Effects of Silica Nanoparticles on the Piezoelectro-Elastic Response of PZT-7A–Polyimide Nanocomposites: Micromechanics Modeling Technique
Abstract
1. Introduction
2. Micromechanical Analysis of Piezoelectric Fibrous Nanocomposites
2.1. Silica-Nanoparticle-Filled Polymer
2.2. Piezoelectric Fiber Composites
3. Results and Discussion
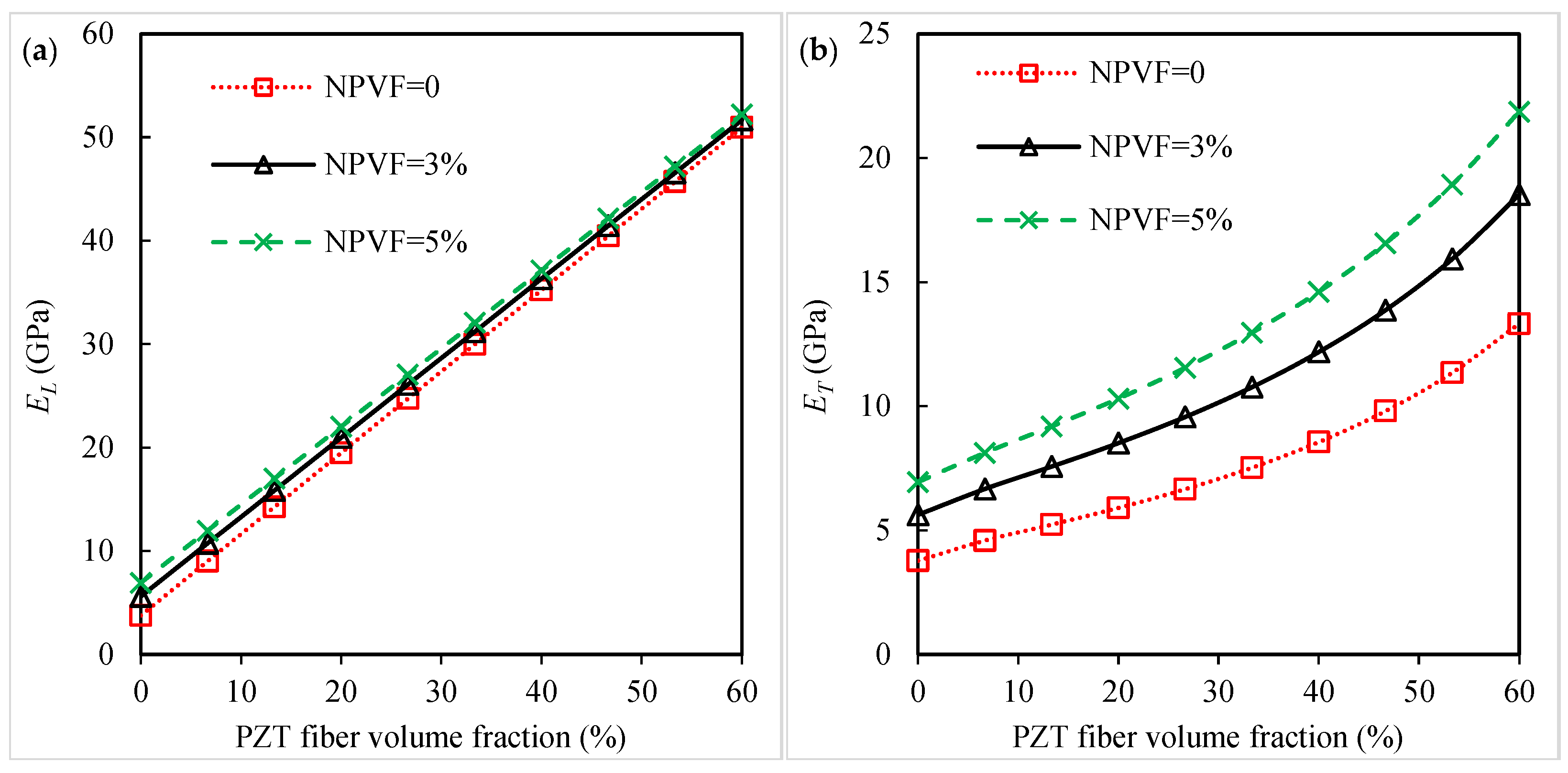
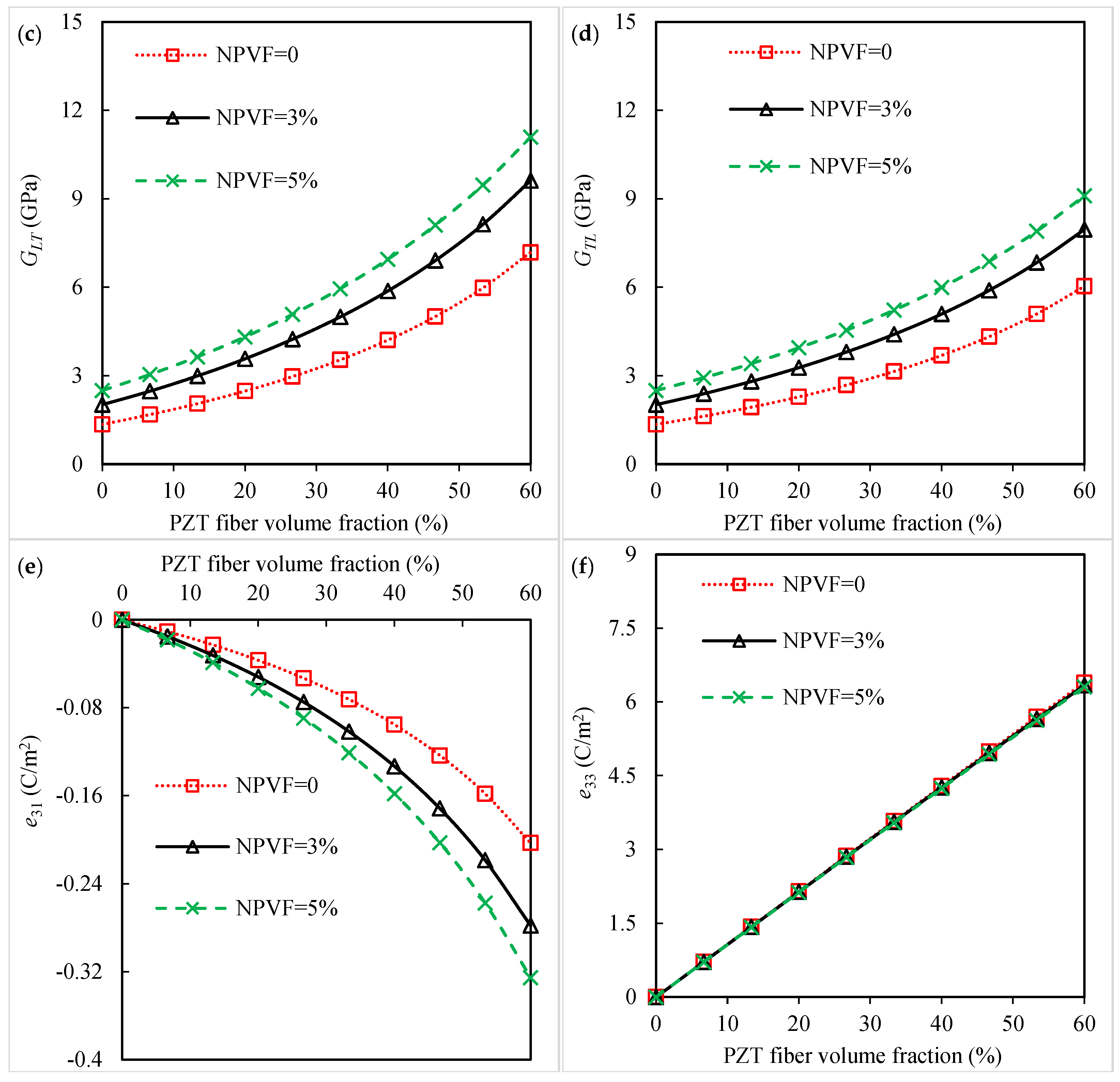
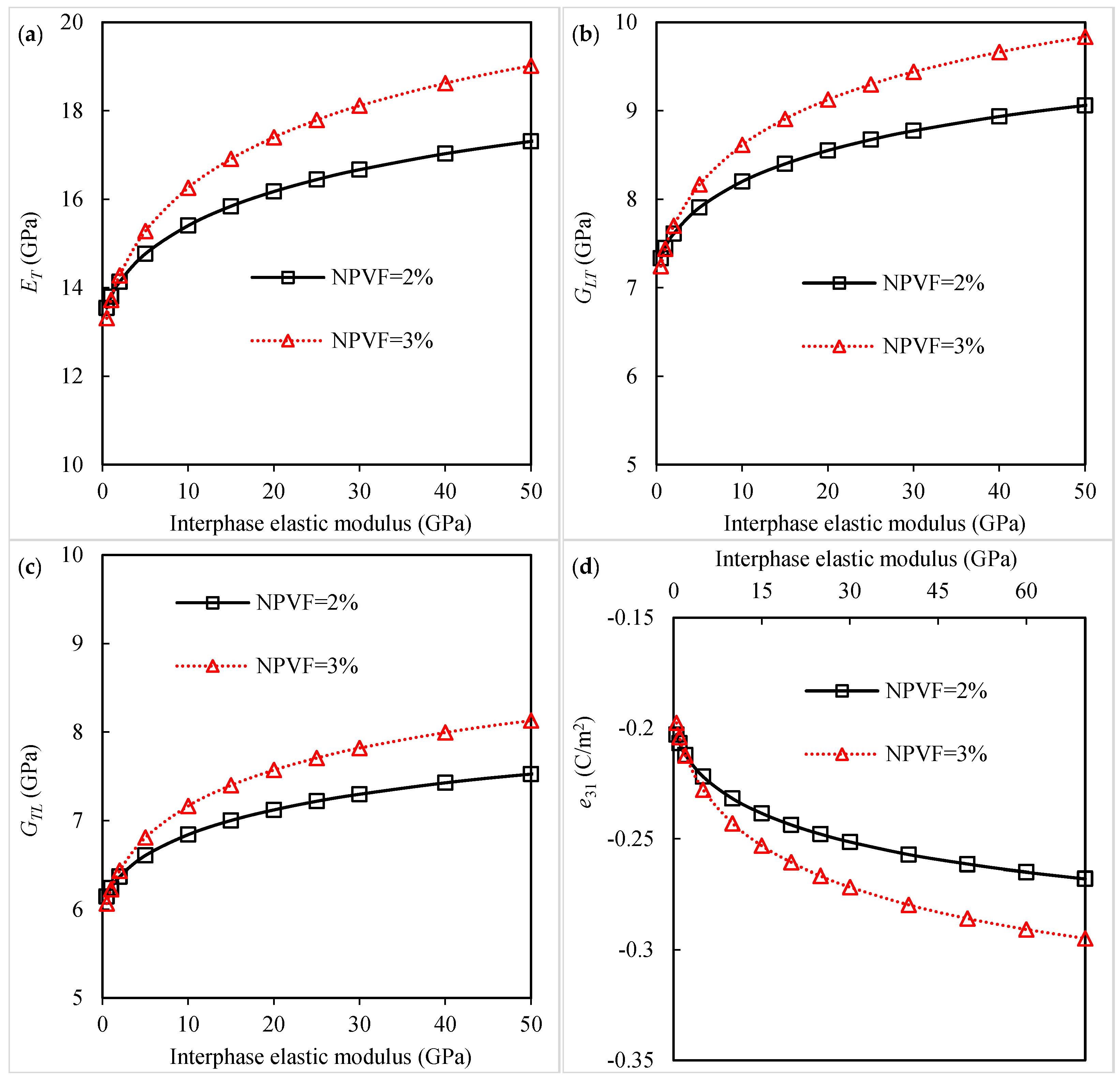
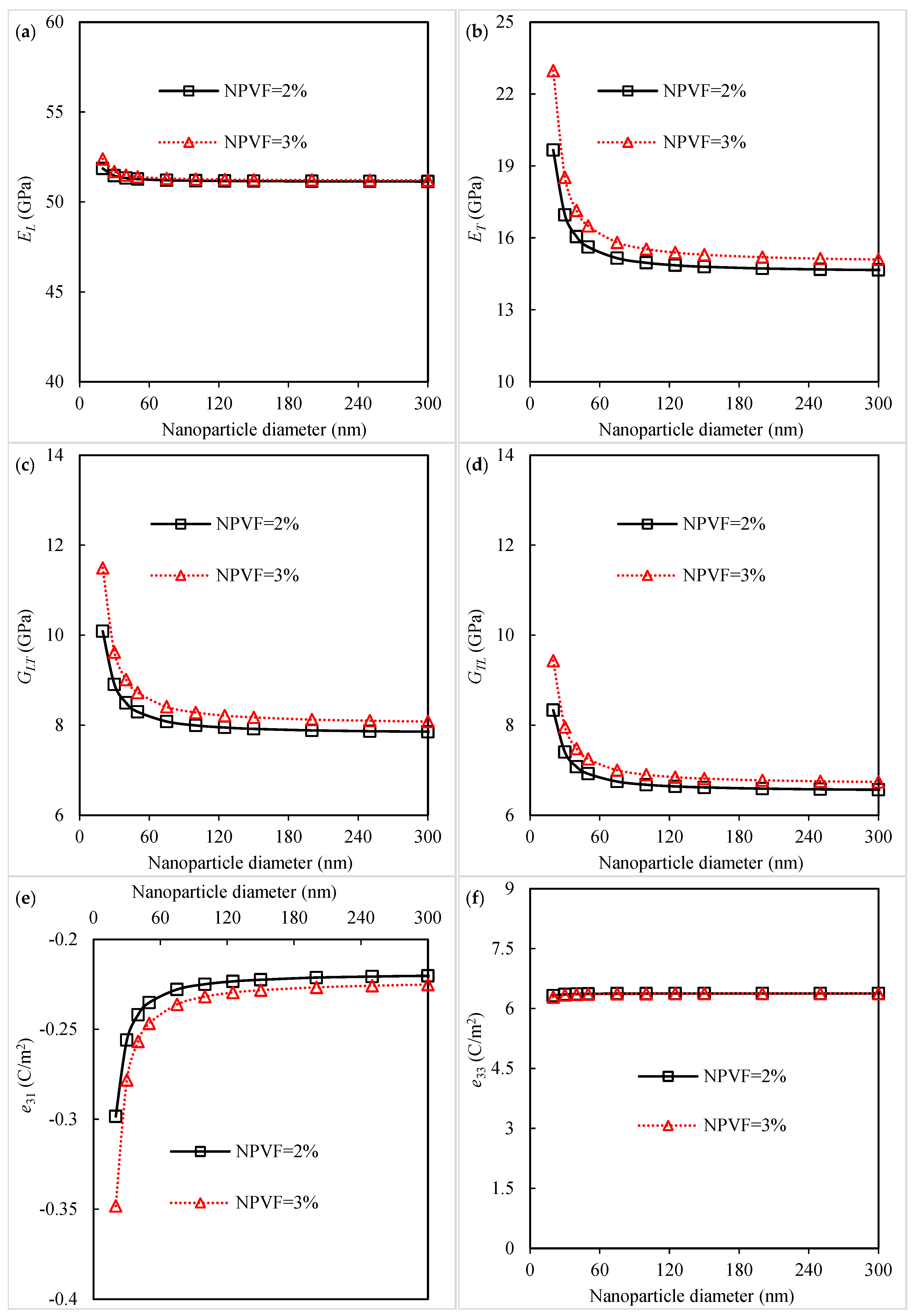
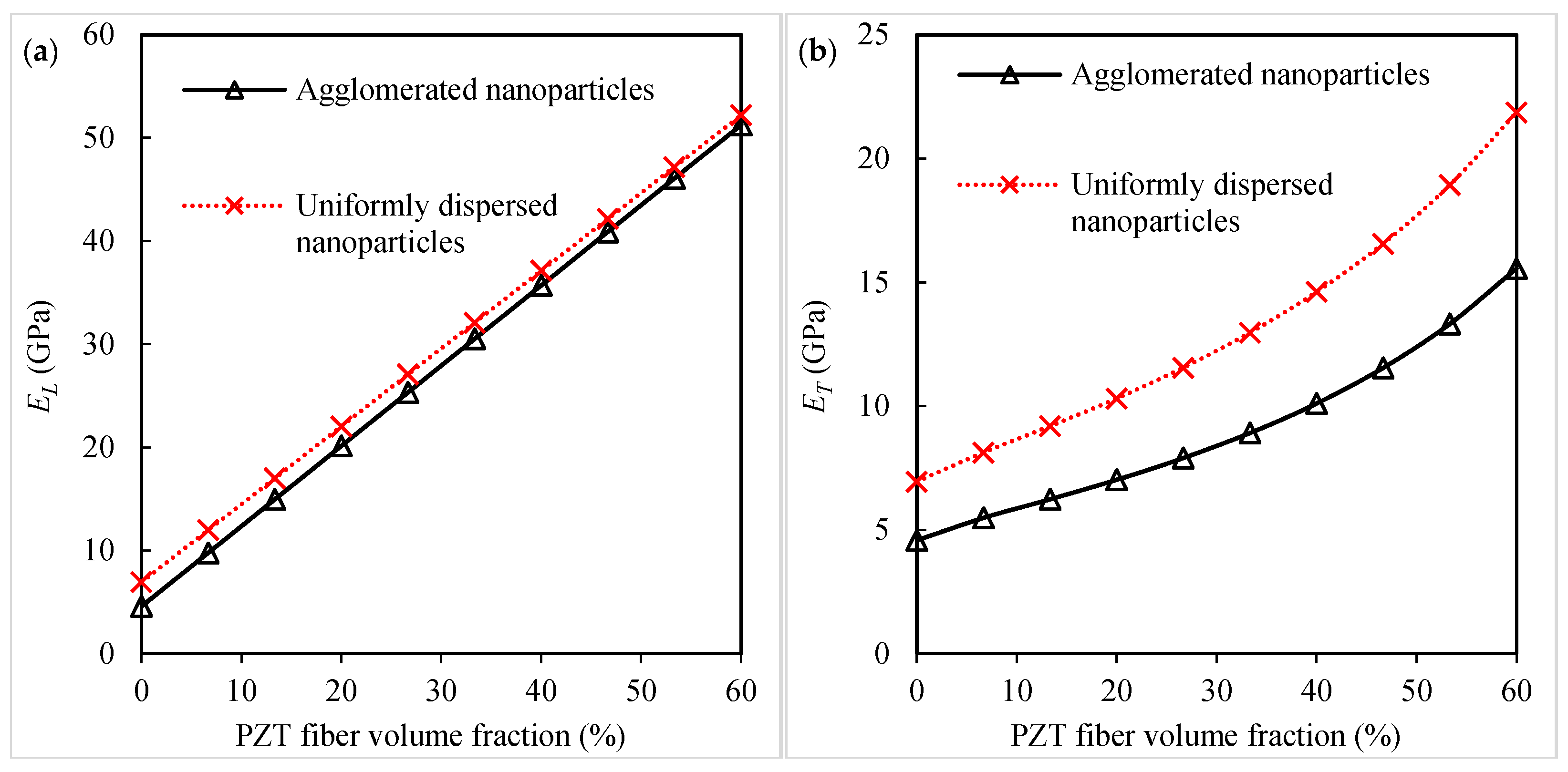
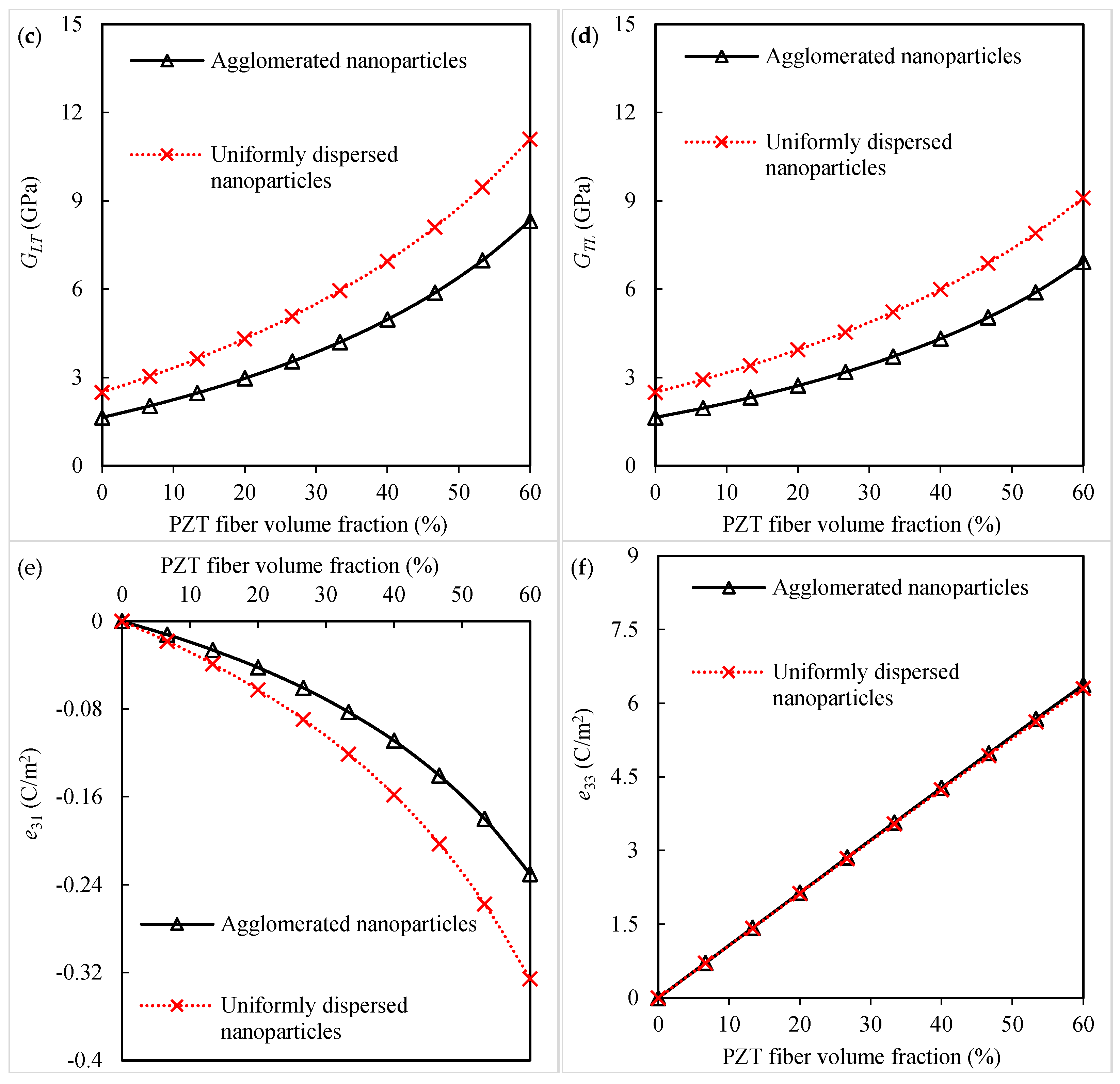
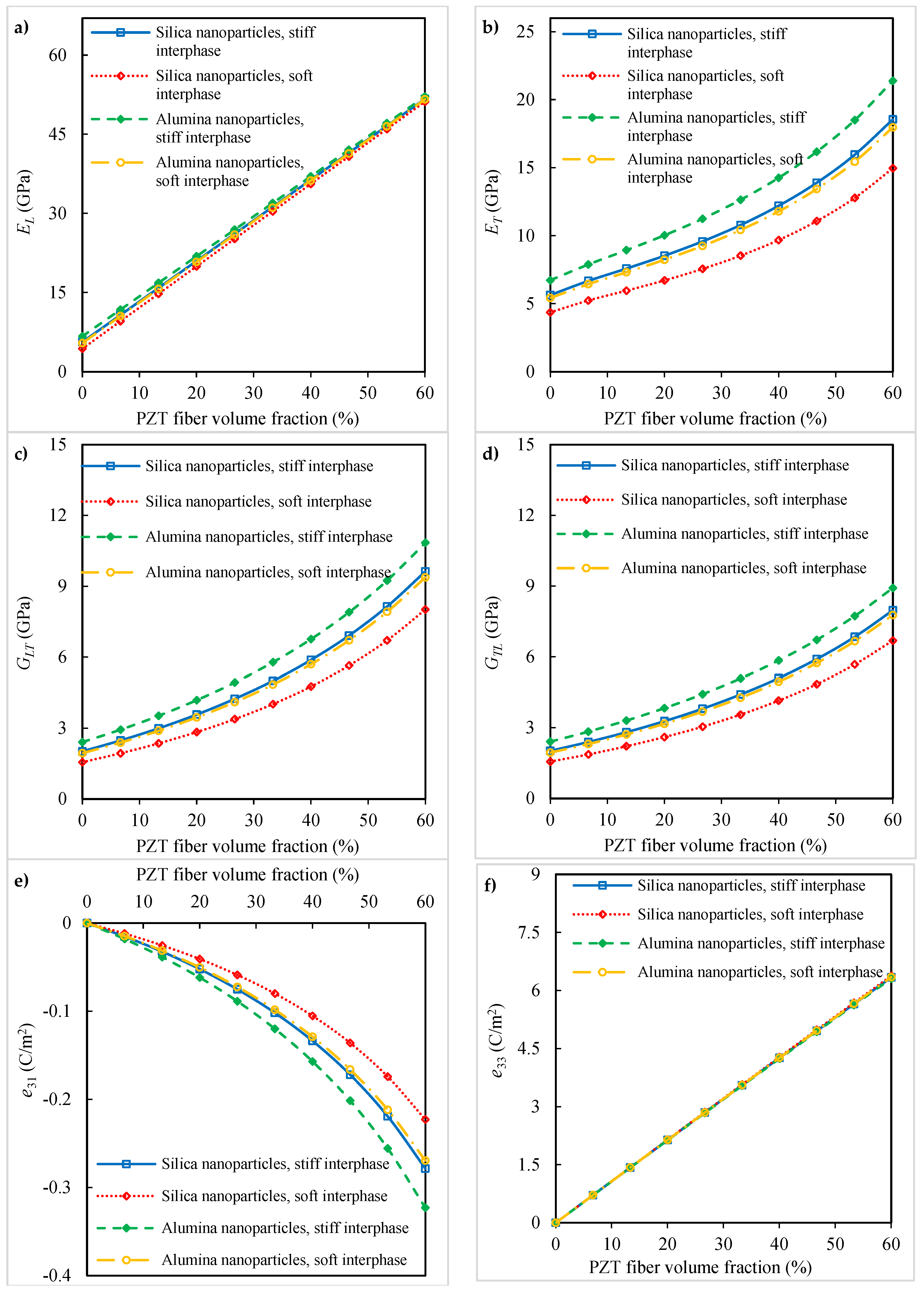
3.1. Piezoelectro-Elastic Response of Piezoelectric Fibrous Nanocomposites
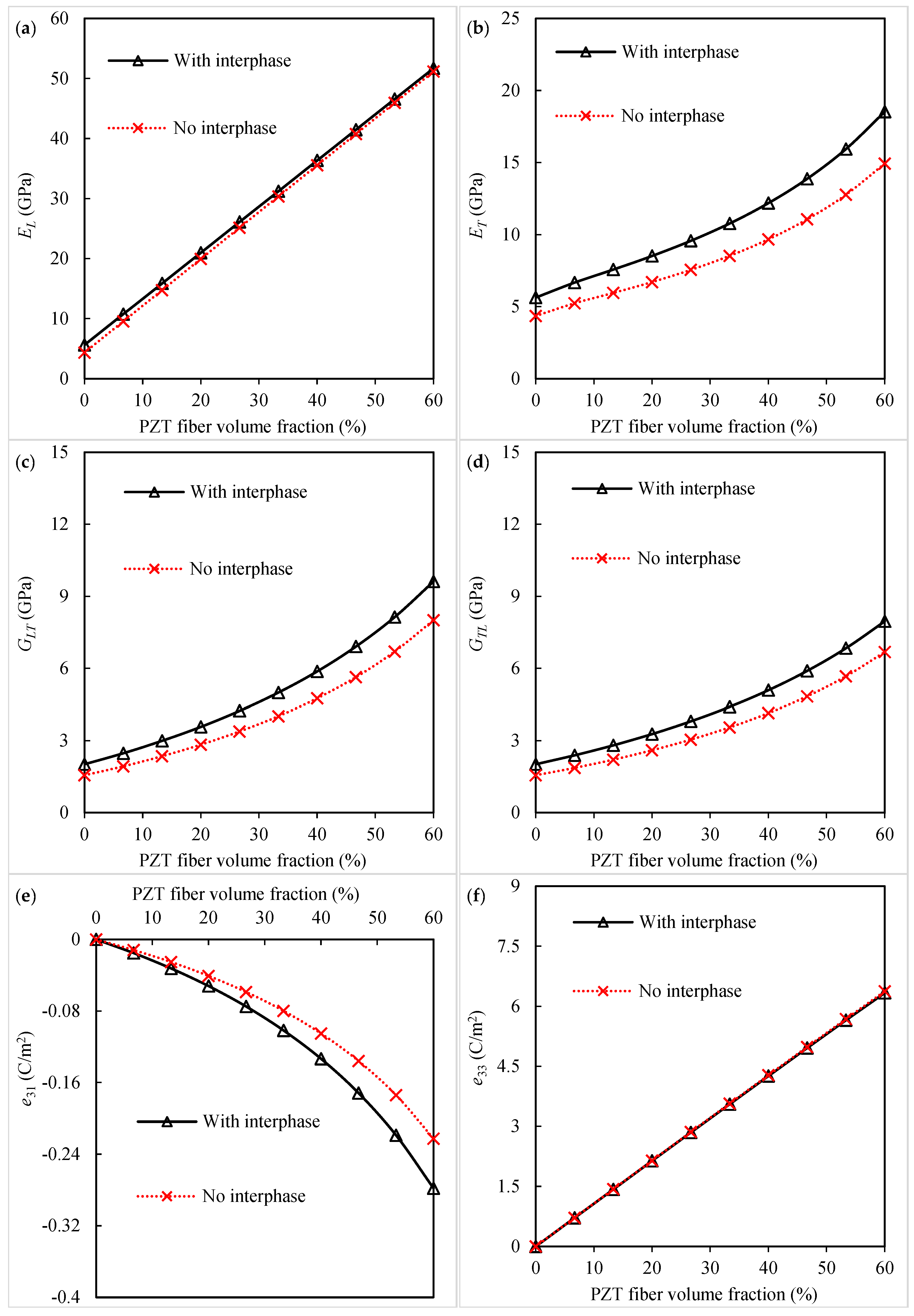
3.2. Comparisons with Experimental and Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, L.F.; Yu, T.C.; Feng, X.; Yang, C.P.; Chen, Y.; Chen, W.; Zhou, J. Dimension dependence of thickness resonance behavior of piezoelectric fiber composites. Mater. Chem. Phys. 2018, 218, 34–38. [Google Scholar] [CrossRef]
- Tan, D.; Yavarow, P.; Erturk, A. Nonlinear elastodynamics of piezoelectric macro-fiber composites with interdigitated electrodes for resonant actuation. Compos. Struct. 2018, 187, 137–143. [Google Scholar] [CrossRef]
- Zhou, B.; Ma, X.; Xue, S. Nonlinear analysis of laminated beams with braided fiber piezoelectric composite actuators. Int. J. Appl. Mech. 2020, 12, 2050043. [Google Scholar] [CrossRef]
- Su, Y.; Li, W.; Yuan, L.; Chen, C.; Pan, H.; Xie, G.; Conta, G.; Ferrier, S.; Zhao, X.; Chen, G.; et al. Piezoelectric fiber composites with polydopamine interfacial layer for self-powered wearable biomonitoring. Nano Energy 2021, 89, 106321. [Google Scholar] [CrossRef]
- He, Z.; Liu, J.; Chen, Q. Higher-order asymptotic homogenization for piezoelectric composites. Int. J. Solids Struct. 2023, 264, 112092. [Google Scholar] [CrossRef]
- Yu, Y.; Narita, F. Evaluation of electromechanical properties and conversion efficiency of piezoelectric nanocomposites with carbon-fiber-reinforced polymer electrodes for stress sensing and energy harvesting. Polymers 2021, 13, 3184. [Google Scholar] [CrossRef]
- Tang, T.; Yu, W. Variational asymptotic micromechanics modeling of heterogeneous piezoelectric materials. Mech. Mater. 2008, 40, 812–824. [Google Scholar] [CrossRef]
- Keramati, Y.; Ansari, R.; Hassanzadeh-Aghdam, M.K. Effect of graphene nano-sheets on the elastic and piezoelectric coefficients of unidirectional PZT-7A/polyimide hybrid composites. J. Intell. Mater. Syst. Struct. 2023, 34, 1548–1560. [Google Scholar] [CrossRef]
- Dhala, S.; Ray, M.C. Micromechanics of piezoelectric fuzzy fiber-reinforced composite. Mech. Mater. 2015, 81, 1–17. [Google Scholar] [CrossRef]
- Al Mahmud, H.; Radue, M.S.; Chinkanjanarot, S.; Pisani, W.A.; Gowtham, S.; Odegard, G.M. Multiscale modeling of carbon fiber-graphene nanoplatelet-epoxy hybrid composites using a reactive force field. Compos. Part B Eng. 2019, 172, 628–635. [Google Scholar] [CrossRef]
- Sahu, R.; Ponnusami, S.A.; Weimer, C.; Harursampath, D. Interface engineering of carbon fiber composites using CNT: A review. Polym. Compos. 2024, 45, 9–42. [Google Scholar] [CrossRef]
- Keramati, Y.; Ansari, R.; Hassanzadeh-Aghdam, M.K.; Umer, U. Micromechanical simulation of thermal expansion, elastic stiffness and piezoelectric constants of graphene/unidirectional BaTiO3 fiber reinforced epoxy hybrid nanocomposites. Acta Mech. 2023, 234, 6251–6270. [Google Scholar] [CrossRef]
- Cui, X.; Liu, J.; Liu, H.; Wu, G. Enhanced interfacial strength and mechanical properties of carbon fiber composites by introducing functionalized silica nanoparticles into the interface. J. Adhes. Sci. Technol. 2019, 33, 479–492. [Google Scholar] [CrossRef]
- Hwayyin, R.N.; Hussien, S.K.; Ameed, A.S. The effect of nano-silica on the mechanical properties of composite polyester/carbon fibers. J. Mech. Eng. Sci. 2022, 16, 9175–9186. [Google Scholar] [CrossRef]
- Zheng, Y.; Ning, R.; Zheng, Y. Study of SiO2 nanoparticles on the improved performance of epoxy and fiber composites. J. Reinf. Plast. Compos. 2005, 24, 223–233. [Google Scholar] [CrossRef]
- Gang, D.; Chilan, C.; Haobin, T.; Zhenhua, L.; Dingzhong, Z.; Kang, Q. The research on the effect of SiO2 and CF on the tensile and tribological properties of PI composite. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 229, 1513–1518. [Google Scholar] [CrossRef]
- Tang, Y.; Ye, L.; Zhang, D.; Deng, S. Characterization of transverse tensile, interlaminar shear and interlaminate fracture in CF/EP laminates with 10 wt% and 20 wt% silica nanoparticles in matrix resins. Compos. Part A Appl. Sci. Manuf. 2011, 42, 1943–1950. [Google Scholar] [CrossRef]
- Hasanzadeh, M.; Ansari, R.; Hassanzadeh-Aghdam, M.K. Evaluation of effective properties of piezoelectric hybrid composites containing carbon nanotubes. Mech. Mater. 2019, 129, 63–79. [Google Scholar] [CrossRef]
- Godara, S.S.; Mahato, P.K. Micromechanical technique based prediction of effective properties for hybrid smart nanocomposites. Mech. Adv. Mater. Struct. 2022, 29, 2065–2073. [Google Scholar] [CrossRef]
- Boutaleb, S.; Zaïri, F.; Mesbah, A.; Nait-Abdelaziz, M.; Gloaguen, J.M.; Boukharouba, T.; Lefebvre, J.M. Micromechanics-based modelling of stiffness and yield stress for silica/polymer nanocomposites. Int. J. Solids Struct. 2009, 46, 1716–1726. [Google Scholar] [CrossRef]
- Kontou, E.; Christopoulos, A.; Koralli, P.; Mouzakis, D.E. The effect of silica particle size on the mechanical enhancement of polymer nanocomposites. Nanomaterials 2023, 13, 1095. [Google Scholar] [CrossRef]
- Sun, L.; Gibson, R.F.; Gordaninejad, F. Multiscale analysis of stiffness and fracture of nanoparticle-reinforced composites using micromechanics and global–local finite element models. Eng. Fract. Mech. 2011, 78, 2645–2662. [Google Scholar] [CrossRef]
- Ray, M.C. Micromechanics of piezoelectric composites with improved effective piezoelectric constant. Int. J. Mech. Mater. Des. 2006, 3, 361–371. [Google Scholar] [CrossRef]
- Dinzart, F.; Sabar, H. Magneto-electro-elastic coated inclusion problem and its application to magnetic-piezoelectric composite materials. Int. J. Solids Struct. 2011, 48, 2393–2401. [Google Scholar] [CrossRef]
- Koutsawa, Y. Overall thermo-magneto-electro-elastic properties of multiferroics composite materials with arbitrary heterogeneities spatial distributions. Compos. Struct. 2015, 133, 764–773. [Google Scholar] [CrossRef]
- Ferreira, P.M.; Machado, M.A.; Vidal, C.; Carvalho, M.S. Modelling electro-mechanical behaviour in piezoelectric composites: Current status and perspectives on homogenisation. Adv. Eng. Softw. 2024, 193, 103651. [Google Scholar] [CrossRef]
- Mishra, N.; Das, K. A Mori–Tanaka based micromechanical model for predicting the effective electroelastic properties of orthotropic piezoelectric composites with spherical inclusions. SN Appl. Sci. 2020, 2, 1206. [Google Scholar] [CrossRef]
- Pan, J.; Bian, L. A physics investigation for influence of carbon nanotube agglomeration on thermal properties of composites. Mater. Chem. Phys. 2019, 236, 121777. [Google Scholar] [CrossRef]
- Mortazavi, B.; Bardon, J.; Ahzi, S. Interphase effect on the elastic and thermal conductivity response of polymer nanocomposite materials: 3D finite element study. Comput. Mater. Sci. 2013, 69, 100–106. [Google Scholar] [CrossRef]
- Ghasemi, A.R.; Hosseinpour, K. The SWCNTs roles in stress/strain distribution of three-phase multilayered nanocomposite cylinder under combined internal pressure and thermo-mechanical loading. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 391. [Google Scholar] [CrossRef]
- Cannillo, V.; Bondioli, F.; Lusvarghi, L.; Montorsi, M.; Avella, M.; Errico, M.E.; Malinconico, M. Modeling of ceramic particles filled polymer–matrix nanocomposites. Compos. Sci. Technol. 2006, 66, 1030–1037. [Google Scholar] [CrossRef]
- Snipes, J.S.; Robinson, C.T.; Baxter, S.C. Effects of scale and interface on the three-dimensional micromechanics of polymer nanocomposites. J. Compos. Mater. 2011, 45, 2537–2546. [Google Scholar] [CrossRef]
- Nematollahi, H.; Mohammadi, M.; Munir, M.T.; Zare, Y.; Rhee, K.Y. Two-Step Method for Predicting Young’s Modulus of Nanocomposites Containing Nanodiamond Particles. J. Mater. Res. Technol. 2024, 33, 2343–2352. [Google Scholar] [CrossRef]
- Pakseresht, M.; Ansari, R.; Hassanzadeh-Aghdam, M.K. An efficient homogenization scheme for analyzing the elastic properties of hybrid nanocomposites filled with multiscale particles. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 3. [Google Scholar] [CrossRef]
- Ji, X.L.; Jing, J.K.; Jiang, W.; Jiang, B.Z. Tensile modulus of polymer nanocomposites. Polym. Eng. Sci. 2002, 42, 983–993. [Google Scholar] [CrossRef]
- Zare, Y. Assumption of interphase properties in classical Christensen–Lo model for Young’s modulus of polymer nanocomposites reinforced with spherical nanoparticles. RSC Adv. 2015, 5, 95532–95538. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Z.; Friedrich, K.; Eger, C. Property improvements of in situ epoxy nanocomposites with reduced interparticle distance at high nanosilica content. Acta Mater. 2006, 54, 1833–1842. [Google Scholar] [CrossRef]
- Naito, K. Tensile properties of polyacrylonitrile-and pitch-based hybrid carbon fiber/polyimide composites with some nanoparticles in the matrix. J. Mater. Sci. 2013, 48, 4163–4176. [Google Scholar] [CrossRef]
- Ji, X.Y.; Cao, Y.P.; Feng, X.Q. Micromechanics prediction of the effective elastic moduli of graphene sheet-reinforced polymer nanocomposites. Model. Simul. Mater. Sci. Eng. 2010, 18, 045005. [Google Scholar] [CrossRef]
- Dastgerdi, J.N.; Marquis, G.; Salimi, M. The effect of nanotubes waviness on mechanical properties of CNT/SMP composites. Compos. Sci. Technol. 2013, 86, 164–169. [Google Scholar] [CrossRef]
- Shi, D.L.; Feng, X.Q.; Huang, Y.Y.; Hwang, K.C.; Gao, H. The effect of nanotube waviness and agglomeration on the elastic property of carbon nanotube-reinforced composites. J. Eng. Mater. Technol. 2004, 126, 250–257. [Google Scholar] [CrossRef]
- Mallik, N.; Ray, M.C. Effective coefficients of piezoelectric fiber-reinforced composites. AIAA J. 2003, 41, 704–710. [Google Scholar] [CrossRef]
- Aboudi, J.; Arnold, S.M.; Bednarcyk, B.A. Micromechanics of Composite Materials: A Generalized Multiscale Analysis Approach; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Odegard, G.M. Constitutive modeling of piezoelectric polymer composites. Acta Mater. 2004, 52, 5315–5330. [Google Scholar] [CrossRef]
- Kuo, M.C.; Tsai, C.M.; Huang, J.C.; Chen, M. PEEK composites reinforced by nano-sized SiO2 and Al2O3 particulates. Mater. Chem. Phys. 2005, 90, 185–195. [Google Scholar] [CrossRef]
- García, M.; van Vliet, G.; ten Cate, M.G.; Chavez, F.; Norder, B.; Kooi, B.; van Zyl, W.E.; Verweij, H.; Blank, D.H.A. Large-scale extrusion processing and characterization of hybrid nylon-6/SiO2 nanocomposites. Polym. Adv. Technol. 2004, 15, 164–172. [Google Scholar] [CrossRef]
- Ray, M.C. The concept of a novel hybrid smart composite reinforced with radially aligned zigzag carbon nanotubes on piezoelectric fibers. Smart Mater. Struct. 2010, 19, 035008. [Google Scholar] [CrossRef]
- Mahmoodi, M.J.; Hassanzadeh-Aghdam, M.K.; Safi, M. Effects of nano-sized silica particles on the off-axis creep performance of unidirectional fiber-reinforced polymer hybrid composites. J. Compos. Mater. 2021, 55, 1575–1589. [Google Scholar] [CrossRef]
- Joshi, P.; Upadhyay, S.H. Effect of interphase on elastic behavior of multiwalled carbon nanotube reinforced composite. Comput. Mater. Sci. 2014, 87, 267–273. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L.; Su, Q.; Zheng, J. Use of unmodified SiO2 as nanofiller to improve mechanical properties of polymer-based nanocomposites. Compos. Sci. Technol. 2013, 89, 52–60. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umer, U.; Abidi, M.H.; Mian, S.H.; Alasim, F.; Aboudaif, M.K. Effects of Silica Nanoparticles on the Piezoelectro-Elastic Response of PZT-7A–Polyimide Nanocomposites: Micromechanics Modeling Technique. Polymers 2024, 16, 2860. https://doi.org/10.3390/polym16202860
Umer U, Abidi MH, Mian SH, Alasim F, Aboudaif MK. Effects of Silica Nanoparticles on the Piezoelectro-Elastic Response of PZT-7A–Polyimide Nanocomposites: Micromechanics Modeling Technique. Polymers. 2024; 16(20):2860. https://doi.org/10.3390/polym16202860
Chicago/Turabian StyleUmer, Usama, Mustufa Haider Abidi, Syed Hammad Mian, Fahad Alasim, and Mohammed K. Aboudaif. 2024. "Effects of Silica Nanoparticles on the Piezoelectro-Elastic Response of PZT-7A–Polyimide Nanocomposites: Micromechanics Modeling Technique" Polymers 16, no. 20: 2860. https://doi.org/10.3390/polym16202860
APA StyleUmer, U., Abidi, M. H., Mian, S. H., Alasim, F., & Aboudaif, M. K. (2024). Effects of Silica Nanoparticles on the Piezoelectro-Elastic Response of PZT-7A–Polyimide Nanocomposites: Micromechanics Modeling Technique. Polymers, 16(20), 2860. https://doi.org/10.3390/polym16202860








