A Precise Prediction of the Chemical and Thermal Shrinkage during Curing of an Epoxy Resin
Abstract
1. Introduction
2. General Theory
2.1. Cure Kinetic Model
2.2. Glass Transition Temperature
2.3. Cure-Dependent Load-Transferring Volumetric Shrinkage
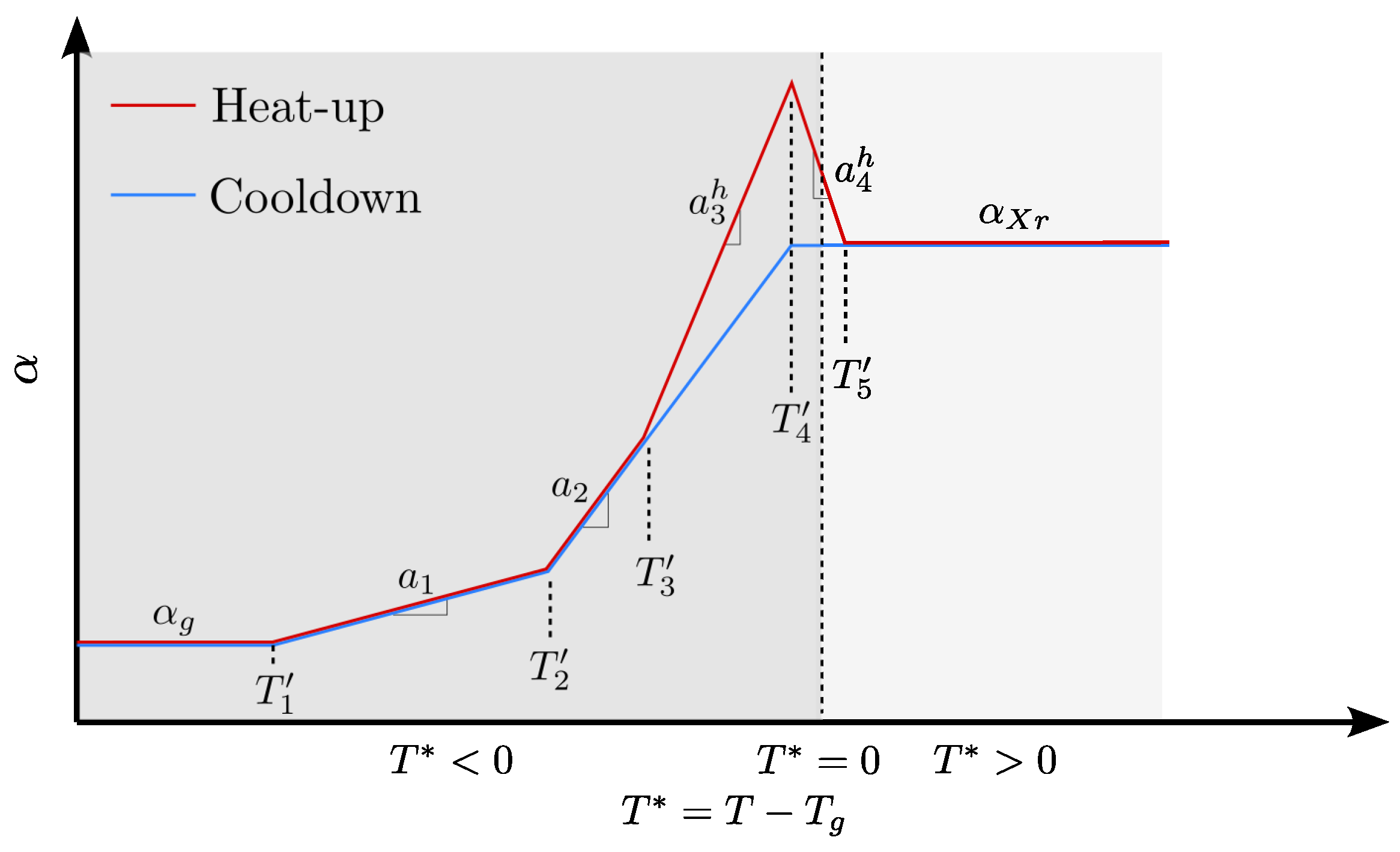
2.4. Complex Thermal Expansion
3. Modelling Constituents
3.1. Thermal Behaviour
3.2. Mechanical Constituents
4. Experimental Method
4.1. Material System
4.2. Reaction Mechanics
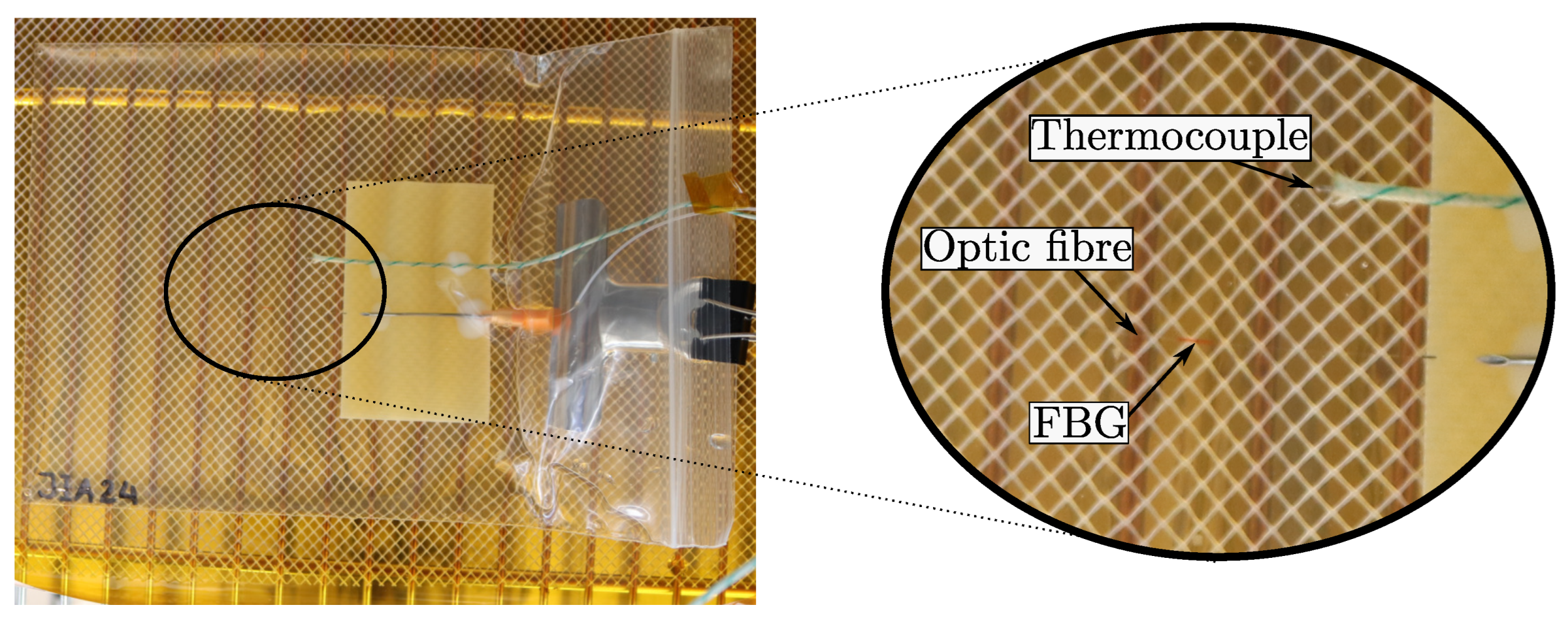
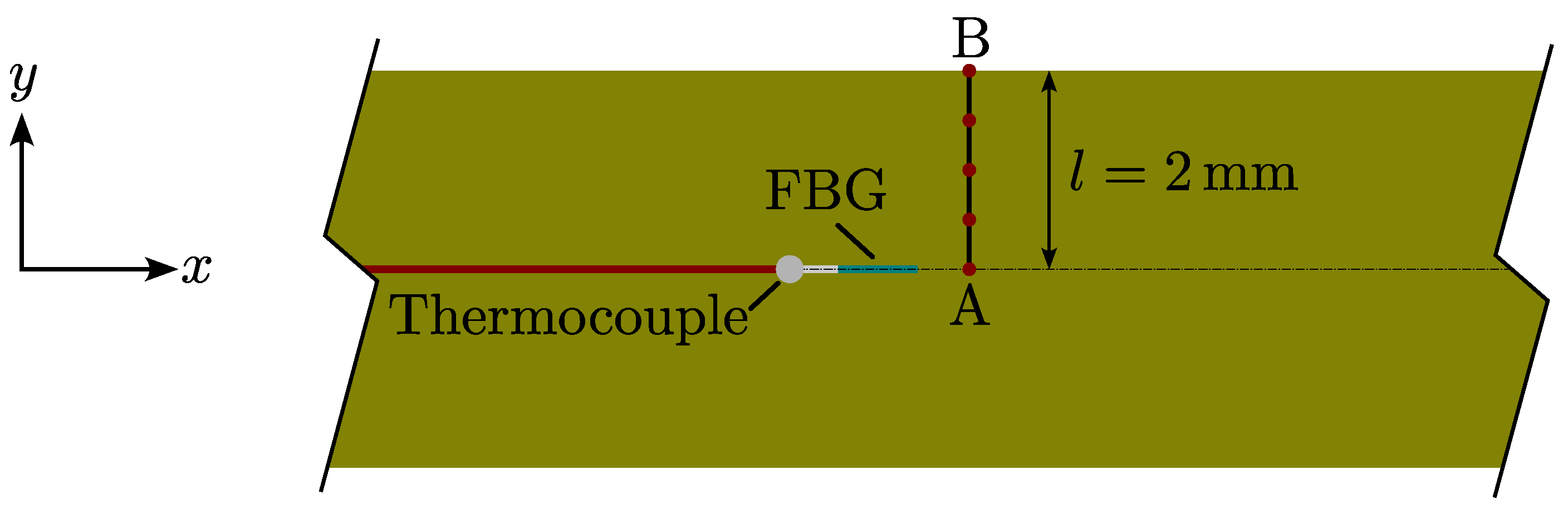
4.3. Experimental Setup
5. Numerical Implementation
5.1. User-Defined Material Heat Transfer—UMATHT
5.2. User-Defined Expansion—UEXPAN
6. Experimental Results
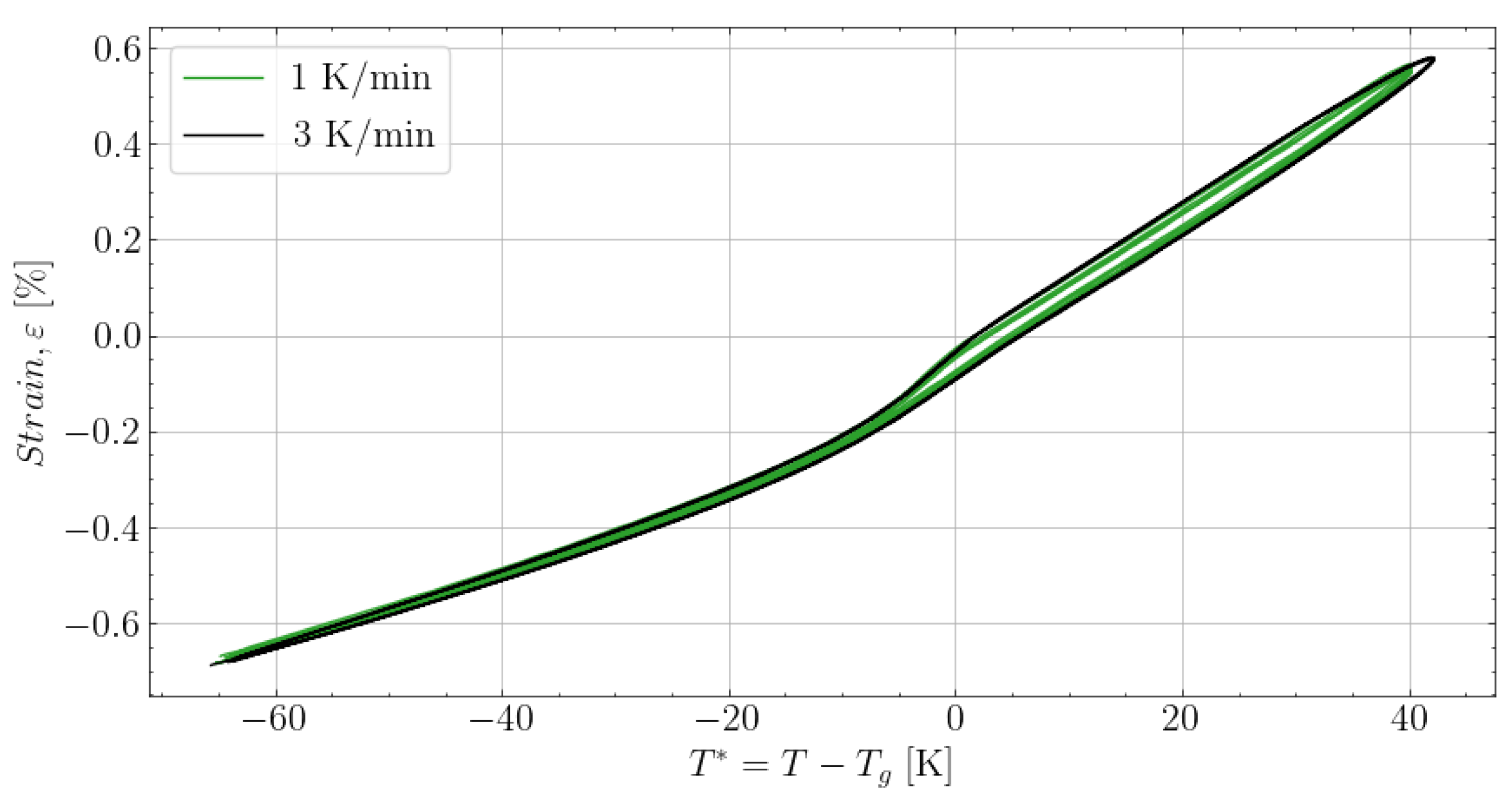
6.1. Cure Experiments
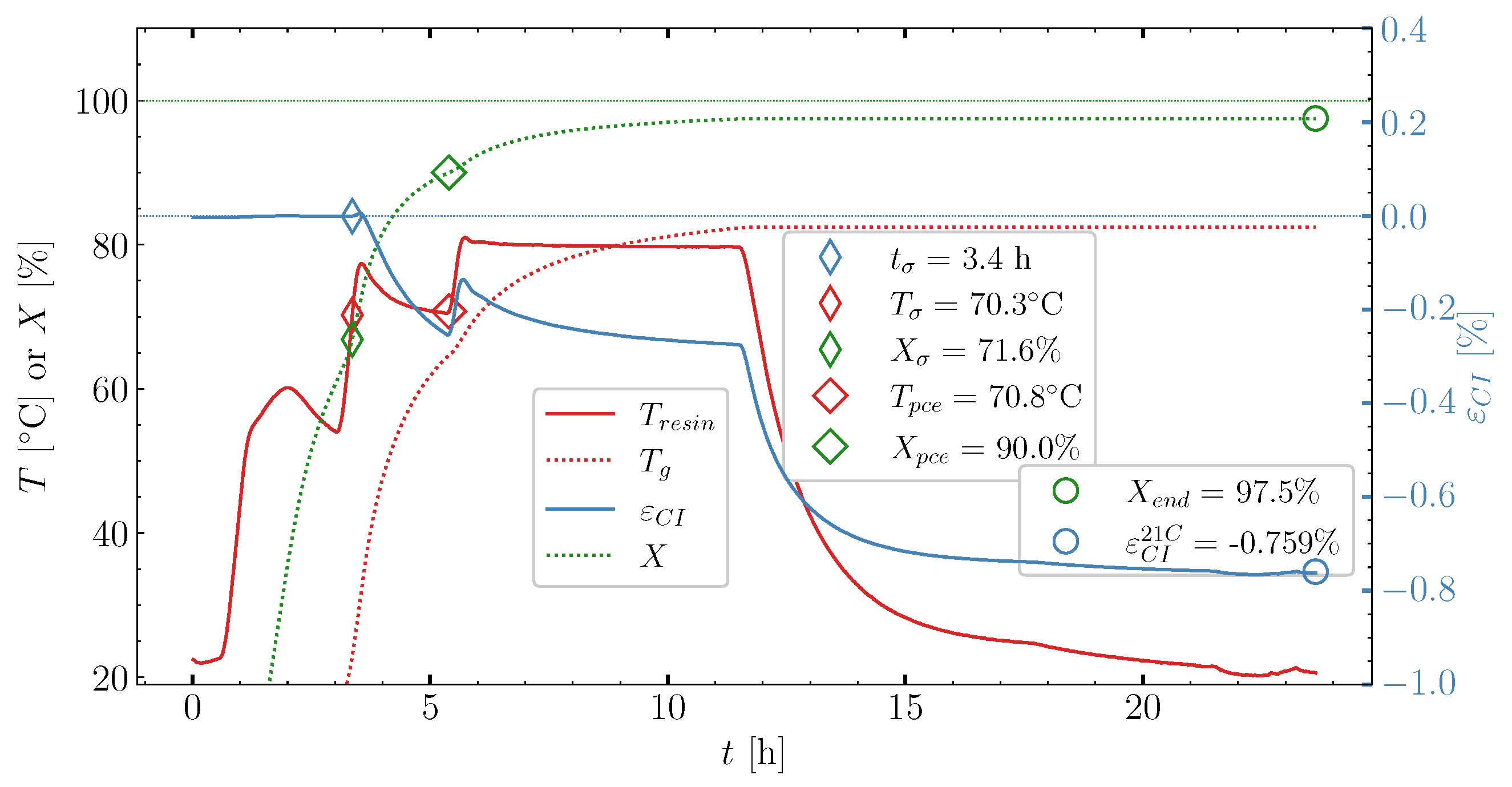
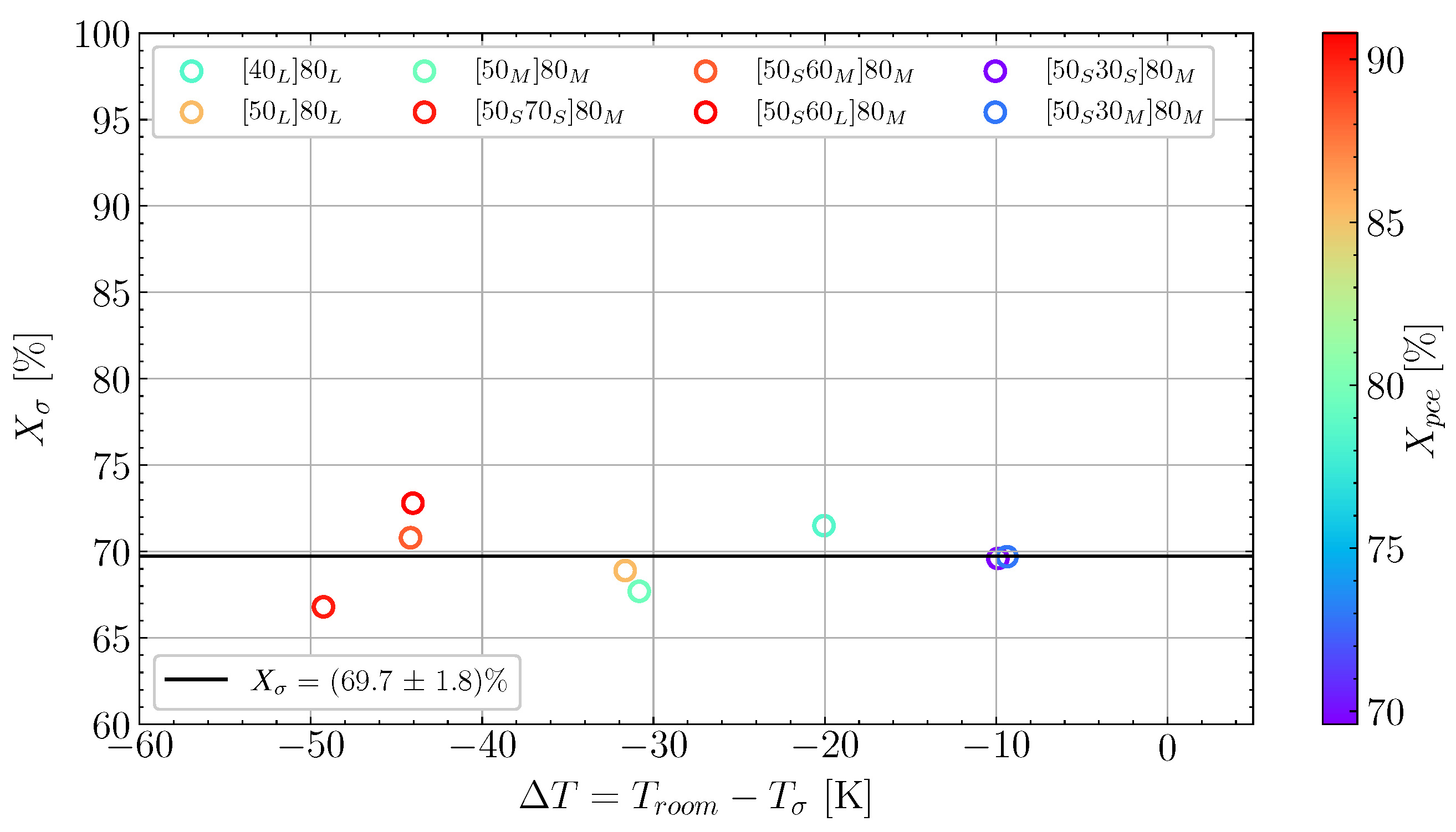
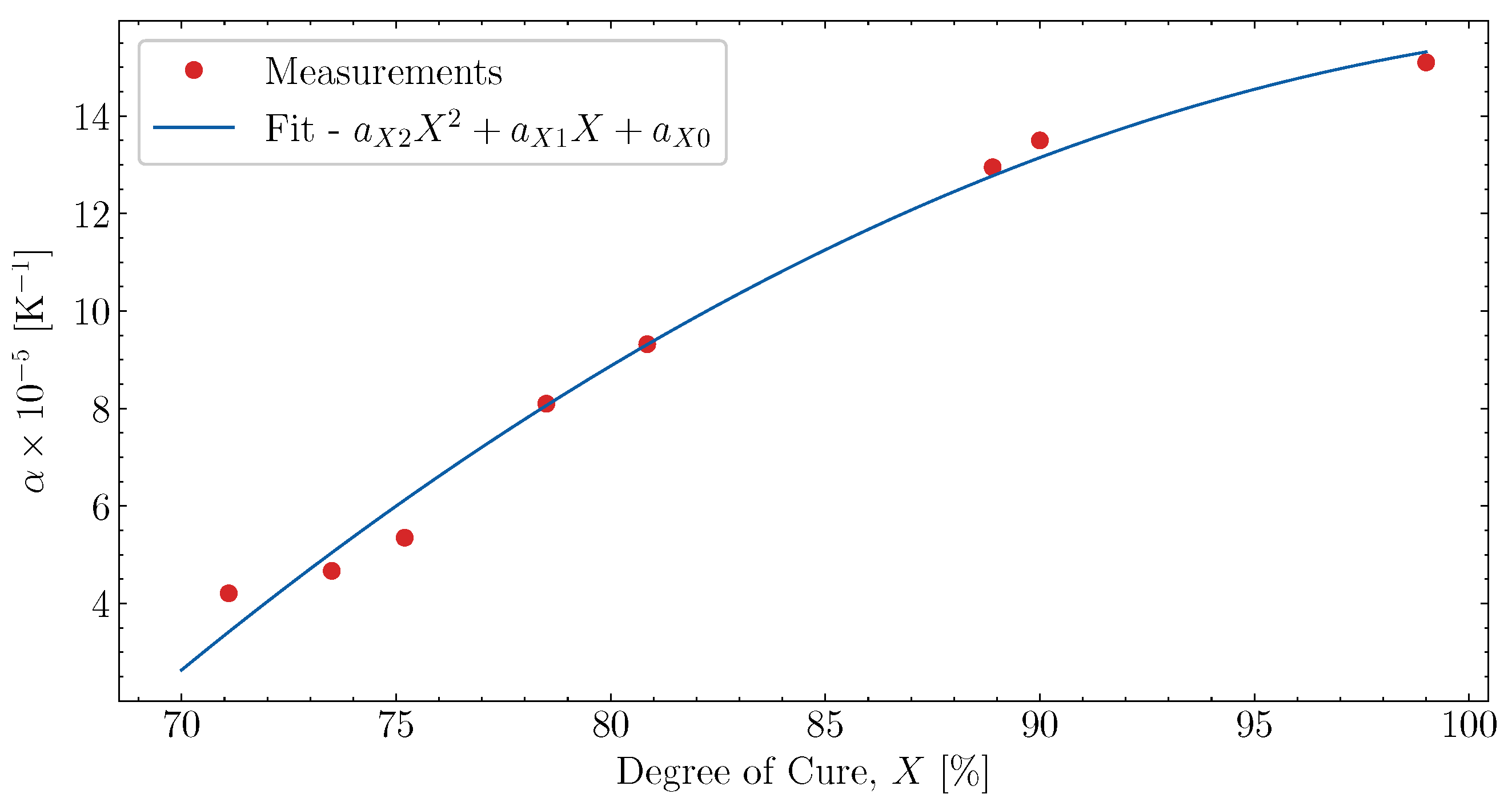
6.2. Determining Volumetric Shrinkage
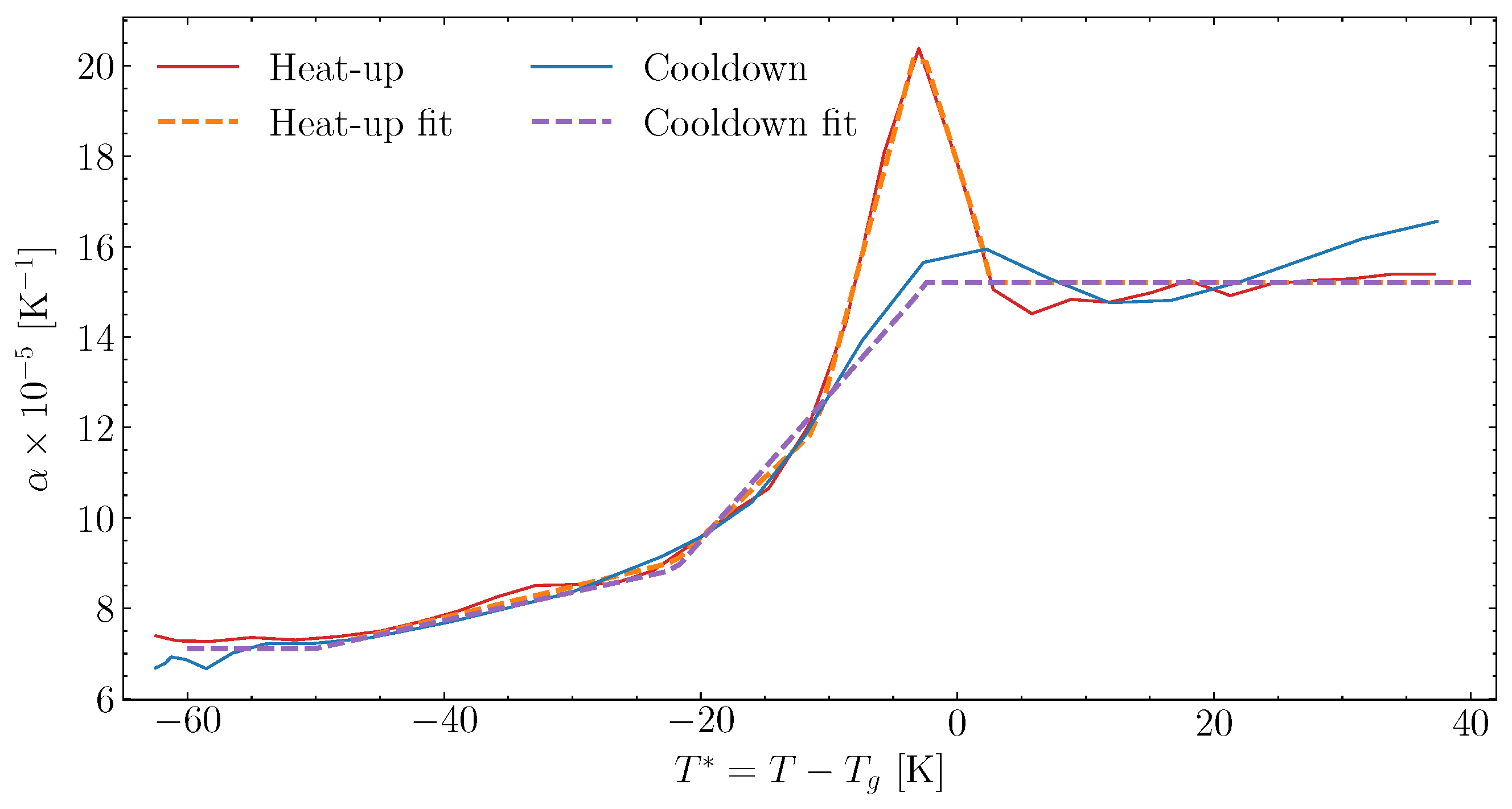
6.3. Fitting of Complex Thermal Expansion
7. Simulation of Cure Shrinkage
Model for the Thermal and Cure-Induced Strain Predicitions
- A
- , (symmetry of heat flow and displacement);
- B
- , , .
- 1. Isothermal— Pre-cure;
- 1. Ramp—Pre-cure;
- 2. Isothermal—Pre-cure;
- 2. Ramp —Pre-cure;
- Isothermal—Post-cure;
- Cooldown after Post-cure.
 and
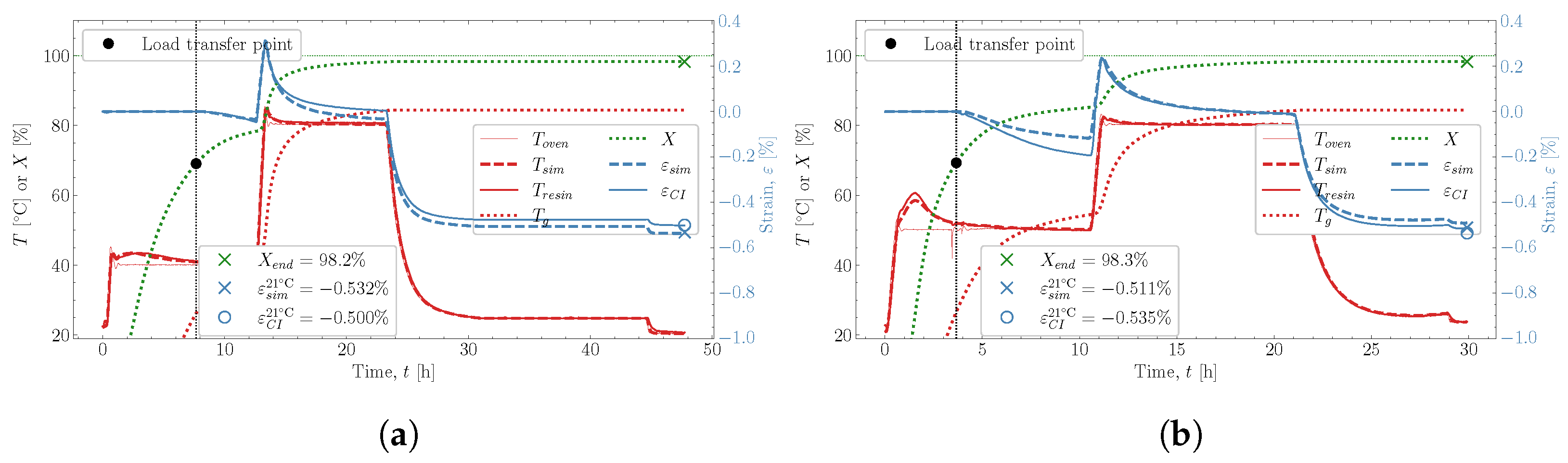
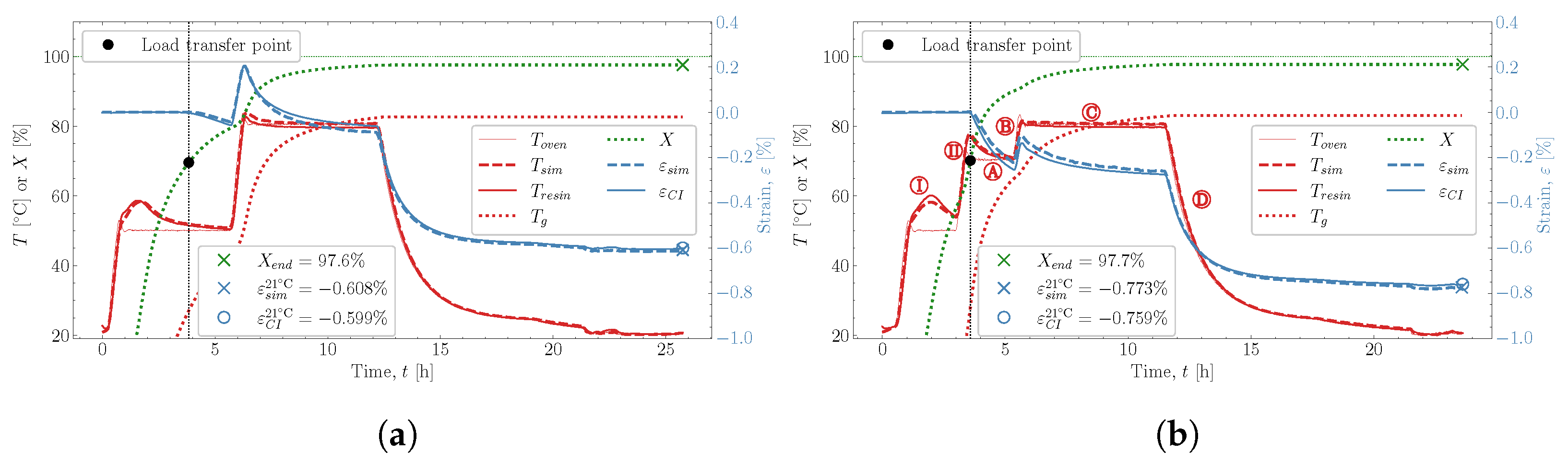
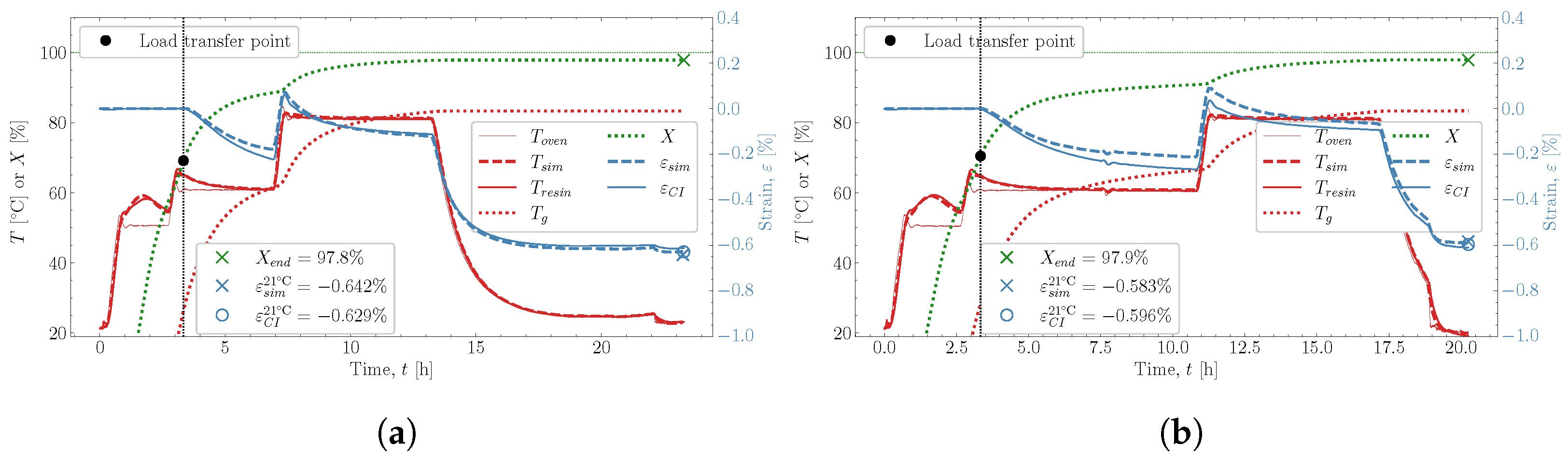
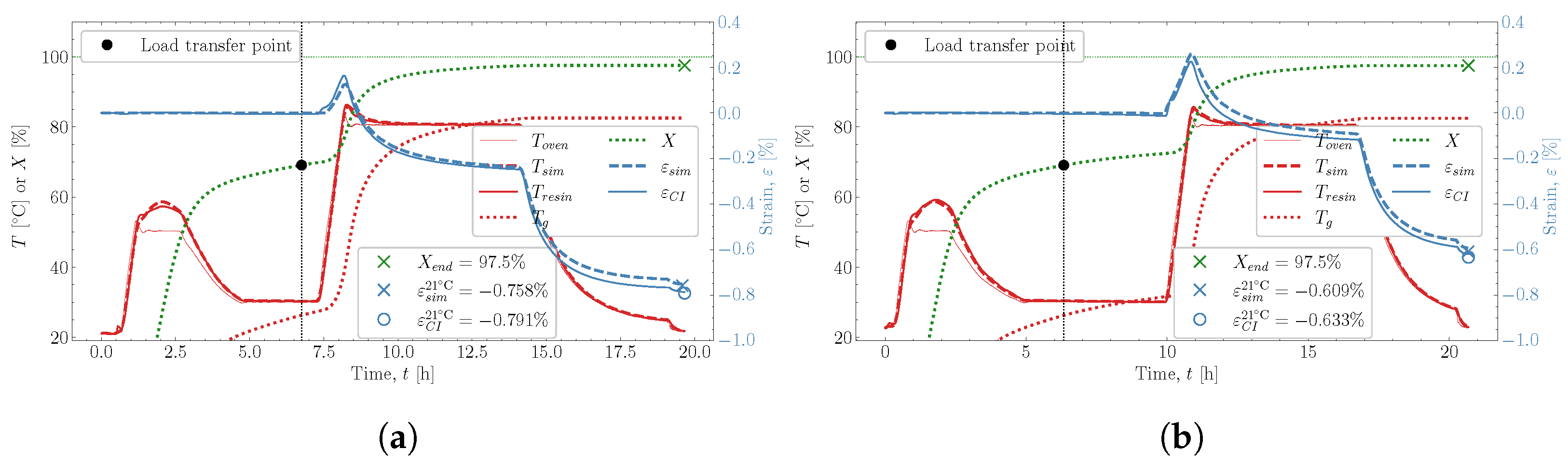
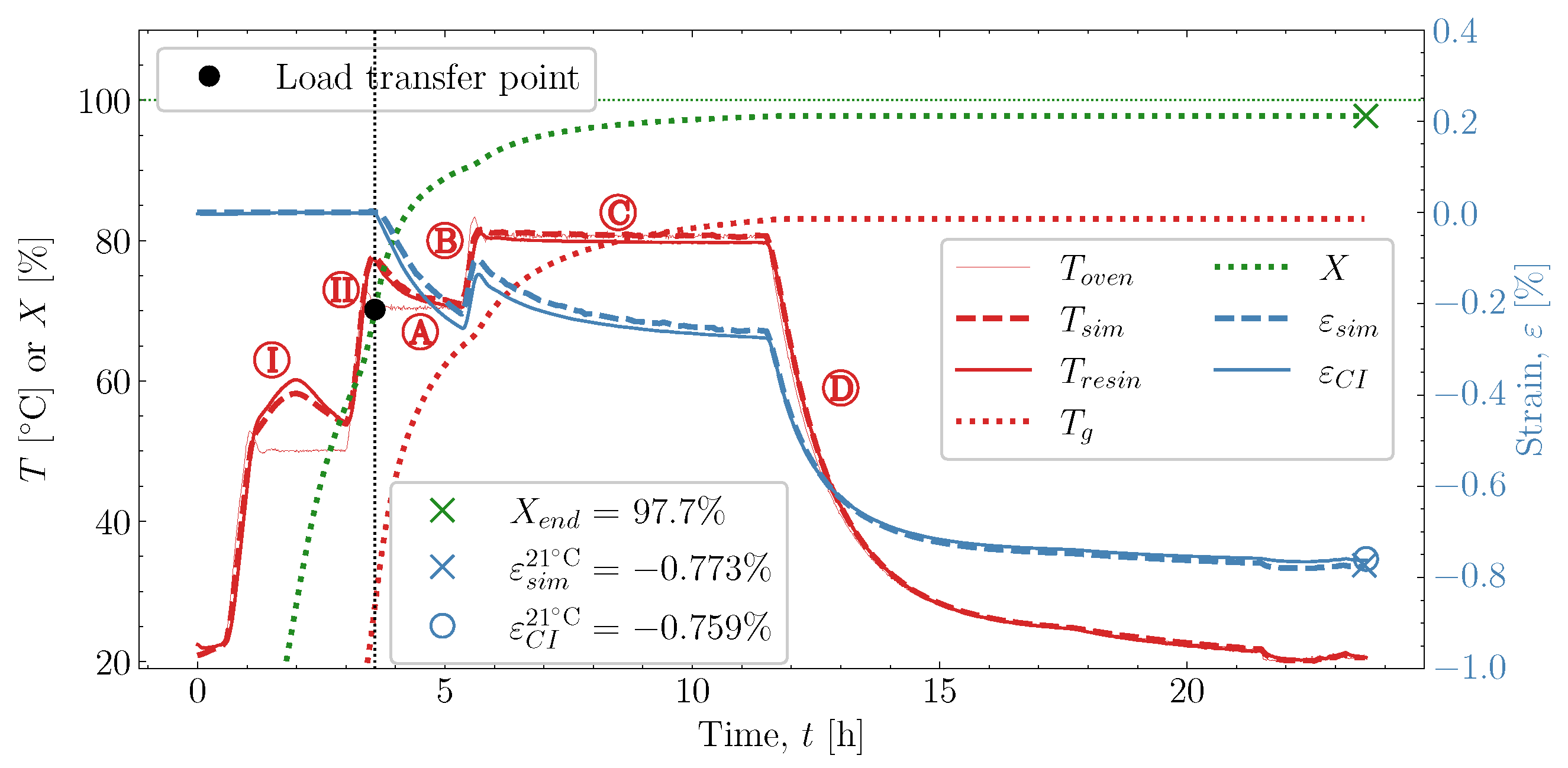
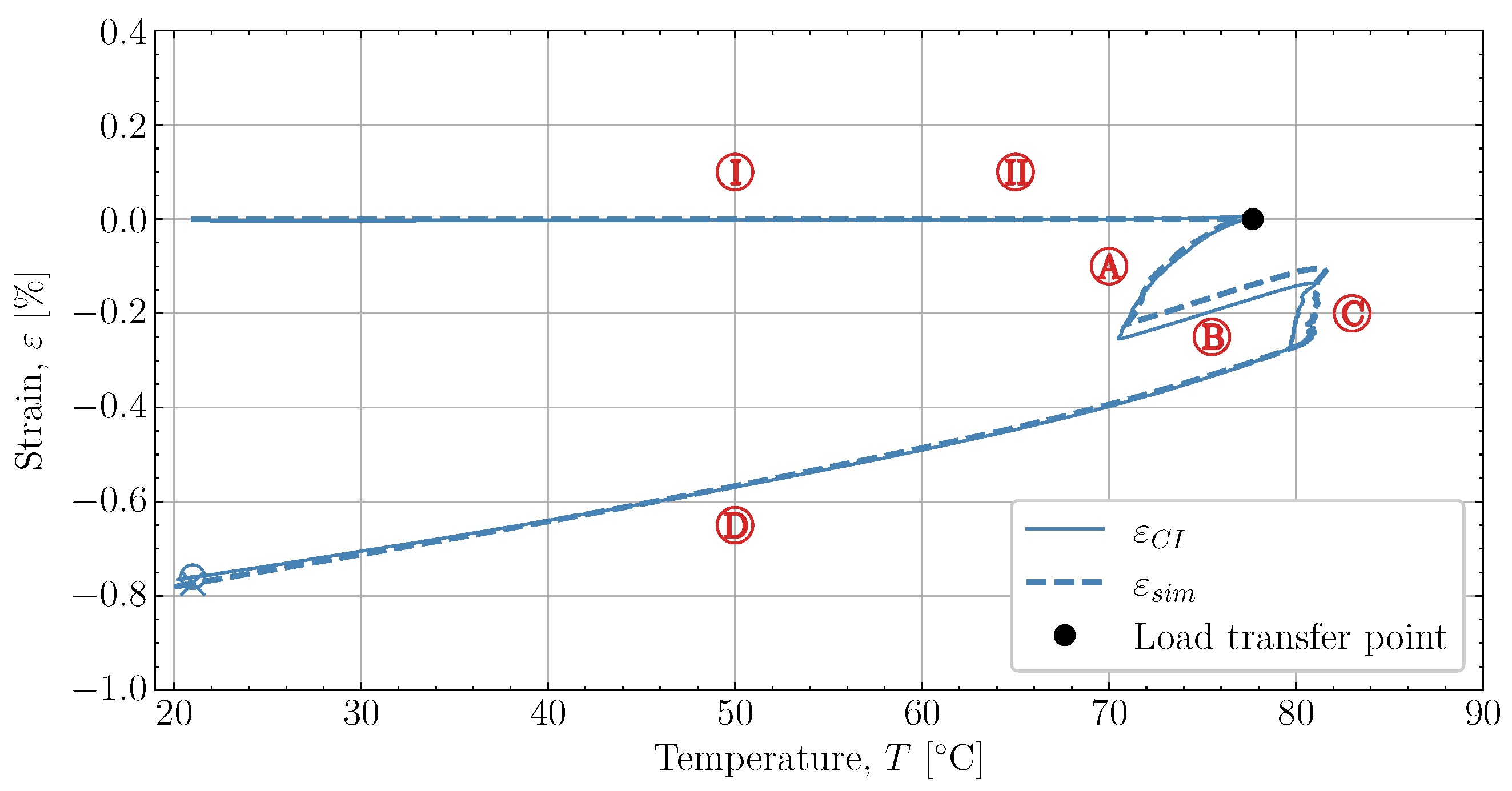
and 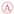 . The predicted temperature by the simulation matches well with the monitored temperature from the thermocouple inside the resin. This is also observed in the remaining eight cases studied, found in Appendix A.
. The predicted temperature by the simulation matches well with the monitored temperature from the thermocouple inside the resin. This is also observed in the remaining eight cases studied, found in Appendix A.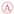 , which is influenced heavily by the thermal and chemical strain occurring simultaneously. Followed by the heat-up
, which is influenced heavily by the thermal and chemical strain occurring simultaneously. Followed by the heat-up 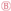 , then the post-cure
, then the post-cure  and the cooldown
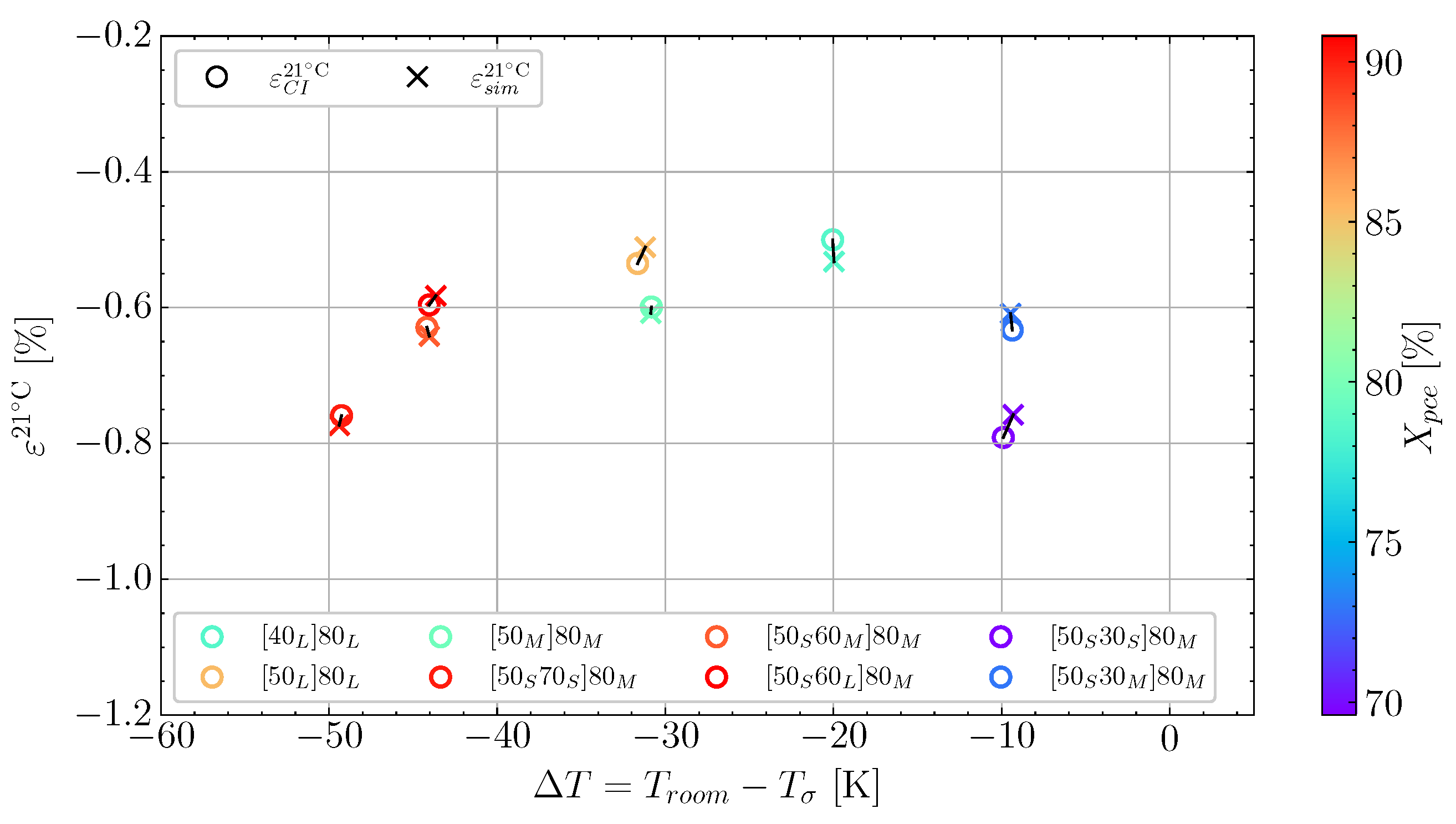
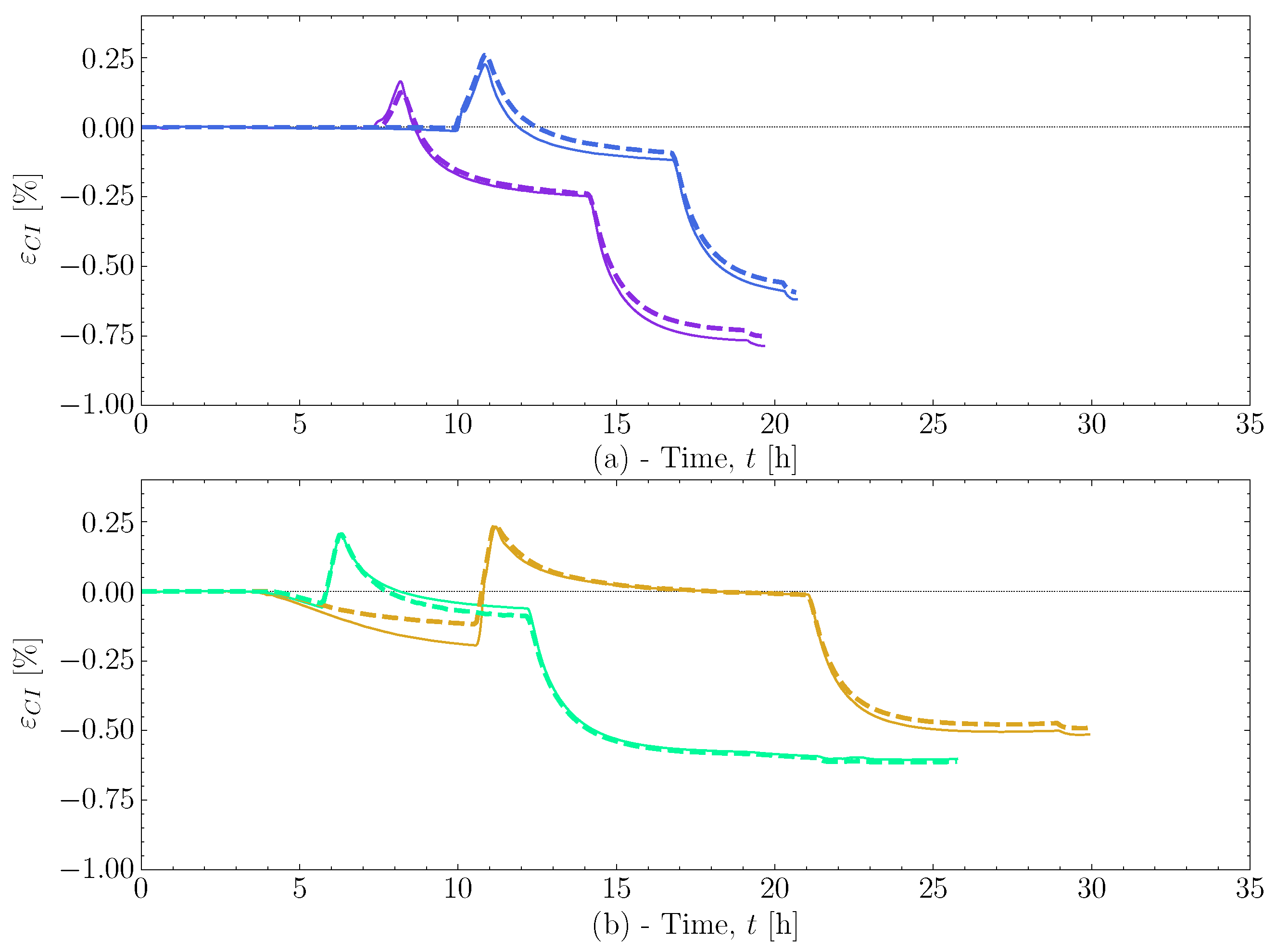
and the cooldown 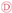 , these also show good correlation between experiment and simulation. At the end of the cure, both the experimental observed cure-induced strain and the simulated are shown in Figure 13, as well as the final value of the simulated X. A comparison of the final simulated degree of cure with the final predicted one based on the thermocouple temperature monitored shown in Figure 3 is relevant. The differences are negligible; thus, the simulated cure development is accurate within the experimentally predicted. In terms of the differences observed between the simulated and measured strain, the deviation relative to the experiment was found to be within 2%. Hence, the simulation is overall satisfactory. The deviations and cure-induced strains observed for all the simulations and corresponding experiments are tabulated in Table 7. The overall deviation was found to be within 2–6% and the average deviation around 3%. With a simulation that matches the observed experimental behaviour well in all cases. The results from both experiments and simulations are available for download [23].
, these also show good correlation between experiment and simulation. At the end of the cure, both the experimental observed cure-induced strain and the simulated are shown in Figure 13, as well as the final value of the simulated X. A comparison of the final simulated degree of cure with the final predicted one based on the thermocouple temperature monitored shown in Figure 3 is relevant. The differences are negligible; thus, the simulated cure development is accurate within the experimentally predicted. In terms of the differences observed between the simulated and measured strain, the deviation relative to the experiment was found to be within 2%. Hence, the simulation is overall satisfactory. The deviations and cure-induced strains observed for all the simulations and corresponding experiments are tabulated in Table 7. The overall deviation was found to be within 2–6% and the average deviation around 3%. With a simulation that matches the observed experimental behaviour well in all cases. The results from both experiments and simulations are available for download [23].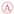 well, although it underestimates the shrinkage somewhat in magnitude. During the following heat-up
well, although it underestimates the shrinkage somewhat in magnitude. During the following heat-up 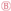 , the expansion observed in the experiment is parallel with the expansion simulated. Therefore, the simulation can capture the expansion and contraction observed experimentally while curing progresses. This is important as the contraction and expansion occurring during
, the expansion observed in the experiment is parallel with the expansion simulated. Therefore, the simulation can capture the expansion and contraction observed experimentally while curing progresses. This is important as the contraction and expansion occurring during 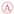 and
and 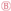 both occur well above . This means that the expansion and contraction should be influenced by curing as per the thermal expansion model applied in Section 2.4.
both occur well above . This means that the expansion and contraction should be influenced by curing as per the thermal expansion model applied in Section 2.4.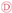 that occurs from
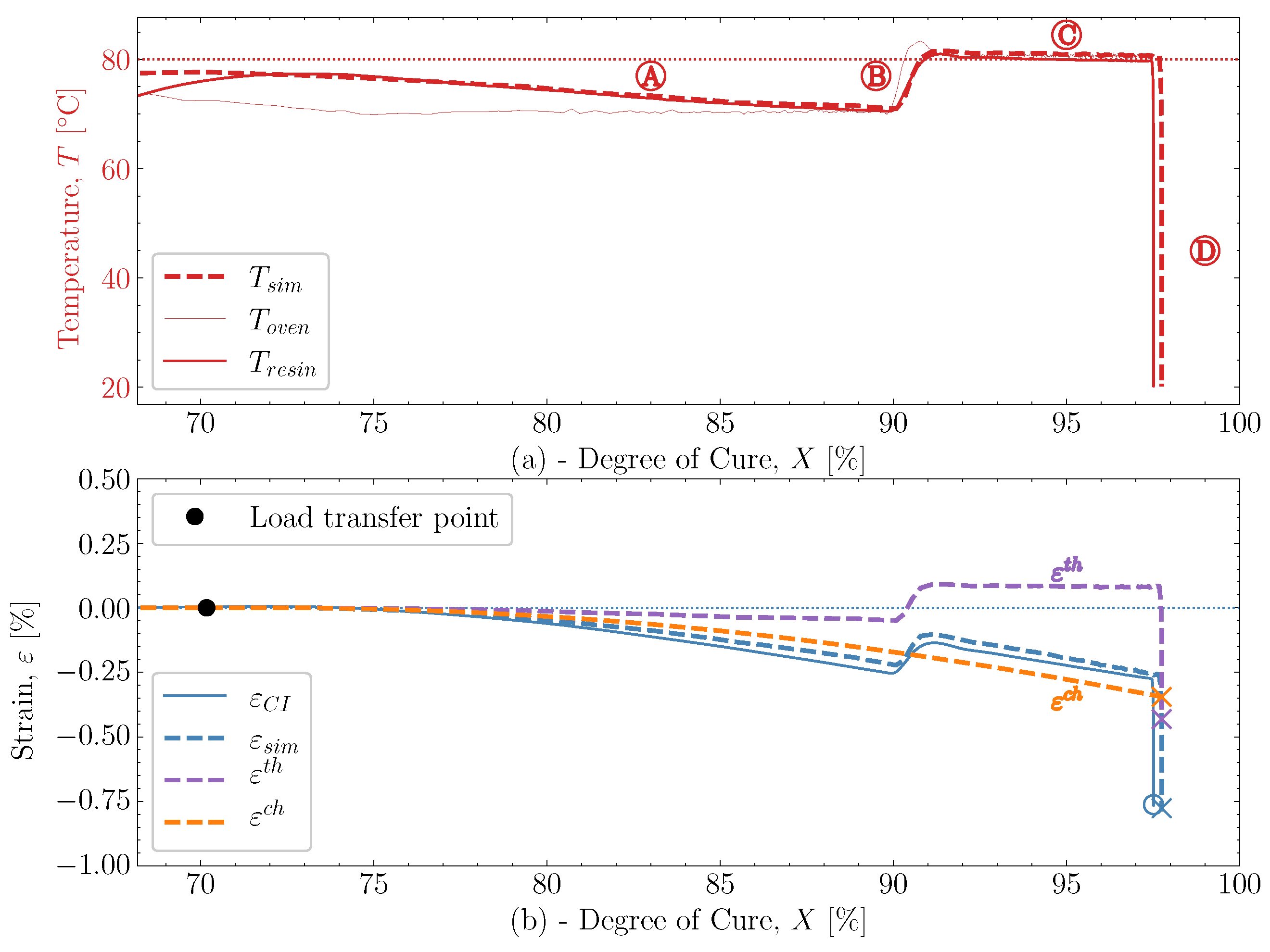
that occurs from  and down to room temperature is unaffected by any significant changes in X and demonstrates that the model can also capture the cured contraction well from just below and until far away from . The simulated strain is plotted as a function of the degree of cure, X, against the experiment in Figure 15, where Figure 15a demonstrates the temperature development of the experiment , simulation and the oven temperature as a function of X. The temperatures of the experiment and simulation agree. There is a slight variation between the oven temperature and the resin temperatures.
and down to room temperature is unaffected by any significant changes in X and demonstrates that the model can also capture the cured contraction well from just below and until far away from . The simulated strain is plotted as a function of the degree of cure, X, against the experiment in Figure 15, where Figure 15a demonstrates the temperature development of the experiment , simulation and the oven temperature as a function of X. The temperatures of the experiment and simulation agree. There is a slight variation between the oven temperature and the resin temperatures.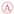 , the simulated thermal strain is also observed to drop. The simulated chemical strain also decreases continuously as the degree of cure increases. It should be possible to check whether the chosen volumetric shrinkage model (4) adapted for the chemical strain matches the experimentally observed behaviour. The simulated strain is seen to under-predict the shrinkage occurring during slightly
, the simulated thermal strain is also observed to drop. The simulated chemical strain also decreases continuously as the degree of cure increases. It should be possible to check whether the chosen volumetric shrinkage model (4) adapted for the chemical strain matches the experimentally observed behaviour. The simulated strain is seen to under-predict the shrinkage occurring during slightly 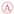 , but follows in parallel with the experimental strain for the duration of
, but follows in parallel with the experimental strain for the duration of  . After that, the curing ends with the cooldown
. After that, the curing ends with the cooldown 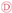 . Even though there generally is this slight offset between experimental and simulated, the offset does not increase or decrease slightly. Indicating that the proposed shrinkage behaviour follows the experimental behaviour well. The simulations are, therefore, quite capable of determining the effects observed experimentally.
. Even though there generally is this slight offset between experimental and simulated, the offset does not increase or decrease slightly. Indicating that the proposed shrinkage behaviour follows the experimental behaviour well. The simulations are, therefore, quite capable of determining the effects observed experimentally.8. Conclusions
- Perform DSC analysis to characterise the cure behaviour and determine the parameters for the cure kinetic model, glass transition temperature evolution, and the enthalpy of the reaction;
- Determine the load transfer initiation in the resin and determine/estimate the load transferring part of the volumetric shrinkage;
- Define the complex nature of the thermal expansion of the specific resin.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Simulation Cases
References
- Nielsen, M.W. Prediction of Process Induced Shape Distortions and Residual Stresses in Large Fibre Reinforced Composite Laminates: With Application to Wind Turbine Blades. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 2013. [Google Scholar]
- Jørgensen, J.B.; Sørensen, B.F.; Kildegaard, C. The effect of residual stresses on the formation of transverse cracks in adhesive joints for wind turbine blades. Int. J. Solids Struct. 2019, 163, 139–156. [Google Scholar] [CrossRef]
- Mortensen, U.A. Process Parameters and Fatigue Properties of High Modulus Composites. Ph.D. Thesis, DTU, Roskilde, Denmark, 2019. [Google Scholar] [CrossRef]
- Miranda Maduro, M.A. Influence of Curing Cycle on the Build-Up of Residual Stresses and the Effect on the Mechanical Performance of Fibre Composites. Ph.D. Thesis, DTU, Roskilde, Denmark, 2021. [Google Scholar]
- Mikkelsen, L.P.; Jørgensen, J.K.; Mortensen, U.A.; Andersen, T.L. Optical fiber Bragg gratings for in-situ cure-induced strain measurements. Zenodo 2023. [Google Scholar] [CrossRef]
- Bogetti, T.A.; Gillespie, J.W. Process-induced stress and deformation in thick-section thermoset composite laminates. J. Compos. Mater. 1990, 26, 626–660. [Google Scholar] [CrossRef]
- Shah, D.U.; Schubel, P.J. Evaluation of cure shrinkage measurement techniques for thermosetting resins. Polym. Test. 2010, 29, 629–639. [Google Scholar] [CrossRef]
- Khoun, L.; Centea, T.; Hubert, P. Characterization methodology of thermoset resins for the processing of composite materials—Case study. J. Compos. Mater. 2010, 44, 1397–1415. [Google Scholar] [CrossRef]
- Johnston, A.A. An Integrated Model of the Development of Process-Induced Deformation in Autoclave Processing of Composite Structures. Ph.D. Thesis, University of of British Columbia, Vancouver, BC, Canada, 1997. [Google Scholar]
- Li, C.; Potter, K.; Wisnom, M.R.; Stringer, G. In-situ measurement of chemical shrinkage of MY750 epoxy resin by a novel gravimetric method. Compos. Sci. Technol. 2004, 64, 55–64. [Google Scholar] [CrossRef]
- Kamal, M.R. Thermoset characterization for moldability analysis. Polym. Eng. Sci. 1974, 14, 231–239. [Google Scholar] [CrossRef]
- Cole, K.C.; Hechler, J.J.; Noel, D. A New Approach to Modeling the Cure Kinetics of Epoxy Amine Thermosetting Resins. 2. Application to a Typical System Based on Bis[4-(diglycidylamino)phenyl] methane and Bis(4-aminophenyl) Sulfone. Macromolecules 1991, 24, 3098–3110. [Google Scholar] [CrossRef]
- Dibenedetto, A.T. Prediction of the Glass Transition Temperature of Polymers: A Model Based on the Principle of Corresponding States. Polym. Sci. Part Polym. Phys. 1987, 25, 1949–1969. [Google Scholar] [CrossRef]
- McKenna, G.B.; Simon, S.L. The glass transition: Its measurement and underlying physics. In Handbook of Thermal Analysis and Calorimetry; Cheng, S.Z.D., Ed.; Elsevier: Springboro Pike Miamisburg, OH, USA, 2002; Chapter 2; pp. 49–104. [Google Scholar]
- Igor, N.; Shardakov, A.N.T. Identification of the temperature dependence of the thermal expansion coefficient of polymers. Polymers 2021, 13, 3035. [Google Scholar] [CrossRef]
- Korolev, A.; Mishnev, M.; Ulrikh, D.V. Non-Linearity of Thermosetting Polymers’ and GRPs’ Thermal Expanding: Experimental Study and Modeling. Polymers 2022, 14, 4281. [Google Scholar] [CrossRef] [PubMed]
- Jørgensen, J.K.; Mikkelsen, L.P.; Andersen, T.L. Cure characterisation and prediction of thermosetting epoxy for wind turbine blade manufacturing. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1293, 012015. [Google Scholar] [CrossRef]
- Hoffman, J.; Khadka, S.; Kumosa, M. Determination of gel point and completion of curing in a single fiber/polymer composite. Compos. Sci. Technol. 2020, 188, 107997. [Google Scholar] [CrossRef]
- Hu, H.; Li, S.; Wang, J.; Zu, L.; Cao, D.; Zhong, Y. Monitoring the gelation and effective chemical shrinkage of composite curing process with a novel FBG approach. Compos. Struct. 2017, 176, 187–194. [Google Scholar] [CrossRef]
- Khadka, S.; Hoffman, J.; Kumosa, M. FBG monitoring of curing in single fiber polymer composites. Compos. Sci. Technol. 2020, 198, 108308. [Google Scholar] [CrossRef]
- Jørgensen, J.K.; Mikkelsen, L.P. Tailored Cure Profiles for Simultaneous Reduction of the Cure Time and Shrinkage of an Epoxy Thermoset. Heliyon 2024, 10, e25450. [Google Scholar] [CrossRef] [PubMed]
- Pascault, J.P.; Williams, R.J. Glass transition temperature versus conversion relationships for thermosetting polymers. J. Polym. Sci. Part Polym. Phys. 1990, 28, 85–95. [Google Scholar] [CrossRef]
- Jørgensen, J.K. Experimental and simulation results of cure-induced strains for a cure study of an conventional epoxy resin. Zenodo 2024. [Google Scholar] [CrossRef]
- Jørgensen, J.K. A thermomechanical finite element subroutine for Abaqus to precisely predict cure-induced strain of an epoxy thermoset. Zenodo 2024. [Google Scholar] [CrossRef]
- McHugh, J.; Fideu, P.; Herrmann, A.; Stark, W. Determination and review of specific heat capacity measurements during isothermal cure of an epoxy using TM-DSC and standard DSC techniques. Polym. Test. 2010, 29, 759–765. [Google Scholar] [CrossRef]
- Wierzbicki, L.; Pusz, A. Thermal conductivity of the epoxy resin filled by low melting point alloy. Arch. Mater. Sci. Eng. 2013, 61, 22–29. [Google Scholar]
- Carson, J.K.; Willix, J.; North, M.F. Measurements of heat transfer coefficients within convection ovens. J. Food Eng. 2006, 72, 293–301. [Google Scholar] [CrossRef]
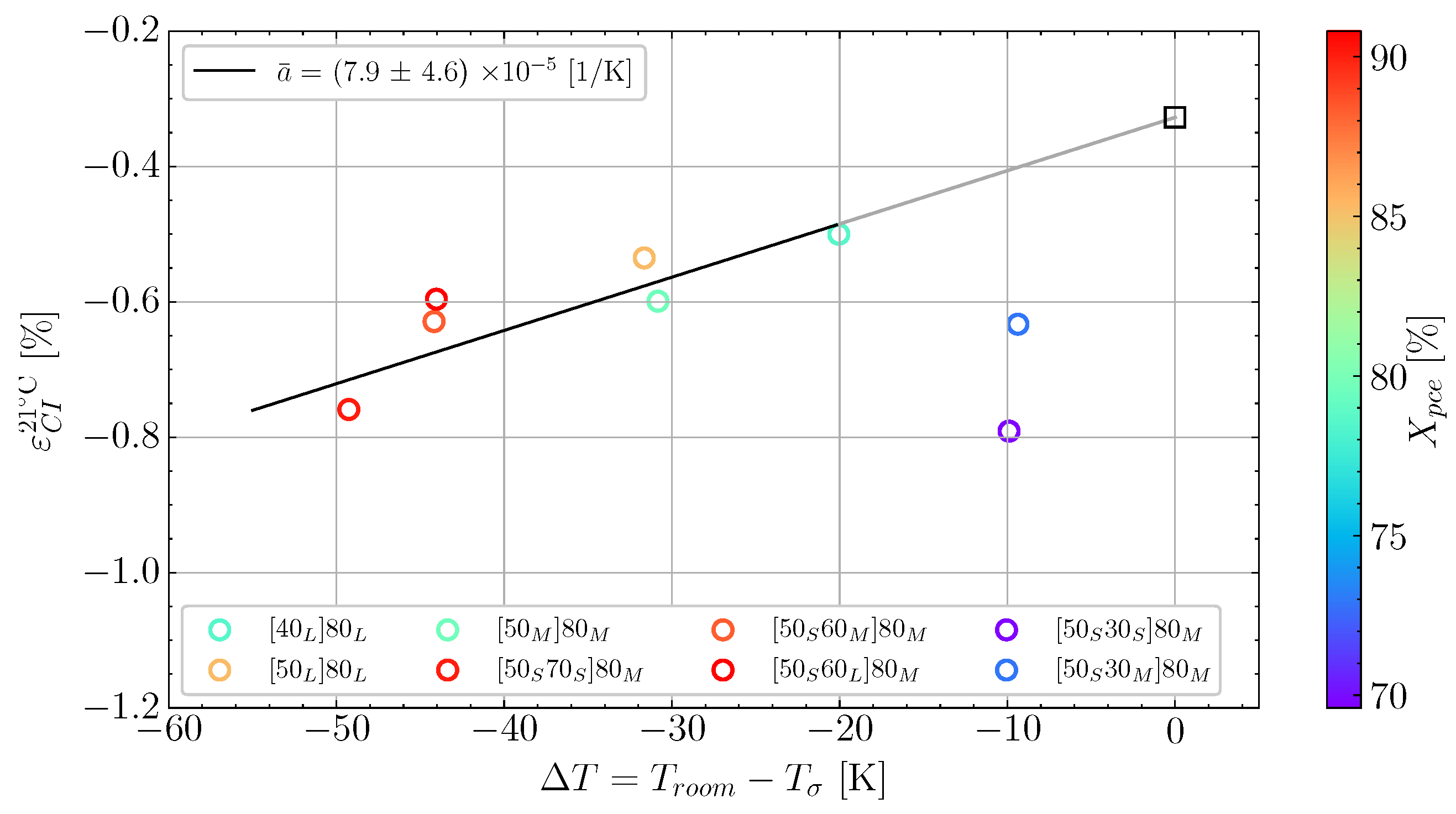
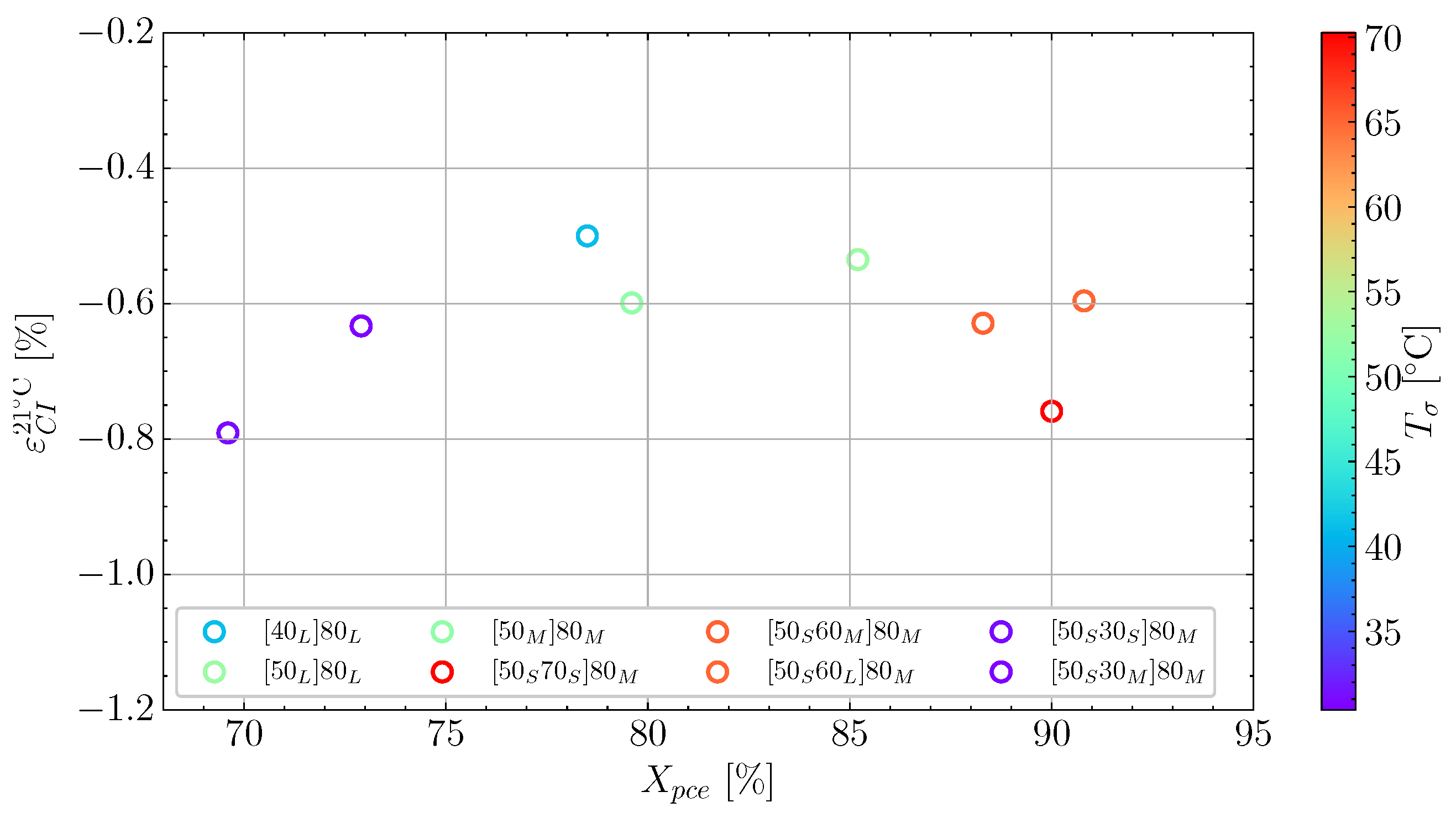
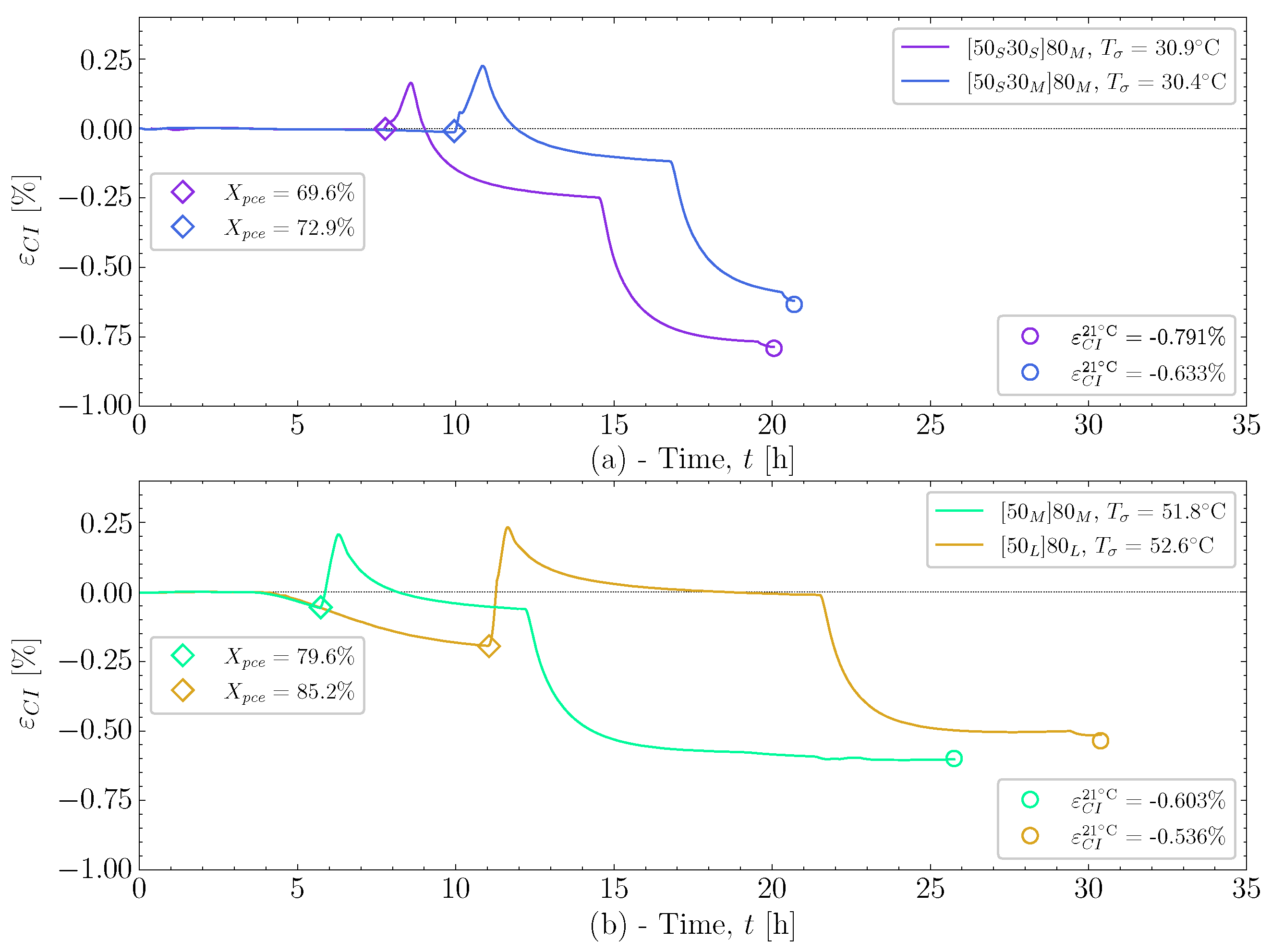
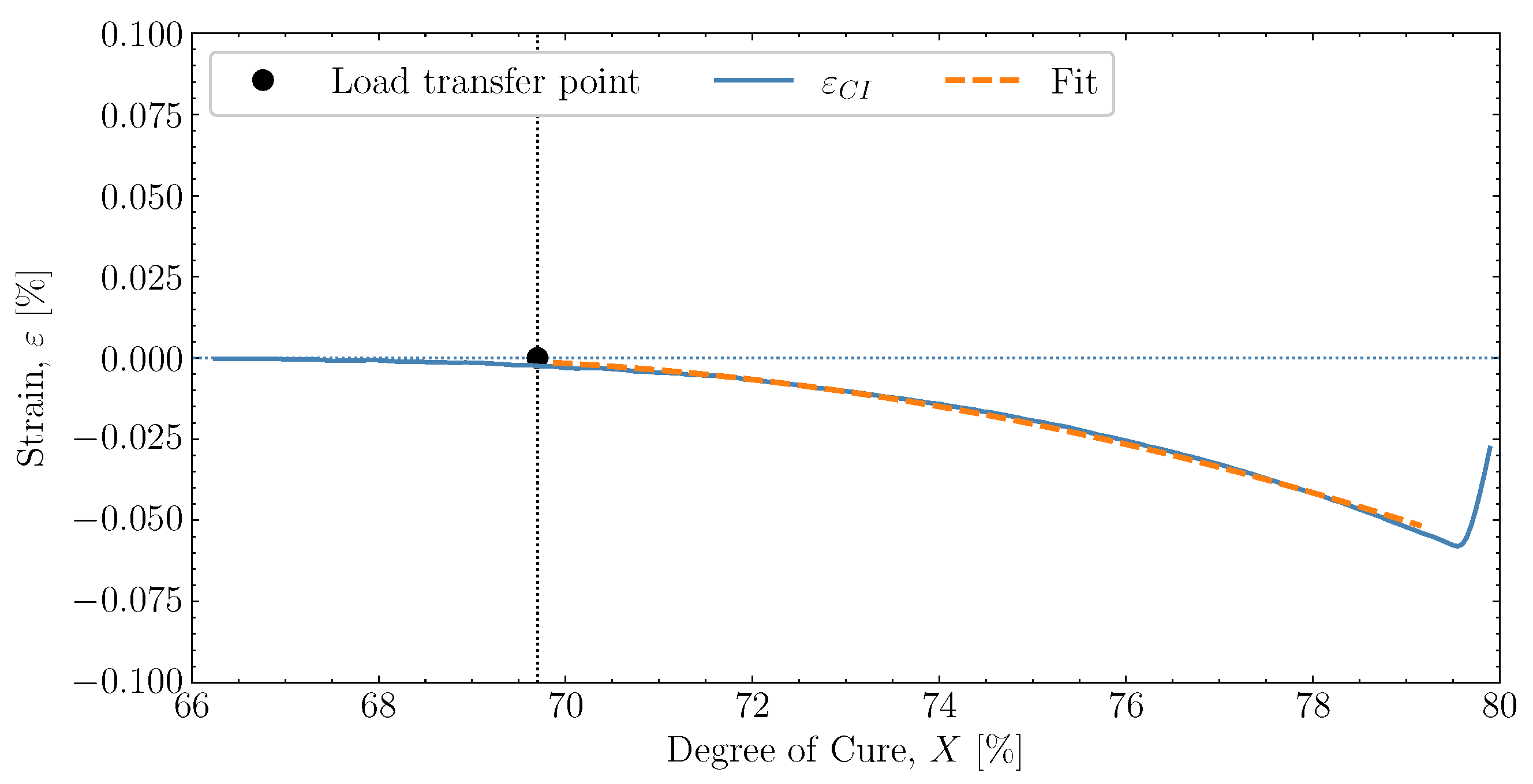
| A [] | [kJ/mol] | n [-] | m [-] | C [-] | [K−1] | [-] | [°C] | [-] | [°C] |
|---|---|---|---|---|---|---|---|---|---|
| 43.7 | −0.885 | −42.0 | 0.487 | 89.0 |
| Cure ID | 1. Pre-Cure | 2. Pre-Cure | Post-Cure | ||||
|---|---|---|---|---|---|---|---|
| [h @ °C] | [h @ °C] | [h @ °C] | [%] | [%] | [%] | [%] | |
| 12 @ 40 | - | 10 @ 80 | 71.6 | 78.5 | 98.3 | −0.500 | |
| 10 @ 50 | - | 10 @ 80 | 68.9 | 85.2 | 98.2 | −0.536 | |
| 5 @ 50 | - | 6 @ 80 | 67.7 | 79.2 | 97.3 | −0.603 | |
| 2 @ 50 | 2 @ 70 | 6 @ 80 | 66.8 | 90.0 | 97.5 | −0.759 | |
| 2 @ 50 | 4 @ 60 | 6 @ 80 | 70.8 | 88.3 | 97.7 | −0.629 | |
| 2 @ 50 | 8 @ 60 | 6 @ 80 | 72.8 | 90.3 | 97.8 | −0.596 | |
| 1.5 @ 50 | 3 @ 30 | 6 @ 80 | 69.6 | 69.6 | 97.4 | −0.791 | |
| 1.5 @ 50 | 6 @ 30 | 6 @ 80 | 69.7 | 72.9 | 97.4 | −0.633 |
| Cure ID | [%] | [%] | [%] |
|---|---|---|---|
| 69.7 | 98.0 | −1.1 |
| [K−1] | [K−2] | [K−2] | [K−2] | [K−2] |
|---|---|---|---|---|
| [K] | [K] | [K] | [K] | [K] |
| −50 | −22 | −11 | −3 | 2.5 |
| [K−1] | [K−1] | [K−1] |
|---|---|---|
| Cure ID | ||||||||
|---|---|---|---|---|---|---|---|---|
| [%] | −0.500 | −0.536 | −0.603 | −0.759 | −0.629 | −0.596 | −0.791 | −0.633 |
| [%] | −0.532 | −0.511 | −0.608 | −0.773 | −0.642 | −0.583 | −0.758 | −0.609 |
| Dev. [%] | 6 | 5 | 2 | 2 | 2 | 2 | 4 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jørgensen, J.K.; Maes, V.K.; Mikkelsen, L.P.; Andersen, T.L. A Precise Prediction of the Chemical and Thermal Shrinkage during Curing of an Epoxy Resin. Polymers 2024, 16, 2435. https://doi.org/10.3390/polym16172435
Jørgensen JK, Maes VK, Mikkelsen LP, Andersen TL. A Precise Prediction of the Chemical and Thermal Shrinkage during Curing of an Epoxy Resin. Polymers. 2024; 16(17):2435. https://doi.org/10.3390/polym16172435
Chicago/Turabian StyleJørgensen, Jesper K., Vincent K. Maes, Lars P. Mikkelsen, and Tom L. Andersen. 2024. "A Precise Prediction of the Chemical and Thermal Shrinkage during Curing of an Epoxy Resin" Polymers 16, no. 17: 2435. https://doi.org/10.3390/polym16172435
APA StyleJørgensen, J. K., Maes, V. K., Mikkelsen, L. P., & Andersen, T. L. (2024). A Precise Prediction of the Chemical and Thermal Shrinkage during Curing of an Epoxy Resin. Polymers, 16(17), 2435. https://doi.org/10.3390/polym16172435








