Polymorph Stability and Free Energy of Crystallization of Freely-Jointed Polymers of Hard Spheres
Abstract
1. Introduction
2. Methodology
2.1. Free Energy Difference between FCC and HCP Polymorphs
2.2. Monte Carlo Simulations
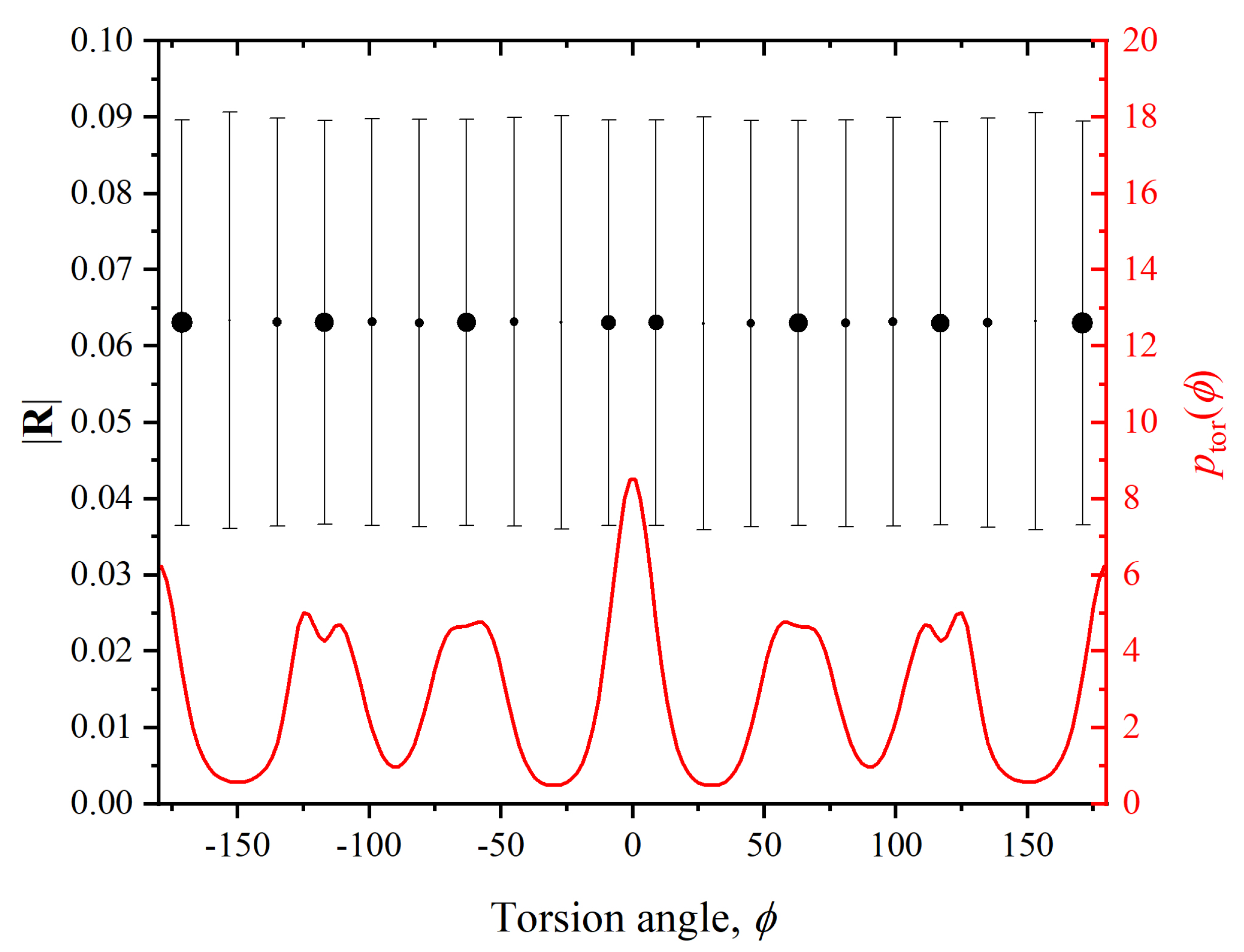
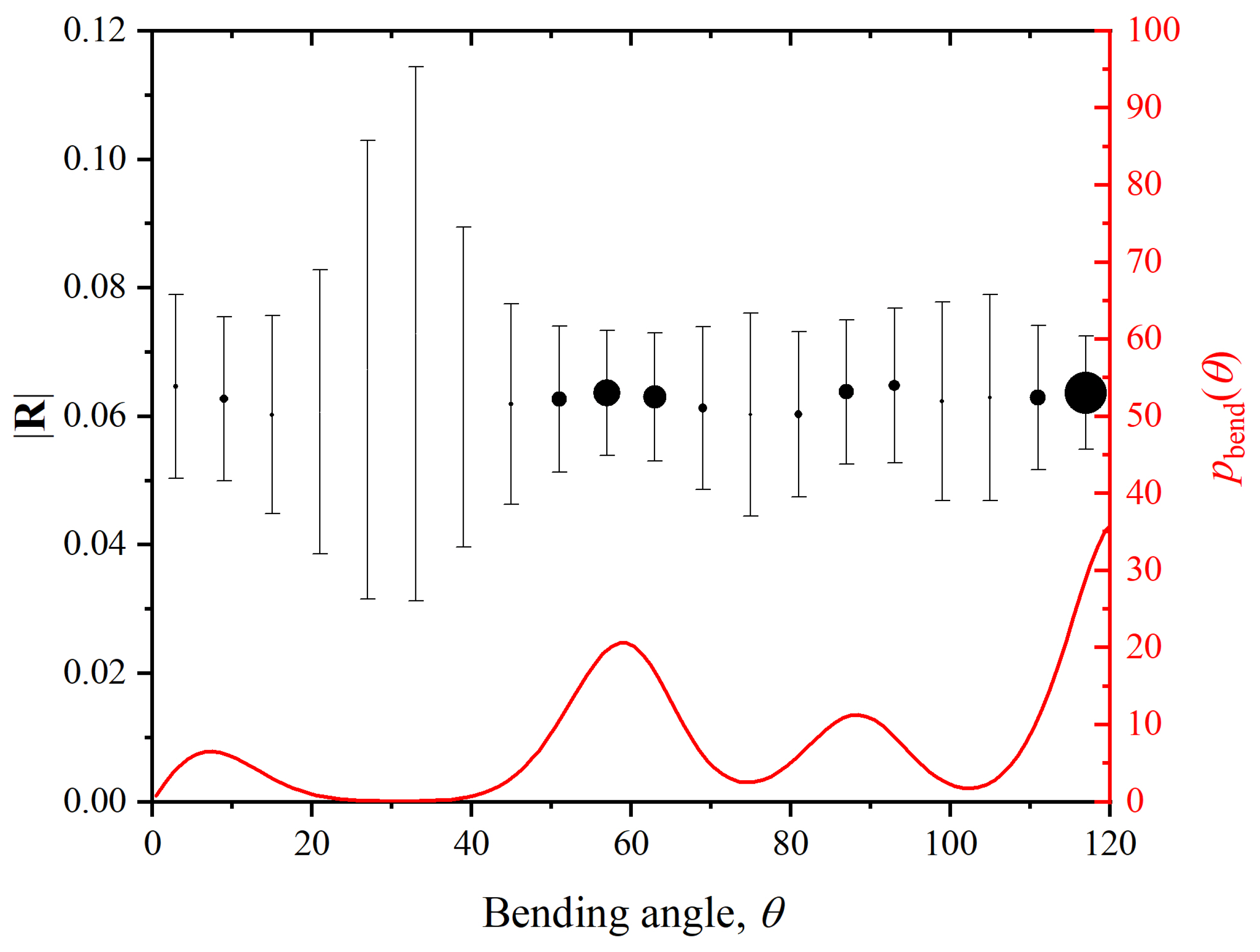
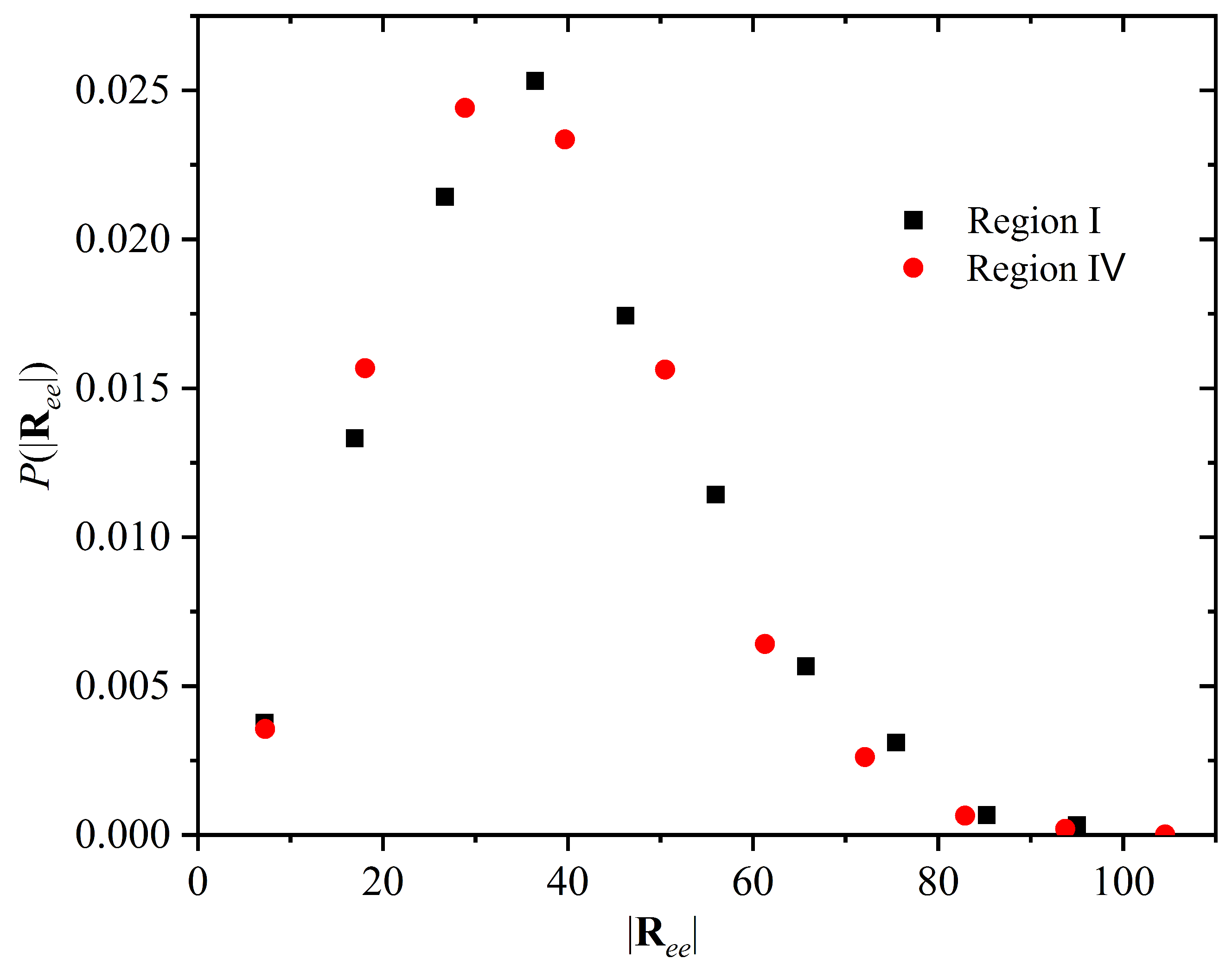
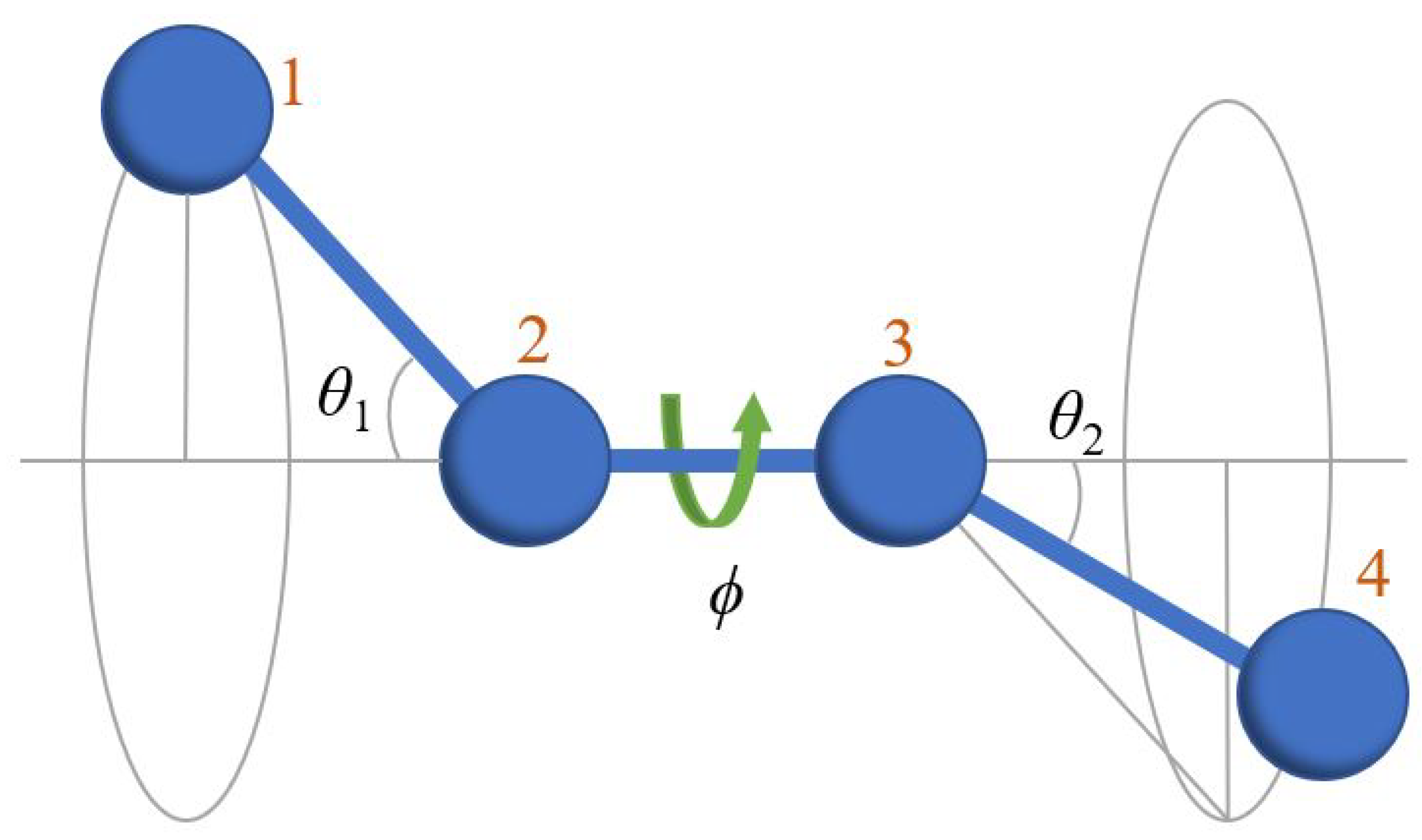
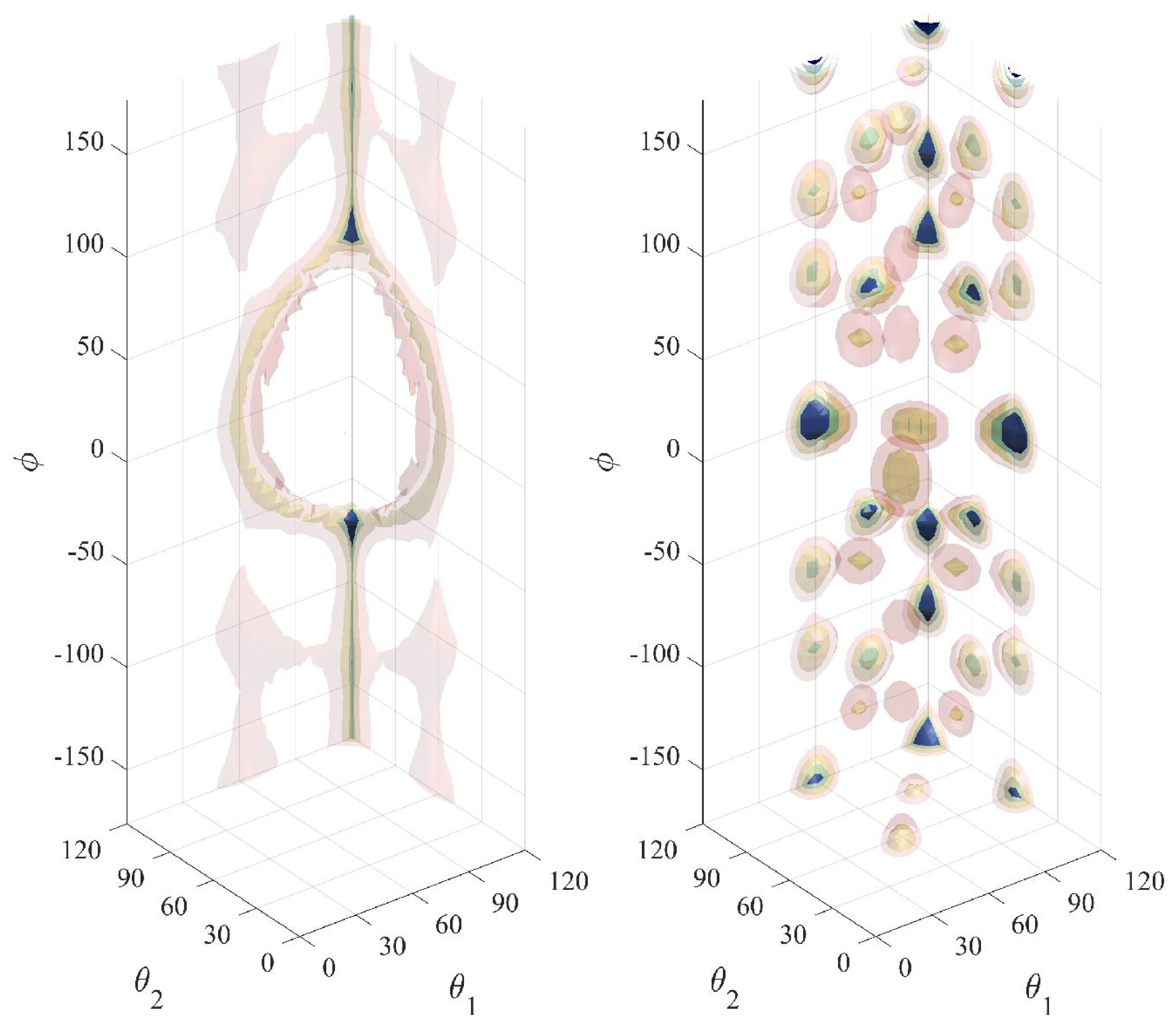
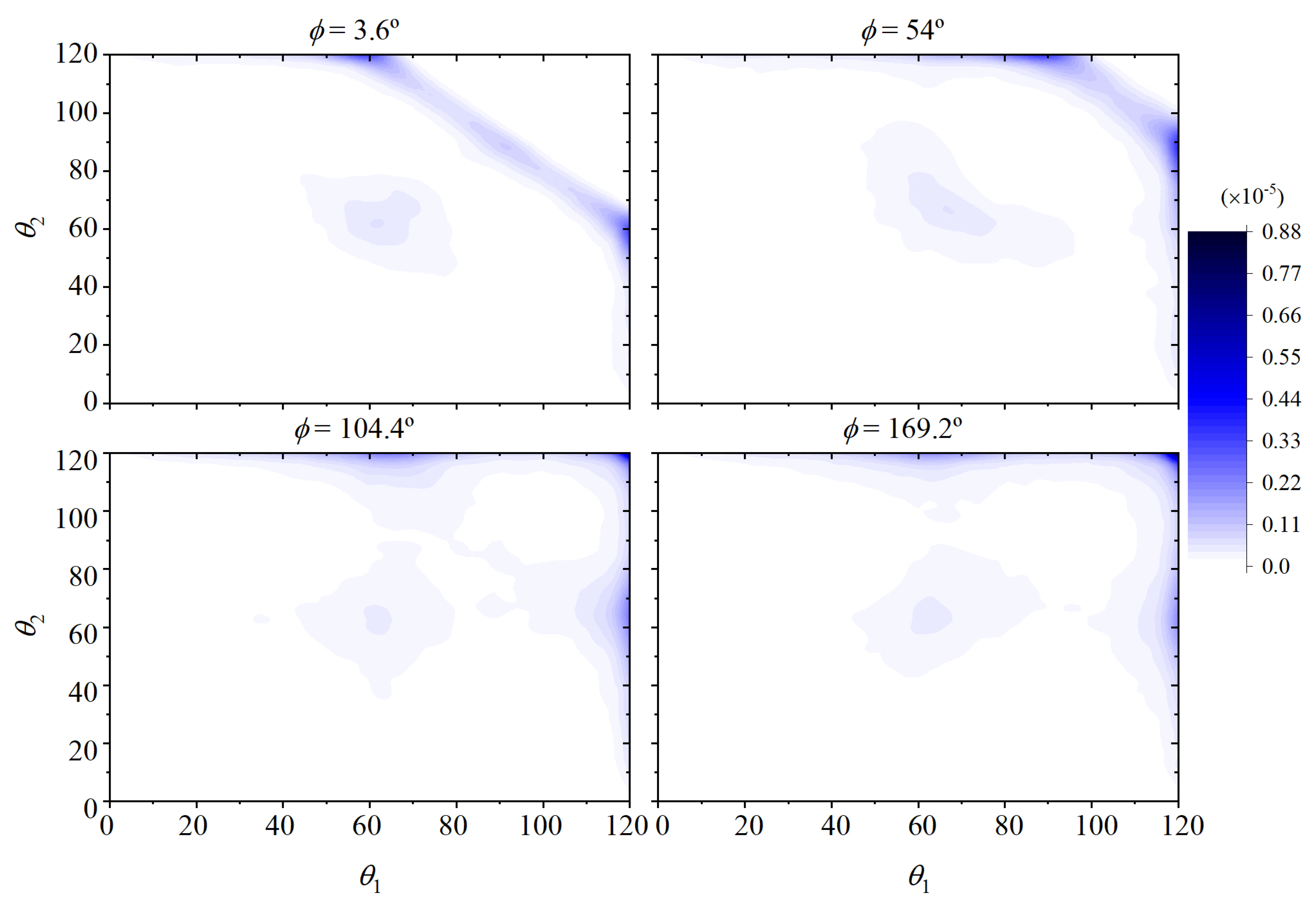
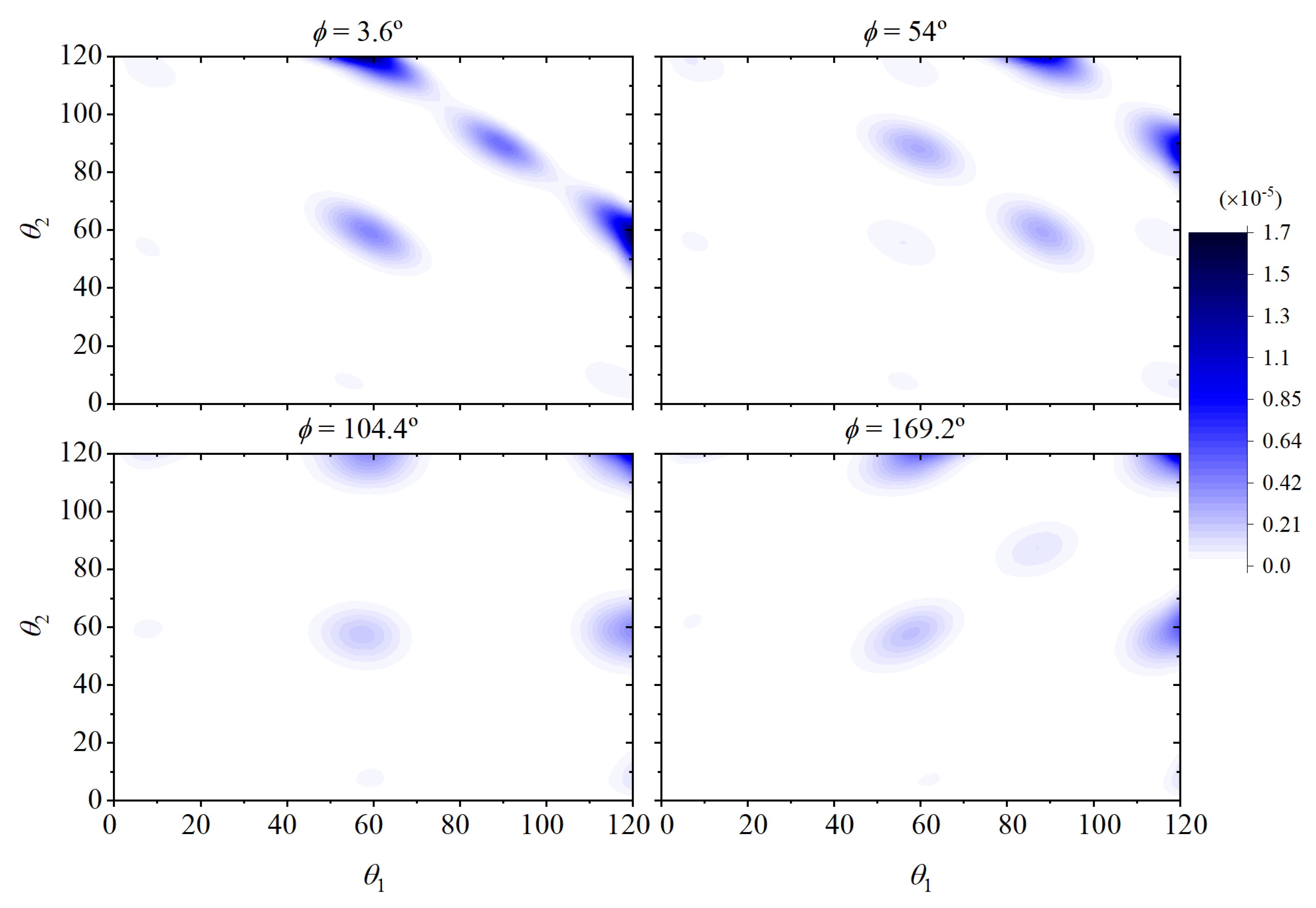
3. Decorrelation of Translational and Conformational Degrees of Freedom
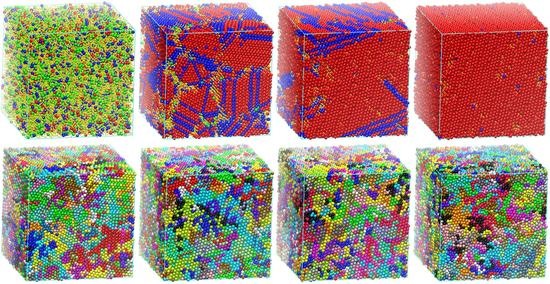
4. Free Energy of Crystallization
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Desouza, L.E.S.; Stamatopoulou, A.; Benamotz, D. Chemical-potentials of hard-sphere solutes in hard-sphere solvents-monte-carlo simulations and analytical approximations. J. Chem. Phys. 1994, 100, 1456–1459. [Google Scholar] [CrossRef]
- Escobedo, F.A.; DePablo, J.J. Chemical potential and dimensions of chain molecules in athermal environments. Mol. Phys. 1996, 89, 1733–1754. [Google Scholar] [CrossRef]
- Meijer, E.J.; Frenkel, D. Colloids dispersed in polymer-solutions—A computer-simulation study. J. Chem. Phys. 1994, 100, 6873–6887. [Google Scholar] [CrossRef]
- Shevchenko, E.V.; Talapin, D.V.; Murray, C.B.; O’Brien, S. Structural characterization of self-assembled multifunctional binary nanoparticle superlattices. J. Am. Chem. Soc. 2006, 128, 3620–3637. [Google Scholar] [CrossRef] [PubMed]
- Campoy-Quiles, M.; Ferenczi, T.; Agostinelli, T.; Etchegoin, P.G.; Kim, Y.; Anthopoulos, T.D.; Stavrinou, P.N.; Bradley, D.D.C.; Nelson, J. Morphology evolution via self-organization and lateral and vertical diffusion in polymer: Fullerene solar cell blends. Nat. Mater. 2008, 7, 158–164. [Google Scholar] [CrossRef]
- Munao, G.; O’Toole, P.; Hudson, T.S.; Costa, D.; Caccamo, C.; Giacometti, A.; Sciortino, F. Phase separation and self-assembly of colloidal dimers with tunable attractive strength: From symmetrical square-wells to Janus dumbbells. Soft Matter 2014, 10, 5269–5279. [Google Scholar] [CrossRef] [PubMed]
- Henzie, J.; Grunwald, M.; Widmer-Cooper, A.; Geissler, P.L.; Yang, P.D. Self-assembly of uniform polyhedral silver nanocrystals into densest packings and exotic superlattices. Nat. Mater. 2012, 11, 131–137. [Google Scholar] [CrossRef]
- Damasceno, P.F.; Engel, M.; Glotzer, S.C. Predictive Self-Assembly of Polyhedra into Complex Structures. Science 2012, 337, 453–457. [Google Scholar] [CrossRef]
- Li, G.; Shrotriya, V.; Huang, J.S.; Yao, Y.; Moriarty, T.; Emery, K.; Yang, Y. High-efficiency solution processable polymer photovoltaic cells by self-organization of polymer blends. Nat. Mater. 2005, 4, 864–868. [Google Scholar] [CrossRef]
- Murray, C.B.; Kagan, C.R.; Bawendi, M.G. Self-organization of cdse nanocrystallites into 3-dimensional quantum-dot superlattices. Science 1995, 270, 1335–1338. [Google Scholar] [CrossRef]
- Pfeifer, R.; Lungarella, M.; Iida, F. Self-organization, embodiment, and biologically inspired robotics. Science 2007, 318, 1088–1093. [Google Scholar] [CrossRef]
- Pusey, P.N.; Vanmegen, W.; Bartlett, P.; Ackerson, B.J.; Rarity, J.G.; Underwood, S.M. Structure of crystals of hard colloidal spheres. Phys. Rev. Lett. 1989, 63, 2753–2756. [Google Scholar] [CrossRef]
- Dolbnya, I.P.; Petukhov, A.V.; Aarts, D.; Vroege, G.J.; Lekkerkerker, H.N.W. Coexistence of rHCP and FCC phases in hard-sphere colloidal crystals. Europhys. Lett. 2005, 72, 962–968. [Google Scholar] [CrossRef]
- Rintoul, M.D.; Torquato, S. Metastability and crystallization in hard-sphere systems. Phys. Rev. Lett. 1996, 77, 4198–4201. [Google Scholar] [CrossRef]
- Schilling, T.; Schope, H.J.; Oettel, M.; Opletal, G.; Snook, I. Precursor-Mediated Crystallization Process in Suspensions of Hard Spheres. Phys. Rev. Lett. 2010, 105. [Google Scholar] [CrossRef] [PubMed]
- Anderson, J.A.; Antonaglia, J.; Millan, J.A.; Engel, M.; Glotzer, S.C. Shape and Symmetry Determine Two-Dimensional Melting Transitions of Hard Regular Polygons. Phys. Rev. X 2017, 7. [Google Scholar] [CrossRef]
- Fuchs, M.; Schweizer, K.S. Structure and thermodynamics of colloid-polymer mixtures: A macromolecular approach. Europhys. Lett. 2000, 51, 621–627. [Google Scholar] [CrossRef]
- Fortini, A.; Dijkstra, M. Phase behaviour of hard spheres confined between parallel hard plates: Manipulation of colloidal crystal structures by confinement. J. Phys.-Condens. Matter 2006, 18, L371–L378. [Google Scholar] [CrossRef]
- Williams, S.R.; Royall, C.P.; Bryant, G. Crystallization of dense binary hard-sphere mixtures with marginal size ratio. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, J.R.; Vega, C.; Valeriani, C.; Frenkel, D.; Sanz, E. Heterogeneous versus homogeneous crystal nucleation of hard spheres. Soft Matter 2019, 15, 9625–9631. [Google Scholar] [CrossRef] [PubMed]
- Medvedev, N.N.; Bezrukov, A.; Shtoyan, D. From amorphous solid to defective crystal. A study of structural peculiarities in close packings of hard spheres. J. Struct. Chem. 2004, 45, S23–S30. [Google Scholar] [CrossRef]
- He, Y.M.; Olivier, B.; Ackerson, B.J. Morphology of crystals made of hard spheres. Langmuir 1997, 13, 1408–1412. [Google Scholar] [CrossRef]
- Pusey, P.N.; Zaccarelli, E.; Valeriani, C.; Sanz, E.; Poon, W.C.K.; Cates, M.E. Hard spheres: Crystallization and glass formation. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2009, 367, 4993–5011. [Google Scholar] [CrossRef]
- Onsager, L. The effects of Shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
- Frenkel, D. Perspective on “The effect of shape on the interaction of colloidal particles”—Onsager L (1949) Ann NY Acad Sci 51: 627. Theor. Chem. Acc. 2000, 103, 212–213. [Google Scholar] [CrossRef]
- Punnathanam, S.; Monson, P.A. Crystal nucleation in binary hard sphere mixtures: A Monte Carlo simulation study. J. Chem. Phys. 2006, 125, 024508. [Google Scholar] [CrossRef]
- Kawasaki, T.; Tanaka, H. Formation of a crystal nucleus from liquid. Proc. Natl. Acad. Sci. USA 2010, 107, 14036–14041. [Google Scholar] [CrossRef]
- O’Malley, B.; Snook, I. Crystal nucleation in the hard sphere system. Phys. Rev. Lett. 2003, 90, 085702. [Google Scholar] [CrossRef]
- Zaccarelli, E.; Valeriani, C.; Sanz, E.; Poon, W.C.K.; Cates, M.E.; Pusey, P.N. Crystallization of Hard-Sphere Glasses. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef]
- Iacopini, S.; Palberg, T.; Schope, H.J. Ripening-dominated crystallization in polydisperse hard-sphere-like colloids. Phys. Rev. E 2009, 79. [Google Scholar] [CrossRef] [PubMed]
- Hoover, W.G.; Ree, F.H. Melting Transition Furthermore, Communal Entropy For Hard Spheres. J. Chem. Phys. 1968, 49, 3609. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T.E. Phase Transition For A Hard Sphere System. J. Chem. Phys. 1957, 27, 1208–1209. [Google Scholar] [CrossRef]
- Gasser, U.; Weeks, E.R.; Schofield, A.; Pusey, P.N.; Weitz, D.A. Real-space imaging of nucleation and growth in colloidal crystallization. Science 2001, 292, 258–262. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.X.; Li, M.; Rogers, R.; Meyer, W.; Ottewill, R.H.; Russell, W.B.; Chaikin, P.M. Crystallization of hard-sphere colloids in microgravity. Nature 1997, 387, 883–885. [Google Scholar] [CrossRef]
- Martelozzo, V.C.; Schofield, A.B.; Poon, W.C.K.; Pusey, P.N. Structural aging of crystals of hard-sphere colloids. Phys. Rev. E 2002, 66, 021408. [Google Scholar] [CrossRef]
- Verhaegh, N.A.M.; Vanduijneveldt, J.S.; Vanblaaderen, A.; Lekkerkerker, H.N.W. Direct observation of stacking disorder in a colloidal crystal. J. Chem. Phys. 1995, 102, 1416–1421. [Google Scholar] [CrossRef]
- Harland, J.L.; vanMegen, W. Crystallization kinetics of suspensions of hard colloidal spheres. Phys. Rev. E 1997, 55, 3054–3067. [Google Scholar] [CrossRef]
- Cheng, Z.D.; Zhu, J.X.; Russel, W.B.; Meyer, W.V.; Chaikin, P.M. Colloidal hard-sphere crystallization kinetics in microgravity and normal gravity. Appl. Opt. 2001, 40, 4146–4151. [Google Scholar] [CrossRef]
- Kegel, W.K.; Dhont, J.K.G. “Aging” of the structure of crystals of hard colloidal spheres. J. Chem. Phys. 2000, 112, 3431–3436. [Google Scholar] [CrossRef]
- Pusey, P.N.; Vanmegen, W. Phase-behavior of concentrated suspensions of nearly hard colloidal spheres. Nature 1986, 320, 340–342. [Google Scholar] [CrossRef]
- Bolhuis, P.G.; Frenkel, D.; Mau, S.C.; Huse, D.A. Entropy difference between crystal phases. Nature 1997, 388, 235–236. [Google Scholar] [CrossRef]
- Woodcock, L.V. Entropy difference between the face-centred cubic and hexagonal close-packed crystal structures. Nature 1997, 385, 141–143. [Google Scholar] [CrossRef]
- Bruce, A.D.; Wilding, N.B.; Ackland, G.J. Free energy of crystalline solids: A lattice-switch Monte Carlo method. Phys. Rev. Lett. 1997, 79, 3002–3005. [Google Scholar] [CrossRef]
- Mau, S.C.; Huse, D.A. Stacking entropy of hard-sphere crystals. Phys. Rev. E 1999, 59, 4396–4401. [Google Scholar] [CrossRef]
- Pronk, S.; Frenkel, D. Can stacking faults in hard-sphere crystals anneal out spontaneously? J. Chem. Phys. 1999, 110, 4589–4592. [Google Scholar] [CrossRef]
- Noya, E.G.; Almarza, N.G. Entropy of hard spheres in the close-packing limit. Mol. Phys. 2015, 113, 1061–1068. [Google Scholar] [CrossRef]
- de Miguel, E.; Marguta, R.G.; del Rio, E.M. System-size dependence of the free energy of crystalline solids. J. Chem. Phys. 2007, 127, 154512. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Malshe, R.; de Pablo, J.J.; Laso, M. Fivefold symmetry as an inhibitor to hard-sphere crystallization. Phys. Rev. E 2011, 83, 061505. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Malshe, R.; Kroger, M.; de Pablo, J.J.; Laso, M. Evolution of fivefold local symmetry during crystal nucleation and growth in dense hard-sphere packings. Soft Matter 2012, 8, 844–858. [Google Scholar] [CrossRef]
- Luchnikov, V.; Gervois, A.; Richard, P.; Oger, L.; Troadec, J.P. Crystallization of dense hard sphere packings—Competition of HCP and FCC close order. J. Mol. Liq. 2002, 96–97, 185–194. [Google Scholar] [CrossRef]
- Richard, P.; Gervois, A.; Oger, L.; Troadec, J.P. Order and disorder in hard-sphere packings. Europhys. Lett. 1999, 48, 415–420. [Google Scholar] [CrossRef]
- Auer, S.; Frenkel, D. Numerical prediction of absolute crystallization rates in hard-sphere colloids. J. Chem. Phys. 2004, 120, 3015–3029. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Burgos, I.; Sanz, E.; Vega, C.; Espinosa, J.R. FCC vs. HCP competition in colloidal hard-sphere nucleation: On their relative stability, interfacial free energy and nucleation rate. Phys. Chem. Chem. Phys. 2021, 23, 19611–19626. [Google Scholar] [CrossRef]
- Leoni, F.; Russo, J. Nonclassical Nucleation Pathways in Stacking-Disordered Crystals. Phys. Rev. X 2021, 11, 031006. [Google Scholar] [CrossRef]
- Koch, H.; Radin, C.; Sadun, L. Most stable structure for hard spheres. Phys. Rev. E 2005, 72, 016708. [Google Scholar] [CrossRef]
- Auer, S.; Frenkel, D. Prediction of absolute crystal-nucleation rate in hard-sphere colloids. Nature 2001, 409, 1020–1023. [Google Scholar] [CrossRef]
- Chen, H.Y.; Ma, H.R. The density profile of hard sphere liquid system under gravity. J. Chem. Phys. 2006, 125. [Google Scholar] [CrossRef]
- Senger, B.; Bafaluy, F.J.; Schaaf, P.; Schmitt, A.; Voegel, J.C. Configurations of adsorbed hard-spheres after diffusion in a gravitational-field. Proc. Natl. Acad. Sci. USA 1992, 89, 9449–9453. [Google Scholar] [CrossRef]
- Hernandez-Guzman, J.; Weeks, E.R. The equilibrium intrinsic crystal-liquid interface of colloids. Proc. Natl. Acad. Sci. USA 2009, 106, 15198–15202. [Google Scholar] [CrossRef]
- Kosinski, P.; Hoffmann, A.C. Extension of the hard-sphere particle-wall collision model to account for particle deposition. Phys. Rev. E 2009, 79, 061302. [Google Scholar] [CrossRef]
- Marechal, M.; Hermes, M.; Dijkstra, M. Stacking in sediments of colloidal hard spheres. J. Chem. Phys. 2011, 135, 034510. [Google Scholar] [CrossRef] [PubMed]
- Dasgupta, T.; Edison, J.R.; Dijkstra, M. Growth of defect-free colloidal hard-sphere crystals using colloidal epitaxy. J. Chem. Phys. 2017, 146, 074903. [Google Scholar] [CrossRef]
- Hoogenboom, J.P.; van Langen-Suurling, A.K.; Romijn, J.; van Blaaderen, A. Epitaxial growth of a colloidal hard-sphere hcp crystal and the effects of epitaxial mismatch on crystal structure. Phys. Rev. E 2004, 69, 051602. [Google Scholar] [CrossRef]
- vanBlaaderen, A.; Ruel, R.; Wiltzius, P. Template-directed colloidal crystallization. Nature 1997, 385, 321–324. [Google Scholar] [CrossRef]
- Zou, L.N.; Cheng, X.; Rivers, M.L.; Jaeger, H.M.; Nagel, S.R. The Packing of Granular Polymer Chains. Science 2009, 326, 408–410. [Google Scholar] [CrossRef] [PubMed]
- Brown, E.; Nasto, A.; Athanassiadis, A.G.; Jaeger, H.M. Strain Stiffening in Random Packings of Entangled Granular Chains. Phys. Rev. Lett. 2012, 108, 108302. [Google Scholar] [CrossRef] [PubMed]
- Vutukuri, H.R.; Demirors, A.F.; Peng, B.; van Oostrum, P.D.J.; Imhof, A.; van Blaaderen, A. Colloidal Analogues of Charged and Uncharged Polymer Chains with Tunable Stiffness. Angew. Chem. Int. Ed. 2012, 51, 11249–11253. [Google Scholar] [CrossRef] [PubMed]
- Verweij, R.W.; Moerman, P.G.; Ligthart, N.E.G.; Huijnen, L.P.P.; Groenewold, J.; Kegel, W.K.; van Blaaderen, A.; Kraft, D.J. Flexibility-induced effects in the Brownian motion of colloidal trimers. Phys. Rev. Res. 2020, 2, 033136. [Google Scholar] [CrossRef]
- McMullen, A.; Holmes-Cerfon, M.; Sciortino, F.; Grosberg, A.Y.; Brujic, J. Freely Jointed Polymers Made of Droplets. Phys. Rev. Lett. 2018, 121, 138002. [Google Scholar] [CrossRef]
- Liu, Z.G.; Yang, Z.; Chen, X.; Tan, R.; Li, G.; Gan, Z.H.; Shao, Y.; He, J.L.; Zhang, Z.B.; Li, W.H.; et al. Discrete Giant Polymeric Chains Based on Nanosized Monomers. JACS Au 2021, 1, 79–86. [Google Scholar] [CrossRef]
- Shakirov, T. Crystallisation in Melts of Short, Semi-Flexible Hard-Sphere Polymer Chains: The Role of the Non-Bonded Interaction Range. Entropy 2019, 21, 856. [Google Scholar] [CrossRef]
- Shakirov, T.; Paul, W. Crystallization in melts of short, semiflexible hard polymer chains: An interplay of entropies and dimensions. Phys. Rev. E 2018, 97, 042501. [Google Scholar] [CrossRef] [PubMed]
- Dietz, J.D.; Hoy, R.S. Two-stage athermal solidification of semiflexible polymers and fibers. Soft Matter 2020, 16, 6206–6217. [Google Scholar] [CrossRef] [PubMed]
- Ni, R.; Dijkstra, M. Effect of bond length fluctuations on crystal nucleation of hard bead chains. Soft Matter 2013, 9, 365–369. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Entropy-Driven Crystallization in Dense Systems of Athermal Chain Molecules. Phys. Rev. Lett. 2009, 103, 045703. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Abrams, C.F.; Laso, M. Modeling of crystal nucleation and growth in athermal polymers: Self-assembly of layered nano-morphologies. Soft Matter 2010, 6, 2160–2173. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The role of bond tangency and bond gap in hard sphere crystallization of chains. Soft Matter 2015, 11, 1688–1700. [Google Scholar] [CrossRef]
- Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Polymorphism and Perfection in Crystallization of Hard Sphere Polymers. Polymers 2022, 14, 4435. [Google Scholar] [CrossRef]
- Ramos, P.M.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Entropy-Driven Heterogeneous Crystallization of Hard-Sphere Chains under Unidimensional Confinement. Polymers 2021, 13, 1352. [Google Scholar] [CrossRef]
- Ramos, P.M.; Herranz, M.; Martinez-Fernandez, D.; Foteinopoulou, K.; Laso, M.; Karayiannis, N.C. Crystallization of Flexible Chains of Tangent Hard Spheres under Full Confinement. J. Phys. Chem. B 2022, 126, 5931–5947. [Google Scholar] [CrossRef]
- Martínez-Fernández, D.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Local and Global Order in Dense Packings of Semi-Flexible Polymers of Hard Spheres. Polymers 2023, 15, 551. [Google Scholar] [CrossRef]
- Pant, P.V.K.; Theodorou, D.N. Variable Connectivity Method For The Atomistic Monte-Carlo Simulation Of Polydisperse Polymer Melts. Macromolecules 1995, 28, 7224–7234. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Laso, M. Monte Carlo scheme for generation and relaxation of dense and nearly jammed random structures of freely jointed hard-sphere chains. Macromolecules 2008, 41, 1537–1551. [Google Scholar] [CrossRef]
- Laso, M.; Karayiannis, N.C. Flexible chain molecules in the marginal and concentrated regimes: Universal static scaling laws and cross-over predictions. J. Chem. Phys. 2008, 128, 174901. [Google Scholar] [CrossRef] [PubMed]
- Stroobants, A.; Lekkerkerker, H.N.W.; Frenkel, D. Evidence for one-dimensional, two-dimensional, and 3-dimensional order in a system of hard parallel spherocylinders. Phys. Rev. A 1987, 36, 2929–2945. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, D. Entropy-driven phase transitions. Physica A 1999, 263, 26–38. [Google Scholar] [CrossRef]
- Eldridge, M.D.; Madden, P.A.; Frenkel, D. Entropy-driven formation of a superlattice in a hard-sphere binary mixture. Nature 1993, 365, 35–37. [Google Scholar] [CrossRef]
- Li, B.; Madras, N.; Sokal, A.D. Critical exponents, hyperscaling, and universal amplitude ratios for two-and three-dimensional self-avoiding walks. J. Stat. Phys. 1995, 80, 661–754. [Google Scholar] [CrossRef]
- Madras, N.; Slade, G. The Self-Avoiding Walk; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Flory, P.J. Statistical Mechanics of Chain Molecules; Hanser-Verlag: Munchen, Germany, 1989. [Google Scholar]
- Ramos, P.M.; Karayiannis, N.C.; Laso, M. Off-lattice simulation algorithms for athermal chain molecules under extreme confinement. J. Comput. Phys. 2018, 375, 918–934. [Google Scholar] [CrossRef]
- Herranz, M.; Santiago, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Crystal, Fivefold and Glass Formation in Clusters of Polymers Interacting with the Square Well Potential. Polymers 2020, 12, 1111. [Google Scholar] [CrossRef]
- Ramos, P.M.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Identification of Local Structure in 2-D and 3-D Atomic Systems through Crystallographic Analysis. Crystals 2020, 10, 1008. [Google Scholar] [CrossRef]
- Schmidt, M.; Fuchs, M. Penetrability in model colloid-polymer mixtures. J. Chem. Phys. 2002, 117, 6308–6312. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. Model. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Alder, B.J. Studies in Molecular Dynamics. V. High-Density Equation of State and Entropy for Hard Disks and Spheres. J. Chem. Phys. 1968, 49, 3688. [Google Scholar] [CrossRef]
- Alder, B.J.; Young, D.A.; Mansigh, M.R.; Salsburg, Z.W. Hard sphere equation of state in close-packed limit. J. Comput. Phys. 1971, 7, 361. [Google Scholar] [CrossRef]
- Anikeenko, A.V.; Medvedev, N.N. Polytetrahedral nature of the dense disordered packings of hard spheres. Phys. Rev. Lett. 2007, 98, 235504. [Google Scholar] [CrossRef] [PubMed]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1988. [Google Scholar]
- Debye, P. The intrinsic viscosity of polymer solutions. J. Chem. Phys. 1946, 14, 636–639. [Google Scholar] [CrossRef]
- Bloch F, W.J.D. Fundamentals of Statistical Mechanics, 2nd ed.; Imperial College Press: London, UK, 2000. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herranz, M.; Benito, J.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Polymorph Stability and Free Energy of Crystallization of Freely-Jointed Polymers of Hard Spheres. Polymers 2023, 15, 1335. https://doi.org/10.3390/polym15061335
Herranz M, Benito J, Foteinopoulou K, Karayiannis NC, Laso M. Polymorph Stability and Free Energy of Crystallization of Freely-Jointed Polymers of Hard Spheres. Polymers. 2023; 15(6):1335. https://doi.org/10.3390/polym15061335
Chicago/Turabian StyleHerranz, Miguel, Javier Benito, Katerina Foteinopoulou, Nikos Ch. Karayiannis, and Manuel Laso. 2023. "Polymorph Stability and Free Energy of Crystallization of Freely-Jointed Polymers of Hard Spheres" Polymers 15, no. 6: 1335. https://doi.org/10.3390/polym15061335
APA StyleHerranz, M., Benito, J., Foteinopoulou, K., Karayiannis, N. C., & Laso, M. (2023). Polymorph Stability and Free Energy of Crystallization of Freely-Jointed Polymers of Hard Spheres. Polymers, 15(6), 1335. https://doi.org/10.3390/polym15061335