Seismic Protection of RC Buildings by Polymeric Infill Wall-Frame Interface
Abstract
1. Introduction
2. Phase I Details
3. Phase II Details
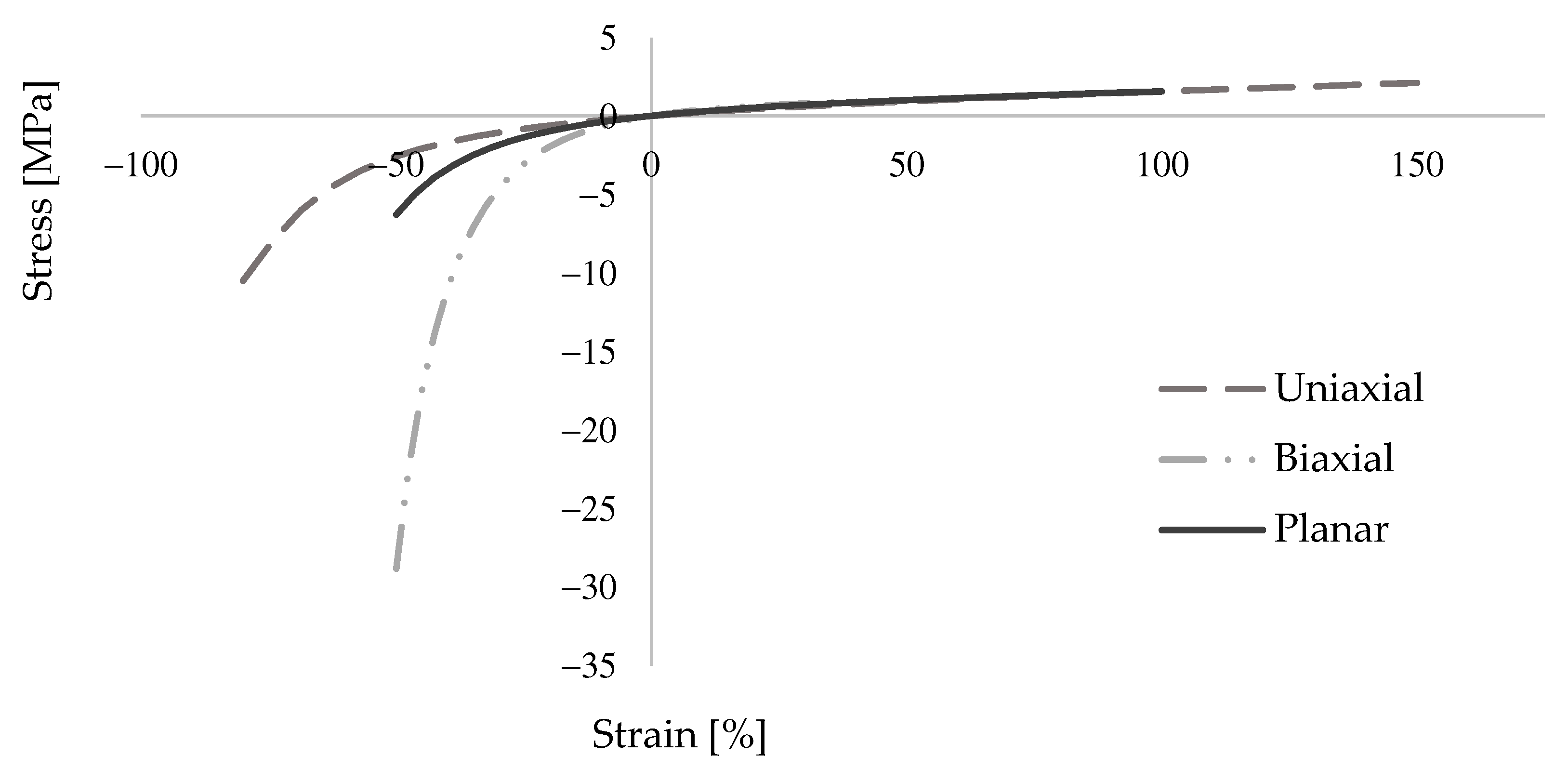
3.1. Material Constitutive Models
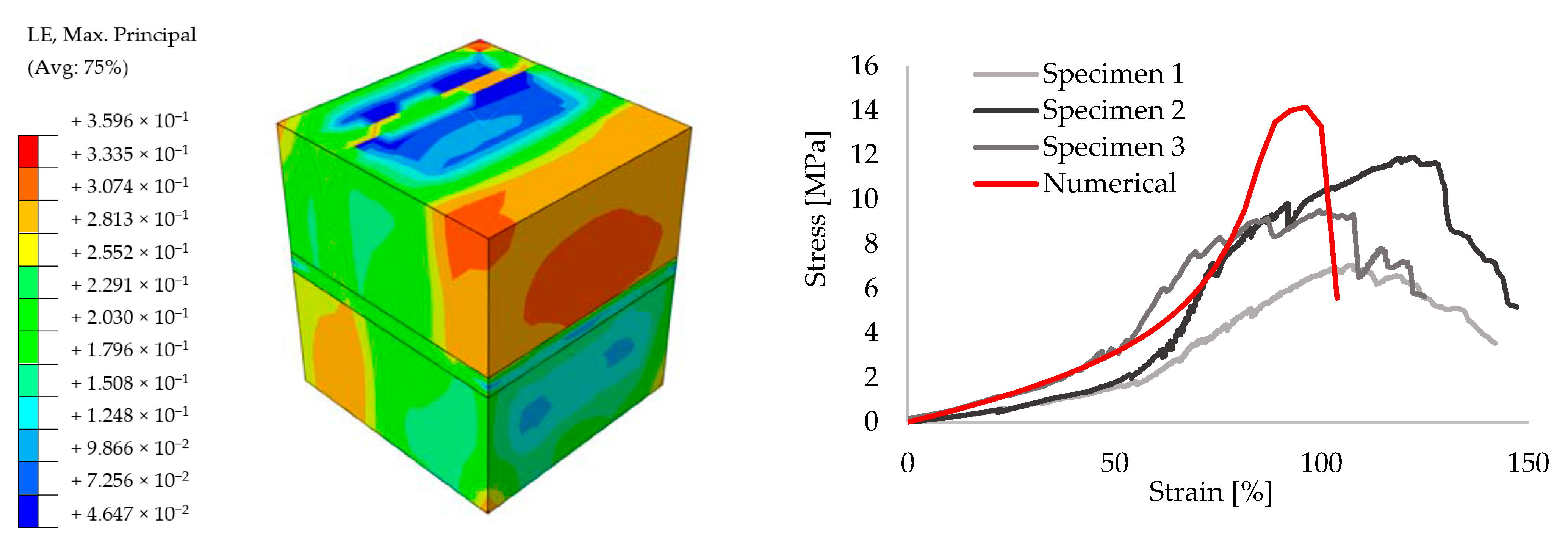
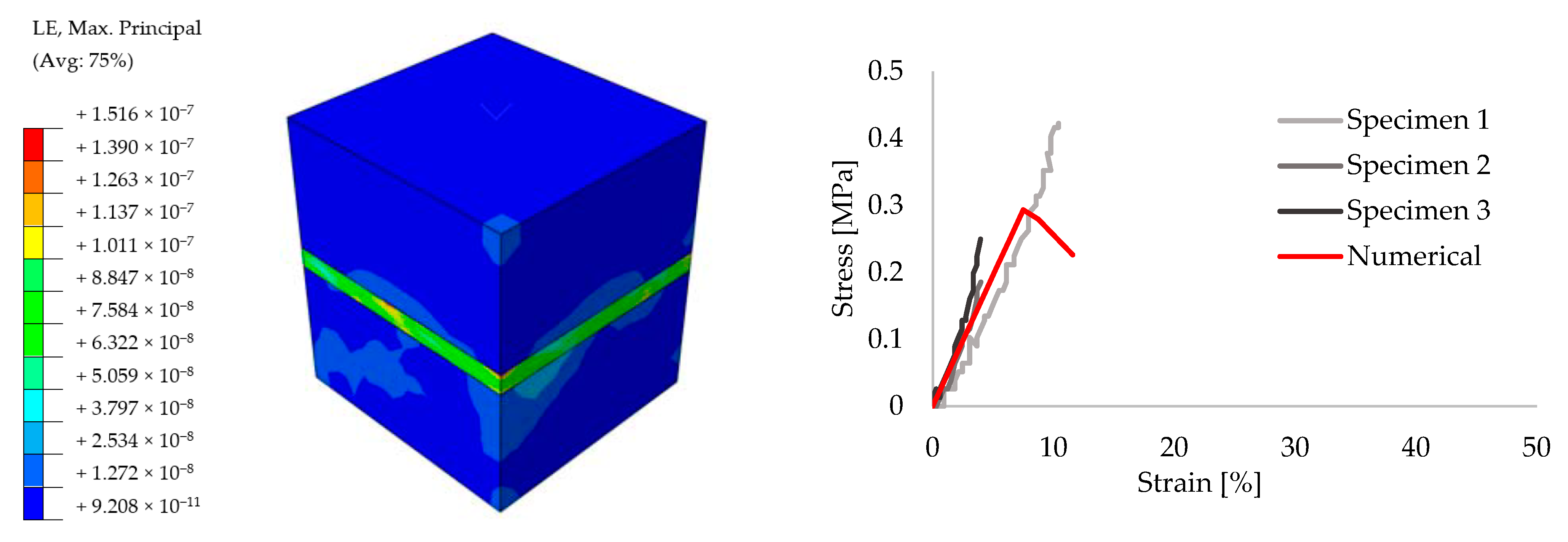
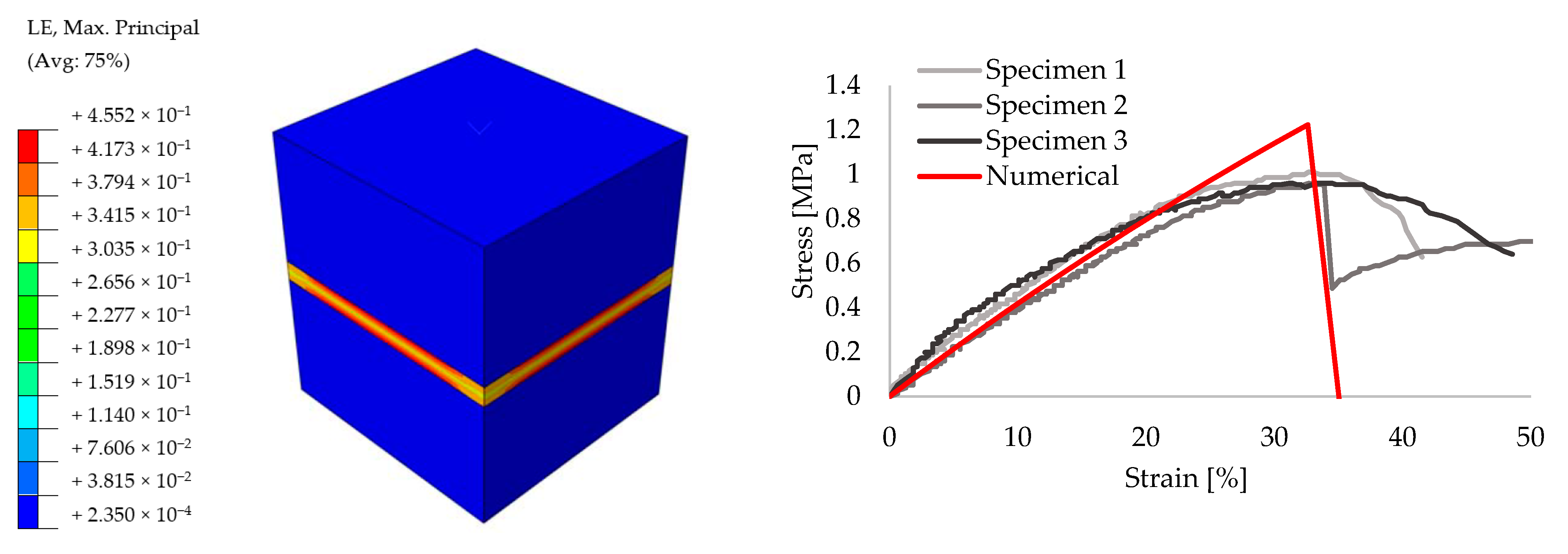
3.2. Small Size Models
3.3. Large Size Models
3.4. Results
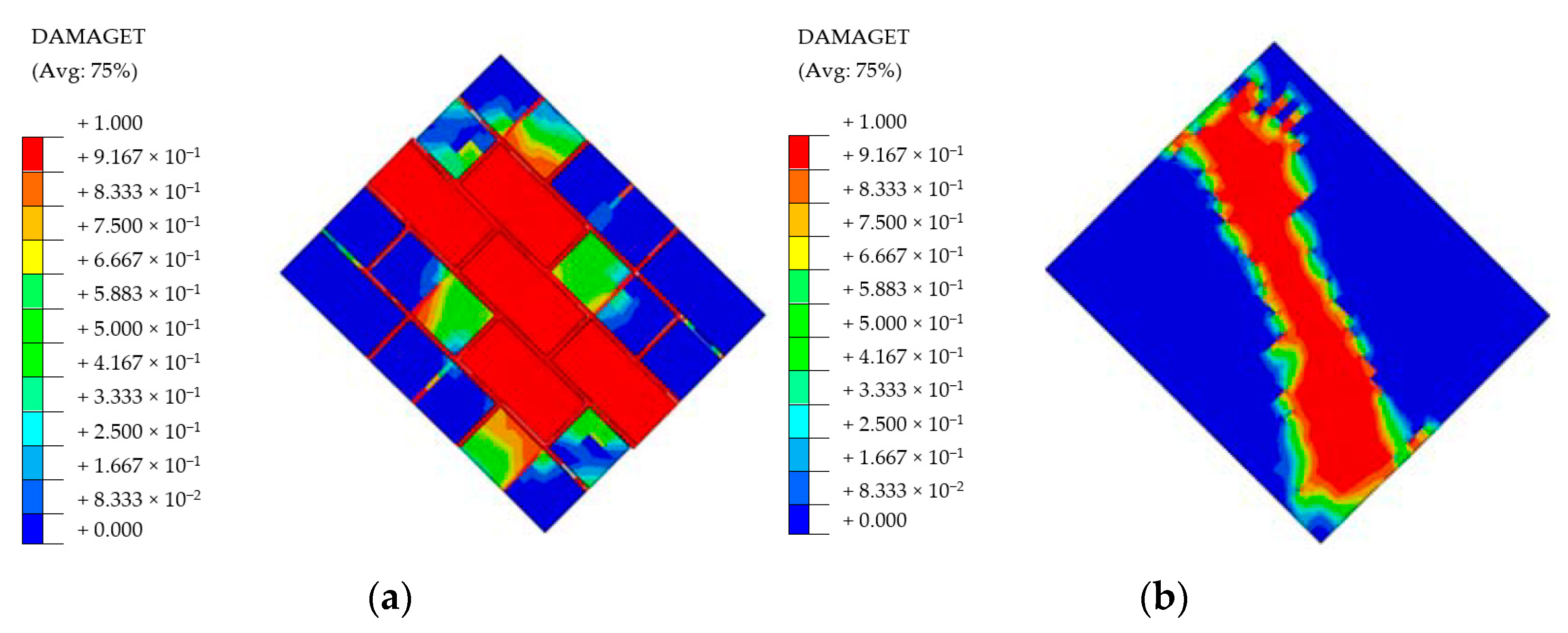
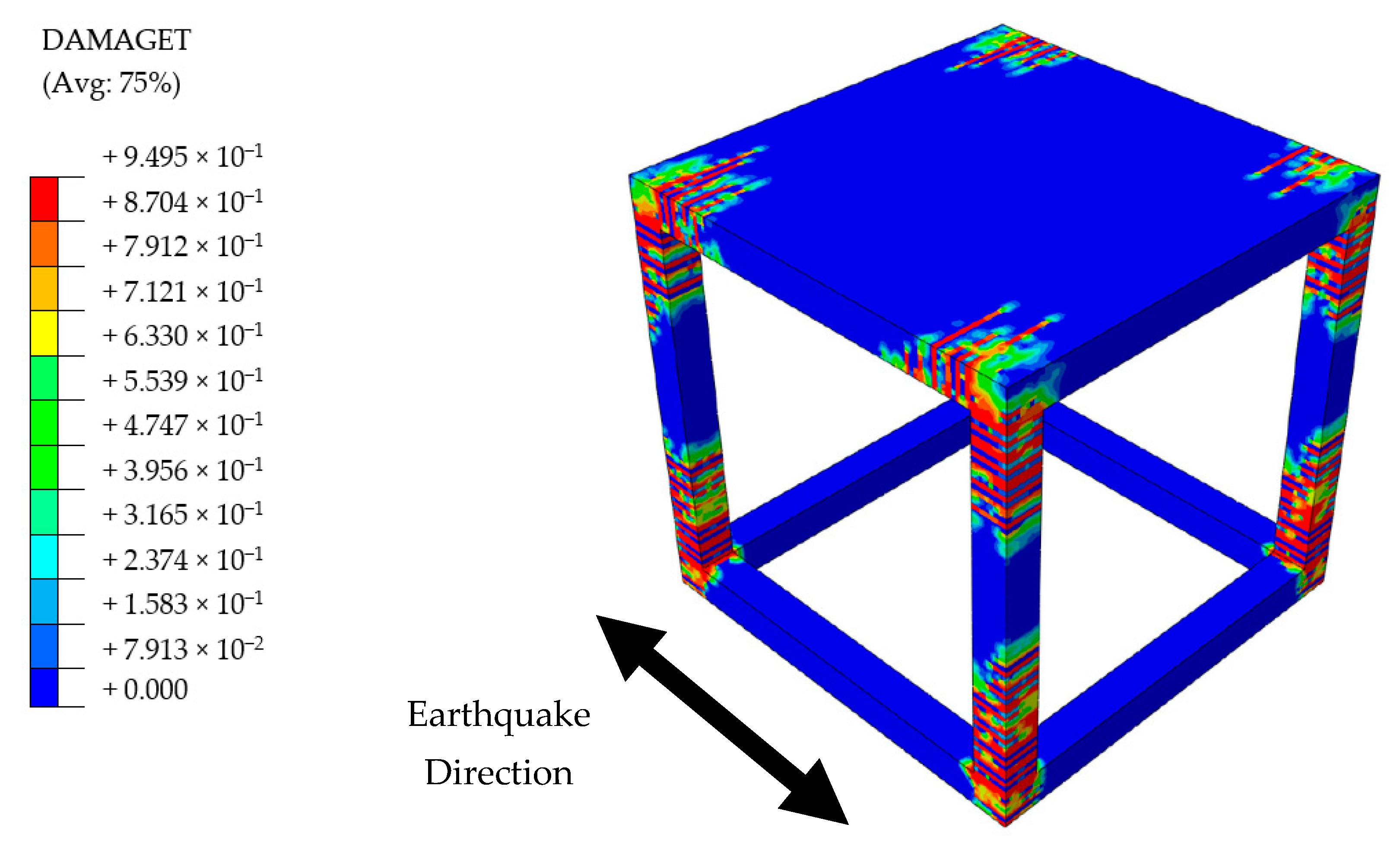
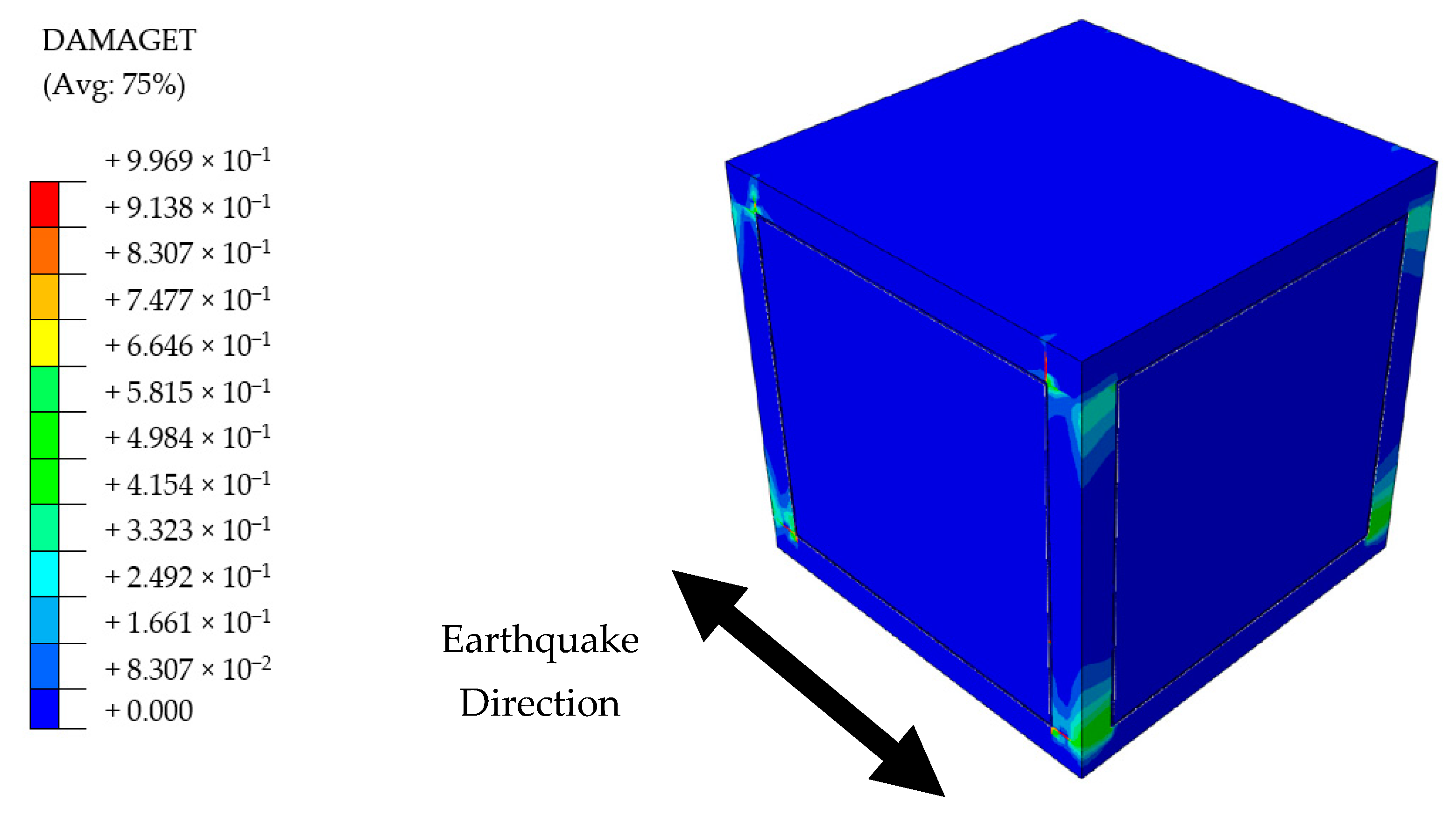
3.4.1. Material Damage Status
3.4.2. Dynamic Characteristics
4. Discussion and Conclusions
- -
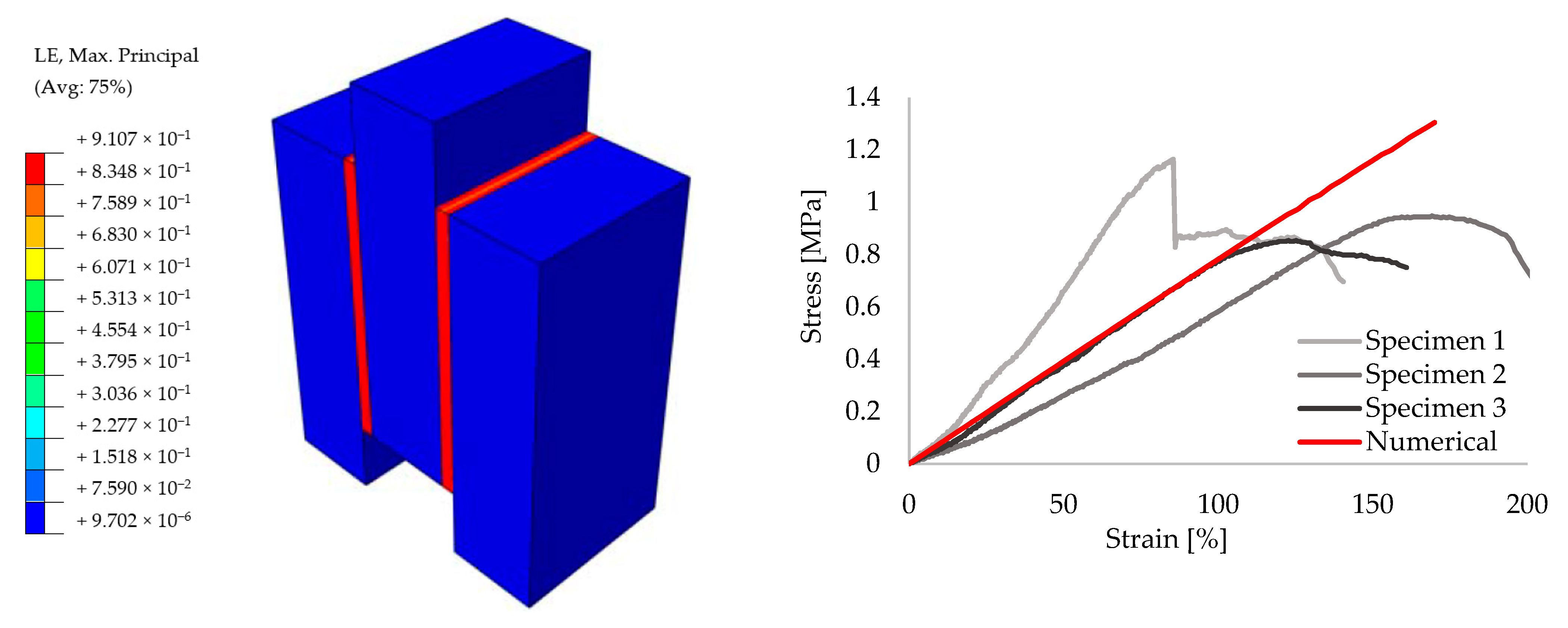
- Large size three-dimensional problems require much information to be taken into account. Therefore, small size specimens were first numerically created in order to obtain an accurate material data for further analyses. Previous experimental results [52] were used while calibrating the models. Once the models provided adequate convergence with the test results, simplified macro wallet tests were performed numerically using the same data. It is shown that PUFJ can be modeled numerically and this approach yields a close match with the test results.
- -
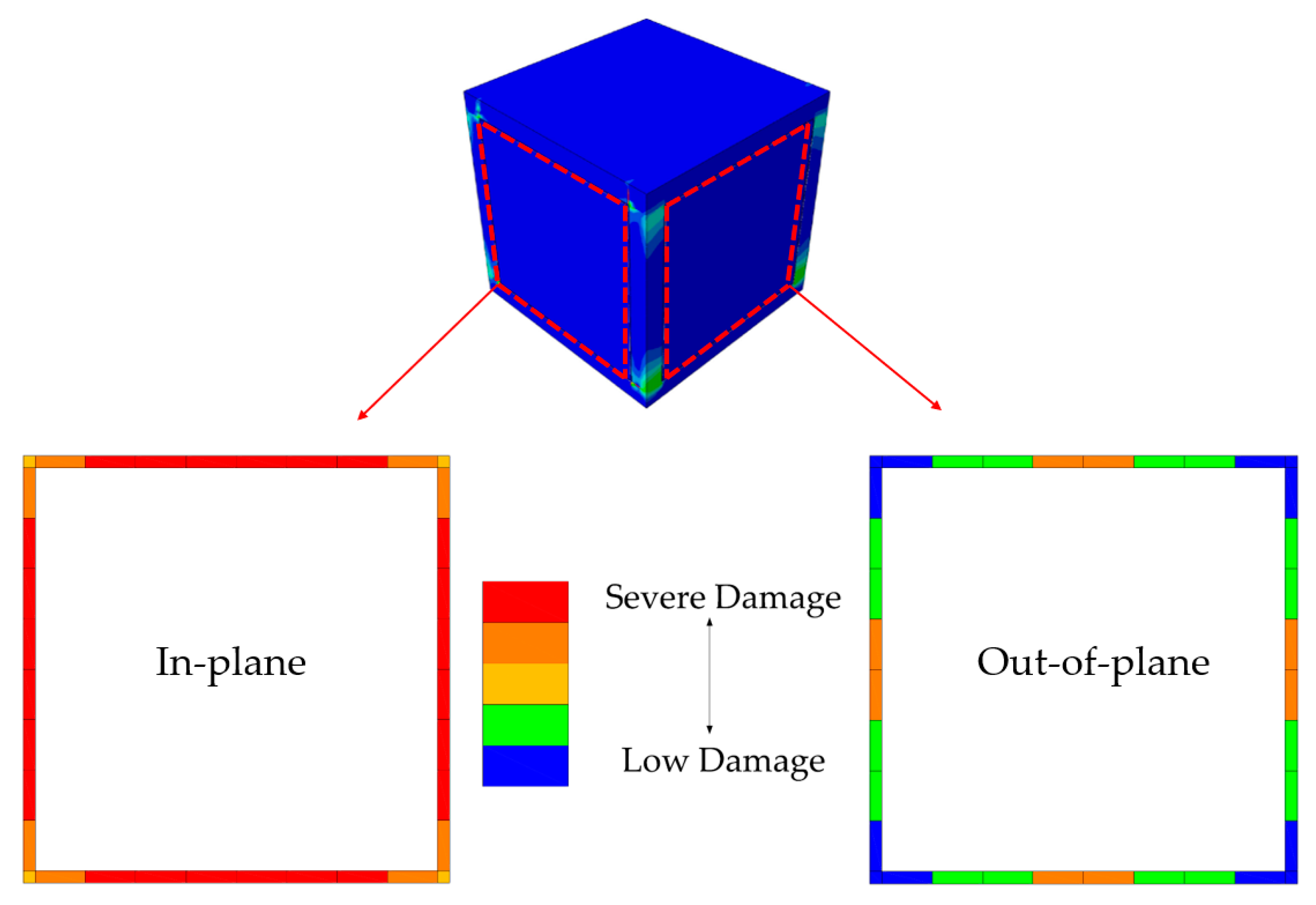
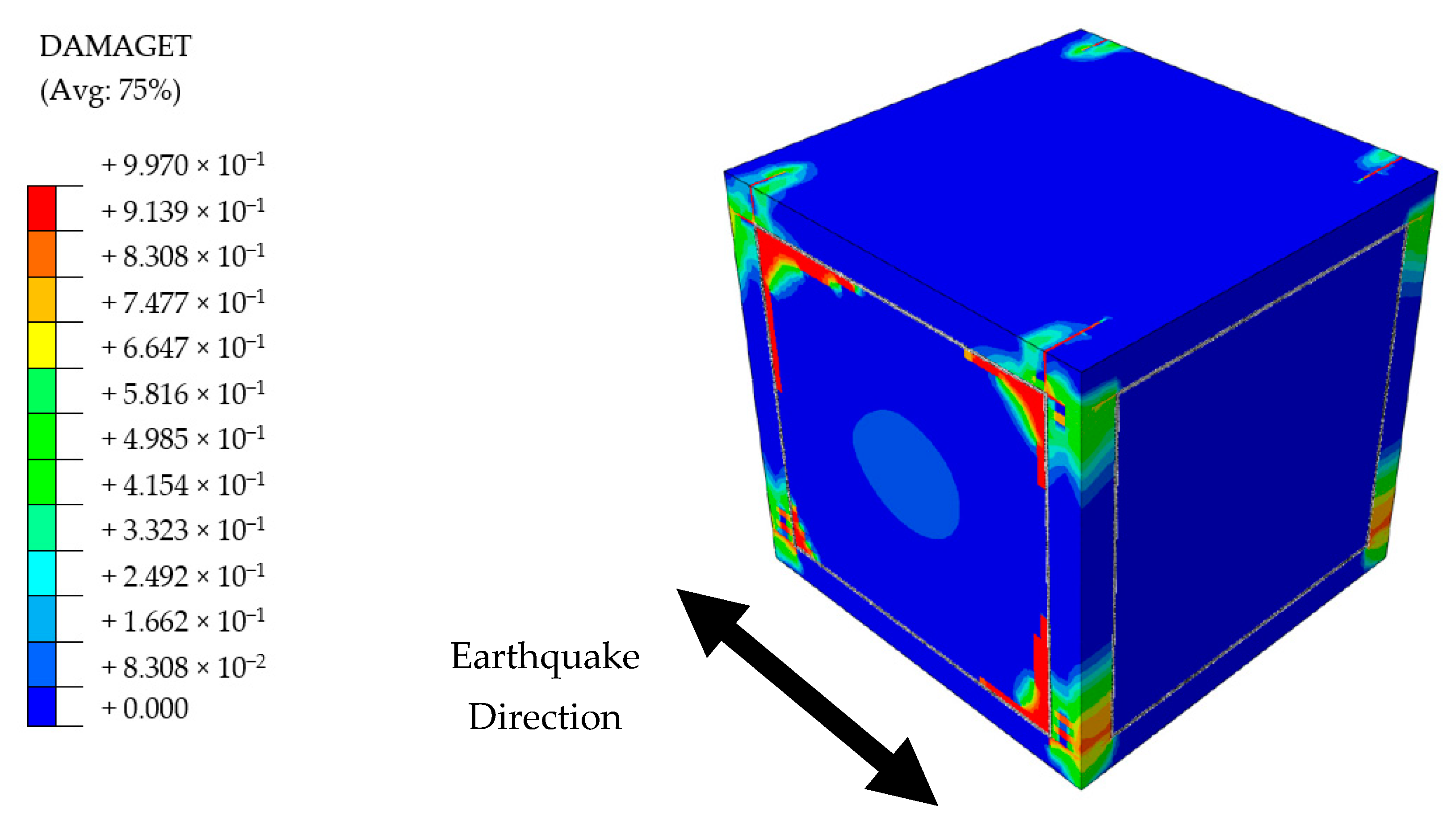
- After this point, the study proceeded by large size models. The structures were biaxially symmetric, hence the seismic excitation was performed only in one direction. Damage levels of each material were investigated at the end of earthquake loading. BF and PUFJ buildings were able to withstand earthquake effects until the end of loading. Meanwhile, TM building suffered severe bonding failure of the mortar around the entire perimeter of masonries, which were located parallel to the loading direction. Especially in real life examples, such in-plane damages progressively cause the total loss of connection strength of the walls and therefore out-of-plane failure is inevitable. Other than that, and excluding the bonding failure in TM building, masonries sustained the internal integrity in both TM and PUFJ buildings, although some tensile corner cracks were observed in the PUFJ type due to the strong bonding features of the polymer. However, it is seen that such damages do not jeopardize the overall structural performance, which was also proven elsewhere [36]. Moreover, all building types experienced concrete cracks in particular regions, mostly concentrated at the column ends as expected. Reinforcement steel did not pass beyond the elastic range, despite the highest stresses were more intense in the vicinity of aforementioned column ends.
- -
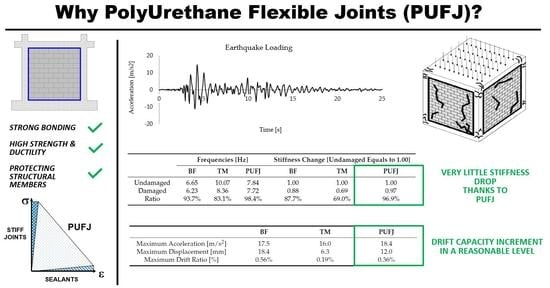
- Frequency analyses were conducted at two stages; at the beginning of horizontal loading for understanding the undamaged state conditions and at the end of earthquake loading for representing the damaged state. Accordingly, TM building had the highest initial frequency value due to the stiff connection around the infill walls, whereas the BF type had the lowest one since there were no walls in this type, which could contribute to the lateral load carrying capacity. The effect of flexible joint implementation was explicit at the damaged states. PUFJ building had very little drop of frequency, meanwhile particularly TM type had relatively harsher frequency reduction. This comparison was more visible when the frequency-based stiffness changes were evaluated. TM building had significant loss of stiffness capacity, reaching to 30% of the initial value. The frequencies obtained during the study have been checked with the results of other researches [65,66]. In Reference [65], the investigated building was damaged, and the measurements and model were made. First natural frequency was equal about 5.5 Hz, but the building was a little bit higher than the structure investigated in the paper. In [66], one-storey undamaged monumental building was investigated. The first natural frequency was equal about 6.5 Hz, which is quite similar to the results listed in Table 2. Furthermore, even though it was not examined in this paper, efficiency of the PUFJ material was tested in [67] against the resonance frequencies. Geometric configuration of the building was very similar of the PUFJ type of building presented in this study, namely a real-size single storey RC structure comprised of brick walls bonded to the frame with PUFJ [37]. It was revealed that various intensities of long-duration (up to 10 min) forced harmonic vibrations were unable to collapse the tested structure, which was previously exposed to the shake table vibrations and was therefore already damaged.
- -
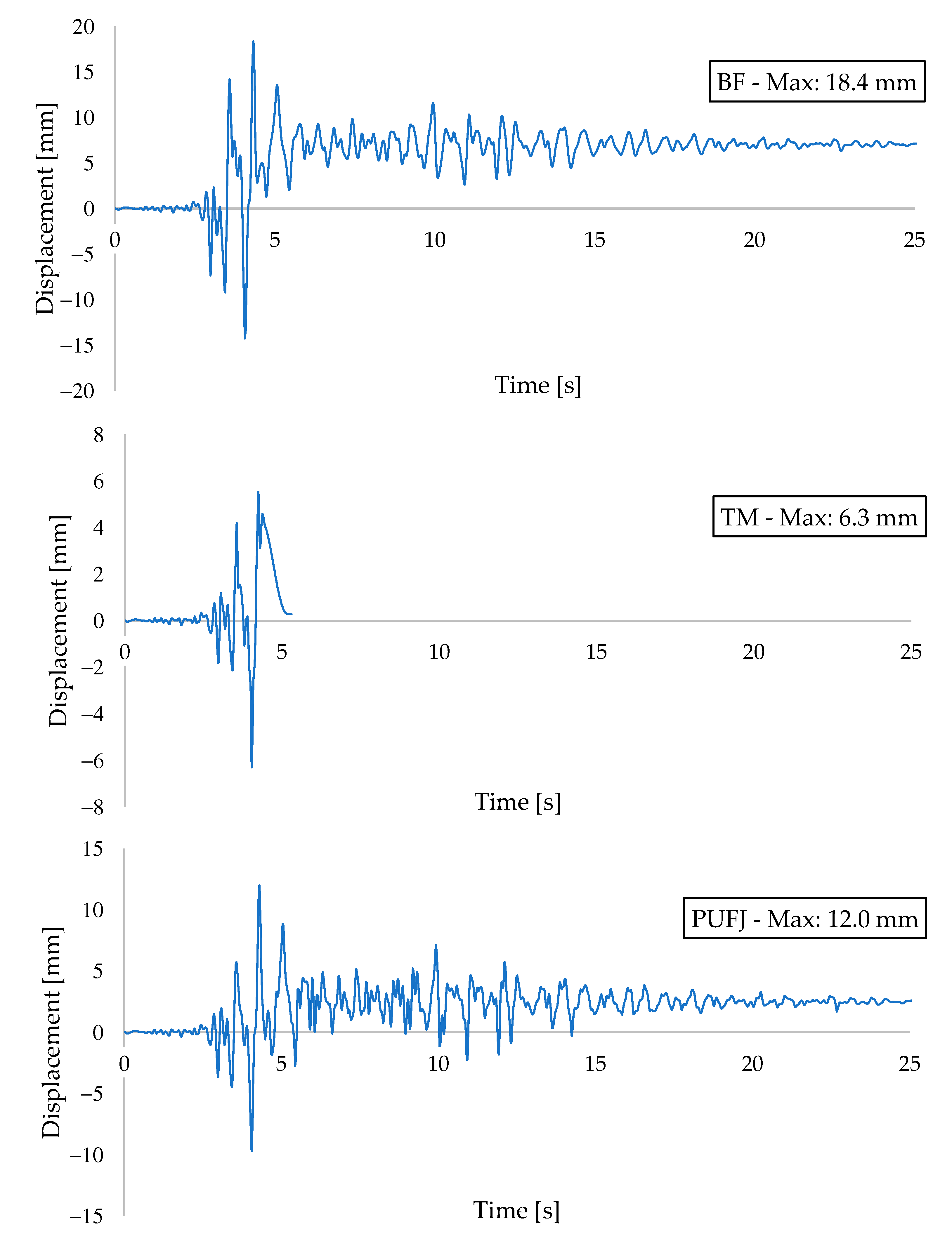
- Acceleration and displacement data was accumulated throughout the loading. The BF building had the highest top slab displacement values and it was visibly the most ductile one among the others. PUFJ type, however, was exposed to the greatest acceleration forces and was able to damp this energy safely. TM building had the lowest peak values of both acceleration and displacement when compared to the other buildings. The system response was weakened due to the bonding failures of the mortar located between the masonries and RC frame.
- -
- As a result of this numerical study and according to the outcomes of previous experimental tests [36,37] of PUFJ, it is seen that the infill wall stability can be sustained even under severe loads. Unlike some proposals, which can be found in the literature and already mentioned in the introduction part of this paper, PUFJ claims to offer a solution to protect the in filled systems against the earthquakes, while at the same time contributing to the drift and strength capacity of the overall system. Implementation of PUFJ is also rather feasible compared to the typical CFRP strips, since any contact surface between the frames and walls can provide sufficient and effective bonding. It can be used on both existing buildings and new to-be-built constructions. For the already built walls, implementation can be done by means of cutting the edges of masonries and injecting the liquid form of polymer in the remained gaps, whereas prefabricated laminates are ideal to be used for the new buildings, which should be placed on the boundaries of frames just before constructing the walls. Implementation details can be found in [36,37]. On the other hand, as previously mentioned, some damages on the wall itself rather than the contact zones might be observed in case of PUFJ implementation. This situation was seen in the experimental tests [36], where hollow-clay bricks were used and also in the numerical analyses of this paper, which predicted potential tensile cracks on the solid clay masonry. While the damages were relatively less compared to the stiff jointed frames and do not seem to pose any risk to the wall stability, further studies on this topic should focus on testing other masonry materials, brick types and different configurations, such as aspect ratios and openings on the walls.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- El-Dakhakhni, W.W.; Elgaaly, M.; Hamid, A.A. Finite element modeling of concrete masonry infilled steel frame. In Proceedings of the 9th Canadian Masonry Symposium, National Research Council (NRC), Ottawa, ON, Canada, June 2001. [Google Scholar]
- Di Trapani, F.; Macalus, G.; Cavaleri, L.; Papia, M. Masonry infills and RC frames interaction: Literature overview and state of the art of macromodeling approach. Eur. J. Environ. Civ. Eng. 2015, 19, 1059–1095. [Google Scholar] [CrossRef]
- Morandi, P.; Hak, S.; Magenes, G. Performance-based interpretation of in-plane cyclic tests on RC frames with strong masonry infills. Eng. Struct. 2018, 156, 503–521. [Google Scholar] [CrossRef]
- Saatcioglu, M.; Mitchell, D.; Tinawi, R.; Gardner, N.J.; Gillies, A.G.; Ghobarah, A.; Anderson, D.L.; Lau, D. The August 17, 1999, Kocaeli (Turkey) earthquake—damage to structures. Can. J. Civ. Eng. 2001, 28, 715–737. [Google Scholar]
- Doğangün, A.; Ural, A.; Sezen, H.; Güney, Y.; Fırat, F.K. The 2011 Earthquake in Simav, Turkey and Seismic Damage to Reinforced Concrete Buildings. Buildings 2013, 3, 173–190. [Google Scholar] [CrossRef]
- Albayrak, U.; Ünlüoğlu, E.; Doğan, M. Effect of infill walls on the seismic performance of an old building. Int. J. Eng. Technol. 2018, 10, 127–131. [Google Scholar] [CrossRef][Green Version]
- Işık, E.; Büyüksaraç, A.; Ekinci, Y.L.; Aydın, M.C.; Harirchian, E. The effect of site-specific design spectrum on earthquake-building parameters: A case study from the Marmara region (NW Turkey). Appl. Sci. 2020, 10, 7247. [Google Scholar] [CrossRef]
- Karami, A.; Shahbazi, S.; Mahdi Kioumarsi, M. A study on the effects of vertical mass irregularity on seismic behavior of BRBFs and CBFs. Appl. Sci. 2020, 10, 8314. [Google Scholar] [CrossRef]
- Miani, M.; Di Marco, C.; Frappa, G.; Pauletta, M. Effects of dissipative systems on the seismic behavior of irregular buildings—Two case studies. Buildings 2020, 10, 202. [Google Scholar] [CrossRef]
- Preti, M.; Migliorati, L.; Giuriani, E. Experimental testing of engineered masonry infill walls for post-earthquake structural damage control. Bull. Earthq. Eng. 2015, 13, 2029–2049. [Google Scholar] [CrossRef]
- Razzaghi, M.S.; Javidnia, M. Evaluation of the effect of infill walls on seismic performance of RC dual frames. Int. J. Adv. Struct. Eng. 2015, 7, 49–54. [Google Scholar] [CrossRef]
- Longo, F.; Wiebe, L.; da Porto, F.; Modena, C. Seismic response history analysis including out-of-plane collapse of unreinforced masonry infill walls in RC frame structures. In Proceedings of the 16th International Brick and Block Masonry Conference, Padova, Italy, 26–30 June 2016. [Google Scholar]
- Crisafulli, F.J.; Carr, A.J. Proposed macro-model for the analysis of infilled frame structures. Bull. N. Z. Soc. Earthq. Eng. 2007, 40, 69–77. [Google Scholar] [CrossRef]
- Asteris, P.G.; Antoniou, S.T.; Sophianopoulos, D.S.; Chrysostomou, C.Z. Mathematical Macromodeling of Infilled Frames: State of the Art. J. Struct. Eng. 2011, 137, 1508–1517. [Google Scholar] [CrossRef]
- FEMA 273. NEHRP Guidelines for the Seismic Rehabilitation of Buildings; Federal Emergency Management Agency: Washington, DC, USA, 1997.
- Eurocode 8: Design of Structures for Earthquake Resistance—Part I: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2005.
- Turkish Seismic Design Code—2018; Turkish Ministry of Interior, Disaster and Emergency Management Presidency: Ankara, Turkey, 2018.
- Asteris, P.G. Lateral stiffness of brick masonry infilled plane frames. J. Struct. Eng. 2003, 129, 1071–1079. [Google Scholar] [CrossRef]
- Kocak, A.; Kalyoncuoglu, A.; Zengin, A. Effect of infill wall and wall openings on the fundamental period of RC buildings. Earthq. Resist. Eng. Struct. IX 2013, 132, 121–131. [Google Scholar]
- Hermanns, L.; Fraile, A.; Alarcon, E.; Alvarez, R. Performance of buildings with masonry infill walls during the 2011 Lorca earthquake. Bull. Earthq. Eng. 2014, 12, 1977–1997. [Google Scholar] [CrossRef]
- Preti, M.; Bolis, V.; Stavridis, A. Design of masonry infill walls with sliding joints for earthquake structural damage control. In Proceedings of the 16th International Brick and Block Masonry Conference, Padova, Italy, 26–30 June 2016. [Google Scholar]
- Totoev, Y.; Al Harthy, A. Semi interlocking masonry as infill wall system for earthquake resistant buildings: A review. J. Eng. Res. 2016, 13, 33–41. [Google Scholar] [CrossRef]
- Misir, I.S.; Ozcelik, O.; Girgin, S.C.; Kahraman, S. Experimental work on seismic behavior of various types of masonry infilled RC frames. Struct. Eng. Mech. 2012, 44, 763–774. [Google Scholar] [CrossRef]
- Vailati, M.; Monti, G. Earthquake-resistant and thermo-insulating infill panel with recycled-plastic joints. In Earthquakes and Their Impact on Society; D’Amico, S., Ed.; Springer Natural Hazards: Cham, Switzerland, 2016; pp. 417–432. [Google Scholar]
- Johnston, H.; Watson, C.; Pampanin, S.; Palermo, A. Shake table testing of an integrated low damage building system. In Proceedings of the 2nd European Conference on Earthquake Engineering and Seismology, Istanbul, Turkey, 25–29 August 2014. [Google Scholar]
- Tasligedik, A.S.; Pampanin, S.; Palermo, A. Low damage seismic solutions for non-structural drywall partitions. In Proceedings of the Vienna Congress on Recent Advances in Earthquake Engineering and Structural Dynamics (VEESD 2013), Vienna, Austria, 28–30 August 2013. [Google Scholar]
- Mohammed, A.A.; Manalo, A.C.; Ferdous, W.; Zhuge, Y.; Vijay, P.V.; Alkinani, A.Q.; Fam, A. State-of-the-art of prefabricated FRP composite jackets for structural repair. Eng. Sci. Technol. Int. J. 2020, 23, 1244–1258. [Google Scholar] [CrossRef]
- Ferdous, W.; Manalo, A.; AlAjarmeh, O.; Mohammed, A.A.; Salih, C.; Yu, P.; Khotbehsara, M.M.; Schubel, P. Static behaviour of glass fibre reinforced novel composite sleepers for mainline railway track. Eng. Struct. 2021, 229, 111627. [Google Scholar] [CrossRef]
- Ferdous, W.; Bai, Y.; Almutairi, A.D.; Satasivam, S.; Jeske, J. Modular assembly of water-retaining walls using GFRP hollow profiles: Components and connection performance. Compos. Struct. 2018, 194, 1–11. [Google Scholar] [CrossRef]
- Erdem, I.; Akyuz, U.; Ersoy, U.; Ozcebe, G. An experimental study on two different strengthening techniques for RC frames. Eng. Struct. 2006, 28, 1843–1851. [Google Scholar] [CrossRef]
- Altin, S.; Anil, O.; Kara, M.E.; Kaya, M. An experimental study on strengthening of masonry infilled RC frames using diagonal CFRP strips. Compos. Part B Eng. 2008, 39, 680–693. [Google Scholar] [CrossRef]
- Yuksel, E.; Ozkaynak, H.; Buyukozturk, O.; Yalcin, C.; Dindar, A.A.; Surmeli, M.; Tastan, D. Performance of alternative CFRP retrofitting schemes used in infilled RC frames. Constr. Build. Mater. 2010, 24, 596–609. [Google Scholar] [CrossRef]
- Kisiel, P. The stiffness and bearing capacity of polymer flexible joint under shear load. Procedia Eng. 2015, 108, 496–503. [Google Scholar] [CrossRef][Green Version]
- Kwiecień, A.; Gams, M.; Rousakis, T.; Viskovic, A.; Korelc, J. Validation of a new hyperviscoelastic model for deformable polymers used for joints between rc frames and masonry infills. Eng. Trans. 2017, 65, 113–121. [Google Scholar]
- Kwiecień, A.; Gams, M.; Viskovic, A.; Kisiel, P.; Korelc, J.; Rousakis, T. Use of polymer flexible joint between RC frames and masonry infills for improved seismic performance. In Proceedings of the SMAR Conference, Zurich, Switzerland, 27–29 August 2017. [Google Scholar]
- Akyildiz, A.T.; Kwiecień, A.; Zając, B.; Triller, P.; Bohinc, U.; Rousakis, T.; Viskovic, A. Preliminary in-plane shear test of infills protected by PUFJ interfaces. In Proceedings of the 17th International Brick/Block Masonry Conference (17thIB2MaC 2020), Kraków, Poland, 5–8 July 2020. [Google Scholar]
- Rousakis, T.; Papadouli, E.; Sapalidis, A.; Vanian, V.; Ilki, A.; Halici, O.F.; Kwiecień, A.; Zając, B.; Hojdys, Ł.; Krajewski, P.; et al. Flexible joints between RC frames and masonry infill for improved seismic performance—Shake table tests. In Proceedings of the 17th International Brick/Block Masonry Conference (17thIB2MaC 2020), Kraków, Poland, 5–8 July 2020. [Google Scholar]
- Zdanowicz, Ł.; Serega, S.; Tekieli, M.; Kwiecień, A. Polymer flexible joint as a repair method of concrete elements: Flexural testing and numerical analysis. Materials 2020, 13, 5732. [Google Scholar] [CrossRef]
- Kwiecień, K.; Kwiecień, A.; Stryszewska, T.; Szumera, M.; Dudek, M. Durability of PS-Polyurethane dedicated for composite strengthening applications in masonry and concrete structures. Polymers 2020, 12, 2830. [Google Scholar] [CrossRef]
- Computers & Structures Inc. SAP2000 v15.2.1. CSI Analysis Reference Manual; Computers & Structures Inc.: Berkeley, CA, USA, 2013. [Google Scholar]
- Dassault Systèmes. Abaqus v2016 Analysis User’s Manual; Dassault Systèmes: Vélizy-Villacoublay, France, 2015. [Google Scholar]
- Hillerborg, A.; Modeer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–782. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–329. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Kytinou, V.K.; Chalioris, C.E.; Karayannis, C.G.; Elenas, A. Effect of steel fibers on the hysteretic performance of concrete beams with steel reinforcement–tests and analysis. Materials 2020, 13, 2923. [Google Scholar] [CrossRef] [PubMed]
- Kytinou, V.K.; Chalioris, C.E.; Karayannis, C.G. Analysis of residual flexural stiffness of steel fiber–reinforced concrete beams with steel reinforcement. Materials 2020, 13, 2698. [Google Scholar] [CrossRef] [PubMed]
- Raza, A.; Khan, Q.Z.; Ahmad, A. Numerical investigation of load carrying capacity of GFRP—Reinforced rectangular concrete members using CDP model in ABAQUS. Adv. Civil Eng. 2019, 21, doi. [Google Scholar] [CrossRef]
- Birtel, V.; Mark, P. Parameterised Finite Element Modelling of RC Beam Shear Failure. In Proceedings of the 19th Annual International ABAQUS Users’ Conference, Boston, MA, USA, 23–25 May 2006. [Google Scholar]
- Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004.
- FIB Model Code for Concrete Structures; International Federation for Structural Concrete: Lausanne, Switzerland, 2010.
- Kaushik, H.B.; Rai, D.C.; Jain, S.K. Stress-strain characteristics of clay brick masonry under uniaxial compression. J. Mater. Civ. Eng. 2007, 19, 728–739. [Google Scholar] [CrossRef]
- Viskovic, A.; Zuccarino, L.; Kwiecień, A.; Zając, B.; Gams, M. Quick seismic protection of weak masonry infilling in filled framed structures using flexible joints. Key Eng. Mater. 2017, 747, 628–637. [Google Scholar] [CrossRef]
- Szczecina, M.; Winnicki, A. Selected aspects of computer modeling of reinforced concrete structures. Arch. Civ. Eng. 2016, 62, 51–64. [Google Scholar] [CrossRef]
- Rewers, I. Numerical analysis of RC beam with high strength steel reinforcement using CDP model. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 1–10. [Google Scholar] [CrossRef]
- Kisiel, P. Model Approach for Polymer Flexible Joints in Precast Elements Joints of Concrete Pavements. Ph.D. Thesis, CUT, Cracow, Poland, 2018. [Google Scholar]
- Kwiecień, A.; Zając, B.; Jankowski, R. Static and dynamic properties of a flexible joint working in cracked historical masonries. In Proceedings of the VI International Conference on Structural Analysis of Historic Construction, SAHC08, Bath, UK, 2–4 July 2008. [Google Scholar]
- Spears, R.E.; Jensen, S.R. Approach for selection of Rayleigh damping parameters used for time history analysis. In Proceedings of the ASME Pressure Vessels and Piping Division Conference, Prague, Czech Republic, 26–30 July 2009. [Google Scholar]
- Eurocode 6: Design of Masonry Structures—Part 1–1: General Rules for Reinforced and Unreinforced Masonry Structures; European Committee for Standardization: Brussels, Belgium, 2005.
- Bernal, D.; Döhler, M.; Kojidi, S.M.; Kwan, K.; Liu, Y. First mode damping ratios for buildings. Earthq. Spectra 2015, 31, 367–381. [Google Scholar] [CrossRef]
- Adnan, A.; Ramli, M.Z.; Abd Razak, S.K.M. Disaster Management and Mitigation for Earthquakes: Are We Ready? In Proceedings of the 9th Asia Pacific Structural Engineering and Construction Conference (APSEC 2015), Kuala Lumpur, Malaysia, 3–5 November 2015. [Google Scholar]
- Blutndell, D.J. Earthquake hazard and risk mitigation. Contemp. Phys. 1981, 22, 335–347. [Google Scholar] [CrossRef]
- Tucker, B.E.; Trumbull, J.G.; Wyss, S.J. Some remarks concerning worldwide urban earthquake hazard and earthquake hazard mitigation. In Issues in Urban Earthquake Risk. NATO ASI Series (Series E: Applied Sciences); Tucker, B.E., Erdik, M., Hwang, C.N., Eds.; Springer: Dordrecht, The Netherlands, 1994; Volume 271, pp. 1–10. [Google Scholar] [CrossRef]
- Shafique, M.; Khan, M.Y. Earthquake Hazards and Risk Mitigation in Pakistan. In Disaster Risk Reduction Approaches in Pakistan; Atta-Ur-Rahman, Khan, A.N., Shaw, R., Eds.; Springer: Tokyo, Japan, 2015; pp. 101–117. [Google Scholar] [CrossRef]
- Thomas, F.; Chaney, R.; Tseng, R. Modelling earthquake hazard. In The Physics of Destructive Earthquakes; Morgan & Claypool Publishers: San Rafael, CA, USA, 2018. [Google Scholar] [CrossRef]
- Lipski, Z.; Mrozek, M.; Mrozek, D. Evolution of the building natural frequency spectrum defined during paraseismical excitation. In Proceedings of the 10th International Conference on New Trends in Statics and Dynamics of Buildings, Bratislava, Slovakia, 3–5 October 2012. [Google Scholar]
- Valašková, V.; Papán, D.; Papánová, Z. Traffic seismicity effect on monumental buildings—Results of case studies. J. Meas. Eng. 2018, 6, 210–217. [Google Scholar] [CrossRef]
- Kwiecień, A.; Rakicevic, Z.; Bogdanovic, A.; Manojlovski, F.; Poposka, A.; Shoklarovski, A.; Rousakis, T.; Ilki, A.; Gams, M.; Viskovic, A. PUFJ and FRPU earthquake protection of infills tested in resonance. In Proceedings of the 1st Croatian Conference on Earthquake Engineering (1CroCEE), Zagreb, Croatia, 22–24 March 2021. [Google Scholar]


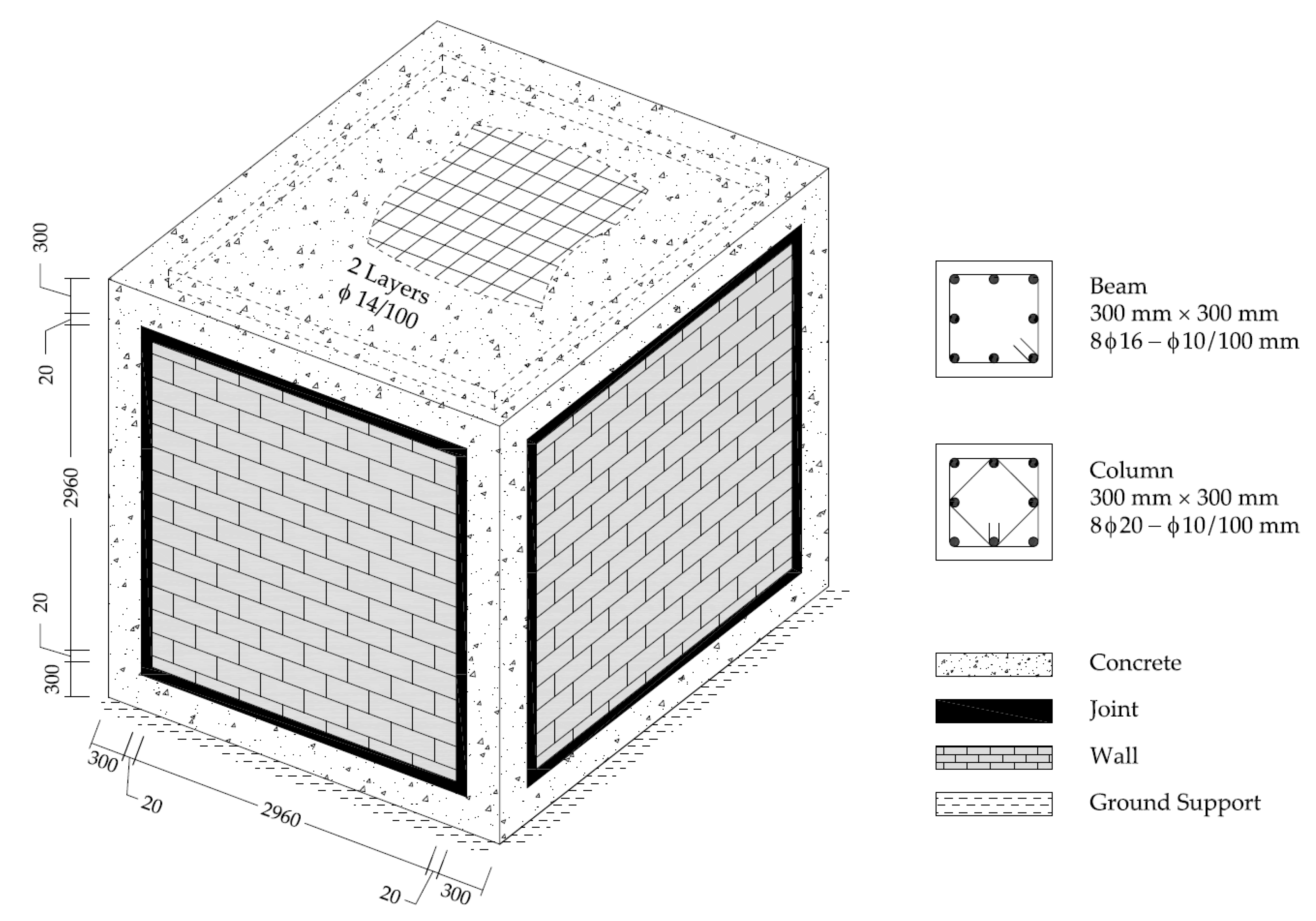

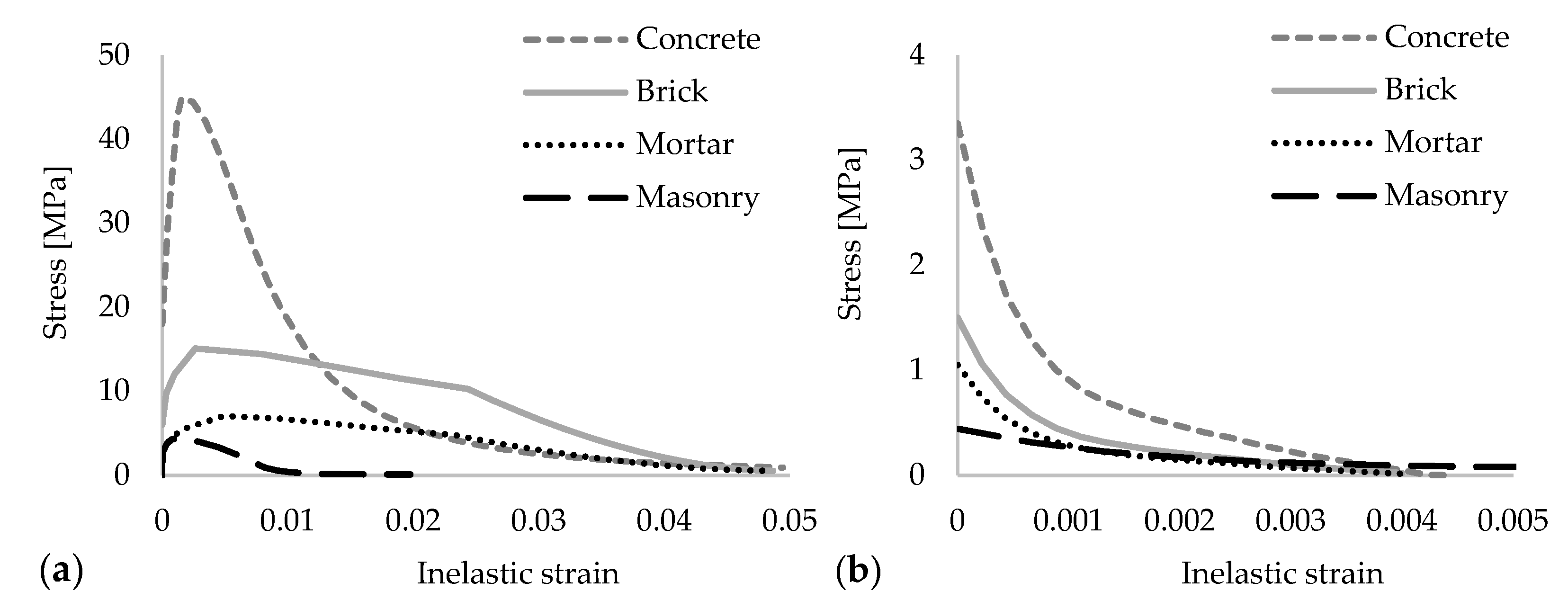

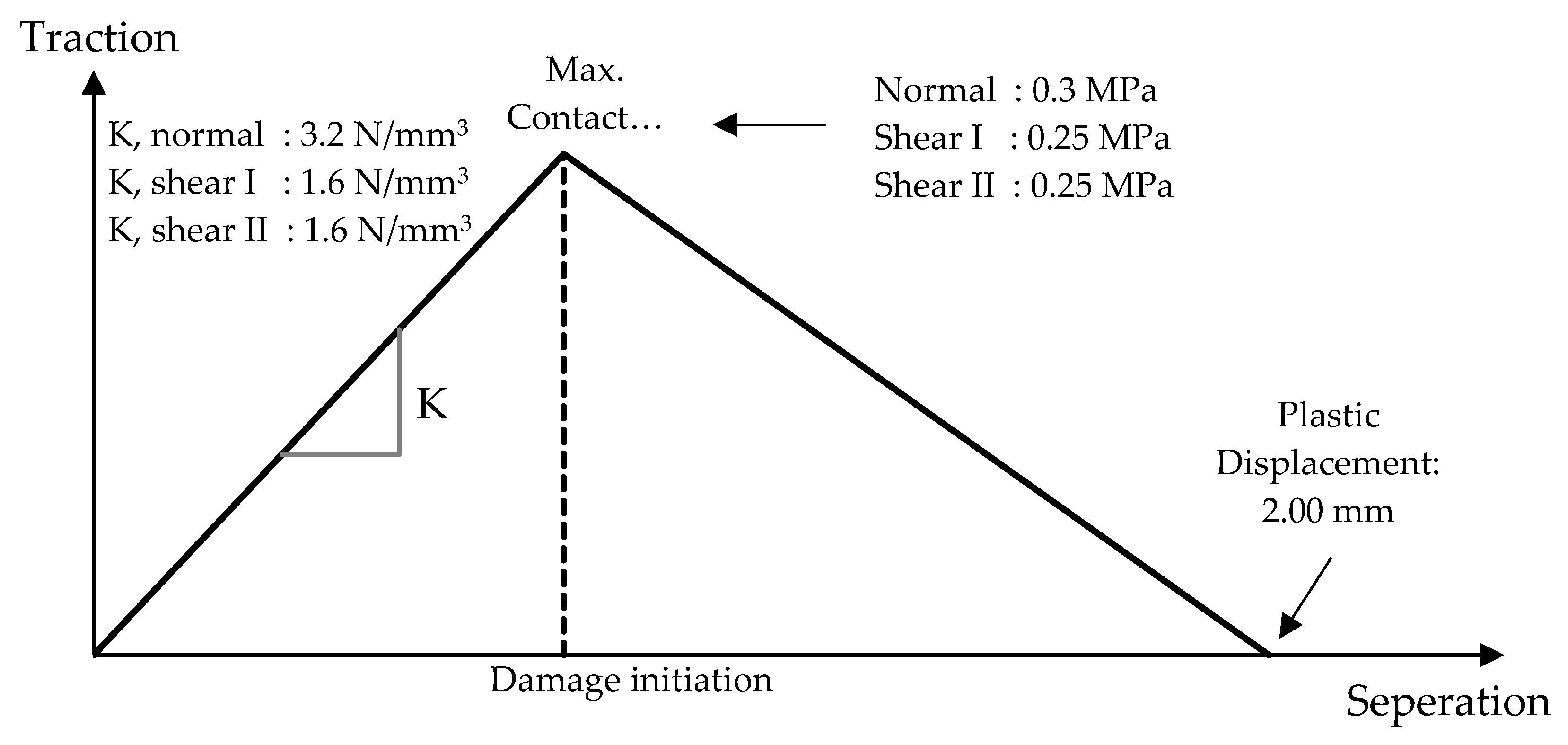








| Elastic Properties | CDP Properties | ||||||
|---|---|---|---|---|---|---|---|
| E [Mpa] | ν | Ψ | ε | σb0/σc0 | Kc | Viscosity Parameter | |
| Brick Unit | 4500 | 0.15 | 30 | 0.1 | 1.16 | 0.67 | 0.001 |
| Concrete | 35,000 | 0.2 | 30 | 0.1 | 1.16 | 0.67 | 0.0001 |
| Mortar | 1400 | 0.2 | 30 | 0.1 | 1.16 | 0.67 | 0.0001 |
| Masonry | 1000 | 0.25 | 30 | 0.1 | 1.16 | 0.67 | 0.05 |
| E | Young’s Modulus | ||||||
| ν | Poisson’s Ratio | ||||||
| Ψ | Dilatation Angle | ||||||
| ε | Flow potential eccentricity | ||||||
| σb0/σc0 | Equibiaxial to uniaxial compressive yield stress ratio | ||||||
| Kc | Stress invariant ratio | ||||||
| Frequencies [Hz] | Stiffness Change [Undamaged Equals to 1.00] | |||||
|---|---|---|---|---|---|---|
| BF | TM | PUFJ | BF | TM | PUFJ | |
| Undamaged | 6.65 | 10.07 | 7.84 | 1.00 | 1.00 | 1.00 |
| Damaged | 6.23 | 8.36 | 7.72 | 0.88 | 0.69 | 0.97 |
| Ratio | 93.7% | 83.1% | 98.4% | 87.7% | 69.0% | 96.9% |
| BF | TM | PUFJ | |
|---|---|---|---|
| Maximum Acceleration [m/s2] | 17.5 | 16.0 | 18.4 |
| Maximum Displacement [mm] | 18.4 | 6.3 | 12.0 |
| Maximum Drift Ratio [%] | 0.56% | 0.19% | 0.36% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akyildiz, A.T.; Kowalska-Koczwara, A.; Hojdys, Ł. Seismic Protection of RC Buildings by Polymeric Infill Wall-Frame Interface. Polymers 2021, 13, 1577. https://doi.org/10.3390/polym13101577
Akyildiz AT, Kowalska-Koczwara A, Hojdys Ł. Seismic Protection of RC Buildings by Polymeric Infill Wall-Frame Interface. Polymers. 2021; 13(10):1577. https://doi.org/10.3390/polym13101577
Chicago/Turabian StyleAkyildiz, Ahmet Tugrul, Alicja Kowalska-Koczwara, and Łukasz Hojdys. 2021. "Seismic Protection of RC Buildings by Polymeric Infill Wall-Frame Interface" Polymers 13, no. 10: 1577. https://doi.org/10.3390/polym13101577
APA StyleAkyildiz, A. T., Kowalska-Koczwara, A., & Hojdys, Ł. (2021). Seismic Protection of RC Buildings by Polymeric Infill Wall-Frame Interface. Polymers, 13(10), 1577. https://doi.org/10.3390/polym13101577