3D Printing of Polymeric Multi-Layer Micro-Perforated Panels for Tunable Wideband Sound Absorption
Abstract
1. Introduction
2. Materials and Methods
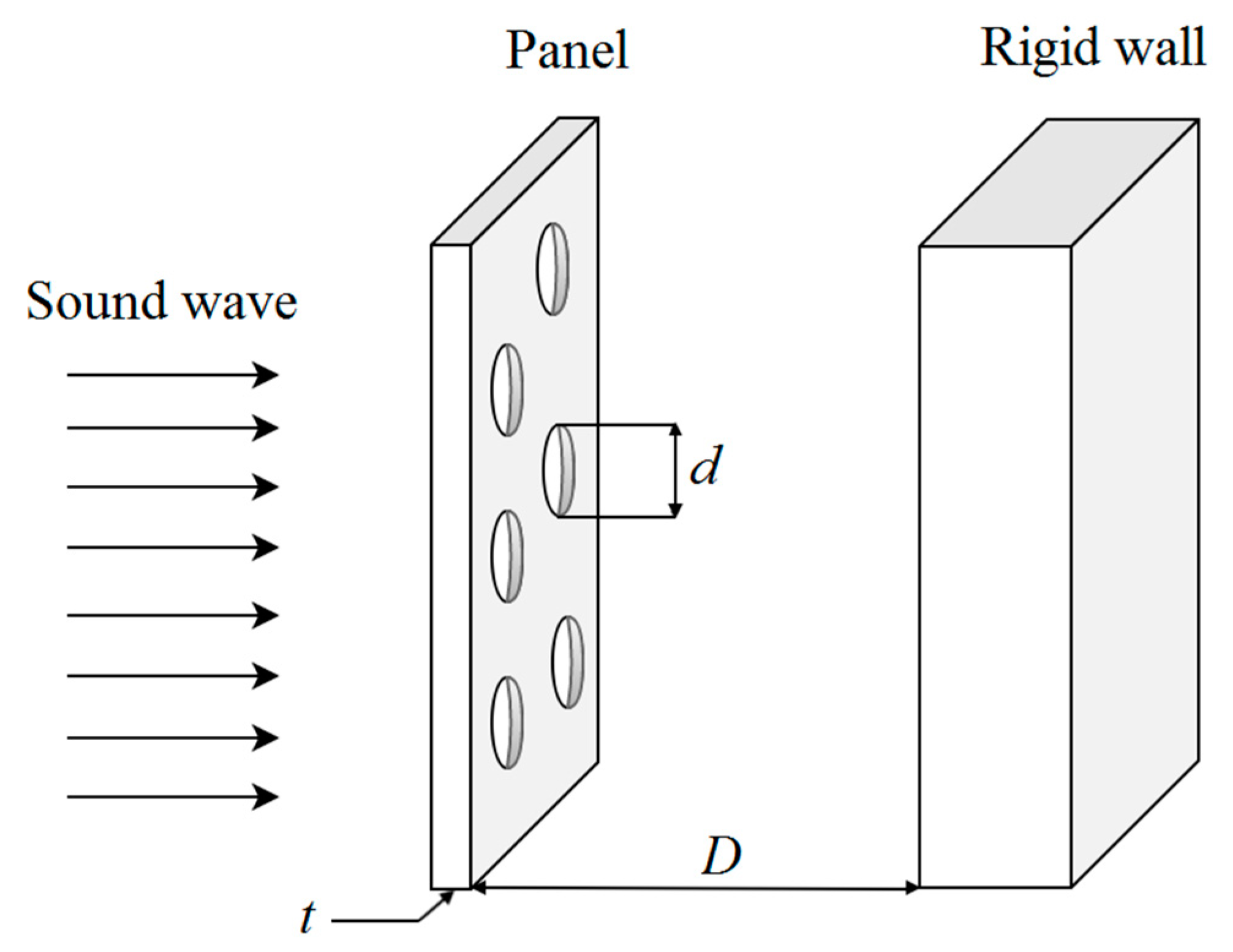
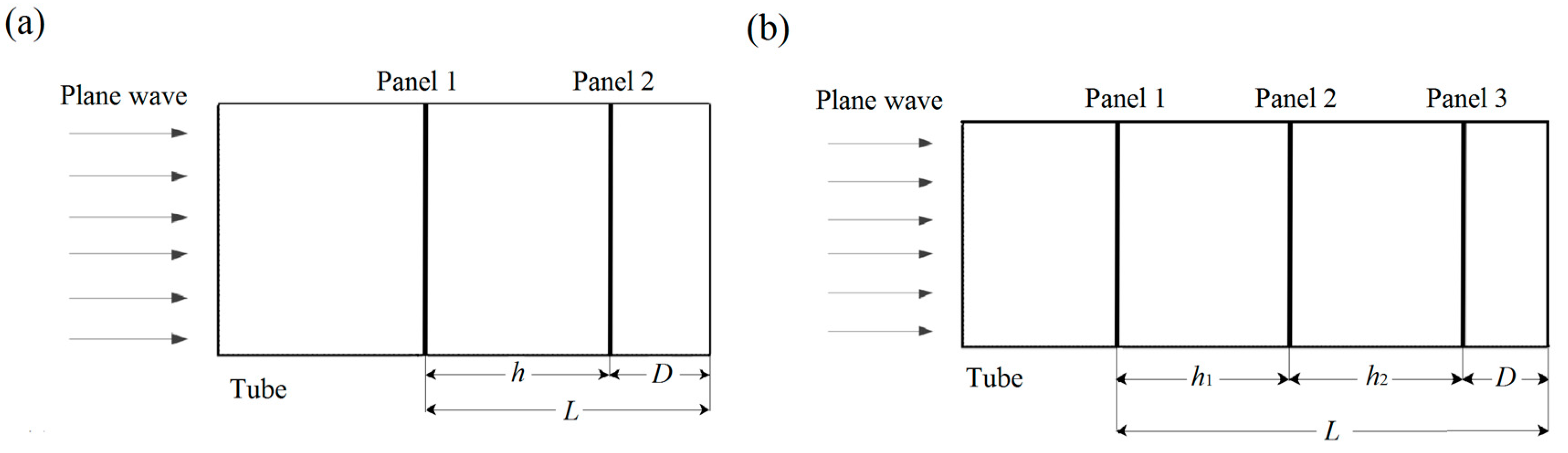
2.1. Theoretical and Numerical Methods
2.2. Experimental Method
3. Results and Discussion
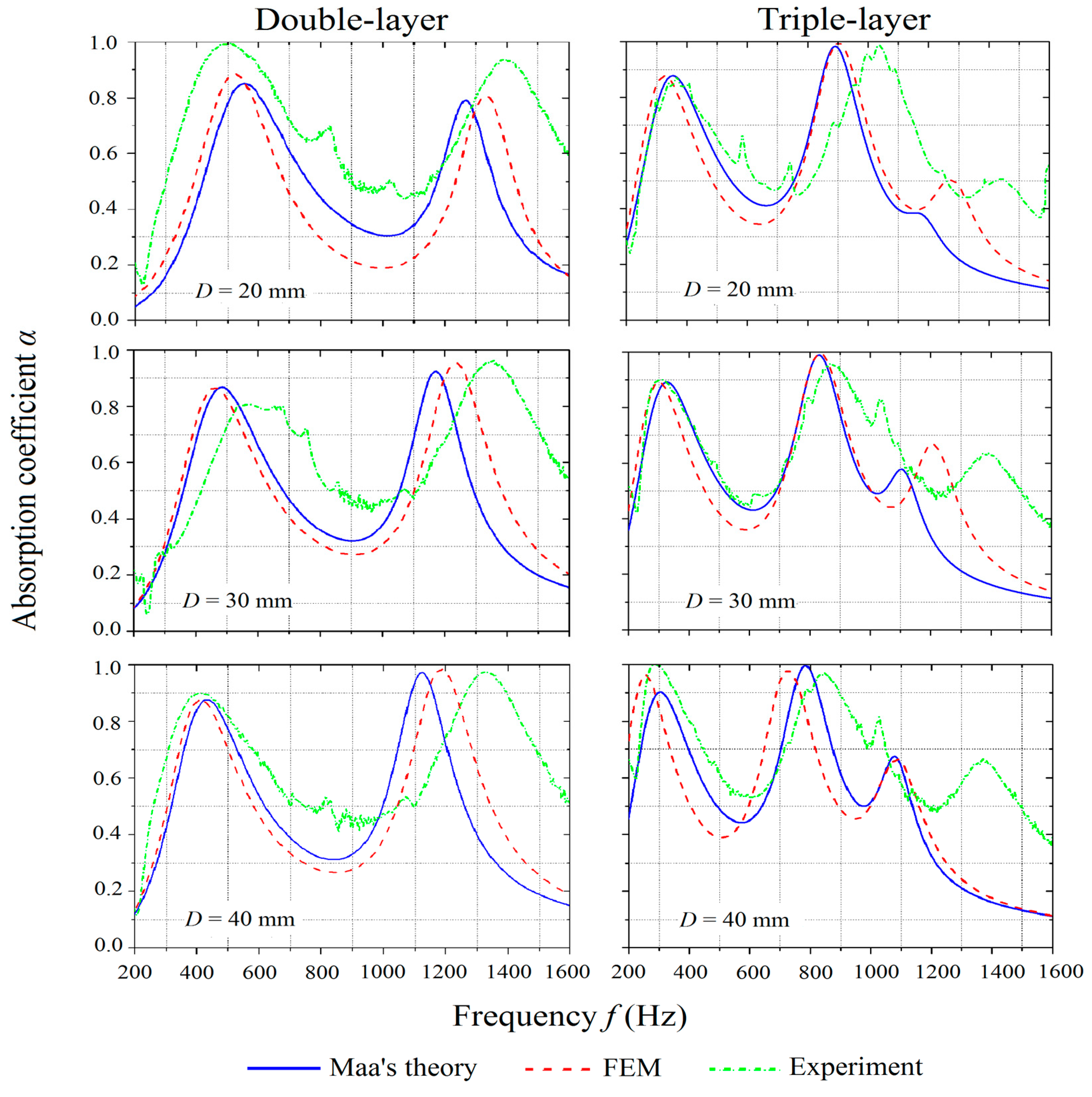
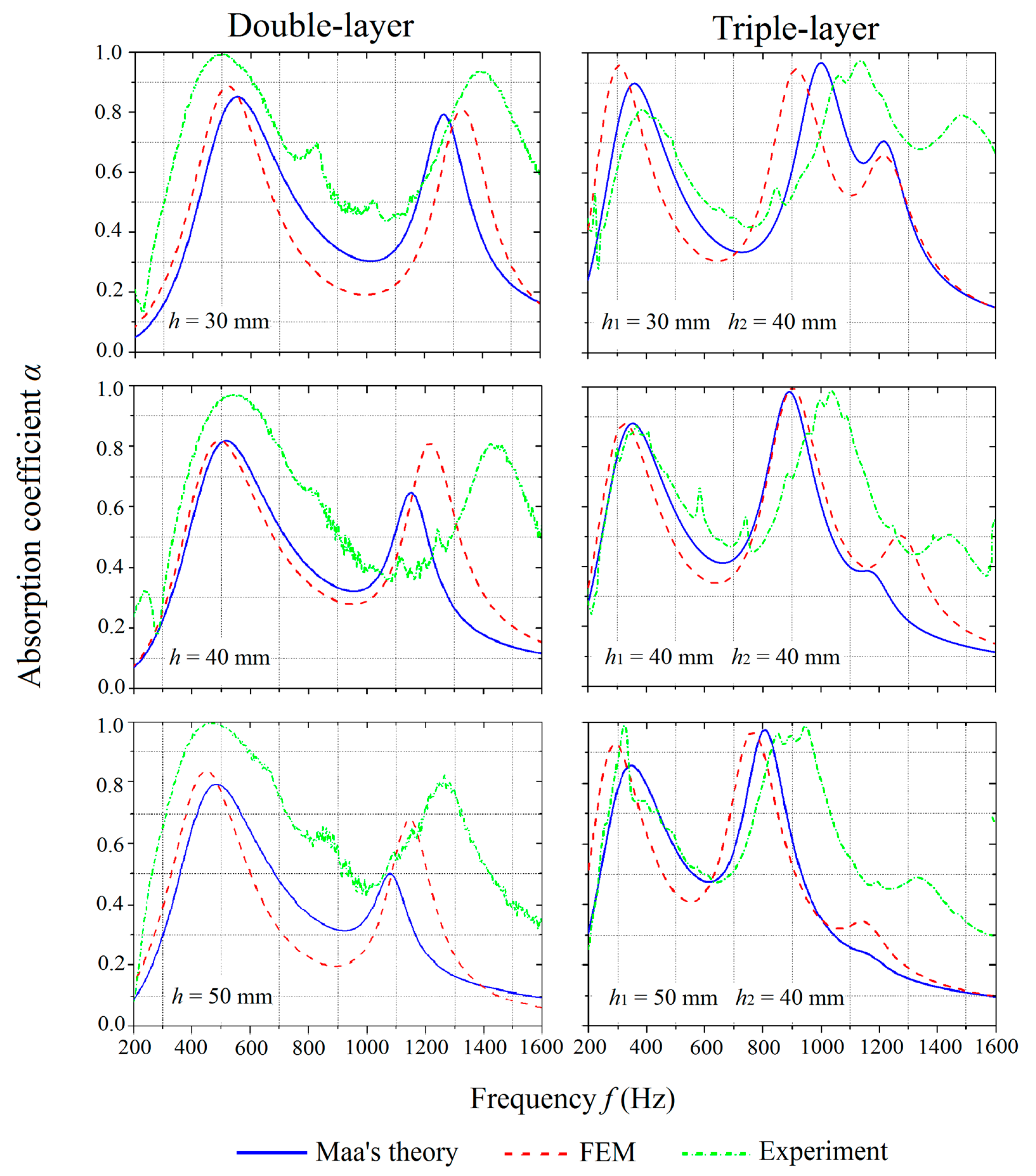
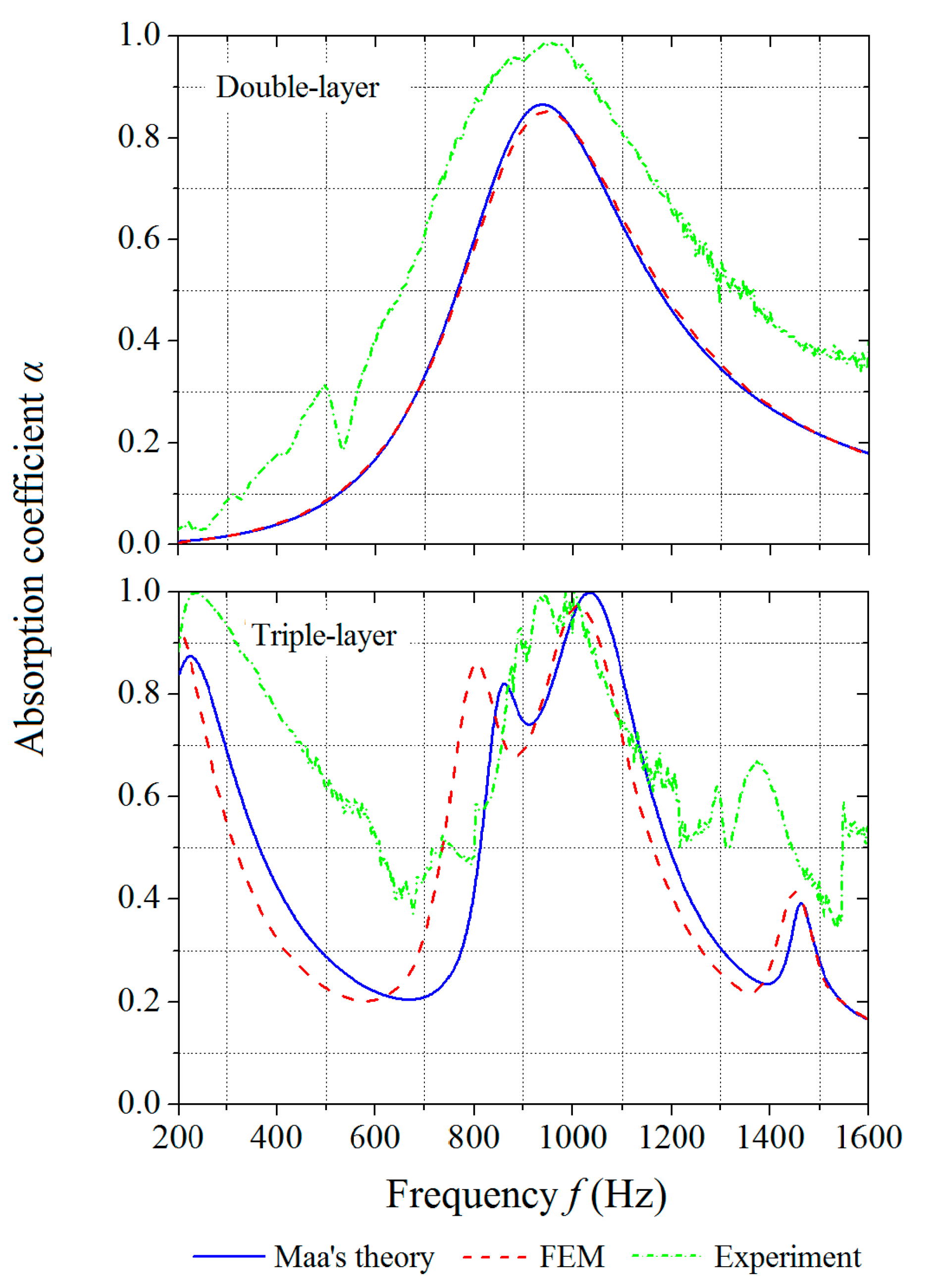
3.1. Effect of the Number of Layers
3.2. Effect of the Air Gap Distance
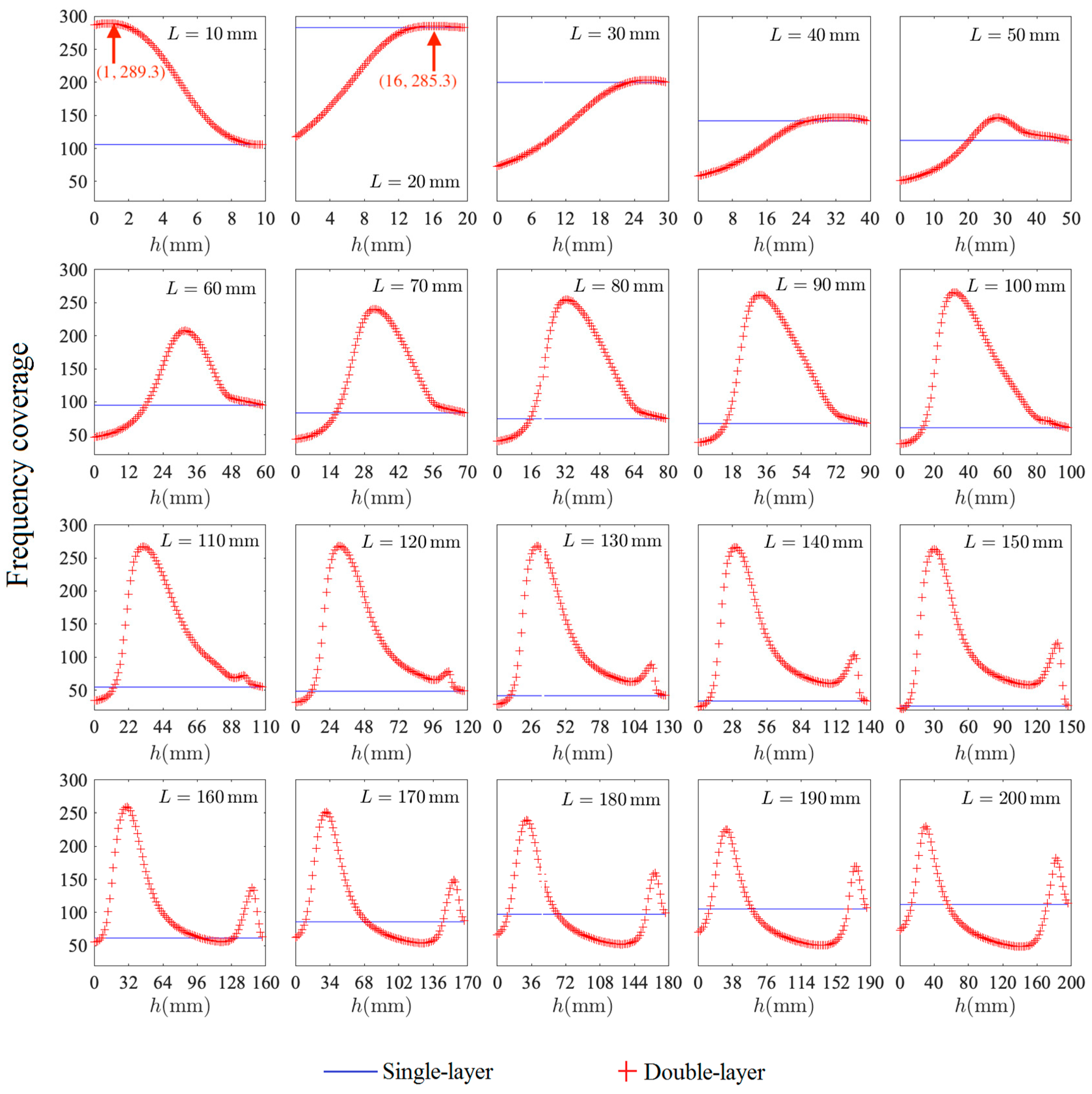
3.3. Effect of the Inter-Layer Distance
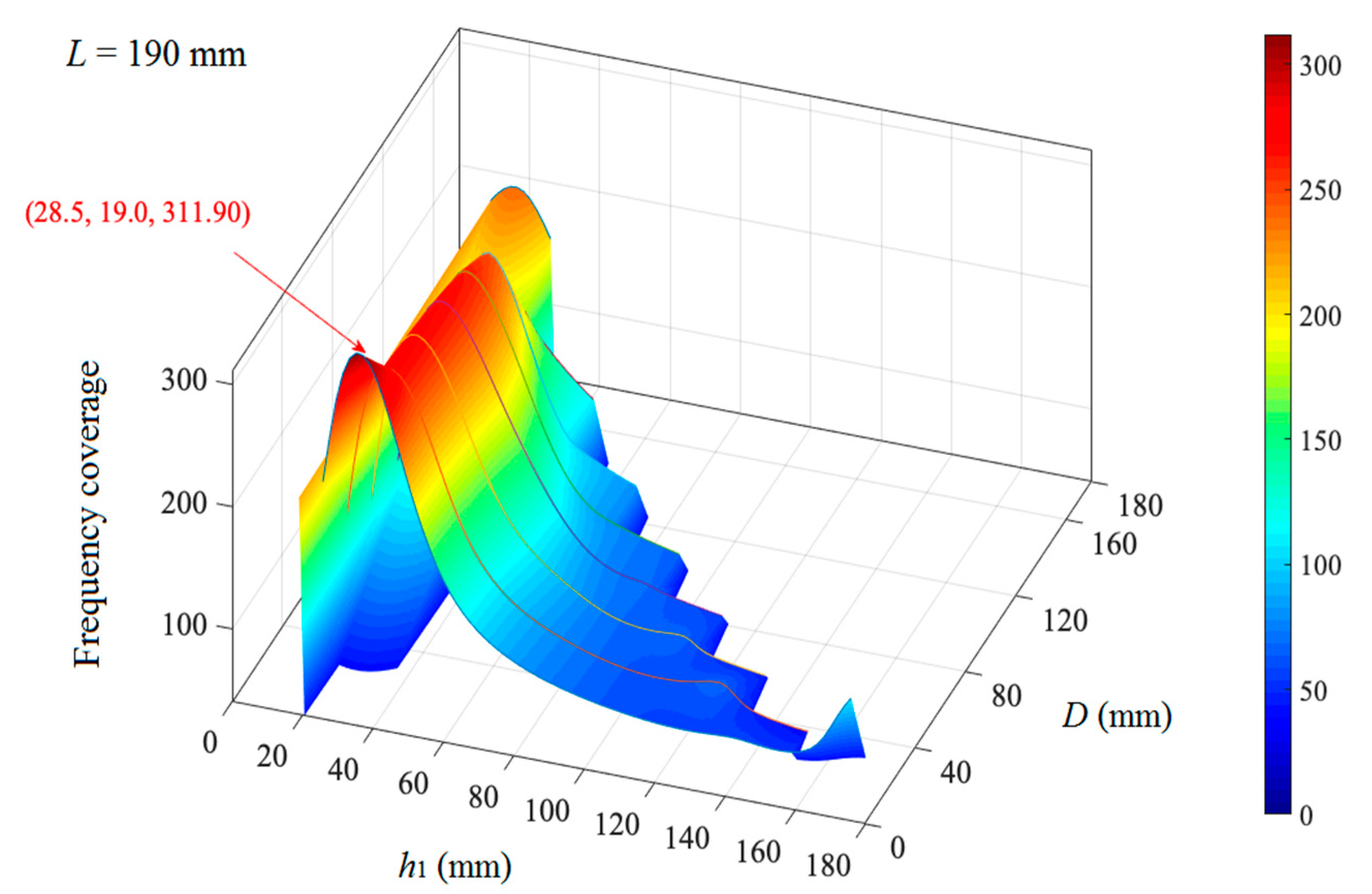
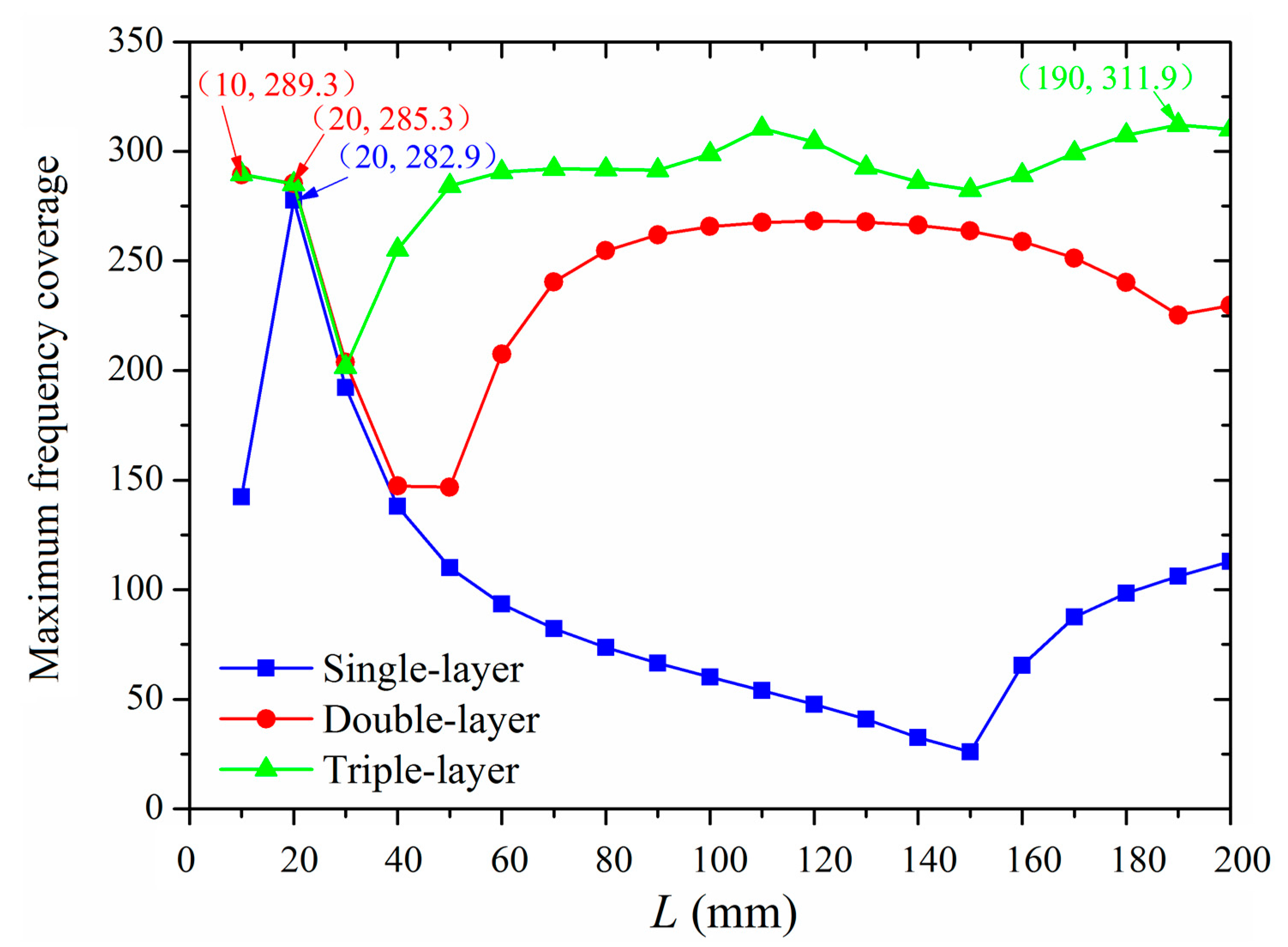
3.4. Structural Optimization for Sound Absorption
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Maa, D.Y. Theory and design of microperforated panel sound-absorbing construction. Sci. Sin. 1975, 18, 55–71. [Google Scholar]
- Maa, D.Y. Microperforated panel wide-band absorber. Noise Control Eng. J. 1987, 29, 77–84. [Google Scholar] [CrossRef]
- Maa, D.Y. Potential of microperforated panel absorber. J. Acoust. Soc. Am. 1998, 104, 2861–2866. [Google Scholar] [CrossRef]
- Wu, M.Q. Micro-perforated panels for duct silencing. Noise Control Eng. J. 1997, 45, 69–77. [Google Scholar] [CrossRef]
- Kang, J.; Brocklesby, M.W. Feasibility of applying microperforated absorbers in acoustic window system. Appl. Acoust. 2005, 66, 669–689. [Google Scholar] [CrossRef]
- Watts, G. Acoustic performance of parallel traffic noise barrier. Appl. Acoust. 1996, 24, 95–119. [Google Scholar] [CrossRef]
- Maa, D.Y. Theory of microslit absorbers. Acta Acust. 2000, 25, 481–485. [Google Scholar]
- Randeberg, R.T. Adjustable slitted panel absorber. Acta Acust. United Acust. 2002, 88, 507–512. [Google Scholar]
- Ning, J.F.; Ren, S.W.; Zhao, G.P. Acoustic properties of micro-perforated panel absorber having arbitrary cross-sectional perforations. Appl. Acoust. 2016, 111, 135–142. [Google Scholar] [CrossRef]
- Sakagami, K.; Nagayama, Y.; Morimoto, M.; Yairi, M. Pilot study on wideband sound absorber obtained by combination of two different microperforated panel (MPP) absorbers. Acoust. Sci. Technol. 2009, 30, 154–156. [Google Scholar] [CrossRef]
- Wang, C.; Huang, L. On the acoustic properties of parallel arrangement of multiple micro-perforated panel absorbers with different cavity depths. J. Acoust. Soc. Am. 2011, 130, 208–218. [Google Scholar] [CrossRef]
- Wang, C.; Cheng, L.; Pan, J.; Yu, G. Sound absorption of a micro-perforated panel backed by an irregular-shaped cavity. J. Acoust. Soc. Am. 2010, 127, 238–246. [Google Scholar] [CrossRef]
- Yairi, M.; Minemura, A.; Sakagami, K.; Morimoto, M. Effect of honeycomb structure in the back cavity on the absorption characteristics of microperforated panel absorbers. J. Acoust. Soc. Am. 2006, 199, 3250. [Google Scholar] [CrossRef]
- Toyoda, M.; Takahashi, D. Sound transmission through a microperforated-panel structure with subdivided air cavities. J. Acoust. Soc. Am. 2008, 124, 3594–3603. [Google Scholar] [CrossRef]
- Gai, X.; Xing, T.; Zhang, B.; Wang, F.; Cai, Z.; Han, Y. Sound absorption of microperforated panel with L shape division cavity structure. Appl. Acoust. 2017, 122, 41–50. [Google Scholar] [CrossRef]
- Sakagami, K.; Matsutani, K.; Morimoto, M. Sound absorption of a double-leaf micro-perforated panel with an air-back cavity and a rigid-back wall: Detailed analysis with a Helmholtz–Kirchhoff integral formulation. Appl. Acoust. 2010, 71, 411–417. [Google Scholar] [CrossRef]
- Ruiz, H.; Cobo, P.; Jacobsen, F. Optimization of multiple-layer microperforated panels by simulated annealing. Appl. Acoust. 2011, 72, 772–776. [Google Scholar] [CrossRef]
- Sakagami, K.; Morimoto, M.; Koike, W. A numerical study of double-leaf microperforated panel absorbers. Appl. Acoust. 2006, 67, 609–619. [Google Scholar] [CrossRef]
- Sakagami, K.; Nakamori, T.; Morimoto, M.; Yairi, M. Double-leaf microperforated panel space absorbers: A revised theory and detailed analysis. Appl. Acoust. 2009, 70, 703–709. [Google Scholar] [CrossRef]
- Kristiansen, U.R.; Vigran, T.E. On the design of resonant absorbers using a slotted plate. Appl. Acoust. 1994, 43, 39–48. [Google Scholar] [CrossRef]
- Cobo, P.; Espinosa, F.M. Proposal of cheap microperforated panel absorbers manufactured by infiltration. Appl. Acoust. 2013, 74, 1069–1075. [Google Scholar] [CrossRef]
- Ruiz, H.; Cobo, P.; Dupont, T.; Martin, B.; Leclaire, P. Acoustic properties of plates with unevenly distributed macroperforations backed by woven meshes. J. Sound Vib. 2012, 132, 3138–3147. [Google Scholar] [CrossRef]
- Yang, D.; Wang, X.; Zhu, M. The impact of the neck material on the sound absorption performance of Helmholtz resonators. J. Sound Vib. 2014, 333, 6843–6857. [Google Scholar] [CrossRef]
- Qian, Y.J.; Kong, D.Y.; Liu, S.M.; Zhao, Z. Investigation on micro-perforated panel absorber with ultra-micro perforations. Appl. Acoust. 2013, 74, 931–935. [Google Scholar] [CrossRef]
- Liu, Z.; Zhan, J.; Fard, M.; Davy, J. Acoustic properties of a porous polycarbonate material produced by additive manufacturing. Mater. Lett. 2016, 81, 296–299. [Google Scholar] [CrossRef]
- Liu, Z.; Zhan, J.; Fard, M.; Davy, J. Acoustic properties of multilayer sound absorbers with a 3D printed micro-perforated panel. Appl. Acoust. 2017, 121, 25–32. [Google Scholar] [CrossRef]
- Shuai, C.; Yang, Y.; Feng, P.; Peng, S.; Guo, W.; Min, A.; Gao, C. A multi-scale porous scaffold fabricated by a combined additive manufacturing and chemical etching process for bone tissue engineering. Int. J. Bioprint. 2018, 4, 133. [Google Scholar]
- Yang, Y.; Wang, G.; Liang, H.; Gao, C.; Peng, S.; Shen, L.; Shuai, C. Additive manufacturing of bone scaffolds. Int. J. Bioprint. 2019, 5, 148. [Google Scholar] [CrossRef]
- Khan, S.Z.; Masood, S.H.; Ibrahim, E.; Ahmad, Z. Compressive behaviour of Neovius Triply Periodic Minimal Surface cellular structure manufactured by fused deposition modelling. Virtual Phys. Prototyp. 2019, 14, 360–370. [Google Scholar] [CrossRef]
- Hao, L.; Savalani, M.M.; Zhang, Y.; Tanner, K.E.; Harris, R.A. Selective laser sintering of hydroxyapatite reinforced polyethylene composites for bioactive implants and tissue scaffold development. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2006, 220, 521–531. [Google Scholar] [CrossRef]
- Ng, W.L.; Chua, C.K.; Shen, Y.F. Print me an organ! Why we are not there yet. Prog. Polym. Sci. 2019, 97, 101145. [Google Scholar] [CrossRef]
- An, J.; Teoh, J.E.M.; Suntornnond, R.; Chua, C.K. Design and 3D printing of scaffolds and tissues. Engineering 2015, 1, 261–268. [Google Scholar] [CrossRef]
- Zhuang, P.; Sun, A.X.; An, J.; Chua, C.K.; Chew, S.Y. 3D neural tissue models: From spheroids to bioprinting. Biomaterials 2018, 154, 113–133. [Google Scholar] [CrossRef]
- Yuan, S.; Shen, F.; Chua, C.K.; Zhou, K. Polymeric composites for powder-based additive manufacturing: Materials and applications. Prog. Polym. Sci. 2019, 91, 141–168. [Google Scholar] [CrossRef]
- Cheah, C.M.; Leong, K.F.; Chua, C.K. Characterization of microfeatures in selective laser sintered drug delivery devices. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2002, 216, 369–383. [Google Scholar] [CrossRef]
- Low, K.H.; Leong, K.F.; Chua, C.K. Characterization of SLS parts for drug delivery devices. Rapid Prototyp. J. 2001, 7, 262–267. [Google Scholar] [CrossRef]
- Chua, C.K.; Leong, K.F. 3D Printing and Additive Manufacturing: Principles and Applications, 5th ed.; World Scientific Publishing: Singapore, 2017. [Google Scholar]
- Setaki, F.; Tenpierik, M.; Turrin, M.; Timmeren, A.V. Acoustic absorbers by additive manufacturing. Build. Environ. 2014, 72, 188–200. [Google Scholar] [CrossRef]
- Berretta, S.; Ghita, O.; Evans, K.E. Morphology of polymeric powders in Laser Sintering (LS): From Polyamide to new PEEK powders. Eur. Polym. J. 2014, 59, 218–229. [Google Scholar] [CrossRef]
- Yuan, S.; Chua, C.K.; Zhou, K. 3D-Printed Mechanical Metamaterials with High Energy Absorption. Adv. Mater. Technol. 2019, 4, 1800419. [Google Scholar] [CrossRef]
- Can, A.; Leclercq, L.; Lelong, J.; Bottledoren, D. Traffic noise spectrum analysis: Dynamic modeling vs. experimental observations. Appl. Acoust. 2010, 71, 764–770. [Google Scholar] [CrossRef]
- Strutt, J.W. Baron Rayleigh, The Theory of Sound; Dover: New York, NY, USA, 1945; Volume II. [Google Scholar]
- Crandall, I.B. Theory of Vibrating Systems and Sound; D. Van Nostrand Company: New York, NY, USA, 1926. [Google Scholar]
- Way, Y.; Pham, D.T.; Dotchev, D.D. Investigation of the Thermal Properties of Different Grades Polyamide 12 (PA12) in Improving Laser Sintering Process (SLS). Appl. Mech. Mater. 2014, 548–549, 294–296. [Google Scholar] [CrossRef]
- Chung, J.Y.; Blaser, D.A. Transfer function method of measuring in-duct acoustic properties. J. Acoust. Soc. Am. 1980, 68, 907–913. [Google Scholar] [CrossRef]
- Manshoori Yeganeh, A.; Movahhedy, M.R.; Khodaygan, S. An efficient scanning algorithm for improving accuracy based on minimising part warping in selected laser sintering process. Virtual Phys. Prototyp. 2019, 14, 59–78. [Google Scholar] [CrossRef]
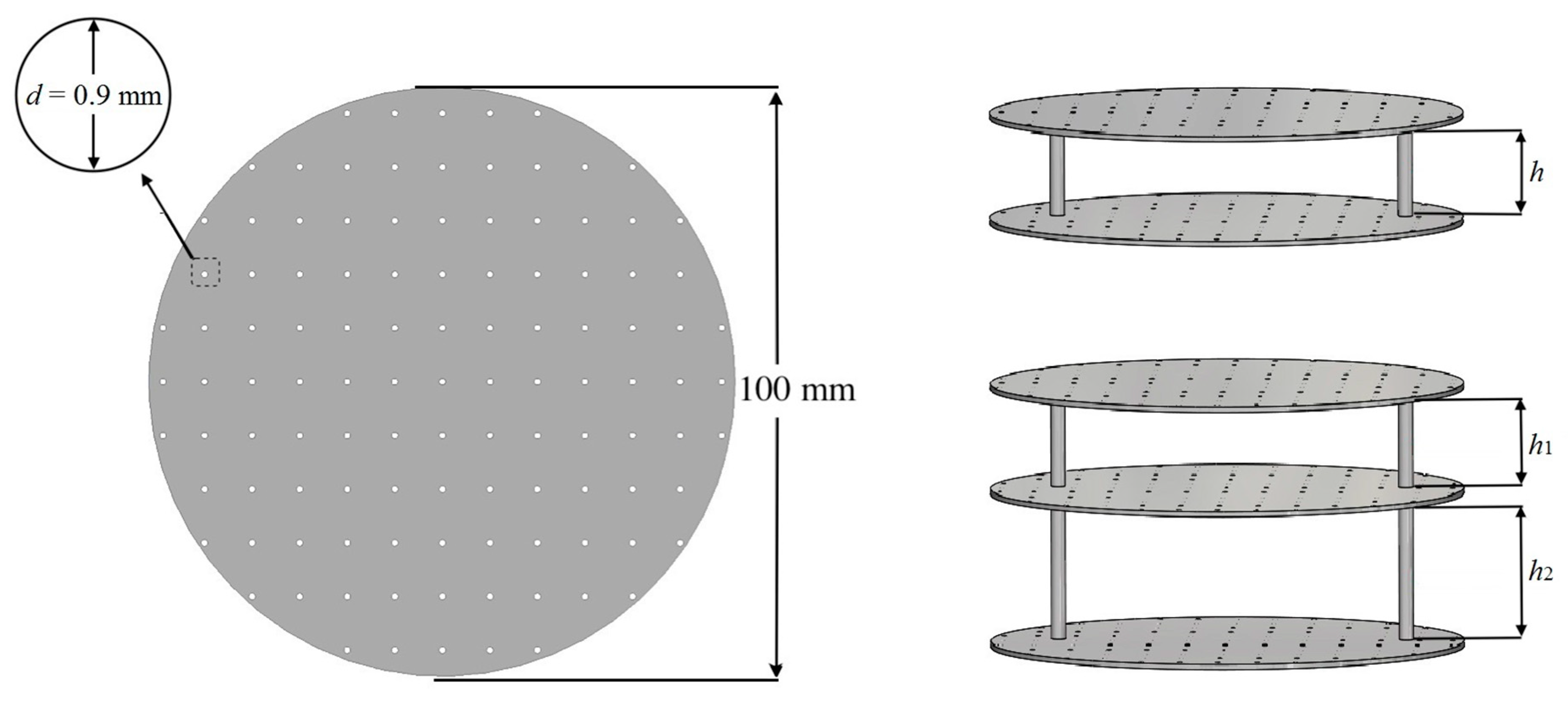



| Sample Number | Number of Layers | Inter-Layer Distances |
|---|---|---|
| MPP_1 | 1 | NA |
| MPP_2 | 2 | h = 30 mm |
| MPP_3 | 2 | h = 40 mm |
| MPP_4 | 2 | h = 50 mm |
| MPP_5 | 3 | h1 = 30 mm, h2 = 40 mm |
| MPP_6 | 3 | h1 = 40 mm, h2 = 40 mm |
| MPP_7 | 3 | h1 = 50 mm, h2 = 40 mm |
| Tensile Modulus (MPa) | Tensile Strength (MPa) | Toughness (J/mm3) | Elongation at Break (%) | Viscosity (Pa·s) at 200 °C |
|---|---|---|---|---|
| 1291 (±12.1) | 44 (±1.3) | 10.18 (±0.9) | 24 (±0.8) | 2616 (±99) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Bai, X.; Zhu, W.; Kiran, R.; An, J.; Chua, C.K.; Zhou, K. 3D Printing of Polymeric Multi-Layer Micro-Perforated Panels for Tunable Wideband Sound Absorption. Polymers 2020, 12, 360. https://doi.org/10.3390/polym12020360
Yang W, Bai X, Zhu W, Kiran R, An J, Chua CK, Zhou K. 3D Printing of Polymeric Multi-Layer Micro-Perforated Panels for Tunable Wideband Sound Absorption. Polymers. 2020; 12(2):360. https://doi.org/10.3390/polym12020360
Chicago/Turabian StyleYang, Wenjing, Xueyu Bai, Wei Zhu, Raj Kiran, Jia An, Chee Kai Chua, and Kun Zhou. 2020. "3D Printing of Polymeric Multi-Layer Micro-Perforated Panels for Tunable Wideband Sound Absorption" Polymers 12, no. 2: 360. https://doi.org/10.3390/polym12020360
APA StyleYang, W., Bai, X., Zhu, W., Kiran, R., An, J., Chua, C. K., & Zhou, K. (2020). 3D Printing of Polymeric Multi-Layer Micro-Perforated Panels for Tunable Wideband Sound Absorption. Polymers, 12(2), 360. https://doi.org/10.3390/polym12020360






