Shock-Driven Decomposition of Polymers and Polymeric Foams
Abstract
1. Introduction
1.1. Shock Physics Background
1.1.1. Basic Concepts
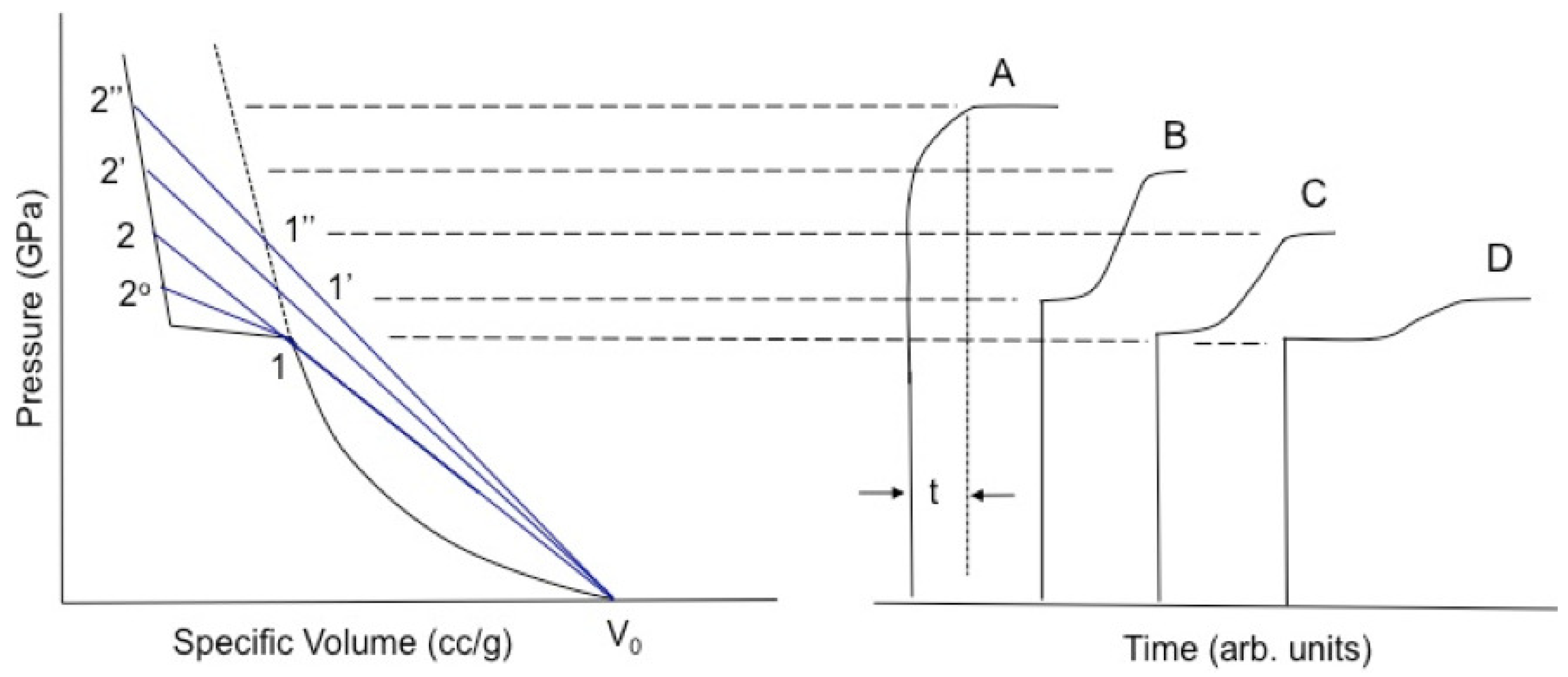
1.1.2. Wave Splitting
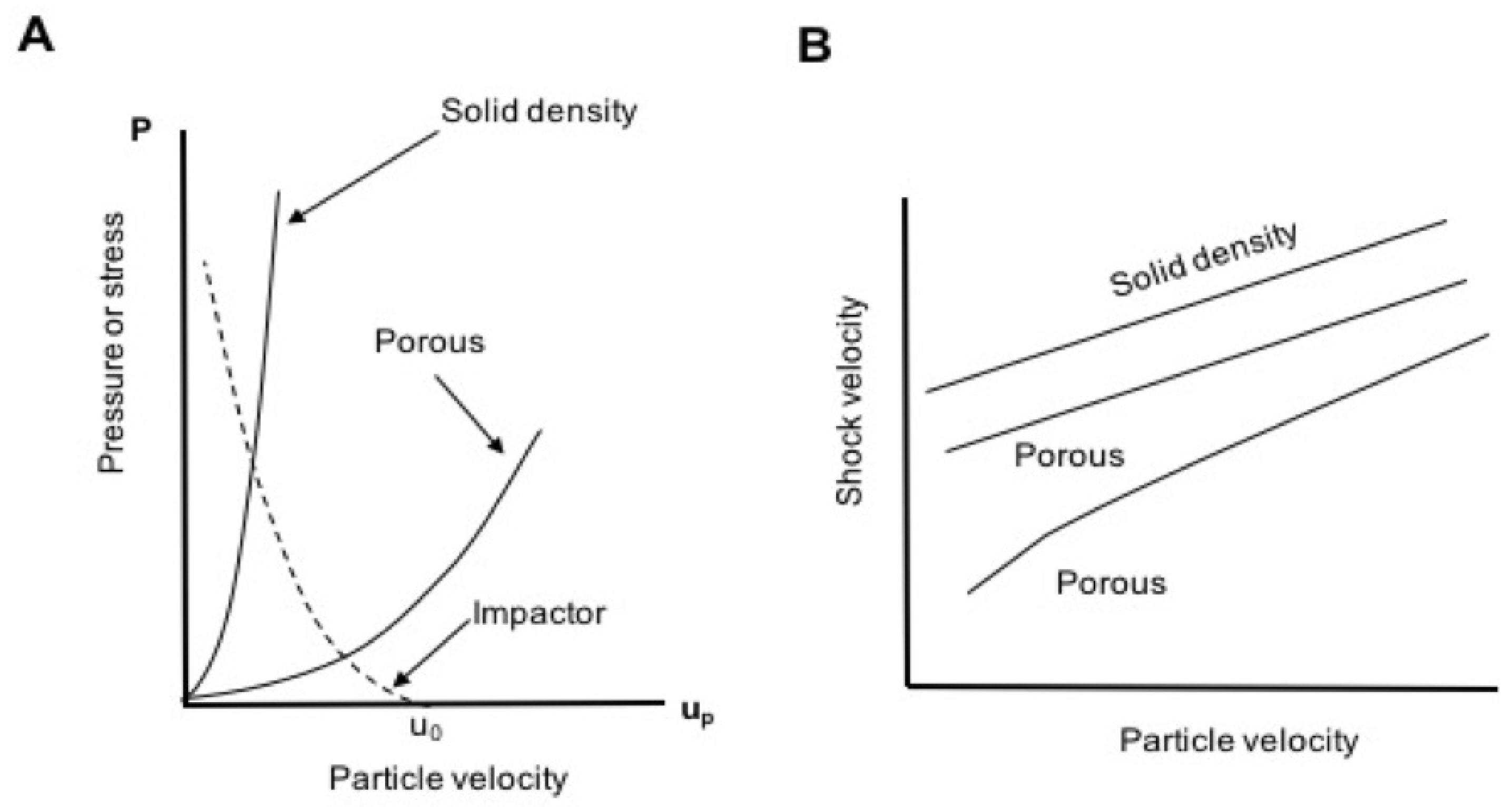
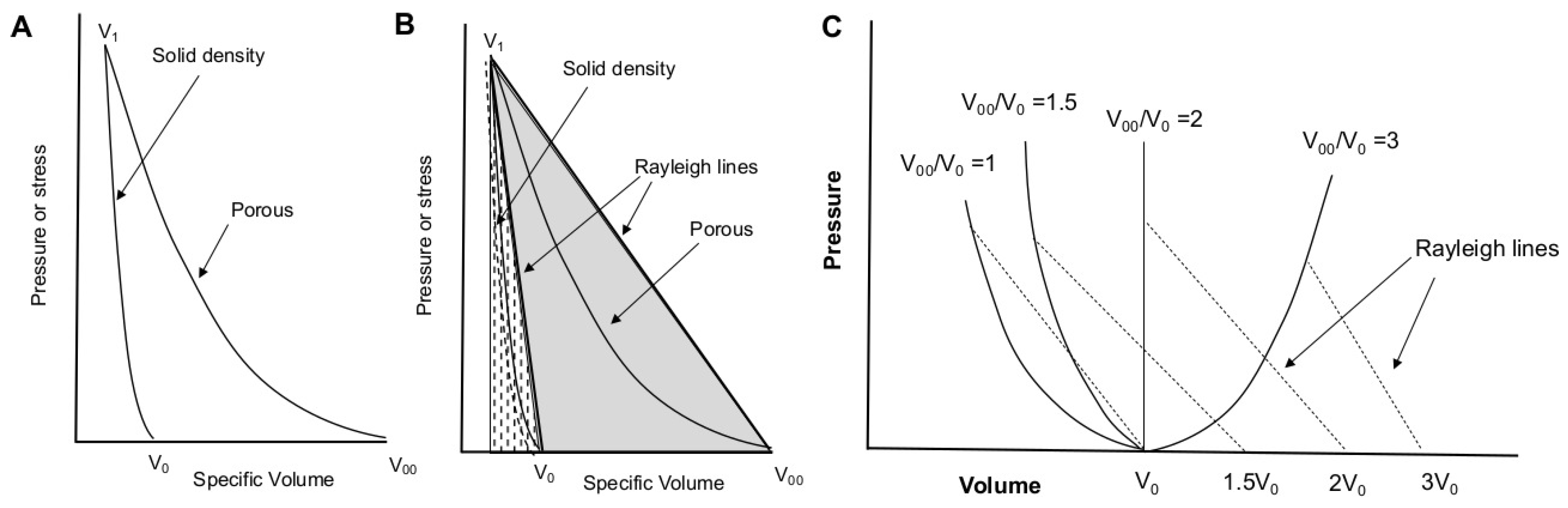
1.1.3. Shockwave Compression of Porous Foams
2. Materials and Methods
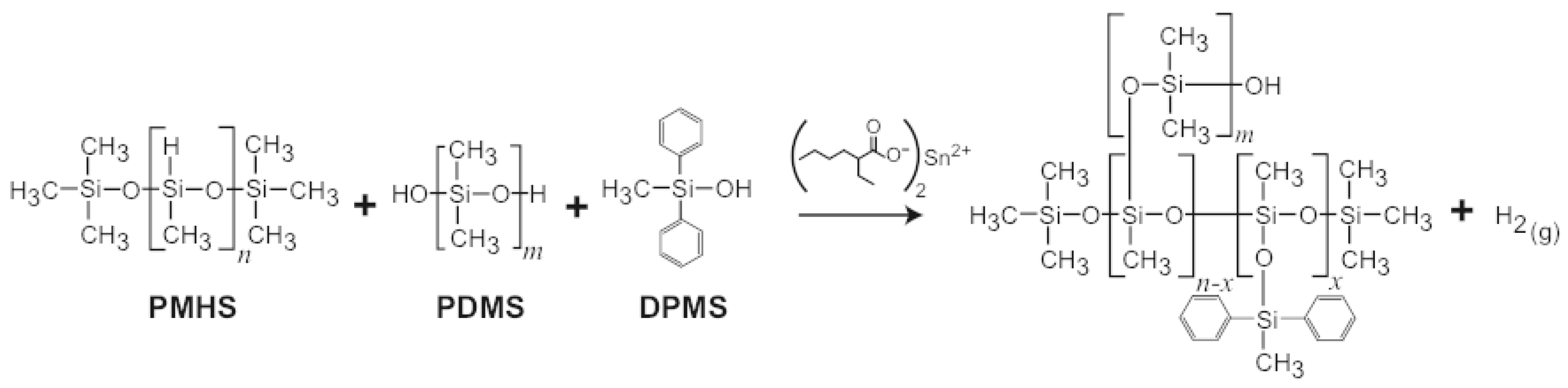
2.1. Materials
2.2. Gas Gun-Driven Plate Impact Experiments
2.3. Equations of State
2.3.1. Global
2.3.2. Thermochemical
3. Results and Discussion
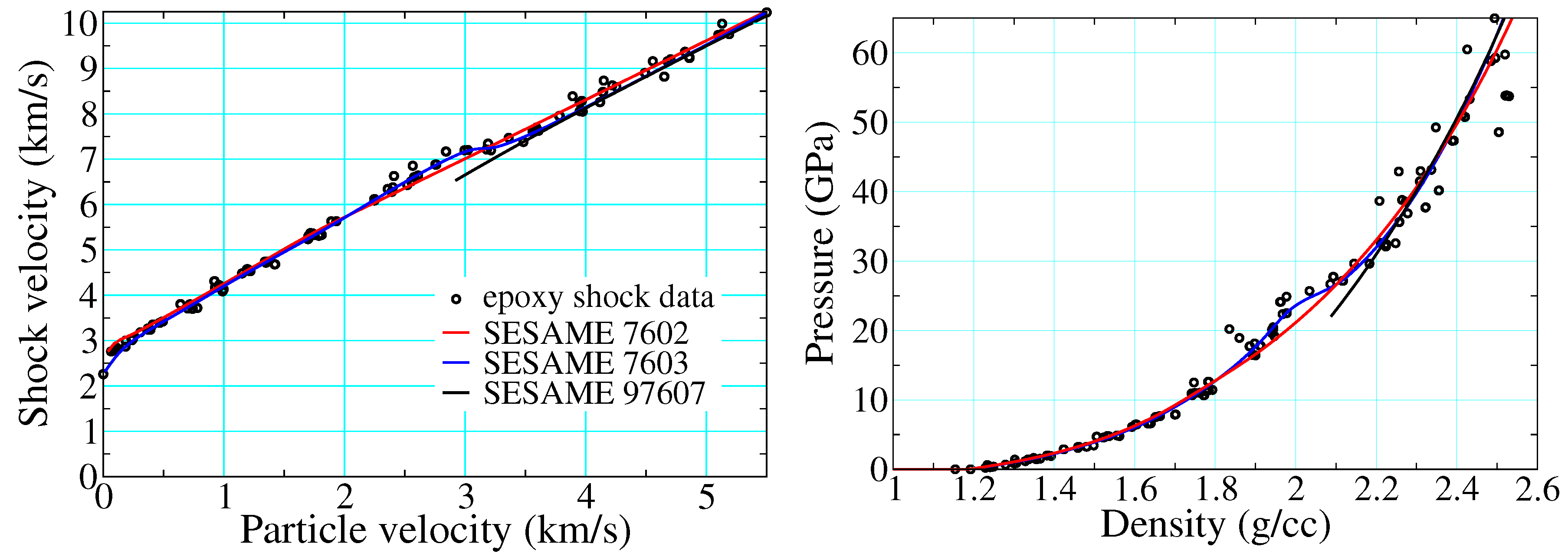
3.1. Polymer Shock Data and Evidence of Decomposition
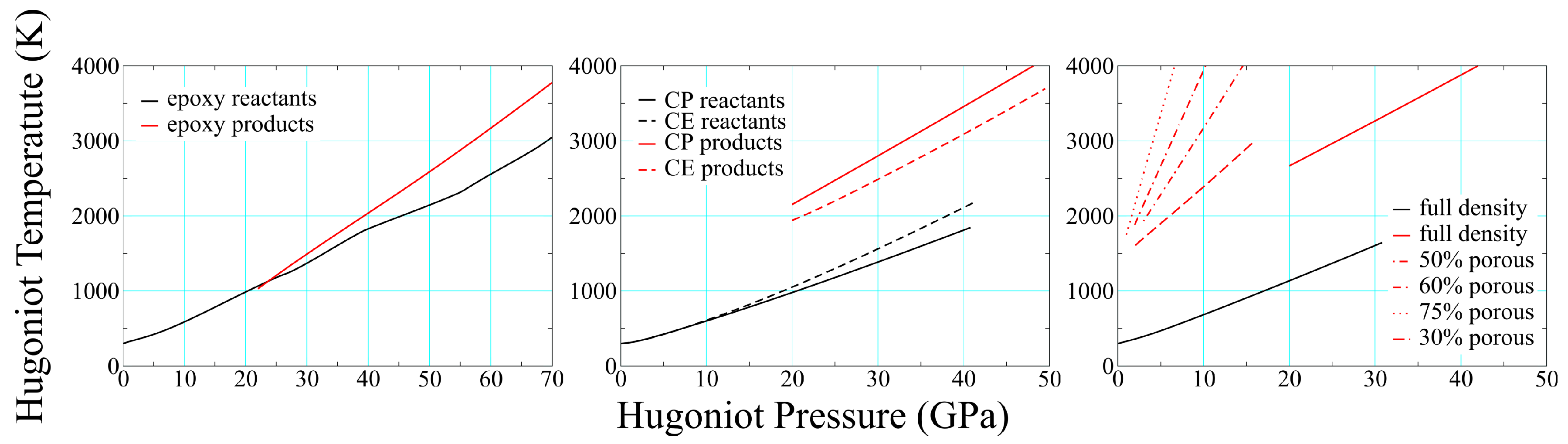
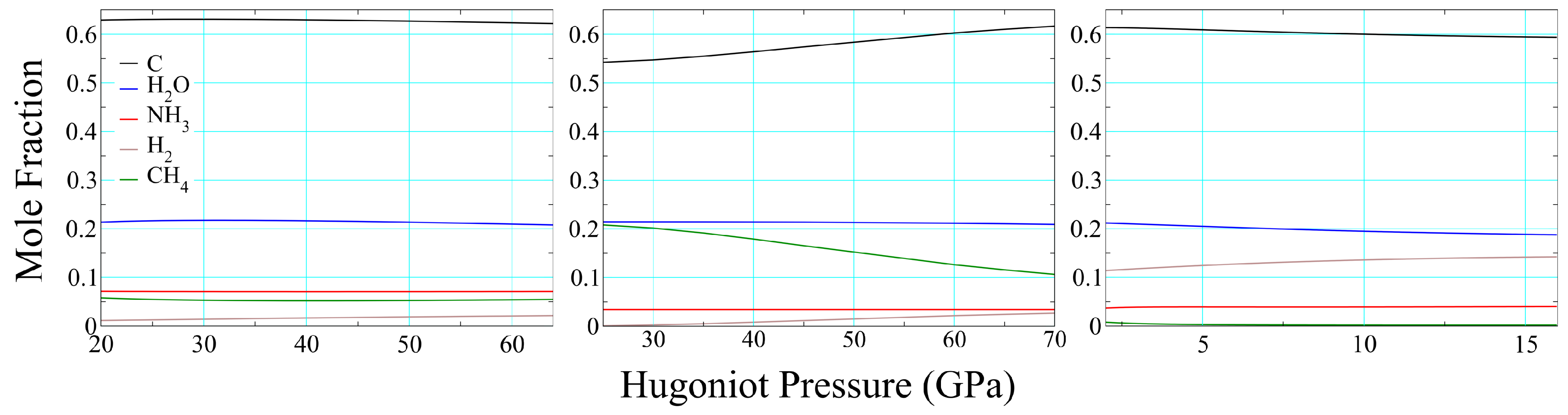
3.2. Product Temperatures and Compositions
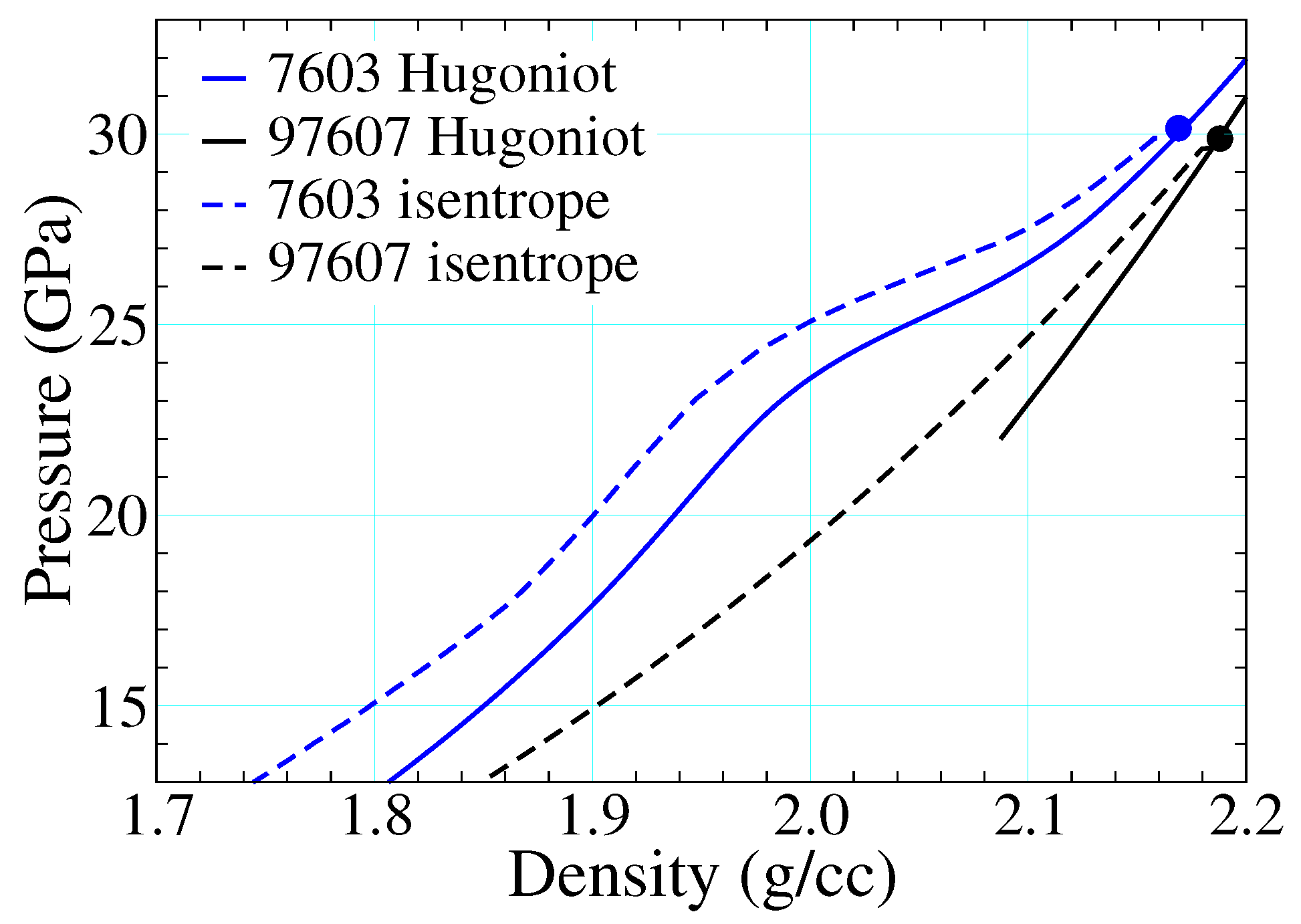
3.3. Porosity and Reaction Thresholds
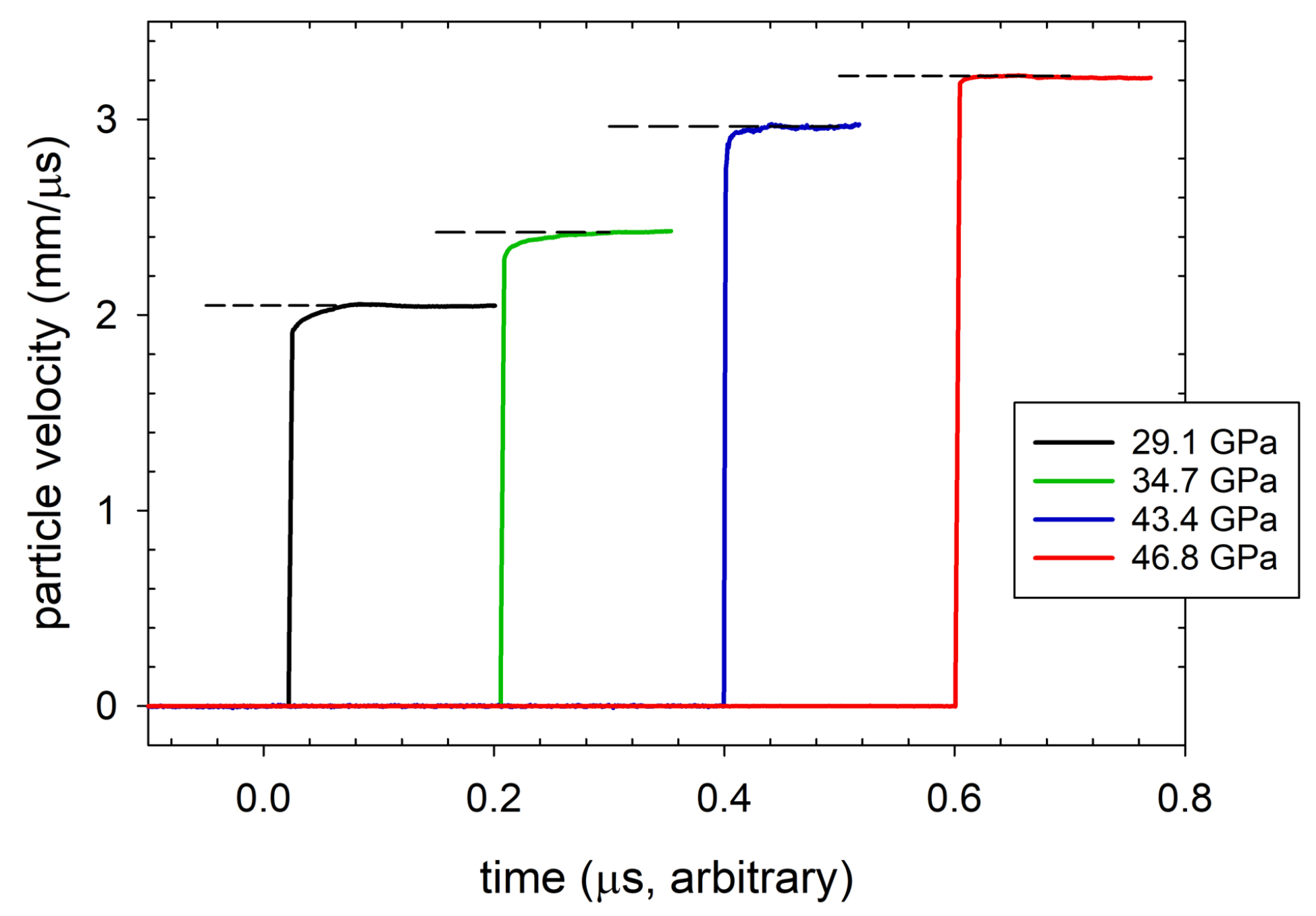
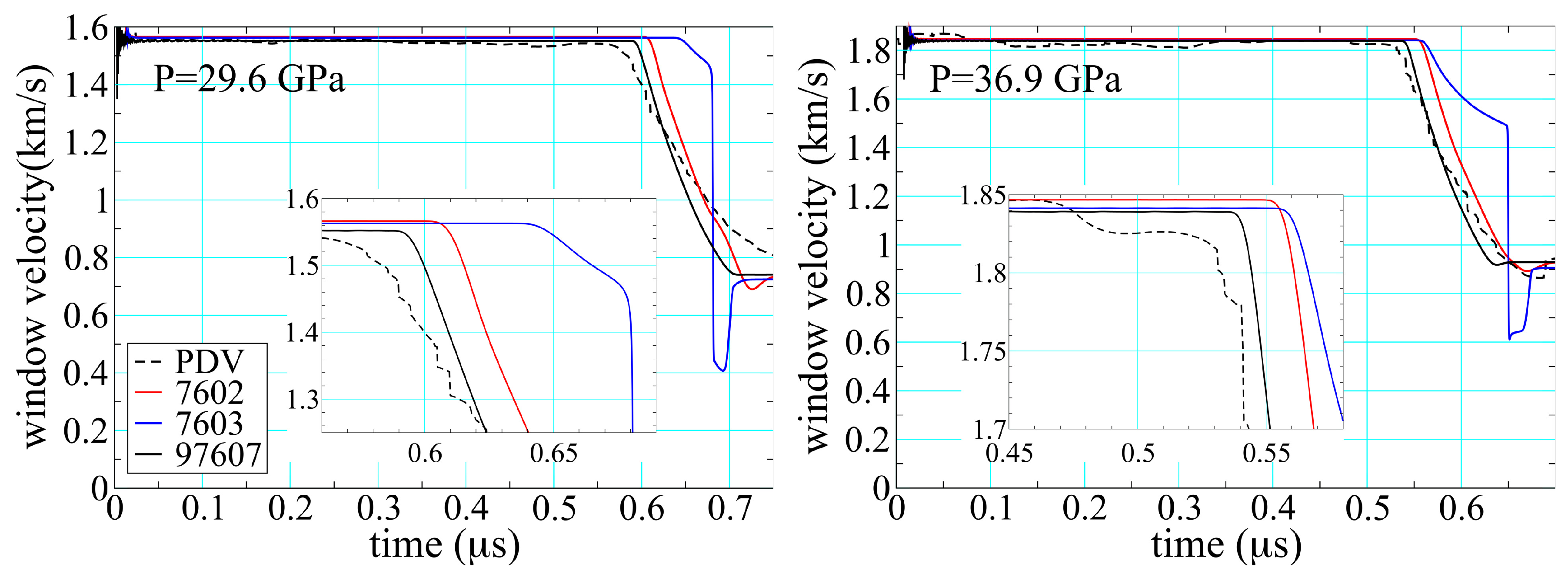
3.4. Wave Profiles
3.5. Reaction Reversibility and Hydrodynamics
4. Conclusions
Future Directions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CE | cyanate ester |
| CM | Carter and Marsh, the authors of Ref. [36] |
| CP | carbon phenolic |
| EOS | equation(s) of state (singular or plural) |
| FSI | front surface impact |
| HE | high explosives |
| LANL | Los Alamos National Laboratory |
| LLNL | Lawrence Livermore National Laboratory |
| PDV | photon Doppler velocimetry |
| PE | polyethylene |
| PTFE | polytetrafluroethylene |
| VISAR | velocity interferometer system for any reflector |
References
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; Wiley: Hoboken, NJ, USA, 1980. [Google Scholar]
- Clements, B.E. A continuum glassy polymer model applicable to dynamic loading. J. Appl. Phys. 2012, 112, 083511. [Google Scholar] [CrossRef]
- Zarzycki, J. Glasses and the Vitreous State; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Coe, J.D. SESAME Equations of State for Stress Cushions and Related Materials; Technical Report LA-UR-15-21390; Los Alamos National Laboratory: Los Alamos, NM, USA, 2015.
- Dattelbaum, D.M.; Coe, J.D.; Rigg, P.A.; Scharff, R.J.; Gammel, J.T. Shockwave response of two carbon fiber-polymer composites to 50 GPa. J. Appl. Phys. 2014, 116, 194308. [Google Scholar] [CrossRef]
- Dattelbaum, D.M.; Coe, J.D.; Kiyanda, C.B.; Gustavsen, R.L.; Patterson, B.M. Reactive, anomalous compression in shocked polyurethane foams. J. Appl. Phys. 2014, 115, 174908. [Google Scholar] [CrossRef]
- Wunderlich, B.; Baur, H. Heat capacities of linear high polymers. Adv. Polym. Sci. 1970, 7, 151–368. [Google Scholar]
- Menikoff, R. Empirical Equations of State for Solids. In Shock Wave Science and Technology Reference Library; Horie, Y., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; Chapter 4. [Google Scholar]
- Fredenburg, D.A.; Koller, D.D.; Rigg, P.A.; Scharff, R.J. High-fidelity Hugoniot analysis of porous materials. Rev. Sci. Instrum. 2013, 84, 013903. [Google Scholar] [CrossRef]
- Fredenburg, D.A.; Lang, J.M.; Coe, J.D.; Scharff, R.J.; Dattelbaum, D.M.; Chisolm, E.D. Systematics of compaction for porous metal and metal-oxide systems. AIP Conf. Proc. 2017, 1793, 120018. [Google Scholar]
- Gourdin, W.H. Dynamic consolidation of metal powders. Prog. Mat. Sci. 1986, 30, 39–80. [Google Scholar] [CrossRef]
- Grady, D.E.; Winfree, N.A. A computational model for polyurethane foam. In Fundamental Issues and Applications of Shock-Wave and High-Strain-Rate Phenomena; Elsevier Science Ltd.: Amsterdam, The Netherlands, 2001; Chapter 61; pp. 485–491. [Google Scholar]
- Mader, C.L.; Carter, W.J. An Equation of State for Shocked Polyurethane Foam; Technical Report LA-4059; Los Alamos National Laboratory: Los Alamos, NM, USA, 1969.
- Kipp, M.E. Polyurethane foam impact experiments and simulations. AIP Conf. Proc. 2000, 505, 313–316. [Google Scholar]
- Boade, R.R. Compression of Porous Copper by Shock Waves. J. Appl. Phys. 1968, 39, 5693–5702. [Google Scholar] [CrossRef]
- Boade, R.R. Principal Hugoniot, Second-Shock Hugoniot, and Release Behavior of Pressed Copper Powder. J. Appl. Phys. 1970, 41, 4542–4551. [Google Scholar] [CrossRef]
- Herrmann, W. Constitutive Equation for the Dynamic Compaction of Ductile Porous Materials. J. Appl. Phys. 1969, 40, 2490–2499. [Google Scholar] [CrossRef]
- Morris, C.E.; Fritz, J.N.; McQueen, R.G. The equation of state of polytetrafluoroethylene to 80 GPa. J. Chem. Phys. 1984, 80, 5203–5218. [Google Scholar] [CrossRef]
- Morris, C.E.; Loughran, E.D.; Mortensen, G.F.; Gray, G.T., III; Shaw, M.S. Shock Induced Dissociation of Polyethylene. In Shock Compression of Condensed Matter; Elsevier: New York, NY, USA, 1989; pp. 687–690. [Google Scholar]
- Graham, R.A. Solids Under High-Pressure Shock Compression; Springer: New York, NY, USA, 1993. [Google Scholar]
- Davison, L.; Graham, R. Shock compression of solids. Phys. Rep. 1979, 55, 255–379. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.O. Supersonic Flow and Shock Waves; Interscience Publications: New York, NY, USA, 1948. [Google Scholar]
- Bancroft, D.; Peterson, E.L.; Minshall, S. Polymorphism of Iron at High Pressure. J. Appl. Phys. 1956, 27, 291–298. [Google Scholar] [CrossRef]
- Forbes, J.W. Shockwave Compression of Condensed Matter: A Primer; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Fortov, V.E.; Lomonosov, I.V. Shock waves and equations of state of matter. Shock Waves 2009, 20, 53–71. [Google Scholar] [CrossRef]
- Duvall, G.E.; Graham, R.A. Phase transitions under shock-wave loading. Rev. Mod. Phys. 1977, 49, 523–579. [Google Scholar] [CrossRef]
- Hayes, D.B. Polymorphic phase transformation rates in shock-loaded potassium chloride. J. Appl. Phys. 1974, 45, 1208–1217. [Google Scholar] [CrossRef]
- Walsh, J.M.; Rice, M.H.; McQueen, R.G.; Yarger, F.L. Shock-Wave Compressions of Twenty-Seven Metals. Equations of State of Metals. Phys. Rev. 1957, 108, 196–216. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Raizer, Y.P. Physics of Shock Waves and High Temperature Hydrodynamic Phenomena; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Mao, H.K.; Chen, X.J.; Ding, Y.; Li, B.; Wang, L. Solids, liquids, and gases under high pressure. Rev. Mod. Phys. 2018, 90, 015007. [Google Scholar] [CrossRef]
- Marsh, S.P. (Ed.) LASL Shock Hugoniot Data; University of California Press: Berkeley, CA, USA, 1980. [Google Scholar]
- Woolfolk, R.; Cowperthwaite, M.; Shaw, R. A “universal” Hugoniot for liquids. Thermochim. Acta 1973, 5, 409–414. [Google Scholar] [CrossRef]
- Olinger, B.; Halleck, P.M.; Cady, H.H. The isothermal linear and volume compression of pentaerythritol tetranitrate (PETN) to 10 GPa (100 kbar) and the calculated shock compression. J. Chem. Phys. 1975, 62, 4480–4483. [Google Scholar] [CrossRef]
- Dick, R.D. Shock compression data for liquids. I. Six hydrocarbon compounds. J. Chem. Phys. 1979, 71, 3203–3212. [Google Scholar] [CrossRef]
- Dattelbaum, D.M. In situ insights into shock-driven reactive flow. AIP Conf. Proc. 2018, 1979, 020001. [Google Scholar]
- Carter, W.J.; Marsh, S.P. Hugoniot Equation of State of Polymers; Technical Report; Los Alamos National Laboratory: Los Alamos, NM, USA, 1995.
- Dremin, A.N.; Savrov, S.D.; Andrievskii, A.N. Investigation of shock initiation to detonation in nitromethane. Combus. Explos. Shock Waves 1965, 1, 1–6. [Google Scholar] [CrossRef]
- Van Thiel, M.; Kusubov, A.S.; Mitchell, A.C. Compendium of Shock Wave Data; Technical Report UCRL-50108; Lawrence Radiation Laboratory: Berkeley, CA, USA, 1967.
- Jensen, B.J.; Gray, G.T.; Hixson, R.S. Direct measurements of the α-ϵ transition stress and kinetics for shocked iron. J. Appl. Phys. 2009, 105, 103502. [Google Scholar] [CrossRef]
- Johnson, J.D. General Features of Hugoniots-II; Technical Report LA-13217-MS; Los Alamos National Laboratory: Los Alamos, NM, USA, 1997.
- Kerley, G.I. A new multiphase equation of state for iron. AIP Conf. Proc. 1994, 309, 903–906. [Google Scholar]
- McQueen, R.G. Equation of state of solids. In High Velocity Impact Phenomena; Kinslow, R., Ed.; Academic Press: New York, NY, USA, 1970; Volume 293–417, pp. 521–568. [Google Scholar]
- Sheffield, S.A.; Dattelbaum, D.M.; Stahl, D.B. In-situ measurement of shock-induced reactive flow in a series of related hydrocarbons. AIP Conf. Proc. 2009, 1195, 145–148. [Google Scholar]
- Sheffield, S.A. Shock-Induced Chemical Reaction in Organic and Silicon Based Liquids. AIP Conf. Proc. 2006. [Google Scholar] [CrossRef]
- Sheffield, S.A. Response of liquid carbon disulfide to shock compression. II. Experimental design and measured Hugoniot information. J. Chem. Phys. 1984, 81, 3048–3063. [Google Scholar] [CrossRef]
- Trunin, R.F. Shock Compression of Condensed Materials; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Maw, J.R.; Whitworth, N.J.; Holland, R.B. Multiple shock compression of polyurethane and syntactic foams. AIP Conf. Proc. 1996. [Google Scholar] [CrossRef]
- Maw, J.R.; Whitworth, N.J. Shock compression and the equation of state of fully dense and porous polyurethane. AIP Conf. Proc. 1998. [Google Scholar] [CrossRef]
- Fredenburg, D.A.; Koller, D.D.; Coe, J.D.; Kiyanda, C.B. The influence of morphology on the low- and high-strain-rate compaction response of CeO2 powders. J. Appl. Phys. 2014, 115, 123511. [Google Scholar] [CrossRef]
- Sheffield, S.A.; Mitchell, D.E.; Hayes, D.B. The equation of state and chemical kinetics for Hexanitrostilbene (HNS) explosive. In Proceedings of the Sixth Symposium (International) on Detonation; Office of Naval Research, Department of the Navy: Arlington, VA, USA, 1976; ACR 221; pp. 748–754. [Google Scholar]
- Clyens, S.; Johnson, W. The dynamic compaction of powdered materials. Mater. Sci. Eng. 1977, 30, 121–139. [Google Scholar] [CrossRef]
- Menikoff, R.; Kober, E.M. Equation of state and Hugoniot locus for porous materials: P-α model revisited. AIP Conf. Proc. 2000. [Google Scholar] [CrossRef]
- Krupnikov, K.K.; Brazhnik, M.I.; Krupnikova, V.P. Shock compression of porous tungsten. Sov. Phys. JETP 1962, 15, 470–476. [Google Scholar]
- Fickett, W.; Davis, W. Detonation: Theory and Experiment; Dover: Mineola, NY, USA, 2000. [Google Scholar]
- Dattelbaum, D.M. Shock Compression of Glass Microballoons. in prepration.
- Simpson, R.; Helm, F. The Shock Hugoniot of Glass Microballoons; Technical Report UCRL-ID-119252; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1994.
- Munson, D.E.; Boade, R.R.; Schuler, K.W. Stress-wave propagation in Al2O3-epoxy mixtures. J. Appl. Phys. 1978, 49, 4797–4807. [Google Scholar] [CrossRef]
- Munson, D.E.; May, R.P. Dynamically Determined High-Pressure Compressibilities of Three Epoxy Resin Systems. J. Appl. Phys. 1972, 43, 962–971. [Google Scholar] [CrossRef]
- Fredenburg, D.A.; Lang, J.M.; Coe, J.D.; Dattelbaum, D.M. Manuscript in preparation.
- Dattelbaum, D.; Gustavsen, R.; Sheffield, S.; Stahl, D.; Scharff, R.; Rigg, P.; Furmanski, J.; Orler, E.; Patterson, B.; Coe, J.D. The dynamic response of carbon fiber-filled polymer composites. EPJ Web Conf. 2012, 26, 02007. [Google Scholar] [CrossRef]
- Dattelbaum, D.M.; Coe, J.D. The dynamic loading response of carbon-fiber-filled polymer composites. In Dynamic Deformation, Damage and Fracture in Composite Materials and Structures; Silberschmidt, V.V., Ed.; Woodhead: Sawston, UK, 2016; Chapter 9; p. 225. [Google Scholar]
- Alcon, R.R.; Robbins, D.L.; Sheffield, S.A.; Stahl, D.B.; Fritz, J.N. Shock Compression of Silicon Polymer Foams with a Range of Initial Densities. AIP Conf. Proc. 2004, 706, 651–654. [Google Scholar]
- Maerzke, K.; Lang, J.M.; Dattelbaum, D.M.; Coe, J.D. Equation of state for SX358 Foams. In preparation.
- Patterson, B.M.; Hamilton, C.E. Dimensional Standard for Micro X-ray Computed Tomography. Anal. Chem. 2010, 82, 8537–8543. [Google Scholar] [CrossRef]
- Patterson, B.M.; Henderson, K.; Smith, Z. Measure of morphological and performance properties in polymeric silicone foams by X-ray tomography. J. Mater. Sci. 2013, 48, 1986–1996. [Google Scholar] [CrossRef]
- Branch, B.; Ionita, A.; Patterson, B.M.; Schmalzer, A.; Clements, B.; Mueller, A.; Dattelbaum, D.M. A comparison of shockwave dynamics in stochastic and periodic porous polymer architectures. Polymer 2019, 160, 325–337. [Google Scholar] [CrossRef]
- Martinez, A.R.; Sheffied, S.A.; Whitehead, M.C.; Olivas, H.D.; Dick, J.J. New LANL gas driven two-stage gun. AIP Conf. Proc. 1994. [Google Scholar] [CrossRef]
- Jones, A.H.; Isbell, W.M.; Maiden, C.J. Measurement of the Very-High-Pressure Properties of Materials using a Light-Gas Gun. J. Appl. Phys. 1966, 37, 3493–3499. [Google Scholar] [CrossRef]
- Vorthman, J.E. Facilities for the study of shock induced decomposition of high explosives. AIP Conf. Proc. 1982, 78, 680–684. [Google Scholar]
- Barker, L.M.; Hollenbach, R.E. Shock-Wave Studies of PMMA, Fused Silica, and Sapphire. J. Appl. Phys. 1970, 41, 4208–4226. [Google Scholar] [CrossRef]
- Barker, L.M.; Hollenbach, R.E. Laser interferometer for measuring high velocities of any reflecting surface. J. Appl. Phys. 1972, 43, 4669–4675. [Google Scholar] [CrossRef]
- Strand, O.T.; Goosman, D.R.; Martinez, C.; Whitworth, T.L.; Kuhlow, W.W. Compact system for high-speed velocimetry using heterodyne techniques. Rev. Sci. Instrum. 2006, 77, 083108. [Google Scholar] [CrossRef]
- Carter, W.J. Hugoniot Equation of State of Some Alkali Halides. High Temp-High Press 1973, 5, 313–318. [Google Scholar]
- Fredenburg, D.A.; Lang, J.M.; Dattelbaum, D.M.; Bennett, L.S. (U) Design Considerations for Obtaining Deep Release in Reacted Epon 828; Technical Report; Los Alamos National Laboratory: Los Alamos, NM, USA, 2016.
- Hooks, D.E.; Lang, J.M.; Coe, J.D.; Dattelbaum, D.M. High pressure deep-release impact experiments on high density and ultra-high molecular weight polyethylene. AIP Conf. Proc. 2018, 1979, 030004. [Google Scholar]
- Lyon, S.P.; Johnson, J.D. SESAME: The Los Alamos National Laboratory Equation of State Database; Technical Report LA-UR-92-3407; Los Alamos National Laboratory: Los Alamos, NM, USA, 1992.
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Oxford University Press: Oxford, UK, 1954; Appendix V. [Google Scholar]
- Thomas, L.H. The calculation of atomic fields. Math. Proc. Camb. Philos. Soc. 1927, 23, 542. [Google Scholar] [CrossRef]
- Fermi, E. Un Metodo Statistico per la Determinazione di alcune Prioprieta dell’Atomo. Rend. Accad. Naz. Lincei 1927, 6, 602–607. [Google Scholar]
- Dirac, P.A.M. Note on Exchange Phenomena in the Thomas Atom. Proc. Camb. Philos. Soc. 1930, 26, 376–385. [Google Scholar] [CrossRef]
- McQuarrie, D.A. Statistical Mechanics; University Science Books: Sausalito, CA, USA, 1976. [Google Scholar]
- Johnson, J.D. A generic model for the ionic contribution to the equation of state. High Press. Res. 1991, 6, 277–285. [Google Scholar] [CrossRef]
- Chisolm, E.D. A Model of Liquids in Wide-Ranging Multiphase Equations of State; Technical Report LA-UR-10-08329; Los Alamos National Laboratory: Los Alamos, NM, USA, 2010.
- Tait, P.G. Report on some of the physical properties of fresh water. Rept. Sci. Results Voy. H.M.S. Challenger. Phys. Chem. 1888, 2, 1–76. [Google Scholar]
- Martin, R.M. Electronic Structure: Basic Theory and Practical Methods; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Bennett, B.I. Computationally Efficient Expression for Obtaining the Zero-Temperature Isotherm in Equations of State; Technical Report LA-08616-MS; Los Alamos National Laboratory: Los Alamos, NM, USA, 1980.
- Smith, W.R.; Missen, R.W. Chemical Reaction Equilibrium Analysis: Theory and Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 1982. [Google Scholar]
- Chase, M.W.J. NIST-JANAF Thermochemical Tables, 4th ed.; American Institute of Physics: New York, NY, USA, 1998. [Google Scholar]
- Ross, M. A high-density fluid-perturbation theory based on an inverse 12th-power hard-sphere reference system. J. Chem. Phys. 1979, 71, 1567–1571. [Google Scholar] [CrossRef]
- Stone, A.J. The Theory of Intermolecular Forces; Oxford University Press: Oxford, UK, 1996; pp. 157–158. [Google Scholar]
- Shaw, M.S.; Johnson, J.D.; Holian, B.L. Effective Spherical Potentials for Molecular Fluid Thermodynamics. Phys. Rev. Lett. 1983, 50, 1141–1144. [Google Scholar] [CrossRef]
- Rowlinson, J.S.; Swinton, F.L. Liquids and Liquid Mixtures, 3rd ed.; Butterworth Scientific: Oxford, UK, 1982. [Google Scholar]
- Ree, F.H. Simple mixing rule for mixtures with exp-6 interactions. J. Chem. Phys. 1983, 78, 409–415. [Google Scholar] [CrossRef]
- Desbiens, N.; Dubois, V.; Matignon, C.; Sorin, R. Improvements of the CARTE Thermochemical Code Dedicated to the Computation of Properties of Explosives. J. Phys. Chem. B 2011, 115, 12868–12874. [Google Scholar] [CrossRef]
- Levashov, P.R.; Khishchenko, K.V.; Lomonosov, I.V.; Fortov, V.E. Database on Shock-Wave Experiments and Equations of State Available via Internet. AIP Conf. Proc. 2004, 706, 87–90. [Google Scholar]
- Maerzke, K.; Coe, J.D.; Ticknor, C.T.; Leiding, J.A.; Gammel, J.T.; Welch, C.F. Equations of state for polyethylene and its shock-driven decomposition products. Manuscript in preparation.
- Dang, N.C.; Bolme, C.A.; Moore, D.S.; McGrane, S.D. Shock Induced Chemistry In Liquids Studied With Ultrafast Dynamic Ellipsometry And Visible Transient Absorption Spectroscopy. J. Phys. Chem. A 2012, 116, 10301–10309. [Google Scholar] [CrossRef] [PubMed]
- Carroll, M.; Holt, A.C. Suggested Modification of the P-α Model for Porous Materials. J. Appl. Phys. 1972, 43, 759–761. [Google Scholar] [CrossRef]
- Dattelbaum, D.M.; Sheffield, S.A. Shock-induced chemical reactions in simple organic molecules. AIP Conf. Proc. 2012, 1426, 627–632. [Google Scholar]
- Lang, J.M.; Fredenburg, D.A.; Coe, J.D.; Dattelbaum, D.M. Deep-release of Epon 828 epoxy from the shock-driven reaction product phase. AIP Conf. Proc. 2018, 1979, 090008. [Google Scholar]
- Olinger, B.; Fritz, J.; Morris, C.E. Equations of State for PEEK, Epon 828, and Carbon Fiber-Epon Composite; Los Alamos National Laboratory: Los Alamos, NM, USA, 1993.
- Gustavsen, R.L.; Dattelbaum, D.M.; Watkins, E.B.; Firestone, M.A.; Podlesak, D.W.; Jensen, B.J.; Ringstrand, B.S.; Huber, R.C.; Mang, J.T.; Johnson, C.E.; et al. Time resolved small angle X-ray scattering experiments performed on detonating explosives at the advanced photon source: Calculation of the time and distance between the detonation front and the x-ray beam. J. Appl. Phys. 2017, 121, 105902. [Google Scholar] [CrossRef]
- Watkins, E.B.; Velizhanin, K.A.; Dattelbaum, D.M.; Gustavsen, R.L.; Aslam, T.D.; Podlesak, D.W.; Huber, R.C.; Firestone, M.A.; Ringstrand, B.S.; Willey, T.M.; et al. Evolution of Carbon Clusters in the Detonation Products of the Triaminotrinitrobenzene (TATB)-Based Explosive PBX 9502. J. Phys. Chem. C 2017, 121, 23129–23140. [Google Scholar] [CrossRef]
- Huber, R.C.; Peterson, J.; Coe, J.D.; Dattelbaum, D.M.; Gibson, L.L.; Gustavsen, R.L.; Sheffield, S.A. Two-wave structure in shock compressed polysulfone. J. Appl. Phys. to be submitted.


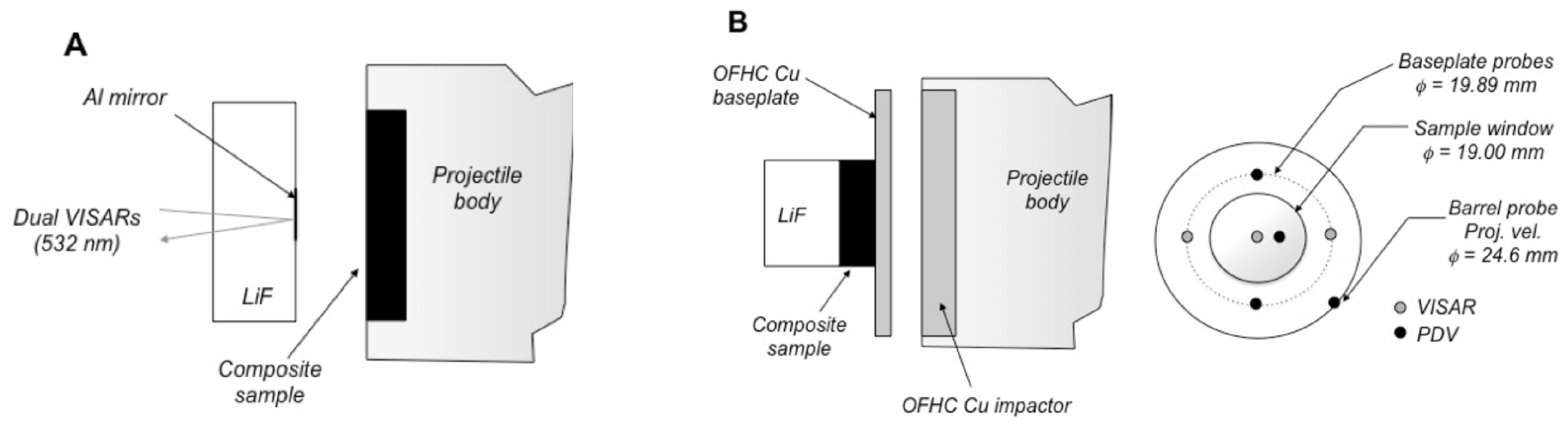
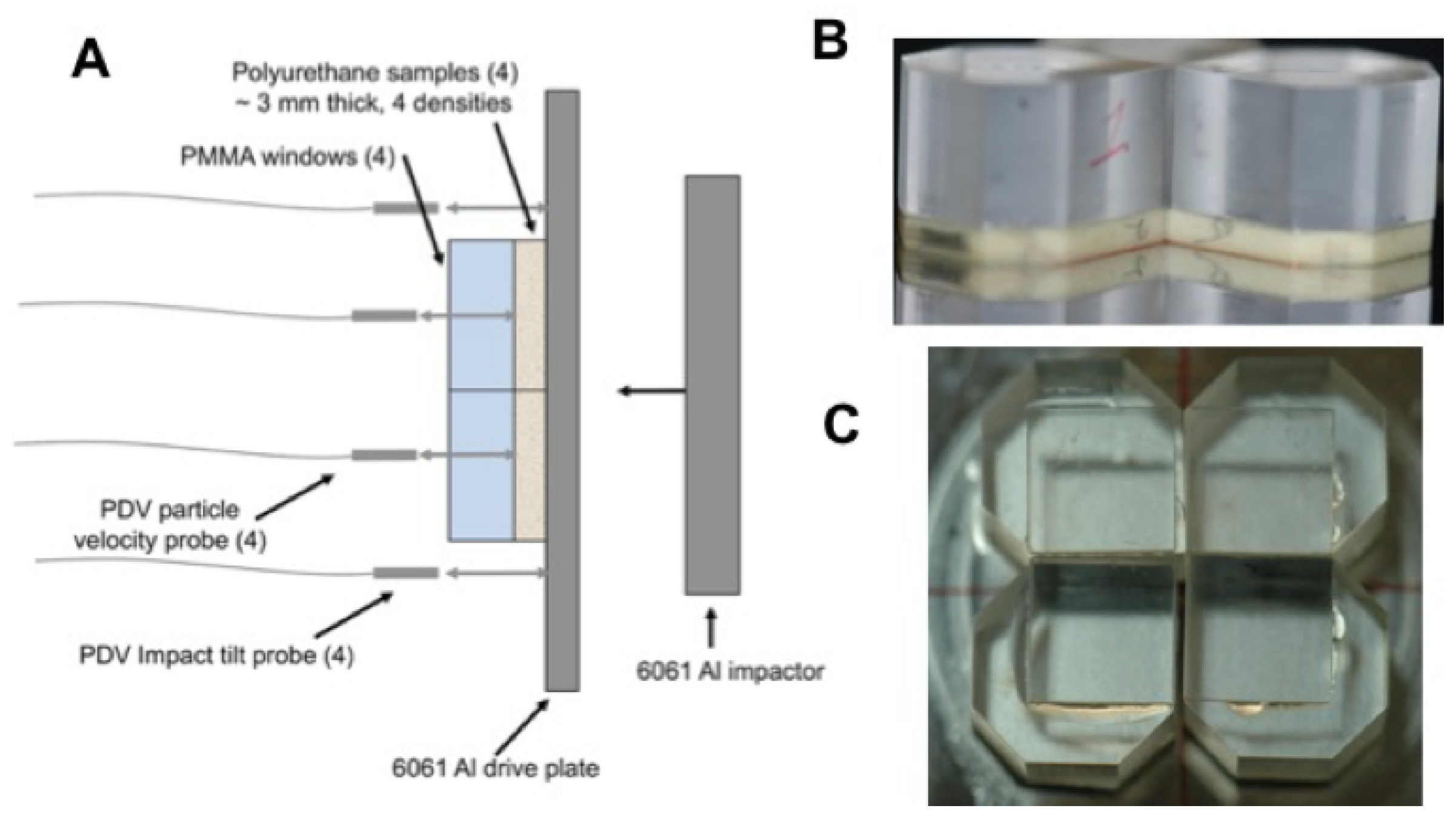
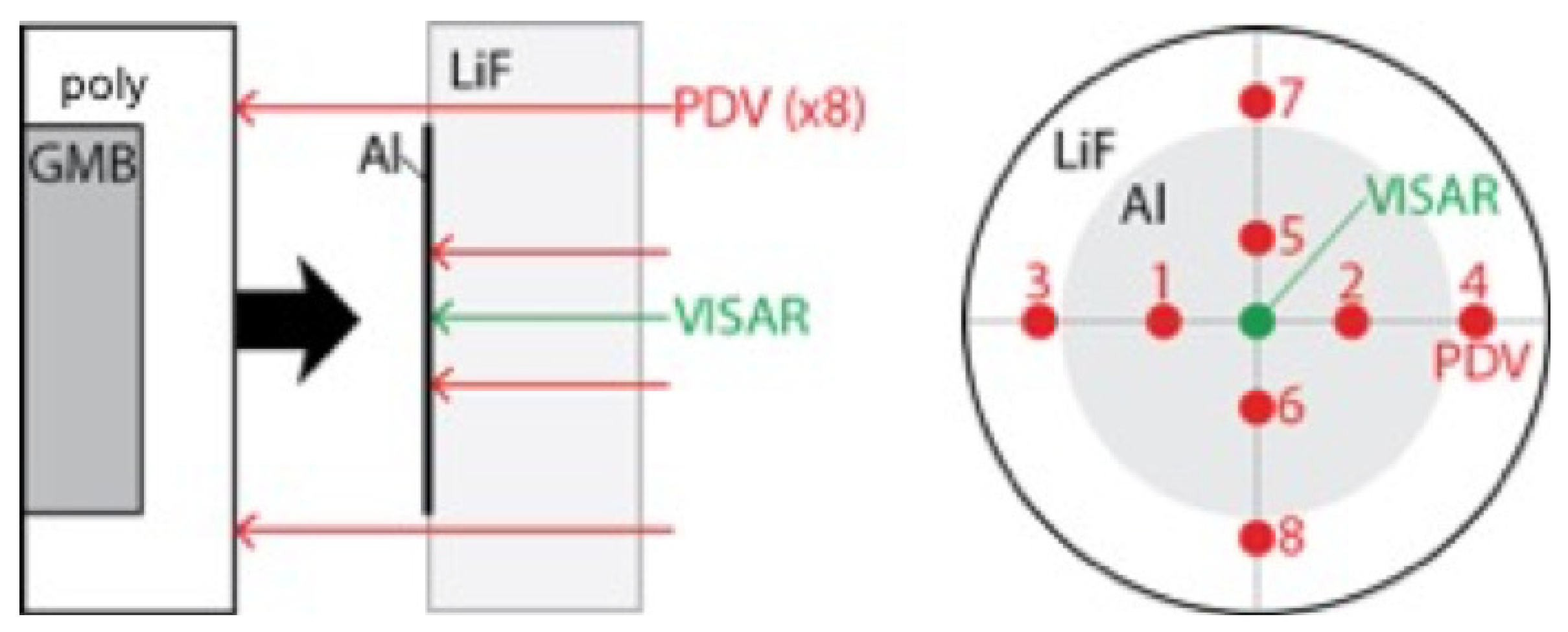
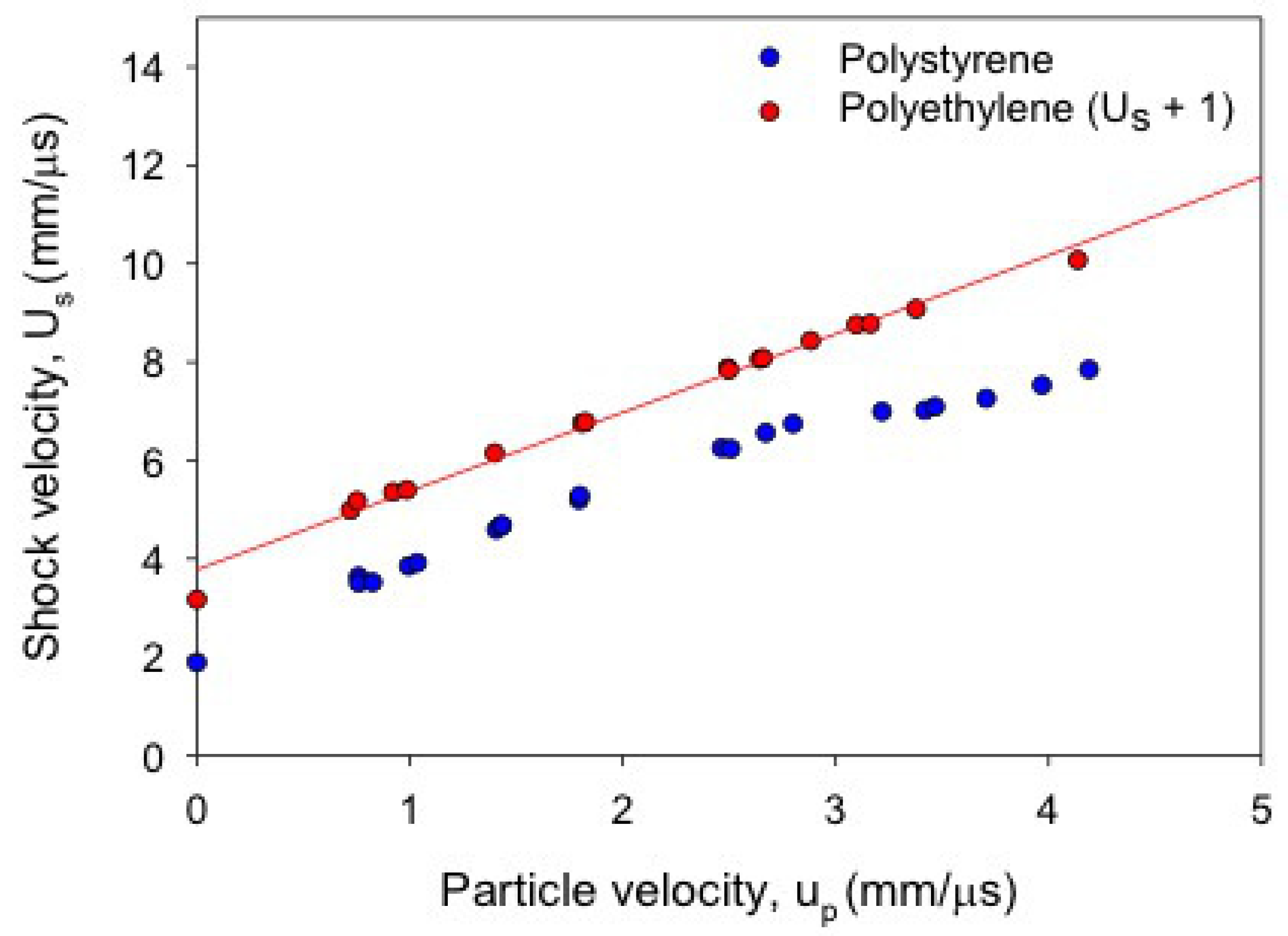

| Material Name | Chemical Formulation (wt %) | Initial Densities (g/cm) |
|---|---|---|
| epoxy | Epon 828 resin (70) | 1.154 |
| Jeffamine T-403 curing agent (30) | ||
| polyurethane | PMDI-based polyurethane (100) | 1.264, 0.867, 0.626, |
| (solid and porous) | 0.451, 0.351 | |
| carbon phenolic | Chopped carbon fibers (56.37) | 1.550–1.555 |
| phenolic polymer resin (35) | ||
| graphite powder (7.75) | ||
| Lithium stearate (<1) | ||
| carbon cyanate ester | carbon fibers (68.5) | 1.555–1.556 |
| cyanate ester resin (31.5) | ||
| SX358 foams | high MW PDMS (43.36) | 0.400–0.500 |
| low MW PDMS (17.19) | ||
| diatomaceous earth (15) | ||
| medium MW PDMS (14.45) | ||
| diphenylmethylsilanol (5) | ||
| PMHS (3) | ||
| tetrapropylorthosilicate (2) |
| Material Name | (GPa) | (%) |
|---|---|---|
| epoxy | 23.1 | 3.9 |
| PMMA | 26.2 | 3.4 |
| PTFE | 41.6 | 1.1 |
| PE (linear) | 24.7 | 0.4 |
| polycarbonate | 20.0 | 11.4 |
| phenolic | 23.2 | 6.7 |
| polysulfone | 18.5 | 12.9 |
| polyurethane | 21.7 | 7.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dattelbaum, D.M.; Coe, J.D. Shock-Driven Decomposition of Polymers and Polymeric Foams. Polymers 2019, 11, 493. https://doi.org/10.3390/polym11030493
Dattelbaum DM, Coe JD. Shock-Driven Decomposition of Polymers and Polymeric Foams. Polymers. 2019; 11(3):493. https://doi.org/10.3390/polym11030493
Chicago/Turabian StyleDattelbaum, Dana M., and Joshua D. Coe. 2019. "Shock-Driven Decomposition of Polymers and Polymeric Foams" Polymers 11, no. 3: 493. https://doi.org/10.3390/polym11030493
APA StyleDattelbaum, D. M., & Coe, J. D. (2019). Shock-Driven Decomposition of Polymers and Polymeric Foams. Polymers, 11(3), 493. https://doi.org/10.3390/polym11030493




