An Integrated Photonic Electric-Field Sensor Utilizing a 1 × 2 YBB Mach-Zehnder Interferometric Modulator with a Titanium-Diffused Lithium Niobate Waveguide and a Dipole Patch Antenna
Abstract
:1. Introduction
2. Theory, Fabrication, and Performance of a Ti: LiNbO3 YBB-MZI Modulator
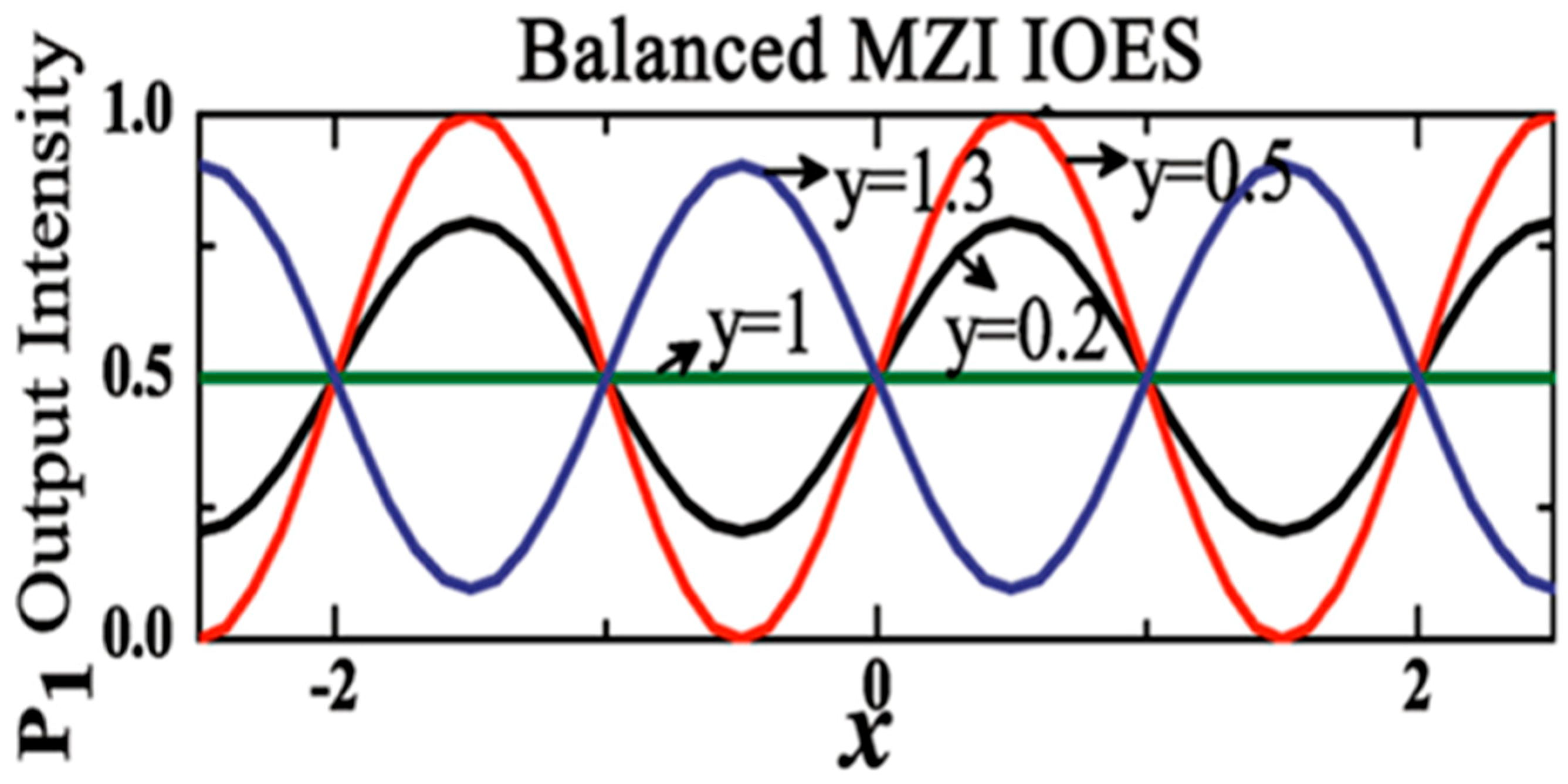
2.1. Device Theory
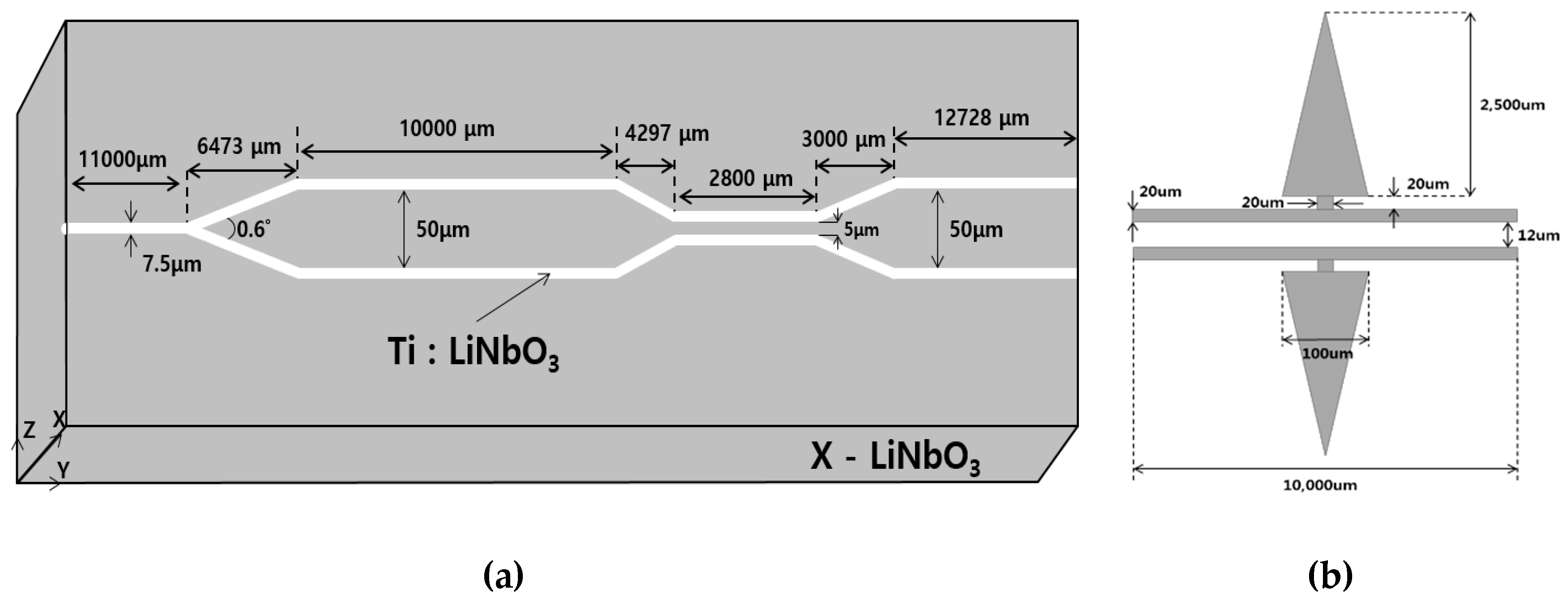
2.2. Designs and Fabrication
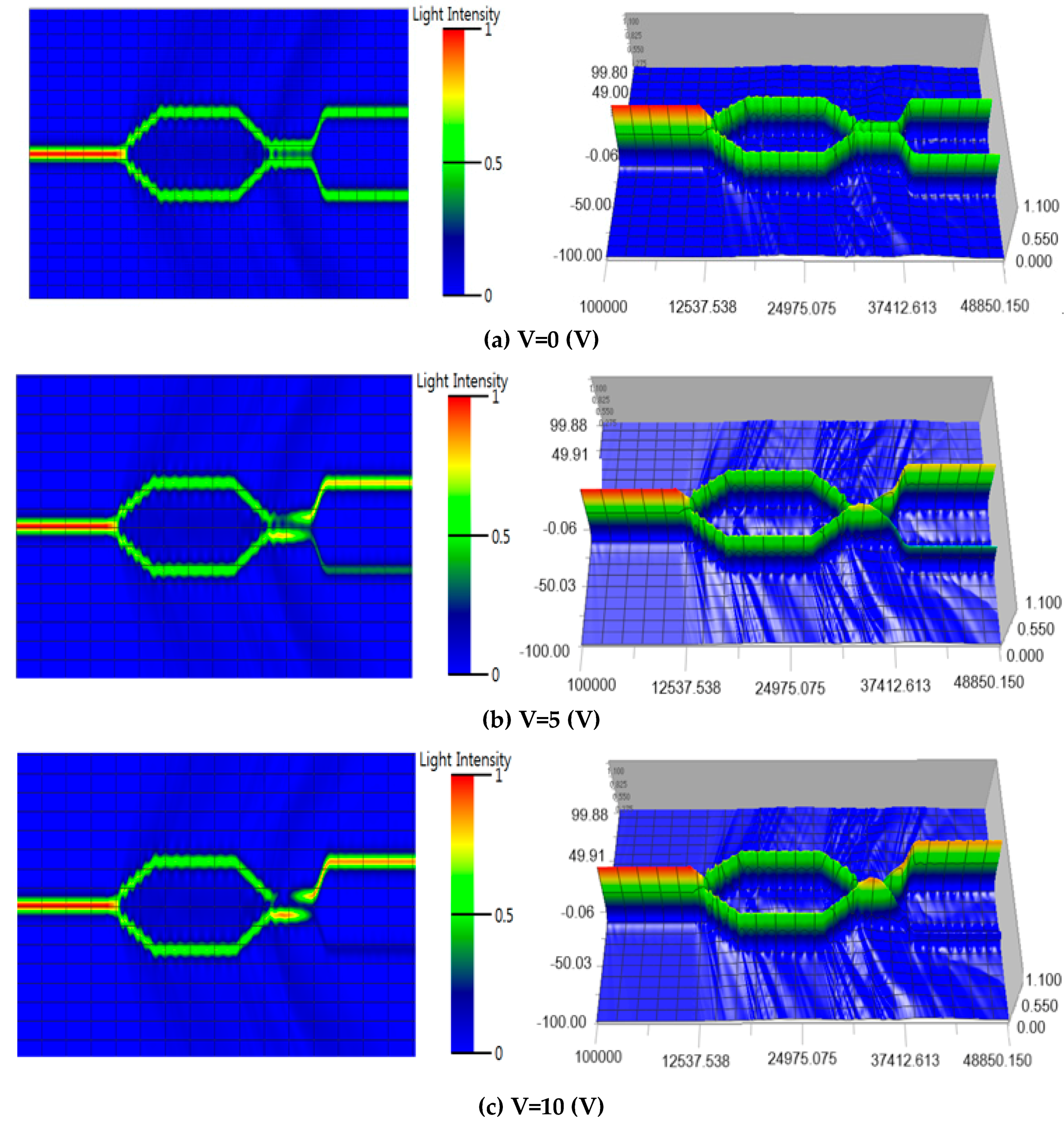
2.3. Performance Evaluations
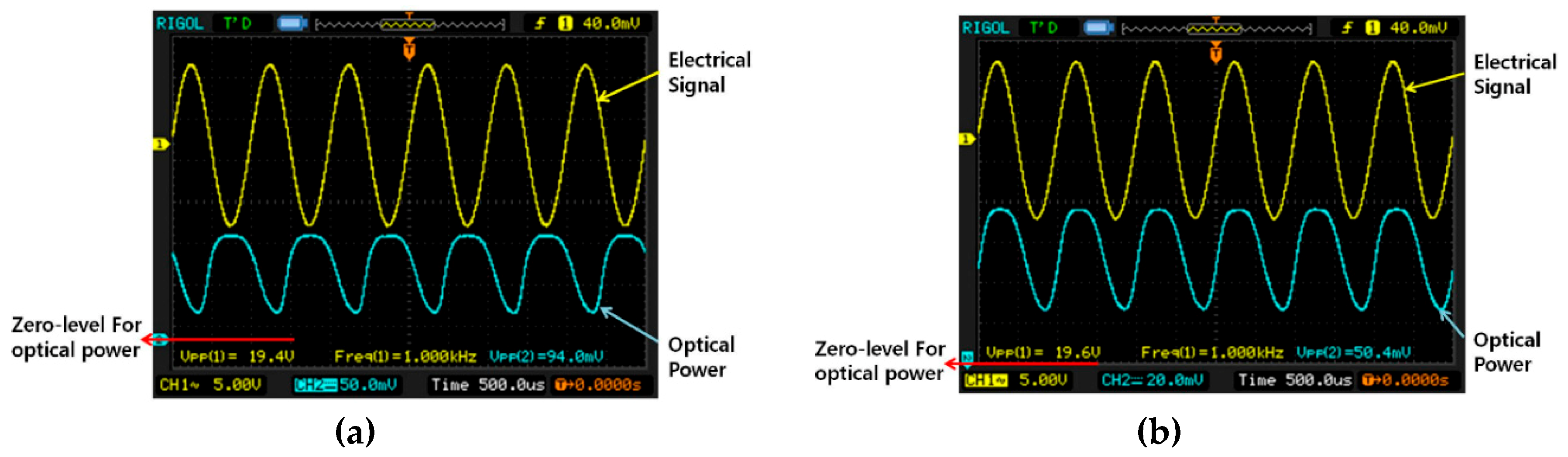
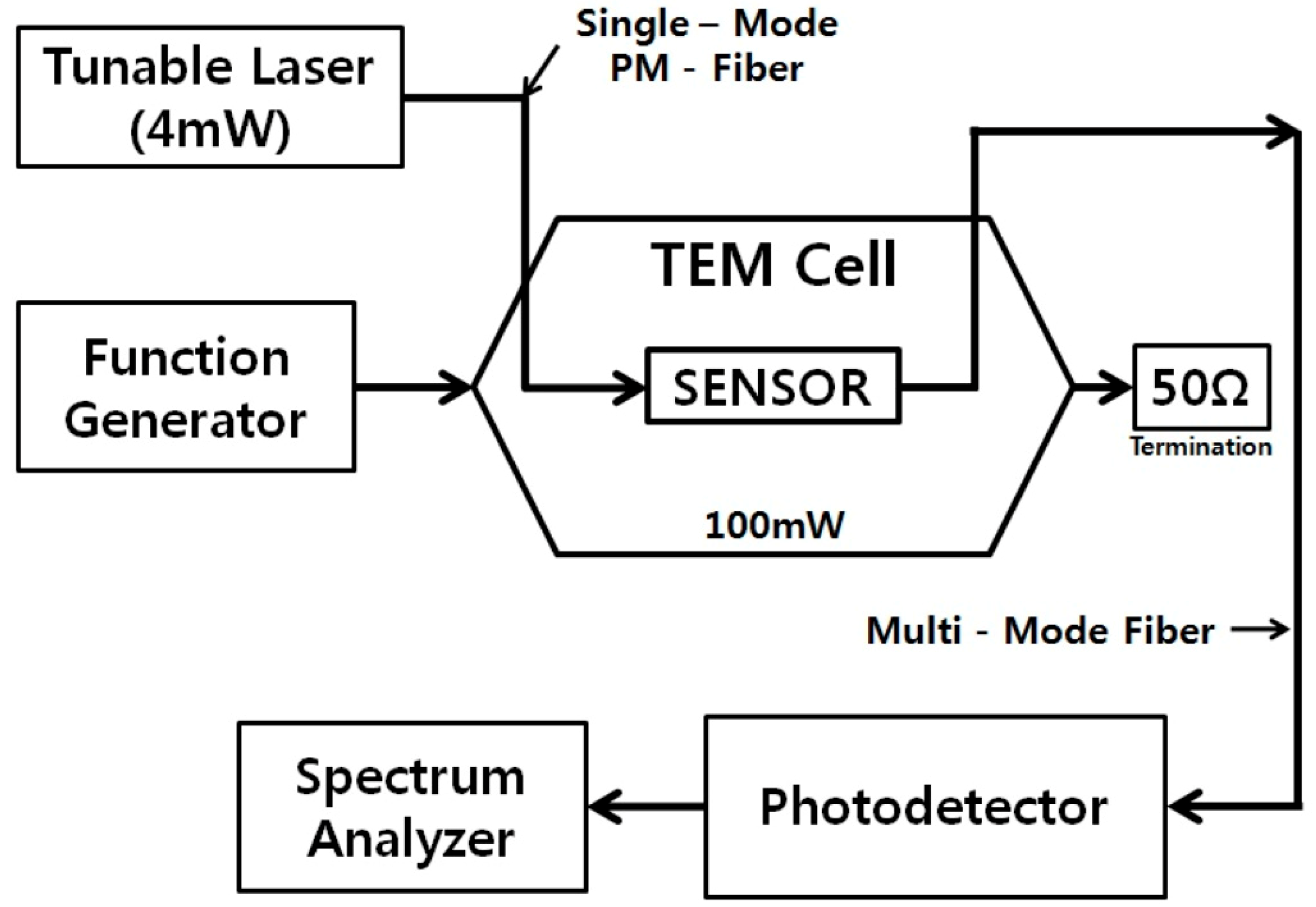
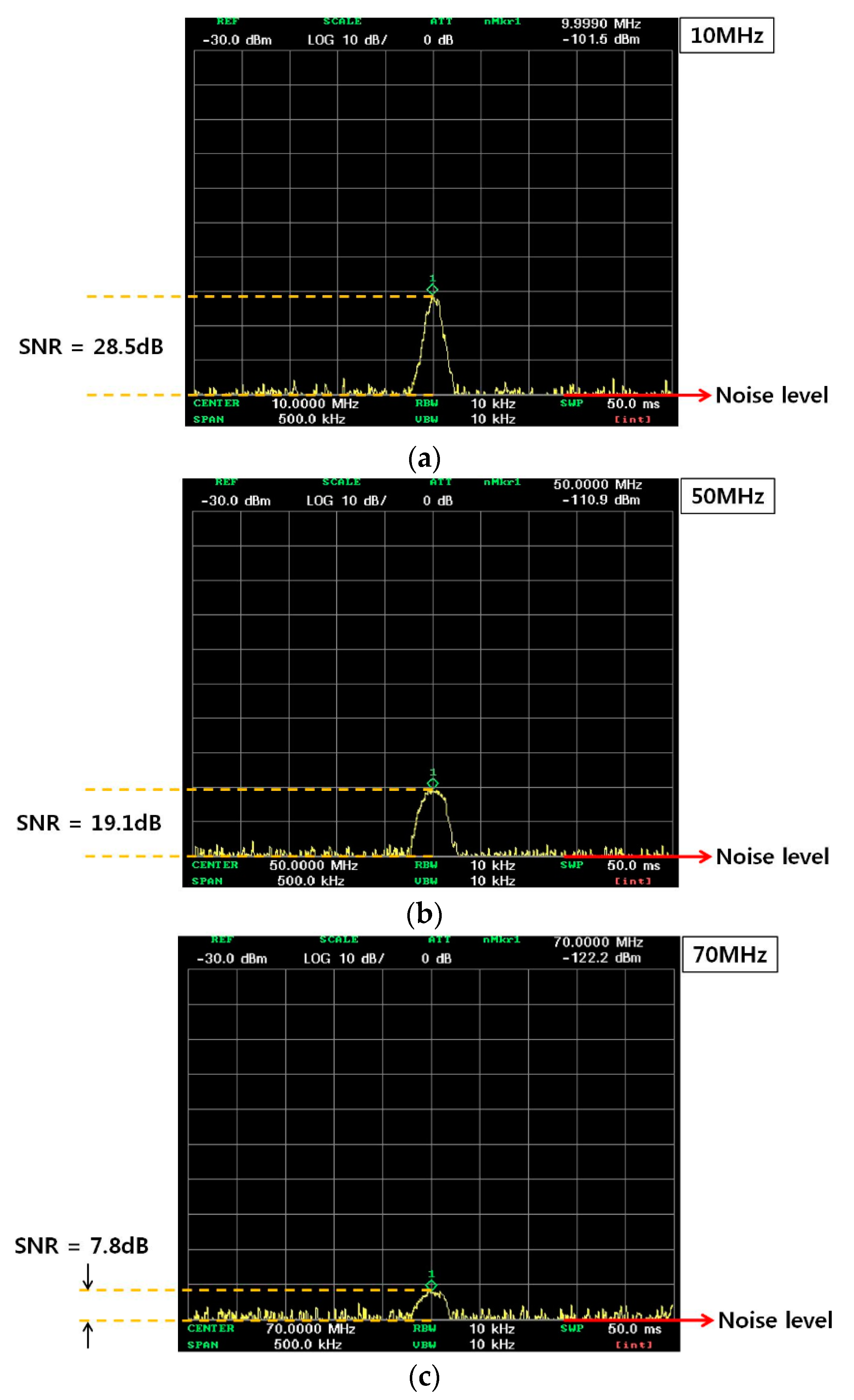
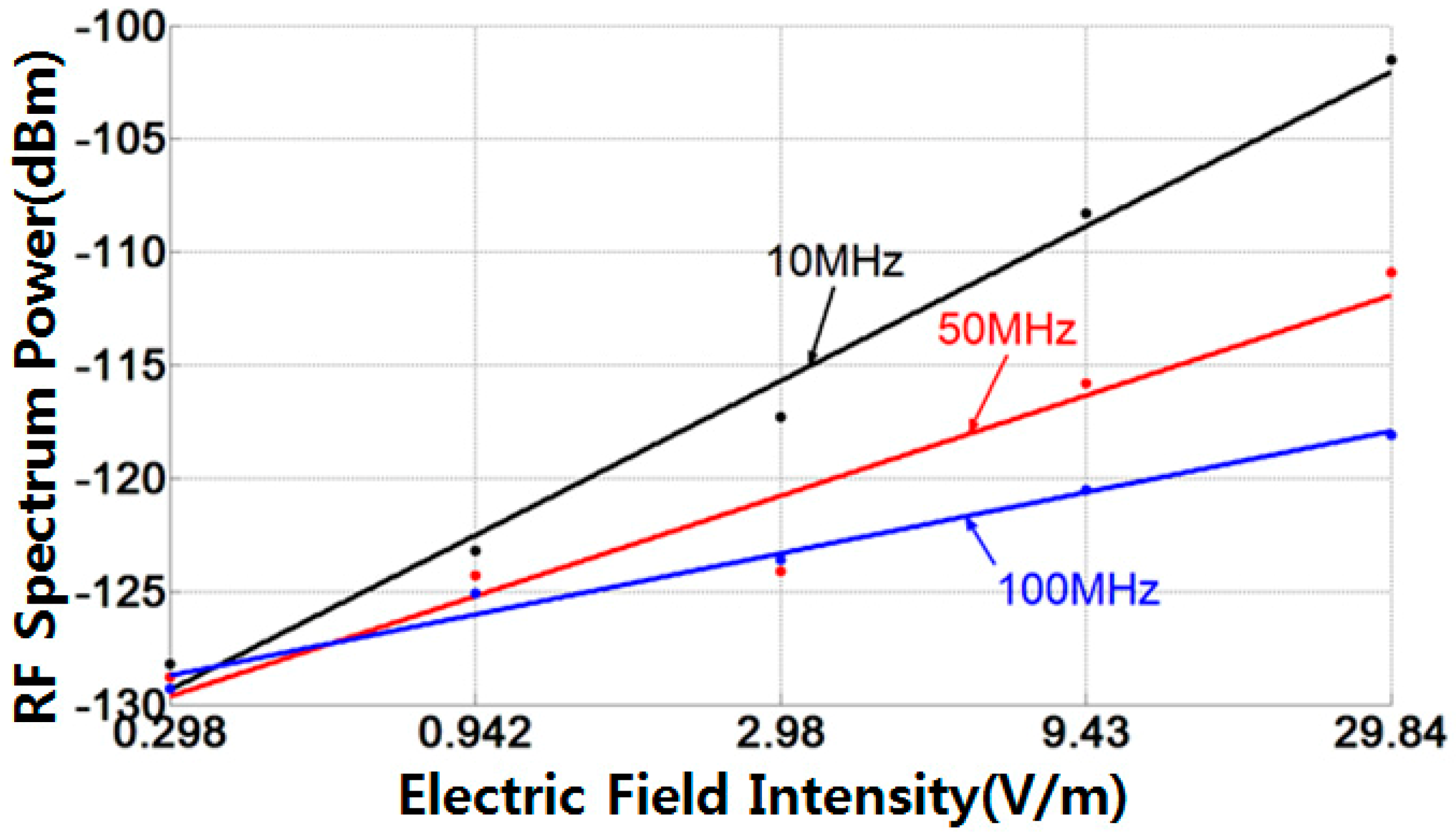
3. Measurement and Experimental Results
3.1. Experimental Setup
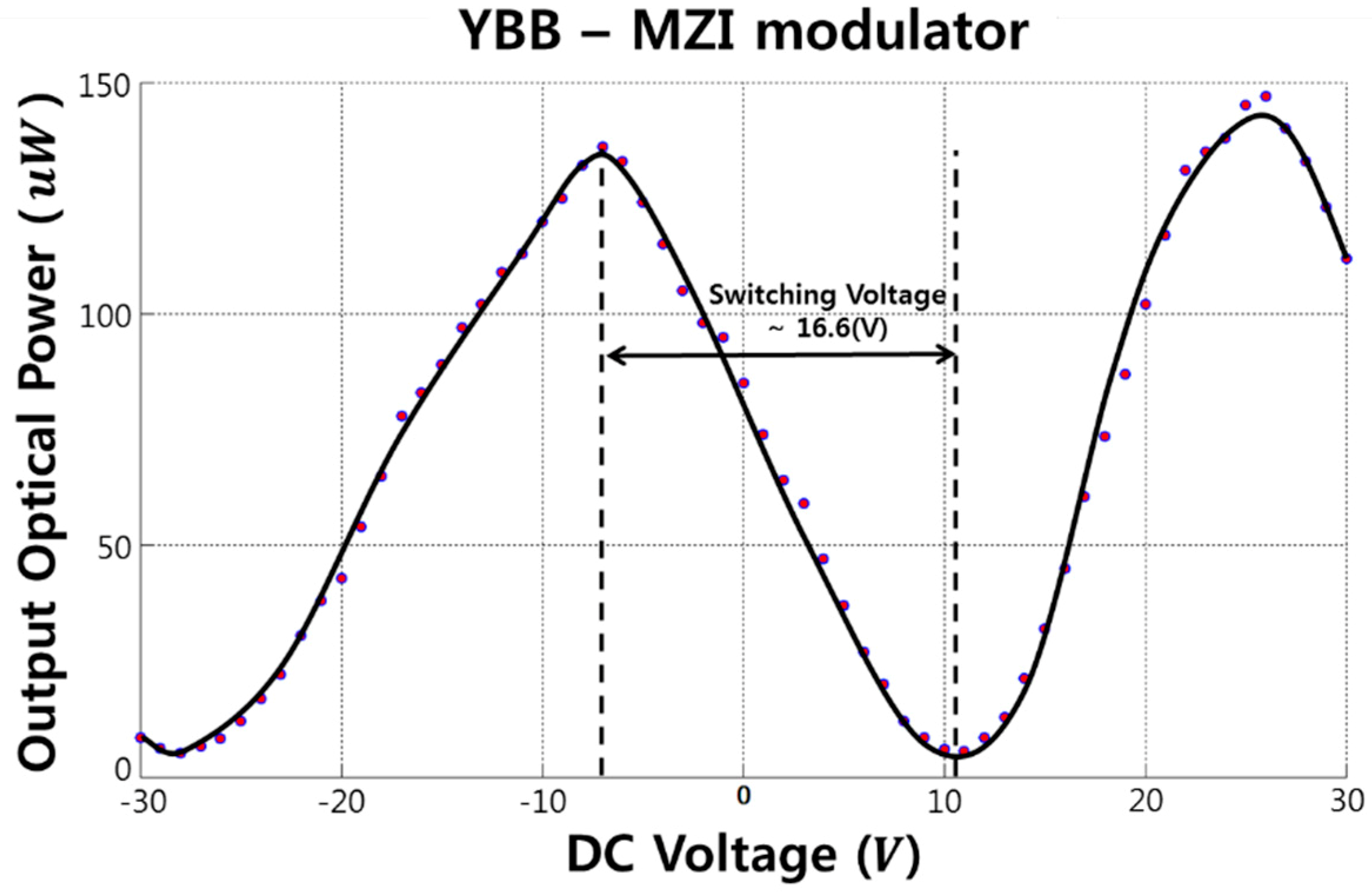
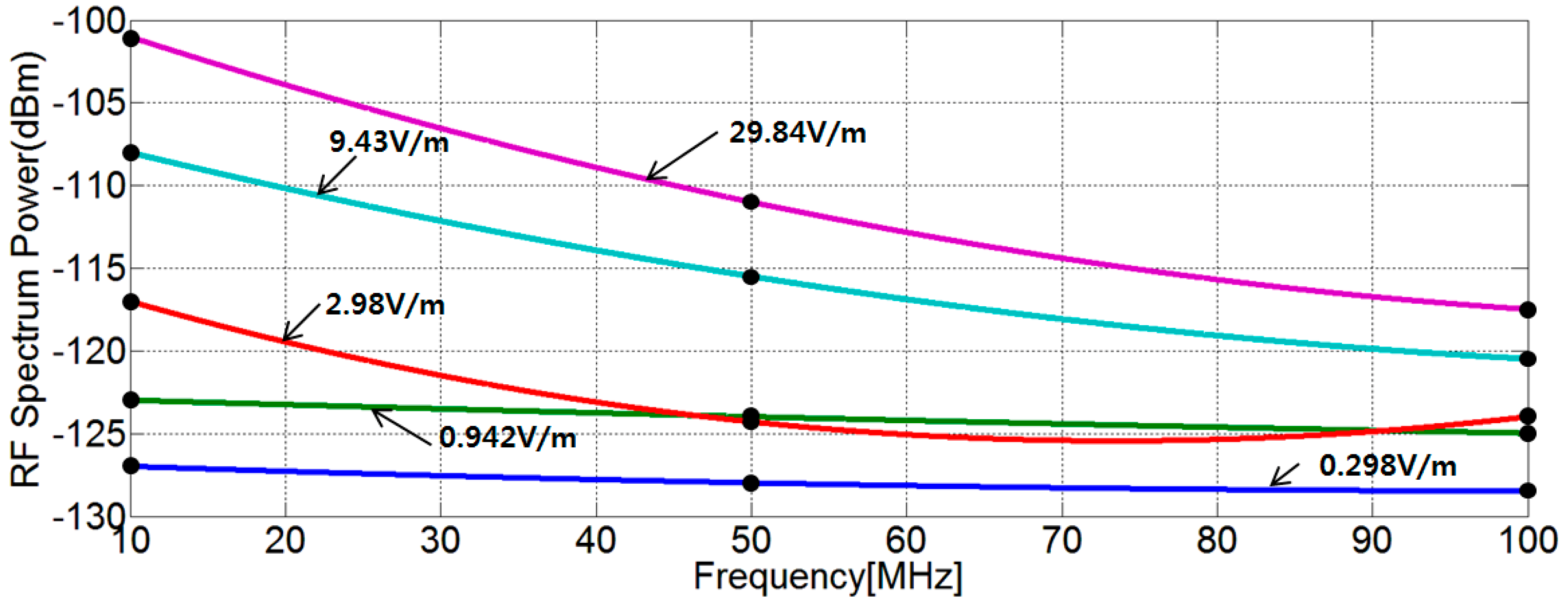
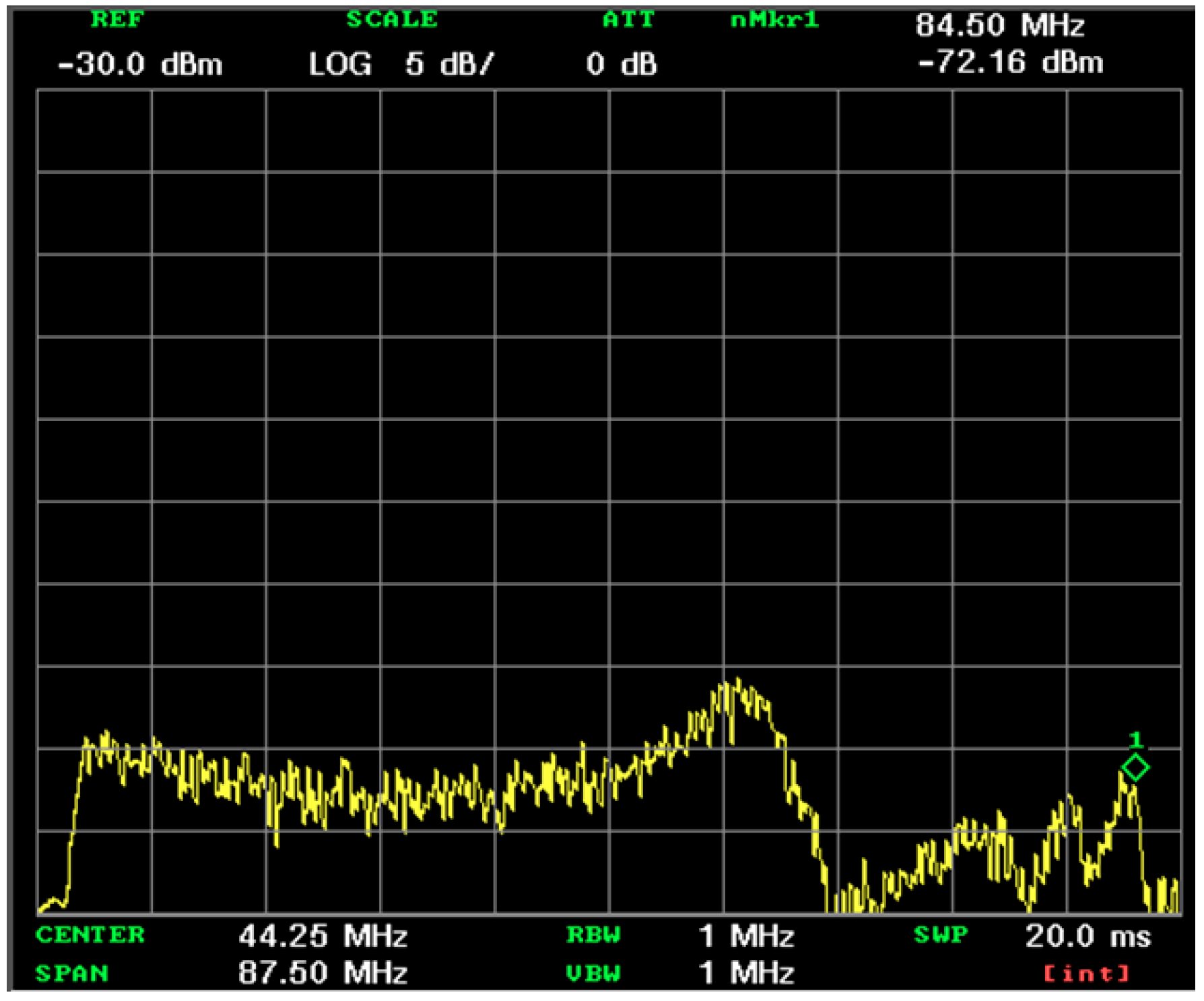
3.2. Test Results and Discussions
4. Conclusions
Funding
Conflicts of Interest
References
- Kuwabara, N.; Tajima, K.; Kobayashi, R.; Amemiya, F. Development and analysis of electric field sensor using LiNbO3 optical modulator. IEEE Trans. Electromagn. Compat. 1992, 34, 391–396. [Google Scholar] [CrossRef]
- Zeng, R.; Wang, B.; Niu, B.; Yu, Z. Development and Application of Integrated Optical Sensors for Intense E-field Measurement. Sensors 2012, 12, 11406–11434. [Google Scholar] [CrossRef] [PubMed]
- Jung, H.S. Photonic Electric-Field Sensor Utilizing an Asymmetric Ti:LiNbO3 Mach-Zehnder Interferometer with a Dipole Antenna. Fiber Integr. Opt. 2012, 31, 343–354. [Google Scholar] [CrossRef]
- Lee, T.H.; Hwang, F.T.; Shay, W.T.; Lee, C.T. Electromagnetc Field Sensor Using Mach-Zehnder Waveguide Modulator. Microw. Opt. Technol. Lett. 2006, 48, 1897–1899. [Google Scholar] [CrossRef]
- Naghski, D.H.; Boyd, J.T.; Jackso, H.E.; Sriram, S.; Kingsley, S.A.; Latess, J. An Integrated Photonic Mach-Zehnder Interferometer with No Electrodes for Sensing Electric Fields. J. Lightwave Technol. 1994, 12, 1092–1098. [Google Scholar]
- Meier, T.; Kostrzewa, C.; Petermann, K.; Schuppert, B. Integrated optical E-field probes with segmented modulator electrodes. J. Lightwave Technol. 1994, 12, 1497–1503. [Google Scholar] [CrossRef]
- Bulmer, C.H.; Burns, W.K. Linear interferometric modulators in Ti:LiNbO3. J. Lightwave Technol. 1984, 2, 512–521. [Google Scholar] [CrossRef]
- An, D.; Shi, Z.; Sun, L.; Taboada, J.M.; Zhou, Q.; Lu, X. Polymeric electro-optic modulator based on 1×2 Y-fed directional coupler. Appl. Phys. Lett. 2005, 76, 98–104. [Google Scholar] [CrossRef]
- Jung, H.S. Electro-optic electric-field sensors utilizing Ti:LiNbO3 1×2 directional coupler with dipole antennas. Opt. Eng. 2013, 52, 064402. [Google Scholar] [CrossRef]
- Thackara, J.I.; Chon, J.C.; Bjorklund, G.C.; Volksen, W.; Burland, D.M. Polymeric electro-optic Mach–Zehnder switches. Appl. Phys. Lett. 1995, 67, 3874–3876. [Google Scholar] [CrossRef]
- Howerton, M.M.; Bulmer, C.H.; Burns, W.K. Linear 1×2 directional coupler for electromagnetic field detection. Appl. Phys. Lett. 1988, 52, 1850–1852. [Google Scholar] [CrossRef]
- Zeng, R.; Wang, B.; Yu, Z.; Ben Niu, B.; Hua, Y. Integrated optical E-field sensor based on balanced Mach-Zehnder inferometer. Opt. Eng. 2011, 50, 114404. [Google Scholar] [CrossRef]
- Twu, R.C. Zn-Diffused 1×2 Balanced-Bridge Optical Switch in a Y-cut Lithium Niobate. IEEE Photonics Tech. Lett. 2007, 19, 1269–1271. [Google Scholar]
- Chiba, A.; Kawanish, T.; Sakamoto, T.; Higuma, K.; Takada, K.; Izutsu, M. Low-Crosstalk Balanced Bridge Interferometric-Type Optical Switch for Optical Signal Routing. IEEE J. Sel. Top. Quant. 2013, 19, 3400307. [Google Scholar] [CrossRef]
- Lee, M.H.; Min, Y.H.; Ju, J.J.; Do, Y.; Park, S.K. Polymeric electrooptic 2 × 2 switch consisting of birfurcation optical active waveguides and a Mach-Zehnder interferometer. IEEE J. Sel. Top. Quant 2013, 7, 812–818. [Google Scholar]
- Schwerdt, M.; Berger, J.; Schuppert, B.; Petermann, K. Integrated Optical E-Field Sensors with a Balanced Detection Scheme. IEEE Trans. Electromagn. Compat. 1997, 39, 386–390. [Google Scholar] [CrossRef]
- Ramaswamy, V.; Divino, M.D.; Standley, R.D. Balanced bridge modulator switch using Ti-diffused LiNbO3 strip waveguides. Appl. Phys. Lett. 1978, 32, 644–646. [Google Scholar]
- Liu, P.L.; Li, B.J.; Trisno, Y.S. In search of a linear electrooptic amplitude modulator. IEEE Photonic. Tech. Lett. 1991, 3, 144–146. [Google Scholar] [CrossRef]
- Webster, M.A.; Austin, M.W.; Winnall, S.T. Balanced-bridge Mach-Zehnder Interferometric Optical Modulator with an Electrical Bandwidth of 30Ghz. In Proceedings of the CLEO/Pacific Rim’97 Conference, Chiba, Japan, 14–18 July 1997. [Google Scholar]
- Nishihara, H.; Haruna, M.; Suhara, T. Optical Integrated Circuits, 1st ed.; McGraw-Hill Book Company: New York, NY, USA, 1985; Chapter 5. [Google Scholar]
- OptiBPM 9.0: Waveguide Optics Design Software; Optiwave Systems Inc.: Ottawa, ON, Canada, 1989.
- Hutcheson, L.D. Integrated Optical Circuits and Components; Marcel Dekker, INC.: New York, NY, USA, 1987; Chapter 3 (Optical Waveguide Fabrication, p70). [Google Scholar]
- Schmidt, R.V. Metal-diffused optical waveguides in LiNbO3. Appl. Phys. Lett. 1974, 25, 458–460. [Google Scholar] [CrossRef]
- Pearsall, T.P.; Chiang, S.; Schmidt, R.V. Study of titanium diffusion in lithium-niobate low-loss optical waveguides by x-ray photoelectron spectroscopy. J. Appl. Phys. 1976, 47, 4794–4797. [Google Scholar] [CrossRef]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, H. An Integrated Photonic Electric-Field Sensor Utilizing a 1 × 2 YBB Mach-Zehnder Interferometric Modulator with a Titanium-Diffused Lithium Niobate Waveguide and a Dipole Patch Antenna. Crystals 2019, 9, 459. https://doi.org/10.3390/cryst9090459
Jung H. An Integrated Photonic Electric-Field Sensor Utilizing a 1 × 2 YBB Mach-Zehnder Interferometric Modulator with a Titanium-Diffused Lithium Niobate Waveguide and a Dipole Patch Antenna. Crystals. 2019; 9(9):459. https://doi.org/10.3390/cryst9090459
Chicago/Turabian StyleJung, Hongsik. 2019. "An Integrated Photonic Electric-Field Sensor Utilizing a 1 × 2 YBB Mach-Zehnder Interferometric Modulator with a Titanium-Diffused Lithium Niobate Waveguide and a Dipole Patch Antenna" Crystals 9, no. 9: 459. https://doi.org/10.3390/cryst9090459
APA StyleJung, H. (2019). An Integrated Photonic Electric-Field Sensor Utilizing a 1 × 2 YBB Mach-Zehnder Interferometric Modulator with a Titanium-Diffused Lithium Niobate Waveguide and a Dipole Patch Antenna. Crystals, 9(9), 459. https://doi.org/10.3390/cryst9090459



