Abstract
Existent methods for determining the composition of lithium niobate single crystals are mainly based on their variations due to changes in their electronic structure, which accounts for the fact that most of these methods rely on experimental techniques using light as the probe. Nevertheless, these methods used for single crystals fail in accurately predicting the chemical composition of lithium niobate powders due to strong scattering effects and randomness. In this work, an innovative method for determining the chemical composition of lithium niobate powders, based mainly on the probing of secondary thermodynamic phases by X-ray diffraction analysis and structure refinement, is employed. Its validation is supported by the characterization of several samples synthesized by the standard and inexpensive method of mechanosynthesis. Furthermore, new linear equations are proposed to accurately describe and determine the chemical composition of this type of powdered material. The composition can now be determined by using any of four standard characterization techniques: X-Ray Diffraction (XRD), Raman Spectroscopy (RS), UV-vis Diffuse Reflectance (DR), and Differential Thermal Analysis (DTA). In the case of the existence of a previous equivalent description for single crystals, a brief analysis of the literature is made.
1. Introduction
Nowadays, more than 50 years after Ballman managed to grow large lithium niobate (LiNbO3; LN) crystals with the Czochralski method [1], synthesizing stoichiometric LN single crystals is still a state-of-the-art matter: The reason behind this is the fact that a Z-cut of a stoichiometric grown crystal costs around 12 times more than one possessing a congruent chemical composition [2]. Compared to this version of the material, while comprehensively studied [3] and well exploited technologically [4,5,6], powders are tacitly considered easier and far less expensive to synthesize. LN powders (LNPws) have served in the past only as survey materials, for example, in the prediction of the nonlinear second order optical capabilities of unavailable single crystals by applying the Kurtz-Perry method in the powdered version [7,8]. Nevertheless, recent developments in LNPws are certainly attracting the attention of scientists and engineers who seek to exploit their potential use in a wide range of applications that span from the construction industry to nonlinear optics.
Cementation materials based on LN have been proposed as a way to improve the air quality of the environment by Artificial Photosynthesis; this is considered important for the reduction of global warming [9]. Regarding LNPws, we emphasize that not only would they be easier than single crystals to implement into cemented materials, but they would also probably enhance the intrinsic surface effects, which are the basis for an improvement of the lifetime of the carriers (photo-generated electrons and holes) involved in Artificial Photosynthesis [10]. Fe-doped LNPws also show, after a post-thermal treatment in a controlled reducing atmosphere, a rather strong ferromagnetic response at room temperature for a doping concentration of the order of 1% mol; this may be considered a first report of the manifestation of ferromagnetism in nanocrystalline LNPws within the regime of very low doping concentrations [11]. Yet in another application based on the powder-in-tube method, a novel fabrication process has been demonstrated for the realization of polarization-maintaining optical fibers [12]. Comprehension of the main mechanism behind this technology, and by looking at the LN mechanical properties [3], it can easily be seen that LNPws are, in principle, good candidates for the fabrication of this type of optical components. Also, possible tuning on the intensity of the Second Harmonic Generation (SHG) that arises from LN micro powders could be ascribed to a proper control of their chemical composition and grain size [13]. This could soon translate into major technical benefits given that neither a critical adjustment of the orientation or temperature in the material (phase matching condition) nor the accurate engineering of a microstructure (quasi-phase matching condition) are substantially needed when the SHG from disordered materials—such as LNPws—are exploited [14].
The performance of LNPws for most of their potentially attributable properties are expected to drastically depend upon their chemical composition (CC), like in the case of single-crystalline LN [3]. Indeed, it has been already demonstrated that size at the nanoscale does not affect the structural symmetry of single LN crystals and that nanosized LN single crystals (down to 5 nm) inherit the nonlinear optical properties from that of large or bulk single crystals [15]: Both the magnitude and the orientation nature of the nonlinear coefficient dmn are preserved. Our work arises from noticing that at least one of the two linear equations that describe the CC of LN single crystals by polarized Raman Spectroscopy measurements [16,17] is not accurate for the case of powders. Hence, it is necessary to properly characterize LNPws, starting by unambiguously determining their CC. Most of the reports found in the literature are only devoted to LN single crystals, where optical and non-optical methods can be found [16,17,18]. Some of the non-optical methods might also be applied to powders; however, in some cases they would not be accessible to everyone, like neutron diffraction methods, and might also give rise to discrepancies like in cases determining the LN CC by measuring the Curie temperature TC. Since temperature is a scalar quantity (light propagates and interacts with matter in vector-like form), it would be permissible to expect a single description of the LN CC in terms of TC that serves for both large single crystals and powders. Interestingly, this is not the case: the systematic measurement of lower TC values (about 10 °C) for LNPws compared to equivalent single crystals has already been addressed and the reason behind this remains unexplained [18].
In this investigation, a custom-made Raman system has been crafted to obtain control on the polarization state of the light at the excitation and detection stages. With this system, verification of the linear equation for the Raman active mode centered at 876 cm−1, as given by Schlarb et al. [16] and Malovichko et al. [17], can be done on stoichiometric (ST) and congruent (CG) lithium niobate single-crystal wafers, according to the provider [2]. Likewise, this serves to calibrate this assembled system and to confidently state that the aforementioned linear equation does not describe LNPws. Then, with a commercially available system, we observed that the linear relationship remains between the CC of LNPws and the linewidth (Γ) of the same Raman mode (876 cm−1), under which in simpler circumstances the polarization state of light at the excitation and detection stages would be disregarded. In accordance to References [16,17,18,19], the accurate determination of the CC of LNPws is proposed by means of a linear fit in terms of the calculated Γ from non-polarized Raman spectra. Yet, the main contribution of this work is based on an a priori probing of the formed phases from 11 different synthesized samples by analysis of X-ray diffraction (XRD) experimental data, while relying on the existent information in the phase diagram that describes the pure LN phase along with its surrounding secondary phases (Figure 1). In this way the linear relationship obtained for the averaged Nb content in the crystallites , in terms of Γ, is affixed to two known or expected values of for the two edges that delimit the pure ferroelectric phase: The boundary with phase LiNb3O8 on one side (Nb excess) and the boundary with phase Li3NbO4 on the other (Li excess).
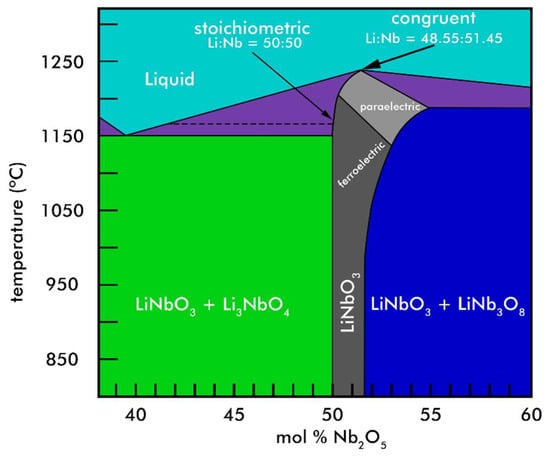
Figure 1.
Schematic phase diagram of the Li2O-Nb2O5 pseudo binary system in the vicinity of LiNbO3—redrawn from the publications by Volk and Wöhlecke [3] and Hatano et al. [20].
The nanocrystalline LNPws are obtained by a mechanochemical-calcination route [21,22]. Gradual addition of Li or Nb has been systematically performed by increasing the mass percentage of a precursor containing the desired ion species. Quantification of secondary-phase percentages is carried out with structure refinement by a standard Rietveld method. An alternative linear equation to determine the CC is also given in terms of the calculated cell volumes by means of the same structure refinement. Additionally, linear fitting of the measured band gap energy (Eg), by means of UV-vis Diffuse Reflectance (DR), is also used for this purpose. Differential Thermal Analysis (DTA) is utilized as a verification technique for specific samples and a fourth empirical equation that describes the CC in terms of the Curie temperature is obtained this way. Scanning Electron Microscopy (SEM) is utilized to verify that the particle size distributions do not vary drastically from one sample to another.
2. Materials and Methods
2.1. Synthesis
High purity lithium carbonate (Li2CO3) and niobium pentoxide (Nb2O5), from Alpha Aesar, were used as starting reagents in a 1:1 molar ratio. The respective masses of the precursors were determined such that 1 g of lithium niobate (LiNbO3; LN) was produced from the following balanced chemical equation:
The resultant product was labeled—and hereafter referred to—as LN-STm (ST: stoichiometric, m: mixture) because, in principle, a LN mixture was obtained after milling with a 1:1 molar ratio in terms of Li and Nb. Variations in the chemical composition (CC) of the final resultant powders were sought by adding, at the milling stage, 1–5% of the mass in one of the precursors (with steps of 1% with resolution of 10−4 g) while keeping the mass of the other precursor constant, in both cases with respect to the masses measured for sample LN-STm (see Appendix A for table). In this way, 10 more samples were synthesized and labeled as LN + 1%LiP, LN + 1%NbP, LN + 2%LiP, and so on up to LN + 5%NbP (P stands for precursor). It must be clarified that the percentages that appear on these labels are not in terms of the ion species solely, but in terms of the whole mass of the precursors that contain them.
The high-energy milling was carried out in an MSK-SFM-3 mill (MTI Corporation) using nylon vials with YSZ balls; a powder:ball ratio of 0.1 was used for each sample preparation. The milling was performed in 30 min cycles, with 30 min pauses to avoid excessive heat inside the milling chamber, until 200 min of effective milling time was reached. Calcination of the resultant materials (amorphous) was done with a Thermo Scientific F21135 furnace in an air atmosphere. All samples were simultaneously calcined with the following programmed routine: 10 °C/min → 600 °C for 30 min → 2 °C/min → 850 °C for 120 min → cooling down slowly to room temperature.
2.2. X-Ray Diffraction
These patterns were measured in air at room temperature using a Bruker D-8 Advance diffractometer with the Bragg-Brentano θ-θ geometry, a source of CuKα radiation (λ = 1.5406 ), a Ni 0.5% CuKβ filter in the secondary beam, and a 1-dimensional position sensitive silicon strip detector (Bruker, Linxeye, Karlsruhe, Germany). The diffraction intensity, as a function of the 2θ angle, was measured between 5.00° and 110.00°, with a step of 0.02° every 38.4 s. Sample LN-STm displays a pure ferroelectric lithium niobate (LN) phase, with Bragg peaks resembling those of the COD-2101175 card previously deposited with the Crystallographic Open Database; supplementary crystallographic data can be obtained free of charge from the Web page of the database [23].
Rietveld refinement was performed using computational package X’Pert HighScore Plus from PANalytical, version 2.2b (2.2.2), released in 2006 [24]. Instructions in the section named Automatic Rietveld Refinement from the HighScore Online Plus Help document were first followed and then adapted for phase quantification of the samples. In short, an archive with information about the atomic coordinates of LN (“2101175.cif”) was downloaded from the Crystallopgraphic Open Database [23]. For the secondary phases LiNb3O8 and Li3NbO4, ICSD-2921 and ICSD-75264 from The Inorganic Crystal Structure Database were used, respectively [25]. The archives were then inserted, along with the experimental data, and Rietveld analysis in “Automatic Mode” was executed, followed by iterative executions in “Semi-automatic Mode,” in which different “Profile Parameters” were allowed to vary until satisfactory indexes of agreement were obtained. The averaged crystallite size was also calculated by Rietveld refinement, following instructions from the Size/Strain Analysis section; a single lanthanum hexaboride (LaB6) crystal was used in this case as the standard sample, analyzed with the ICSD-194636 card.
2.3. Raman Spectroscopy
Two Raman systems were employed in this investigation: One custom-made and one of standard use and commercially available. The former allowed for the set-up of different experimental conditions in terms of the polarization state of light at the incident-on-sample and detection stages, including non-polarized, parallel polarized (p), and cross polarized (s) situations. Adopting the so-called Porto’s formalism, these experimental conditions were , and , respectively; where, in general, A(BC)D stands for light propagating in the A direction with linear polarization B, before the sample, while selective detection is done on the D direction with polarization C [26].
The commercially available system only featured the non-polarized configuration. It was a Witec alpha300R Confocal-Raman microscope with a 532 nm source of excitation wavelength and 4–5 cm−1 of spectral resolution. With this equipment, the Raman spectra were collected in the range 100–1200 cm−1 at room temperature and light incident on the normal component of the sample with a power of 3.4 mW; a Nikon 10 objective was used to focus the incoming light on a 1:5 mm spot. An intensity of approximately 11Wcm−2 was delivered to the sample. The customized open-air Raman system consisted of an excitation beam output of a continuous wave diode laser at 638 nm wavelength with a power of 37 mW (Innovative photonic solution). The beam was linearly polarized from variable angle mounting and transmitted through a beam splitter to focus the excitation beam into the sample by an aspherized achromatic lens (NA = 0.5, Edmund optics). The excitation spot diameter measured at the focus point had a ~10 μm radius. The collected Raman scattered light from the sample through the aspheric lens and the beam splitter was focused by two silver coated mirrors and one bi-convex lens into a fiber Raman Stokes probe (InPhotonics) that was connected to a QE65 Raman Pro spectrometer (Ocean optics) for a Raman shift range detection between 250–3000 cm−1. In its use for the characterization of the powders, the light at λ = 638 nm was incident at razing angle with P = 10 mW. The Raman spectra were collected in the range 200–1200 cm−1 at room temperature with a spectral resolution of 8 cm−1. In this case, a laser intensity of approximately 3 kWcm−2 was delivered to the sample. Due to technical issues, most of the utilized experimental conditions were different from one Raman system to another—it is shown how this did not alter the obtained results, except for the detection mode which in both cases was fixed at the backscattering-detection mode (Figure 2).
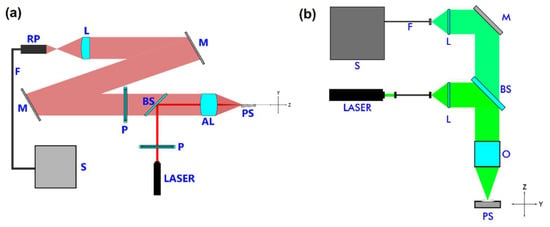
Figure 2.
Scheme of the experimental configurations used for the acquisition of Raman spectra: (a) Custom-made featuring both configurations, polarized and non-polarized; (b) commercially available featuring only non-polarized measurements. From left to right: RP—Raman probe, F—filter, M—mirror, L—lens, P—polarizer, BS—beam splitter, AL—aspheric lens, PS—powdered sample, S—spectrometer, O—objective.
2.4. UV-Vis Diffuse Reflectances and Differential Thermal Analysis
An Ocean Optics USB2000+ UV-VIS Spectrometer and an R400-Angle-Vis Reflection probe were used to collect the diffuse reflectance (DR) spectra of the samples and an Ocean Optics DH-2000-BAL Deuterium-Halogen light source was utilized. Commercially available aluminum oxide (Al2O3) was chosen as the standard reference. Precautions were taken so that the approximations necessary to apply the Kubelka-Munk Theory were accomplished [27,28,29]. These approximations are, mainly speaking, a preparation of the sample being thick enough so that the measured reflectance does not change with further increasing of this parameter (avoidance of Fresnel reflection) and an averaged size of the particles being smaller than such thickness, but larger relative to the wavelength (scattering independent of the wavelength).
The first of these experimental conditions was fulfilled by using a self-supporting pressed powder rectangular mount (3 × 3 × 3 mm); in all the experiments, an amount of approximately 1 g of powder was deposited. The second requirement was fulfilled by determination of the average size particle in the powders, using a field emission Scanning Electron Microscopy (SEM), with a JEOL JSM 5600-LV microscope (V = 20 kV, at 1500×, Mitaka, Tokyo, Japan). The micrographs were analyzed with ImageJ software: The edge length histograms were obtained from statistical analysis of at least 200 particles. Lastly, we followed the recommendation of grinding the powders in an agate mortar for a few minutes to avoid sample heterogeneity and regular reflection [29]: All samples were ground for 10 min before measurements.
On the other hand, the Curie temperatures for the samples LN-STm, LN + 1%NbP, LN + 2%NbP, and LN + 3%NbP were measured using differential scanning calorimetry (DSC) equipment coupled to thermogravimetry (TGA), SDT Q600 of TA instruments. The calorimeter was calibrated with respect to the copper melting point (1084 °C). The samples were analyzed in a wide temperature range between room temperature and 1200 °C, at a heating rate of 20 °C/min under a nitrogen atmosphere and using alumina containers. The ferroelectric-paraelectric state transition was observed around 1050–1080 °C. Subsequently, the samples were analyzed in four cooling cycles from 500 °C to 1200 °C at the same heating rate, 20 °C/min, and the process was seen to be reproducible, indicating that there was no permanent change in the volume of the pseudo-ilmenites.
3. Results and Discussion
3.1. X-Ray Diffraction
The obtained XRD pattern for sample LN-STm is shown in the bottom line of Figure 3a. The corresponding pattern of single crystalline LN is in agreement with the one indexed in COD-2101175 [23]. The difference, for all samples, between the obtained XRD patterns (Iexp) and their respective calculated patterns by means of Rietveld refinement (Iref) is also shown in the upper half of this figure; for the secondary phases LiNb3O8 and Li3NbO4, ICSD-2921 and ICSD-75264 from The Inorganic Crystal Structure Database were used, respectively [25]. For all cases, this difference function tends to a common baseline, so that neither the formation of thermodynamically stable phases (other than LiNbO3, Li3NbO4, and LiNb3O8) nor the presence of one of the precursors in an interstitial fashion can be deduced, that is, without participating in the formation of one of the involved phases. As seen in this figure, most of the synthesized powders resulted in a pure ferroelectric LN phase, except for samples LN + 4%NbP and LN + 5%NbP (blue lines). Figure 4 and Table 1 have been added for a better visualization of this argument. A loss of Li equivalent to the loss of 5 mol % Li2CO3 could be hastily addressed for the central sample LN-STm due to the calcination process. Nevertheless, this information can also be interpreted as having no loss of Li and thus the assumption of a non-ideal sensitivity for the XRD technique must be taken. In other words, a detection threshold of 5.0 mol % Li2CO3 = 1.4 mol % Nb2O5 exists for ‘seeing’ a secondary phase by the XRD analysis, combined with the structure refinement, done in this investigation. This assumption has been taken into account in this investigation, thus defining the boundaries that delimit the pure ferroelectric LN phase for samples LN-STm (Li excess) and LN+3%NbP (Nb excess). For the calculation of mol % equivalence between precursors, the values for the relative atomic masses of Li and Nb have been used as presented in the Periodic Table provided by the Royal Society of Chemistry [30].
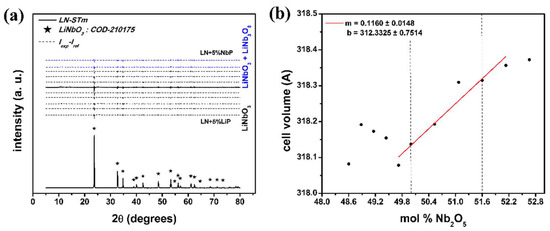
Figure 3.
XRD results: (a) Experimental pattern of sample LN-STm and, for all samples, the differences between experimental and their respective calculated patterns with Rietveld refinement. The central sample, LN-STm, is distinguished from the rest by the solid line; (b) cell volume as a function of mol % Nb precursor. The edges of the ferroelectric pure LN phase are represented by the vertical dashed lines.
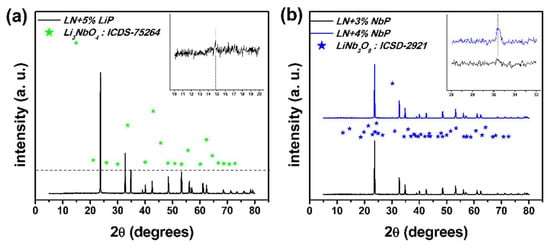
Figure 4.
X-ray diffraction patterns close to the boundaries of the pure ferroelectric LN phase: (a) Under the assumption of no loss of Li, sample LN-STm is on the excess of the Li boundary; (b) sample LN + 3%NbP is on the excess of Nb boundary.

Table 1.
Phase percentages present in the synthesized samples, along with the calculated cell volumes and relevant agreement indices of the refinement process.
The calculated cell volumes are plotted in Figure 3b, as a function of the averaged Nb content in the crystallites , as calculated by the previous procedure (re-labeling of the samples in terms of their predicted CC). A clear linear trend exists for a CC range of 49.7–52.1 mol % Nb2O5. Hence, for future reference, we first propose the determination of for LNPws in this CC range with the following equation:
where Vcell stands for the cell volume in (angstrom)3 units, calculated by a standard structure refinement method. The 0.5 mol % uncertainty is determined by the sum of the uncertainty associated to the linear fitting (0.14 mol % Nb2O5) and half the longer step in the Nb precursor (0.53/2 = 0.27 mol % Nb2O5), both multiplied by the square root of the averaged goodness of fit factor for the six involved samples (). The uncertainty associated with the linear fitting has been determined following several calculations according to Baird [31].
Justification of the Assumption made in the X-Ray Diffraction Analysis
The reasoning behind the assumption made can be summarized in three main points. First, a good agreement can be seen with the phase diagram (Figure 1), upon which by close inspection, around T = 850 °C, a CC range of approximately 1.7 mol % Nb2O5 is deduced for the pure ferroelectric LN phase. In this investigation, the observed range goes from the ST point 50.0 mol % (sample LN-STm) to a near-CG point 53.0 − 1.4 = 51.6 mol % (sample LN + 3%NbP), that is 1.6 mol % Nb2O5. A direct explanation would not be found for an estimated range of 4.4 mol % Nb2O5 if this assumption had not been taken. Secondly, under these circumstances it follows that, out of 11 synthesized samples, only samples LN-STm, LN + 1%NbP, LN + 2%NbP, and LN+3%NbP resulted to have a pure ferroelectric LN phase. It will be soon shown that, for all the performed studies, unmistakable linear relationships happen to exist among these samples and their corresponding experimental parameters (related to the CC); a striking, very sensitive, deviation from these trends is observed for all samples out of this range, in some cases even under the consideration only of neighbor samples such as LN + 1%LiP and LN + 4%NbP. Lastly, besides the well-known difficulties to produce single-phase ST LN at temperatures used in solid-state reactions (T ≥ 1200 C) [32,33], much ambiguity can be found in the literature concerning deviation from stoichiometry in the formation of LNPws at calcination temperatures near T = 850 °C. While only one work is found to report no loss of Li after two 16-hour reaction periods at 1120 °C [34], other authors have observed the loss of Li at 600–800 °C within at least three different investigations [33,35,36]. However, these methods of synthesis are very different from each other, except for those in the works published in 2006 (Liu et al.) [33] and 2008 (Liu et al.) [36], which are aqueous soft-chemistry methods. The deviation from stoichiometry tendency in the formation of LNPws through aqueous soft-chemistry methods, in comparison to non-aqueous (as in this investigation), has already been identified [37]. Besides, high-energy milling has previously been proposed as a method to prevent loss of Li, in contrast to Pechini’s method, sol-gel, and coprecipitation [21].
It is also worth mentioning that De Figueiredo et al. [38] had a similar observation in their investigation: They had a small amount of non-reacted Li2CO3 not detected by XRD, but only identified after DTA and Infrared Spectroscopy; the LNPws were synthesized via mechanical alloying. They explained this observation by assuming that the number and size of the Li2CO3 nanocrystals were sufficiently low and small to not being detected by XRD. Hence, the assumption taken of no loss of Li and the existence of a detection threshold of 1.4 mol % Nb2O5 in XRD might have been justified with these lines. This detection threshold can be considered unique and expected to change according to different experimental variables and analysis tools, including spatial and temporal size of the step during the experiment, brand, and model of equipment utilized, as well as the software used for Rietveld refinement, among others.
3.2. Raman Spectroscopy
Verification of the linear equation for the Raman active mode centered at 876 cm−1 [16,17] was done by using the assembled Raman system (Figure 2a) on the aforementioned stoichiometric (ST) and congruent (CG) lithium niobate (LN) wafers. Even though the experimental conditions therein described were not exactly reproduced, this could be accomplished within the given absolute accuracy and, thus, calibration of this equipment could be done. At this instance, use of the equation for the Raman band located at 876 cm−1 has been done [16,17]. A detailed description of the phonon branches of single crystal LN and their assignment can be found elsewhere [39,40]. No specifications regarding the resolution of the Raman bands or fitting techniques are given by Schlarb et al. [16] or Malovichko et al. [17], although these procedures are critical for achieving great accuracy in the determination of the LN CC [16,39,40,41]. Moreover, it is not clearly stated whether the complete linewidth (Γ), or just the halfwidth, is to be entered in this equation.
The resolution of this Raman band was explored, after normalization of the full spectra, by two distinct line shape fittings: Gaussian and Lorentzian. The Full Width at Half Maximum (FWHM; Γ) was extracted from the fitting (Origin Pro 8) and used in the calculations. Change of the intercept value from 53.29 to 54.8 had also been tried, as suggested whenever no polished single crystals are available [16]. From all the calculations performed, we noticed that only for those (halfwidths) under a Lorentzian fit and using the intercept value of 54.8, the calculated Li contents follow this equation within the uncertainty of 0.2% mol, which “govern the absolute accuracy of the described method” [16]. The values obtained by this calculation were 50.3 mol % for the ST wafer and 48.5 mol % for the CG one. Thus, this approach has been adopted for the investigation with the LNPws. Before presenting these results, one more point needs to be further discussed.
It can be argued that the value of 50.3 mol % for the ST wafer goes out of the uncertainty range, thus not justifying the implications made above. Nevertheless, it must be noticed that the experimental conditions used in this investigation are subtly different from those described by Schlarb et al. [16] and Malovichko et al. [17]. Succinctly, they used an experimental Z(YY)X configuration (using Porto’s convention [26]), whereas for our case, given certain technical limitations, a configuration was used in this investigation. Besides, no direct statement concerning the propagation of light along an axis of the crystals studied is done by these authors, but it can be inferred that they excited along the crystallographic Z-axis by recalling the condition of zero (or small) phonon directional dispersion to simplify their adjustments (band resolution) [16]. In our case, wafers with Z-cuts were used, upon which light was made to impinge on normal to the surface. The incident radiation then propagates in a plane containing the extraordinary axis, inducing in this way short-range atomic forces (extraordinary refractive index) that compete to long-range atomic forces behind the splitting of longitudinal optic (LO) and transverse optic (TO) phonons [42]. Significant changes in the Raman spectra of LN single crystals, especially in the position of the bands located at 153 cm−1 and 578 cm−1 (red and blue shifts), have already been identified and addressed to the overlapping of the LO and TO lattice vibrations [42,43,44]. Such an overlapping is clearly a drawback for band resolution and it might be the reason behind the discrepancy between predicted and measured values; interestingly, this is only relevant in single crystals of ST composition.
Application of the same procedure to the synthesized LNPws gives unsatisfactory results, according to the implications obtained from the XRD analysis (re-labeling of the samples in terms of their predicted CC, Figure 3b). As expected, the same occurs if this is applied to the non-polarized Raman spectra. It worsens considering the Raman band is located at 153 cm−1, where the corresponding linear equation is used, and the Raman spectra are measured with the commercially available Raman system (Witec), which features recording of intensity in the range 0–200 cm−1. However, well defined linear trends can be seen for the calculated Raman halfwidths around the pure LN ferroelectric phase, but only for the case of the band at 876 cm−1 as measured under non-polarized experimental conditions. For both situations (Witec and self-assembled systems), the trend is of an increasing halfwidth with decreasing Li content; surprisingly, despite the great differences between both experimental configurations and conditions (Figure 2), both trends are very similar. This feature can also be seen for the positions of the bands (xc), and it remains for the resultant values of the halfwidths divided by the positions (Γ/2xc). Figure 5b shows how this Γ/2xc parameter relates to the Nb content of the synthesized powders, as determined by XRD analysis. Given the similarity between the results obtained by both experimental configurations, this graph represents the average of such results. For sample LN-STm, the Raman spectra measured with the Witec system are shown in Figure 5a; these closely resemble those obtained in polycrystalline LN by Repelin et al. [40].
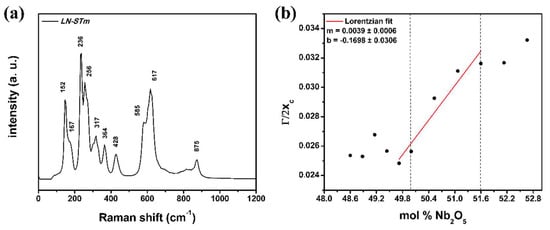
Figure 5.
Results obtained by Raman Spectroscopy: (a) Non-polarized Raman spectra of the central sample LN-STm, obtained with the commercially available Raman system; (b) Linear trend upon which Equation (3) is based for the case of band resolution with a Lorentzian fit, averaged calculated data from those obtained by two distinct Raman systems.
As the resolution of this Raman band (876 cm−1) by means of a Gaussian fitting does not entail significant changes either, the following equations are proposed for the determination of in LNPws:
where Γi stands for the FWHM in cm−1 of the Raman band around 876 cm−1, resolved by linear fitting either using a Lorentzian or a Gaussian line shape, denotes the center of this Raman band. Normalization of the full Raman spectra precedes the linear fitting and, regardless of the line shape, enlargement around this band is suggested, extending it as much as possible (precise determination of the baseline) and applying a single or double-peak fitting, rather than performing a multi-peak fitting to the full Raman spectra. Like in the XRD analysis, the uncertainty is determined by summation over half the longer step in the Nb precursor (0.53/2 = 0.27 mol % Nb2O5), the uncertainty associated to the linear fitting (0.12 mol % Nb2O5 (0.23 mol % Nb2O5) for the Lorentzian (Gaussian) case), and dividing by the square root of the averaged (five involved samples) reduced χ2 fit factor obtained in the resolution of the band (). Once more, the uncertainty associated to the linear fitting is determined following several calculations according to Baird [31].
Lastly, the fact that the trend remains linear is not surprising. Scott and Burns [34] have previously demonstrated this, based on experimentation; showing in this way that the Raman spectra from poly-crystalline LN inherits the essential features of those from single crystal LN [45]. Conceptually, this can be understood by recalling the intrinsic nature of LN to deviate from the stoichiometric point. Under regular circumstances, LN contains high amounts of intrinsic defects such as anti-site Nb ions (NbLi), which are compensated by their charge-compensating Li vacancies (VLi) [3,46]. Such a substitution mechanism imposes fundamental changes on the electronic structure, inducing in this way, variations in the macroscopic dielectric tensor of LN [16]. Yet, because in this substitution mechanism gradual Nb increments are proportional to the decreasing of Li, the variations of the dielectric tensor are expected to be linear, as far as the Nb-Li interchange is sufficiently small.
3.3. UV-Vis Diffuse Reflectances and Differential Thermal Analysis
The sensitivity of the chemical composition (CC) of lithium niobate (LN) to the fundamental band gap or fundamental absorption edge has been previously reported for LN single crystals [47,48]. Kovács et al. have given a corresponding linear equation with different sets of fitting parameters, depending on the character of the refractive index (ordinary and extraordinary), and the definition of the absorption edge (either as corresponding to a value in the absorption coefficient of 20 cm−1 or 15 cm−1) [48]. There is no point in using this equation to describe the CC of LNPws, since these terms (refractive index and absorption coefficient) make no sense when related to powders.
In this investigation, the direct measurements of the DR spectra for the 11 samples are transformed to the Kubelka-Munk (K-M) or remission function , straightforwardly with the acquisition software (Spectra Suite). Since this function is a proxy of the actual absorption spectrum [29], these data are used to find the fundamental absorption edge for all the samples. For practical purposes, a direct band gap is assumed for LN—notice that it could also be assumed to be indirect [49]. Thus, under this assumption, the fundamental band gap is proportional to the square of the remission function, as is shown in Figure 6a,b. The Nb content of LNPws is linearly related to the fundamental band gap Eg (Figure 6c). Equation (4) allows us to accurately determine the Nb content of a determined sample, in terms of Eg (in eV units).
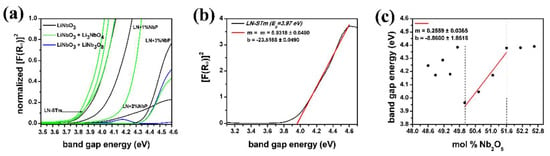
Figure 6.
Graphics derived from analysis of the data obtained by UV-vis Diffuse Reflectance measurements: (a) Normalized Kubelka-Munk or remission functions in terms of the energy of the light in eV units; (b) Demonstration of the determination of the onset for sample LN-STm (assuming a direct interband transition) to determine the fundamental band gap energy; (c) Fundamental band gap energy as a function of mol % Nb precursor.
Interaction of light with matter at a fundamental level must be considered in the DR and Raman Spectroscopy techniques. In other words, because of the ubiquitous randomness of the media, strong scattering effects are present in both Rayleigh (crystallite size) and Mie scattering (particle size). The study of the intensity and angular distribution of the scattered field by the powders has not been done on this investigation; however, certainty of the results obtained by these techniques is expected under certain limits if no large variations in the crystallite and particle average sizes are found. Considering all the synthesized samples, the resultant average crystallites are distributed in a 100–300 nm range, with overall mean and standard deviation values of 157 and 58 nm, respectively. Also, for four randomly chosen samples, the distributions in particle size were determined by statistical analysis of micrographs obtained by Scanning Electron Microscopy (SEM). The obtained distributions were very similar and the centers (xc) of these distributions fall within a band 1 μm thick, centered at 2.6 μm, as shown in Figure 7.
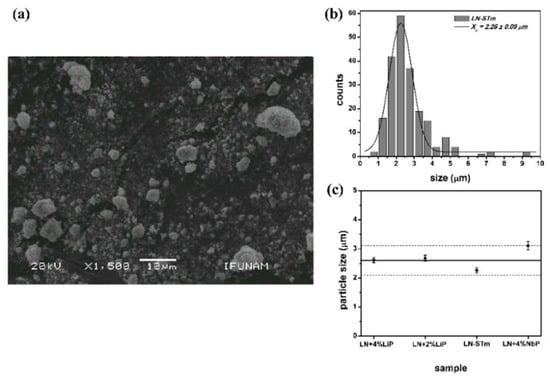
Figure 7.
Information derived from SEM: (a) and (b) Micrograph and particle size distribution for sample LN-STm, respectively; (c) Centers of the particle size distributions obtained for four randomly-chosen samples.
Regarding the ferroelectric-paraelectric phase transition, a change in the crystalline structure of LN occurs in which the symmetry of the system increases [3]. This second-order phase transition is described by the Landau order-disorder theory, where a finite discontinuity in the heat capacity of the system having this transition has been addressed as a direct thermodynamic consequence [50]. Figure 8a shows the difference in temperature between the reference container for each of the studied samples; with this technique, only samples presenting a pure LN ferroelectric phase have been investigated. The Curie temperatures are determined by the extrapolated departure from the baseline, these being plotted in Figure 8b in terms of the Nb content. A nonlinear quadratic trend better describes this relation, with fitting coefficients A = 18623.560, B = -667.969, and C = 6.383; as expected, this is also the case for LN single crystals [51]. Nevertheless, use of the linear fitting coefficients is done in the analysis that follows, so that a simple calculation of an uncertainty value follows by use of Equation (5), where the Curie temperature TC, is in Celsius.
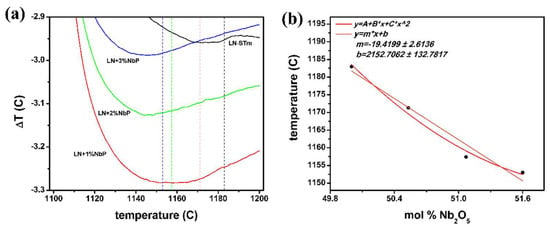
Figure 8.
Thermometric results: (a) Curie temperatures as a function of mol % Nb precursor; (b) Obtained curves for samples within the pure LN phase. The Curie temperatures are determined by extrapolation of the departure from the baseline.
Use of this equation gives an estimate of TC = 1181.56 °C (1153.41 °C for a ST (CG) powder); whereas, with the quadratic expression, it is of 1182.61 °C and 1153.01 °C, respectively. These values vary in no more than 0.1%. Regarding single crystals, a variation of 0.7% can be found for the Curie temperatures calculated for these CCs, by use of equations reported in two independent investigations [51,52]. Using the equation given by Bordui et al. [52], the calculated values are TC = 1206.47 °C (1149.83 °C) for the ST (CG) crystal. Thus, contrary to what was believed, not a unique description of the LN CC regardless of its version (powder or single crystal) can be formulated by DTA either. This observation of the TC being lower for ST LNPws, with respect to ST LN crystals, has been previously noticed [36], apart from the observations highlighted in the introduction. A straight explanation of this subtlety cannot be found nowadays in the literature. A classic theoretical development shows that the energy of the vibrations within the structure is the dominant contribution to the heat capacity—if the elastic response of a crystal is a linear function of the applied forces [53]. Thus, it is inferred that this might be explained under consideration of anharmonic crystal interactions, that is, phonon-phonon coupling. Still, further investigations on these matters are needed.
Lastly, it is acknowledged that in contrast to pioneering works (on LN single crystals, References [16] and [17]) the Equations (2)–(5) here give the averaged Nb content in the crystallites instead of . Although a simpler comparison with data in the literature could have been attained by putting these equations in terms of , it was decided to do it in terms of because of a simpler interpretation and association with a phase diagram describing LN, like that given in Figure 1. It has been noticed that most of the phase diagrams existent in the literature to describe LN, not to say all, are presented in terms of Nb2O5 mol %. This is readily understood since even in the fabrication of large LN single crystals, melts of Nb2O5 and another compound containing Li are used [3,20]. The equivalent equations in terms of are given in Appendix B.
3.4. Grinding of a Single Crystal
The bought single crystal with stoichiometric composition, described above, was turned into powder with ST composition. Low-energy grinding with an agate mortar was employed discontinuously in several steps until an averaged particle size of 1.6 μm (checked by SEM) was reached. In some instances, commercial acetone (purity ≥ 99.5%, Sigma-Aldrich) was used to ease the grinding, especially during its initial stages. Verification of Equations (2) and (3) was sought by repeating the experimental procedures performed on the synthesized powders; in the case of Raman Spectroscopy (RS), only the commercially available system (Witec alpha 300R) was used. The results obtained are shown in Table 2. While RS does imply a chemical composition according to what was expected, stoichiometrically (50 mol % Nb2O5), the structure refinement does not. This can be attributed to changes of the lattice parameter (lattice distortion) due to a variable local lattice strain frequently observed in nanocrystalline materials, induced by excess of volume at the grain boundaries [54]. Remarkably, our powdered single crystal differs from the synthesized powders in the averaged crystallite size: On the latter, a myriad of nanosized crystals (100–300 nm) form large particles of the order of 2–3 μm (see Figure 7c), while on the former it can be argued that crystallite size equals the particle size; actually, the applied Rietveld refinement for the calculation of the averaged crystallite size of the grinded crystal does not converge. These implications must be confirmed and scrutinized by further investigation. Lastly, since Equation (3) is strongly dependent on the XRD analysis (re-labeling of the samples in terms of their predicted CC), the Raman results shown in Table 2 demonstrate the reliability of our method.

Table 2.
Estimated chemical composition for the grinded single crystal.
4. Conclusions
Despite the increasing interest in lithium niobate powders (LNPws) due to their importance in possible applications in actual and future nanooptoelectronic devices, as well as the facility to produce them in large quantities, an accurate and trusting method to determine their chemical composition (CC) does not exist, to the best of our knowledge. Therefore, in this work a first step is given in this direction by developing a facile method based mainly on imposing X-Ray Diffraction (XRD) as a seed characterization technique. Raman Spectroscopy, UV-vis Diffuse Reflectance and Differential Thermal Analysis enrich this work, representing various alternatives for the independent and accurate determination of the CC of LNPws. An empirical equation that describes this fundamental property in terms of a corresponding experimental parameter is given for each of these four characterization techniques.
We wish to underline here the main aspects of our method. It is primarily based on the quantification of pure and secondary phase percentages by XRD, followed by Rietveld structure refinement. Secondly, relying on the LN phase diagram, the CCs of the studied samples are inferred, and thereafter labeled in terms of the Nb content in the crystallites. Lastly, having done this, any of the mentioned characterization techniques can be used to relate such a labeling with their corresponding experimental parameter. In the case of a user who wants to determinate the CC of LNPws only, he/she would only need to perform the last step and make use of any of Equations (2)–(5), respectively. On the other hand, in the case of wanting to describe other powders apart from LNPws, the whole method (three main steps described above) might be further applied inasmuch as akin materials are to be investigated, lithium tantalate (LiTaO3) powders for example.
The validity of this methodology is proven self-consistently with the determination of the CC of several samples, where the content of Li and Nb is varied in a controlled way. According to a paramount observation made in the peer reviewing process of this article, the main shortcoming of this investigation is the large uncertainty associated with Equations (2)–(5). Rigorously, they should not be used for a practical composition determination and, instead, it only could be stated with more confidence that, by using these equations, the composition of a LN powder would be closer to the stoichiometric or congruent compositions, or rather in an intermediate state. However, both, the resolution and the associated uncertainties of this methodology, can be significantly improved by analyzing larger quantities of powder. As mentioned in the details related to the uncertainty calculations and given after introducing Equations (2) and (3), the major contribution to uncertainty emerges from the determination of the boundaries of the pure ferroelectric LN phase: Determined by dividing the 1.6 mol % Nb2O5 by three increasing steps of Nb content, and then dividing by 2 (0.53/2 = 0.27 mol % Nb2O5). The associated uncertainty to Equations (2)–(5) can be significantly reduced if a larger number of samples are synthesized in this range, which can be more easily achieved if larger quantities of powder are prepared. As an example, it is expected that by synthesizing approximately 10 g of powder, around 40 points would be available for analysis if the increasing step is fixed at 0.1% in the mass of the Nb precursor, resulting in a decrease in the overall uncertainties of about 50–80% (noticing that the uncertainty associated with the linear fitting would also be reduced significantly). Conclusively, although it is acknowledged that the proposed equations are not universal in the sense that they may only describe the CC of LNPws with specific physical properties (crystallite and particle dimensions), this work paves the way to furnish a general description and claims the attention of the community advocated to this field to broaden the present results. For a more general description, besides the synthesis of larger number of samples, the influence of other experimental factors and parameters such as the method of synthesis, the beam spot size, the intensity of light (Raman Spectroscopy), the averaged crystallite and particle size, and randomness, among others, should be considered in future investigations.
No full credit for all the ideas developed in this work is to be taken. The idea of determining the CC of LNPws by means of a linear fit to data obtained from Raman spectra was first conceived in the pioneering work of Scott and Burns in 1972 [34]. Indeed, no equation is given in this work, but it could be easily extracted from Figure 3 (in Reference [34]) to describe LNPws instead of LN single crystals; again, it would not be easy to decide whether the complete linewidth (Γ), or just the halfwidth, is to be entered in such a hypothetical equation, and if a Lorentizian or Gaussian distribution is to be used. The work of Scott and Burns is also a pioneer to the ideas conceived by Schlarb et al. [16] and Malovichko et al. [17], whom later in 1993 exploited this fruitful result and demonstrated that other optical processes, besides Raman Spectroscopy, resulted into data that fit linearly with the LN CC. Also, regarding Equation (2), the previous observation of an increase of the lattice parameters or cell volume with increasing Nb content is also acknowledged [55]. An equation is formulated in Reference [18] from the data given in [55]. Interestingly, equation (4) in Reference [18] is almost the same as Equation (A1), given in Appendix B, if the slope and intercept values of the latter are divided by a constant value of 2.58; the very small discrepancy might be attributed to variation in the local lattice strain, as discussed above where the results of grinding a LN single crystal of stoichiometric composition are presented. At last, apart from providing four distinct alternatives to describe accurately the CC of LNPws (instead of single crystalline LN), what is innovative in the present work is the self-consistency character of the whole method: no other technique is needed to confirm the CC of the powders since the determination of the pure ferroelectric LN phase boundaries by XRD analysis suffices for this purpose. The four distinct methods are based on standard characterization techniques, accessible nowadays to large scientific communities in developing countries.
Author Contributions
Conceptualization, O.S.-D., C.D.F.-R. and R.F.; methodology, O.S.-D. and C.D.F.-R.; software, O.S.-D.; validation, A.S.P.-R. and S.H.-L.; formal analysis, O.S.-D.; investigation, O.S.-D., C.J.V., C.D.F.-R., E.V.-S. and S.H.-L.; resources, C.J.V., R.F., E.V.-S. and J.-A.R.-E.; writing—original draft preparation, O.S.-D.; writing—review and editing, J.-A.R.-E.; visualization, C.D.F.-R. and A.S.P.R.; supervision, R.F. and J.-A.R.-E.; project administration, J.-A.R.-E.; funding acquisition, J.-A.R.-E.
Funding
This research was funded by CONACyT, and partially funded by PIIF-3-2018 and UNAM-PAPIIT [grant numbers IN112919, IN114317].
Acknowledgments
The authors wish to acknowledge the technical assistance of Antonio Morales Espino and Manuel Aguilar Franco. The assistance from Alicia Torres and Maricruz Rocha (Laboratorio de Análisis de Materiales, UTCJ) with the milling of the samples is also acknowledged. O.S.-D. thanks CONACyT scholarship grant and Laboratorio Universitario de Caracterización Espectroscópica (LUCE), ICAT-UNAM for providing equipment for Raman spectroscopy measurements. The authors also thank the revision of the final English text by Fernando Funakoshi.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
In the following table the measured values for the masses of the precursors used in each of the 11 synthesis procedures are given.
| Sample | Nb2O5 Mass (g) | Li2CO3 Mass (g) | Sample | Nb2O5 Mass (g) | Li2CO3 Mass (g) |
| LN+5%LiP | 0.8989 | 0.2622 | LN+1%NbP | 0.9079 | 0.2498 |
| LN+4%LiP | 0.8988 | 0.2598 | LN+2%NbP | 0.9167 | 0.2496 |
| LN+3%LiP | 0.8991 | 0.2574 | LN+3%NbP | 0.9259 | 0.2497 |
| LN+2%LiP | 0.8990 | 0.2547 | LN+4%NbP | 0.9348 | 0.2498 |
| LN+1%LiP | 0.8989 | 0.2523 | LN+5%NbP | 0.9438 | 0.2498 |
| LN-STm | 0.8990 | 0.2498 |
Appendix B
Equations in terms of the averaged Li content in the crystallites would also be useful, especially when comparing to measurements on single crystals described elsewhere [16,17,18]. Equations (2)–(5) in terms of are:
References
- Ballman, A.A. Growth of Piezoelectric and Ferroelectric Materials by the Czochralski Technique. J. Am. Ceram. Soc. 1965, 48, 112–113. [Google Scholar] [CrossRef]
- MTI Corporation, LiNbO3 & Doped. Available online: http://www.mtixtl.com/linbo3.aspx (accessed on 29 January 2019).
- Volk, T.; Wöhlecke, M. Point Defects in LiNbO3. In Springer Series in Materials Science. Lithium Niobate. Defects, Photorefraction and Ferroelectric Switching, 1rst ed.; Hull, R., Osgood, R.M., Jr., Parisi, J., Warlimont, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 115, pp. 9–50. ISBN 978-3-540-70765-3. [Google Scholar]
- Weis, R.S.; Gayklord, T.K. Lithium Niobate. Summary of Physical Properties and Crystal Structure. Appl. Phys. A 1985, 37, 191–203. [Google Scholar] [CrossRef]
- Luo, R.; Jiang, H.; Rogers, S.; Liang, H.; He, Y.; Lin, Q. On-chip second-harmonic generation and broadband parametric down-conversion in a lithium niobate microresonator. Opt. Exp. 2017, 25, 24531–24539. [Google Scholar] [CrossRef] [PubMed]
- Pang, C.; Li, R.; Li, Z.; Dong, N.; Cheng, C.; Nie, W.; Bötger, R.; Zhou, S.; Wang, J.; Chen, F. Lithium Niobate Crystal with Embedded Au Nanoparticles: A New Saturable Absorber for Efficient Mode-Locking of Ultrafast Laser Pulses at 1µm. Adv. Opt. Mater. 2018, 6, 1800357. [Google Scholar] [CrossRef]
- Kurtz, S.K.; Perry, T.T. A Powder Technique for the Evaluation of Nonlinear Optical Materials. J. Appl. Phys. 1968, 39, 3798–3812. [Google Scholar] [CrossRef]
- Aramburu, I.; Ortega, J.; Folcia, C.L.; Etxebarria, J. Second harmonic generation by micropowders: A revision of the Kurtz-Perry method and its practical application. Appl. Phys. B: Lasers Opt. 2014, 116, 211–233. [Google Scholar] [CrossRef]
- Nath, R.K.; Zain, M.F.M.; Kadhum, A.A.H. Artificial Photosynthesis using LiNbO3 as Photocatalyst for Sustainable and Environmental Friendly Construction and Reduction of Global Warming: A Review. Catal. Rev. Sci. Eng. 2013, 56, 175–186. [Google Scholar] [CrossRef]
- Yang, W.C.; Rodriguez, B.J.; Gruverman, A.; Nemanich, R.J. Polarization-dependent electron affinity of LiNbO3 surfaces. Appl. Phys. Lett. 2004, 85, 2316–2318. [Google Scholar] [CrossRef]
- Fierro-Ruíz, C.D.; Sánchez-Dena, O.; Cabral-Larquier, E.M.; Elizalde-Galindo, J.T.; Farías, R. Structural and Magnetic Behavior of Oxidized and Reduced Fe Doped LiNbO3 Powders. Crystals 2018, 8, 108. [Google Scholar] [CrossRef]
- Kudinova, M.; Humbert, G.; Auguste, J.L.; Delaizir, G. Multimaterial polarization maintaining optical fibers fabricated with powder-in-tube technology. Opt. Mater. Express 2017, 10, 3780–3790. [Google Scholar] [CrossRef]
- Sánchez-Dena, O.; García-Ramírez, E.V.; Fierro-Ruíz, C.D.; Vigueras-Santiago, E.; Farías, R.; Reyes-Esqueda, J.A. Effect of size and composition on the second harmonic generation from lithium niobate powders at different excitation wavelengths. Mater. Res. Express 2017, 4, 035022. [Google Scholar] [CrossRef]
- Skipetrov, S.E. Disorder is the new order. Nature 2004, 432, 285–286. [Google Scholar] [CrossRef]
- Knabe, B.; Buse, K.; Assenmacher, W.; Mader, W. Spontaneous polarization in ultrasmall lithium niobate nanocrystals revealed by second harmonic generation. Phys. Rev. B 2012, 86, 195428. [Google Scholar] [CrossRef]
- Schlarb, U.; Klauer, S.; Wesselmann, M.; Betzler, K.; Wöhlecke, M. Determination of the Li/Nb ratio in Lithium Niobate by Means of Birefringence and Raman Measurements. Appl. Phys. A 1993, 56, 311–315. [Google Scholar] [CrossRef]
- Malovichko, G.I.; Grachev, V.G.; Kokanyan, E.P.; Schirmer, O.F.; Betzler, K.; Gather, B.; Jermann, F.; Klauer, S.; Schlarb, U.; Wöhlecke, M. Characterization of stoichiometric LiNbO3 grown from melts containing K2O. Appl. Phys. A: Mater. Sci. Process. 1993, 56, 103–108. [Google Scholar] [CrossRef]
- Wöhlecke, M.; Corradi, G.; Betzler, K. Optical methods to characterise the composition and homogeneity of lithium niobate single crystals. Appl. Phys. B 1996, 63, 323–330. [Google Scholar] [CrossRef]
- Zhang, Y.; Guilbert, L.; Bourson, P.; Polgár, K.; Fontana, M.D. Characterization of short-range heterogeneities in sub-congruent lithium niobate by micro-Raman spectroscopy. J. Phys. Condens. Matter 2006, 18, 957–963. [Google Scholar] [CrossRef]
- Hatano, H.; Liu, Y.; Kitamura, K. Growth and Photorefractive Properties of Stoichiometric LiNbO3 and LiTaO3. In Photorefractive Materials and Their Applications 2, 1st ed.; Günter, P., Huignard, J.P., Eds.; Springer Series in Optical Sciences: New York, NY, USA, 2007; pp. 127–164. [Google Scholar]
- Kong, L.B.; Chang, T.S.; Ma, J.; Boey, F. Progress in synthesis of ferroelectric ceramic materials via high-energy mechanochemical technique. Prog. Mater. Sci. 2008, 53, 207–322. [Google Scholar] [CrossRef]
- Suryanarayana, C. Mechanical alloying and milling. Prog. Mater. Sci. 2001, 46, 1–184. [Google Scholar] [CrossRef]
- Crystallographic Open Database, Information for card entry 2101175. Available online: http://www.crystallography.net/cod/2101175.html (accessed on 29 January 2019).
- Degen, T.; Sadki, M.; Bron, E.; König, U.; Nènert, W. The HighScore suite. Powder Diffr. 2014, 29, S13–S18. [Google Scholar] [CrossRef]
- FIZ Karlsruhe ICSD, ICDS- Inorganic Crystal Structure Database. Available online: www2.fiz-karlsruhe.de/icsd_home.html (accessed on 29 January 2019).
- Porto, S.P.S.; Krishnan, R.S. Raman Effect of Corundum. J. Chem. Phys. 1967, 47, 1009–1011. [Google Scholar] [CrossRef]
- Kubelka, P. New Contributions to the Optics of Intensely Light-Scattering Materials. Part I. J. Opt. Soc. Am. 1948, 38, 448–457. [Google Scholar] [CrossRef]
- Kubelka, P. New Contributions to the Optics of Intensely Light-Scattering Materials. Part II: Nonhomogeneous Layers. J. Opt. Soc. Am. 1954, 44, 330–335. [Google Scholar] [CrossRef]
- Torrent, J.; Barrón, V. Diffuse Reflectance Spectroscopy. In Methods of Soil Analysis Part5—Mineralogical Methods, 1st ed.; Ulery, A.L., Drees, R., Eds.; Soil Science Society of America: Wisconsin, WI, USA, 2008; pp. 367–385. [Google Scholar]
- The Royal Society of Chemistry, Periodic Table. Available online: http://www.rsc.org/periodic-table (accessed on 29 January 2019).
- Baird, D.C. Experimentation: An Introduction to Measurement Theory and Experiemtn Design, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995; pp. 129–133. [Google Scholar]
- Kalinnikov, V.T.; Gromov, O.G.; Kunshina, G.B.; Kuz’min, A.P.; Lokshin, E.P.; Ivanenko, V.I. Preparation of LiTaO3, LiNbO3, and NaNbO3 from Peroxide Solutions. Inorg. Mater. 2004, 40, 411–414. [Google Scholar] [CrossRef]
- Liu, M.; Xue, D.; Luo, C. Wet chemical synthesis of pure LiNbO3 powders from simple niobium oxide Nb2O5. J. Alloys Compd. 2006, 426, 118–122. [Google Scholar] [CrossRef]
- Scott, B.A.; Burns, G. Determination of Stoichiometry Variations in LiNbO3 and LiTaO3 by Raman Powder Spectroscopy. J. Am. Ceram. Soc. 1972, 55, 225–230. [Google Scholar] [CrossRef]
- Liu, M.; Xue, D. An efficient approach for the direct synthesis of lithium niobate powders. Solid State Ionics 2006, 177, 275–280. [Google Scholar] [CrossRef]
- Liu, M.; Xue, D.; Li, K. Soft-chemistry synthesis of LiNbO3 crystallites. J. Alloys Compd. 2008, 449, 28–31. [Google Scholar] [CrossRef]
- Nyman, M.; Anderson, T.M.; Provencio, P.P. Comparison of Aqueous and Non-aqueous Soft-Chemical Syntheses of Lithium Niobate and Lithium Tantalate Powders. Cryst. Growth Des. 2009, 9, 1036–1040. [Google Scholar] [CrossRef]
- De Figueiredo, R.S.; Messaia, A.; Hernandes, A.C.; Sombra, A.S.B. Piezoelectric lithium niobate obtained by mechanical alloying. J. Mater. Sci. Lett. 1998, 17, 449–451. [Google Scholar] [CrossRef]
- Pezzotti, G. Raman spectroscopy of piezoelectrics. J. Appl. Phys. 2013, 113, 211301. [Google Scholar] [CrossRef]
- Repelin, Y.; Husson, E.; Bennani, F.; Proust, C. Raman spectroscopy of lithium niobate and lithium tantalite. Force field calculations. J. Phys. Chem. Solids 1999, 60, 819–825. [Google Scholar] [CrossRef]
- Thermo Fisher Scientific, Application Note: Curve Fitting in Raman and IR Spectroscopy. Available online: https://www.thermofisher.com/search/results?query=Curve%20Fitting%20in%20Raman&focusarea=Search%20All (accessed on 29 January 2019).
- Tuschel, D. The Effect of Microscope Objectives on the Raman Spectra of Crystals. Spectroscopy 2017, 32, 14–23. [Google Scholar]
- Maïmounatou, B.; Mohamadou, B.; Erasmus, R. Experimental and theoretical directional dependence of optical polar phonons in the LiNbO3 single crystal: New and complete assignment of the normal mode frequencies. Phys. Status Solidi B 2016, 253, 573–582. [Google Scholar] [CrossRef]
- Yang, X.; Lang, G.; Li, B.; Wang, H. Raman Spectra and Directional Dispersion in LiNbO3 and LiTaO3. Phys. Status Solidi B 1987, 142, 287–300. [Google Scholar] [CrossRef]
- Balanevskaya, A.É.; Pyatigorskaya, L.I.; Shapiro, Z.I.; Margolin, L.N.; Bovina, E.A. Determination of the composition of LiNbO3 specimens by Raman spectroscopy. J. Appl. Spectrosc. 1983, 38, 491–493. [Google Scholar] [CrossRef]
- Kovács, L.; Kocsor, L.; Szaller, Z.; Hajdara, I.; Dravecz, G.; Lengyel, K.; Corradi, G. Lattice Site of Rare-Earth Ions in Stoichiometric Lithium Niobate Probed by OH− Vibrational Spectroscopy. Crystals 2017, 7, 230. [Google Scholar] [CrossRef]
- Redfield, D.; Burke, W.J. Optical absorption edge of LiNbO3. J. Appl. Phys. 1974, 45, 4566–4571. [Google Scholar] [CrossRef]
- Kovács, L.; Ruschhaupt, G.; Polgár, K.; Corradi, G.; Wöhlecke, M. Composition dependence of the ultraviolet absorption edge in lithium niobate. Appl. Phys. Lett. 1997, 70, 2801–2803. [Google Scholar] [CrossRef]
- Thierfelder, C.; Sanna, S.; Schindlmayr, A.; Schmidt, W.G. Do we know the band gap of lithium niobate? Phys. Satus Solidi C 2010, 7, 362–365. [Google Scholar] [CrossRef]
- Devonshire, A.F. Theory of ferroelectrics. Adv. Phys. 1954, 3, 85–130. [Google Scholar] [CrossRef]
- O’Bryan, H.M.; Gallagher, P.K.; Brandle, C.D. Congruent Composition and Li-Rich Phase Boundary of LiNbO3. J. Am. Ceram. Soc. 1985, 68, 493–496. [Google Scholar] [CrossRef]
- Bordui, P.F.; Norwood, R.G.; Jundt, D.H.; Fejer, M.M. Preparation and characterization of off-congruent lithium niobate crystals. J. Appl. Phys. 1992, 71, 875–879. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 7th ed.; John Wiley & Sons: New York, NY, USA, 1996; pp. 99–130. [Google Scholar]
- Quin, W.; Nagase, T.; Umakoshi, Y.; Szpunar, J.A. Relationship between microstrain and lattice parameter change in nanocrystalline materials. Philos. Mag. Lett. 2008, 88, 169–179. [Google Scholar] [CrossRef]
- Iyi, N.; Kitamura, K.; Izumi, F.; Yamamoto, J.K.; Hayashi, T.; Asano, H.; Kimura, S. Comparative study of defect structures in lithium niobate with different compositions. J. Sol. State Chem. 1992, 101, 340–352. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).