Abstract
High-pressure single-crystal synchrotron X-ray diffraction data for galenobismutite, PbBi2S4 collected up to 20.9 GPa, were fitted by a third-order Birch-Murnaghan equation of state, as suggested by a FE-fE plot, yielding V0 = 697.4(8) Å3, K0 = 51(1) GPa and K’ = 5.0(2). The axial moduli were M0a = 115(7) GPa and Ma’ = 28(2) for the a axis, M0b = 162(3) GPa and Mb’ = 8(3) for the b axis, M0c = 142(8) GPa and Mc’ = 26(2) for the c axis, with refined values of a0, b0, c0 equal to 11.791(7) Å, 14.540(6) Å 4.076(3) Å, respectively, and a ratio equal to M0a:M0b:M0c = 1.55:1:1.79. The main structural changes on compression were the M2 and M3 (occupied by Bi, Pb) movements toward the centers of their respective trigonal prism bodies and M3 changes towards CN8. The M1 site, occupied solely by Bi, regularizes the octahedral form with CN6. The eccentricities of all cation sites decreased with compression testifying for a decrease in stereochemical expression of lone electron pairs. Galenobismutite is isostructural with calcium ferrite CaFe2O4, the suggested high pressure structure can host Na and Al in the lower mantle. The study indicates that pressure enables the incorporation of other elements in this structure, increasing its potential significance for mantle mineralogy.
1. Introduction
Galenobismutite PbBi2S4 is a Bi-sulfosalt usually found in hydrothermal veins or associated with fumarolic deposits [1,2]. Like other Bi-minerals, it has an important role in the reconstruction of the formation of ore deposits as it is sensitive to physical–chemical fluctuations and can constrain the genesis of ore.
According to sulfosalt classification [3] galenobismutite is classified among commensurate composite derivatives of cannizzarite in a sub-group with angelaite, Cu2AgPbBiS4 [4], nuffieldite, Cu1.4Pb2.4Bi2.4Sb0.2S7 [5] and weibullite, Ag0.33Pb5.33Bi8.33(S,Se)18 [6]. It has a distinctly different crystal structure from the chemically (stoichiometrically) similar berthierite FeSb2S4 [7], garavellite FeSbBiS4 [8] and clerite MnSb2S4 [9] which form a berthierite isotypic series [3].
Chemical substitution of Sb for Bi and Fe for Pb are common in gelenobismutite. It is illustrated by galenobismutite from Beiya porphyry- and skarn-type deposits that contain Sb up to 0.39% and Fe up to 0.42% [10]. Selenium can replace sulfur in galenobismutite. In galenobismutite from Vulcano Island (Italy) [1] heterogeneous distribution of selenium in the Sulphur sites was found, with a total amount of up to 0.13 atoms of Se per formula unit. Moreover, galenobismutite from Vulcano shows an unusual presence of Cl, according to the coupled heterovalent substitution scheme: Pb2+ + Cl− = Bi3+ + S2− [2].
The crystal structure of galenobismutite is orthorhombic, space group Pnam, and was described firstly by Wickman [11], then by Iitaka and Nowacki [12], and later classified by Makovicky [13] as being representative of a specific subgroup of cannizzarite-type structures.
The crystal structure contains three cation positions. M1 has a slightly distorted octahedral coordination and forms fragments of galena-like structure two octahedra wide by sharing edges with a conjugated M1 octahedron. M2 is surrounded by seven S atoms forming a “lying” (prism axis is perpendicular to the c crystal axis) mono-capped trigonal prism. M3 polyhedron is a “standing” (prism axis parallel to the c crystal axis) bi-capped trigonal prism (CN8) with one of the capping ligands relatively distant, so the coordination can also be described as a 7+1 (Figure 1).
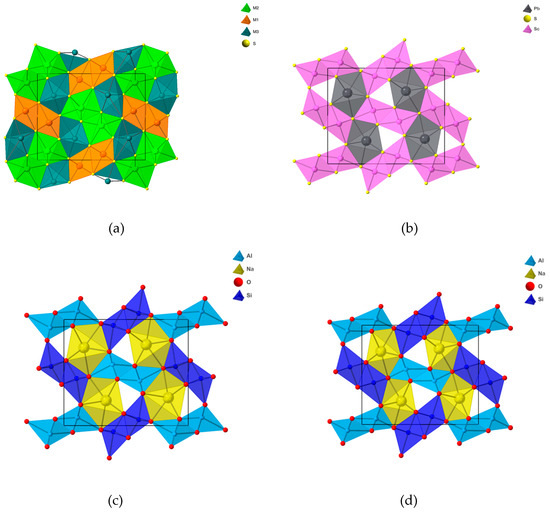
Figure 1.
Crystal structures of: (a) galenobismutite, projected along [001] with x axis on the vertical and y axis on the horizontal line; (b) PbSc2S4 [19]; (c) NaAlSiO4 at room pressure [16]; (d) NaAlSiO4 at 35 GPa [20].
The determination of the distribution of Bi and Pb in the three sites by refinement of X-ray diffraction data is practically impossible due to the similar number of electrons (83 and 82, respectively). It is therefore based on the bond valence calculations. According to Pinto et al. [1], who used bond lengths, bond valences and geometrical characteristics of the coordination polyhedral to interpret the occupancy on the M1, M2 and M3 positions. M1 is considered fully occupied by Bi, while M2 and M3 are mixed sites dominated by Bi and Pb, respectively.
The configuration of this structure, isotypic with calcium ferrite (CF) CaFe2O4, is of a particular interest for high pressure mineral physics. Finger and Hazen [14] include among the seven structure-types with exclusively six-coordinated silicon NaAlSiO4 [15,16], the analogue of CF. This structure bears a close relationship to hollandite, another VISi -coordinated structure type. Both structures consist of double octahedral chains which are joined to form ‘tunnels’ parallel to c that accommodate the alkali or alkaline-earth cations. In hollandite four double chains form square tunnels, whereas in CF four double chains define triangular tunnels.
Akaogi et al. [17] were the first who synthesized NaAlSiO4 with CF structure at pressures higher than 18–20 GPa. Tutti et al. [18] found that this phase is stable at pressure up to at least 70–75 GPa and temperatures 800–2200 °C indicating it as an important carrier of Na and Al in the lower Mantle.
The most regular CF-type structure known is that of PbSc2S4 ([19], Figure 1b). The reported crystal structure of NaAlSiO4 ([16], Figure 1c), obtained from a powder sample, has a substantially more distorted octahedral coordination. Dubrovinsky et al. [20] reported the structure of NaAlSiO4 at 35 GPa, likewise done on a powder sample (Figure 1d). The data suggest that the M1 coordination becomes more regular without significant contraction, whereas M2 and Na coordinations significantly contract keeping their general shapes. Compared to the other CF structures, galenobismutite differs in having CN7 coordination of the M2 site and a significantly distorted coordination of the M3 site. M1 coordination is eccentric, unlike in PbSc2S4 or NaAlSiO4. The increased CN of M2 and distortions of the other two coordinations in galenobismutite are explained as a stereochemical effect of the lone electron pair of Bi3+ [21].
The first high-pressure study of galenobismutite was done by Olsen et al [21] at pressures up to 8.9 GPa with single crystal X-ray diffraction. They found a bulk modulus of K0 equal to 43.9(7) GPa and a K’ of 6.9 (3). No phase transition was observed in this pressure range and, interestingly, although the stereochemical activity of Lone Electron Pair (LEP)’s decreased with pressure, the structure did not approach the CF isotype but moved further away from its typical configuration, keeping its distinct character [21].
The present paper extends the study of the baric behavior of galenobismutite over a significantly larger pressure range, up to 20.9 GPa, by a synchrotron single crystal X-ray diffraction study in order to obtain a more complete picture of its behavior under high pressure. Really the relevance of high pressure single crystal X-ray diffraction data with respect those from high pressure powder diffraction was very recently highlight in several papers i.e. [22,23].
2. High Pressure Experiments
The HP synchrotron single-crystal X-ray diffraction experiments were carried out at ID-15B beamline at ESRF (Grenoble) dedicated to the determination of structural properties of solids at high pressure using angle-dispersive-diffraction with diamond anvil cells. A membrane-type Diamond Anvil Cell with an opening angle of +/−32 degrees, equipped with 600 µm diamond culets was used. Helium was used as a pressure transmitting medium. According to Singh [24] helium is superior in ensuring near to hydrostatic conditions at pressures of 20 GPa or over compared to argon.
Ruby sphere was loaded as a fluorescent P calibrant together with the galenobismutite sample (80 × 10 × 20 μm3) in the 300 μm hole in the center of a pre-indented stainless steel gasket of 80 μm thickness. Pressure was measured before and after each data collection.
The sample-to-detector distance was 279.88 mm and calibrated, along with the wavelength, using Si standard and Fit2D software [25]. The same synthetic sample of galenobismutite used in Olsen et al 2007 was selected to collect the present set of measurements, to avoid differences in compressibility ascribable to different chemical compositions in the samples.
The X-ray beam was monochromatized to a wavelength of 0.41125 Å and focused down to 10 × 10 µm area. Data were collected with a DAC rotating 64° around the ω-axis (from −32 to +32°) with angular step of 0.5° and counting time of 1s per step. The scattered radiation was collected by a MAR555 flat panel detector, with 430 × 350 mm (555mm diagonal) active area.
The extraction and correction of the intensity data, merging of reflections, and the refinements of the crystal lattice parameters were done by means of the CrysAlis software (Agilent technologies) [26]. Measurements were performed at different pressures from 0.5 to 20.9 GPa on increasing pressure, and at 16.43, 8.12, and 2.1 GPa on decreasing pressure to evaluate the reversibility and hysteresis phenomena of structural changes. The absorption correction was applied by means of ABSORB-7 software [27].
The structure refinements were carried out with ShelXle [28] on F2. Scattering curves for neutral atoms were used. Table 1 summarizes details of data collection and structure refinements up to 20.9 GPa. Final atomic coordinates and isotropic displacement factors are listed in Table 2. Bond lengths, polyhedral volumes and polyhedral distortion parameters at different pressures, are reported in Table 3. Cif files with the hkl, i.e., the Miller indices of the collected reflections, of individual refinements are in Table S1 (deposited).

Table 1.
Details of data refinements, lattice parameters, and density at different pressures.

Table 2.
Final atomic coordinates and isotropic displacement factors at different pressures.
3. Results
3.1. Compressibility
The evolution of the unit-cell of galenobismutite with pressure is reported in Figure 2 and in Table 1. The behavior of the cell parameters shows no discontinuities in the investigated pressure range and indicates that no phase transition occurs in galenobismutite structure up to 20.9 GPa. The volume-pressure data were fitted with a third-order Birch-Murnaghan equations-of-state, using the EOSFIT7-GUI software [29], as suggested by fE-FE, namely the “Eulerian finite strain” versus “normalized stress” plot [30], (Figure 3). The third order Birch-Murnaghan Equation of State (EoS) fit yields V0 = 697.4(8) Å3, K0 = 51(1) GPa and K’ = 5.0(2). The bulk modulus and the first derivative values were in good agreement with the values obtained from the fE-FE plot [30]. The intercept value and the slope obtained by a linear regression give FE0 and K’ values equal to 51(1) GPa and 4.8(8), respectively.
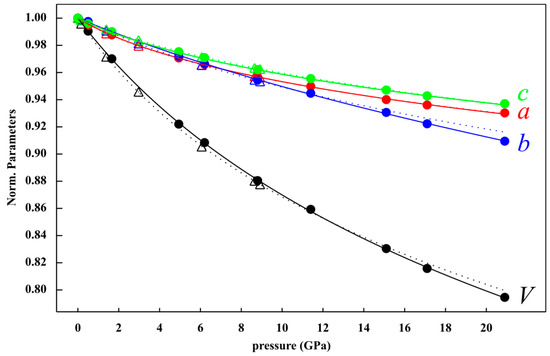
Figure 2.
Evolution of the unit cell volume and a, b, c lattice parameters normalized to the values at room conditions as a function of pressure (GPa), fitted by a third-order Birch-Murnaghan EoS. Olsen et al. [21] data are shown by stippled lines and triangles for comparison.
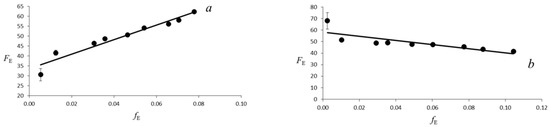
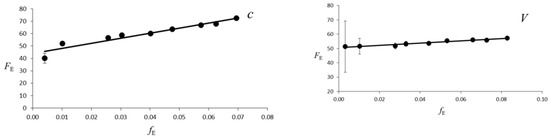
Figure 3.
Evolution of the Eulerian finite strain fE versus the “normalized stress” FE. The solid line is the weighted linear fit of the data for V, a, b and c lattice parameters.
The lattice parameter moduli, calculated using a third-order Birch-Murnaghan equation of state, were for the axis M0a = 115(7) GPa and Ma’ = 28(2), for the b axis M0b = 162(3) GPa and Mb’ = 8(3), for the c axis M0c = 142(8) GPa and Mc’ = 26(2), with refined values of a0 11.791(7) Å, b0 = 14.540(6) Å, c0 = 4.076(3) Å, respectively. Since the results gave large differences in M’ parameters, the lattice parameter moduli were calculated using the second order Birch-Murnaghan equation of state, fixing M’ to 12 in order to evaluate the anisotropic behavior. The results of this fitting give M0a 191 (9) GPa with a0 equal to 11.74 (2) Å, M0b = 123(5) GPa with b0 equal to 14.96 (2) Å and M0c = 226 (10) GPa with c0 equal to 4.058(6) Å. The compressional anisotropy of crystallographic axes, showed that b and c were the most and the least compressible lattice parameters, respectively, with the anisotropic ratio M0a:M0b:M0c = 1.55:1:1.84.
Density of galenobismutite changed from 7.243 g/cm3 at 0.5 GPa to 9.029 g/cm3 at 20.9 GPa, with an increase of about 22% in the investigated pressure range.
To compare the present data with those of other sulfides of metalloids from literature (galena [31], bismuthinite [32], stibnite [33], chalcostibite [34], lillianite [35], heyrovskyite [36], berthierite [37]) a K’ vs K0 plot was elaborated (Figure 4). In the plot, the confidence ellipses at 90 and 68 % of confidence level for the present data and those reported by Olsen et al. [21] are shown. In order to allow a more direct comparison of K0 and K’ calculated with the two data sets and to evaluate if the observed differences were due to the different pressure range, we also calculated K0 and K’ restricting our data to the same pressure range investigated by Olsen et al [21]. We observed a strong negative correlation between K’ and K0 in agreement with the data presented by Olsen et al. [21]. However, the ellipsoides for the two data sets did not overlap, even if they are quite close. The reason might be that the results of Olsen et al. [21] were biased by an unequal distribution of pressures at which the data were measured.
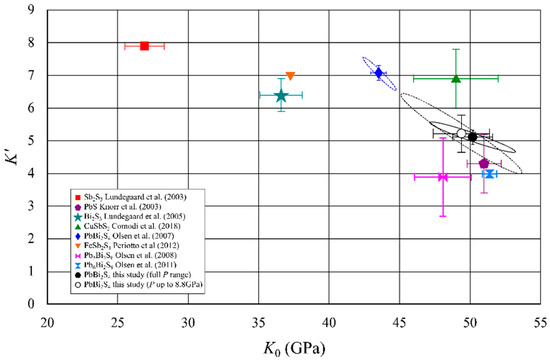
Figure 4.
Bulk Moulus (K0) vs its pressure derivative (K’) for different sulfides. Confidence ellipses at 90% of confidence level are reported for K0 and K’ calculated with the present data collected up to 20.9 GPa (solid black line) as well as with data limited at 8.8 GPa (stippled black line). Confidence ellipse at 90% for Olsen et al. [21] data is also shown (stippled blue line).
K0 and K’ values for galena (Figure 4), PbS, before the phase transition, were very close to those observed for galenobismutite. On the other hand, K0 for bismuthinite, Bi2S3, were significantly lower (Figure 4). Olsen et al. [21] suggested an empirical relation between the bulk modulus of galenobismutite and those of PbS and Bi2S3 corresponding to the proportion of Bi and Pb in galenobismutite: KPbBi2S4 = (2KBi2S3 + KPbS)/3. Although this relation holds approximately for the data from the previous study, the present corrected data for galenobismutite does not support this observation. We can conclude that a simple relation between a bulk modulus for a complex composition cannot be derived straightforwardly from the bulk moduli of its simpler constituents [38] even if they contain the same general structural modules (like in sulfosalts). Obviously, a more complex cooperative mechanism between the structural modules should be involved [39]. For sulfosalts it is important to take into account that they contain cations with active lone electron pairs (LEPs), which can strongly affect the polyhedral distortion, and the overall structural compressibility to different extents. Sb3+ LEP’s stereochemical activity is generally higher than that of Bi3+, evaluated from the measurements of the eccentricity of Sb and Bi polyhedra at room pressure conditions, which show larger difference in interatomic Sb-S distances compared to Bi-S ones. Under high pressure, the polyhedra become more regular and the eccentricity reduces more rapidly for Sb3+ polyhedra with respect to those of Bi3+, because the longest interatomic contacts in atomic coordinations generally compress faster than the shortest ones. As a consequence, Sb sulfosalts have bulk moduli lower than the corresponding Bi sulfosalts, as illustrated by the isomorphic chalcostibite-emplectite series [34].
Pb2+ also contains a LEP, but it is generally less expressed than that of Bi3+. LEP of Pb2+ is even fully suppressed in several structures, like in galena or the earlier mentioned PbSc2S4. To the best of our knowledge the only observed regular coordination of Bi3+ is the octahedral coordination in the mineral kupcikite, Cu4Bi5S10 [40,41]. It is interesting that the pressure can force coordinations with suppressed LEP to a structure with highly expressed stereochemical activity through phase transition [35,36,42].
Very few theoretical calculations provide an analysis of the relation between electronic structure, lone electron pairs and structural geometrical parameters. Olsen et al 2011 [43], by using SIESTA DFT code considered the effect of pressure in Bi2S3 and compared the theoretical with experimental data. Their data on the effective Bi s-p hydridization support the origin of the stereochemically active lone pair and its evolution with pressure increases.
A comparison of the bulk modulus of galenobismutite to those of CF type structures shows much larger differences. Dubrovinsky et al. [20] reported the CF type NaAlSiO4 bulk modulus measured up 40 GPa. Their data gave a very high bulk modulus of 220 GPa and its pressure derivative was equal to 4.1(1), similar to the values measured for other compounds with a calcium ferrite structure. For example, the value of K0, with K’ fixed to 4, of MgAl2O4 measured by Yutani et al. [44] was 241(1) GPa, whereas K0 measured for Fe3O4 by Haavik et al. [45] was 202(7) GPa, with K’ equal to 4. The general rule, suggested by Anderson et al. [46], KV = constant, where V represents the molar volume (36.58cm3/mol for NaAlSiO4, 36.13 cm3/mol for MgAl2O4 and 41.89 cm3/mol for Fe3O4), seems to be followed by this group of calcium ferrite structures [20]. In comparison, galenobismutite has a higher molar volume (105.0 cm3/mol) but, at the same time, a much lower bulk modulus, resulting in a violation of the Anderson’s relation. This is most probably due to a large difference in chemistry, influenced by both cation and anion electronic configurations and especially by the presence of cation LEPs in galenobismutite.
3.2. Structural Evolution with Pressure
The M1, M2 and M3 polyhedral evolution with pressure was analyzed through changes in bond lengths and polyhedral volumes reported in Table 3.
Figure 5 and Figure 6 show the changes of bond distances and volumes with pressure. The bulk moduli of M1, M2 and M3 polyhedra, calculated as the reciprocals of linear compressibilities are 114 (3) GPa, 86(2) GPa and 84(2) GPa, respectively. The values agree with the general relationship suggested by Finger and Hazen [14], which relates the polyhedral bulk moduli to inverse of the mean cation-anion distances for several oxides, silicates as well as sulfides and selenides and several other types of compounds.
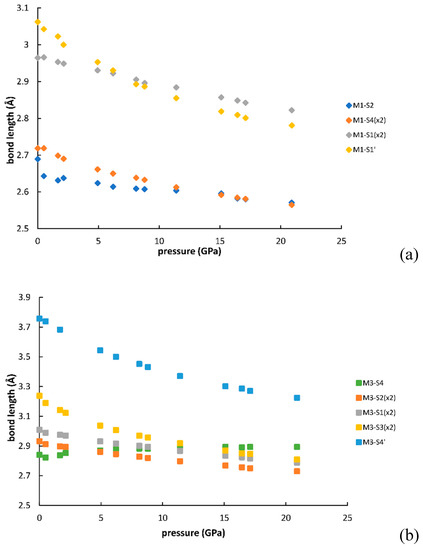
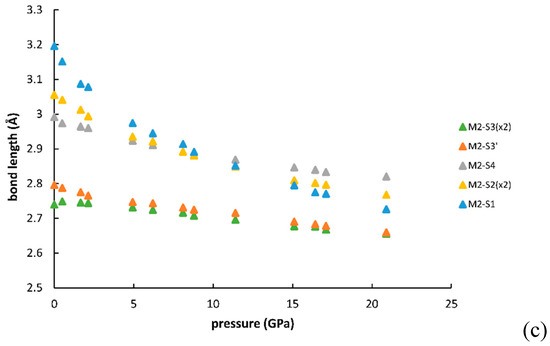
Figure 5.
Evolution of the bond distances with pressure for M1 (a), M2 (b), M3(c) polyhedra.
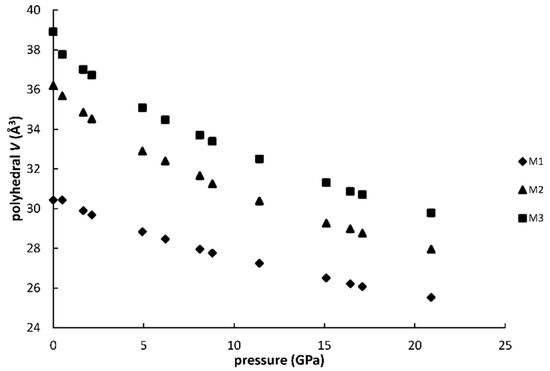
Figure 6.
Variation of polyhedral volume for M1 (a), M2 (b), M3 (c) polyhedra with pressure.
The distortion parameters of the coordination polyhedra can give an additional insight in the compressibility behavior of atomic coordinations. Figure 7 shows the development of the eccentricities, asphericities and shape distortions (or volume distortions [47]). For M3 we calculated the parameters for both CN7 and CN8, because of its specific character. The eccentricities of all coordinations decreased continuously with pressure but much faster for M2 and M3 than for M1. After 4 GPa M1 reached the most eccentric coordination in spite of its smallest CN. It is interesting that the eccentricity of M3 related to only the closest seven S atoms levels off after 12 GPa and does not show further changes with pressure. However, for CN8 it continued to decrease, due to a continuous approach of the eight S atom. The asphericities showed much smaller changes with pressure. Note that M1 from the start had negligible asphericity, meaning that all six S atoms fit practically perfectly to a common sphere. It is interesting that the asphericity of the M3 coordination for CN7 actually increased with pressure, in spite of a constant decrease in asphericity calculated for CN8. It must, however, be noted that the asphericity for CN8 was significantly higher. The shape distortion, which shows the departure of the arrangement of ligands compared to an ideal polyhedron, shows an increase with pressure for all coordination polyhedra. The parameters are in all cases calculated compared to the ideal polyhedron which shows the smallest VS/VP ratio for a given CN, where VS and VP are the volumes of the circumscribed sphere and the polyhedron, respectively. For CN6 this is the regular octahedron, for CN7 the regular pentagonal bipyramid and for CN8 the “maximum volume” bisdisphenoid. Compared to the latter two, an ideal monocapped trigonal prism would have a “shape distortion” of 0.159, and an ideal bicapped trigonal prism would have a “shape distortion” of 0.073. In this respect, the values calculated for M2 and M3 (both for CN7 and for CN8) are actually a sign of approaching the shapes closer to ideal monocapped, respectively bicapped trigonal prism. M1, however, departed more from an ideal octahedron shape with increasing pressure.
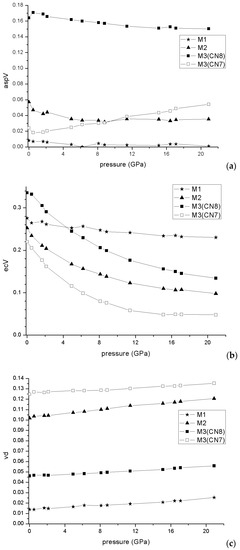
Figure 7.
Asphericity (a), Eccentricity (b) and shape distortion (c) evolution with pressure for M1, M2, and M3 polyhedra.
The orientation and expression of a LEP can be calculated from the relative positions of the central atom in a coordination and the centroid of the ligand arrangement [48]. The black spheres in Figure 8 have their centers in centroids of coordinations, thus, they illustrate the orientations and the expressions of the LEPs of cations.
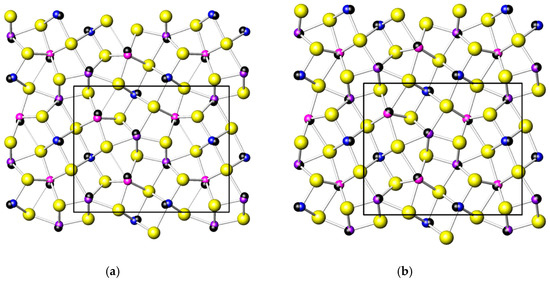
Figure 8.
Galenobismutite at room pressure (a) and at 20.9 GPa (b). Black spheres are centered on centroids of coordinations and indicate the orientations of M1, M2 and M3 lone electron pairs.
Taking into account the changes in bond distances and distortion parameters plus the global aspects of the crystal structure, the changes that occur in galenobismutite under increasing pressure can be summarized as follows: The main change is that both M2 and M3 atoms move towards the centers of the bodies of respective trigonal prisms. It can be visually verified by comparing the crystal structures at 1 bar and 20.9 GPa, as represented in Figure 8, and by checking the development of the bond lengths, as in Figure 5. Here, the atoms making the body of the trigonal prism were two S3 atoms, two S2 atoms plus S3 and S1 for M2. Note that bond distances to these six S atoms showed a merging tendency with increasing pressure. The distance to the capping S4 atom decreased with a much lower gradient than the ones to two S2 plus S1 atom (that are longer at 1 bar) and actually became the longest one from 12 GPa on. In the case of M3, two S2, two S1 and two S3 atoms formed the prism body and one can observe the same tendency of merging the bond distances up to approximately 10 GPa; above this pressure they became the shortest bond distances in the coordination polyhedron. It is true that the longest distance to one of the capping S4 atoms had a significant decrease during the whole measurement range, but with a gradient that was similar to the one of the two S3 atoms belonging to prism body. On the contrary, the distance to the other S4 capping atom actually slightly increased under compression. This all testifies also in this case that M3 moves inside the body of the trigonal prism with a consequence that it also moves away from the closest capping S4 atom. As the distance to the other one largely decreases due to its approach to the prism body, the two distances to the capping S atoms show a merging tendency and we can assume that the coordination’s character changes from the 7+1 type towards the real CN8, becoming a more regular bicapped trigonal prism (also confirmed by the values of the shape distortion in Figure 7c).
The changes in the M1 coordination were very small compared to M2 and M3. The eccentricity of this site changed very little (Figure 7a) as the difference between the three shortest and three longest bonds remained almost the same (Figure 5a). There was actually a slight but constant increase in the distortion of the octahedral shape (Figure 7c). The main change in this coordination is due to the polyhedral accommodation to the contraction of the b axis that had the largest compressibility (Figure 2 and Figure 8a). The expression of the LEP of M1 slightly changed, but its orientation, seen from the atomic nucleus, changed more significantly from the diagonal one, oriented towards the space between the two neighboring M1 coordinations, to a direction along the b axis (Figure 8b). The changes in the expression of LEPs of M2 and M3 were more significant and their orientations changed to directions closer to the M2-capping S and M3-most distant capping S, in accordance to the movement of M2 and M3 towards the centers of their respective trigonal prisms.
4. Discussion and Conclusion
The comparison of data collected at different pressures on galenobismutite allows the following conclusions:
- (a)
- The structural evolution is completely reversible with pressure increase up to 20.9 GPa. The same values were measured increasing and decreasing the pressure and the same equation of state is measured by using values collected increasing or decreasing pressure. No evidence of hysteresis in the changes were observed, meaning that the changes are completely elastic.
- (b)
- The change in atomic coordinations bring the M3 coordination polyhedron closer to the shape observed in other members of the CF structural family (from CN7+1 to CN8). However, unlike other CF crystal structures, M2 keeps and even equalizes its seven-fold coordination with increasing pressure. This emphasizes the specific character of galenobismutite in this structural family. We suggest that the main reason is a comparatively large size of the M2 cation, comparable to that of the M3, unlike the other examples of CF structures, where M2 is significantly smaller than M3.
- (c)
- The structure remains stable at very high pressures (up to 20 GPa) notwithstanding the moderate bulk modulus, at least under the structural point of view, since there are no incompatible distances up to 20.9 GPa. All sulfur-sulfur distances, which could indicate instability of the structure, remained quite large with the shortest S3-S4 distance equal to 3.140 Å.
- (d)
- Calcium ferrite structure type reveals enough flexibility in incorporating various element combinations through the example of galenobismutite. Thus, not only Al and Na, incompatible in the periclase or perovskite crystal structures under the lower mantle conditions, can be considered to prefer this structure type, but it might incorporate also some other important or less abundant elements or combinations of elements.
Supplementary Materials
The following is available online at https://www.mdpi.com/2073-4352/9/4/210/s1, Table S1: HKL at different pressure of galenobismutite.
Author Contributions
Conceptualization, P.C. and T.B.-Z.; methodology, M.H. and I.C.; software, M.H., I.C. and A.Z.; formal analysis, A.Z., data curation, A.Z.; writing of original draft preparation, P.C. and T.B.-Z.; writing—review and editing, P.C., T.B.-Z., A.Z.
Funding
This research received no external funding.
Acknowledgments
The European Synchrotron Facility is acknowledged for allocating beam-time for the experiment ES-723 (main proposer P.C.).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pinto, D.; Balic-Zunic, T.; Garavelli, A.; Makovicky, E.; Vurro, F. Comparative crystal-structure of Ag-free lillianite and galnbismutite from Vulcano, Aeolian Island, Italy. Can. Mineral. 2006, 44, 159–175. [Google Scholar] [CrossRef]
- Pinto, D.; Balic-Zunic, T.; Bonaccorsi, E.; Bordaev, Y.S.; Garavelli, A.; Garbarino, C.; Makovicky, E.; Mozgova, N.; Vurro, F. Rare Sulfosalts from Vulcano, Aeolian Island, Italy. VII. Cl-bearing galenobismutite. Can. Mineral. 2006, 44, 443–457. [Google Scholar] [CrossRef]
- Moëlo, Y.; Makovicky, E.; Mozgova, N.N.; Jambor, J.L.; Cook, N.; Pring, A.; Paar, W.; Nickel, E.H.; Graeser, S.; Karup-Møller, S.; et al. Sulfosalt systematics: A review. Report of the sulpfosalt sub-committee of the IMA Commission on Ore Mineralogy. Eur. J. Mineral. 2008, 20, 7–46. [Google Scholar]
- Brodtkorb, M.K.; Paar, W. Angelaíta en la paragénesis del distrito Los Manantiales, provincia del Chubut: Una nueva especie mineral. Rev. Assoc. Geol. Argent. 2004, 59, 787–789. [Google Scholar]
- Moëlo, Y.; Meerschaut, A.; Makovicky, E. Refinement of the crystal structure of nuffieldite, Pb2Cu1.4(Pb0.4Bi0.4Sb0.2)Bi2S7: Structural relationships and genesis of complex lead sulfosalt structures. Can. Mineral. 1997, 35, 1497–1508. [Google Scholar]
- Mumme, W.G. Seleniferous lead–bismuth sulphosalts from Falun, Sweden:Weibullite, wittite, and nordströmite. Am. Mineral. 1980, 65, 789–796. [Google Scholar]
- Buerger, M.J. The crystal structure of berthierite. Am. Mineral. 1936, 21, 205–206. [Google Scholar]
- Bindi, L.; Menchetti, S. Garavellite, FeSbBiS4, from the Caspari mine, North Rhine-Westphalia, Germany: Composition, physical properties and determination of the crystal structure, Locality: Caspari mine, North Rhine-Westphalia, Germany. Mineral. Petrol. 2005, 85, 131–139. [Google Scholar] [CrossRef]
- Bente, K.; Edenharter, A. Rontgenographische strukturanalyse von MnSb2S4 und strukturverfeinerung, von berthierit, FeSb2S4. Z. Krist. 1989, 185, 31–33. [Google Scholar]
- Zhou, H.; Sun, X.; Fu, Y.; Lin, H.; Jiang, L. Mineralogy and mineral chemistry: Constrains of ore genesis of the Beiya giant porphyry-skarn gold deposit, southwestern China. Ore Geol. Rev. 2016, 79, 408–424. [Google Scholar] [CrossRef]
- Wickman, F.E. The crystal structure of galenobismutite PbBi2S4. Ark. Miner. 1951, 1, 219. [Google Scholar]
- Iitaka, Y.; Nowacki, W. A re-determination of the crystal structure of galenobismutite PbBi2S4. Acta Crystallogr. 1962, 15, 691–698. [Google Scholar] [CrossRef]
- Makovicky, E. The building principles and classification of bismith-lead sulfosalts and related compounds. Fortschr. Miner. 1981, 59, 137–190. [Google Scholar]
- Finger, L.W.; Hazen, R.M. Systematic of high-pressure silicate structures. Rev. Mineral. Geochem. 2000, 41, 123–155. [Google Scholar] [CrossRef]
- Liu, L.G. High pressure NaAlSiO4: The first silicate calcium ferrite isotype. Geophys. Res. Lett. 1977, 4, 183–186. [Google Scholar] [CrossRef]
- Yamada, H.; Matsui, Y.; Ito, E. Crystal-chemical characterization of NaAlSiO4 with the CaFe2O4 structure. Mineral. Mag. 1983, 47, 177–181. [Google Scholar] [CrossRef][Green Version]
- Akaogi, M.; Tanaka, A.; Kobayashi, M.; Fikushima, N.; Suzuki, T. High pressure transformation in NaAlSiO4 and thermodynamic properties of jadeite, nepheline and calcium ferrite-type phase. Phys. Earth Plant. Inter. 2002, 130, 49–58. [Google Scholar] [CrossRef]
- Tutti, F.; Dubrovisky, L.; Saxena, S.K. High pressure phase transformation of jadeite and stability of NaAlSiO4 with calcium-ferrite type structure in the lower mantle conditions. Geophs. Res. Lett. 2000, 27, 2025–2028. [Google Scholar] [CrossRef]
- Shemet, V.; Gulay, L.; Stepien-Damm, J.; Pietraszko, A.; Olekseyuk, I. Crystal structure of the Sc2PbX4 (X = S and Se) compounds. J. Alloy. Compd. 2006, 407, 94–97. [Google Scholar] [CrossRef]
- Dubrovinsk, L.S.; Dubrovinskaia, N.A.; Prokopenko, V.B.; Le Bihan, T. Equation of state and crystal structure of NaAlSiO4 with calcium-ferrite type structure in the conditions of the lower mantle. High Press. Res. 2002, 22, 495–499. [Google Scholar] [CrossRef]
- Olsen, L.A.; Balic-Zunic, T.; Makovicky, E.; Ullrich, A.; Miletich, R. Hydrostatic compression of galenobismutite (PbBi2S4): Elastic properties and high-pressure crystal chemistry. Phys. Chem. Miner. 2007, 34, 467–475. [Google Scholar] [CrossRef]
- Ruiz-Fuertes, J.; Friedrich, A.; Errandonea, D.; Segura, A.; Morgenroth, W.; Rodríguez-Hernández, P.; Muñoz, A.; Meng, Y. Optical and structural study of the pressure-induced phase transition of CdWO4. Phys. Rev. B 2017, 95, 174105. [Google Scholar] [CrossRef]
- Comboni, D.; Lotti, P.; Gatta, G.D.; Lacalamita, M.; Mesto, E.; Merlini, M.; Hanfland, M. Amstrongite at non-ambient conditions: An in-situ high pressure single-crystal X-ray diffraction study. Microporous Mesoporous Mater. 2019, 274, 171–175. [Google Scholar] [CrossRef]
- Singh, A.K. Strength of solid helium under high pressure. J. Phys. Conf. Ser. 2012, 377, 012007. [Google Scholar] [CrossRef]
- Hammersley, A.P.; Svensson, S.O.; Hanfland, M.; Fitch, A.N.; Hausermann, D. Two-dimensional detector software: From real detector to idealized image or two-theta scan. High Press. Res. 1996, 14, 235–245. [Google Scholar] [CrossRef]
- Oxford Diffraction. CrysAlis(Pro); Oxford Diffraction Ltd.: Abingdon, UK, 2006. [Google Scholar]
- Angel, R.; Gonzalez-Platas, J. ABSORB–7 and ABSORB-GUI for single crystal absorption correction. J. Appl. Crystall. 2013, 46, 252–254. [Google Scholar] [CrossRef]
- Hubschle, C.B.; Sheldrick, G.M.; Dittrich, B. ShelXle: A Qt graphical user interface for29 SHELXL. J. Appl. Cryst. 2011, 44, 1281–1284. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Platas, J.; Alvaro, M.; Nestola, F.; Angel, R. EOSFIT7-GUI: A new graphycal user interface for equation of state calculation, analyses and teaching. J. Appl. Cryst. 2016, 49, 1377–1382. [Google Scholar] [CrossRef]
- Angel, R.J. Equation of state. In High Temperature and High Pressure Crystal Chemistry; Hazen, R.M., Downs, R.T., Eds.; Reviews in Mineralogy and Geochemistry; Mineralogical Society of America: Chantilly, VA, USA, 2000; Volume 41, pp. 117–211. [Google Scholar]
- Knorr, K.; Ehm, L.; Hytha, M.; Winkler, B.; Depmeier, W. The high-pressure α/β phase transition in lead sulphide (PbS)—X-ray powder diffraction and quantum mechanical calculations. Eur. Phys. J. 2003, 31, 297–303. [Google Scholar] [CrossRef]
- Lundegaard, L.; Makovicky, E.; Boffa Ballaran, T.; Balic-Zunic, T. Crystal structure and cation lone electron pair activity of Bi2S3 between 0 and 10 GPa. Phys. Chem. Miner. 2005, 32, 578–584. [Google Scholar] [CrossRef]
- Lundegaard, L.F.; Miletich, R.; Balic-Zunic, T.; Makovicky, E. Equation of state and crystal structure of Sb2S3 between 0 and 10 GPa. Phys. Chem. Miner. 2003, 30, 463–468. [Google Scholar] [CrossRef]
- Comodi, P.; Guidoni, F.; Nazzareni, S.; Balic-Zunic, T.; Zucchini, A.; Makoviscky, E.; Prakapenka, V. A high-pressure phase transition in chalcostibite, CuSbS2. Eur. J. Miner. 2018, 30, 491–505. [Google Scholar] [CrossRef]
- Olsen, L.A.; Balić-Žunić, T.; Makovicky, E. High-pressure anisotropic distortion of Pb3Bi2S6: A pressure-induced, reversible phase transition with migration of chemical bonds. Inorg. Chem. 2008, 47, 6756–6762. [Google Scholar] [CrossRef]
- Olsen, L.A.; Friese, K.; Makovicky, E.; Balić-Žunić, T.; Morgenroth, W.; Grzechnik, A. Pressure induced phase transition in Pb6Bi2S9. Phys. Chem. Miner. 2011, 38, 1–10. [Google Scholar] [CrossRef]
- Periotto, B.; Balic-Zunic, T.; Nestola, F. The role of the Sb3+ lone electron pairs and Fe2+ coordination in the high-pressure behavior of berthierite. Can. Mineral. 2012, 50, 201–218. [Google Scholar] [CrossRef]
- Comodi, P.; Mellini, M.; Zanazzi, P.F. Scapolites: Variation of structure with pressure and possible role in the storage of fluids. Eur. J. Mineral. 1990, 2, 195–202. [Google Scholar] [CrossRef]
- Gatta, G.D.; Comodi, P.; Zanazzi, P.F.; Boffa Ballaran, T. Anomalous elastic behaviour and high-pressure structural evolution of zeolite levyne. Am. Mineral. 2005, 90, 645–652. [Google Scholar] [CrossRef]
- Mariolacos, K.; Kupčik, V.; Ohmasa, M.; Miehe, G. The Crystal Structure of Cu4Bi5S10 and its Relation to the Structures of Hodrushite and Cuprobismutite. Acta Cryst. 1975, 31, 703–708. [Google Scholar] [CrossRef]
- Topa, D.; Makovicky, E.; Balić-Žunić, T.; Paar, W.H. Kupčikite, Cu3.4Fe0.6Bi5S10, a new Cu-Bi sulfosalt from Felbertal, Austria, and its crystal structure. Can. Mineral. 2003, 41, 1155–1166. [Google Scholar] [CrossRef][Green Version]
- Grzechnik, A.; Friese, K. Pressure-induced orthorhombic structure of PbS. J. Phys. Condens. Matter 2010, 22, 095402. [Google Scholar] [CrossRef]
- Olsen, L.A.; Lopez-Solano, J.; Garcia, A.; Balic-Zinic, T.; Makovicky, E. Dependence of lone pair of bismuth on coordination environment and pressure: Ab Initio study on Cu4Bi5S10 and Bi2S3. J. Solid State Chem. 2010, 18, 2133–2143. [Google Scholar] [CrossRef]
- Yutani, M.; Yagi, T.; Yusa, H.; Irifune, T. Compressibility of calcium ferrite-type MgAl2O4. Phys. Chem. Miner. 1997, 24, 340–344. [Google Scholar] [CrossRef]
- Haavik, C.; Stolen, S.; Fjellvag, H.; Hanfland, M.; Häusermann, D. Equation of state of magnetite and its high-pressure modification: Thermodynamics of the Fe-O system at high pressure. Am. Mineral. 2000, 85, 514–523. [Google Scholar] [CrossRef]
- Anderson, O.L. Equation of State of Solids for Geophysics and Ceramic Science; Oxford University Press: New York, NY, USA, 1994; p. 495. [Google Scholar]
- Makovicky, E.; Balić-Žunić, T. New measure of distortion for coordination polyhedra. Acta Cryst. 1998, 54, 766–773. [Google Scholar] [CrossRef]
- Balić Žunić, T.; Makovicky, E. Determination of the Centroid or “the Best Centre” of a Coordination Polyhedron. Acta Cryst. 1996, 52, 78–81. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).