Investigation on the Thermal Deformation Behavior of the Nickel-Based Superalloy Strengthened by γ′ Phase
Abstract
:1. Introduction
2. Experimental Procedure
3. Results and Analysis
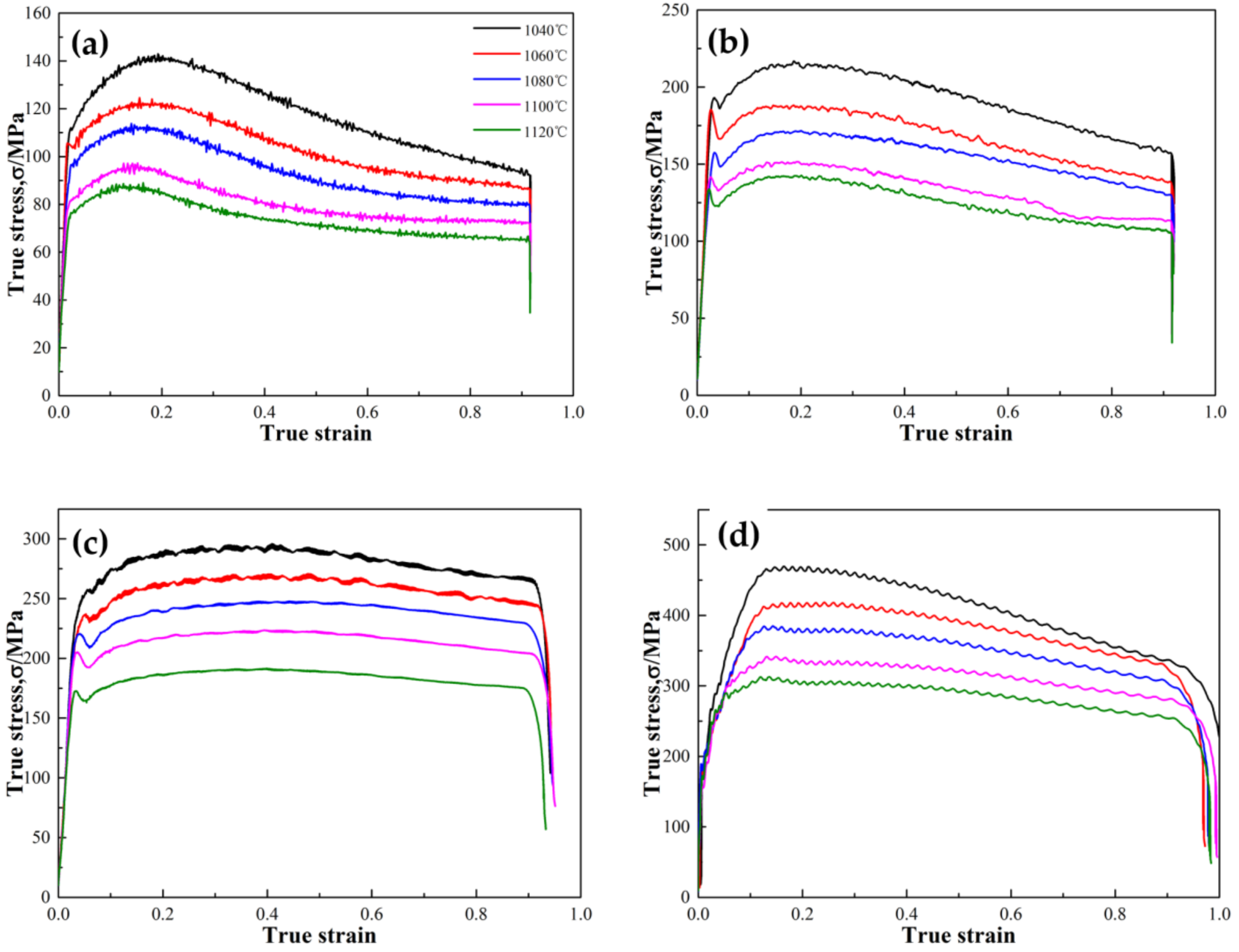
3.1. Stress–Strain Curves
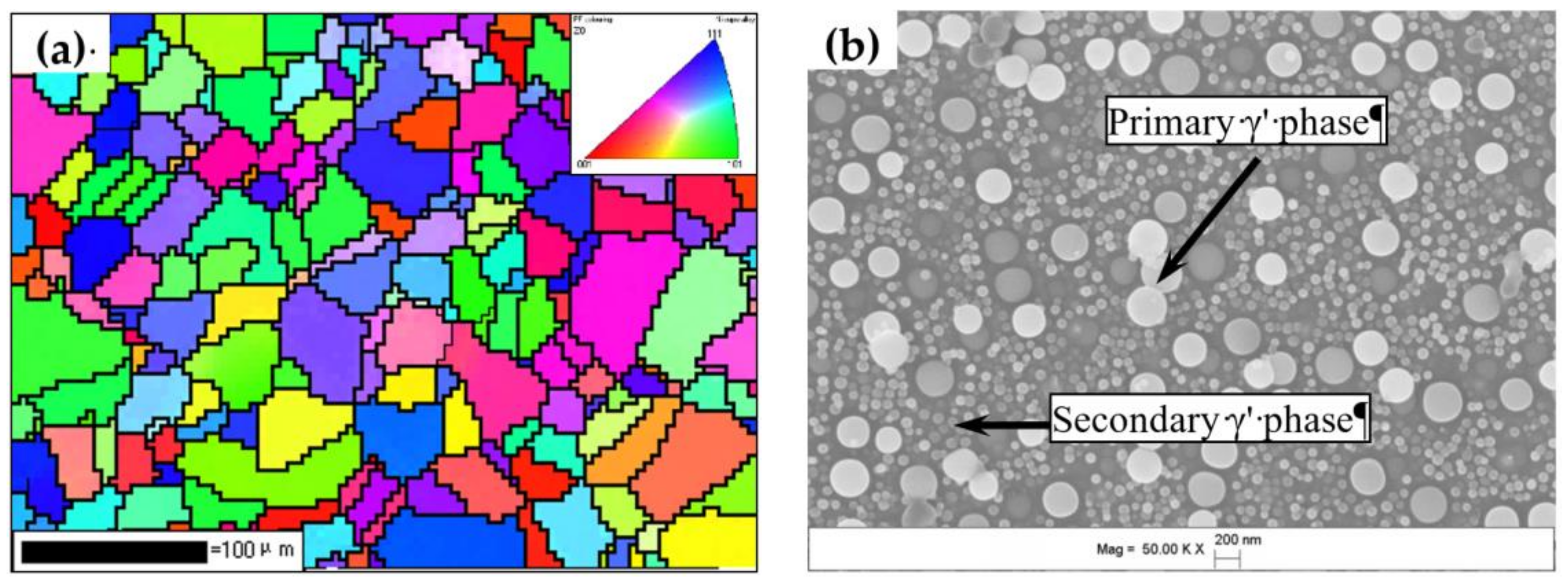
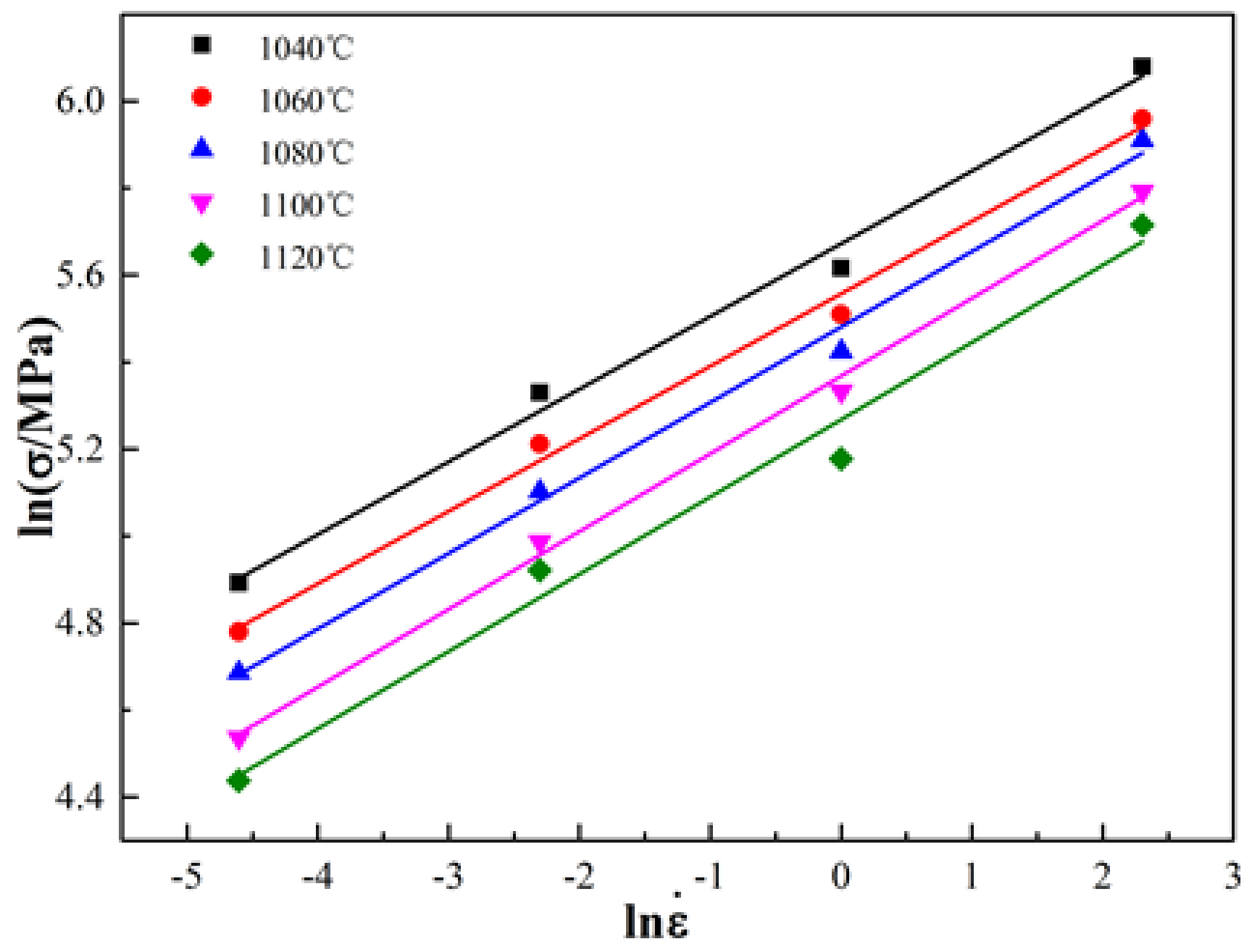
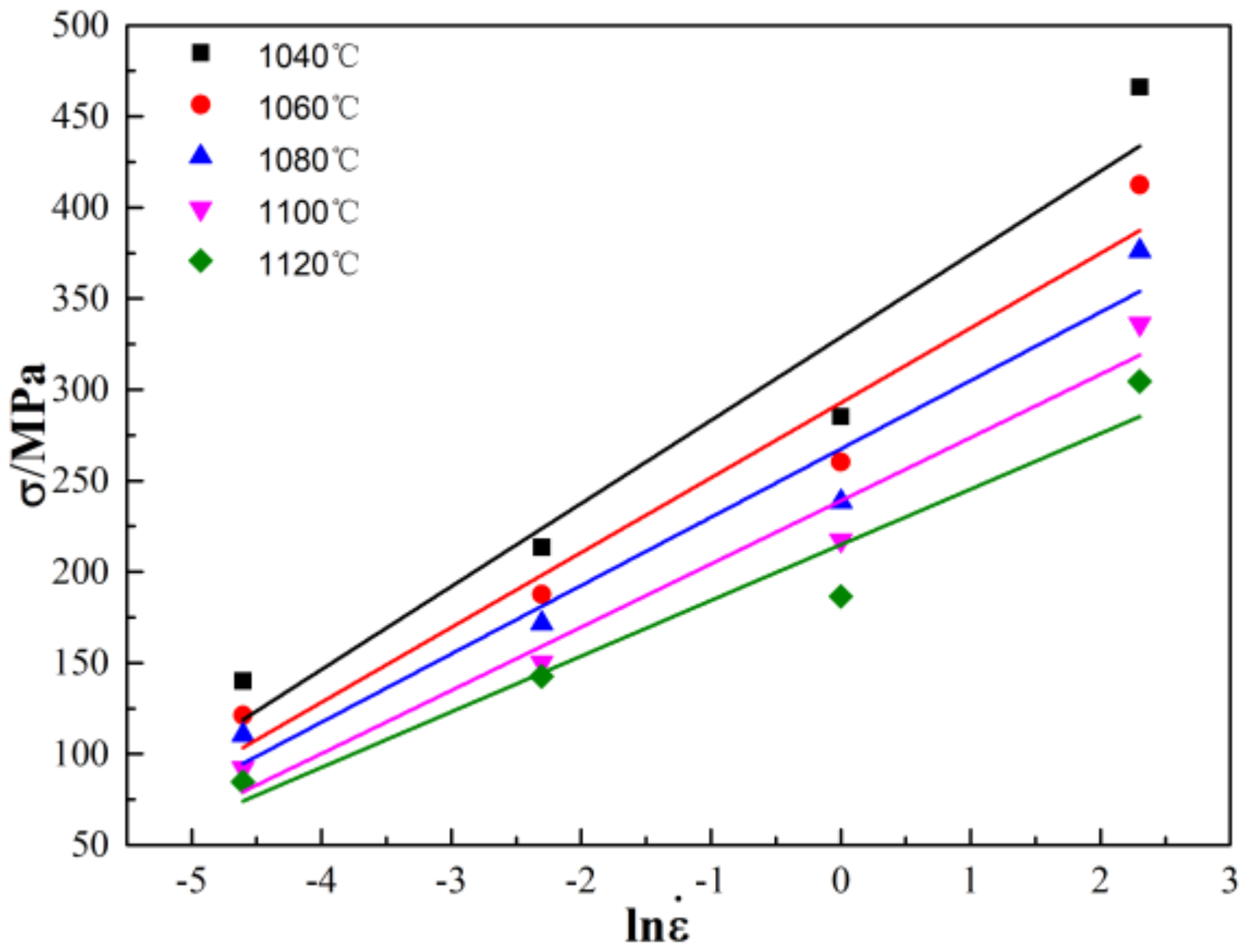
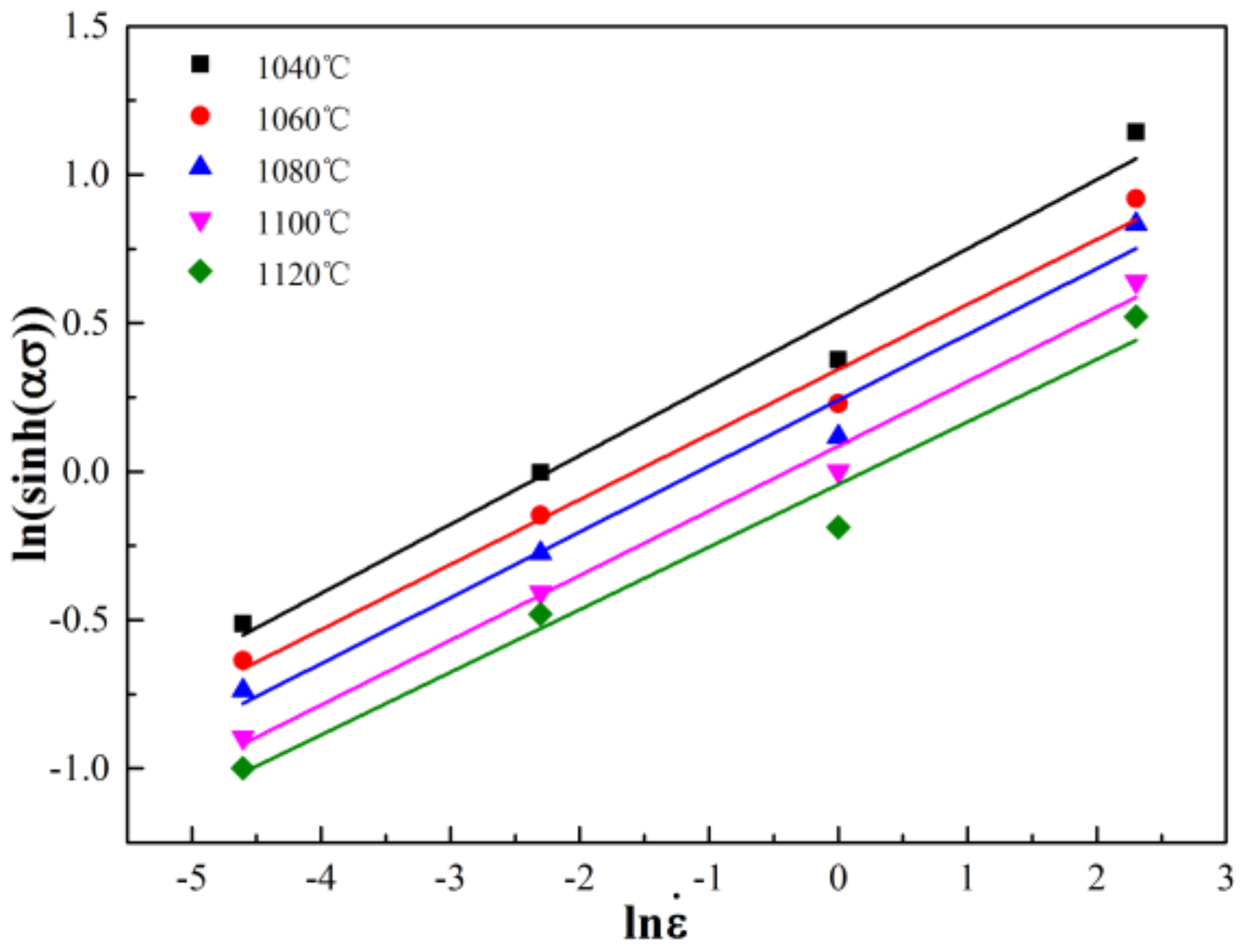
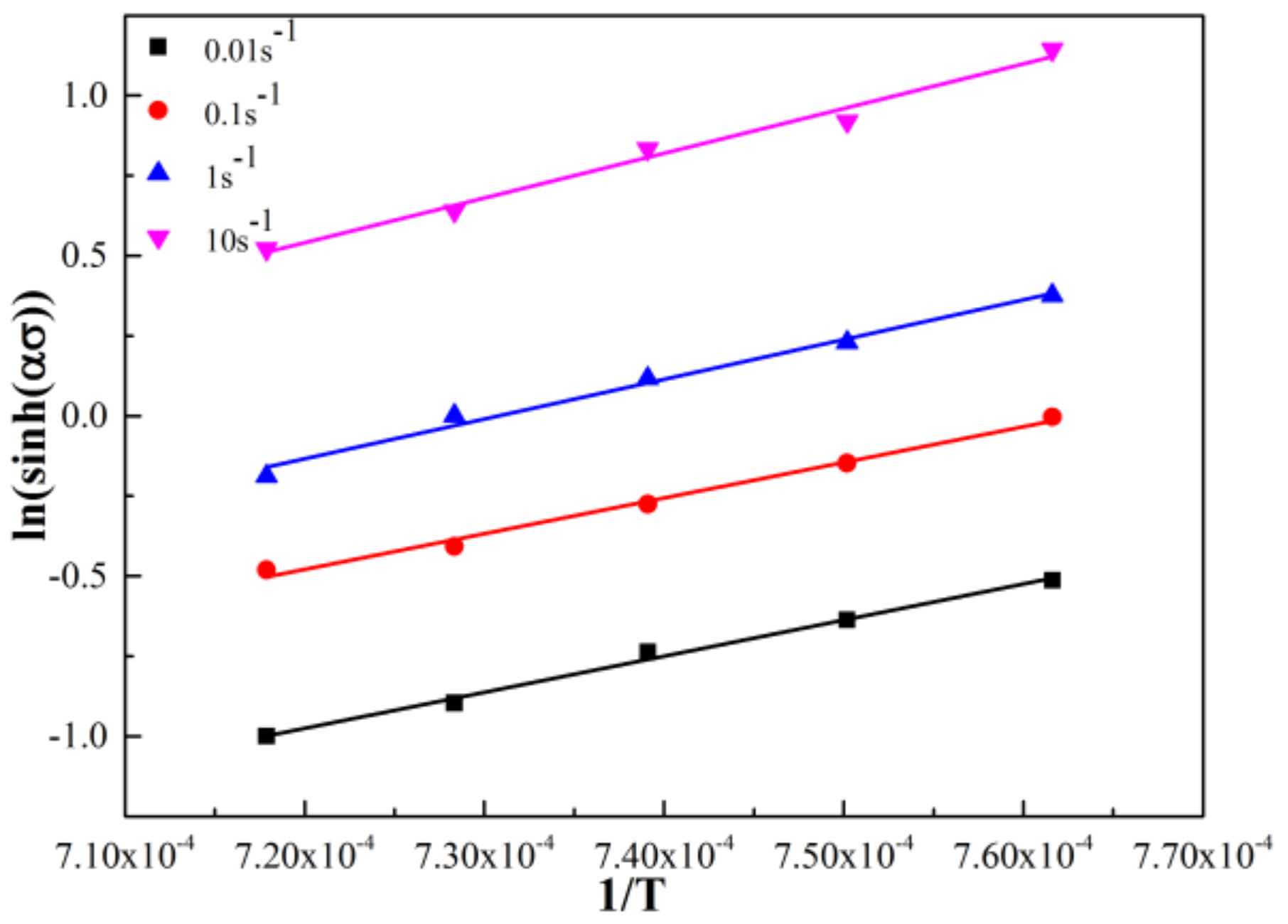
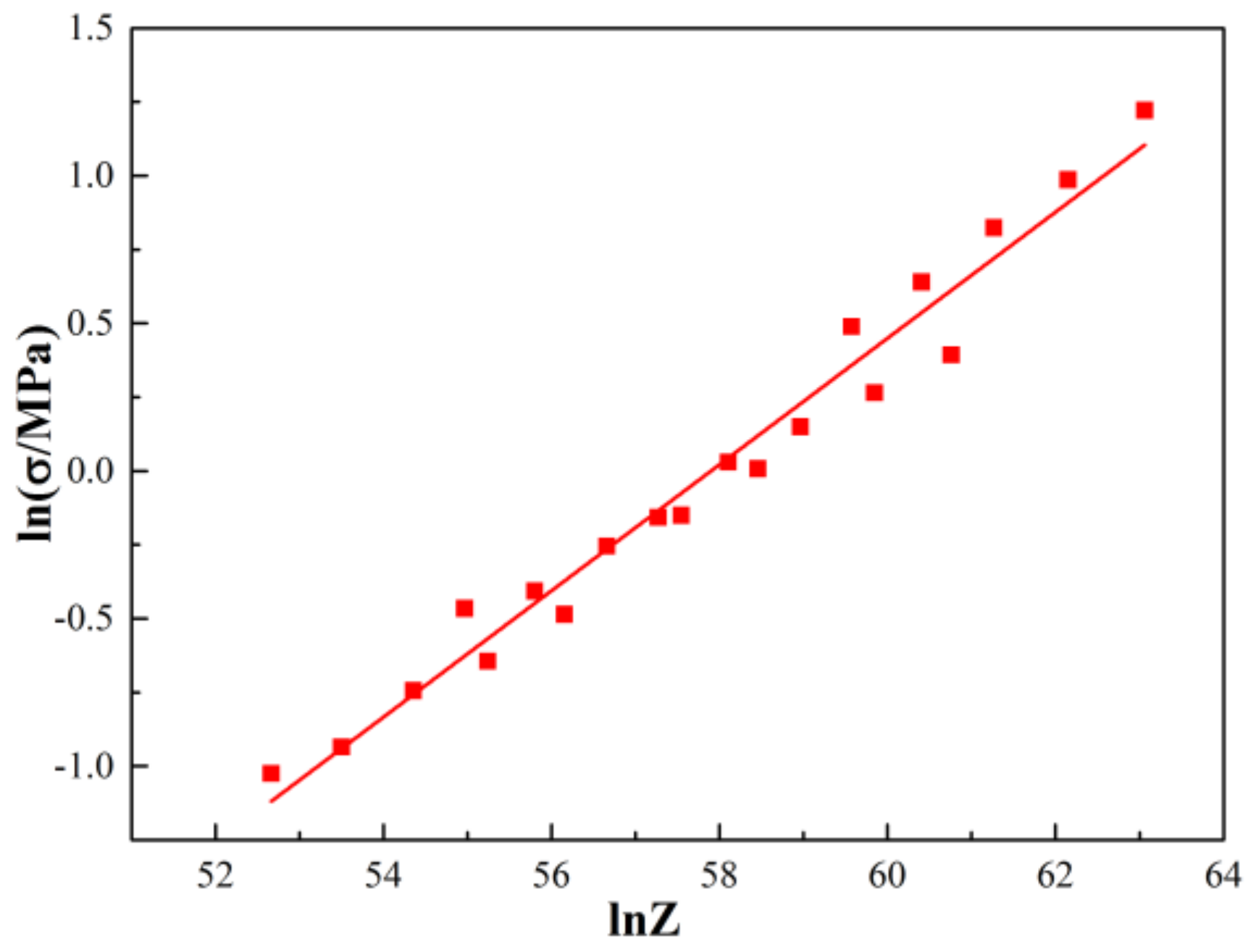
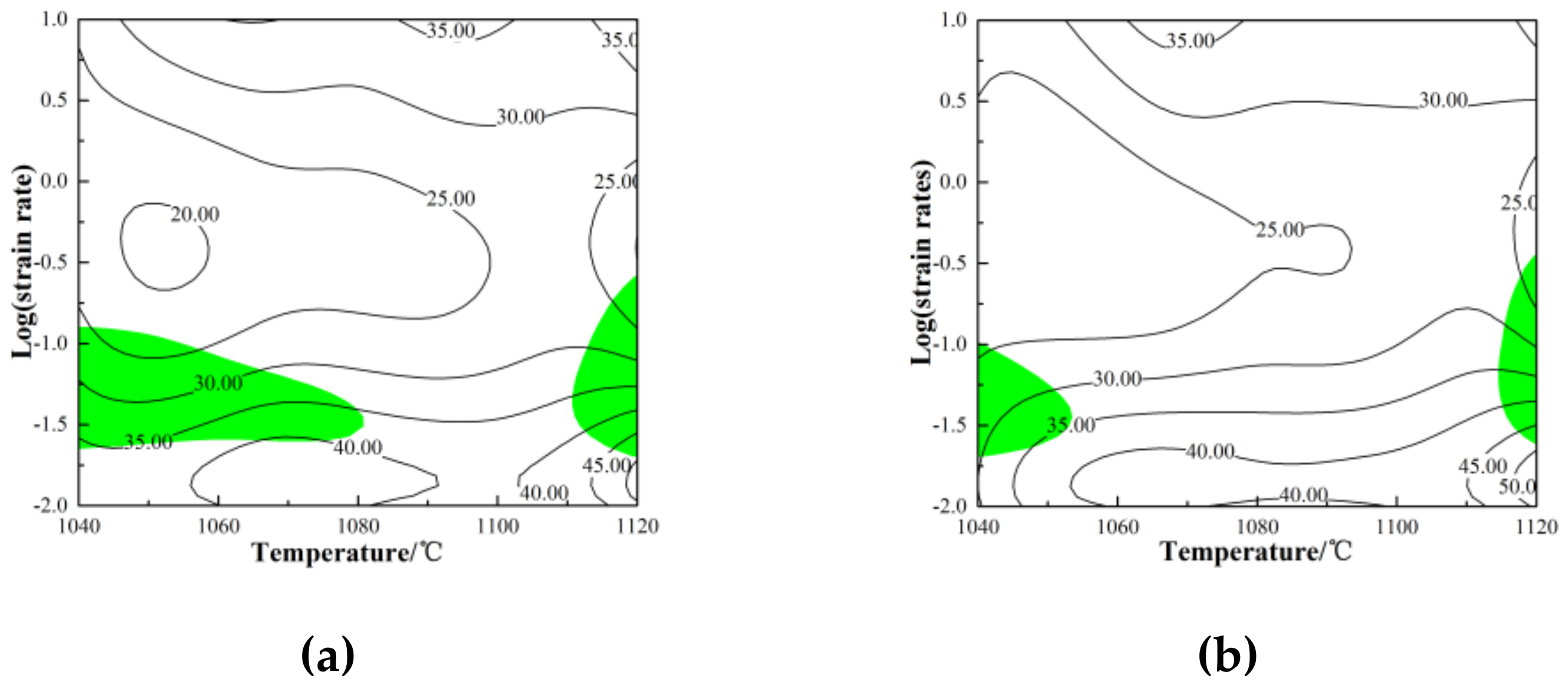
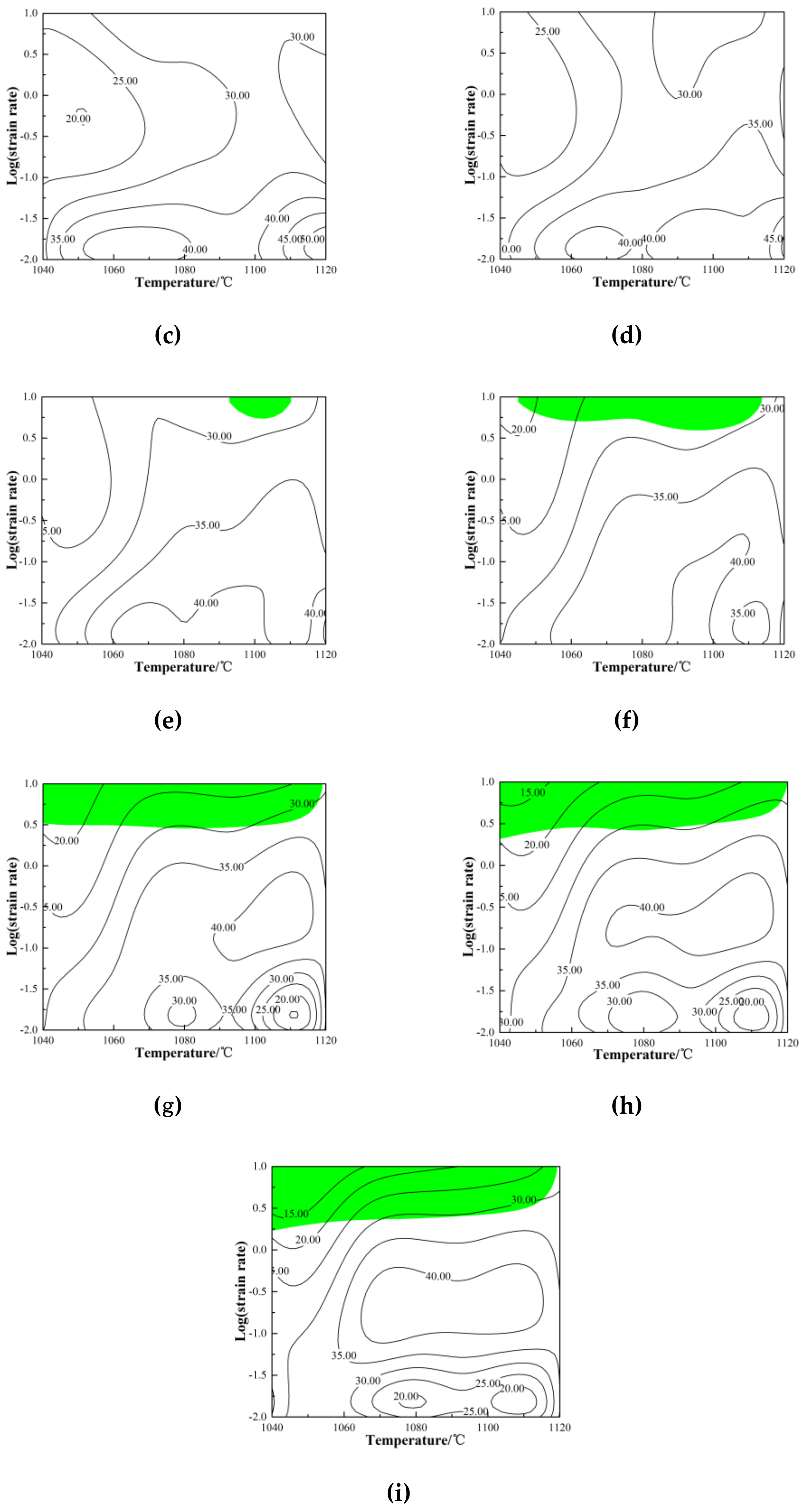
3.2. Deformation Behavior
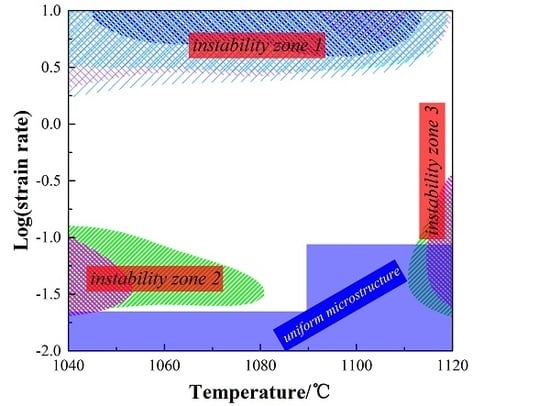
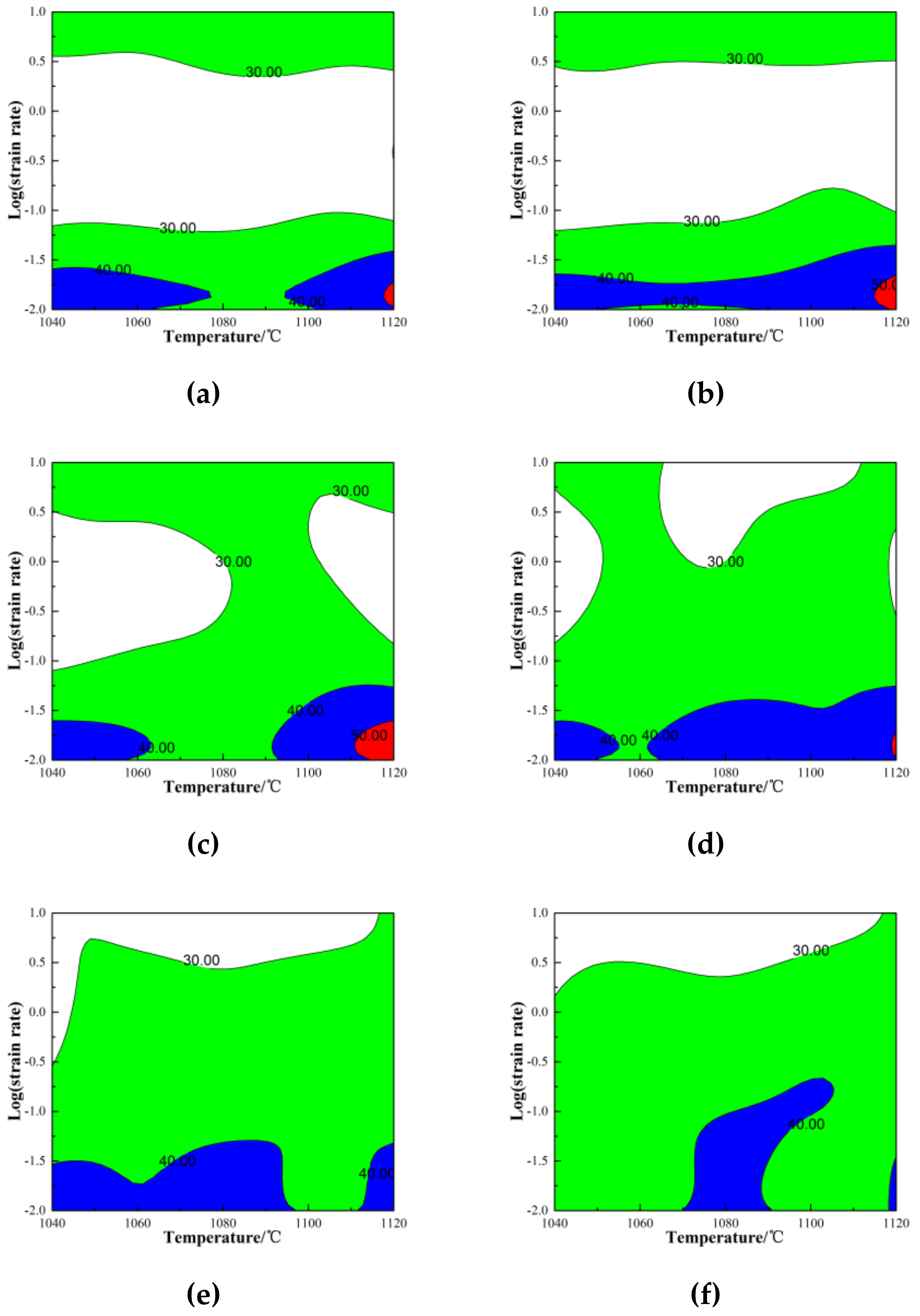
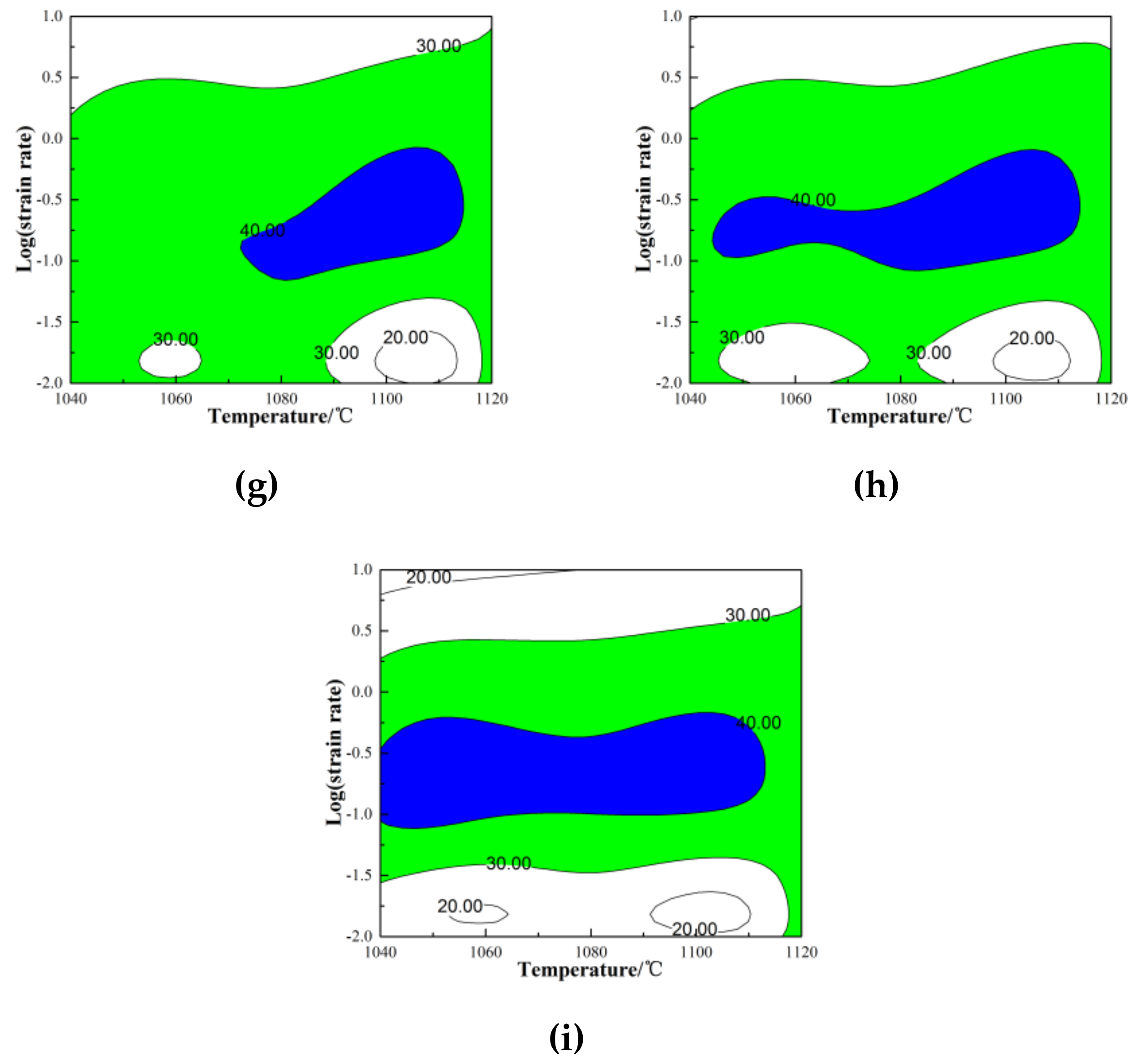
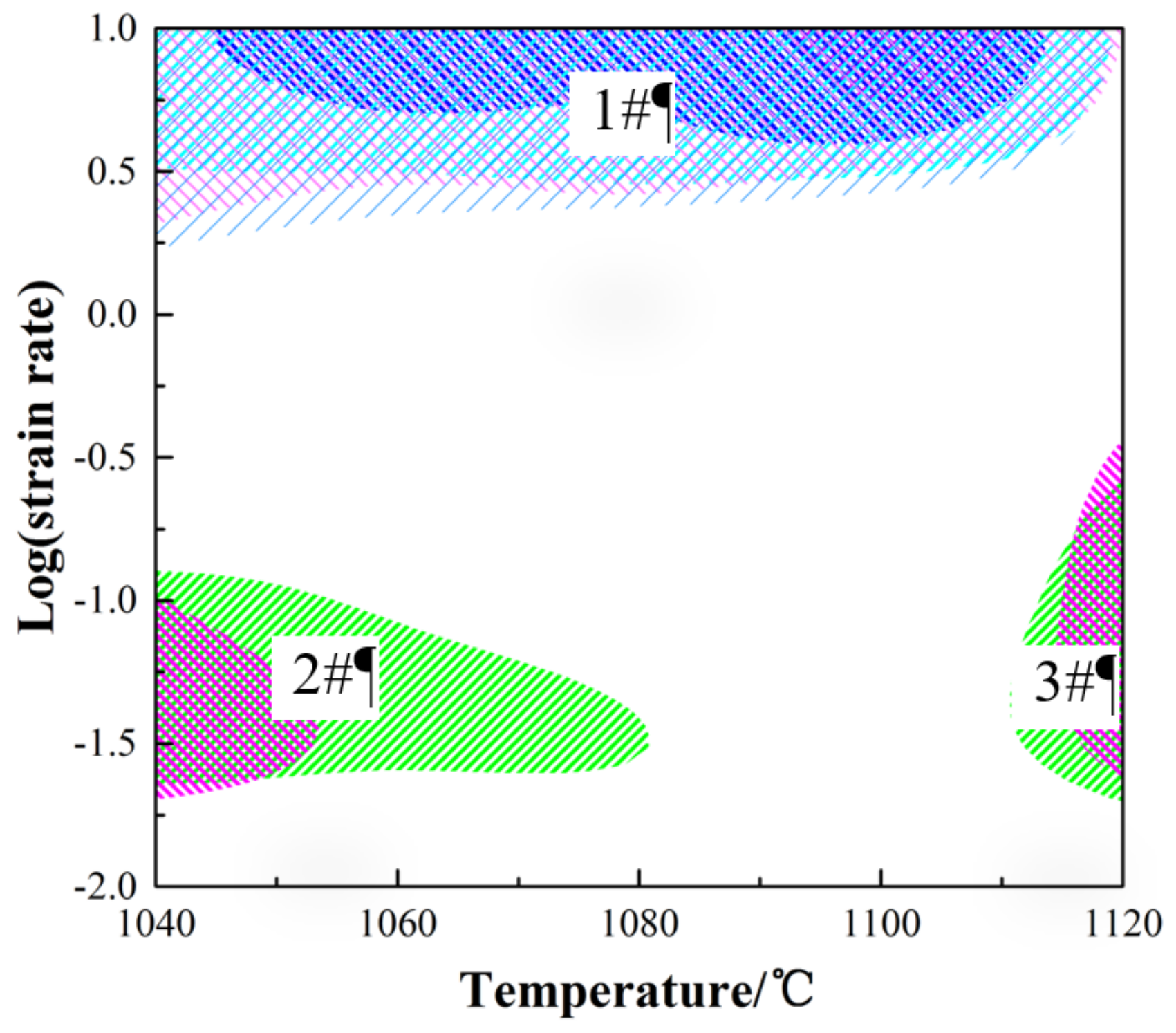
3.3. Processing Maps
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Chang, K.; Liu, X. Effect of γ′ content on the mechanical behavior of the WASPALOY alloy system. Mater. Sci. Eng. A 2001, 308, 1–8. [Google Scholar] [CrossRef]
- Weber, J.H.; Banerjee, M.K. Nickel-Based Superalloys: Alloying Reference Module in Materials Science and Materials Engineering; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Stone, H.J.; Holden, T.M.; Reed, R.C. On the generation of microstrains during the plastic deformation of Waspaloy. Acta Mater. 1999, 47, 4435–4448. [Google Scholar] [CrossRef]
- Olovsj, S.; Nyborg, L. Influence of microstructure on wear behaviour of uncoated WC tools in turning of Alloy 718 and Waspaloy. Wear 2012, 282, 12–21. [Google Scholar] [CrossRef]
- Oja, M.; Ravi Chandran, K.S.; Tryon, R.G. Orientation Imaging Microscopy of fatigue crack formation in Waspaloy: Crystallographic conditions for crack nucleation. Int. J. Fatigue 2010, 32, 551–556. [Google Scholar] [CrossRef]
- Kelekanjeri, V.S.; Gerhardt, R.A. Characterization of microstructural fluctuations in Waspaloy exposed to 760 °C for times up to 2500 h. Electrochim. Acta 2006, 51, 1873–1880. [Google Scholar] [CrossRef]
- Sinha, N.K.; Sinha, S. High-temperature yield strength and its dependence on primary creep and recovery. Mater. Sci. Eng. A 2011, 528, 5366–5378. [Google Scholar] [CrossRef]
- Attallah, M.M.; Preuss, M. 2-Inertia Friction Welding (IFW) for aerospace applications A2. In Welding and Joining of Aerospace Materials; Woodhead Publishing: Cambridge, UK, 2012; pp. 25–74. [Google Scholar]
- Chamanfar, A.; Jahazi, M.; Gholipour, J.; Wanjara, P.; Yue, S. Maximizing the integrity of linear friction welded Waspaloy. Mater. Sci. Eng. A 2012, 555, 117–130. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Wei, D.; Hu, J.; Li, Y. A comparative study on modified Zerilli–Armstrong, Arrhenius-type and artificial neural network models to predict high-temperature deformation behavior in T24 steel. Mater. Sci. Eng. A 2012, 536, 216–222. [Google Scholar] [CrossRef]
- Xiao, X.; Liu, G.Q.; Hu, B.F.; Zheng, X.; Wang, L.N.; Chen, S.J.; Ullah, A. A comparative study on Arrhenius-type constitutive equations and artificial neural network model to predict high-temperature deformation behaviour in 12Cr3WV steel. Comput. Mater. Sci. 2012, 62, 227–234. [Google Scholar] [CrossRef]
- Han, Y.; Qiao, G.; Sun, J.; Zou, D. A comparative study on constitutive relationship of as-cast 904L austenitic stainless steel during hot deformation based on Arrhenius-type and artificial neural network models. Comput. Mater. Sci. 2013, 67, 93–103. [Google Scholar] [CrossRef]
- Peng, W.; Zeng, W.; Wang, Q.; Yu, H. Comparative study on constitutive relationship of as-cast Ti60 titanium alloy during hot deformation based on Arrhenius-type and artificial neural network models. Mater. Des. 2013, 51, 95–104. [Google Scholar] [CrossRef]
- Shao, J.C.; Xiao, B.L.; Wang, Q.Z.; Ma, Z.Y.; Liu, Y.; Yang, K. Constitutive flow behavior and hot workability of powder metallurgy processed 20 vol.%SiCP/2024Al composite. Mater. Sci. Eng. A 2010, 527, 7865–7872. [Google Scholar] [CrossRef]
- Quan, G.; Ku, T.; Song, W.; Kang, B. The workability evaluation of wrought AZ80 magnesium alloy in hot compression. Mater. Des. 2011, 32, 2462–2468. [Google Scholar] [CrossRef]
- Park, N.; Yeom, J.; Na, Y. Characterization of deformation stability in hot forging of conventional Ti–6Al–4V using processing maps. J. Mater. Process. Technol. 2002, 130, 540–545. [Google Scholar] [CrossRef]
- Anil Kumar, V.; Gupta, R.K.; Narayana Murty, S.V.S.; Prasad, A.D. Hot workability and microstructure control in Co20Cr15W10Ni cobalt-based superalloy. J. Alloy Compd. 2016, 676, 527–541. [Google Scholar] [CrossRef]
- Zhang, P.; Hu, C.; Ding, C.; Zhu, Q.; Qin, H. Plastic deformation behavior and processing maps of a Ni-based superalloy. Mater. Des. 2015, 65, 575–584. [Google Scholar] [CrossRef]
- Kong, Y.; Chang, P.; Li, Q.; Xie, L.; Zhu, S. Hot deformation characteristics and processing map of nickel-based C276 superalloy. J. Alloy Compd. 2015, 622, 738–744. [Google Scholar] [CrossRef]
- Liu, Y.; Ning, Y.; Nan, Y.; Liang, H.; Li, Y.; Zhao, Z. Characterization of hot deformation behavior and processing map of FGH4096–GH4133B dual alloys. J. Alloy Compd. 2015, 633, 505–515. [Google Scholar] [CrossRef]
- Jiang, H.; Dong, J.; Zhang, M.; Zheng, L.; Yao, Z. Hot deformation characteristics of Alloy 617B nickel-based superalloy: A study using processing map. J. Alloy Compd. 2015, 647, 338–350. [Google Scholar] [CrossRef]
- Zhu, Y.; Zeng, W.; Feng, F.; Sun, Y.; Han, Y.; Zhou, Y. Characterization of hot deformation behavior of as-cast TC21 titanium alloy using processing map. Mater. Sci. Eng. A 2011, 528, 1757–1763. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Li, H.Z.; Li, Z.; Wang, H.; Liu, B. Constitutive modeling and processing map for elevated temperature flow behaviors of a powder metallurgy titanium aluminide alloy. J. Mater. Process. Technol. 2009, 209, 5363–5370. [Google Scholar] [CrossRef]
- Luo, J.; Li, M.; Yu, W.; Li, H. Effect of the strain on processing maps of titanium alloys in isothermal compression. Mater. Sci. Eng. A 2009, 504, 90–98. [Google Scholar] [CrossRef]
- Ghasemi, E.; Zarei-Hanzaki, A.; Farabi, E.; Tesa, K.; JGer, A.; Rezaee, M. Flow softening and dynamic recrystallization behavior of BT9 titanium alloy: A study using process map development. J. Alloy Compd. 2017, 695, 1706–1718. [Google Scholar] [CrossRef]
- Chi, J.; Cai, Z.; Li, L. Optimization of spinning process parameters for long thin-walled cylinder of TC11 alloy based on processing map. Int. J. Adv. Manuf. Technol. 2018, 97, 1961–1969. [Google Scholar] [CrossRef]
- Guo, L.; Yang, S.; Yang, H.; Zhang, J. Processing map of as-cast 7075 aluminum alloy for hot working. Chin. J. Aeronaut. 2015, 28, 1774–1783. [Google Scholar] [CrossRef]
- Yang, Y.; Xie, Z.; Zhang, Z.; Li, X.; Wang, Q.; Zhang, Y. Processing maps for hot deformation of the extruded 7075 aluminum alloy bar: Anisotropy of hot workability. Mater. Sci. Eng. A 2014, 615, 183–190. [Google Scholar] [CrossRef]
- Jenab, A.; Karimi Taheri, A. Experimental investigation of the hot deformation behavior of AA7075: Development and comparison of flow localization parameter and dynamic material model processing maps. Int. J. Mech. Sci. 2014, 78, 97–105. [Google Scholar] [CrossRef]
- Zhang, G.; Zhou, Z.; Sun, H.; Zou, L.; Wang, M.; Li, S. Hot deformation behavior and processing map of a 9Cr ferritic/martensitic ODS steel. J. Nucl. Mater. 2014, 455, 139–144. [Google Scholar] [CrossRef]
- Pu, E.; Zheng, W.; Xiang, J.; Song, Z.; Li, J. Hot deformation characteristic and processing map of superaustenitic stainless steel S32654. Mater. Sci. Eng. A 2014, 598, 174–182. [Google Scholar] [CrossRef]
- Sun, H.M.; Li, M.Q.; Liu, Y.G. Development of processing map coupling grain size for the isothermal compression of 300 M steel. Mater. Sci. Eng. A 2014, 595, 77–85. [Google Scholar] [CrossRef]
- Cheng, Y.; Du, H.; Wei, Y.; Hou, L.; Liu, B. Metadynamic recrystallization behavior and workability characteristics of HR3C austenitic heat-resistant stainless steel with processing map. J. Mater. Process. Technol. 2016, 235, 134–142. [Google Scholar] [CrossRef]
- Chamanfar, A.; Jahazi, M.; Gholipour, J.; Wanjara, P.; Yue, S. Evolution of flow stress and microstructure during isothermal compression of Waspaloy. Mater. Sci. Eng. A 2014, 615, 497–510. [Google Scholar] [CrossRef]
- Nayan, N.; Gurao, N.P.; Narayana Murty, S.V.S.; Jha, A.K.; Pant, B.; George, K.M. Microstructure and micro-texture evolution during large strain deformation of Inconel alloy IN718. Mater. Charact. 2015, 110, 236–241. [Google Scholar] [CrossRef]
- McQueen, H.J.; Ryan, N.D. Constitutive analysis in hot working. Mater. Sci. Eng. A 2002, 322, 43–63. [Google Scholar] [CrossRef]
- Guo, S.; Li, D.; Pen, H.; Guo, Q.; Hu, J. Hot deformation and processing maps of Inconel 690 superalloy. J. Nucl. Mater. 2011, 410, 52–58. [Google Scholar] [CrossRef]
- Srinivasan, N.; Prasad, Y.V. Microstructural control in hot working of IN-718 superalloy using processing map. Metall. Mater. Trans. A 1994, 25, 2275–2284. [Google Scholar] [CrossRef]

| Elements | Ni | Cr | Co | Mo | Ti | Al | Mn |
|---|---|---|---|---|---|---|---|
| Wt.% | Balance | 19.15 | 13.9 | 4.57 | 3.18 | 1.46 | 0.005 |
| Fe | C | Zr | S | P | Cu | Si | B |
| 0.25 | 0.05 | 0.058 | <0.005 | <0.010 | 0.005 | 0.089 | 0.007 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Liu, D.; Wang, J.; Shi, Y.; Zheng, Y.; Hu, Y. Investigation on the Thermal Deformation Behavior of the Nickel-Based Superalloy Strengthened by γ′ Phase. Crystals 2019, 9, 125. https://doi.org/10.3390/cryst9030125
Wang H, Liu D, Wang J, Shi Y, Zheng Y, Hu Y. Investigation on the Thermal Deformation Behavior of the Nickel-Based Superalloy Strengthened by γ′ Phase. Crystals. 2019; 9(3):125. https://doi.org/10.3390/cryst9030125
Chicago/Turabian StyleWang, Haiping, Dong Liu, Jianguo Wang, Yongzhao Shi, Yong Zheng, and Yang Hu. 2019. "Investigation on the Thermal Deformation Behavior of the Nickel-Based Superalloy Strengthened by γ′ Phase" Crystals 9, no. 3: 125. https://doi.org/10.3390/cryst9030125
APA StyleWang, H., Liu, D., Wang, J., Shi, Y., Zheng, Y., & Hu, Y. (2019). Investigation on the Thermal Deformation Behavior of the Nickel-Based Superalloy Strengthened by γ′ Phase. Crystals, 9(3), 125. https://doi.org/10.3390/cryst9030125