On Crystal Mosaicity in Single Crystal Ni-Based Superalloys
Abstract
:1. Introduction
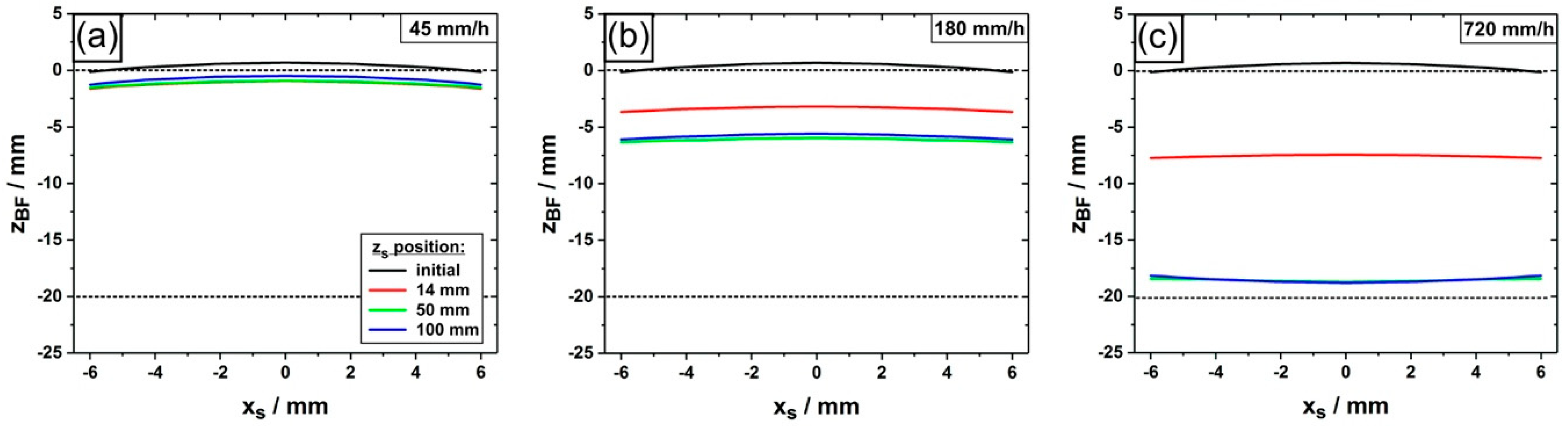
2. Materials and Methods
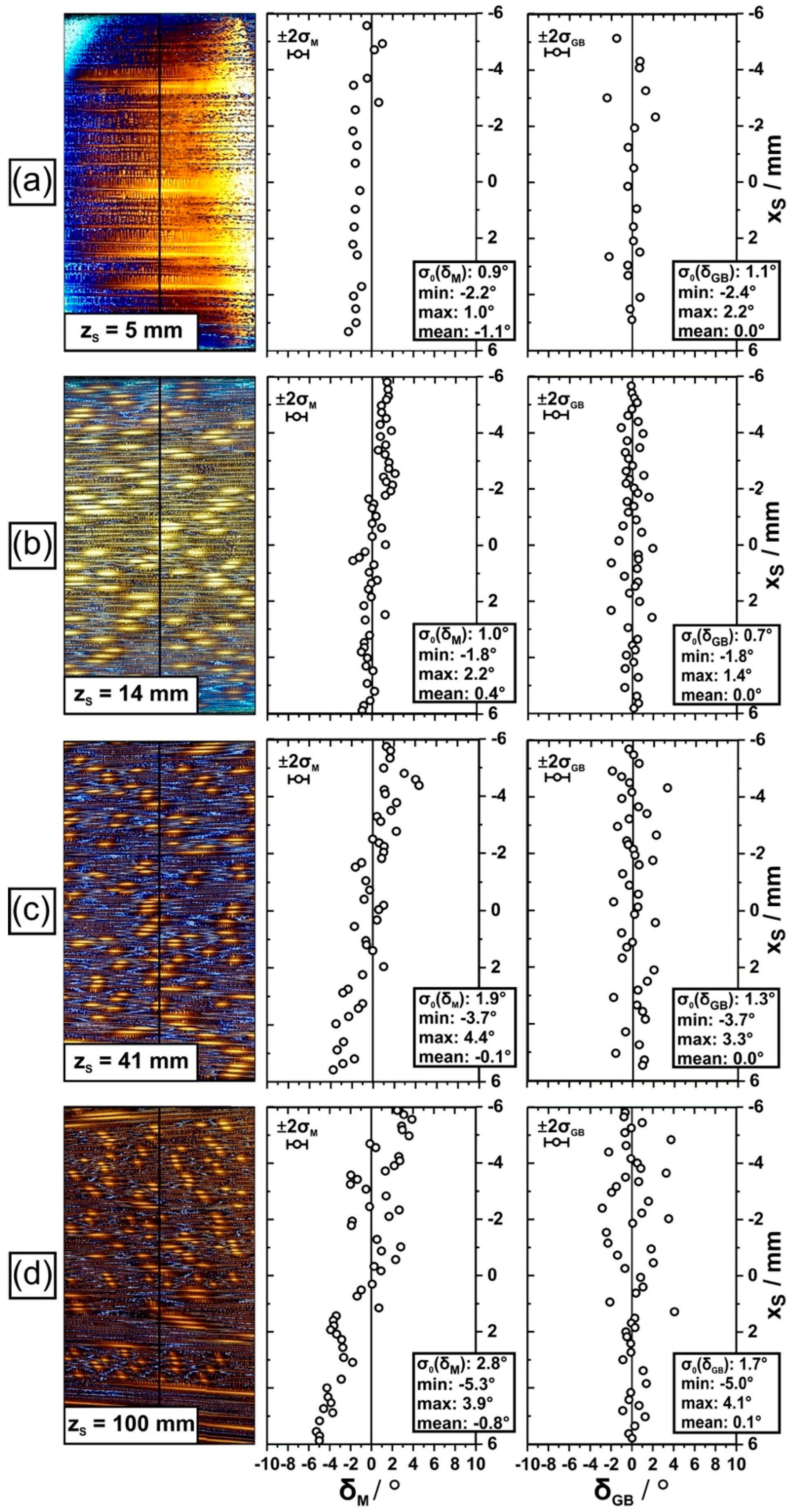
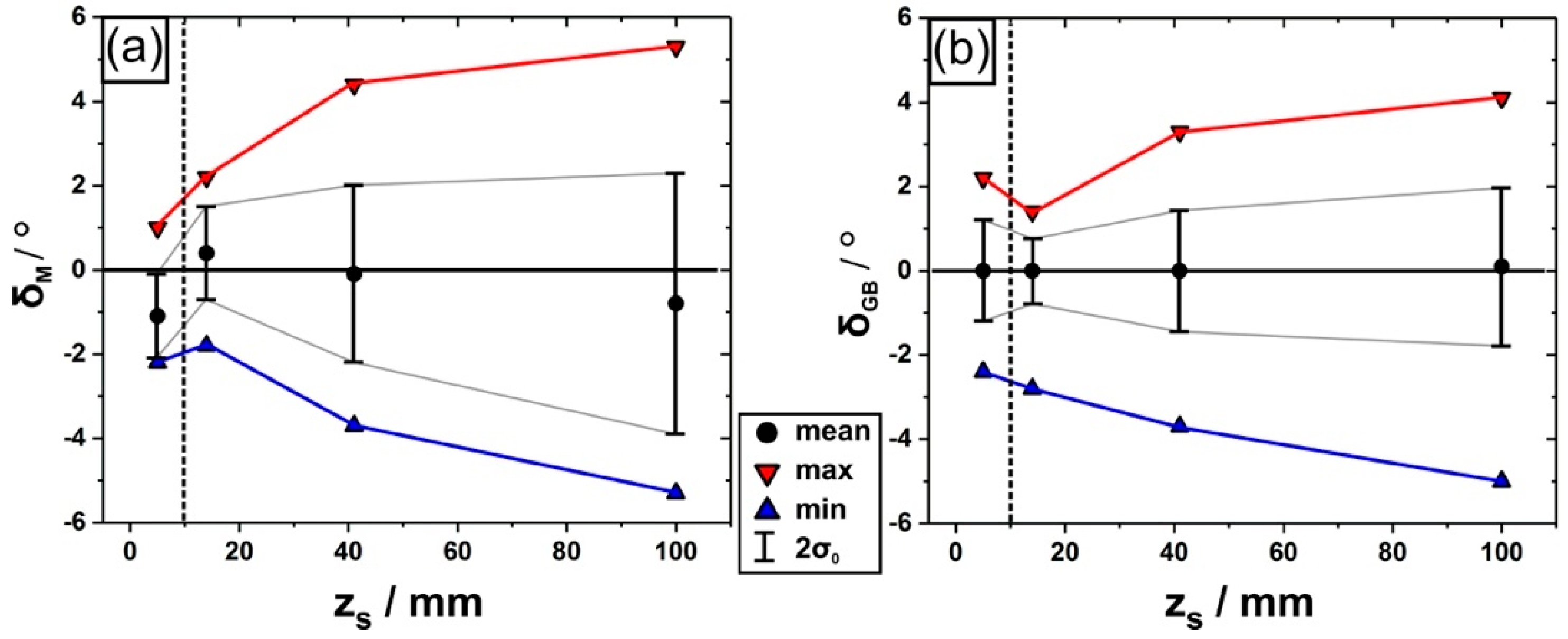
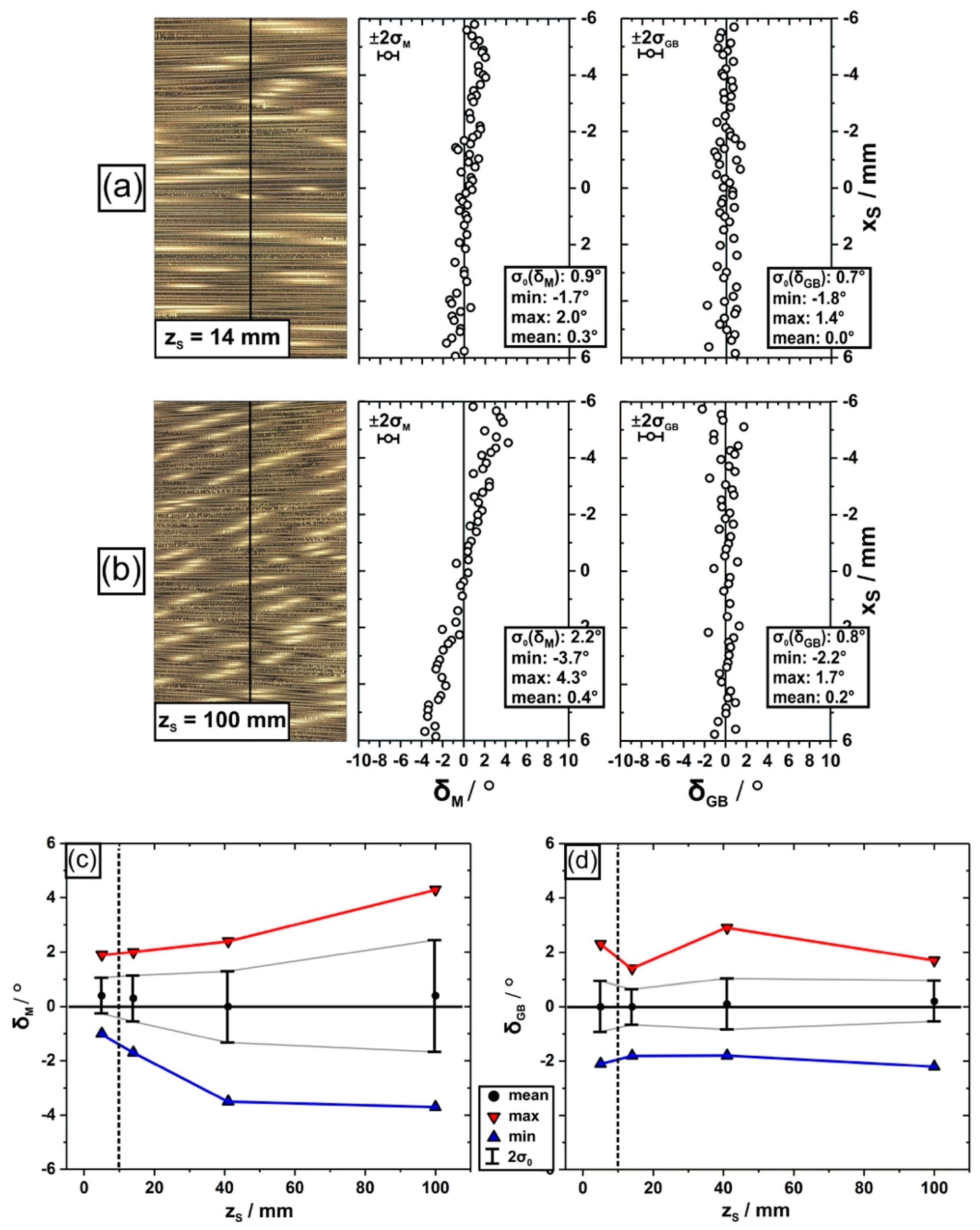
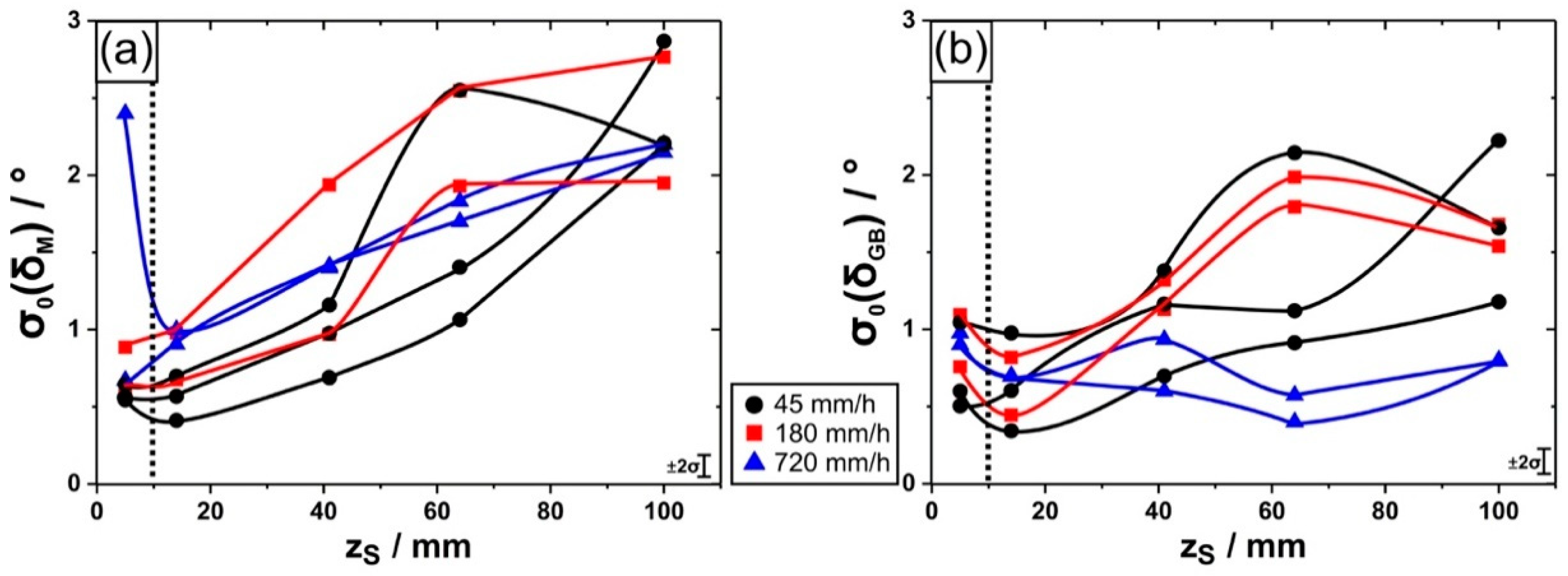
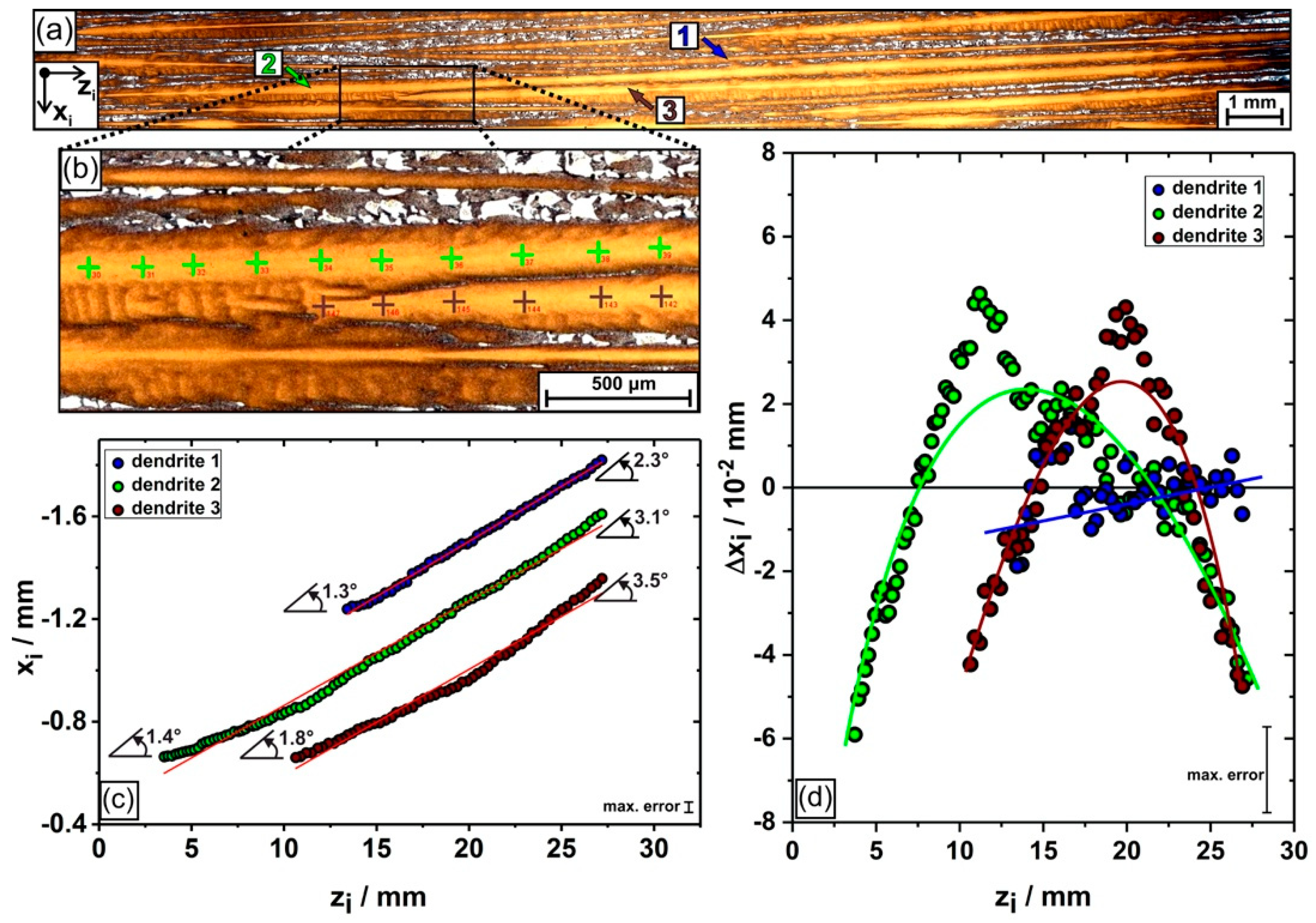
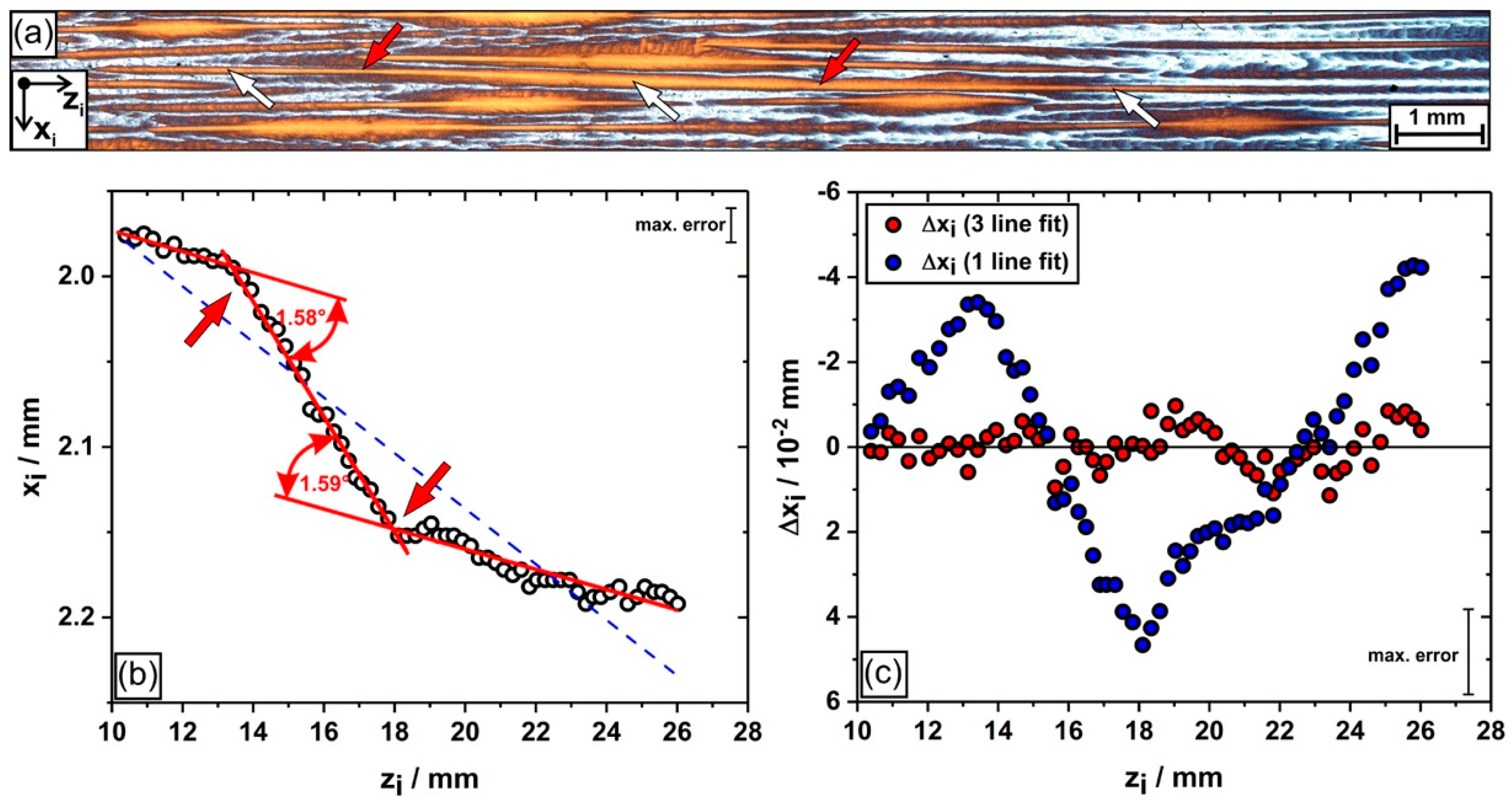
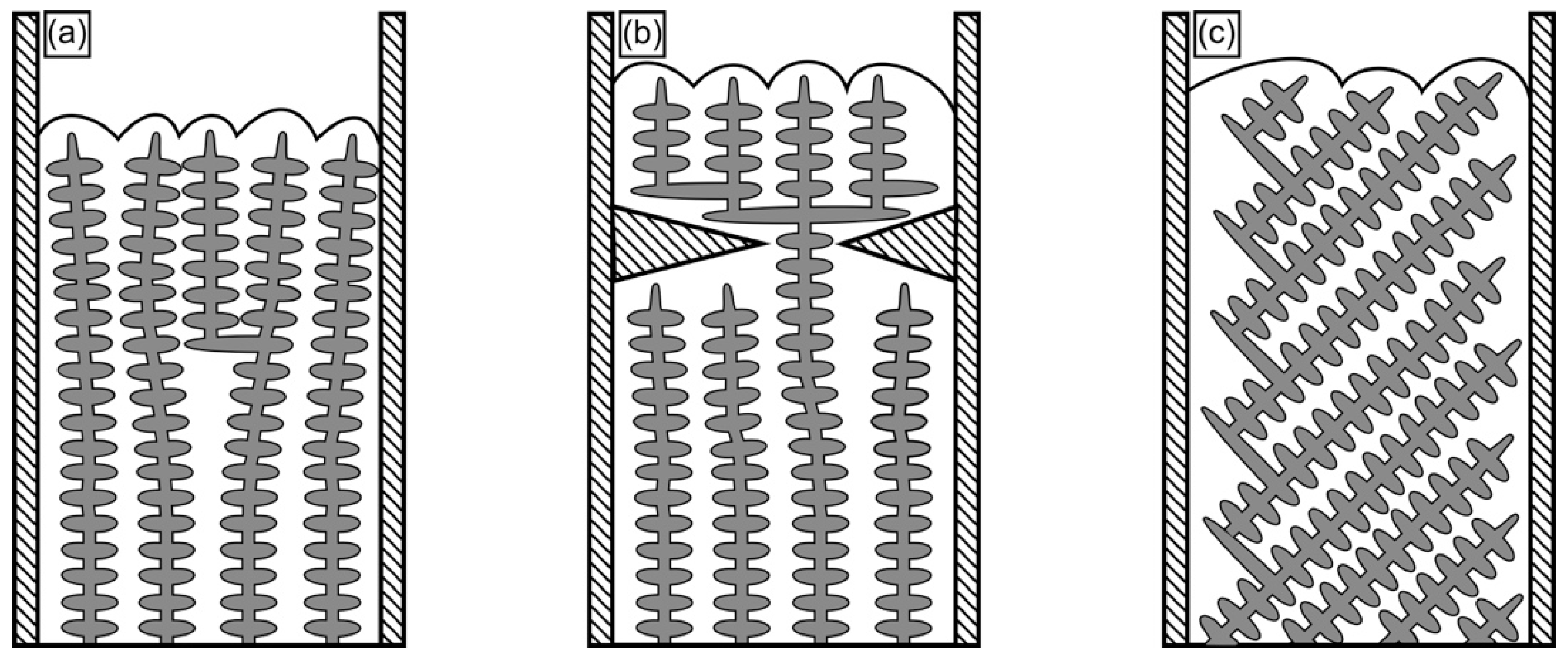
3. Results
4. Discussion
5. Conclusions
- 1)
- Crystal mosaicity represents an inherent feature of dendritic single crystal superalloy microstructures related to elementary stochastic processes which govern solidification.
- 2)
- Two sources of mosaicity have been identified: First, mosaicity is inherited from the seed crystal which is used to impose crystallographic target directions. Second, the degree of mosaicity increases by dendrite deformation, while the average dendrite/crystal orientations remain constant.
- 3)
- Almost every single crystal investigated in the present study has its own mosaicity fingerprint. Two crystals always differ in this respect, even when they were made using identical processing conditions. Small differences in the orientation spread of the seed crystals, as well as small stochastic orientation deviations, continuously accumulate during solidification. This eventually results in individual misorientation types and it represents an experimental evidence for the chaotic nature of mosaicity evolution.
- 4)
- We provide direct evidence for dendrite bending in a seeded Bridgman growth process. It was observed that continuous or sudden bending affects the growth directions of dendrites. It was observed that some dendrites continuously bend by ≈1.7° within a 25-mm growth interval.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Reed, R.C. The Superalloys—Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- McLean, M. Directionally Solidified Materials for High Temperature Service; The Metals Society: London, UK, 1983. [Google Scholar]
- Pollock, T.M.; Tin, S. Nickel-based superalloys for advanced turbine engines: Chemistry, microstructure and properties. J. Propuls. Power 2006, 22, 361–374. [Google Scholar] [CrossRef]
- Evans, R.W.; Wilshire, B. Creep of Metals and Alloys; Institute of Metals: London, UK, 1985. [Google Scholar]
- Ilschner, B. Hochtemperatur-Plastizität: Warmfestigkeit und Warmverformbarkeit Metallischer und Nichtmetallischer Werkstoffe; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1973; Volume 23. [Google Scholar]
- Bürgel, R.; Maier, H.J.; Niendorf, T. Hochtemperaturlegierungen. In Handbuch Hochtemperatur-Werkstofftechnik; Bürgel, R., Maier, H.J., Niendorf, T., Eds.; Vieweg+Teubner Verlag: Wiesbaden, Germany, 2011; pp. 340–484. [Google Scholar]
- Cadek, J. Creep in Metallic Materials; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Quested, P.N.; McLean, M. Solidification morphologies in directionally solidified superalloys. Mater. Sci. Eng. 1984, 65, 171–180. [Google Scholar] [CrossRef]
- Versnyder, F.I.; Shank, M.E. The development of columnar grain and single crystal high temperature materials through directional solidification. Mater. Sci. Eng. 1970, 6, 213–247. [Google Scholar] [CrossRef]
- Kubiak, K.; Szeliga, D.; Sieniawski, J.; Onyszko, A. The unidirectional crystallization of metals and alloys (turbine blades). In Handbook of Crystal Growth (Second Edition)—Bulk Crystal Growth: Growth Mechanisms and Dynamics; Rudolph, P., Ed.; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Hallensleben, P.; Schaar, H.; Thome, P.; Jöns, N.; Jafarizadeh, A.; Steinbach, I.; Eggeler, G.; Frenzel, J. On the evolution of cast microstructures during processing of single crystal Ni-base superalloys using a Bridgman seed technique. Mater. Des. 2017, 128, 98–111. [Google Scholar] [CrossRef]
- Pollock, T.M.; Murphy, W.H. The breakdown of single-crystal solidification in high refractory nickel-base alloys. Metall. Mater. Trans. A 1996, 27, 1081–1094. [Google Scholar] [CrossRef]
- Hobbs, R.A.; Tin, S.; Rae, C.M.F. A castability model based on elemental solid-liquid partitioning in advanced nickel-base single-crystal superalloys. Metall. Mater. Trans. A 2005, 36, 2761–2773. [Google Scholar] [CrossRef]
- Zhou, Y.Z.; Volek, A.; Singer, R.F. Influence of solidification conditions on the castability of nickel-base superalloy IN792. Metall. Mater. Trans. A 2005, 36, 651–656. [Google Scholar] [CrossRef]
- Parsa, A.B.; Wollgramm, P.; Buck, H.; Somsen, C.; Kostka, A.; Povstugar, I.; Choi, P.P.; Raabe, D.; Dlouhy, A.; Müller, J.; et al. Advanced scale bridging microstructure analysis of single crystal Ni-base superalloys. Adv. Eng. Mater. 2015, 17, 216–230. [Google Scholar] [CrossRef]
- Nörtershäuser, P.; Frenzel, J.; Ludwig, A.; Neuking, K.; Eggeler, G. The effect of cast microstructure and crystallography on rafting, dislocation plasticity and creep anisotropy of single crystal Ni-base superalloys. Mater. Sci. Eng. A 2015, 626, 305–312. [Google Scholar] [CrossRef]
- Lopez-Galilea, I.; Huth, S.; Fries, S.G.; Warnken, N.; Steinbach, I.; Theisen, W. Microsegregation and Secondary Phase Formation During Directional Solidification of the Single-Crystal Ni-Based Superalloy LEK94. Metall. Mater. Trans. A 2012, 43, 5153–5164. [Google Scholar] [CrossRef]
- Steinbach, I. Effect of interface anisotropy on spacing selection in constrained dendrite growth. Acta Mater. 2008, 56, 4965–4971. [Google Scholar] [CrossRef]
- Matache, G.; Stefanescu, D.M.; Puscasu, C.; Alexandrescu, E.; Buhrig-Polaczek, A. Investigation of solidification microstructure of single crystal CMSX-4 superalloy—experimental measurements and modelling predictions. Int. J. Cast Met. Res. 2015, 28, 323–336. [Google Scholar] [CrossRef]
- Pyczak, F.; Devrient, B.; Neuner, F.; Mughrabi, H. The influence of different alloying elements on the development of the γ/γ′ microstructure of nickel-base superalloys during high-temperature annealing and deformation. Acta Mater. 2005, 53, 3879–3891. [Google Scholar] [CrossRef]
- Qu, S.; Fu, C.M.; Dong, C.; Tian, J.F.; Zhang, Z.F. Failure analysis of the 1st stage blades in gas turbine engine. Eng. Fail. Anal. 2013, 32, 292–303. [Google Scholar] [CrossRef]
- Hong, J.P.; Ma, D.X.; Wang, J.; Wang, F.; Dong, A.P.; Sun, B.D.; Bührig-Polaczek, A. Geometrical effect of freckle formation on directionally solidified superalloy CM247 LC components. J. Alloy Compd. 2015, 648, 1076–1082. [Google Scholar] [CrossRef]
- Ma, D.X.; Zhou, B.; Buhrig-Polaczek, A. Investigation of freckle formation under various solidification conditions. In Euro Superalloys 2010; Heilmaier, M., Ed.; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2011; Volume 278, pp. 428–433. [Google Scholar]
- Auburtin, P.; Wang, T.; Cockcroft, S.L.; Mitchell, A. Freckle formation and freckle criterion in superalloy castings. Metall. Mater. Trans. B 2000, 31, 801–811. [Google Scholar] [CrossRef]
- Yang, C.; Liu, L.; Zhao, X.; Zhang, J.; Sun, D.; Fu, H. Formation of stray grains during directional solidification of a superalloy AM3. Appl. Phys. A 2013, 114, 979–983. [Google Scholar] [CrossRef]
- Zhou, Y.Z. Formation of stray grains during directional solidification of a nickel-based superalloy. Scr. Mater. 2011, 65, 281–284. [Google Scholar] [CrossRef]
- Aveson, J.W.; Tennant, P.A.; Foss, B.J.; Shollock, B.A.; Stone, H.J.; D’Souza, N. On the origin of sliver defects in single crystal investment castings. Acta Mater. 2013, 61, 5162–5171. [Google Scholar] [CrossRef]
- Yardley, V.; Povstugar, I.; Choi, P.P.; Raabe, D.; Parsa, A.B.; Kostka, A.; Somsen, C.; Dlouhy, A.; Neuking, K.; George, E.P.; et al. On local phase equilibria and the appearance of nanoparticles in the microstructure of single-crystal Ni-base superalloys. Adv. Eng. Mater. 2016, 18, 1556–1567. [Google Scholar] [CrossRef]
- Fan, X.; Guo, Z.; Wang, X.; Yang, J.; Zou, J. Morphology evolution of γ′ precipitates in a powder metallurgy Ni-base superalloy. Mater. Charact. 2018, 139, 382–389. [Google Scholar] [CrossRef]
- Serin, K.; Göbenli, G.; Eggeler, G. On the influence of stress state, stress level and temperature on gamma-channel widening in the single crystal superalloy CMSX-4. Mater. Sci. Eng. A 2004, 387, 133–137. [Google Scholar] [CrossRef]
- Darwin, C.G. XCII. The reflexion of X-rays from imperfect crystals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1922, 43, 800–829. [Google Scholar] [CrossRef]
- Bellet, D. Etude Des Textures des Superalliages Monocristallins Par Diffraction et Diffusion Des Rayonnements: X,[Gamma] et Neutrons. Ph.D. Thesis, Université Joseph Fourier (Grenoble), Grenoble, France, 1990. [Google Scholar]
- Klam, H.; Blank, E. The growth of modern superalloy single crystals. In Proceedings of the First Conference on Advanced Materials and Processes (EUROMAT’89), Aachen, Germany, 22–24 November 1989; pp. 407–412. [Google Scholar]
- Brückner, U.; Epishin, A.; Link, T. Local X-ray diffraction analysis of the structure of dendrites in single-crystal nickel-base superalloys. Acta Mater. 1997, 45, 5223–5231. [Google Scholar] [CrossRef]
- Kurz, W.; Fisher, D.J. Fundamentals of Solidification, 4th ed.; Trans Tech Publ.: Aedermannsdorf, Switzerland, 2005. [Google Scholar]
- Boettinger, W.J.; Coriell, S.R.; Greer, A.L.; Karma, A.; Kurz, W.; Rappaz, M.; Trivedi, R. Solidification microstructures: Recent developments, future directions. Acta Mater. 2000, 48, 43–70. [Google Scholar] [CrossRef]
- Dantzig, J.A.; Rappaz, M. Solidification; EFPL Press: Lausanne, France, 2009. [Google Scholar]
- D’Souza, N.; Newell, M.; Devendra, K.; Jennings, P.A.; Ardakani, M.G.; Shollock, B.A. Formation of low angle boundaries in Ni-based superalloys. Mater. Sci. Eng. A 2005, 413, 567–570. [Google Scholar] [CrossRef]
- Bogdanowicz, W.; Albrecht, R.; Sieniawski, J.; Kubiak, K. The subgrain structure in turbine blade roots of CMSX-4 superalloy. J. Cryst. Growth 2014, 401, 418–422. [Google Scholar] [CrossRef]
- Bogdanowicz, W.; Albrecht, R.; Onyszko, A.; Sieniawski, J. Characterization of Single-Crystal Turbine Blades by X-Ray Diffraction Methods. In Applied Crystallography Xxii; Stroz, D., Dercz, G., Eds.; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2013; Volume 203–204, pp. 63–66. [Google Scholar]
- Onyszko, A.; Bogdanowicz, W.; Sieniawski, J. Structural perfection of a single crystal nickel-based CMSX-4 superalloy. In Electron Microscopy Xiv; Stroz, D., Prusik, K., Eds.; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2012; Volume 186, pp. 151–155. [Google Scholar]
- Newell, M.; D’Souza, N.; Green, N.R. Formation of low angle boundaries in Ni-based superalloys. Int. J. Cast Met. Res. 2009, 22, 66–69. [Google Scholar] [CrossRef]
- Newell, M.; Devendra, K.; Jennings, P.A.; D’Souza, N. Role of dendrite branching and growth kinetics in the formation of low angle boundaries in Ni–base superalloys. Mater. Sci. Eng. A 2005, 412, 307–315. [Google Scholar] [CrossRef]
- Siredey, N.; Lesoult, G.; Lacaze, J. Evolution during Solidification of the Array of Dendritic Primary Axes of Am1 Superalloy Single Grains in Relation with Their Crystalline Quality. In High Temperature Materials for Power Engineering; Springer: Dordrecht, The Netherlands, 1990; Parts 1–2; pp. 1309–1318. [Google Scholar]
- Siredey, N.; Boufoussi, M.B.; Denis, S.; Lacaze, J. Dendritic growth and crystalline quality of nickel-base single grains. J. Cryst. Growth 1993, 130, 132–146. [Google Scholar] [CrossRef]
- Schaefer, R.; Black, D.; Vaudin, M.; Mueller, B.; Giamei, A. Geometry and mechanisms of dendrite misalignments in superalloy single crystals. In Proceedings of the 4th Decennial International Conference on Solidification Processing, Sheffield, UK, 7–10 July 1997; pp. 37–40. [Google Scholar]
- Aveson, J.W.; Reinhart, G.; Nguyen-Thi, H.; Mangelinck-Noël, N.; Tandjaoui, A.; Billia, B.; Goodwin, K.; Lafford, T.A.; Baruchel, J.; Stone, H.J.; et al. Dendrite bending during directional solidification. In Superalloys 2012; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 615–624. [Google Scholar]
- Aveson, J.W.; Reinhart, G.; Nguyen-Thi, H.; Mangelinck-Noel, N.; D’Souza, N.; Stone, H.J. Origins of misorientation defects in single crystal castings:aA time resolved in situ synchrotron x-ray radiography study. In Eurosuperalloys 2014—2nd European Symposium on Superalloys and Their Applications; Guedou, J.Y., Chone, J., Eds.; EDP Sciences: Les Ulis, France, 2014; Volume 14. [Google Scholar]
- Reinhart, G.; Nguyen-Thi, H.; Mangelinck-Noël, N.; Baruchel, J.; Billia, B. In Situ Investigation of Dendrite Deformation During Upward Solidification of Al-7wt.%Si. JOM-US 2014, 66, 1408–1414. [Google Scholar] [CrossRef]
- Doherty, R.D. Comments on “Mechanical deformation of dendrites by fluid flow during the solidification of undercooled melts”. Scr. Mater. 2003, 49, 1219–1222. [Google Scholar] [CrossRef]
- Uehara, T.; Tsujino, T. Phase field simulation of stress evolution during solidification. J. Cryst. Growth 2005, 275, e219–e224. [Google Scholar] [CrossRef]
- Uehara, T.; Fukui, M.; Ohno, N. Phase field simulations of stress distributions in solidification structures. J. Cryst. Growth 2008, 310, 1331–1336. [Google Scholar] [CrossRef]
- Wagner, A.; Shollock, B.A.; McLean, M. Grain structure development in directional solidification of nickel-base superalloys. Mater. Sci. Eng. A 2004, 374, 270–279. [Google Scholar] [CrossRef]
- Dragnevski, K.; Mullis, A.M.; Walker, D.J.; Cochrane, R.F. Mechanical deformation of dendrites by fluid flow during the solidification of undercooled melts. Acta Mater. 2002, 50, 3743–3755. [Google Scholar] [CrossRef]
- Mullis, A.M.; Walker, D.J.; Battersby, S.E.; Cochrane, R.F. Deformation of dendrites by fluid flow during rapid solidification. Mater. Sci. Eng. A 2001, 304–306, 245–249. [Google Scholar] [CrossRef]
- Pilling, J.; Hellawell, A. Mechanical deformation of dendrites by fluid flow. Metall. Mater. Trans. A 1996, 27, 229–232. [Google Scholar] [CrossRef]
- Rappaz, M.; Blank, E. Combined X-ray microdiffraction and topography experiment for microstructural analysis of heterogeneous materials. J. Mater. Sci. 1987, 22, 896–906. [Google Scholar] [CrossRef]
- Brückner, U.; Epishin, A.; Link, T.; Dressel, K. The influence of the dendritic structure on the γ/γ’-lattice misfit in the single-crystal nickel-base super-alloy CMSX-4. Mater. Sci. Eng. A 1998, 247, 23–31. [Google Scholar] [CrossRef]
- Husseini, N.S.; Kumah, D.P.; Yi, J.Z.; Torbet, C.J.; Arms, D.A.; Dufresne, E.M.; Pollock, T.M.; Wayne Jones, J.; Clarke, R. Mapping single-crystal dendritic microstructure and defects in nickel-base superalloys with synchrotron radiation. Acta Mater. 2008, 56, 4715–4723. [Google Scholar] [CrossRef]
- Bogdanowicz, W.; Albrecht, R.; Sieniawski, J.; Kubiak, K.; Onyszko, A. Correlation between SEM and X-Ray diffraction imaging of structure in single-crystal Ni-based superalloy. Solid State Phenom. 2012, 186, 135–138. [Google Scholar] [CrossRef]
- Whitesell, H.S.; Li, L.; Overfelt, R.A. Influence of solidification variables on the dendrite arm spacings of Ni-based superalloys. Met. Mater. Trans. B 2000, 31, 546–551. [Google Scholar] [CrossRef]
- Corel Draw X5. Available online: https://www.coreldraw.com (accessed on 12 January 2019).
- Rueden, C.T.; Schindelin, J.; Hiner, M.C.; DeZonia, B.E.; Walter, A.E.; Arena, E.T.; Eliceiri, K.W. ImageJ2: ImageJ for the next generation of scientific image data. BMC Bioinform. 2017, 18, 529. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Thome, P.; Medghalchi, S.; Frenzel, J.; Schreuer, J.; Eggeler, G. Ni-Base Superalloy Single Crystal (SX) Mosaicity Characterized by the Rotation Vector Base Line Electron Back Scatter Diffraction (RVB-EBSD) Method. Ultramicroscopy 2019. Submitted. [Google Scholar]
- Quested, P.N.; Brooks, R.F.; Chapman, L.; Morrell, R.; Youssef, Y.; Mills, K.C. Measurement and estimation of thermophysical properties of nickel based superalloys. Mater. Sci. Technol. 2009, 25, 154–162. [Google Scholar] [CrossRef]
- Chase, M.W., Jr. NIST-JANAF Thermochemical Tables, Monograph No. 9, 4th ed.; NIST: Washington, DC, USA, 1998.
- Picard, S.; Burns, D.T.; Roger, P. Measurement of the Specific Heat Capacity of Graphite, Rapport BIPM-2006/01; International Bureau of Weights and Measures: Sèvres, France, 2006. [Google Scholar]
- Material data sheets/personal communications from/with furnace component manufacturers. 2016.
- Chang, C.E.; Wilcox, W.R. Control of interface shape in the vertical bridgman-stockbarger technique. J. Cryst. Growth 1974, 21, 135–140. [Google Scholar] [CrossRef]
- Potts, H.; Wilcox, W.R. Thermal fields in the Bridgman-Stockbarger technique. J. Cryst. Growth 1985, 73, 350–358. [Google Scholar] [CrossRef]
- Hellawell, A.; Sarazin, J.R.; Steube, R.S. Channel Convection in partially solidified Systems. Philos. Trans. R. Soc. A 1993, 345, 507–544. [Google Scholar] [CrossRef]
- Liu, S.; Lu, S.-Z.; Hellawell, A. Dendritic array growth in the systems NH4Cl–H2O and [CH2 CN]2–H2O: The detachment of dendrite side arms induced by deceleration. J. Cryst. Growth 2002, 234, 740–750. [Google Scholar] [CrossRef]
- Mullis, A.M. Growth induced dendritic bending and rosette formation during solidification in a shearing flow. Acta Mater. 1999, 47, 1783–1789. [Google Scholar] [CrossRef]
- Warren, J. Dendritic Crystals: Rule of thumb breaks down. Nat. Mater. 2006, 5, 595–596. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.N.; Kim, K.-H.; Lee, Y.-G.; Choi, C.-H. Factors determining crystal orientation of dendritic growth during solidification. Mater. Chem. Phys. 1997, 47, 154–158. [Google Scholar] [CrossRef]


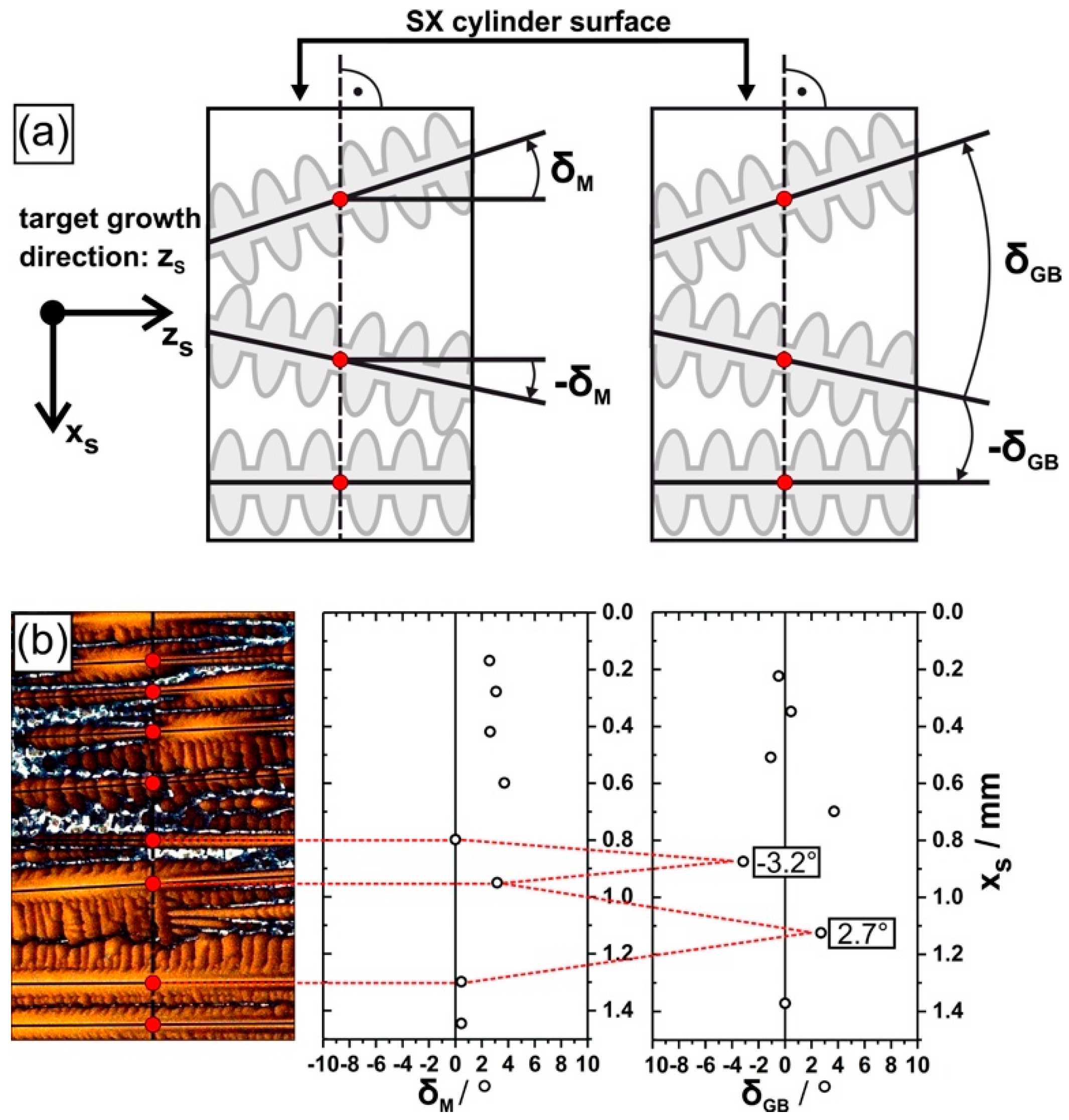
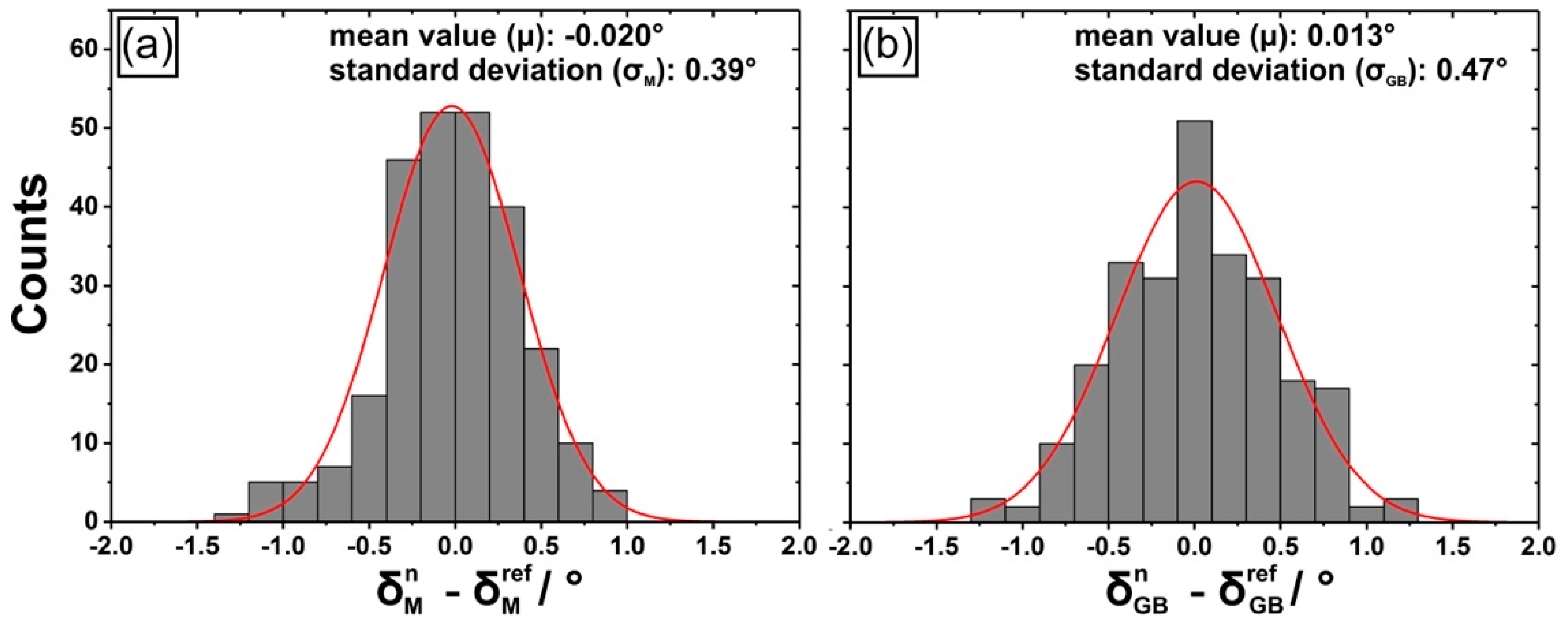
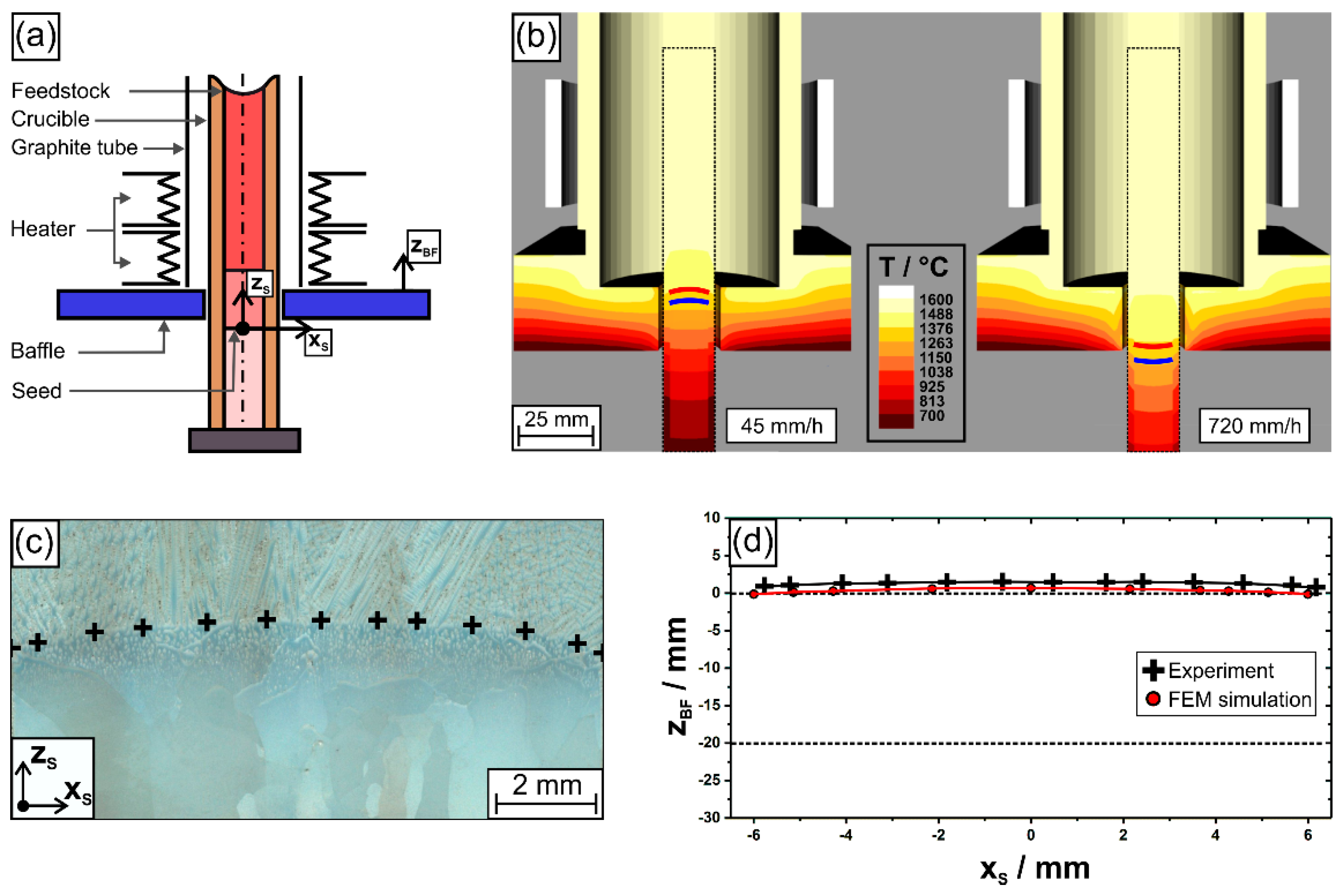


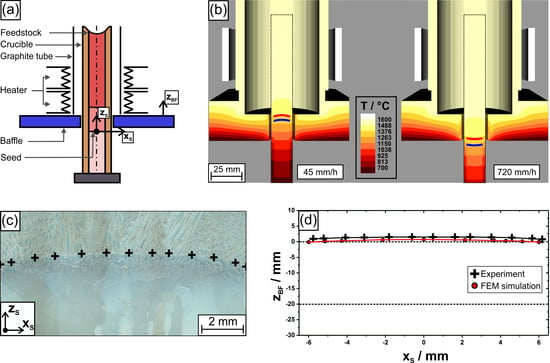
| Withdrawal Rate (mm/h) | PDAS (µm) |
|---|---|
| 45 | 243 |
| 180 | 205 |
| 720 | 148 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hallensleben, P.; Scholz, F.; Thome, P.; Schaar, H.; Steinbach, I.; Eggeler, G.; Frenzel, J. On Crystal Mosaicity in Single Crystal Ni-Based Superalloys. Crystals 2019, 9, 149. https://doi.org/10.3390/cryst9030149
Hallensleben P, Scholz F, Thome P, Schaar H, Steinbach I, Eggeler G, Frenzel J. On Crystal Mosaicity in Single Crystal Ni-Based Superalloys. Crystals. 2019; 9(3):149. https://doi.org/10.3390/cryst9030149
Chicago/Turabian StyleHallensleben, Philipp, Felicitas Scholz, Pascal Thome, Helge Schaar, Ingo Steinbach, Gunther Eggeler, and Jan Frenzel. 2019. "On Crystal Mosaicity in Single Crystal Ni-Based Superalloys" Crystals 9, no. 3: 149. https://doi.org/10.3390/cryst9030149
APA StyleHallensleben, P., Scholz, F., Thome, P., Schaar, H., Steinbach, I., Eggeler, G., & Frenzel, J. (2019). On Crystal Mosaicity in Single Crystal Ni-Based Superalloys. Crystals, 9(3), 149. https://doi.org/10.3390/cryst9030149