2.1. On Indirect-Transitions Lasing
A paper by Dumke dated September 1962 [
7] can be assigned as a fundamental work devoted to this laser mechanism. Although it deals with a theoretical prediction of the effect under consideration, it is not a deeply theoretically conceived article. Dumke does not go into detailed quantum-mechanical calculations but he writes the paper as simple as possible to make it understandable also (or primarily) to experimenters. He applies empirical—at that time already very well known—data on the optical absorption coefficient in the neighborhood of the absorption edge and combines it with a simple kinetic approach describing an excited semiconductor along with possible losses of its recombination radiation in an optical Fabry-Perot resonator.
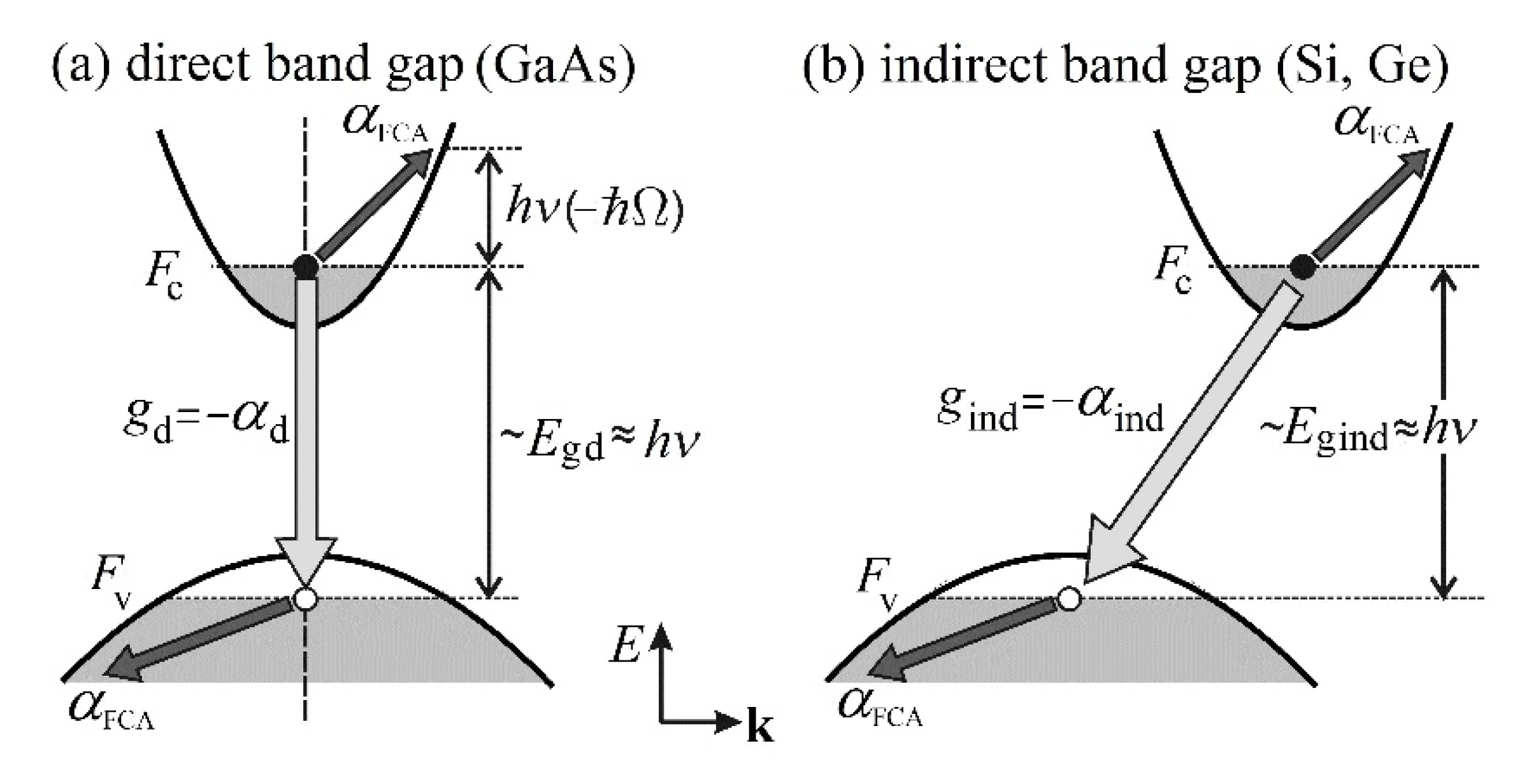
What matters is that Dumke was the first to point out correctly the crucial importance of losses of the generated radiation due to free carrier absorption (FCA). This is the primary loss mechanism in indirect gap semiconductors: an electron residing in the conduction-band valley (a valence-band hole residing in the valence-band maximum), upon absorbing a proper photon, goes to a state within the same band with a simultaneous change of its wave-vector (see
Figure 2). (The energy difference between the band extremum and the final electron/hole state equals approximately the absorbed photon energy.) This process therefore requires, much like the interband emission (or absorption) of radiation in indirect semiconductors, phonon participation to conserve momentum. The two phenomena are thus comparable in magnitude. Such a reabsorption of the radiation generated by electron–hole recombination across the band gap is unavoidable; the details of the band structure of a particular semiconductor are then of crucial importance for deciding which process prevails. In direct gap materials the FCA losses are, of course, negligible in comparison with the high amplification by stimulated emission due to direct radiative transitions at
k = 0. This is what Dumke clearly states in his paper for the case of GaAs.
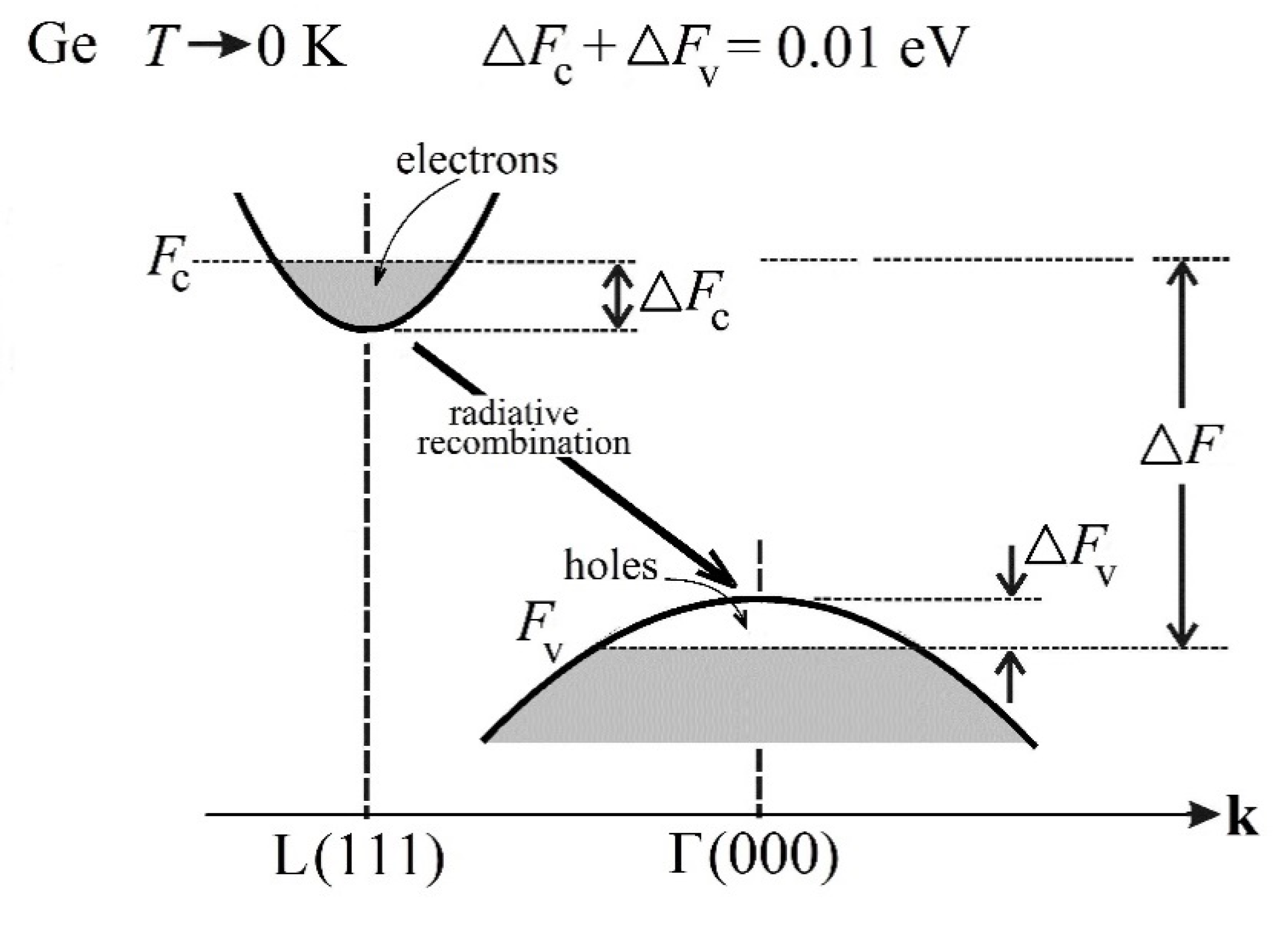
On the other hand, by using available experimental data on the electron–hole effective masses, the relevant absorption cross-sections etc., Dumke comes to the conclusion that lasing due to indirect transitions in Ge and Si would not be possible. This conclusion was found to be valid even in the most favorable case when, at low temperatures, total inversion population of levels is achieved with electron/hole densities about 1.10
18 cm
−3 (
Figure 3). This is because Dumke’s calculations yielded the value of the amplification (gain) coefficient due to indirect gap stimulated emission in Ge to be –
gind =
αind = 0.24 cm
−1, while the FCA absorption coefficient turned out to be
αFCA = 7 cm
−1, or much larger than |
gind|. The loss therefore predominated the gain.
Thus, Dumke’s conclusion was rather pessimistic [
7]:” in Ge maser action (the terminology of laser physics was in its infancy at the beginning of the 60s. Since it was masers who were predecessors of lasers, the maser terminology was adapted first, so that “maser action” means what is called “lasing” nowadays), using either the indirect or indirect exciton transitions, would be prevented by absorption due to free carriers… Silicon is even a more unlikely candidate since the cross-sections for free carrier absorption are an order of magnitude larger than in Ge.”
It is correct to note that Dumke’s article was preceded by some other works dealing also with the considerations about lasers and indirect semiconductors, in particular Ge [
8,
9]. However, these papers did not receive a wider response. With the benefit of hindsight it turns out that their authors either underestimated the FCA effect or their ideas about lasing in semiconductors were not fully correct. Readers interested in the general history of semiconductor lasers are referred to a review article [
10].
Next, extensive and theoretically well-grounded work dealing with the possibility of generating coherent laser radiation in indirect semiconductors was a paper by Adams and Landsberg at the 9th International Conference on the Physics of Semiconductors in Moscow 1968 [
11]. Unlike Dumke, the authors proceed from explicit quantum-mechanical formulas for the absorption coefficient of direct (1st order perturbation theory) and indirect (2nd order perturbation theory) transitions close to the absorption edge. They consider low temperatures only (
T = 0 K) and take into account resonator losses due to both the partial mirror transparency and reabsorption (predominantly by FCA). Nevertheless, they estimate also the active medium internal loss caused by light scattering.
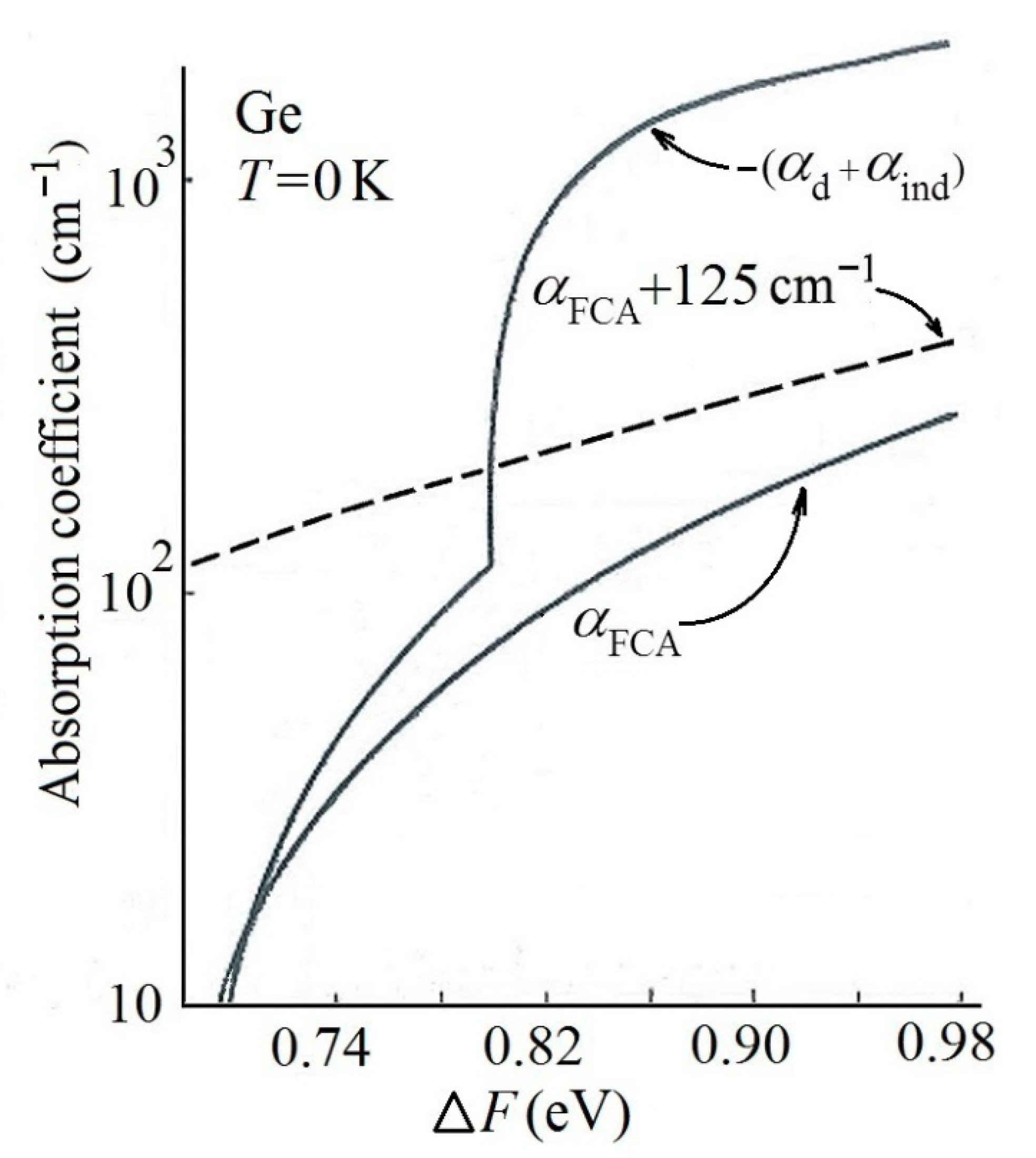
Their results, formulated in a general way, are illustrated via the specific case of Ge, see
Figure 4. It displays the sum of the calculated amplification coefficients, that is, the negative absorption coefficients –(
αd +αind) in the direct and indirect gaps, respectively, together with the FCA loss coefficient
αFCA, both as a function of the quasi-Fermi level separation ∆
F (for the definition of ∆
F, see
Figure 3). When the authors added to the calculated
αFCA also a (rather arbitrarily) estimated loss term of 125 cm
−1 owing to light scattering plus the useful loss caused by the radiation output from the resonator, they came to a similar conclusion as Dumke: indirect lasing would not be possible because the losses in the indirect bandgap (0.7–0.8 eV) would be greater than the amplification (optical gain). However, it might be questionable whether the authors were not led to this conclusion rather purposely trying to support ex post all the unsuccessful attempts to demonstrate indirect lasing in Ge (?)
On the other hand, the direct band gap lasing should, in principle, not be hindered by anything, claimed the authors [
11]. We shall see later to what extent they were right in this point.
The mentioned theoretical works [
7,
11] along with the vain empirical effort towards a Ge laser led to a quite obvious conclusion: it appeared necessary to increase in some way the rate of radiative recombination in the indirect band gap, that is, to increase the value of the gain coefficient |–
αind|. In this respect, it was a US patent by Robert H. Rediker entitled “Method and Apparatus for Enhancing Radiation from Indirect Gap Semiconductors” that turned out very interesting [
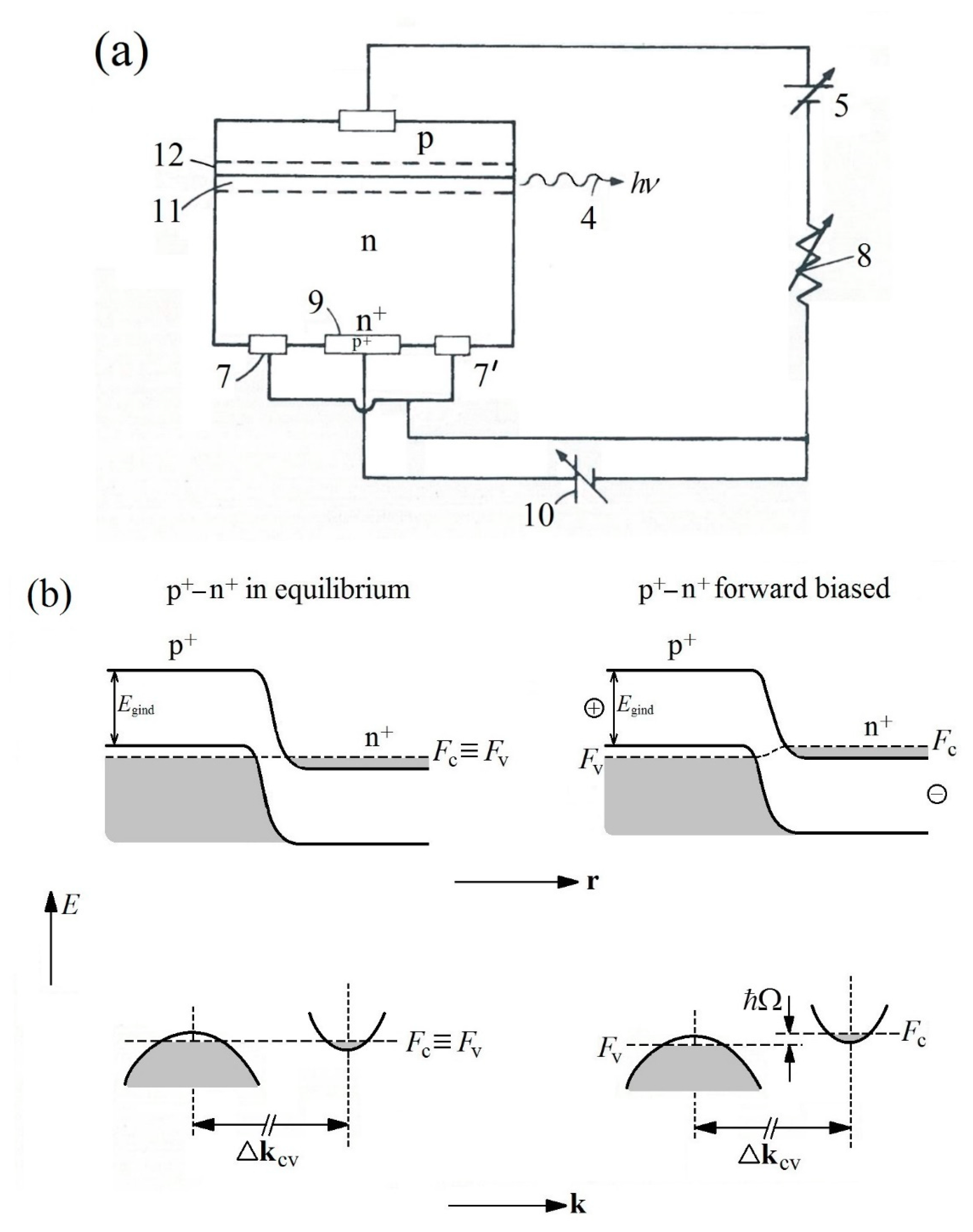
12]. The patent was granted to the author by the US Patent Office on January 18, 1972. Rediker suggests a relatively simple semiconductor device sketched in
Figure 5a whose operation is explained as follows: In a Ge or Si forward-biased p-n junction (diode) denoted 11 and 12 electrical injection of minority carriers takes place due to a potential source 5 and a variable resistance 8, creating thereby an inverted population in the energy bands. This inversion will stay there for a comparatively very long time, hundreds of microseconds or some milliseconds, since the electron–hole recombination rate is low (so far nothing new). However, if we succeed to create in the device a very high density of phonons, the rate of indirect recombination increases dramatically (it scales with the phonon density [
13]) and an intense laser pulse is emitted in the wavy-line direction 4. (This direction is determined by the optical resonator, whose mirrors are represented by polished lateral faces of the device.)
Well, how to create the required amount of important phonons? That is the main Rediker idea. He supposes to build into the device a p
+–n
+ junction 9, that is, a junction between heavily doped Si or Ge regions. This junction, being forward biased via ohmic contacts 7–7’ and a variable electric potential 10, enables electrons to tunnel from n
+ to p
+. During the tunneling a change in the electron
k-vector is imposed which is accompanied by the emission of phonons (
Figure 5b). The resulting phonon avalanche, provided it has a proper timing, will spread from the junction 9 towards the 11/12 diode and will “sweep” the electrons accumulated in the conduction band down to the valence-band hole states. This will result in the intense output laser pulse 4 mentioned above.
The idea is certainly original and appealing. However, in practice it never worked. We can only guess about the reasons. For instance, the following explanation may be plausible: The phonon avalanche will not enhance only the radiative transitions across the band gap but also the absorption processes within the bands due to FCA (
Figure 2), for they are non-vertical, indirect effects of the same order. Thus, one can perhaps say ex nihilo, nihilo fit (out of nothing, nothing becomes).
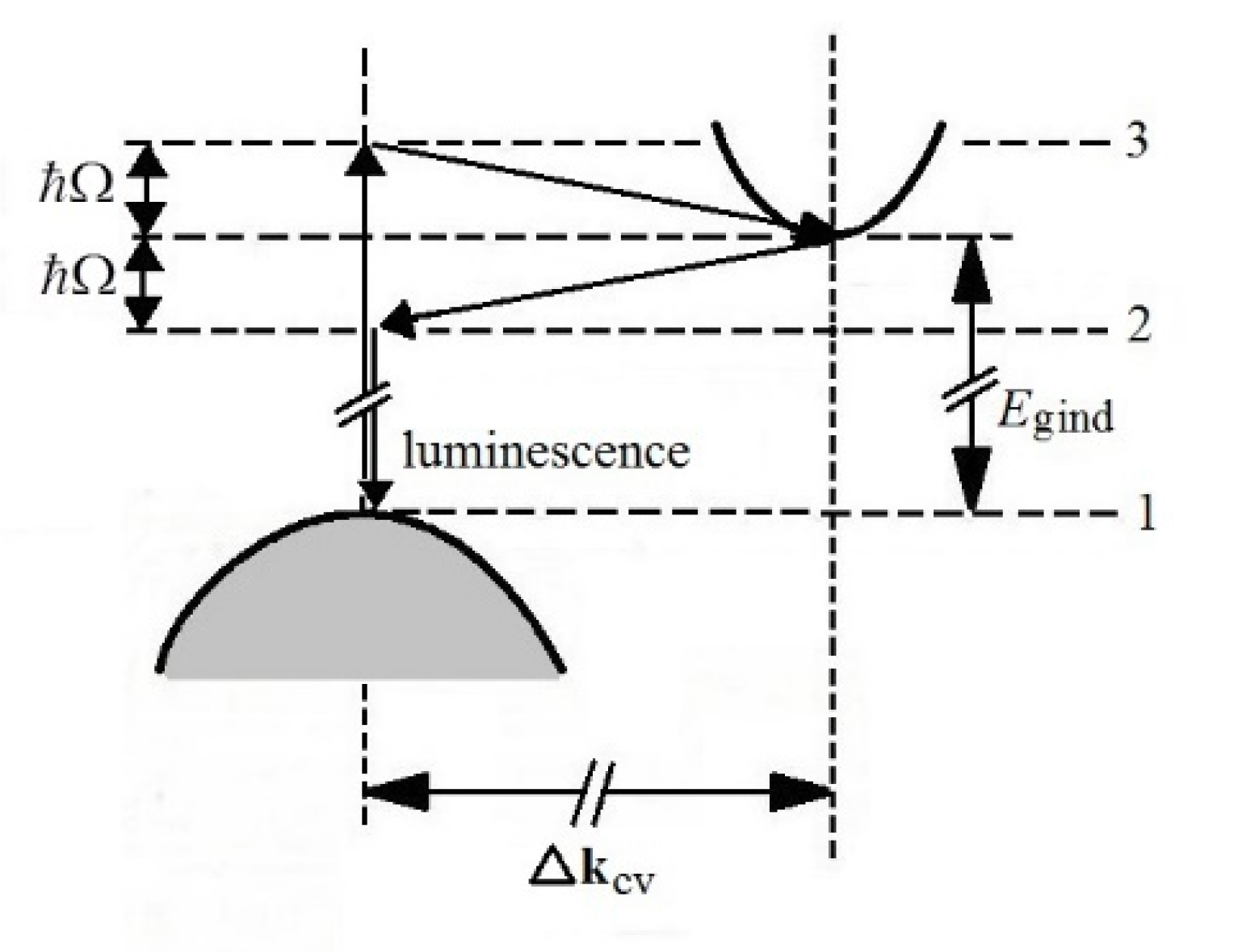
A rather long period followed when (to the best of the authors’ knowledge) no noticeable paper appeared. The problems of semiconductor indirect lasing continued to irritate physicists, though. As late as in 2003 Trupke et al. published an article titled “Optical gain in materials with indirect transitions” [
14], in which they theoretically analyze indirect optical transitions using a simple model two-level system. Thus, unlike [
7,
11], they do not consider any specific band structure of a particular semiconductor. They point to the fact that optical gain can be achieved with indirect transitions, in principle, even without inverted population, provided the temperature is very low and the luminescence photon energy is smaller than the energy gap by one (
ħΩ) or several phonon energy. It is somewhat like a three-level laser system, see
Figure 6. However, the question is whether a true coherent laser beam arising from stimulated emission of radiation can be generated in this way. In addition, reducing the energy of the emitted photons, that is, increasing their wavelength
λ will inevitably lead to an increase in the FCA losses since
αFCA ~ λ2 [
15,
16].
In 2009 S. J. Byrnes in his de facto unpublished work “Lasing in single-crystal silicon through phonon pumping: A feasibility study” [
17] revived the idea about the favorable phonon-avalanche impact on the electron-hole recombination rate, this time explicitly in silicon. His considerations are based on the analysis of the indirect-transitions matrix element (2nd order perturbation theory). Unlike the Rediker’s approach [
12], Byrnes does not take into account the phonon creation by electron tunneling but, instead, by illuminating the active Si region with a suitable infrared laser beam. Such a beam will generate in silicon two phonons from every absorbed photon; the resonance creation of a single phonon by a single photon of the same energy is forbidden in Si because of the momentum conservation law (therefore, it is not a pump laser
hν ≥ 1.12 eV (= energy band gap) creating the inverted population. This has to be present simultaneously also, of course, or alternatively electrical injection of electrons and holes may be used). For example, assuming the creation of one TO(X) phonon and one TA(L) phonon, an IR laser emitting at
λ ~ 18 μm would be used. Byrnes aims to accelerate the radiative recombination at least 100 times. This should be enough to overcome all losses including FCA (even if the author does not apply such an explicit formulation). He finds that to achieve this goal, a very short laser pulse (shorter than 30 ps which is a TO-phonon lifetime) would be required that would create approx. 4.10
21 cm
−3 additional phonons. However, Byrnes does not consider it experimentally achievable. His conclusion is therefore completely contrary to the Rediker’s idea about the easy realization of a high phonon density and, thereby, also the initiation of laser action in indirect band gap.
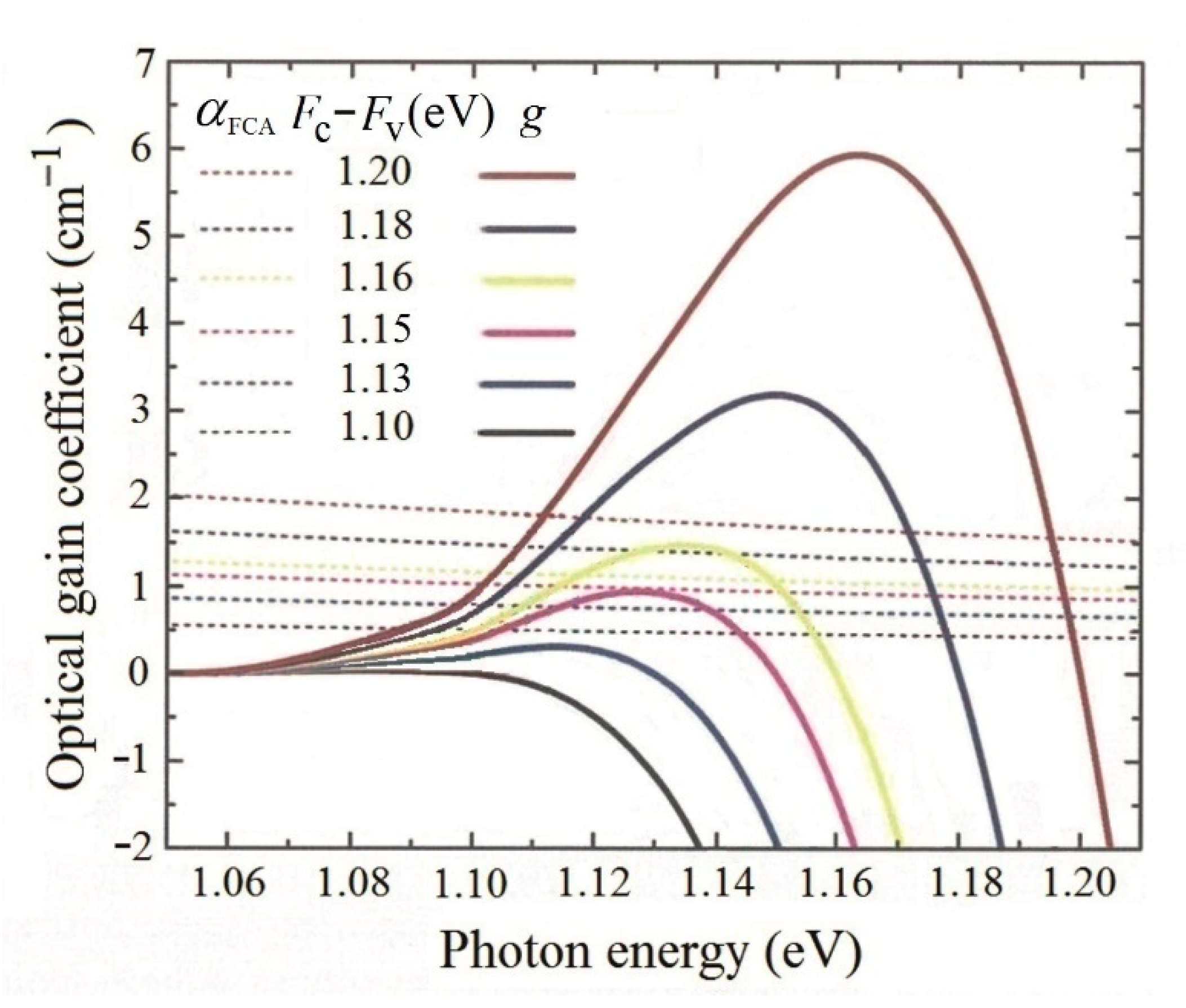
Finally, quite recently a paper titled “Optical gain coefficient of silicon: a theoretical study” appeared [
18]. This is probably the most detailed theoretical analysis of the absorption/gain coefficient of the indirect transitions in Si ever published. The author C.-Y. Tsai from National University, Taiwan, takes into consideration eight contributions to these transitions in the 2nd order of perturbation theory (two types of phonons: TO(X) = 57 meV, TA(X) = 19 meV, at each of them the possibility of both phonon absorption and emission, virtual states mediating the transitions occurring both in the Γ and X points of the 1st Brillouin zone). The result is displayed in
Figure 7 together with the theoretically calculated rival FCA curves.
Judging by this figure, optical gain (material gain, not modal, like in the other discussed papers) at the energy of emitted photons of 1.13 eV should overcome the FCA losses if the quasi-Fermi levels separation ∆
F is greater than 1.15 eV. However, it should be noted that the author does not take into account the additional unavoidable losses (light scattering, end loss caused by the resonator output mirror). Due to a very delicate balance between the small gain—a few cm
−1 only—and the FCA absorption (
Figure 7), those latent losses might negate the author’s rather optimistic conclusion to a considerable extent. Additionally, Tsai does not quote the electron and hole concentrations in the bands required to assure that ∆
F = 1.15 eV. From his previous work [
19], however, it can be estimated that they should be as high as 5.10
19–1.10
20 cm
−3, which might already present some experimental difficulties.
Let us have a partial summary. Out of the six works we have discussed, three are negative as for the chance of indirect-gap lasing, while the remaining three tend to be more positive about the matter. Thus, it is basically undecided—and it has been going like this for over 50 years.
Now let us look at what physical mechanisms have been proposed to achieve inverted population and lasing via direct transitions in the 1st Brillouin zone center (Γ-point, k = (0,0,0)).
2.2. On Direct-Transitions Lasing
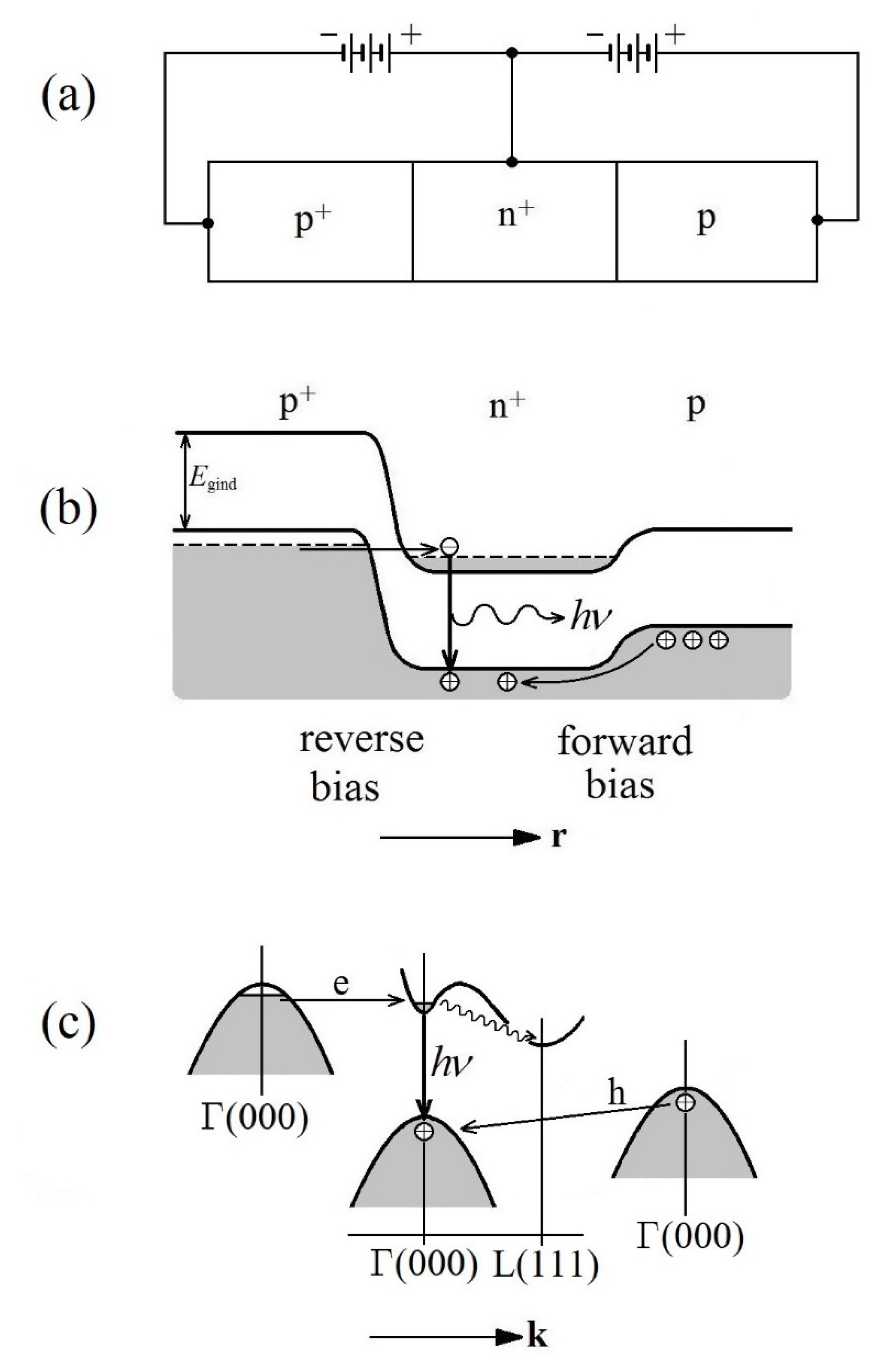
The first idea about how to realize a semiconductor device enabling laser action in a direct band gap, in particular in Ge, appeared already in 1963. It was put forward by S. Wang et al. from the University of California, Berkeley, [
20,
21] and shortly after that this idea was checked experimentally in Bell Telephone Laboratories [
22]. The device in question was a transistor structure shown schematically in
Figure 8a, whereas panel 8b displays the physical phenomena occurring within it as represented in real (
r–) space: a p
+–n
+ junction on the left is heavily doped on both sides, so that when
reverse biased it facilitates electron tunneling to the central part (base). Simultaneously a n
+–p junction on the right works as an ordinary diode and, consequently, under
forward bias it injects holes to the base (both the p–n junctions are thus biased in the opposite way compared to an ordinary bipolar transistor). There, the radiative recombination of the tunneling electrons with the injected holes occurs. It is important to realize how these processes can be visualized in
k-space; we can learn this from the inspection of panel 8c. The electrons tunnel (provided the doping level is high enough) from the
k = 0 state at the valence band top to a state with the same
k-value in the conduction band. Thus, in the base they occur in the conduction band minimum at the Γ-point. Neither of the holes change their
k-vector value during injection; consequently, upon the injection they remain at the valence band top Γ-point. In the transistor base thereby the inverted population is created at
k = 0, and the electrons may recombine radiatively in a very efficient way with the holes, via a direct transition. If the transistor is placed in a suitable optical resonator, it starts to emit a coherent laser beam.
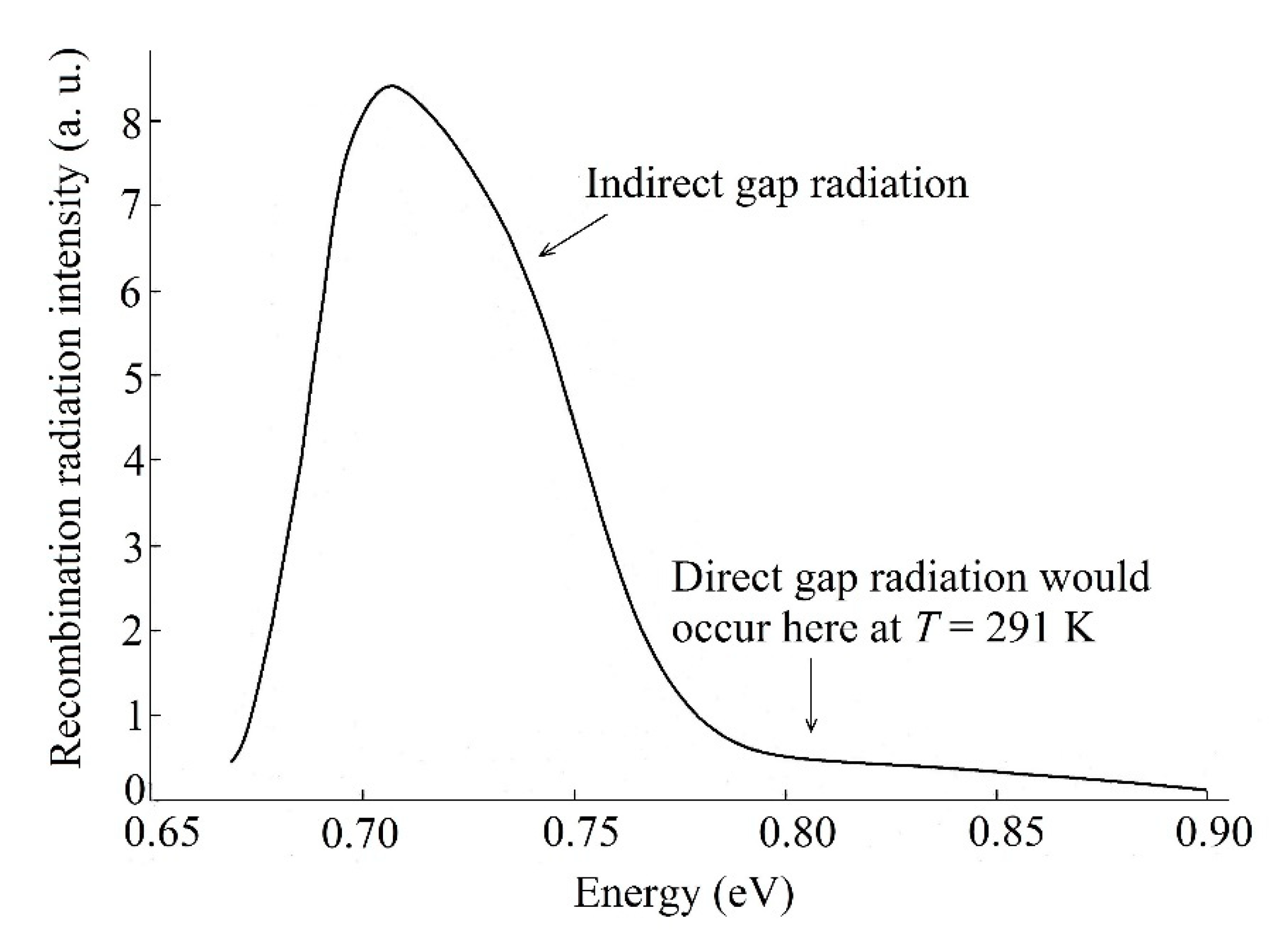
That is at least what Wang and his colleagues hoped for. However, the reality turned out somewhat differently—it did not work. Although it appeared possible to detect experimentally IR electroluminescence emerging from the device at
T = 77 K [
20], the subsequent study of its spectral composition revealed [
22] that it arose from the usual indirect recombination of the electrons at the L(1,1,1) valley with the holes at the Γ(0,0,0) maximum, see
Figure 9. The luminescent photon energy ~ 0.70 eV in this figure corresponds very well to the indirect band gap value in Ge.
The spectrum shown in
Figure 9 was acquired without applying any emitter-base voltage. Logically then, no electron tunneling to the base could have occurred and thus the observed radiation was solely due to the indirect L → Γ recombination close to the forward-biased base-collector junction. (The existence of this kind of electron–hole recombination was known very well at that time; observation of the relevant electroluminescence had already been reported in 1952 [
23].) What was of utmost importance, however, was that no change in the spectrum occurred when repeatedly applying (reverse) bias to the emitter—no observable shift of the curve towards higher photon energy appeared, only sometimes the luminescence intensity at 0.70 eV slightly increased.
Where did Wang and his coworkers make a mistake? Basically, they neglected the fact that for the tunneling electrons, finding themselves in the conduction band valley at
k = 0, a very efficient and fast competitive channel opens—apart from the radiative recombination—to get rid of the excess energy: a non-radiative transition (the so-called intervalley scattering) to the lower-lying conduction band valleys at four L(1,1,1) points, see the wavy line in
Figure 8c. To put it simply, the number of holes injected to the base would have to be enormously high in order to enable the electrons at
k = 0 to recombine with at least some of them, before the electrons are scattered to the L-points. However, numerical estimates had shown that even at the highest applicable hole current densities (beyond which the transistor becomes irreversibly damaged) the hole concentration at the p
+–n
+ junction emitter-base remains still about 100 times lower than would be necessary [
22].
Thus even this Wang’s idea, certainly very remarkable, did not become a reality.
In their internal Memorandum, however, Chynoweth et al. [
22] express another interesting idea in response to a question they had asked themselves: “Is it possible to prevent the electrons from quickly leaving Γ for L?” Yes, they respond, in case that germanium is such a heavily n-doped material that the electron quasi-Fermi level is high enough to assure complete filling of all four L-valleys by electrons. In consequence of this filling the electrons “overflow” to the Γ-valley (
Figure 10) and, thus, electron scattering Γ
7− →L
6+will be prevented because all potential final states in the L
6+indirect valleys will be fully occupied. Moreover, this will make inverted population and lasing in the Γ-point possible, if only a suitable pumping of the non-equilibrium carriers across the band gap is added. The authors, however, were not sure about the feasibility of achieving experimentally the necessary donor concentration; they estimated it to be as high as 10
20 donor/cm
3, which was at the edge of material cohesion.
Let us now move forward in time by more than 45 years, to 2009. The group of Jurgen Michel from MIT, Cambridge, USA, publishes a paper “Direct gap optical gain of Ge on Si at room temperature” [
24] in which they report on the realization of the idea about the favorable effect of heavy doping on optical gain in germanium direct band gap. However, to accomplish this, the authors had to make one small but important modification of the approach proposed by the Bell Lab workers: To reduce the indispensable donor concentration they subjected the doped germanium to a modest tensile deformation. The deformation had caused the conduction band edge in the neighborhood of the Γ
7− point to shift slightly downwards, reducing thereby the L
6+ valley depth. Consequently, lower electron density sufficed to fill the -L-valleys: The relevant donor concentration of 1.10
19 donor/cm
3, that is, lower by one order of magnitude in comparison with what Chynoweth et al. [
22] feared, proved to be sufficient. The corresponding tensile strain was achieved by Liu et al. [
24] in that they allowed a thin Ge layer to grow on a silicon substrate and afterwards annealed the sample at a high temperature. The remainder, that is, the introduction of the strain into the sample, was provided by a large difference in the thermal expansion between Ge and Si.
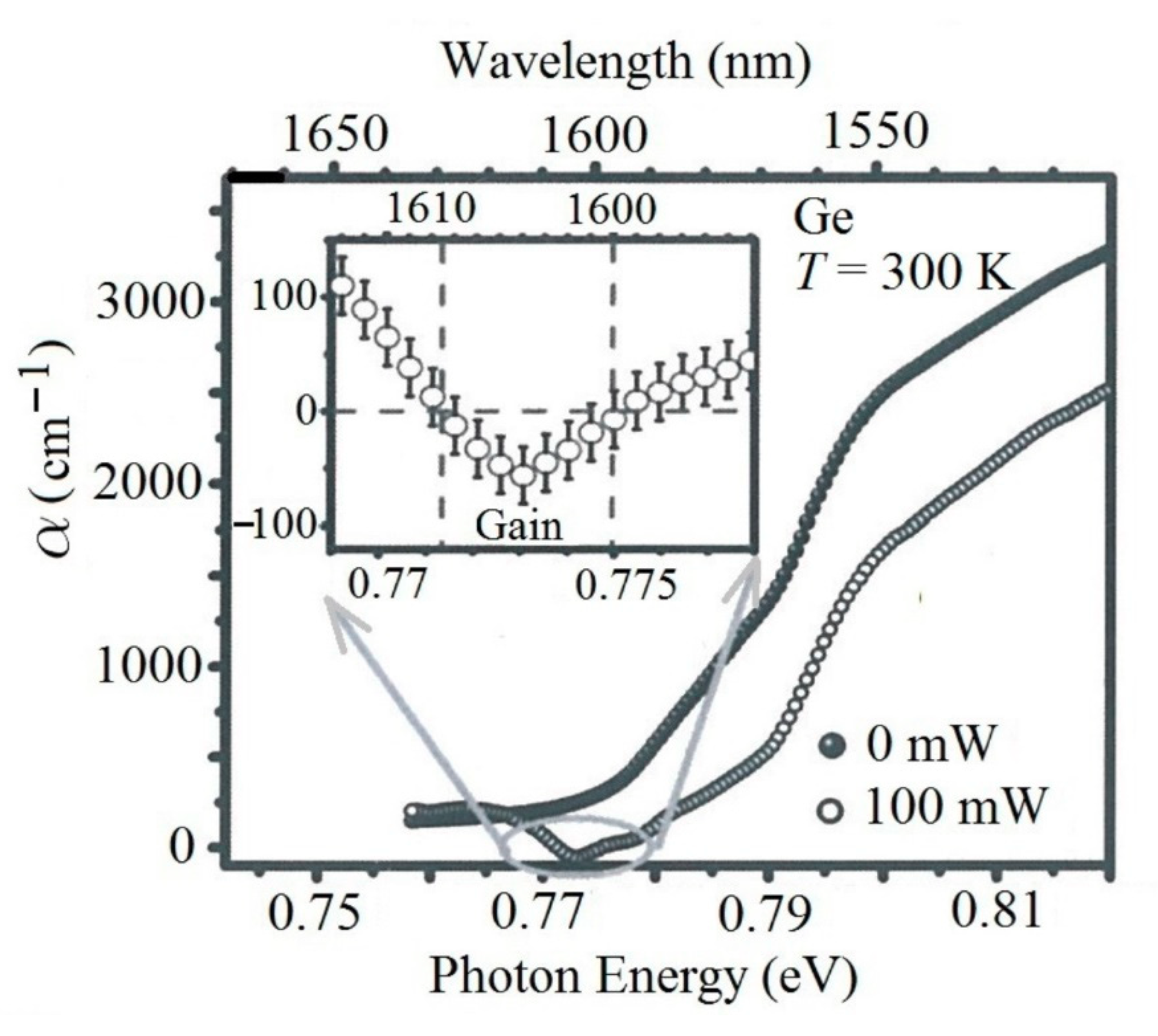
Figure 11 displays the optical absorption coefficient of strained n
+–germanium under optical pumping with a c.w. laser at a wavelength of 1480 nm [
24]. A negative value of the absorption coefficient (around −50 cm
−1) at ~ 1605 nm indicated unambiguously the attainment of near-IR optical gain (a slight red shift of the photon energy against
Figure 9 is due to the embedded tensile strain. This, by the way, serves a strong evidence for the reality of achieving such a strain via the preparative technique applied in Ref. [
24]).
Soon after, an article on “genuine” laser action under optical pumping (
T = 300 K) followed from the same laboratory: strained n
+–germanium was placed in an optical resonator [
25]. A few years later the Institute of Semiconductor Engineering in Stuttgart reported on n
+–germanium lasing induced by carrier electrical injection [
26], and papers dealing with similar effects in Ge nanostructures also appeared [
27]. It is worth noting that direct-transition laser action was reported also in GeSn alloy, without mechanically introducing strain [
28].
Sixty years after the birth of the first laser, it seems therefore that the issue of lasing in germanium (and silicon) has been solved (?) Well, we would rejoice prematurely. The success in generating stimulated emission from germanium spontaneous luminescence, even under electrical pumping, can be undoubtedly declared a great victory of semiconductor science and technology. However, the time has changed. What would be welcome with enthusiasm in the 1960s, leaves today most physicists and engineers rather unexcited because the material base of the electronics and microelectronics has moved from germanium to silicon.
One may ask a logical question now: Is it not feasible to perform in Si a similar band structure engineering as in Ge, that is, to facilitate lasing in direct band gap at k = 0 via concerted action of a heavy n-doping with application of a tensile strain?
2.3. What about Silicon?
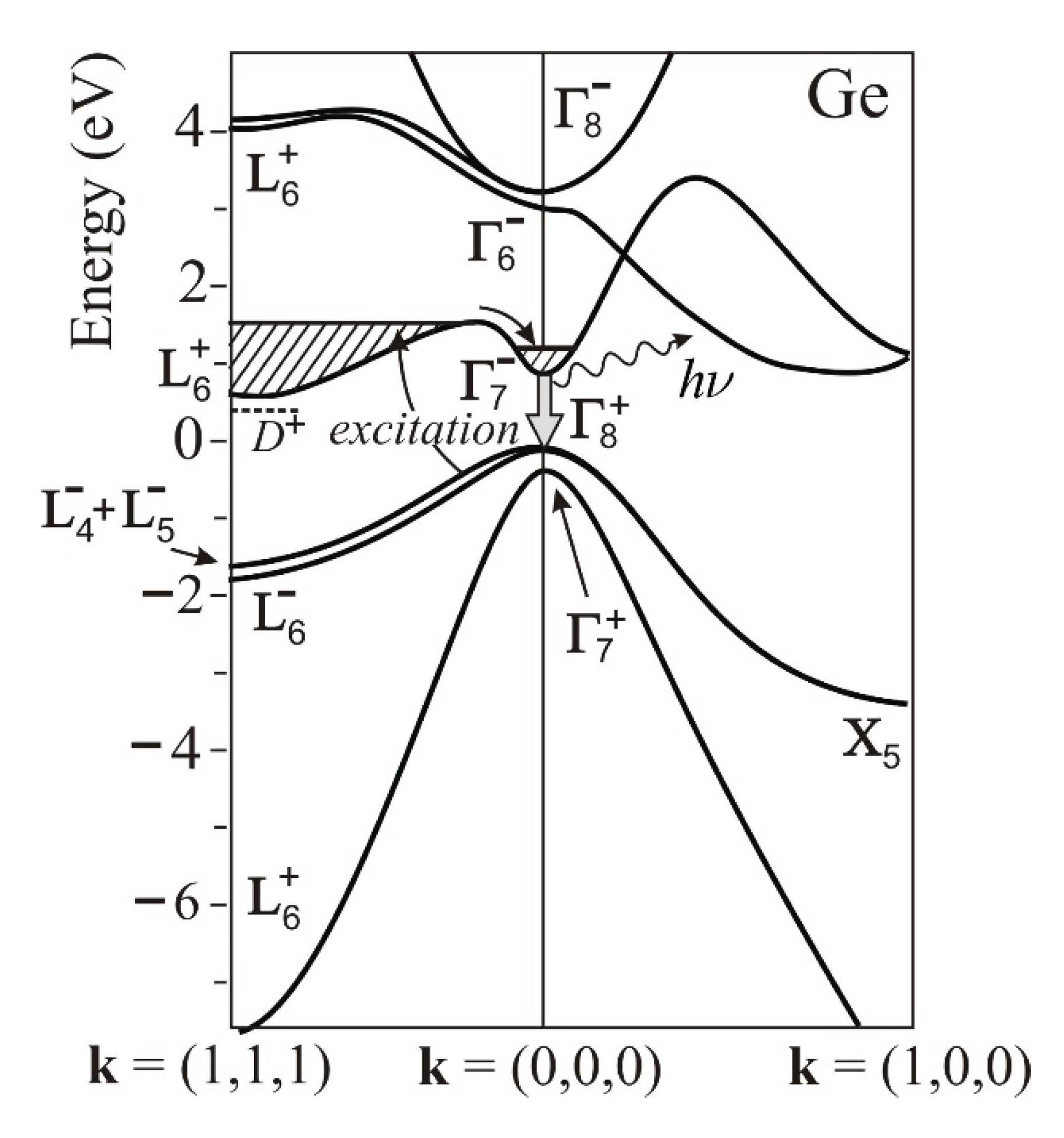
In order to be able to answer the above question concerning Si band structure engineering, let us compare in detail the band structures of Si and Ge in
Figure 1. Even if in both the semiconductors the optical absorption edge is owing to indirect transitions, there are two important differences:
In germanium, the energy separation between the direct gap (Γ
8+ – Γ
7−) width and that of the indirect one (Γ
8+ – L
6+) is relatively small, about 0.15 eV only. On the other hand, in silicon this energy difference amounts to ~2.2 eV (see
Figure 1; (Γ
25’– Γ
15) is the direct gap, (Γ
25’– X
1) the indirect one). It is thus by one order of magnitude larger.
In silicon, as opposed to Ge, no valley occurs at the Γ-point conduction-band local extremum. In general, it can be said that Si is the only one among the commonly known semiconductors which does not possess a local conduction band minimum at Γ. (A noteworthy feature foreshadowing, maybe, a certain privileged position of silicon among semiconductors?)
It follows from the first difference that in order to fill all six X1-conduction-band valleys by electrons, silicon would have to be much more heavily n-doped than Ge. A rough estimate gives the requested donor concentration of ~1.7.1022 cm−3. Since crystalline silicon contains 5.1022 Si atoms per cubic centimeter, this would mean that every third Si atom would have to be replaced by a donor (e.g., phosphorus P) atom. However, such a material then would no longer be silicon but a kind of Si/P alloy with substantially modified physical properties (apart from the fact that such an alloy would probably be unstable in a solid state).
The second difference implies the following: Even if, hypothetically, the conduction band valleys were filled with electrons up to the Γ15 level, the electrons would hardly stay in the Γ15 state for a sufficiently long time. In all probability they would scatter very quickly to the lower lying L1 conduction-band valleys. (The analogy of an electron with a mechanical ball that has an unstable position at the top of a hill and rolls into the valley is fully correct here.) It is therefore not feasible to apply the band-structure-engineering protocol used in the case of Ge also to Si.
Thus, how to reduce the X1-valleys depth and to create a local minimum at the Γ15 conduction-band state in Si? Is it even possible? Is there any point in attempting it? The answer may be provided by nanostructures, more specifically by silicon quantum dots (SiQDs).
The very fact that SiQDs are able to exhibit much stronger photoluminescence than bulk Si at room temperature was discovered in 1990 when L. Canham at Royal Signals and Radar Establishment, GB, observed, by a naked eye, visible photoluminescence of porous silicon under a UV lamp [
29]. Porous silicon is a sponge-like structure prepared by etching bulk silicon with hydrofluoric acid; it consists of tiny Si micro- and nanoparticles and nanowires. Interestingly, porous silicon has been known since 1956 when, by chance, it was prepared in Bell Laboratories by a research worker Arthur Uhlir Jr.
The discovery of luminescent porous silicon stimulated, in the coming years, great interest in quantum dots based on this indirect-gap semiconductor. Various methods had appeared to prepare SiQDs and to stabilize their properties in time, because it turned out that the luminescence of porous silicon degraded, even if rather slowly, in time. In spite of a considerable increase in efficiency of the radiative processes in SiQDs compared to bulk Si, the exciton radiative lifetime in SiQDs still remained long, in the order of hundred microseconds, that is, by about four orders of magnitude longer than in direct semiconductors. This had led to a general consensus that, despite the relatively efficient luminescence, the optical transitions remained still indirect. Even when positive optical gain was found in SiQDs by several laboratories [
30,
31,
32], the coveted link SiQDs—optical resonator—lasing has not been realized up to now. Here, a big problem appeared to be, besides FCA, the overall optical quality of the material, that is, the losses due to light scattering. Small SiQDs (with the diameter of a few nanometers) tend to agglomerate to larger clusters sized up to several hundred nanometers, especially in high concentrations indispensable to achieve optical gain. Such clusters, being comparable in size with the wavelength of visible light, then scatter very efficiently the emitted luminescence radiation. To maximize optical gain in substances based on Si QDs it is therefore necessary (i) to increase further the efficiency of the radiative transitions, (ii) on the contrary, to diminish loss due to light scattering and (iii) to reduce the loss due to FCA.
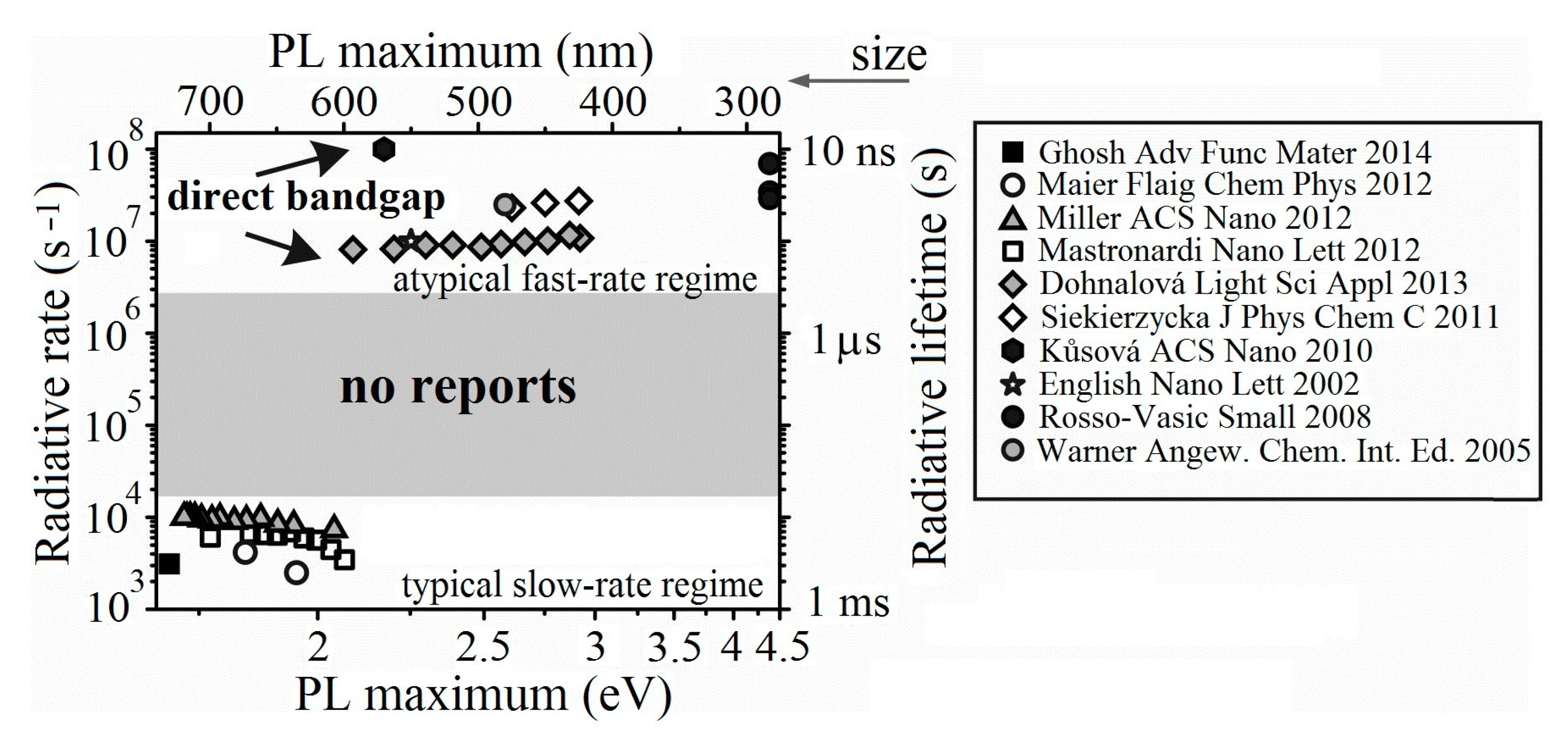
It was not before 2014 when two groups published theoretical calculations, initiated by experimental observations, that in certain configuration even SiQDs may possess direct band gap and, by means of it, may further increase their radiative recombination rate by several orders of magnitude [
33,
34]. The degree to which the radiative rates were improved is illustrated in
Figure 12, which summarizes experimentally reported radiative rates in SiQDs. Furthermore, the relevant SiQDs which supplied very interesting experimental results [
35,
36] had been prepared in the form of a stable colloidal dispersion, which was optically clear. In both the cases, in order to get the direct gap, it was necessary to combine quantum confinement (i.e., a small size of SiQDs) with a suitable surface coverage. To explain the physical background of the direct gap appearance under these conditions, two slightly different theoretical opinions were invoked. Now however, it is advisable to make a small digression.
Till now, our discussion has been led in terms of the direct or indirect band gap. The electronic band structure as such is, however, strictly valid in the case of an infinite crystal only, being applicable as a very good approximation to bulk semiconductors containing 1023 atoms/cm3, but this approach might already be questionable in quantum dots consisting of a few hundreds of atoms. Despite objections from the theorists’ side, the notion of band structure and of a direct/indirect band gap had been used intuitively by experimenters because of the observed parallels between bulk semiconductors and the corresponding quantum dots (not only in silicon).
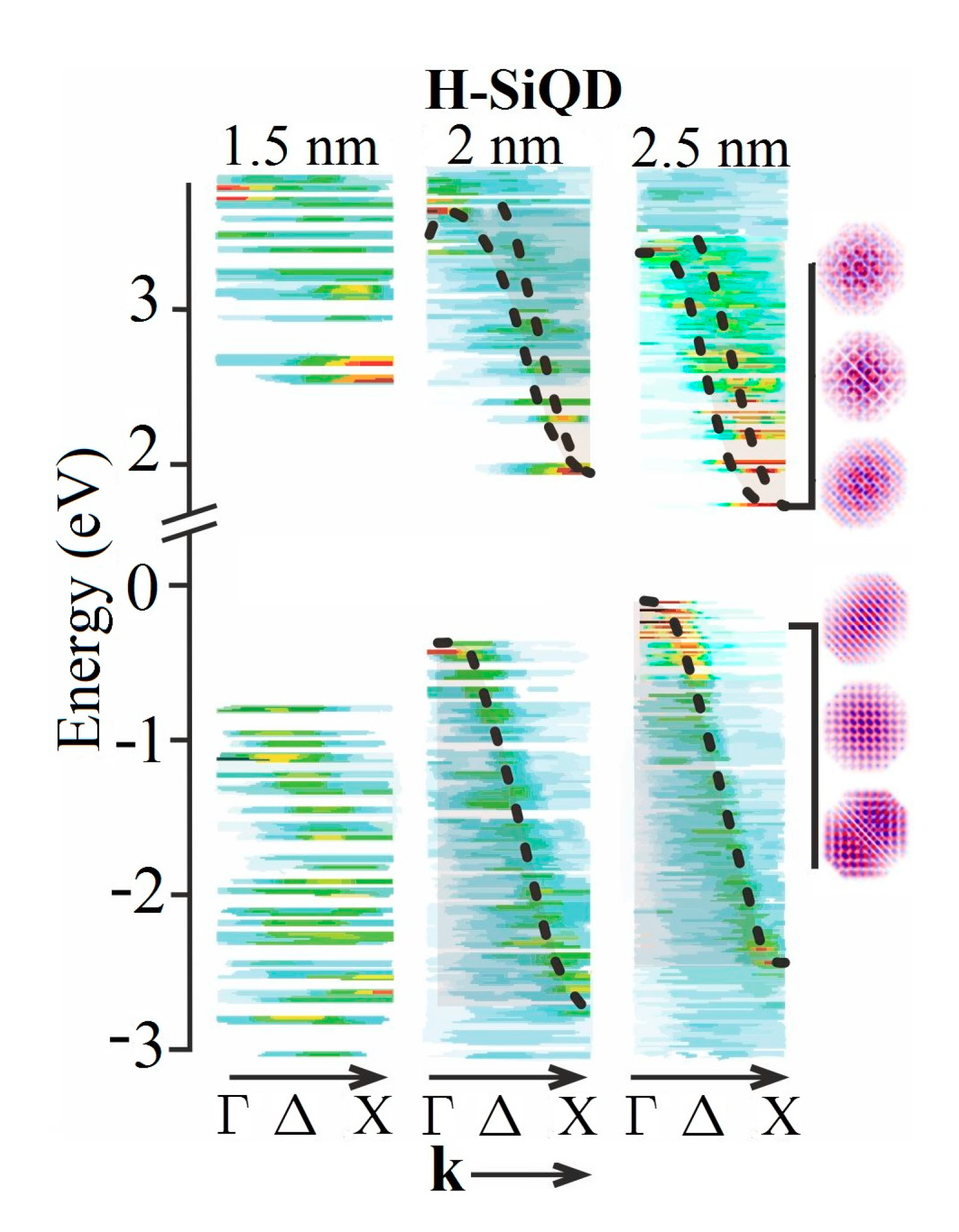
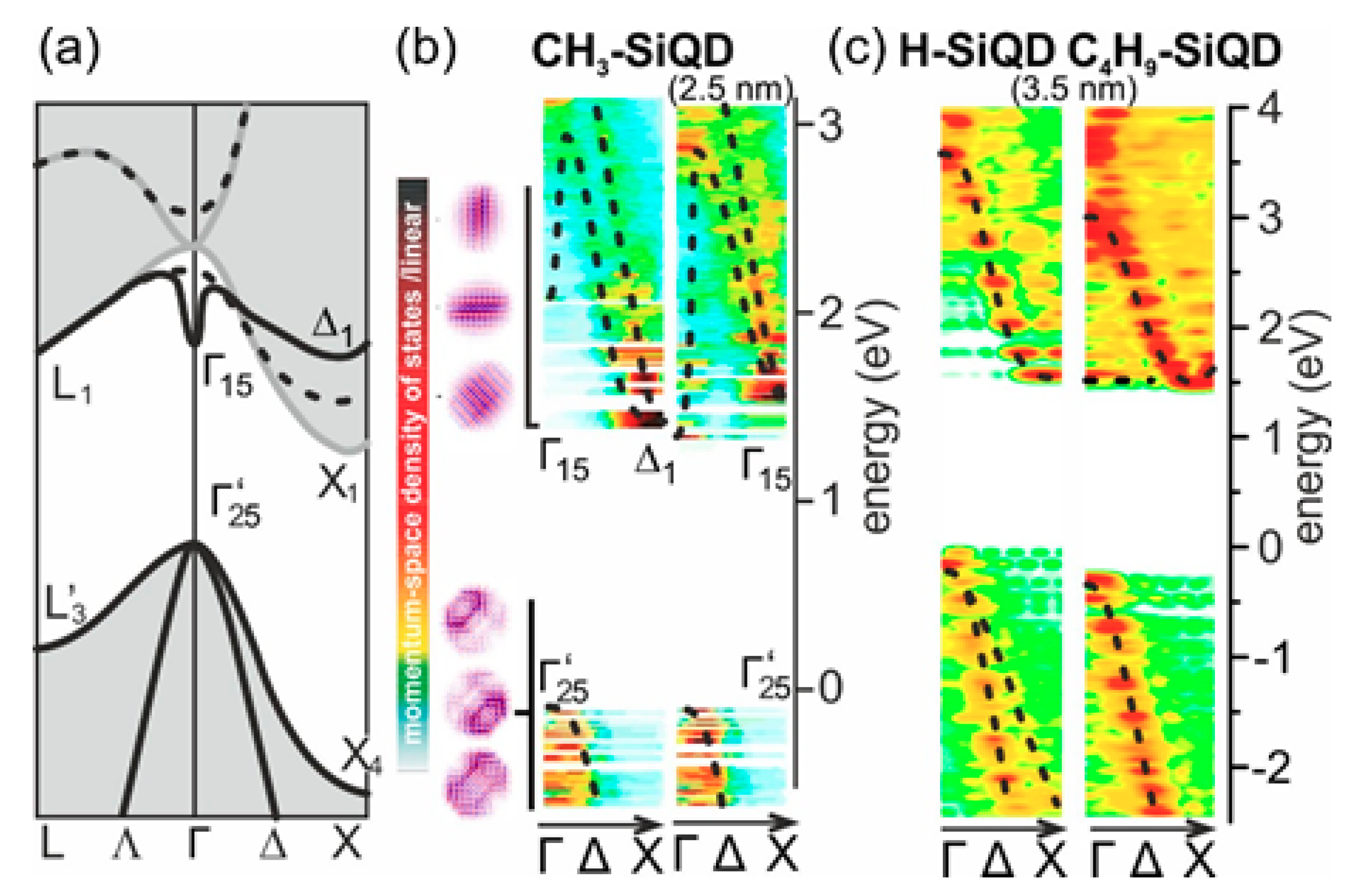
The issue of SiQDs band structure has only been clarified in 2013 in a theoretical study where the calculated SiQDs wave functions in
r-space were projected to reciprocal (
k-) space and thus was also obtained their band structure [
37]. It turned out that, for SiQDs larger than a certain size (~1.8 nm), the band structure constructed in this way copied (with some limitations) very well that of bulk Si, see
Figure 13. Unlike bulk Si, however, the band structure of quantum dots was found “fuzzy”. It means that instead of sharp band edges that occur in bulk Si, these edges were formed now by maxima in the electron wave function distribution over reciprocal space; of course, this distribution does not fall to zero in the neighborhood and/or between the maxima but keeps a certain non-zero level. The fuzzy character of wave functions has confirmed the correctness of calculations because this fuzziness follows immediately from Heisenberg uncertainty relations (the localization of the SiQD electron wave function in
r-space implies the delocalization of the relevant electron momentum in reciprocal space); this had been intuitively used previously to describe the observed acceleration of radiative recombination in SiQDs in comparison with bulk Si.
What makes the situation rather complicated is that, in quantum dots, the efficiency of radiative recombination cannot be judged solely according to the overlap of electron and hole wave functions in reciprocal space. The band structure concept in bulk crystals is based on conceiving electrons in semiconductors as plane waves, which means that these electrons are implicitly spread over the whole semiconductor volume, their space overlap being thus automatically ensured. Quantum dots have, with regard to their volume, comparatively large surface and thus surface effects are of increasing importance for the wave functions and optical properties manifestation. A surface of “pure” SiQDs in ambient atmosphere is strongly reactive (oxidizing); that is why real SiQDs have always foreign atoms attached on their surface, be it naturally or intentionally grown oxide or another protective layer (typically alkyls, for instance). The impact of surface termination on electron wave functions is sizeable, it affects especially the extent of the wave function localization in real space, that is, whether the wave function is “nicely spread” over the whole quantum dot volume or whether it is “sucked out” towards the surface or towards any other part of the crystalline core. A nice example of bulk-like wave function is that of a hydrogen-capped SiQD as shown in
Figure 13. Therefore, the electron–hole wave function overlap in real space is—besides the direct or indirect band gap—another important parameter that determines the efficiency of radiative processes.
Now we are able to understand better how the direct gap in SiQDs originates. In both mentioned cases of observing the fast direct luminescence [
35,
36], the SiQDs surface was covered by short alkyl groups (in particular methyl –CH
3 and butyl –C
4H
9 ones, respectively). This type of surface termination is beneficial for achieving a homogeneous distribution of electron/hole wave functions (close to the band gap) in real space, much like in a bulk material, see
Figure 14. It means that the wave functions are well “spread” over the quantum dot interior, not localized in a particular site. Such wave functions are important from two viewpoints: (i) The electronic and optical properties of such a quantum dot will actually be analogous to bulk silicon and (ii) the localization of the wave function in real space will not significantly reduce the efficiency of radiative transitions.
Let us now return to the methyl-terminated SiQDs. As sketched in
Figure 14a, the appearance of direct gap was explained in terms of a combination of two abovementioned phenomena: Quantum confinement and tensile strain, the latter being present just due to the covalently-bonded methyl groups [
33]. Quantum confinement affects the silicon band structure in such a way that the direct conduction band local maximum at the Γ-point shifts downwards while, on the contrary, the indirect conduction band edge (a local minimum) close to the X-point shifts upwards. Therefore, the band extrema approach each other. A similar result can be obtained by applying tensile strain onto the crystalline core of the quantum dot, by increasing slightly its lattice constant. Concerted action of quantum confinement and tensile strain then results in such a shift of the conduction band extrema that the maximum and minimum levels equalize each other, in consequence of which the direct optical transitions outweigh indirect ones. Importantly, this is accompanied by two additional effects: First, the upward shift of the indirect local minimum X
1 makes the band gap wider against bulk Si, reducing thereby the FCA losses. Second, as shown by theoretical calculations by Kůsová et al. [
33] a local band minimum is formed around the Γ
15 state instead of the bulk-related maximum. Thus, all the attributes requested to obtain efficient direct-gap radiative recombination are met!
It is worth noting that the combination of both phenomena (quantum confinement and tensile strain) is imperative even if they “act in the same direction”. Neither it is enough to prepare a sufficiently small nanoparticle with a sizeable quantum confinement but lacking completely the mechanical strain, nor to take a relatively large nanoparticle with a negligible quantum confinement and tense it strongly (it would be mechanically destroyed).
For similar reasons, large mechanical strain alone cannot be applied to bulk silicon—the deformation needed to induce direct band gap would be too large (the requested stretch of lattice constant by about 6%). Moreover, real stretching of the bulk crystal is, in contrast to compression, a technically difficult matter. In this respect, the quantum dots offer several advantages over bulk crystals: (i) Thanks to the phenomenon of quantum confinement the requested mechanical strain is smaller, (ii) due to their small size the quantum dots are able to tolerate better the mechanical stress without lattice defects and (iii) the mechanical stress can be realized simply by means of a strongly covalently bonded surface layer. Such a layer is represented just by the short methyl groups that can be thought of as “open umbrellas” stretching—due to steric hindrance—the quantum dots crystalline core.
The second mentioned work dealing with direct gap SiQDs (those covered by butyl groups [
34]) then offered an alternative validation of the direct gap development, namely, that based on electronegativity of the surface layer. Electronegativity is a measure of the tendency to attract a shared (bonding) pair of electrons. This property of the surface coverage turns out to be of importance mainly for the conduction band shape because the attraction of electrons towards the surface (in real space) implies an increase in the conduction-band density of states in the Γ-point of the first Brillouin zone (reciprocal space). The band structures resulting from the corresponding calculations are shown in
Figure 14c. This, in its turn, enhances the predominance of direct transitions. However, even in this case one has to deal with SiQDs, not with bulk Si, because (i) the phenomenon of quantum confinement itself increases the rate of radiative transitions and (ii) an electronegative surface of bulk Si would not have the same effect in view of a much smaller surface/volume ratio.
It is very likely that a complete theoretical explanation of the occurrence of direct transitions will require involvement of both the mechanical strain and surface electronegativity, or their combination. Despite strong experimental evidence one can hardly claim that any theoretical computation so far has been able to confirm as high acceleration of the radiative recombination rate as observed in experiment. Theoretical calculations addressing the impact of electronegativity [
34] were performed with the aid of tight-binding empirical methods where some of the input parameters may be slightly varied and, consequently, these methods are considered less reliable. On the other hand, the approach applied to calculate the band structure engineering owing to mechanical strain was quite rigorous (density functional theory, DFT) but, in this case, it appeared necessary to increase artificially the calculated strain in order to achieve the agreement between theory and experiment, see also
Figure 14b [
33]. Here, it is suggested to explore further experimental parameters, not considered by the theory till now, which might increase the rate of radiative processes; for instance the quantum dot shape (slightly elongated instead of strictly spherical) or a partial degree of surface termination. From the rigorous theoretical point of view, the potential of these parameters remains unclear. This incomplete theoretical understanding makes any goal-directed preparation of fast-direct-luminescent SiQDs difficult.
The colloidal SiQDs exhibiting the fast direct radiative transitions seem an ideal candidate to attain inverted population and across-gap lasing in silicon. Nevertheless, against SiQDs with indirect band gap, positive optical gain in this medium has not been reported yet (which sounds paradoxical). The production of samples with SiQD density high enough to achieve optical gain is impeded by extremely time-consuming preparation techniques. The other issue is under what experimental conditions it is possible to ensure in such a system necessary inverted population. Despite these difficulties, at the moment these modified SiQDs are very likely the best candidate for the active laser medium based on silicon.