1. Introduction
Angular/spatial filtering devices based on photonic crystals (PhCs) [
1,
2] provide diffraction of the angular components of an incident beam. The effect of a PhCs-based spatial/angular filtering device that works on a spatial frequency spectrum relies on an angular band-gap [
3,
4,
5,
6,
7]. For spatial filtering, a range of angular components of a beam can be removed due to the angular band-gaps, that is, the waves can be reflected in a backward direction [
3,
4,
5] or deflected at large angles in a forward one [
6,
7].
Furthermore, double-periodic photonic structures enable manipulation of the zero diffraction order of a transmitted beam [
8]. For example, some angular components of an incident light source diffract from the zero diffraction order to the other orders at resonance conditions. On the other hand, some angular components, out of resonance, directly propagate through the PhCs. In this way, low-angle-pass or high-angle-pass filtering devices are achievable through a proper interplay among the grating characteristics.
In particular, the PhCs filtering has been already implemented for intracavity angular filtering in an integrated platform such as microchip lasers [
9]. Such a PhCs-based confocal filtering device presents an alternative method for replacing conventional filtering devices [
10], but has a critical disadvantage that is the presence of an optical axis [
11]. Therefore, the transmitted axisymmetric concentric ring structures result in the limitation of angular filter merely for on-axis incident light.
It is noted that there have been other approaches to spatial filtering such as passive [
12] or light-induced [
13] Bragg gratings and pulse-induced population density gratings [
14]. However, these alternative methods require not only more sophisticated schemes but additional optical components, leading to limited applications in the compact micro-systems. Therefore, more compact PhCs-based angular filters are desirable solutions for the use in the microlasers, e.g., autocloned PhCs, which preserves the initial modulation during the deposition of multilayers [
15]. For example, a multilayered photonic microstructure based on a sinusoidal or braze profile was demonstrated experimentally as one of the most compact PhCs-based angular filters [
16]. However, this proposed filter presents the weak filtering performance, so further investigation is required for practical use. For example, a compact filter with a transverse invariance performs both the narrow angular bandwidth and the high efficiency. The filtering for the application of such a compact filter toward a Gaussian beam has not been well studied in the prior study [
16]. Although the fabrication of the autocloned PhCs has been demonstrated experimentally [
17,
18], it is still unavoidable that the variation of the amplitude (Amp) of the harmonic modulation of the autoclaved PhCs increases with the number of layers [
19]. Further studies for feasible parameters in fabrication such as less number of layers are a concern.
In this paper, we provide a numerical study of an angular/spatial filtering based on multilayered PhCs gratings with a harmonically modulated substrate profile. The multilayered gratings are all-dielectric and periodic, where the variation of the periods or wavelength results in a low- or high-angle-pass filter. A spectral width (SW), defined as the full spectral width at half maximum (FWHM), is calculated by using the finite-difference time-domain (FDTD) method [
20]. To enhance the spatial filtering, we focus on narrowing filtering angular distributions by the design of the low-angle-pass filter and the results are compared with the study in [
16].
2. Numerical Far-Field Simulations for Autocloned PhCs
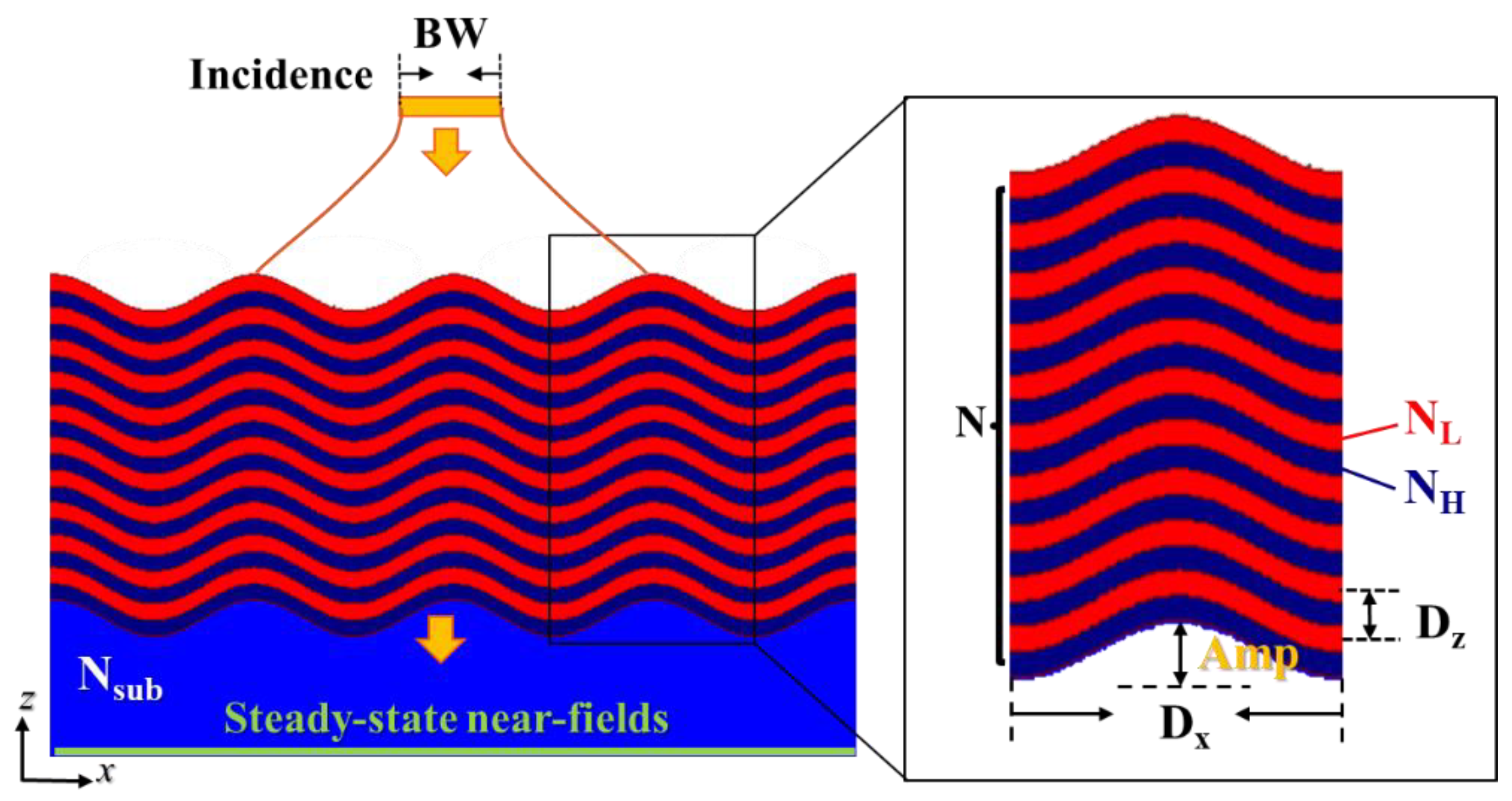
The configuration of the proposed multilayered PhCs grating for spatial filtering is schematically shown in
Figure 1. The multilayers consisting of alternating high-refractive-index (N
H) and low-refractive-index (N
L) layers with the number of layers (N) on top of a grating substrate (N
sub) that results in a sinusoidal profile with a peak-to-peak Amp. Such a multilayered grating with a sinusoidal profile provides a transversal and a longitudinal modulations of the period (D
x) and an alternating thicknesses (D
z) of the multilayers. The thicknesses of the high- and low-refractive-index layers are equal to D
z/2. The wavelength of the incident light is equal to λ = 582 nm and a transverse electric (TE) polarization is considered. A more detailed calculation procedure is further described in the following section, Method.
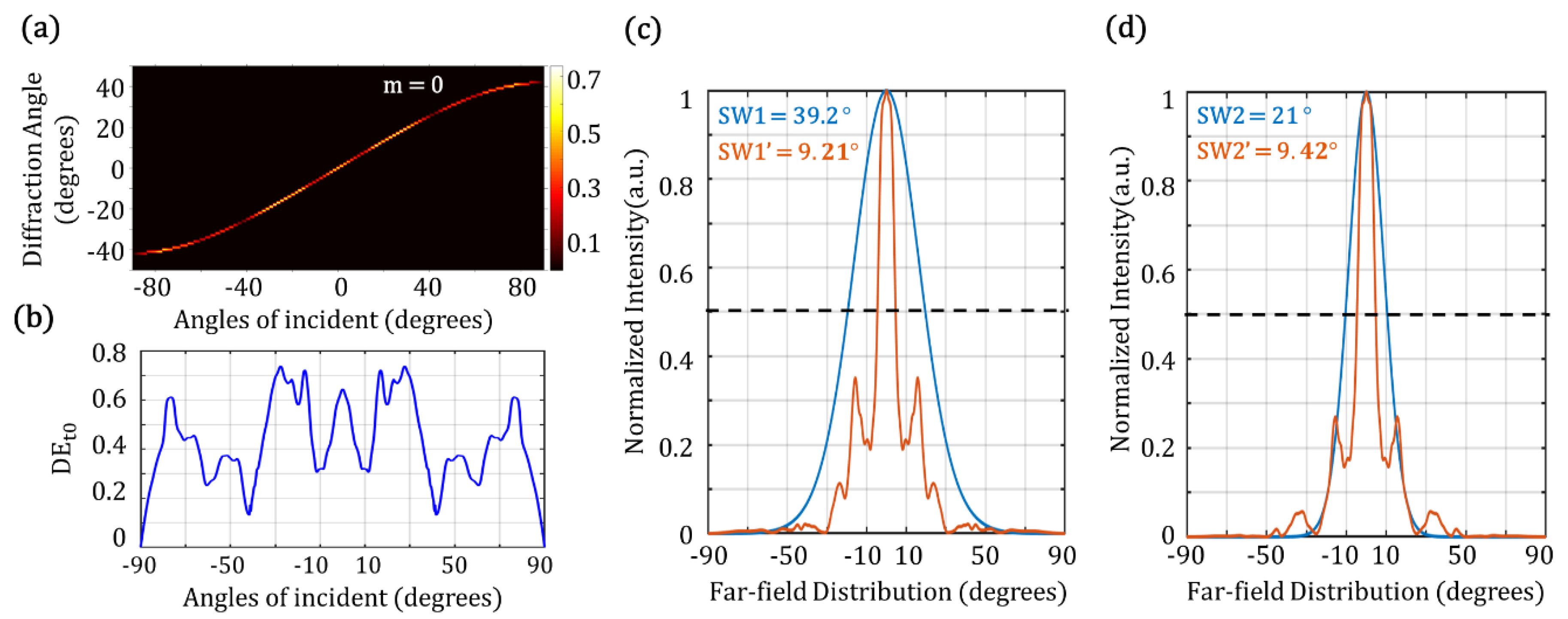
We first analyze diffraction patterns of the periodic multilayered structure by using a rigorous coupled-wave analysis (RCWA) method [
21] and its 0th-order transmission is as plotted in
Figure 2a. The parameters of the studied structure are identical as those in [
16]: N = 33 layers, Dx = 1.67 μm, D
z = 0.24 μm, N
Sub = 1.5, N
H = 1.42, and N
L = 1.3. Since the parameter of Amp was not mentioned in [
16], we found the narrowest SW by scanning Amp up to 0.5 μm. The narrowest SW of 9.21° is obtained for Amp = 0.27 μm. Furthermore, the angular dependence of the 0th-order diffraction efficiency (DE
t0) (
Appendix A Method) presents a low-pass filtering design where the angular components at around 10° are removed or coupled out to the others, as shown in
Figure 2b. Thus, the far-field distribution of a Gaussian beam, regarded as different plane-wave components at different angles of incidence, can be narrowed down.
Figure 2c,d show that the filtered far-field distributions for two incident beams with different beam widths (BW1= 1 λ and BW2 = 2 λ). Their filtered SWs, SW1’ (9.21°) and SW2’ (9.42°), are narrower than SW1 (39.2°) and SW2 (20.99°), respectively.
3. Minimum SWs for Different Configurations of Autocloned PhCs
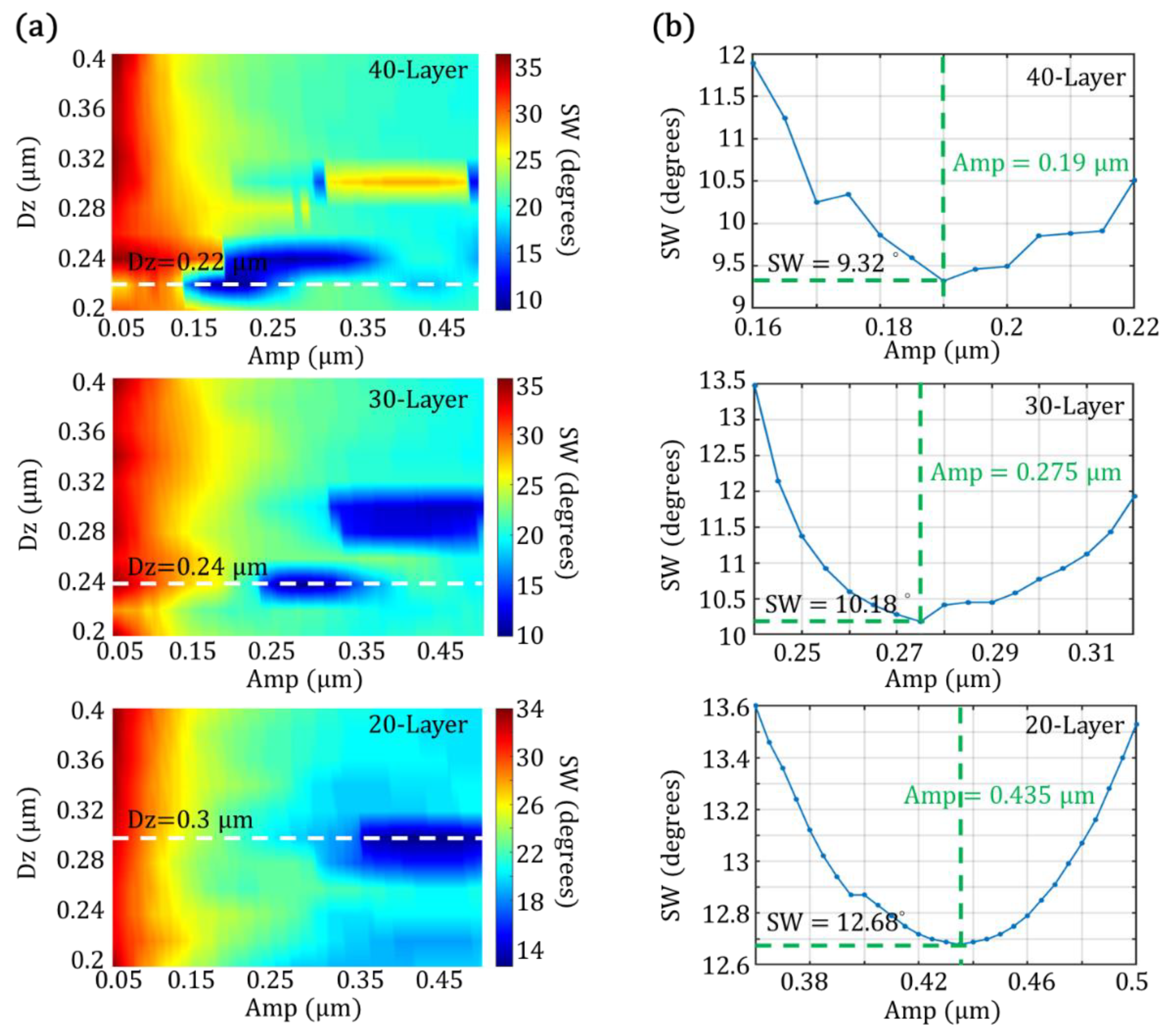
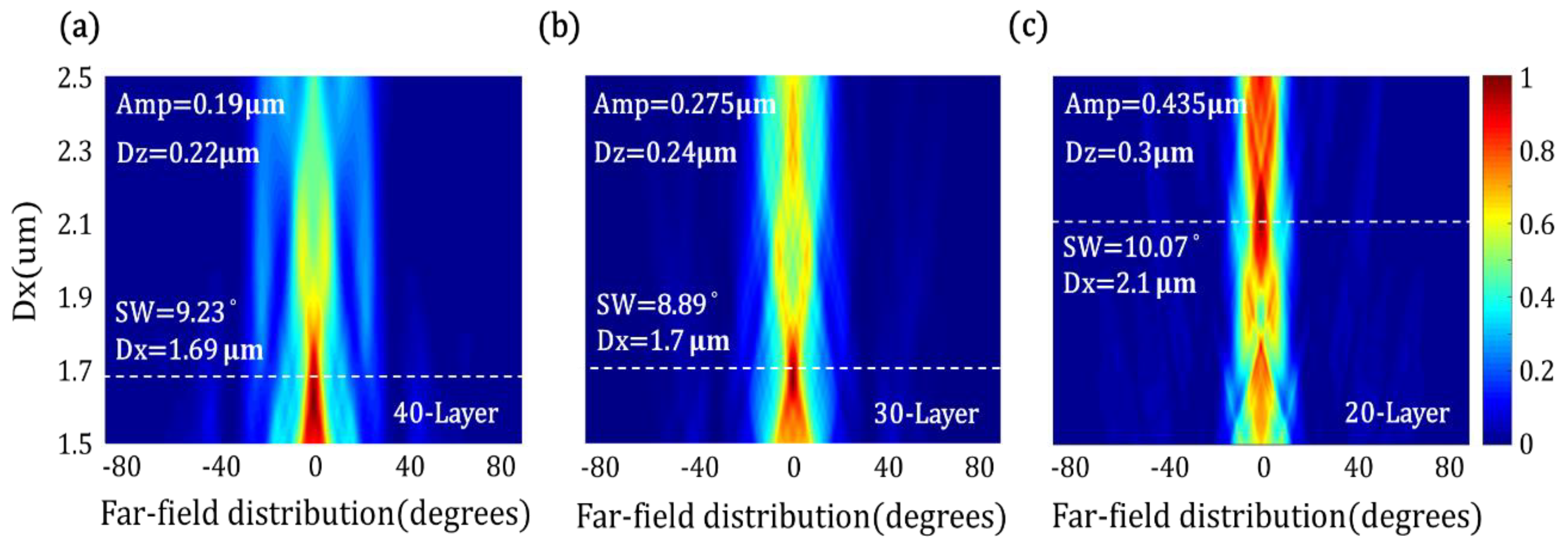
In this section, a series of numerical calculations is executed for the best filtering effect. We focus on scanning structural parameters such as Amp and Dz for obtaining a narrow FWHM of SW. First, three configurations of the wavy structures are considered with different layer numbers (N = 40, 30, and 20). Three related maps of their SWs are calculated by scanning two parameters Amp from 0.005 to 0.5 μm and Dz from 0.2 to 0.4 μm, as shown in
Figure 3a. It is noted that their transversal periods are identical, referred to [
15].
The smallest SWs for the 40-, 30-, and 20-layer configurations are found at the longitudinal periods Dz of 0.22, 0.24, and 0.3 μm, respectively. The corresponding variances of the SWs at the specific Dz, highlighted by white dashed lines in
Figure 3a, are shown in
Figure 3b. The optimal Amps of these three harmonic structures with N = 40, 30, and 20 are 0.19, 0.275, and 0.435 μm, respectively. As a result, in the three configurations with the different layer numbers, the 40-layer structure presents the smallest SW of 9.32° where BW of 1 λ is considered.
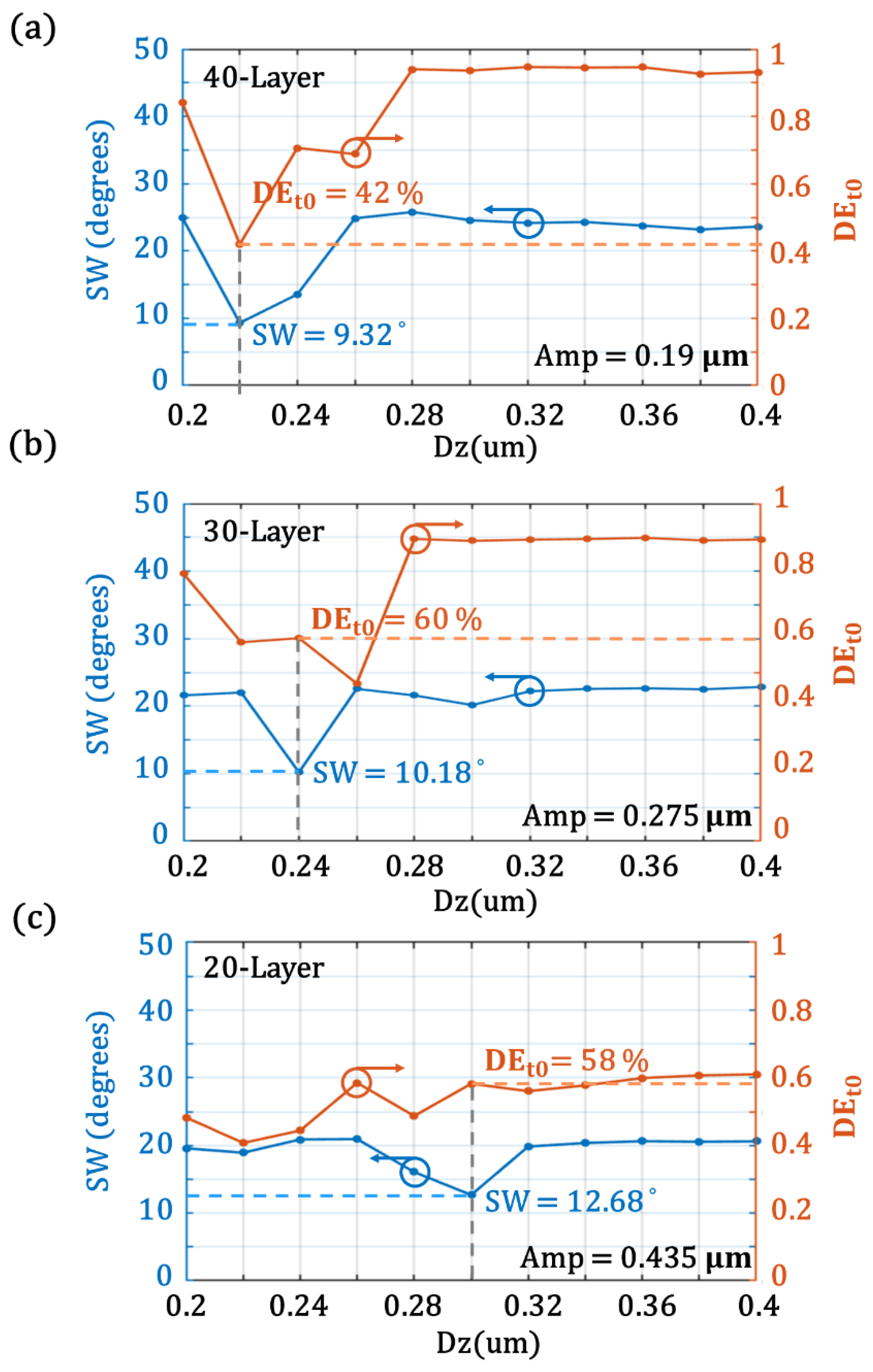
Furthermore, the diffraction efficiency for the center of the filtered beam is also considered as depicted in
Figure 4. The variations of the SW and DE
t0 with respect to Dz are studied for the three different configurations of the wavy structures. The SWs of 9.32°, 10.18°, and 12.68° and DE
t0 values of 42%, 60%, and 58% are achievable for the 40-, 30-, and 20-layer structures, respectively. Although the narrowest SW of 9.32° of a filtering beam is achievable by the configuration with 40 layers, it brings in the lowest diffraction efficiency.
For all the above simulations, the transversal period Dx of 1.67 μm is considered for the low-pass filtering design. As generally known, the transversal period of PhCs plays an important role in diffraction patterns. As the transversal period Dx is changed, the far-field distribution changes dramatically, leading to the low- and high-pass filtering effects. Hence,
Figure 5 shows the variation of far-field distributions by varying Dx for three configurations with 40-, 30-, and 20-layer structures. The best low-angle-pass filtering performance (SW = 8.89° and DE
t0 = 60%) is found at the 30-layer structure with Amp = 0.275 μm, Dz = 0.24 μm, and Dx = 1.7 μm.
A more optimal parameter Dx of 1.7 μm is found after scanning the far-field distribution with respect to Dz, as shown in
Figure 4. Even though the longitudinal period Dx of 1.67 μm is considered for the previously studied structure, it has shown that the procedure of the search of optimal parameters such as Amp, layers, and Dz for the low-pass angular filtering is beneficial. For example, as shown in
Figure 3 and
Figure 4, we obtain SWs of 12.68° and 9.32° and DE
t0 values of 58% and 42% for the two configurations with 20 layers and 40 layers, respectively. Although the 40-layer structure presents stronger spatially filtering, it requires more layers to achieve the narrower SW; however, the DE
t0 is lower.
Furthermore, the number of layers is also a concern for the fabrication of a wavy-like multilayered structure because the experimental modulation of the wavy structure may be reduced with the increased number of layers [
19]. Even if the fabrication of the 20-layer structure may be controllable, a weaker filtering effect is obtained. Obviously, the fabricating feasibility concerning the number of layers should be also considered at the stage in the design process. Therefore, a series of the analysis of structural parameters is helpful to define the optimization range and consider fabrication feasibility.
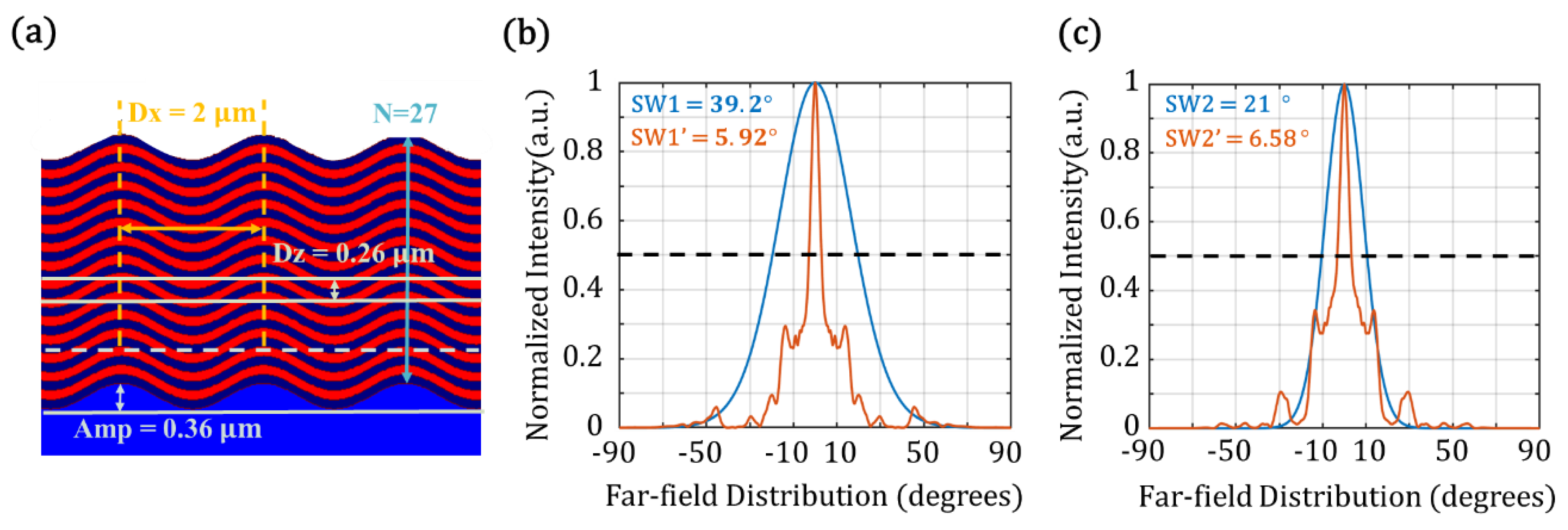
In our work, the optimization of this wavy structure by using the simplex method has been demonstrated, as shown in
Figure 6. All parameters of the multilayered structure are optimized simultaneously and the target of the optimization is to realize a low-pass filter design that achieves the narrowest SW for a Gaussian beam. To ensure fabrication feasibility, the optimizing range of the number of the layer should not be more than 40 layers. The optimizing ranges of Amp and the longitudinal period Dz should be less than 0.5 μm and 0.4 μm, respectively, as referred to the previous study. As a result, the final optimal parameters of the structure are obtained as follows: N = 27, Amp = 0.36 μm, Dz = 0.26 μm, and Dx = 2 μm. The far-field distributions in
Figure 6b,c show the narrowest SW1’ = 5.92° and SW2’ = 6.58° for two Gaussian beams with BW1 = λ and BW2 = 2λ, respectively. The DE
t0 of the optimal result is 64%. The narrower SW and the higher diffraction efficiency are achieved by the optimized structure with the less number of layer, compared with that of the previous study. Therefore, the optimizing results not only present the best spatial filtering to narrow the SW, but also demonstrate the use of the structures with fewer layers is a more feasible approach to a manufacturing process.
4. Conclusions
This paper has demonstrated the PhCs filtering effect for a light beam. The autocloned PhCs present transversal and longitudinal periods, the key element to modulate spatial spectra. The paper has studied different configurations of the multilayered structures based on the harmonic modulation. The narrowest SW of 8.89° and the diffraction efficiency of 60% are obtained for a 30-layer structure after a series of the scanning procedure in the structural parameters.
Considering feasible fabrication, the optimization has been further studied for practical use by using the simplex method. The number of layers N for our optimal structure is reduced to 27 and a stringer spatial filtering performance provides an SW of 5.92° and the diffraction efficiency of 0th transmission is 64%. For an autocloned PhC with several layers, another approach, such as an autocloned blazed modulation, could be more applicable for fabrication, although the fabrication of a tilted blazed profile is not as simple as that of the sinusoidal modulation.