Interaction of Dislocations and Interfaces in Crystalline Heterostructures: A Review of Atomistic Studies
Abstract
1. Introduction
- In Section 2, TBs of metals and alloys interact with screw and non-screw lattice dislocations.
- Section 3 focuses on the interaction of dislocations with low-angle grain boundaries (LAGBs) and high-angle grain boundaries (HAGBs).
- In Section 4, the interaction of bimetal interfaces— covering coherent, semi-coherent, and incoherent interfaces—with dislocations is reviewed.
- Section 5 focuses on metal/nonmetal interfaces interacting with both metal dislocations and nonmetal dislocations.
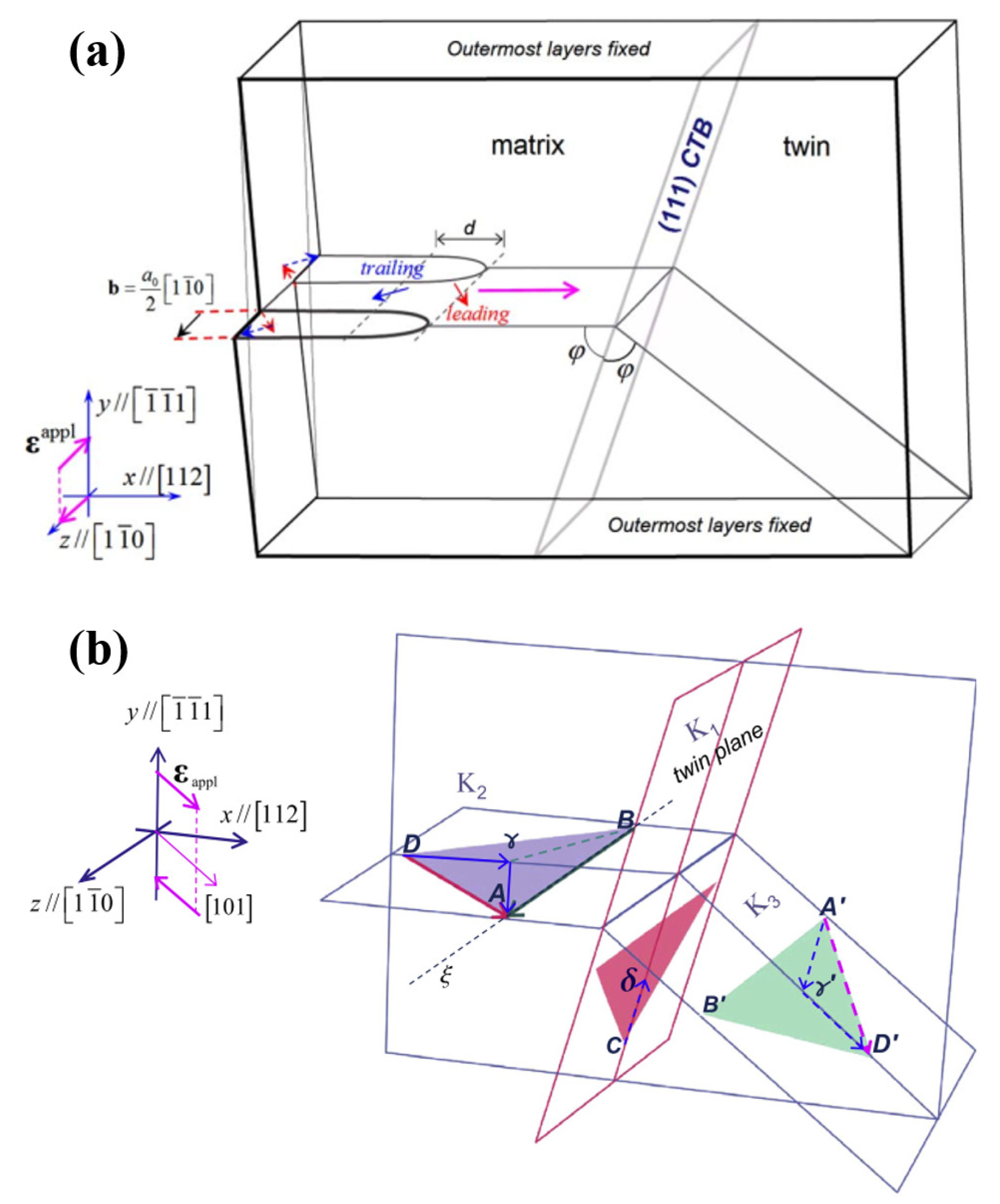
2. The Interaction of Dislocations and TBs
2.1. Screw Dislocations Interacting with Coherent TBs
2.2. Non-Screw Dislocations Interacting with Coherent TBs
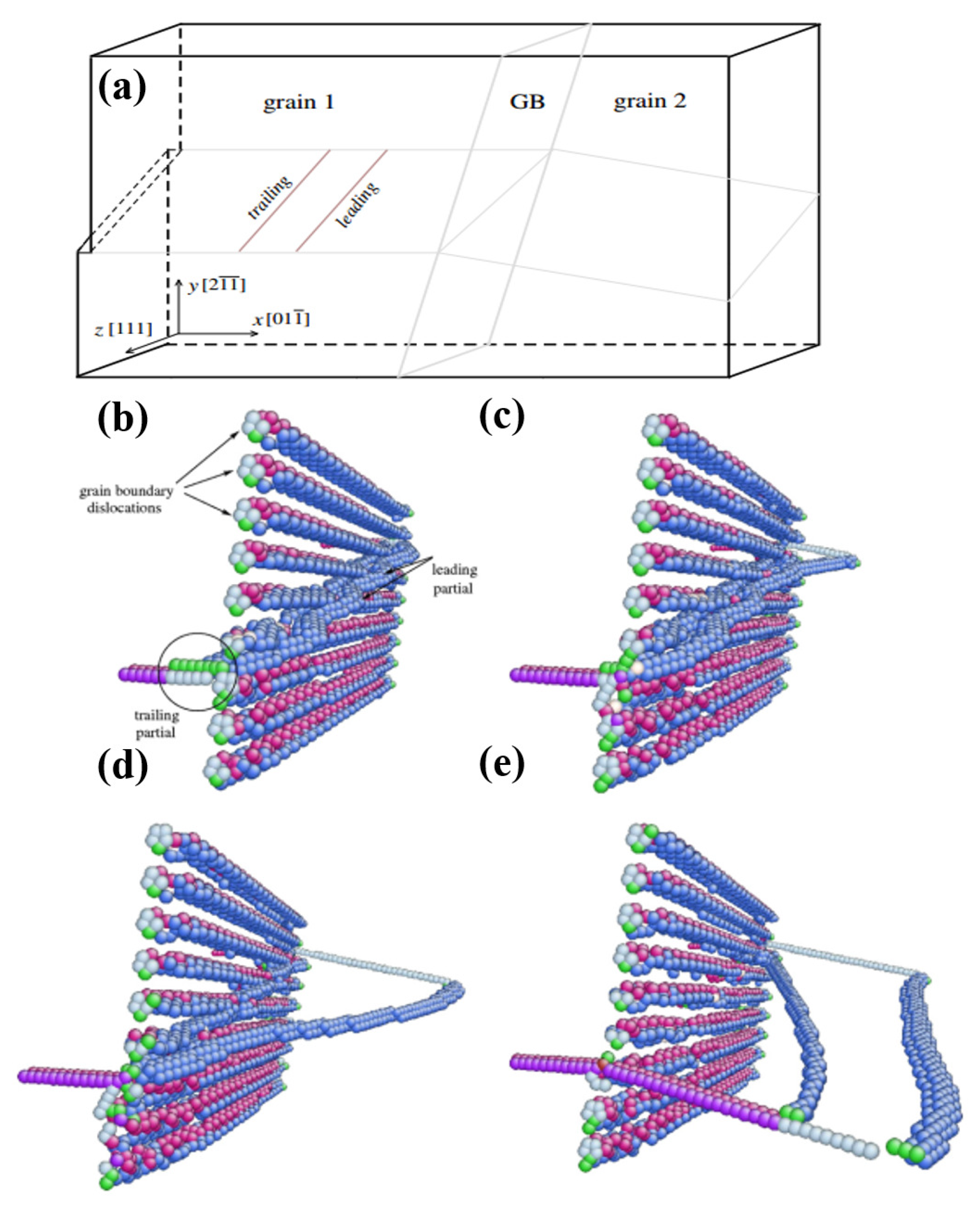
3. The Interaction of Dislocations and GBs
3.1. Dislocations Interacting with LAGBs
3.2. Dislocations Interacting with HAGBs
3.3. Dislocation Pile-Ups Interacting with GBs
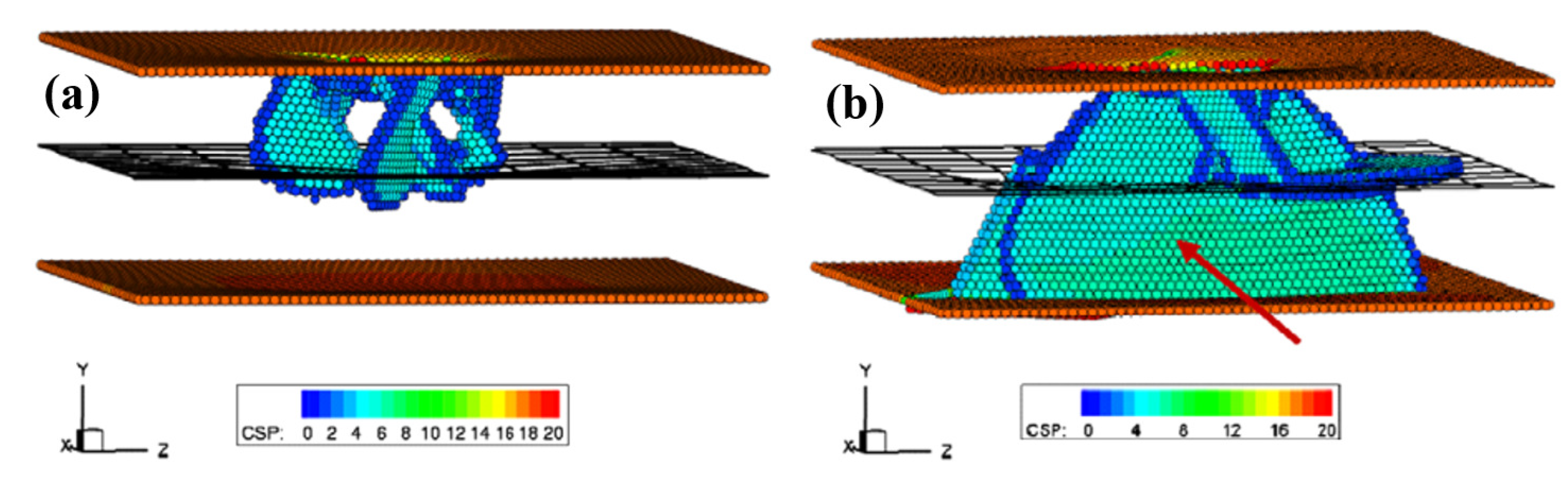
4. The Interaction of Dislocations and Bi-Metal Interfaces
4.1. The Interaction of Dislocations and Coherent Interfaces
4.2. The Interaction of Dislocations and Semi-Coherent Interfaces
4.3. The Interaction of Dislocations and Incoherent Interfaces
5. The Interaction of Dislocations and Metal/Non-Metal Interfaces
5.1. Interaction of Metal Dislocations and Metal/Non-Metal Interfaces
5.2. Interaction of Non-Metal Dislocations with Metal/Nonmetal Interfaces
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Molecular dynamics | MD |
| face-centered-cubic | fcc |
| body-centered-cubic | bcc |
| twin boundary | TB |
| grain boundary | GB |
| low-angle grain boundary | LAGB |
| high-angle grain boundary | HAGB |
| grain boundary dislocation | GBD |
References
- Lesuer, D.R.; Syn, C.K.; Sherby, O.D.; Wadsworth, J.; Lewandowski, J.J.; Hunt, W.H. Mechanical behaviour of laminated metal composites. Int. Mater. Rev. 1996, 41, 169–197. [Google Scholar] [CrossRef]
- Misra, A.; Hirth, J.P.; Hoagland, R.G. Length-scale-dependent deformation mechanisms in incoherent metallic multilayered composites. Acta Mater. 2005, 53, 4817–4824. [Google Scholar] [CrossRef]
- Fang, T.H.; Li, W.L.; Tao, N.R.; Lu, K. Revealing extraordinary intrinsic tensile plasticity in gradient nano-grained copper. Science 2011, 331, 1587–1590. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Hoagland, R.G.; Liu, X.Y.; Misra, A. The influence of interface shear strength on the glide dislocation-interface interactions. Acta Mater. 2011, 59, 3164–3173. [Google Scholar] [CrossRef]
- Ke, L. Making strong nanomaterials ductile with gradients. Science 2014, 345, 1455–1456. [Google Scholar] [CrossRef]
- Lu, L.; Chen, X.; Huang, X.; Lu, K. Revealing the Maximum Strength in Nanotwinned Copper. Science 2009, 323, 607–610. [Google Scholar] [CrossRef]
- Li, N.; Wang, J.; Misra, A.; Zhang, X.; Huang, J.Y.; Hirth, J.P. Twinning dislocation multiplication at a coherent twin boundary. Acta Mater. 2011, 59, 5989–5996. [Google Scholar] [CrossRef]
- Wang, Y.B.; Sui, M.L. Atomic-scale in situ observation of lattice dislocations passing through twin boundaries. Appl. Phys. Lett. 2009, 94, 737. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations, 2nd ed.; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Sutton, A.P.; Balluffi, R.W. Interfaces in Crystalline Materials; Clarendon Press: Oxford, UK, 1996. [Google Scholar]
- Lim, L.C. Slip-twin interactions in nickel at 573K at large strains. Scr. Metall. 1984, 18, 1139–1142. [Google Scholar] [CrossRef]
- Shen, Z.; Wagoner, R.H.; Clark, W.A.T. Dislocation pile-up and grain boundary interactions in 304 stainless steel. Scr. Metall. 1986, 20, 921–926. [Google Scholar] [CrossRef]
- Lee, T.C.; Robertson, I.M.; Birnbaum, H.K. TEM in situ deformation study of the interaction of lattice dislocations with grain boundaries in metals. Philos. Mag. A 1990, 62, 131–153. [Google Scholar] [CrossRef]
- Lee, T.C.; Robertson, I.M.; Birnbaum, H.K. An In Situ transmission electron microscope deformation study of the slip transfer mechanisms in metals. Metall. Trans. A 1990, 21, 2437–2447. [Google Scholar] [CrossRef]
- Zheng, S.J.; Wang, J.; Carpenter, J.S.; Mook, W.M.; Dickerson, P.O.; Mara, N.A.; Beyerlein, I.J. Plastic instability mechanisms in bimetallic nanolayered composites. Acta Mater. 2014, 79, 282–291. [Google Scholar] [CrossRef]
- Li, N.; Wang, J.; Huang, J.Y.; Misra, A.; Zhang, X. In situ TEM observations of room temperature dislocation climb at interfaces in nanolayered Al/Nb composites. Scr. Mater. 2010, 63, 363–366. [Google Scholar] [CrossRef]
- Van Swygenhoven, H. Grain boundaries and dislocations. Science 2002, 296, 66–67. [Google Scholar] [CrossRef] [PubMed]
- Schioøtz, J.; Jacobsen, K.W. A maximum in the strength of nanocrystalline copper. Science 2003, 301, 1357–1359. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.H.; Gumbsch, P.; Ma, E.; Albe, K.; Lu, K.; Hahn, H.; Gleiter, H. The interaction mechanism of screw dislocations with coherent twin boundaries in different face-centred cubic metals. Scr. Mater. 2006, 54, 1163–1168. [Google Scholar] [CrossRef]
- Jin, Z.H.; Gumbsch, P.; Albe, K.; Ma, E.; Lu, K.; Gleiter, H.; Hahn, H. Interactions between non-screw lattice dislocations and coherent twin boundaries in face-centered cubic metals. Acta Mater. 2008, 56, 1126–1135. [Google Scholar] [CrossRef]
- Salehinia, I.; Wang, J.; Bahr, D.; Zbib, H. Molecular dynamics simulations of plastic deformation in Nb/NbC multilayers. Int. J. Plast. 2014, 59, 119–132. [Google Scholar] [CrossRef]
- Zhang, Z.; Urbassek, H.M. Dislocations penetrating an Al/Si interface. AIP Adv. 2017, 7. [Google Scholar] [CrossRef]
- Cao, A.J.; Wei, Y.G. Molecular dynamics simulation of plastic deformation of nanotwinned copper. J. Appl. Phys. 2007, 102, 422. [Google Scholar] [CrossRef]
- Wu, Z.X.; Zhang, Y.W.; Srolovitz, D.J. Dislocation–twin interaction mechanisms for ultrahigh strength and ductility in nanotwinned metals. Acta Mater. 2009, 57, 4508–4518. [Google Scholar] [CrossRef]
- Zhu, T.; Ju, L. Ultra-strength materials. Prog. Mater. Sci. 2010, 55, 710–757. [Google Scholar] [CrossRef]
- Yuasa, M.; Masunaga, K.; Mabuchi, M.; Chino, Y. Interaction mechanisms of screw dislocations with and twin boundaries in Mg. Philos. Mag. 2014, 94, 285–305. [Google Scholar] [CrossRef]
- Fang, Q.; Sansoz, F. Influence of intrinsic kink-like defects on screw dislocation–coherent twin boundary interactions in copper. Acta Mater. 2017, 123, 383–393. [Google Scholar] [CrossRef]
- Hall, E.O. The Deformation and Ageing of Mild Steel: III Discussion of Results. Proc. Phys. Soc. 2002, 64, 495. [Google Scholar] [CrossRef]
- Petch, N.J. The cleavage strength of polycrystals. J. Iron Steel Inst. 1953, 174, 25. [Google Scholar]
- Yamakov, V.; Wolf, D.; Phillpot, S.R.; Mukherjee, A.K.; Gleiter, H. Dislocation processes in the deformation of nanocrystalline aluminium by molecular-dynamics simulation. Nat. Mater. 2002, 1, 45–48. [Google Scholar] [CrossRef]
- Liu, B.; Eisenlohr, P.; Roters, F.; Raabe, D. Simulation of dislocation penetration through a general low-angle grain boundary. Acta Mater. 2012, 60, 5380–5390. [Google Scholar] [CrossRef]
- Yun, G.; Jin, Z. Interaction between lattice dislocations and low-angle grain boundaries in Ni via molecular dynamics simulations. Mol. Simul. 2017, 43, 1–7. [Google Scholar]
- Bachurin, D.V.; Weygand, D.; Gumbsch, P. Dislocation-grain boundary interaction in 〈111〉 textured thin metal films. Acta Mater. 2010, 58, 5232–5241. [Google Scholar] [CrossRef]
- Kacher, J.; Robertson, I.M. Quasi-four-dimensional analysis of dislocation interactions with grain boundaries in 304 stainless steel. Acta Mater. 2012, 60, 6657–6672. [Google Scholar] [CrossRef]
- Tschopp, M.A.; McDowell, D.L. Dislocation nucleation in Σ3 asymmetric tilt grain boundaries. Int. J. Plast. 2008, 24, 191–217. [Google Scholar] [CrossRef]
- Tucker, G.J.; Tschopp, M.A.; Mcdowell, D.L. Evolution of structure and free volume in symmetric tilt grain boundaries during dislocation nucleation. Acta Mater. 2010, 58, 6464–6473. [Google Scholar] [CrossRef]
- Guleryuz, E.; Mesarovic, S.D. Dislocation nucleation on Grain Boundaries: Low angle twist and asymmetric tilt boundaries. Crystals 2016, 6, 77. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, S.; Jeon, J.B.; Kim, Y.J.; Lee, B.J.; Oh, S.H.; Han, S.M. Effect of a high angle grain boundary on deformation behavior of Al nanopillars. Scr. Mater. 2015, 107, 5–9. [Google Scholar] [CrossRef]
- Tucker, G.J.; Aitken, Z.H.; Greer, J.R.; Weinberger, C.R. The mechanical behavior and deformation of bicrystalline nanowires. Model. Simul. Mater. Sci. Eng. 2013, 21. [Google Scholar] [CrossRef]
- Dewald, M.P.; Curtin, W.A. Multiscale modelling of dislocation/grain-boundary interactions: I. Edge dislocations impinging on Σ11 (113) tilt boundary in Al. Philos. Mag. 2007, 87, 4615–4641. [Google Scholar] [CrossRef]
- Dewald, M.P.; Curtin, W.A. Multiscale modelling of dislocation/grain boundary interactions. II. Screw dislocations impinging on tilt boundaries in Al. Philos. Mag. 2007, 87, 4615–4641. [Google Scholar] [CrossRef]
- Dewald, M.; Curtin, W.A. Multiscale modeling of dislocation/grain-boundary interactions: III. 60∘ dislocations impinging on Σ3, Σ9 and Σ11 tilt boundaries in Al. Model. Simul. Mater. Sci. Eng. 2011, 19, 055002. [Google Scholar] [CrossRef]
- Lee, T.C.; Robertson, I.M.; Birnbaum, H.K. Prediction of slip transfer mechanisms across grain boundaries. Scr. Metall. 1989, 23, 1467. [Google Scholar] [CrossRef]
- Rao, S.I.; Hazzledine, P.M. Atomistic Simulations of Dislocation-Interface Interactions in the Cu-Ni Multilayer System. Philos. Mag. A 1999, 80, 2011–2040. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, R.F.; Zhou, C.Z.; Beyerlein, I.J.; Misra, A. Interface dislocation patterns and dislocation nucleation in face-centered-cubic and body-centered-cubic bicrystal interfaces. Int. J. Plast. 2014, 53, 40–55. [Google Scholar] [CrossRef]
- Shao, S.; Medyanik, S.N. Dislocation-interface interaction in nanoscale fcc metallic bilayers. Mech. Res. Commun. 2010, 37, 315–319. [Google Scholar] [CrossRef]
- Spearot, D.E.; Jacob, K.I.; Mcdowell, D.L. Nucleation of dislocations from [0 0 1] bicrystal interfaces in aluminum. Acta Mater. 2005, 53, 3579–3589. [Google Scholar] [CrossRef]
- Saraev, D.; Miller, R.E. Atomistic simulation of nanoindentation into copper multilayers. Model. Simul. Mater. Sci. Eng. 2005, 13, 1089. [Google Scholar] [CrossRef]
- Capolungo, L.; Spearot, D.E.; Cherkaoui, M.; Mcdowell, D.L.; Qu, J.; Jacob, K.I. Dislocation nucleation from bicrystal interfaces and grain boundary ledges: Relationship to nanocrystalline deformation. J. Mech. Phys. Solids 2007, 55, 2300–2327. [Google Scholar] [CrossRef]
- Hoagland, R.G.; Mitchell, T.E.; Hirth, J.P.; Kung, H. On the strengthening effects of interfaces in multilayer fee metallic composites. Philos. Mag. A 2002, 82, 643–664. [Google Scholar] [CrossRef]
- Frank, F. Martensite. Acta Metall. 1953, 1, 15–21. [Google Scholar] [CrossRef]
- Hirth, J.; Pond, R.; Hoagland, R.; Liu, X.Y.; Wang, J. Interface defects, reference spaces and the Frank–Bilby equation. Prog. Mater. Sci. 2013, 58, 749–823. [Google Scholar] [CrossRef]
- Yan, J.W.; Zhu, X.F.; Yang, B.; Zhang, G.P. Shear stress-driven refreshing capability of plastic deformation in nanolayered metals. Phys. Rev. Lett. 2013, 110. [Google Scholar] [CrossRef] [PubMed]
- Hoagland, R.G.; Hirth, J.P.; Misra, A. On the role of weak interfaces in blocking slip in nanoscale layered composites. Philos. Mag. 2006, 86, 3537–3558. [Google Scholar] [CrossRef]
- Zbib, H.M.; Overman, C.T.; Akasheh, F.; Bahr, D. Analysis of plastic deformation in nanoscale metallic multilayers with coherent and incoherent interfaces. Int. J. Plast. 2011, 27, 1618–1639. [Google Scholar] [CrossRef]
- Surappa, M.K.; Rohatgi, R.K. Preparation and properties of cast aluminium-ceramic particle composites. J. Mater. Sci. 1981, 16, 983. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Riahi, A.R.; Alpas, A.T. Indentation-induced subsurface damage in silicon particles of Al–Si alloys. Mater. Sci. Eng. A 2009, 527, 387–396. [Google Scholar] [CrossRef]
- Xia, S.; Qi, Y.; Perry, T.; Kim, K.S. Strength characterization of Al/Si interfaces: A hybrid method of nanoindentation and finite element analysis. Acta Mater. 2009, 57, 695–707. [Google Scholar] [CrossRef]
- Zhang, Z.; Urbassek, H.M. Dislocation-based strengthening mechanisms in metal-matrix nanocomposites: A molecular dynamics study of the influence of reinforcement shape in the Al-Si system. Comput. Mater. Sci. 2018, 145, 109–115. [Google Scholar] [CrossRef]
- Wei, Y.; Ayoub, G.; Salehinia, I.; Mansoor, B.; Zbib, H. Deformation mechanisms in Ti/TiN multilayer under compressive loading. Acta Mater. 2017, 122, 99–108. [Google Scholar]
- Szlufarska, I. Atomistic simulations of nanoindentation. Mater. Today 2006, 9, 42–50. [Google Scholar] [CrossRef]
- Lu, C.; Gao, Y.; Michal, G.; Deng, G.; Huynh, N.N.; Zhu, H.; Liu, X.; Tieu, A.K. Experiment and molecular dynamics simulation of nanoindentation of body centered cubic iron. J. Nanosci. Nanotechnol. 2009, 9, 7307. [Google Scholar] [CrossRef]
- Zhang, Z.; Urbassek, H.M. Indentation into an Al/Si composite: Enhanced dislocation mobility at interface. J. Mater. Sci. 2018, 53, 799–813. [Google Scholar] [CrossRef]
- Li, Z.; Guo, Q.; Li, Z.; Fan, G.; Xiong, D.B.; Su, Y.; Zhang, J.; Zhang, D. Enhanced Mechanical Properties of Graphene (Reduced Graphene Oxide)/Aluminum Composites with a Bioinspired Nanolaminated Structure. Nano Lett. 2015, 15, 8077–8083. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Shao, C.; Wang, S.; Luo, X.; Zheng, K.; Urbassek, H.M. Interaction of Dislocations and Interfaces in Crystalline Heterostructures: A Review of Atomistic Studies. Crystals 2019, 9, 584. https://doi.org/10.3390/cryst9110584
Zhang Z, Shao C, Wang S, Luo X, Zheng K, Urbassek HM. Interaction of Dislocations and Interfaces in Crystalline Heterostructures: A Review of Atomistic Studies. Crystals. 2019; 9(11):584. https://doi.org/10.3390/cryst9110584
Chicago/Turabian StyleZhang, Zhibo, Cancan Shao, Shuncheng Wang, Xing Luo, Kaihong Zheng, and Herbert M. Urbassek. 2019. "Interaction of Dislocations and Interfaces in Crystalline Heterostructures: A Review of Atomistic Studies" Crystals 9, no. 11: 584. https://doi.org/10.3390/cryst9110584
APA StyleZhang, Z., Shao, C., Wang, S., Luo, X., Zheng, K., & Urbassek, H. M. (2019). Interaction of Dislocations and Interfaces in Crystalline Heterostructures: A Review of Atomistic Studies. Crystals, 9(11), 584. https://doi.org/10.3390/cryst9110584




