Design and Optimization of Proton Exchanged Integrated Electro-Optic Modulators in X-Cut Lithium Niobate Thin Film
Abstract
1. Introduction
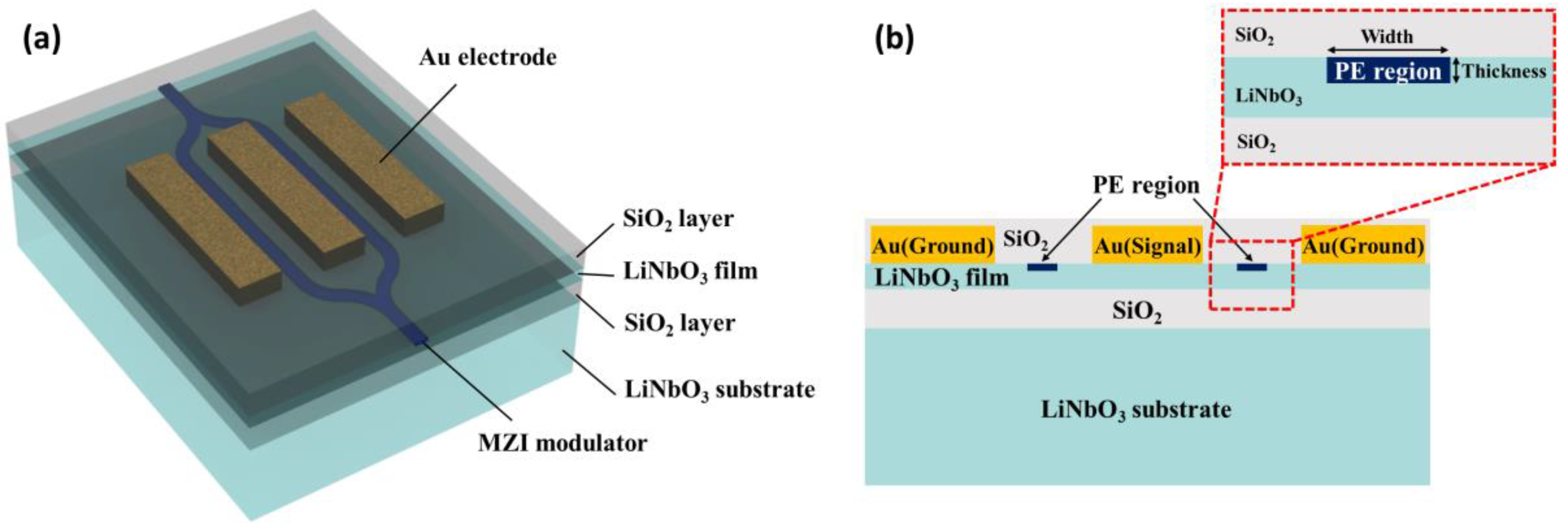
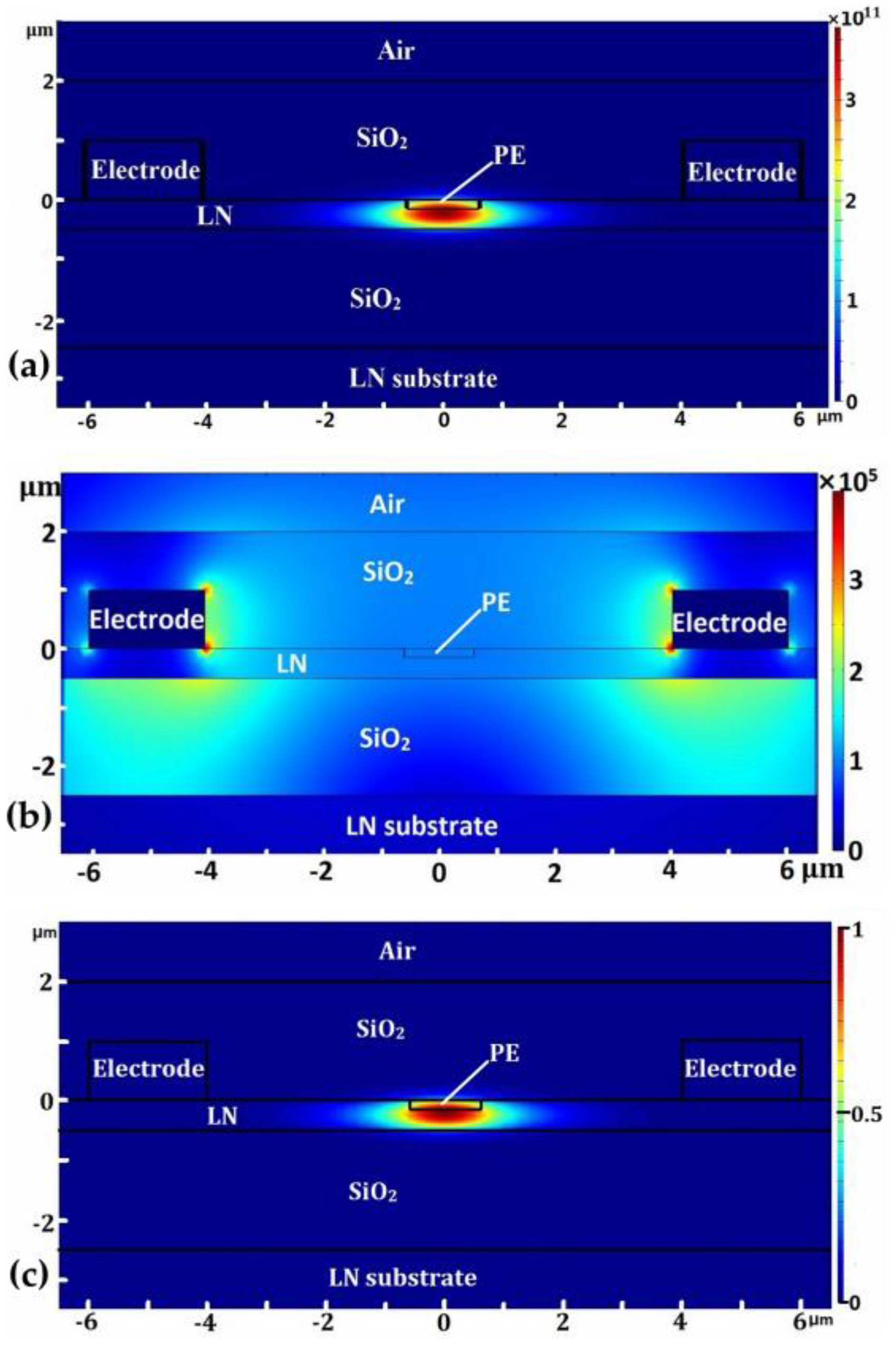
2. Device Design and Methods
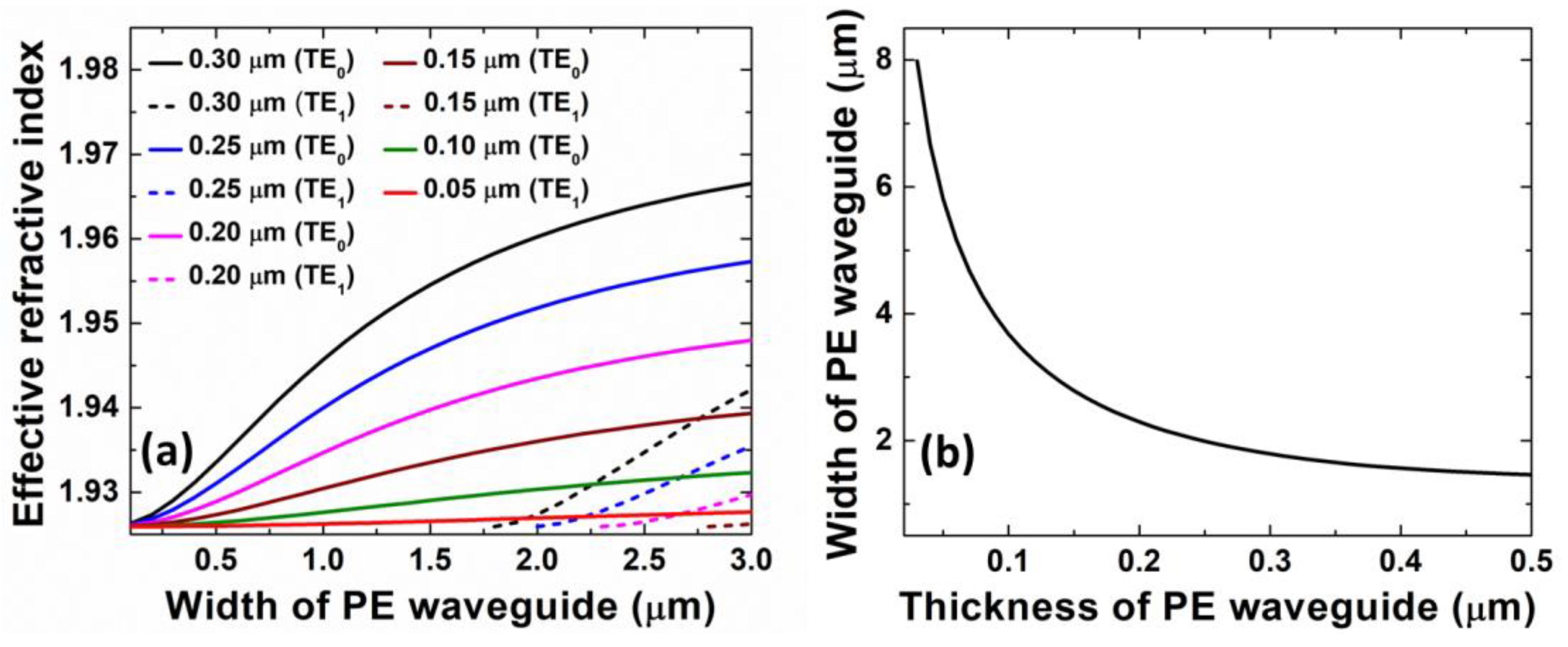
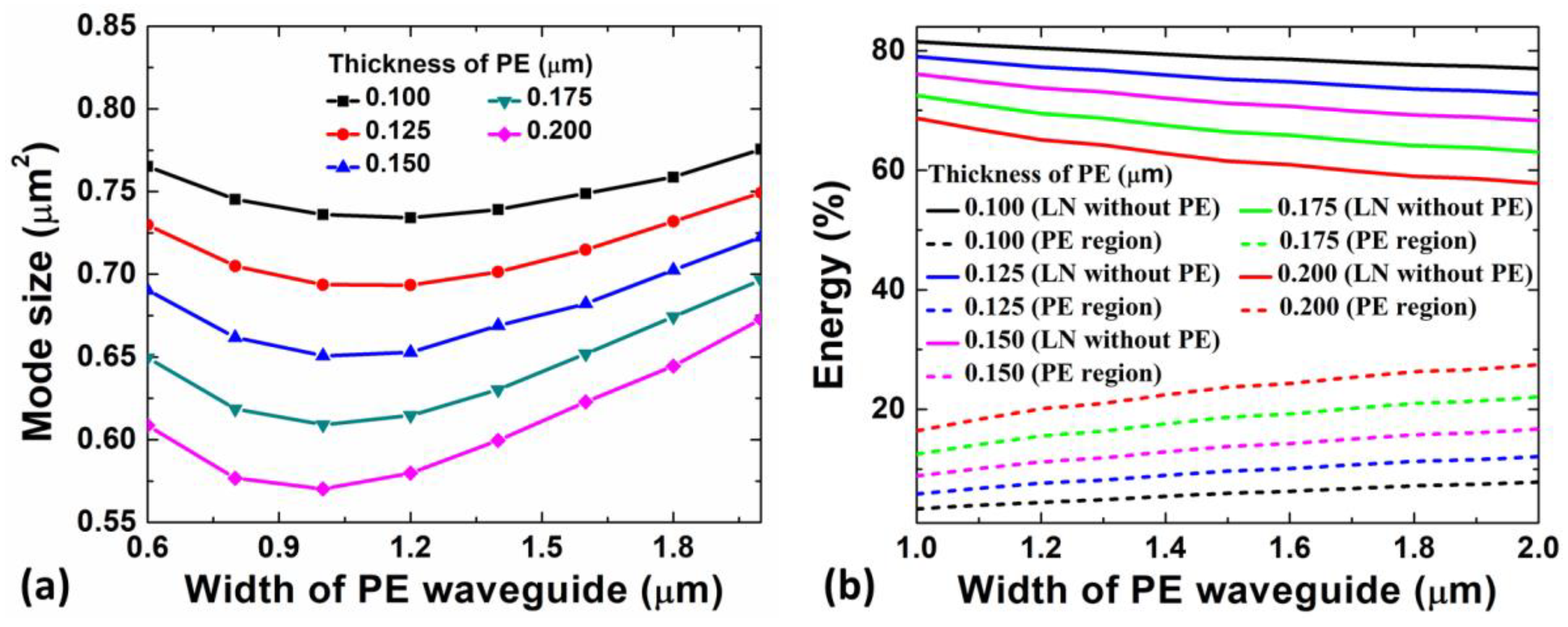
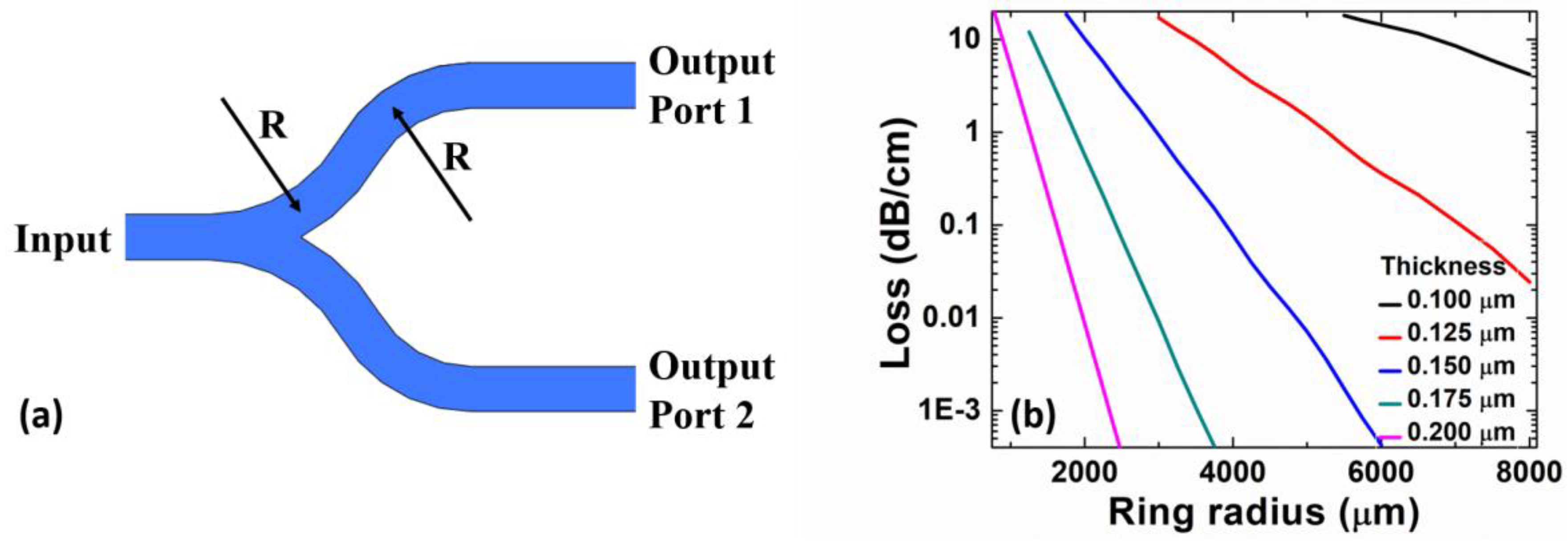
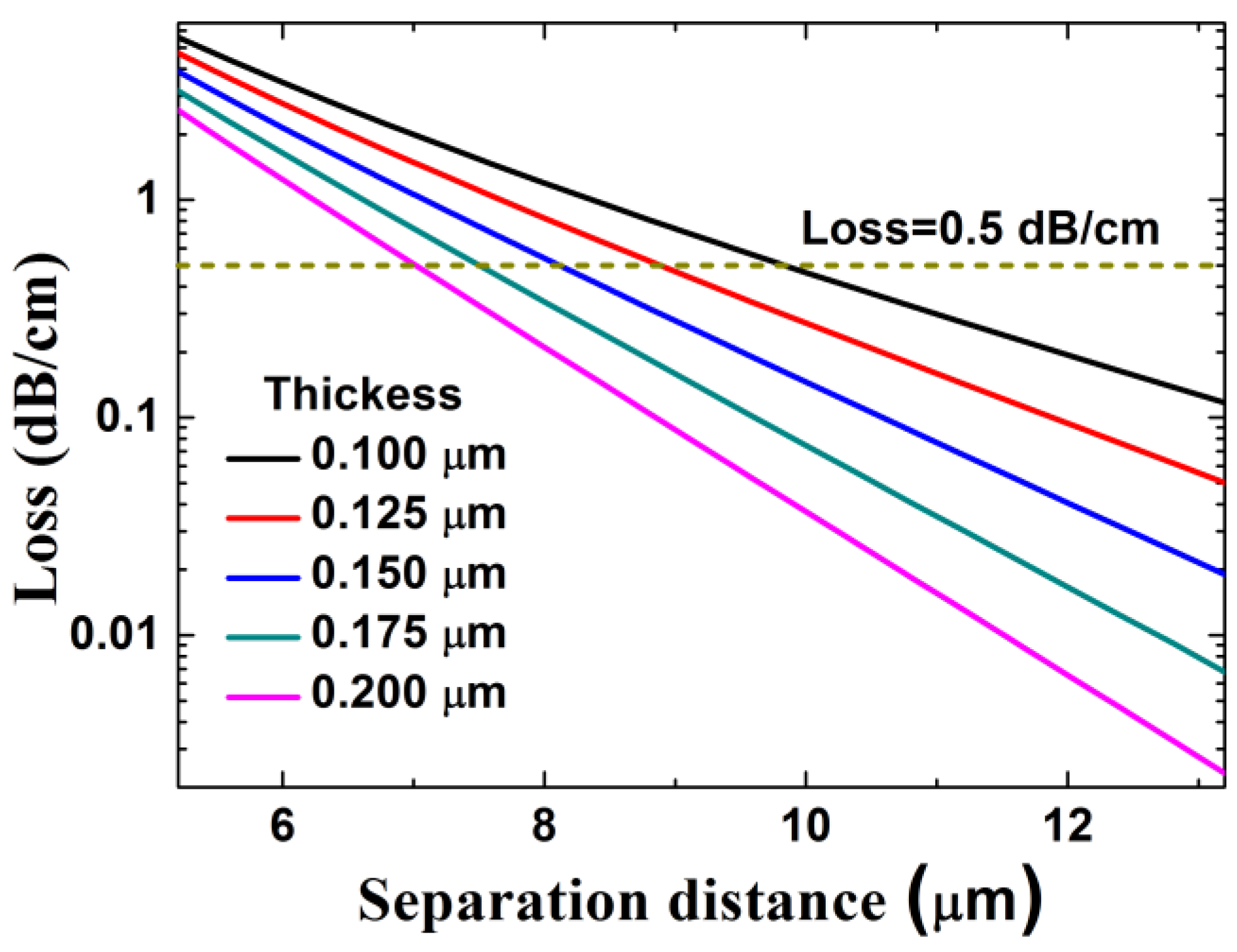
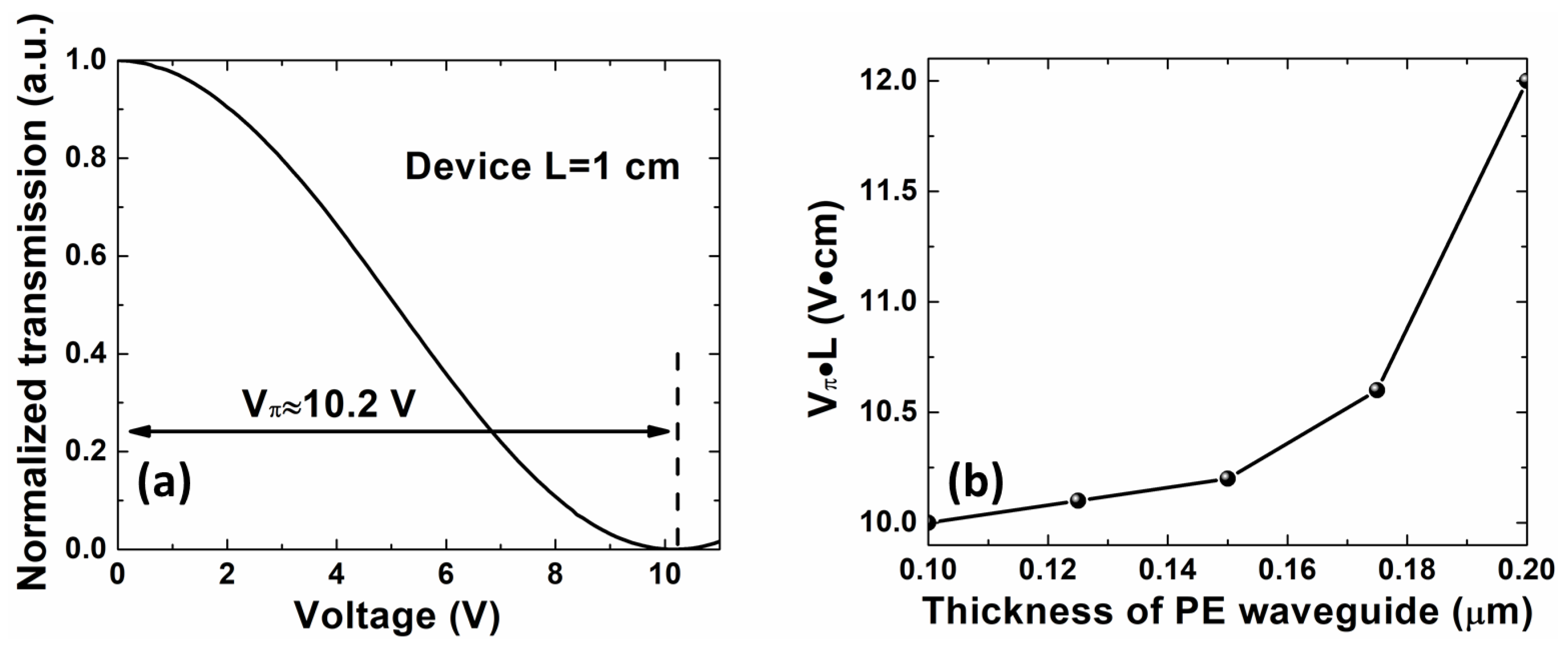
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Honardoost, A.; Safian, R.; Rao, A.; Fathpour, S. High-Speed Modeling of Ultracompact Electrooptic Modulators. J. Light. Technol. 2018, 36, 5893–5902. [Google Scholar] [CrossRef]
- Janner, D.; Tulli, D.; García-Granda, M.; Belmonte, M.; Pruneri, V. Micro-structured integrated electro-optic LiNbO3 modulators. Laser Photonics Rev. 2019, 3, 301–313. [Google Scholar] [CrossRef]
- Chuang, R.W.; Hsu, M.T.; Chang, Y.C.; Lee, Y.J.; Chou, S.H. Integrated multimode interference coupler-based Mach–Zehnder interferometric modulator fabricated on a silicon-on-insulator substrate. IET Optoelectron. 2012, 6, 147–152. [Google Scholar] [CrossRef]
- Chen, H.W.; Kuo, Y.H.; Bowers, J.E. High speed hybrid silicon evanescent Mach-Zehnder modulator and switch. Opt. Express 2008, 16, 20571–20576. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Shao, S.; Zhang, L.; Fu, X.; Yang, L. Method to improve the linearity of the silicon Mach-Zehnder optical modulator by doping control. Opt. Express 2016, 24, 24641–24648. [Google Scholar] [CrossRef]
- Kitoh, T. Recent progress on arrayed-waveguide grating multi/demultiplexers based on silica planar lightwave circuits. Proc. SPIE 2008, 7135, 713503. [Google Scholar]
- Maru, K.; Mizumoto, M.; Uetsuka, H. Demonstration of Flat-Passband Multi/Demultiplexer Using Multi-Input Arrayed Waveguide Grating Combined with Cascaded Mach-Zehnder Interferometers. J. Light. Technol. 2007, 25, 2187–2197. [Google Scholar] [CrossRef]
- Cahill, L.W. The modelling of integrated optical power splitters and switches based on generalised Mach-Zehnder devices. Opt. Quantum Electron. 2004, 36, 165–173. [Google Scholar] [CrossRef]
- Cherchi, M. Design scheme for Mach–Zehnder interferometric coarse wavelength division multiplexing splitters and combiners. J. Opt. Soc. Am. B 2006, 23, 1752–1756. [Google Scholar] [CrossRef]
- Weis, R.S.; Gaylord, T.K. Lithium niobate: Summary of physical properties and crystal structure. Appl. Phys. A 1985, 37, 191–203. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, M.; Chen, X.; Bertrand, M.; Shams-Ansari, A.; Chandrasekhar, S.; Winzer, P.; Lončar, M. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 2018, 562, 101–104. [Google Scholar] [CrossRef] [PubMed]
- He, M.; Xu, M.; Ren, Y.; Jian, J.; Ruan, Z.; Xu, Y.; Gao, S.; Sun, S.; Wen, X.; Zhou, L.; et al. High-performance hybrid silicon and lithium niobate Mach–Zehnder modulators for 100 Gbit s−1 and beyond. Nat. Photonics 2019, 13, 359–364. [Google Scholar] [CrossRef]
- Weigel, P.O.; Zhao, J.; Fang, K.; Al-Rubaye, H.; Trotter, D.; Hood, D.; Mudrick, J.; Dallo, C.; Pomerene, A.T.; Starbuck, A.L.; et al. Bonded thin film lithium niobate modulator on a silicon photonics platform exceeding 100 GHz 3-dB electrical modulation bandwidth. Opt. Express 2018, 26, 23728–23739. [Google Scholar] [CrossRef] [PubMed]
- Mercante, A.J.; Shi, S.; Yao, P.; Xie, L.; Weikle, R.M.; Prather, D.W. Thin film lithium niobate electro-optic modulator with terahertz operating bandwidth. Opt. Express 2018, 26, 14810–14816. [Google Scholar] [CrossRef]
- Rao, A.; Patil, A.; Rabiei, P.; Honardoost, A.; Desalvo, R.; Paolella, A.; Fathpour, S. High-performance and linear thin-film lithium niobate Mach–Zehnder modulators on silicon up to 50 GHz. Opt. Lett. 2016, 41, 5700–5703. [Google Scholar] [CrossRef]
- Poberaj, G.; Hu, H.; Sohler, W.; Günter, P. Lithium niobate on insulator (LNOI) for micro-photonic devices. Laser Photonics Rev. 2012, 6, 488–503. [Google Scholar] [CrossRef]
- Han, H.; Cai, L.; Hu, H. Optical and structural properties of single-crystal lithium niobate thin film. Opt. Mater. 2015, 42, 47–51. [Google Scholar] [CrossRef]
- Xiang, B.; Guan, J.; Jiao, Y.; Wang, L. Fabrication of ion-sliced lithium niobate slabs using helium ion implantation and Cu–Sn bonding. Phys. Status Solidi (A) 2014, 211, 2416–2420. [Google Scholar] [CrossRef]
- Hu, H.; Ricken, R.; Sohler, W. Lithium niobate photonic wires. Opt. Express 2009, 17, 24261–24268. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, C.; Cheng, R.; Shams-Ansari, A.; Lončar, M. Monolithic ultra-high-Q lithium niobate microring resonator. Optica 2017, 4, 1536–1537. [Google Scholar] [CrossRef]
- Honardoost, A.; Juneghani, F.A.; Safian, R.; Fathpour, S. Towards subterahertz bandwidth ultracompact lithium niobate electrooptic modulators. Opt. Express 2019, 27, 6495–6501. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.; Mahmoud, A.; Piazza, G. Low-loss waveguides on Y-cut thin film lithium niobate: Towards acousto-optic applications. Opt. Express 2019, 27, 9794–9802. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.; Kong, R.; Wang, Y.; Hu, H. Channel waveguides and y-junctions in x-cut single-crystal lithium niobate thin film. Opt. Express 2015, 23, 29211–29221. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.; Wang, M.; Xu, J.; Qi, J.; Chu, W.; Fang, Z.; Zhang, J.; Zhou, J.; Qiao, L.; Chai, Z.; et al. Long Low-Loss-Litium Niobate on Insulator Waveguides with Sub-Nanometer Surface Roughness. Nanomaterials 2018, 8, 910. [Google Scholar] [CrossRef] [PubMed]
- Ganshin, V.A.; Korkishko, Y.N. Proton exchange in lithium niobate and lithium tantalate single crystals: Regularities and specific features. Phys. Status Solidi (A) 1990, 119, 11–25. [Google Scholar] [CrossRef]
- Canali, C.; Carnera, A.; Mea, G.D.; Mazzoldi, P.; Shukri, S.M.A.; Nutt, A.C.G.; Rue, R.M.D.L. Structural characterization of proton exchanged LiNbO3 optical waveguides. J. Appl. Phys. 1986, 59, 2643–2649. [Google Scholar] [CrossRef]
- Xu, C.L.; Huang, W.P.; Stern, M.S.; Chaudhuri, S.K. Full-vectorial mode calculations by finite difference method. IEE Proc. Optoelectron. 1994, 141, 281–286. [Google Scholar] [CrossRef]
- Scarmozzino, R.; Gopinath, A.; Pregla, R.; Helfert, S. Numerical techniques for modeling guided-wave photonic devices. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 150–162. [Google Scholar] [CrossRef]
- Scarmozzino, R.; Osgood, R.M. Comparison of finite-difference and Fourier-transform solutions of the parabolic wave equation with emphasis on integrated-optics applications. J. Opt. Soc. Am. A 1991, 8, 724–731. [Google Scholar] [CrossRef]
- Han, H.; Xiang, B.; Zhang, J. Simulation and analysis of single-mode microring resonators in lithium niobate thin film. Crystals 2018, 8, 342. [Google Scholar] [CrossRef]
- Méndez, A.; Paliza, G.D.L.; Garcia-Cabanes, A.; Cabrera, J.M. Comparison of the electro-optic coefficient r33 in well-defined phases of proton exchanged LiNbO3 waveguides. Appl. Phys. B 2001, 73, 485–488. [Google Scholar] [CrossRef]
- Schlarb, U.; Betzler, K. A generalized sellmeier equation for the refractive indices of lithium niobate. Ferroelectrics 1994, 156, 99–104. [Google Scholar] [CrossRef]
- Lumerical Solutions. Available online: http://www.lumerical.com/ (accessed on 25 August 2019).
- Chung, Y.; Dagli, N. An assessment of finite difference beam propagation method. IEEE J. Quantum Electron. 1990, 26, 1335–1339. [Google Scholar] [CrossRef]
- Wooten, E.; Kissa, K.; Yi-Yan, A.; Murphy, E.; Lafaw, D.; Hallemeier, P.; Maack, D.; Attanasio, D.; Fritz, D.; McBrien, G.; et al. A review of lithium niobate modulators for fiber-optic communications systems. IEEE J. Quantum Electron. 2000, 6, 69–82. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.; Xiang, B.; Lin, T.; Chai, G.; Ruan, S. Design and Optimization of Proton Exchanged Integrated Electro-Optic Modulators in X-Cut Lithium Niobate Thin Film. Crystals 2019, 9, 549. https://doi.org/10.3390/cryst9110549
Han H, Xiang B, Lin T, Chai G, Ruan S. Design and Optimization of Proton Exchanged Integrated Electro-Optic Modulators in X-Cut Lithium Niobate Thin Film. Crystals. 2019; 9(11):549. https://doi.org/10.3390/cryst9110549
Chicago/Turabian StyleHan, Huangpu, Bingxi Xiang, Tao Lin, Guangyue Chai, and Shuangchen Ruan. 2019. "Design and Optimization of Proton Exchanged Integrated Electro-Optic Modulators in X-Cut Lithium Niobate Thin Film" Crystals 9, no. 11: 549. https://doi.org/10.3390/cryst9110549
APA StyleHan, H., Xiang, B., Lin, T., Chai, G., & Ruan, S. (2019). Design and Optimization of Proton Exchanged Integrated Electro-Optic Modulators in X-Cut Lithium Niobate Thin Film. Crystals, 9(11), 549. https://doi.org/10.3390/cryst9110549






