1. Introduction
Phononic crystals (PCs) are periodic structures made up of two or more kinds of materials (solid-solid or fluid-solid) with different acoustic impedance [
1,
2,
3]. Due to their ability to forbid propagation of acoustic or elastic waves through band gaps induced by Bragg scattering or local resonance, PCs have received significant attention in the applications of wave manipulation, vibration suppression, wave guiding, and so on [
4,
5,
6]. Although fluid-solid PCs have been one of the research focuses in the past years, in most literature fluid only serves as a constituent or a medium through which acoustic waves propagate [
7,
8,
9,
10,
11]. Conventionally, accelerometers (e.g., [
8,
12] for flexural waves) or ultrasonic immersion transmission technique (e.g., [
9,
11] for longitudinal waves) are used to detect the transmission spectra of phononic crystals.The fluid-structure interaction (FSI) on tuning the band-gap or transmission properties of the PCs are seldom addressed. As a promising method for the PCs to adapt to different operation conditions, tuning band gaps through solid-fluid coupling is currently receiving attention. To actively control the localized modes for guiding or filtering waves, Jin et al. theoretically investigated the dynamics of a phononic crystal plate with hollow and liquid-filled pillars [
7]. Casadei and Bertoldi realized self-regulation of dispersion properties by coupling incident aerodynamic flow to a slender beam carrying a periodic array of local resonators [
12]. In fact, in addition to band gap tuning, knowledge about the influence of fluids coupled to PC beams or plates on elastic band-gap and transmission properties is fundamental to a variety of potential applications for the PCs, from environmental or liquid sensing to structural design or vibration control in the marine environment.
In fluid-solid coupling, hydrodynamic loadings may contain the contributions of added mass (i.e., the proportionality constant of the inertial force to the acceleration of the solid) and/or viscous damping (i.e., the proportionality constant of the viscous force to the velocity of the solid). A wide range of research on FSI of non-periodic structures submerged in a fluid have laid a foundation for the study of the fluid-solid coupling on the PCs, particularly vibration characteristics of slender beams subjected to hydrodynamic loadings. Eysden and Sader presented theoretical analysis of the resonant frequencies of rectangular cantilever beams immersed in fluid applicable to large Reynolds number [
13]. Green and Sader studied the increase of hydrodynamic loading on an infinitely long rigid cylinder immersed in a viscous fluid undergoing small amplitude oscillations [
14]. Naik et al. experimentally investigated the dynamic response of a resonant cantilever beam in a viscous fluid by considering the influence of liquid properties and the gap height between the beam and the solid boundary [
15]. Generally, in modeling fluid-solid coupling for submerged structures, several challenges and factors need to be addressed compared with structural modeling performed in vacuo. These factors include the dimensions or shapes of the structures with respect to fluid damping, amplitude of vibration, viscosity of the fluid, and the influence of the fluid boundary conditions. Viscosity of the water plays a dominant role when the submerged structures being considered are of microscopic size. However, for structures of macroscopic size immersed in fluid, viscous damping can be neglected and the fluid can be assumed to be inviscid in nature [
13].
Although some studies on the FSI problem have provided experimental comparisons on structural dynamics (e.g., [
15,
16,
17,
18]), few experimental research focused on the transmission properties of structures immersed in fluid. In this paper, we investigate the lowering of the flexural wave band gaps of a PC beam through fluid-solid coupling. First, we present the spectral element method (SEM) to determine the band structure and displacement transmission of the PC beam, in which the influence of hydrodynamic loading on the PC beam is considered. Then, we present a fiber Bragg grating (FBG) displacement sensing system and employ the FBG system to directly detect the displacement transmission of the PC beam partially or fully immersed in a water tank. Finite element method (FEM) simulations are also provided for comparisons. To the authors’ best knowledge, this is the first experimental study on FSI of the PC beam using the point-wise FBG displacement sensing technique.
2. Modeling of Fluid-Solid Coupling by Spectral Element Method
We investigate a periodic binary straight beam of macroscopic size immersed in water as illustrated in
Figure 1a. Water is assumed to be incompressible and inviscid in nature. Each segment of the periodic binary straight beam has the same dimension (length
, width
, and height
). The spectral element method (SEM) [
19] is used to analyze the influence of hydrodynamic loadings on the flexural wave band-gap properties and displacement transmission of the PC beam. The PC beam is located away from the boundary of the fluid domain and thus the boundary influence on the dynamic of the PC beam can be neglected.
First, we consider a single beam segment in a unit cell as shown in
Figure 1b. The governing equation of the free bending vibration of a partially or fully submerged Timoshenko beam is described by
where
is the transverse displacements,
is the slope due to bending,
is the area moment of inertia about the bending axis,
is the mass density of the beam segment,
is the effective added mass density of fluid (relating to the depth of the surrounding fluid),
is the Young’s modulus,
is the shear modulus,
is the shear correction factor, and
is the cross-section area [
20]. The shear correction factor (also known as shear coefficient) accounts for the variation of the shear stress across the cross section of the phononic crystal beam and it is dependent on the shape of the cross section. The shear correction factor is shown to be related to the Poisson’s ratio
(e.g., for rectangle cross section it is
and for circle cross section it is
[
21]). Note that the surrounding fluid does not contribute to the rotational inertia of the beam segment. In Equation (1), the effect of the hydrodynamic loading is taken into account by introducing the effective mass density of fluid (here the water) to modify the density of the beam segment in air. The consideration of the added mass and neglection of the viscosity are often used in modeling non-micro Bernoulli-Euler beam structures fully or partially immersed in fluid [
22,
23,
24].
The mode shape functions of
and
are assumed in the spectral forms as [
25]
where the wavenumbers (i.e.,
) are obtained by solving the dispersion equation of the beam segment. The four wavenumbers are respectively represented as [
20]
where
and
respectively represent the rightward and leftward traveling waves,
and
respectively represent the rightward and leftward near-field decaying waves,
,
, and
. Following the symbol in [
20], we introduce new subscripts
and
for simplification of the symbols for later derivations.
Obviously, the wavenumbers and mode shape functions of the beam segment are influenced by the added mass of the fluid.
The spectral components of the applied transverse shear forces
and bending moments
of the submerged beam segment has the relationships to displacement and bending slope as
The spectral beam elements are related to the nodal shear forces and bending moments in the two ends of the beam segment as
where
is the nodal displacement of the
beam segment (i.e.,
) and
is the dynamic stiffness matrix, represented as
where the sub-matrix in Equation (6) are respectively
where
with
Now we consider flexural wave propagation in an infinite submerged PC beam. The Floquet boundary condition,
, is applied on a single unit cell (as shown in
Figure 1a, where
is the wave propagation constant. To obtain the band structure of the infinite PC beam immersed in water, the spectral element matrix of the two segments in a unit cell is assembled. The equation of motion of the unit cell coupling with fluid in spectral form can be written as
where
,
, and
are respectively the nodal displacement in the left, middle, and right of the unit cell and
and
are respectively the left and right nodal loading forces, namely,
Note that in Equation (10) we define two kinds of spectral beam elements with the same geometry but made of two different materials
(stands for aluminum) and
(stands for PMMA). In addition, the sub-matrix for each material in Equation (10) are again derived based on Equations (6)–(9). The degrees of freedom (DOFs) in the middle point connecting to the two beam segments can be eliminated by relating
to
and
(i.e.,
Thus, Equation (10) can be further reduced as
where
Applying the Floquet boundary condition, Equation (13) can be reformulated by matrix transformation as
where
is the transmission matrix obtained from spectral beam elements, given by
From the eigenvalue problem of Equation (15), one can calculate propagation constant and the band structure of the submerged PC beam can accordingly be obtained.
For a finite PC beam immersed in water under excitation of harmonic loadings, the global stiffness matrix of the entire beam is obtained after assembling the spectral stiffness matrix of each spectral beam elements. The equation of motion of the PC beam coupling with fluid in spectral form is given by
where
is the nodal displacement vector in the form of
,
is the loading force vector with dimension of
, and the global dynamic stiffness matrix of the beam is given by
Finally, the flexural displacement transmission of the submerged beam can be obtained by the definition of
where
and
are respectively the displacement amplitudes on the two ends of the submerged PC beam.
3. Experimental and Theoretical Validation and Discussion
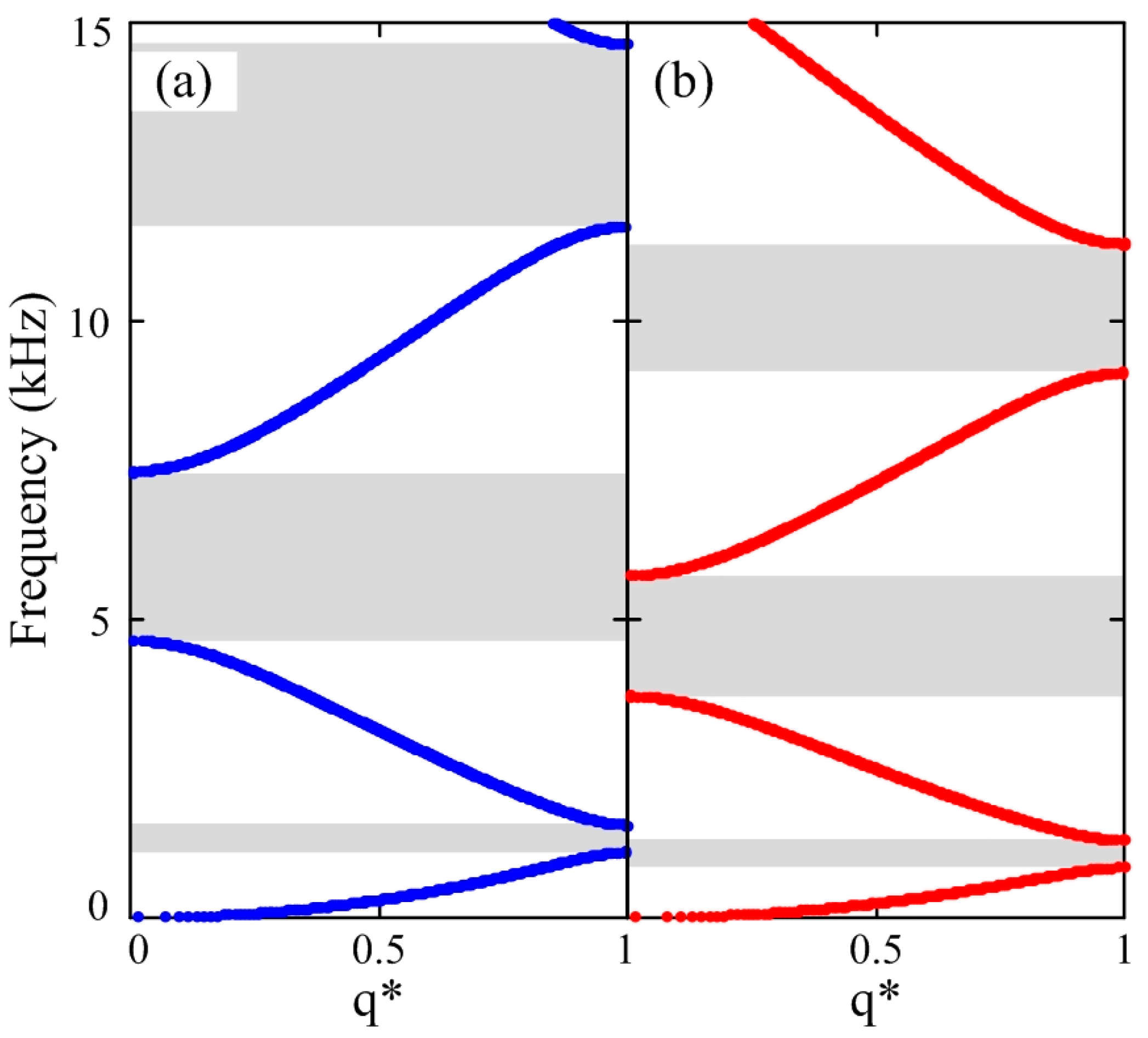
First, we compare the band structures of an infinite PC beam in vacuo (i.e., practically in air) and in water to see the influence of the added mass of fluid on the band-gap properties.
Figure 2 shows the band structures of a PC beam in vacuo (
Figure 2a) and in water (
Figure 2b) calculated by the SEM, in which the complete band gaps are shaded and the wavenumbers are normalized for the unit cell (i.e.,
). The PC beam consists of two materials, 6061 aluminum and PMMA. Each of the two materials (i.e., 6061 aluminum and PMMA) has the size of 0.045 m (length)
0.015 m (width)
0.01 m (height). The elastic constants of the PC beam used in the SEM calculation are
,
,
,
, and
. The Poisson’s ratio of the two materials is 0.33. In the calculation of the band structures, the PC beam is assumed to be far away from the boundary of the fluid domain and thus the effective added mass density of fluid is set as the mass density of water as
[
24]. For the dry PC beam in air,
is set as zero in SEM calculation. Three Bragg-scattering-induced band gaps can be seen in
Figure 2 within 0–15 kHz. From
Figure 2 we can see that both the center frequency and the gap widths decrease when the effect of the surrounding fluid is taken into account as an added mass applied on the phononic crystal beam. As a result, the effective mass density of the submerged phononic crystal beam is increased and accordingly the frequency ranges of the pass- and stop-bands decrease. The effect of the added mass on lowering the pass-bands as well as the stop-bands gets larger as the frequency increases. Obviously, the band-gap properties can be tuned via interaction with the surrounding fluid.
The relationships between the related band-gap parameters and the dimensions of the PC beam (i.e.,
, where
and
are respectively different calculated 3D dimensions and the dimensions of the submerged PC beam considered in
Figure 2) are listed in
Table 1. The considered band-gap parameters include the band-gap width
, the center frequency
, and the absolute and relative shift of the center frequency. The relative shift of center frequency is calculated as the percentage of shift of the center frequency due to fluid-solid coupling related to the center frequency of the dry PC beam (i.e., in air). The relative size of the band gap, which can be an important design parameter of phononic crystals, is also calculated in
Table 1 as the ratio between band-gap width and the corresponding center frequency [
26,
27],
where
and
are respectively the frequencies of upper and lower edge limits of the considered band gap and
is the center frequency of the band gap. From
Table 1 we can see that, the relative size of the band gaps and the relative shift of the center frequencies of the submerged PC beam are influenced or lowered in the same way with almost identical values (compared with the same band gap) by the fluid-solid coupling. On the other hand, different dimensions of the submerged PC beam only leads to a different absolute shift of the band gaps and band-gap widths.
Then, an FBG displacement sensing system is employed to directly detect the displacement transmission of a finite PC beam in air, partially, or fully immersed in water. A fiber Bragg grating (FBG) is a periodic perturbation of the refractive index in a length of fiber core capable of selectively reflecting a particular wavelength of light according to Bragg reflection. Unless the cladding of the FBG are partially removed by side-polishing or hydrofluoric (HF) acid etching, submerged FBGs are intrinsically insensitive to surrounding fluid because of the well-screened core mode coupling [
28]. The FBG, often used as strain sensors for structural health monitoring [
29], has not been used as point-wise displacement sensors in the applications of the phononic crystals until the work recently published in [
30]. Based on the fiber Bragg grating (FBG) sensing technique proposed in [
30], we setup an FBG displacement sensing system to measure the displacement transmission of the submerged PC beam. To the authors’ best knowledge, this is the first experimental study of fluid-solid coupling on the PC beam through displacement transmission using the point-wise FBG displacement sensing technique.
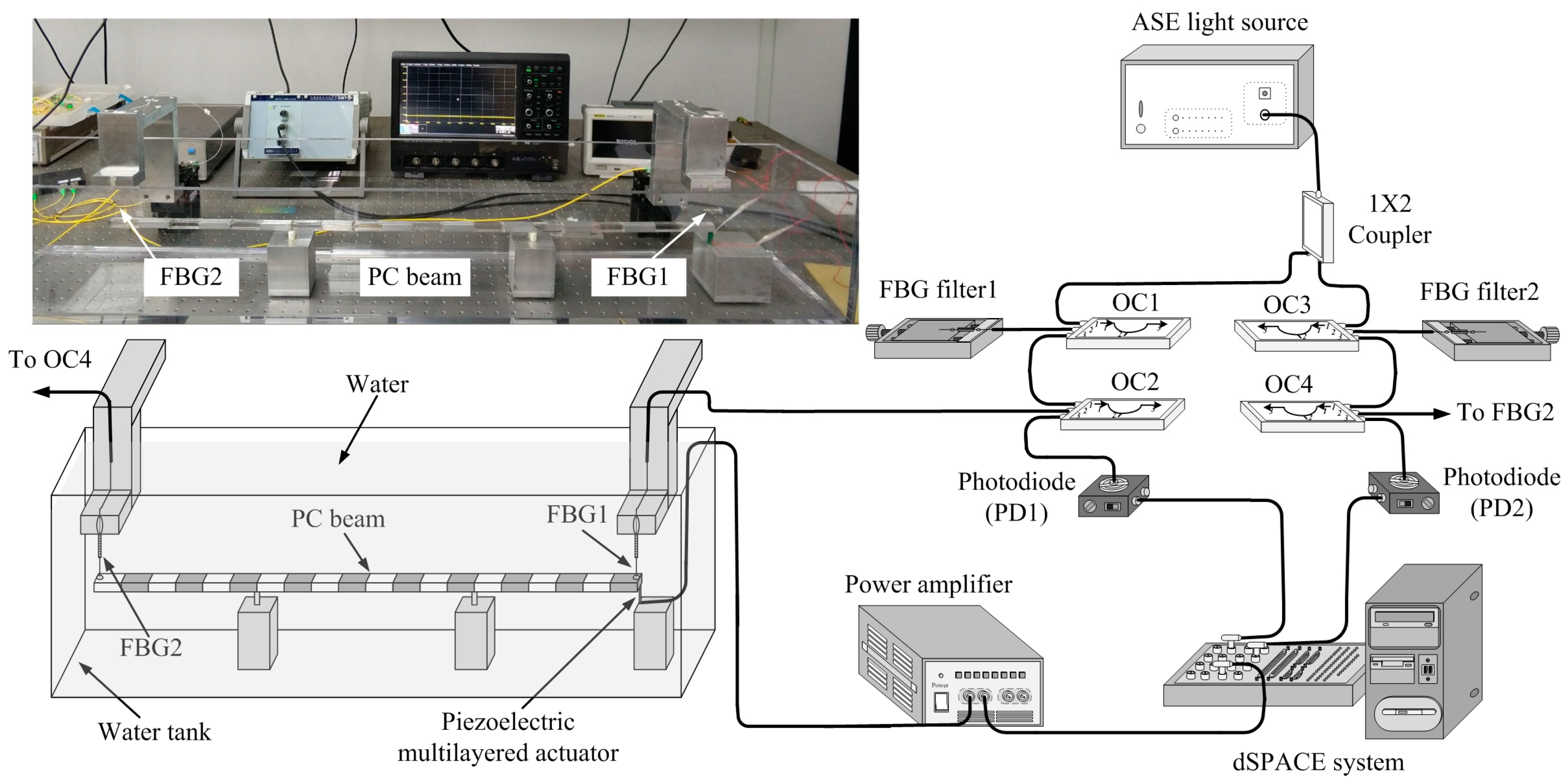
Figure 3 shows the experimental setup and the corresponding fiber Bragg grating (FBG) displacement sensing system. There are 10 unit cells in total along the PC beam. The size of the PC beam is the same as that considered in
Figure 2. The PC beam is placed in a water tank and only two points of the PC beam are rested on two soft rubbers. The bottom surface of the PC beam is 0.1 m away from the bottom of the water tank. The size of the water tank is 1.2 m (length) × 0.2 m (width) × 0.2 m (height). Note that the size of the water tank is relatively large compared to the cross-sectional area of the PC beam. Thus, reflected pressure field from the wall of the water tank is negligible.
In the FBG sensing system, a C-band amplified spontaneous emission (ASE) light source (China-Fiber Optics, Shanghai, China) is split into two paths by a coupler and sent to two FBG sensors (i.e., FBG1 and FBG2) and the corresponding FBG demodulation systems (i.e., FBG filter1 and FBG filter2). Two 3-port directional optical circulators (OCs) are set up in each demodulation system to guide the light beam. Photodiodes (PDA10CS, InGaAs amplified detector, Thorlabs, Newton, NJ, USA) are employed to convert the light to electrical signals and are connected to a dSPACE system (dSPACE GmbH, Paderborn, Germany) for displacement transmission measurement. The grating lengths of the FBG sensors and FBG filters are both 10 mm. One end of the FBG sensor is point-wisely glued to the sensing point (i.e., the extreme end of the PC beam) by epoxy glues. The other end of the FBG sensor is glued to a vertical translated stage. By careful matching the initial Bragg wavelength of the FBG sensor and the corresponding FBG filter, the Bragg wavelength shift of the FBG sensor during vibration of the PC beam can be linearly demodulated. In the experimental setup shown in
Figure 3, FBG1 serves as an input sensor and FBG2 an output sensor.
To obtain the displacement transmission, white noise random signals are generated by the dSPACE DS1104 system and sent to a piezoelectric multilayered actuator (AE0505D16, Thorlabs, Newton, NJ, USA) to excite flexural wave propagation in the PC beam. To prevent electric leakage, the wires of the piezoelectric multilayered actuator are carefully wrapped with an insulating layer of epoxy glues. The responses of FBG1 and FBG2 within 20 s are recorded in the dSPACE DS1104 system. The displacement transmission is then obtained from calculating the relationship , where is the auto-spectral density function of the input random displacement (detected by the FBG1) and is the cross-spectral density function between the input random and transmitted displacements (obtained by FBG2).
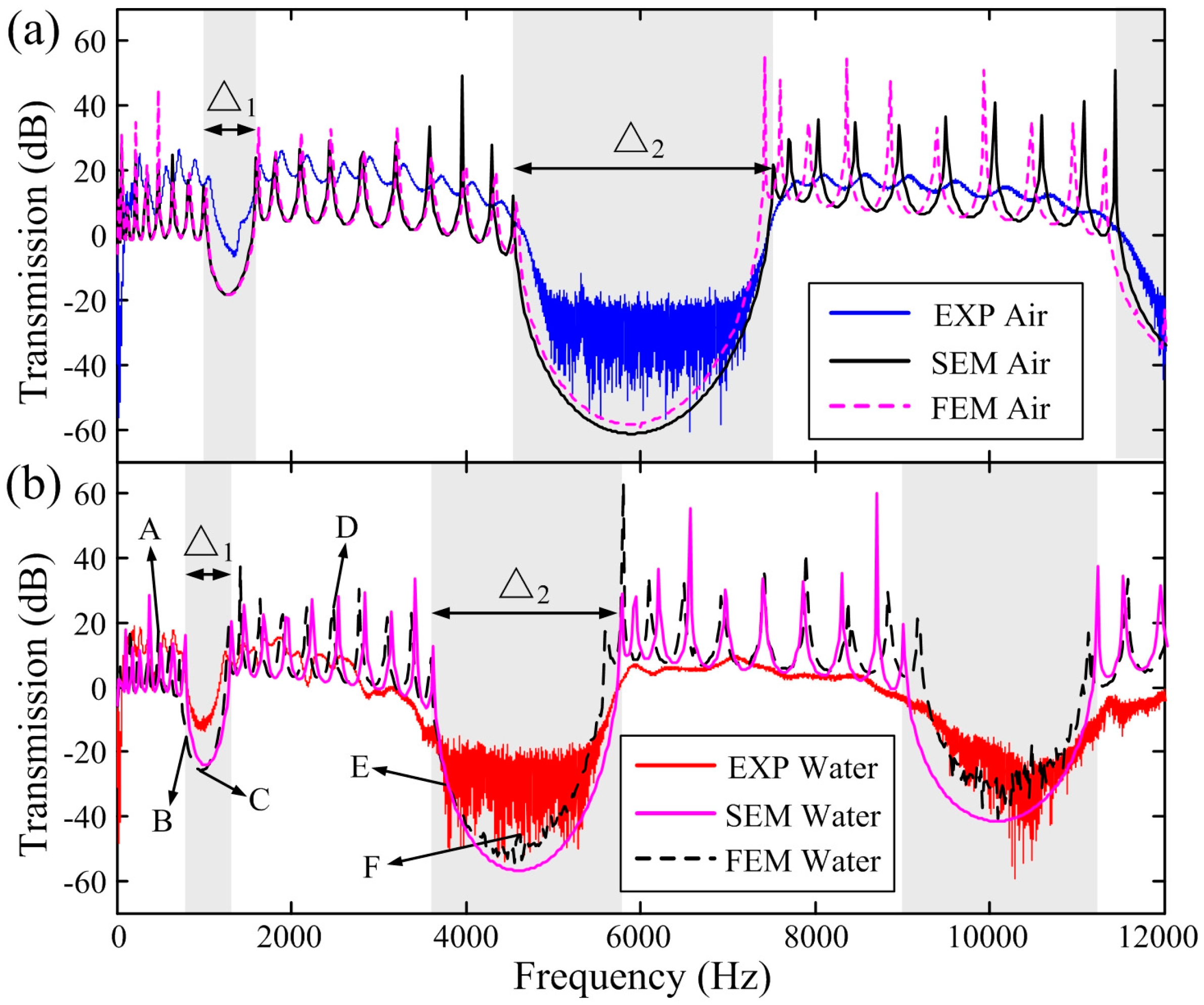
The identified displacement transmissions when the PC beam is respectively excited in air and in a water tank full of water are shown in
Figure 4, compared with the results obtained by the SEM (i.e., using Equation (18)) and FEM performed by the COMSOL Multiphysics
® software (Comsol Inc., Stockholm, Sweden). In SEM simulations, the coupling of the water is considered as an added mass applied on the dry PC beam. In FEM analysis, instead of simply applying the added mass, the acoustic-solid interaction module is selected in which the water is set as a pressure acoustic model and the space of the water is set the same as the experimental condition. The acoustic-solid interaction module first calculates the frequency response and mode shapes of the linear PC beam and then feeds the information of the dynamics of the solid back to the acoustic domain. The acoustic pressure field is calculated by solving the frequency-domain Helmholtz equation for sound pressure in water [
31]. A normal acceleration boundary condition is then considered to feed back the frequency response of the PC beam to the acoustic field. Note that the structural damping, which can be considered in the modeling of the PC beam by introducing a complex Young’s modulus that leads to decaying wave propagation, is neglected in both SEM and FEM simulations. The structural damping mainly reduces the vibration amplitudes near the resonant frequencies and has no influence on the band-gap locations [
32]. Despite the neglection of the structural damping in SEM/FEM simulations, good agreement can be obtained in
Figure 4 between the experimental, theoretical, and numerical results both in air and water.
The results shown in
Figure 4 clearly indicate that the FBG sensors immersed in water are indeed intrinsically insensitive to surrounding fluid and can possess good point-wise displacement sensing performance even in water. In addition, the lowering of the band gaps and decreasing of the band-gap widths can still be observed in the experimental, SEM, and FEM results for the finite PC beam. Strong damping of the resonant peaks is observed when the PC beam is immersed in water. As the frequency gets higher, discrepancy between the SEM, FEM, or experimental results can be observed. Without the coupling of the water (i.e.,
Figure 4a) and when the wavelength in the PC beam is not small compared to the beam thickness, the frequency responses calculated by the SEM can be regarded as accurate due to the fact it uses exact dynamic stiffness matrices [
20]. However, structural modeling using SEM is limited to simple geometry, loads, and boundary conditions. On the other hand, FEM can be applied to structures of complicated geometry or boundary conditions but the accuracy of FEM is based on the finite element discretization [
32]. Thus, increasing element numbers in FEM analysis can reduce the high-frequency (i.e., small wavelength) discrepancy. In the presence of water, good agreements between SEM, FEM, and FBG experimental results especially at low frequencies indicates that both the added mass in SEM and the acoustic-solid interaction module in FEM are capable of analyzing the considered fluid-solid coupling problem for low-order band gaps.
The normal velocity of the fluid is equal to that of the structure at the fluid-structure interface. The vibration modes in vacuo are assumed to be preserved when the PC beam is immersed in water and each mode shape generates corresponding surface pressure distributions (e.g., see [
33,
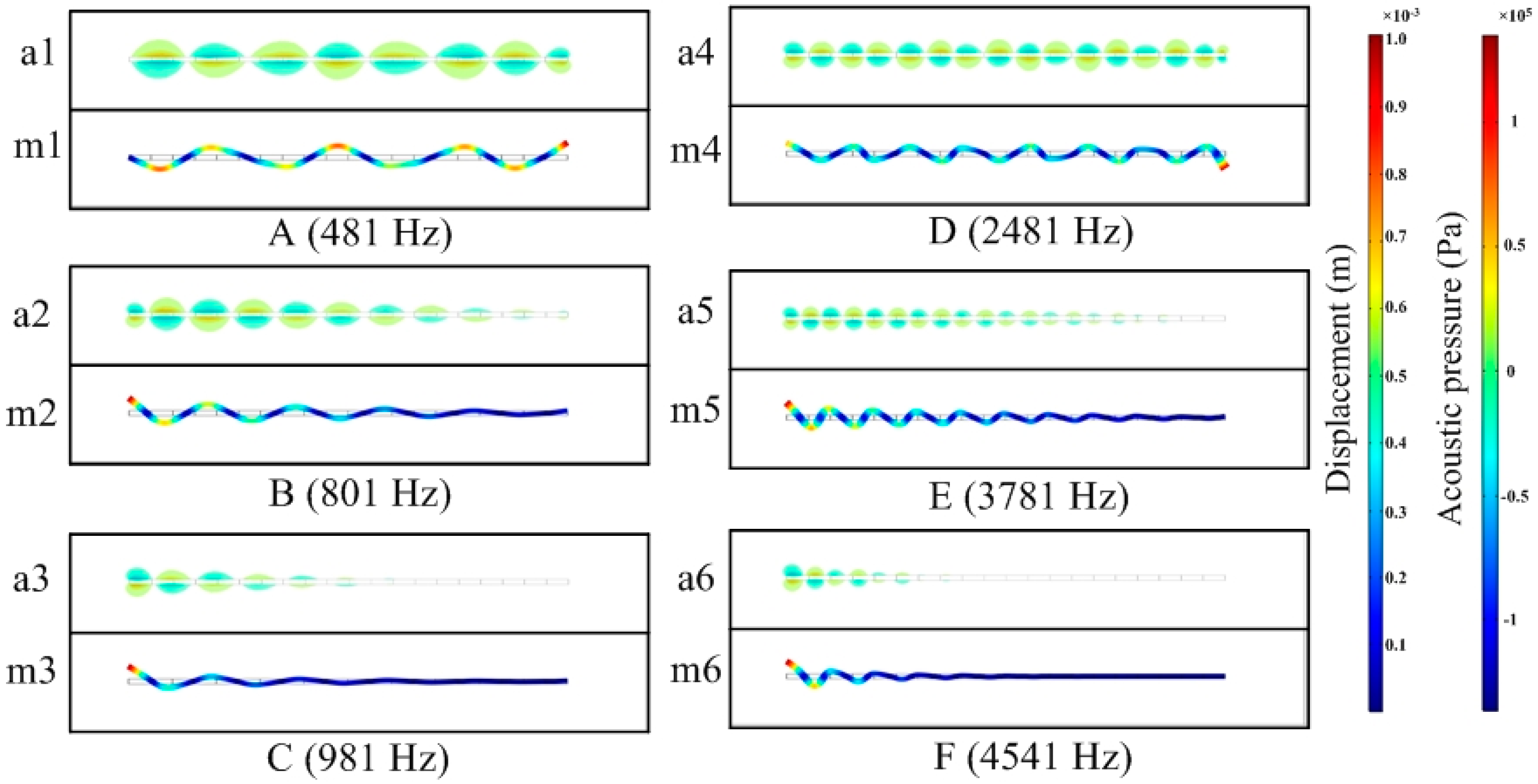
34]). To demonstrate the coupling of the water to the dynamics of the PC beam, we select representative frequencies in
Figure 4 to show the corresponding steady-state vibration profiles of the PC beam and the acoustic pressure field by COMSOL. The frequencies of the selected vibration profiles are marked as A to F in
Figure 4, including resonant peaks in pass bands (i.e., A = 481 Hz, D = 2481 Hz), lower edge of the first band gap (i.e., B = 801 Hz, E = 3781 Hz), and center of the band gaps (i.e., C = 981 Hz, F = 4541 Hz). The results are shown in
Figure 5. We can see clear correspondence, such as the nodal points, between the vibration profiles and the interacted acoustic field in the water at these frequencies. Inside the band gaps, the acoustic pressure field decays along the PC beam. In addition, even for the resonant frequencies at pass bands (i.e., “A” and “D”), the intensity of the acoustic pressure field also gets stronger close to the excitation point. Thus, the energy of the acoustic pressure is decayed away from the excitation point instead of uniformly distributed along the PC beam. The correspondences in
Figure 5 also suggest that employing the acoustic-solid interaction module in FEM is equivalent to considering the added mass of fluid on the PC beam. Despite the correspondence between the vibration modes and acoustic pressure field, we note that the vibration of the submerged PC beam is mainly considered and the absorption of structure-borne sound in water and their influence on the vibrations is neglected in our work. In addition, the influence of the wall of the water tank can be neglected at the considered frequency ranges.
In
Table 2, we compare the first and the second band-gap widths (i.e., denoted as “
” and “
”), the center frequencies in the band gaps, and shift of the center frequencies obtained in
Figure 2 (i.e., band structure, denoted in
Table 2 as “BS”) and
Figure 4 (i.e., displacement transmissions). The results show that the discrepancies between the FEM and experimental results for center frequencies are less than 5%, indicating that the proposed FBG displacement sensing system is suitable to be applied in fluid-solid coupling problem. The center frequencies and their shifts in the band gaps of the band structure and the displacement transmission obtained by the SEM calculations are closely related as shown in
Table 2. Larger inconsistency is found for the band-gap widths in the first band gap. We observe that a practical finite PC beam possesses larger band-gap widths than the ideal infinite PC beam. For the first band gap, the relative size of the band gap
is larger in the presence of water for the band structure, SEM, FEM, and FBG experimental results. For many applications, the larger relative size of the band gap is preferable [
26,
27]. However, it is interesting to note that while decreasing the band-gap width and the center frequency, the relative size of the band gap also decreases for the second band gap when there is fluid-solid coupling.
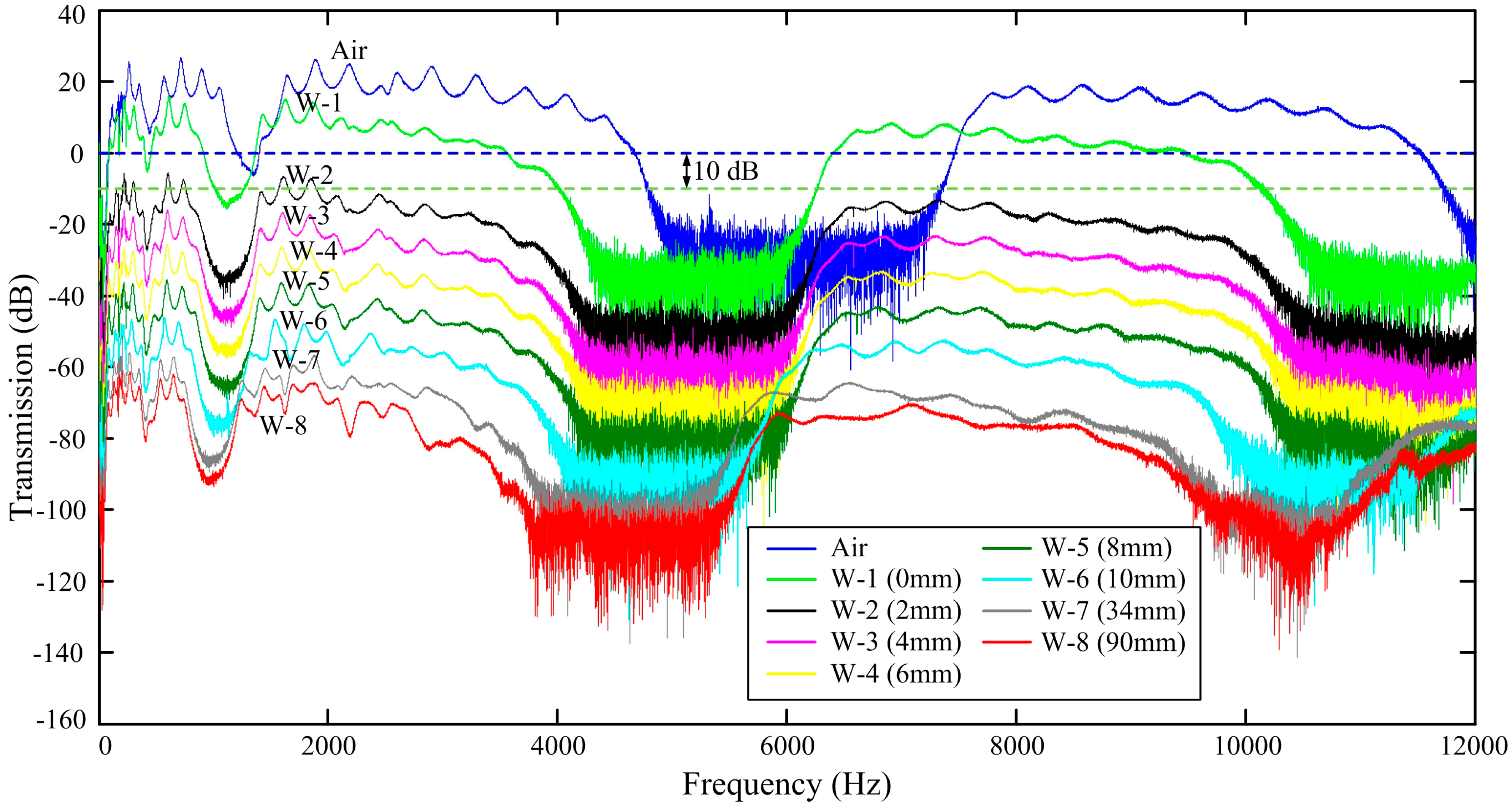
Next, to clearly demonstrate the influence of the coupling of the water on the displacement transmission and the band gaps, we detect the displacement transmissions of the PC beam with different immersed depths.
Figure 6 shows the experimental results performed in different operation conditions (i.e., in air, fully, or partially immersed in water). During the experiments, the water is first filled to the bottom surface of the PC beam, then the water depth is increased with an increment of 2 mm until the top surface of the PC beam is immersed with a layer of water. Then, the water is filled to the lower edge of the fiber grating and finally the water tank is full of water. We obtain the displacement transmission at these operation conditions. The experimental results performed in air and fully immersed in water have been plotted in
Figure 4 and we plot them again in
Figure 6 for the purpose of comparisons. There are nine displacement transmissions, in which W-1 is the result when the water just touches the bottom surface of the PC beam, W-2 to W-6 are the results of the PC beam immersed with different water depths, W-7 is the result when the lower edge of the grating section touches the water surface, and W-8 is the result when the water tank is full of water. Except for the results in air, each result shown in
Figure 6 is shifted 10 dB for clearer observation. The shift of 10 dB is illustrated in the case of W-1, in which the 0 dB lines (i.e., blue dashed line for the case in air and green dashed line for the case in W-1) are shifted 10 dB downward.
The band-gap widths, center frequencies, and percentage of shifts of the center frequencies for different operation conditions are listed in
Table 3. The water depths listed in
Table 3 are measured from the bottom surface of the PC beam. In addition, 0 mm in
Table 3 means the bottom surface of the PC beam is just wet. From
Figure 6 and
Table 3 we can see that, the resonant peaks and band gaps shift to lower frequencies as more surface area of the PC beam immersed in water. From
Table 3 we can also see that the percentage of shift of the center frequencies are very close but the absolute shifts of the center frequencies gets larger for higher-order band gaps. First, from the results of W-2, W-3, W-4, and W-5 (i.e., partially immersed in water with different water depths), we can see that the variations of the displacement properties are not much compared to those properties when the bottom surface of the PC beam just touches the water (i.e., W-1). However, significant shifts of the center frequencies can be found by comparing the dry PC beam and the case of W-1. When the PC beam is partially immersed in water, the submerged part of the PC beam has larger effective density due to the added mass than the density of the dry part of the PC beam [
23]. The increasing of the effective density decreases the pass bands and the band gaps. After the top surface of the PC beam touches the water (i.e., in the case of W-6 and the top surface of the PC beam is wet), larger shifts of the band gaps as well as resonant peaks can again be observed due to additional fluid-interaction of pressure field from the top surface of the PC beam.
From the results of W-7 (i.e., the water just reaches the lower edge of the grating) and W-8 (i.e., the water tank is full of water), we can again validate that the FBG displacement sensors are very suitable to detect dynamic responses of the submerged PCs. In fact, the reflected light spectrum of the FBG sensors almost remains unchanged for the FBG sensors immersed in water or not. Thus, the differences in W-7 and W-8 are not attributed to the coupling of the water to the light in fiber but to the added mass of the water on the PC beam for different water depths. Finally, as the water depth increases, the structural damping interacted with water gets stronger and the amplitudes of the resonant peaks at pass bands are decreased. In fact, some modes are merged during fluid-solid interaction [
33,
34].