Reliability and Failure Probability Analysis of Al-Mg-Si/Al2O3–SiC Composites Cast Under Different Mold Conditions Using Classical and Bayesian Weibull Models
Abstract
1. Introduction
2. Material and Method
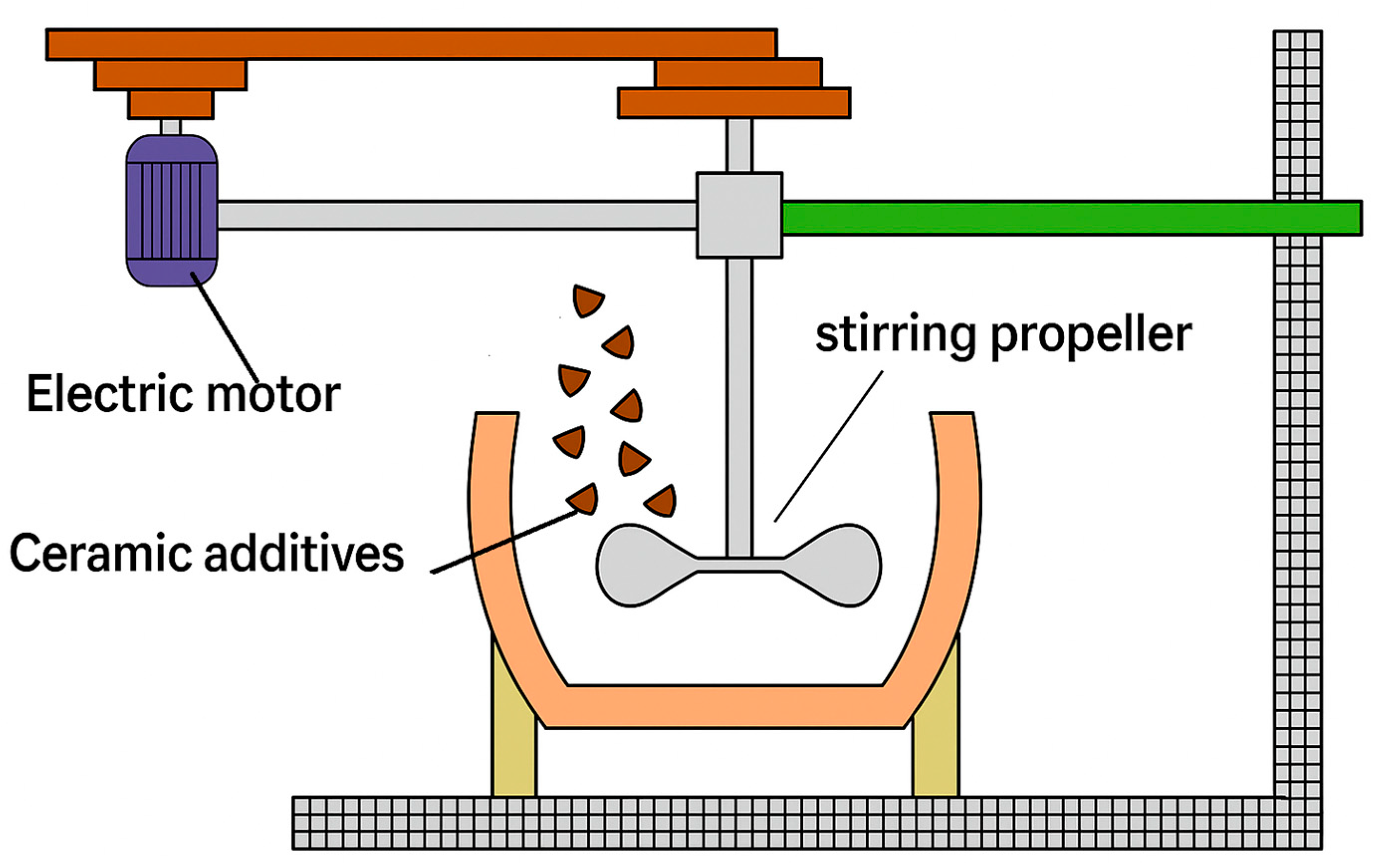
2.1. Stir Casting
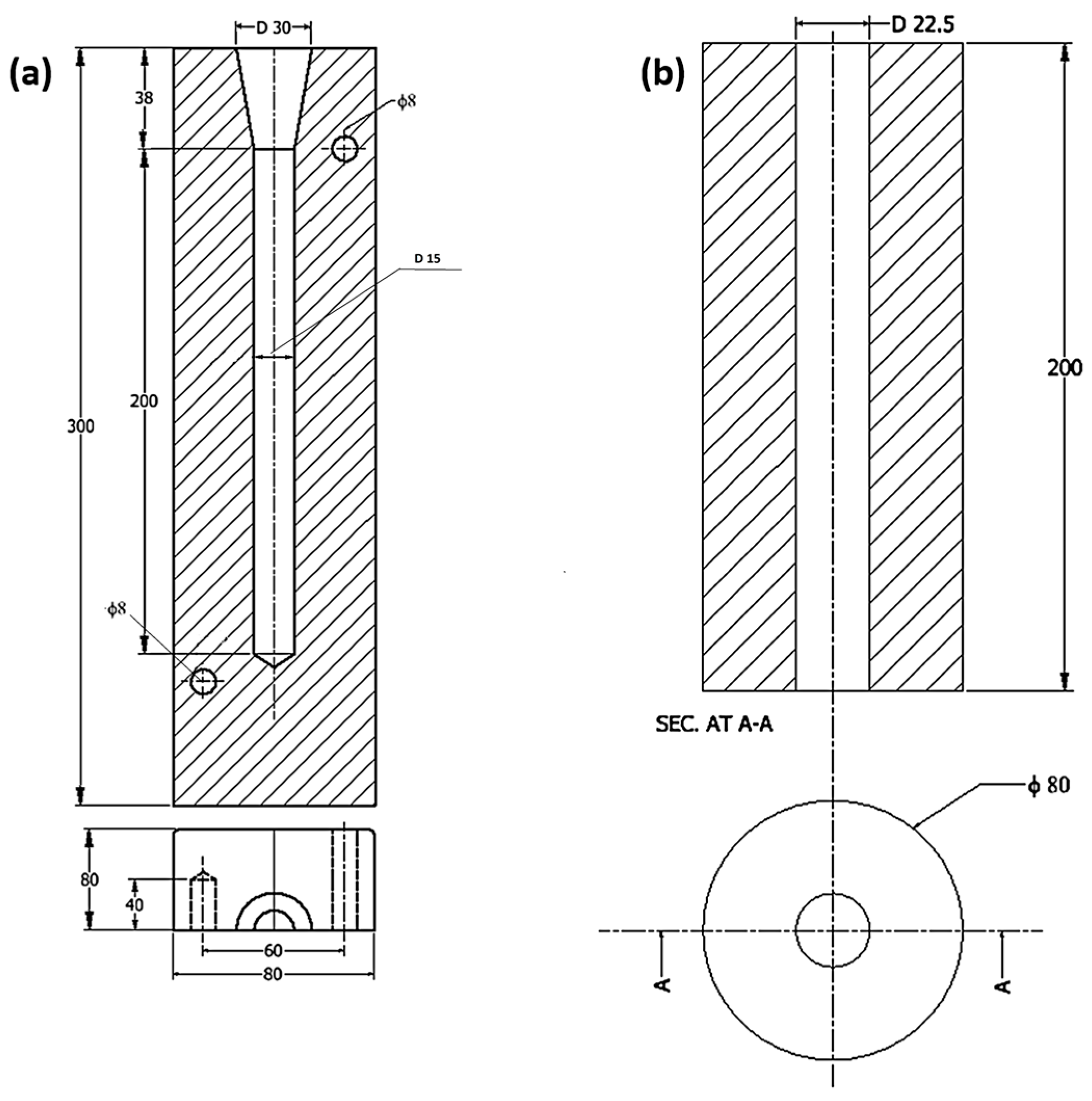
2.2. Compression Test
3. Statical Analysis
3.1. Weibull-Based Statistical and Reliability Study
3.2. Lifelines (Frequentist Weibull)
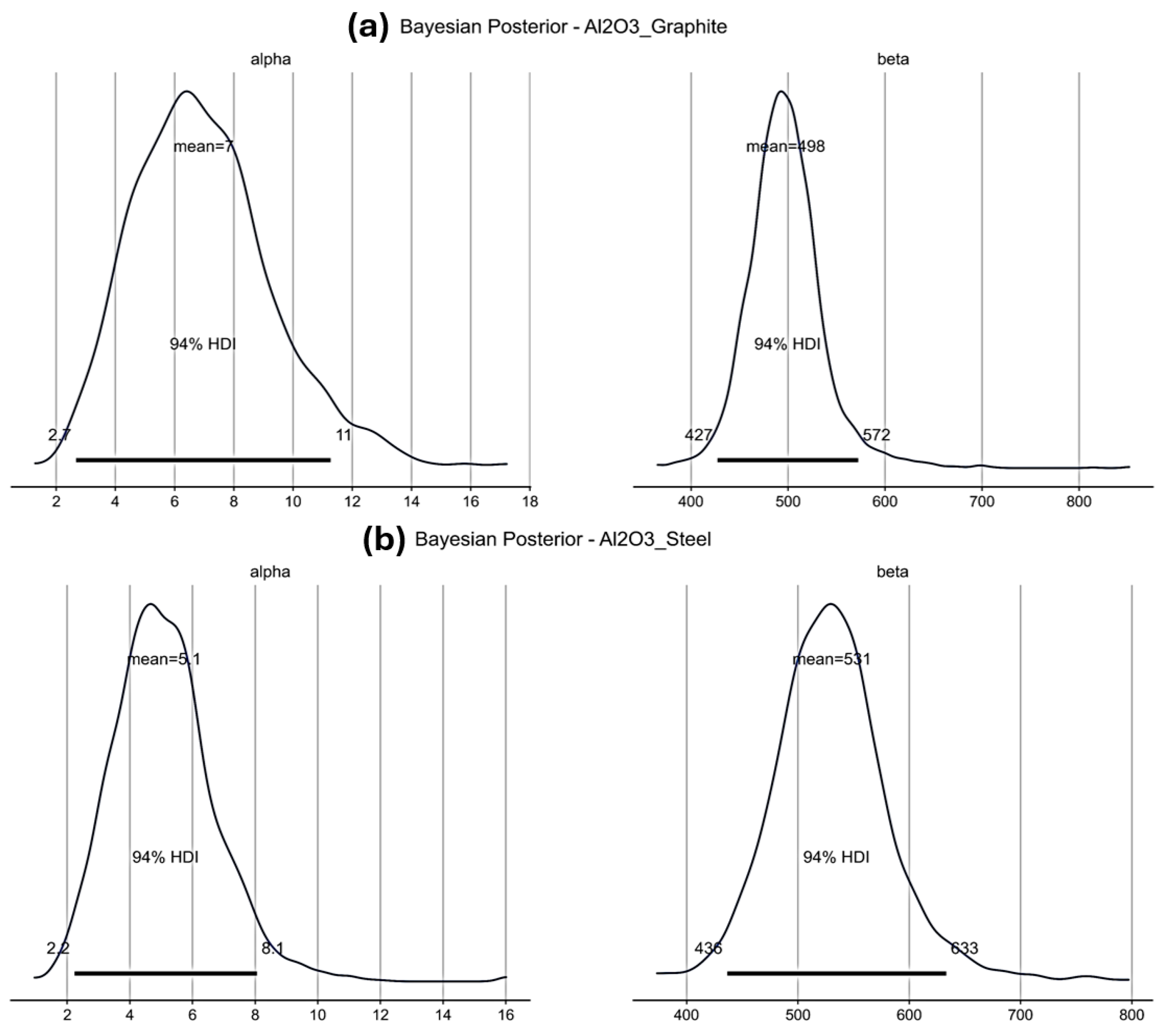
3.3. Bayesian Reliability Analysis (Bayesian Weibull)
4. Results and Discussion
4.1. Experimental Results
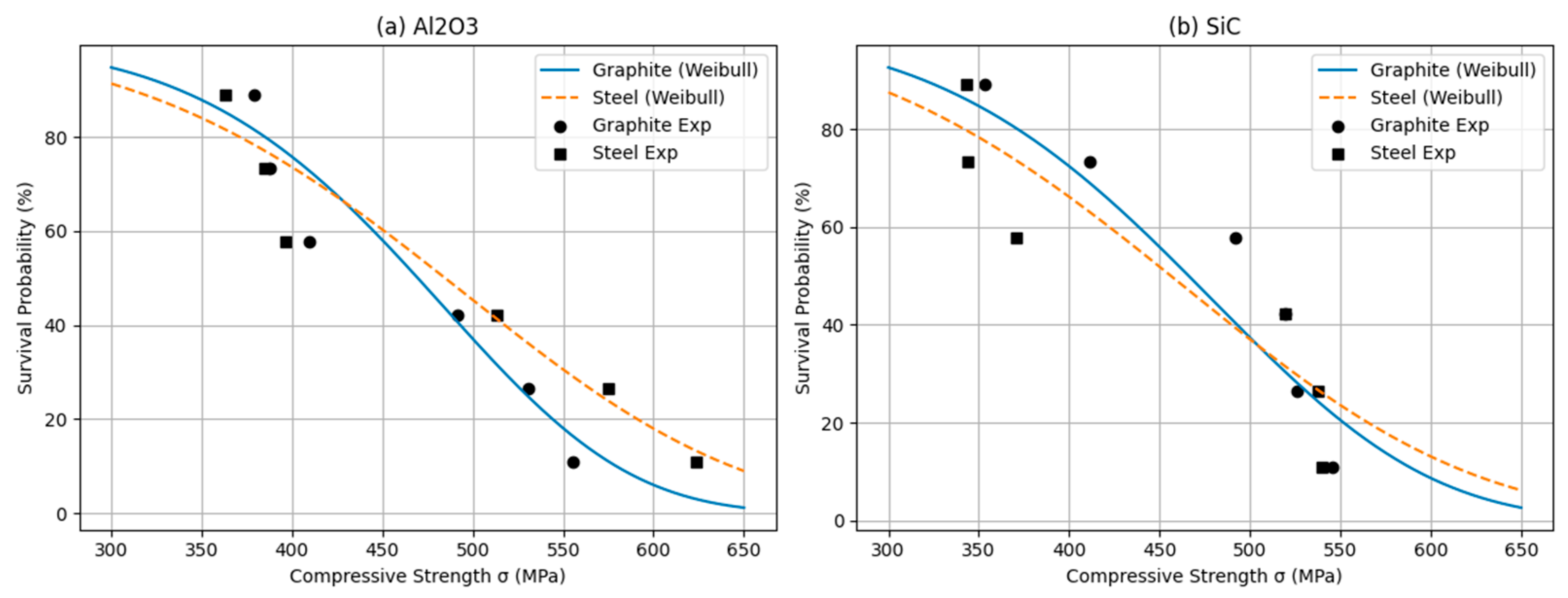
4.2. Weibull Distribution Analysis
4.3. Bayesian Model Analysis
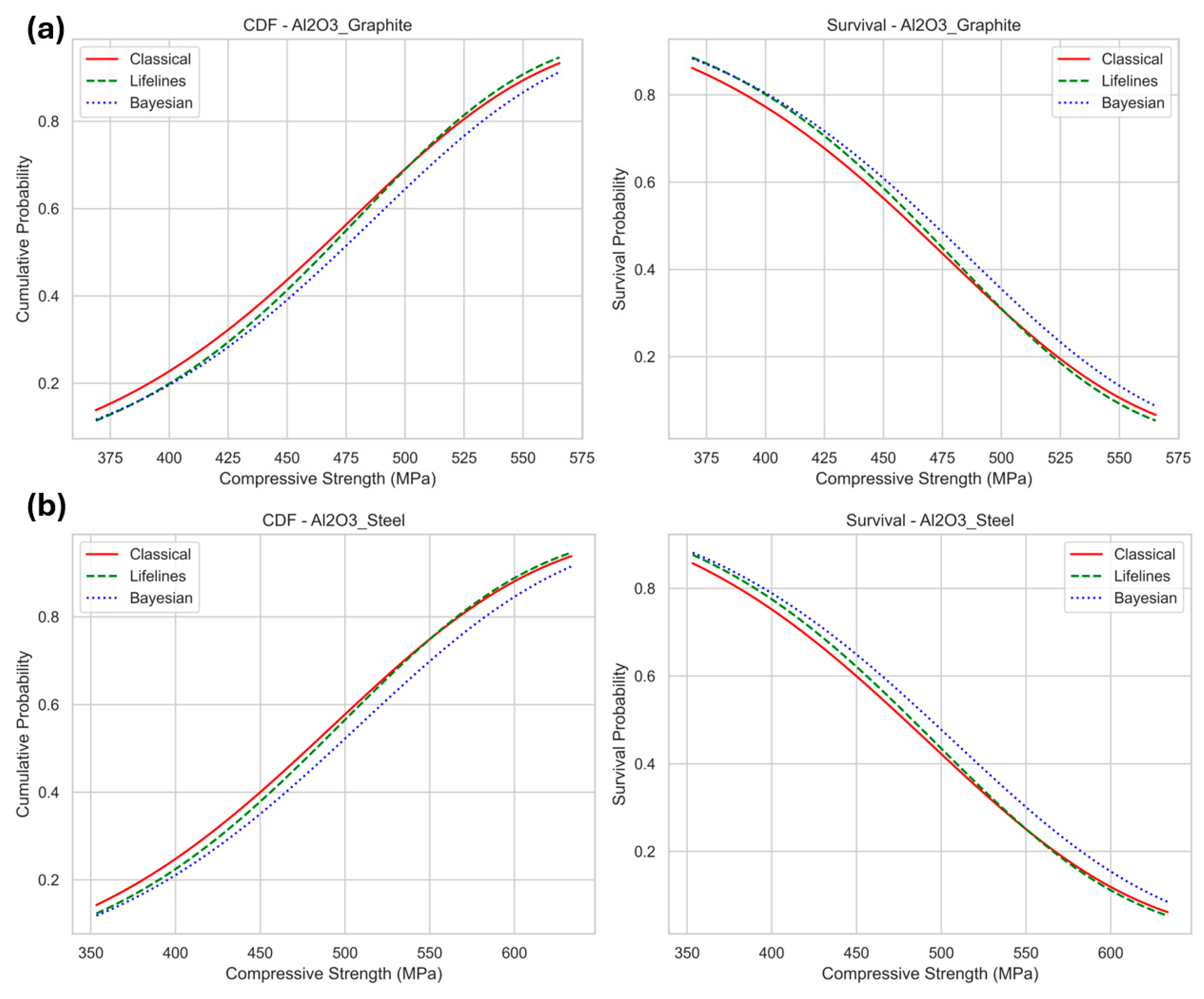
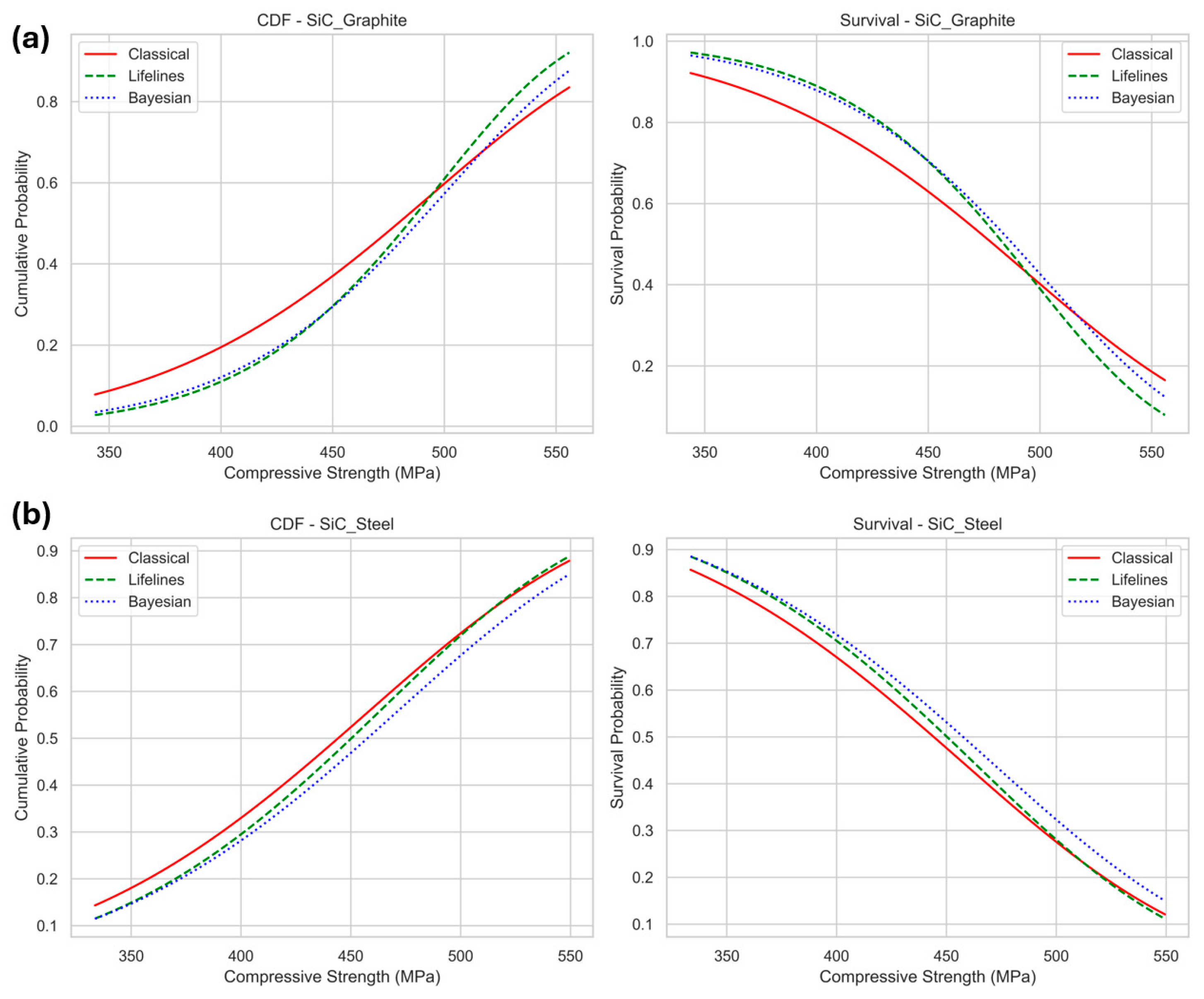
4.4. Comparison of Weibull Distribution Analysis (Classic) with Lifelines and Bayesian Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Biswal, S.R.; Sahoo, S. A Comparative Analysis on Physical and Mechanical Properties of Aluminum Composites with AlO and WS Reinforcement. In Recent Advances in Mechanical Engineering; Springer: Berlin/Heidelberg, Germany, 2023; pp. 597–603. [Google Scholar]
- Sujatha, S. Valuation of Strength Enhancement in Heat Treated SiC Nanoparticles Reinforced 2024 Aluminum Alloy Metal Matrix Composites Using FEA. Master’s Thesis, College of Engineering, JNT University, Hyderabad, India, 2024. [Google Scholar]
- Abdellah, M.Y.; Fadhl, B.M.; El-Ainin, H.M.A.; Hassan, M.K.; Backar, A.H.; Mohamed, A.F. Experimental Evaluation of Mechanical and Tribological Properties of Segregated Al-Mg-Si Alloy Filled with Alumina and Silicon Carbide through Different Types of Casting Molds. Metals 2023, 13, 316. [Google Scholar] [CrossRef]
- Lee, S.; Suh, D.; Kwon, D. Microstructure and fracture of SiC-particulate-reinforced cast A356 aluminum alloy composites. Metall. Mater. Trans. A 1996, 27, 3893–3901. [Google Scholar] [CrossRef]
- Chakrapani, P.; Suryakumari, T. Mechanical properties of aluminium metal matrix composites—A review. Mater. Today Proc. 2021, 45, 5960–5964. [Google Scholar] [CrossRef]
- Girimurugan, R.; Pugazhenthi, R.; Suresh, T.; Maheskumar, P.; Vairavel, M. Prediction of mechanical properties of hybrid aluminium composites. Mater. Today Proc. 2021, 39, 712–716. [Google Scholar] [CrossRef]
- Sugimura, Y.; Suresh, S. Effects of sic content on fatigue crack growth in aluminum alloys reinforced with SiC particles. Metall. Trans. A 1992, 23, 2231–2242. [Google Scholar] [CrossRef]
- Kumar, G.V.; Panigrahy, P.P.; Nithika, S.; Pramod, R.; Rao, C. Assessment of mechanical and tribological characteristics of Silicon Nitride reinforced aluminum metal matrix composites. Compos. Part B Eng. 2019, 175, 107138. [Google Scholar] [CrossRef]
- Tiryakioğlu, M. Weibull analysis of mechanical data for castings II: Weibull mixtures and their interpretation. Metall. Mater. Trans. A 2015, 46, 270–280. [Google Scholar] [CrossRef]
- Khashaba, U. Fatigue and reliability analysis of unidirectional GFRP composites under rotating bending loads. J. Compos. Mater. 2003, 37, 317–331. [Google Scholar] [CrossRef]
- Cohen, D. Application of reliability and fiber probabilistic strength distribution concepts to composite vessel burst strength design. J. Compos. Mater. 1992, 26, 1984–2014. [Google Scholar] [CrossRef]
- Yang, J.; Liu, B.; Shu, D.; Li, H.; Yang, Q.; Hu, T.; Wang, Z.; Zeng, Y.; Huang, J.; Tang, X. Effect of ultra vacuum assisted high pressure die casting on the mechanical properties of Al-Si-Mn-Mg alloy. J. Alloys Compd. 2025, 1026, 180531. [Google Scholar] [CrossRef]
- Skejić, D.; Dokšanović, T.; Čudina, I.; Mazzolani, F.M. The basis for reliability-based mechanical properties of structural aluminium alloys. Appl. Sci. 2021, 11, 4485. [Google Scholar] [CrossRef]
- Jung, J.; Yoon, J.I.; Park, H.K.; Kim, J.Y.; Kim, H.S. Bayesian approach in predicting mechanical properties of materials: Application to dual phase steels. Mater. Sci. Eng. A 2019, 743, 382–390. [Google Scholar] [CrossRef]
- Fernandez-Zelaia, P.; Joseph, V.R.; Kalidindi, S.R.; Melkote, S.N. Estimating mechanical properties from spherical indentation using Bayesian approaches. Mater. Des. 2018, 147, 92–105. [Google Scholar] [CrossRef]
- Sun, G.; Li, Z.; Jiao, Y.; Wang, Q. Application of Bayesian Statistics in Analyzing and Predicting Carburizing-Induced Dimensional Changes in Torsion Bars. Metals 2025, 15, 546. [Google Scholar] [CrossRef]
- Vafadar, F.; Collins, S.; Fink, G. Bayesian modeling of finger joints’ tensile and bending properties considering censored data. Eur. J. Wood Prod. 2025, 83, 110. [Google Scholar] [CrossRef]
- Yang, J.; Liu, B.; Shu, D.; Li, H.; Yang, Q.; Hu, T.; Wang, Z.; Zeng, Y.; Haung, J.; Tang, X. Effect of Casting Pressure on Porosity, Microstructure, and Mechanical Properties of Large Die Casting Aluminum Alloy Parts. Int. J. Met. 2025, 1–15. [Google Scholar] [CrossRef]
- Wang, S.; Tokgoz, A.; Huang, Y.; Zhang, Y.; Feng, J.; Sastry, P.; Sun, C.; Figg, N.; Lu, Q.; Sutcliffe, M.P.F. Bayesian inference-based estimation of normal aortic, aneurysmal and atherosclerotic tissue mechanical properties: From material testing, modeling and histology. IEEE Trans. Biomed. Eng. 2019, 66, 2269–2278. [Google Scholar] [CrossRef] [PubMed]
- Hashim, J. The production of cast metal matrix composite by a modified stir casting method. J. Teknol. (Sci. Eng.) 2001, 35, 9–20. [Google Scholar] [CrossRef]
- Aqida, S.N.; Ghazali, M.I.; Hashim, J. Effect of porosity on mechanical properties of metal matrix composite: An overview. J. Teknol. (Sci. Eng.) 2004, 40, 17–32. [Google Scholar] [CrossRef]
- Ravichandran, M.; Meignanamoorthy, M.; Chellasivam, G.P.; Vairamuthu, J.; Kumar, A.S.; Stalin, B. Effect of Stir Casting Parameters on Properties of Cast Metal Matrix Composite. Mater. Today Proc. 2020, 22, 2606–2613. [Google Scholar] [CrossRef]
- Morsiya, C.; Pandya, S. EffEct of stir caSting ProcESS ParamEtErS and StirrEr BladE gEometry on mEchanical ProPErtiES of al mmcS—A Review. Arch. Metall. Mater. 2023, 68, 1473–1495. [Google Scholar] [CrossRef]
- Gugulothu, B.; Nagarajan, N.; Pradeep, A.; Saravanan, G.; Vijayakumar, S.; Rao, J.; Vijayan, V. Analysis of Mechanical Properties for Al-MMC Fabricated through an Optimized Stir Casting Process. J. Nanomater. 2022, 2022, 2081189. [Google Scholar] [CrossRef]
- Baisane, V.; Sable, Y.; Dhobe, M.; Sonawane, P. Recent development and challenges in processing of ceramics reinforced Al matrix composite through stir casting process: A Review. Int. J. Eng. Appl. Sci. 2015, 2, 257814. [Google Scholar]
- Aqida, S.; Ghazali, M.; Hashim, J. The effects of stirring speed and reinforcement particles on porosity formation in cast MMC. J. Mech. 2003, 16, 22–30. [Google Scholar]
- Sajjadi, S.; Ezatpour, H.; Beygi, H. Microstructure and mechanical properties of Al–Al2O3 micro and nano composites fabricated by stir casting. Mater. Sci. Eng. A 2011, 528, 8765–8771. [Google Scholar] [CrossRef]
- Alam, M.T.; Ansari, A.H. X-ray diffraction analysis and microstructural examination of al-sic composite fabricated by stir casting. Int. J. Sci. Technol. Manag. 2015, 4, 941–956. [Google Scholar]
- Kaufman, J.G. Introduction to Aluminum Alloys and Tempers; ASM International: Almere, The Netherlands, 2000. [Google Scholar]
- Ei-Aini, H.A.; Mohamed, K.; Mohammed, Y.H. Effect of mold types and cooling rate on mechanical properties of Al alloy 6061 within ceramic additives. In Proceedings of the 2nd International Conference on Energy Engineering ICEE-2, Manama, Bahrain, 18–22 December 2010. [Google Scholar]
- Hassan, M.K.; Mohammed, Y.; Abu, E. Improvement of Al-6061 alloys mechanical properties by controlling processing parameters. Int. J. Mech. Mechatron. Eng. 2012, 12, 14–18. [Google Scholar]
- Kaczmar, J.; Pietrzak, K.; Włosiński, W. The production and application of metal matrix composite materials. J. Mater. Process. Technol. 2000, 106, 58–67. [Google Scholar] [CrossRef]
- Anyalebechi, P.N. Analysis of the effects of alloying elements on hydrogen solubility in liquid aluminum alloys. Scr. Metall. Et Mater. 1995, 33, 1209–1216. [Google Scholar] [CrossRef]
- ASTM, E. Standard Test Methods of Compression Testing of Metallic Materials at Room Temperature; ASTM International: West Conshohocken, PA, USA, 2000; pp. 98–105. [Google Scholar]
- Tanimoto, T.; Amijima, S.; Ishikawa, H. A reliability analysis approach to fatigue life dispersion of laminated glass fiber composite materials. Mech. Behav. Mater. 1980, 207–216. [Google Scholar]
- NN_Developer. Logic to Caluclate Shape and Scale Parameter in Survival Analysis. Available online: https://stats.stackexchange.com/questions/618645/logic-to-caluclate-shape-and-scale-parameter-in-survival-analysis (accessed on 13 June 2023).
- The PyMC Development Team. Weibull Distribution—PyMC v5.10.1 Documentation. 2024. Available online: https://www.pymc.io/projects/docs/en/v5.10.1/api/distributions/generated/pymc.Weibull.html (accessed on 1 August 2025).
- Data Camp. Probability Distributions in Python. Available online: https://projector-video-pdf-converter.datacamp.com/25923/chapter3.pdf (accessed on 28 July 2025).
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Liang, G.; Ali, Y.; You, G.; Zhang, M.-X. Effect of cooling rate on grain refinement of cast aluminium alloys. Materialia 2018, 3, 113–121. [Google Scholar] [CrossRef]
- Barbero, E.; Fernández-Sáez, J.; Navarro, C. Statistical analysis of the mechanical properties of composite materials. Compos. Part B Eng. 2000, 31, 375–381. [Google Scholar] [CrossRef]



| Wt.% Additives | σ (Al2O3) (MPa) | SDV (Al2O3) | %Error (Al2O3) | σ (SiC) (MPa) | SDV (SiC) | %Error (SiC) | % Height Reduction (Al2O3) | % Height Reduction (SiC) |
|---|---|---|---|---|---|---|---|---|
| 0 | 504.88 | 9.06 | 5.23 | 504.88 | 5.23 | 5.23 | 39 | 39 |
| 0.5 | 378.87 | 27.07 | 15.62 | 411.72 | 26.32 | 15.19 | 30.7 | 34.8 |
| 1 | 530.37 | 1.06 | 0.61 | 545.92 | 3.37 | 1.95 | 47.7 | 39 |
| 2 | 409.30 | 17.27 | 9.97 | 373.36 | 14.54 | 8.39 | 26.8 | 26.8 |
| 3 | 387.69 | 18.30 | 10.50 | 353.61 | 0.9 | 0.52 | 29 | 19.7 |
| 4 | 555.43 | 29.12 | 16.81 | 525.98 | 3.7 | 2.13 | 54.4 | 49.7 |
| 8 | 491.85 | 26.40 | 15.29 | 519.61 | 12.30 | 7.10 | 41.9 | 43.1 |
| Wt.% Additives | σ (Al2O3) (MPa) | SDV (Al2O3) | %Error (Al2O3) | σ (SiC) (MPa) | SDV (SiC) | %Error (SiC) | % Height Reduction (Al2O3) | % Height Reduction (SiC) |
|---|---|---|---|---|---|---|---|---|
| 0 | 513.30 | 30.07 | 17.36 | 513.31 | 30.07 | 17.36 | 52.6 | 52.6 |
| 0.5 | 396.85 | 32.64 | 18.82 | 370.57 | 22.31 | 12.88 | 34.3 | 38.1 |
| 1 | 513.29 | 5.91 | 3.42 | 519.12 | 25.73 | 14.86 | 46 | 48.6 |
| 2 | 384.73 | 1.81 | 1.04 | 343.66 | 9.18 | 5.30 | 42 | 30.5 |
| 3 | 363.29 | 13.56 | 7.80 | 343.50 | 2.58 | 1.49 | 38 | 25.8 |
| 4 | 574.77 | 19.08 | 11.02 | 539.46 | 16.93 | 9.77 | 50 | 59.8 |
| 8 | 623.53 | 24.99 | 14.42 | 537.65 | 3.59 | 2.07 | 41 | 34.4 |
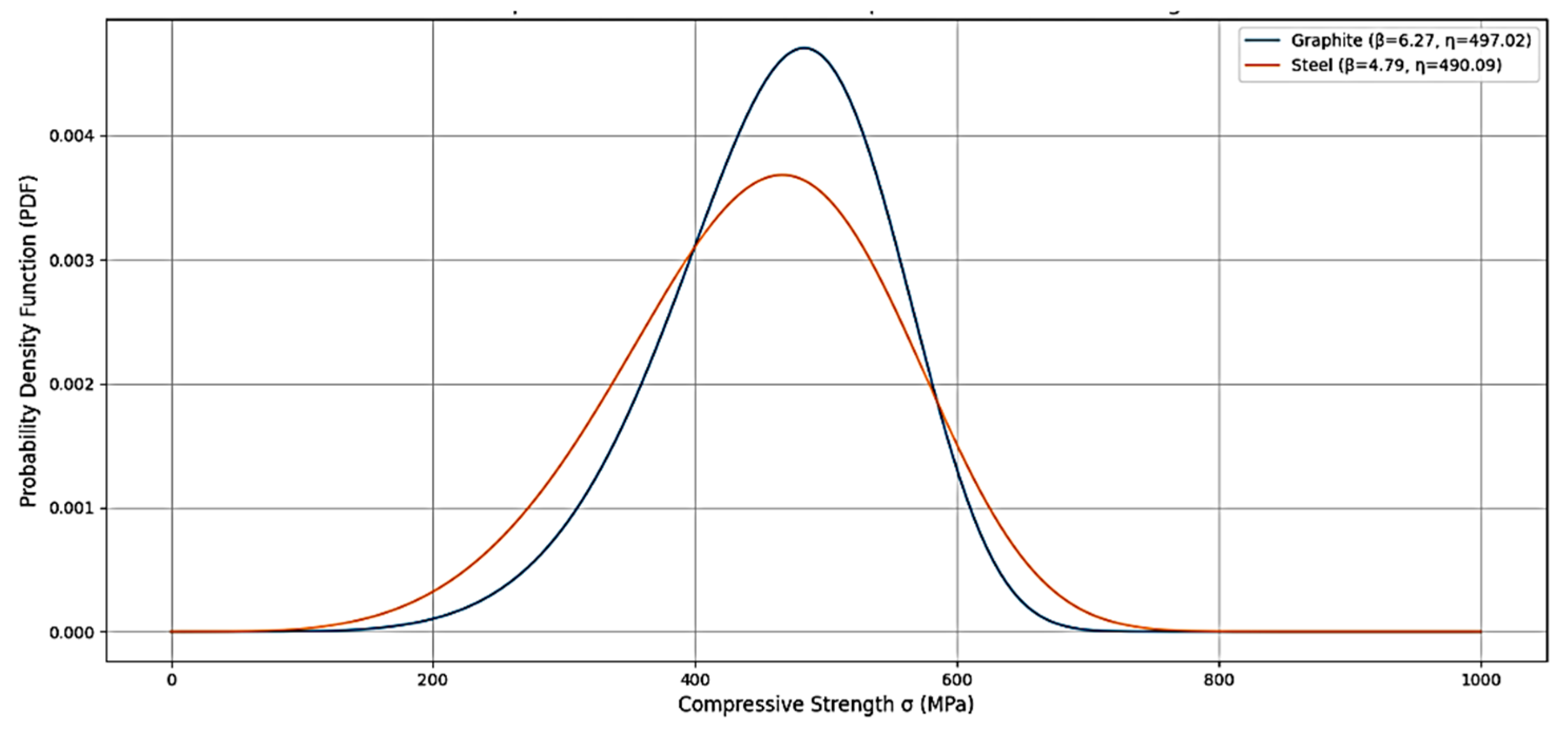
| Material | Mold Type | Shape β | Scale η (MPa) | R2 (Goodness of Fit) | Interpretation |
|---|---|---|---|---|---|
| Al2O3 | Graphite | 6.27 | 497.02 | 0.911 | Narrow failure distribution, more uniform strength, better reliability |
| SiC | Graphite | 5.49 | 497.34 | 0.911 | |
| Al2O3 | Steel | 4.66 | 523.19 | 0.912 | |
| SiC | Steel | 4.79 | 490.09 | 0.821 | Wider failure distribution → more scatter in strength, less consistent performance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdellah, M.Y.; Alabdullah, F.T.; Alshqaqeeq, F.; Hassan, M.K. Reliability and Failure Probability Analysis of Al-Mg-Si/Al2O3–SiC Composites Cast Under Different Mold Conditions Using Classical and Bayesian Weibull Models. Crystals 2025, 15, 791. https://doi.org/10.3390/cryst15090791
Abdellah MY, Alabdullah FT, Alshqaqeeq F, Hassan MK. Reliability and Failure Probability Analysis of Al-Mg-Si/Al2O3–SiC Composites Cast Under Different Mold Conditions Using Classical and Bayesian Weibull Models. Crystals. 2025; 15(9):791. https://doi.org/10.3390/cryst15090791
Chicago/Turabian StyleAbdellah, Mohammed Y., Fadhel T. Alabdullah, Fadhel Alshqaqeeq, and Mohamed K. Hassan. 2025. "Reliability and Failure Probability Analysis of Al-Mg-Si/Al2O3–SiC Composites Cast Under Different Mold Conditions Using Classical and Bayesian Weibull Models" Crystals 15, no. 9: 791. https://doi.org/10.3390/cryst15090791
APA StyleAbdellah, M. Y., Alabdullah, F. T., Alshqaqeeq, F., & Hassan, M. K. (2025). Reliability and Failure Probability Analysis of Al-Mg-Si/Al2O3–SiC Composites Cast Under Different Mold Conditions Using Classical and Bayesian Weibull Models. Crystals, 15(9), 791. https://doi.org/10.3390/cryst15090791






