Abstract
Ascorbic Acid (AA), an important biomolecule present in relatively high concentrations in blood and other biological fluids, has been rarely investigated with reference to its effect on the biological mineralization–demineralization processes. To our knowledge, the present work is one of an extremely limited few found in the literature in which the effect of the presence of AA in mineralizing or demineralizing electrolyte solutions is addressed in a quantitative way. We have used the constant saturation method for the accurate measurement of the rates of crystal growth of hydroxyapatite (HAP, Ca5(PO4)3OH), the model compound of the inorganic component of the hard tissues of higher mammals. It was found that both crystal growth and dissolution were accelerated significantly. The increase in crystal growth rates showed stronger dependence on the solution supersaturation (120% increase for the highest and 460% for the lowest) in the presence of 0.1 mM of AA, pH 7.40, 37 °C, 0.15 M NaCl. The dissolution rate increase was less dependent (average of ca. 300% increase). It was concluded from the detailed characterization of the solid that the acceleration effect was due to the uptake of AA on the HAP surface.
1. Introduction
The most thermodynamically stable calcium phosphate crystal phase, hydroxyapatite [Ca5(PO4)3OH, HAP], is the model compound of the phosphate biominerals of the hard tissues of higher mammals. HAP is commonly encountered not only in osteogenesis but also in pathological biomineralization, including heart valves calcification [1,2,3], coronary calcification [4,5], intraocular lenses (IOL), especially hydrophilic [6,7,8,9,10], and in numerous other occasions [11]. In all cases, the mineralizing tissues are in contact with body fluids, which are highly supersaturated with respect to more than one calcium phosphate crystalline phase [12]. The mineralization/demineralization processes take place in the presence of a variety of molecules, both of high and low molecular weight, which influence both the kinetics of the respective processes but also the crystal characteristics (morphology, surface charge, bonding, etc.) [13,14,15,16,17].
Biomaterials based on HAP and other calcium phosphate mineral phases have been broadly used because of their chemical and structural similarity with the mineral component of the hard tissues of higher mammals [18,19]. Hard tissues and/or implanted biomaterials are in contact with biological fluids, the composition of which is quite complex due to the presence of a large variety of substances, from inorganic metal ions and anionic species to smaller and larger molecular weight organic molecules. The investigation of mineralization and/or demineralization processes in complex media like simulated body fluids, although useful, do not allow for the full understanding of the role of specific compounds or molecules on the ubiquitous processes of mineralization/demineralization [20].
Among the significant components of human plasma is ascorbic acid (AA); the normal concentration levels are in the range of 8.8–17.6 mg/L (50–100 μM) [21,22], while in the aqueous humor it reaches levels of the order of 1–2 mM [23]. As such, AA has attracted research interest because it is a strong antioxidant. However, studies concerned with the role of the presence of AA in the biological mineralization and demineralization processes are scarce in the literature. Investigations on the crystal growth and/or dissolution of biominerals, mainly calcium phosphates, are missing to our knowledge from the related literature. It has been reported that variations in L-ascorbate (vitamin C) concentrations can have a marked effect on mineralization in vitro [24]. Supplementation of diet with AA has been reported to beneficially interfere with the process of arterial wall calcification [25]. On the other hand, there are reports from experiments in animals that AA in combination with inorganic orthophosphate increases Ca deposition [26]. Increased AA concentrations have been associated with higher risk for stone formation [27]. Concerning, therefore, the formation of biominerals, in particular calcium phosphates, reports are contradictory concerning the effect of the presence of AA in the calcification process. Concerning the opposite process, i.e., demineralization, which consists of the process of dissolution of calcium phosphates and/or other biominerals, prolonged contact of the mineral deposits with AA and other chemical compounds forming strong chelates with calcium favored their dissolution [28,29].
From the limited reports so far, it may be concluded that AA plays an important role at the solid/electrolyte interfaces, and it is for this reason that it has been used for the preparation of nanocomposites with HAP, which are stabilized by hydrogen bonding between the carbonyl group of ascorbic acid and HAP [30]. The incorporation of AA in HAP-based scaffolds and the bioactivity of the respective biomaterials were improved since they accelerated osteoblast proliferation and, at the same time, they eliminated the activity of free radicals released during inflammation [31].
The purpose of the present investigation was to clarify the role of AA in the mineralization of the most thermodynamically stable calcium phosphate, HAP, considered to be the main inorganic component of the hard tissues of mammals, in the presence of various levels of concentrations of AA. The crystal growth of HAP in the absence and in the presence of AA was investigated from measurements of the kinetics of crystallization of HAP from supersaturated solutions, mimicking the composition of body fluids. Using the constant composition approach [32], the measurements of the rates of crystal growth allowed for the more accurate investigation of the interaction of AA with HAP. Moreover, the opposite process, the dissolution of HAP from undersaturated solutions with respect to HAP, again at constant driving force, was investigated both in the absence and in the presence of AA. It is interesting to note that despite the importance both of AA and HAP, the information available concerning quantitative data and measurements of mineralization/demineralization processes is limited. Measurements of the electrokinetic charge of HAP particles in the absence and in the presence of AA provided useful insight on the interaction of AA with HAP surface. These studies are important for the development of novel biomaterials based on calcium phosphates and also for the possible decalcification of materials wherever possible. The present work is, to our knowledge, the first time that a systematic study of HAP crystal growth and dissolution kinetics in the presence of AA is reported in the literature.
2. Materials and Methods
2.1. Solutions
All solutions were prepared using doubly distilled RO-treated water (TDW) (specific conductivity 0.5 × 10−6 μS·cm−1). Stock calcium chloride and sodium dihydrogen phosphate solutions were prepared from crystalline calcium chloride dihydrate (CaCl2·2H2O) and sodium dihydrogen phosphate (NaH2PO4) (Merck, Puriss., Darmstadt, Germany), respectively. Calcium chloride solutions were standardized with standard Ethylene Diamino Tetraacetic Acid (EDTA) solutions, prepared from the crystalline disodium salt (Na2EDTA, Merck), using murexide indicator and by atomic absorption spectrometry (air-acetylene flame, Perkin Elmer AAnalyst 300, Norwalk, CT, USA). The orthophosphate stock solutions were standardized with potentiometric titrations with standard sodium hydroxide solutions (Merck, Titrisol, Darmstadt, Germany) and by spectrophotometric analysis using the vanadomolybdate method spectrophotometrically (Perkin Elmer lambda 35, Norwalk, CT, USA) [13]. Sodium chloride stock solutions were prepared from the crystalline solid dried overnight at 105 °C, without any further purification. The standard sodium hydroxide solutions used for pH adjustment were checked regularly with potentiometric titrations of carefully weighted quantities of potassium hydrogen phthalate previously dried overnight at 105 °C. Standard hydrochloric acid (HCl) solutions were prepared from concentrated standards (Merck, Titrisol, Darmstadt, Germany) and the solutions were re-checked by potentiometric titrations with standard sodium hydroxide solutions.
2.2. Preparation of HAP Seed Crystals
For the crystal growth experiments, HAP seed crystals were prepared by precipitation as follows: Equal volumes of CaCl2 (0.5 M) and KH2PO4 (0.3 M) solutions were equilibrated at 70 °C. Next, the pH of the phosphate solution was adjusted to 10.0 and it was transferred to a water jacketed reactor, thermostatted at 70 °C by circulating water, and was stirred by a motorized stirrer. The calcium chloride solution was added dropwise at a constant rate of ca. 2.5 mL/min. The addition was completed past 2 h. During the calcium solution addition, the solution pH was measured withdrawing aliquots and adjusted by the addition of potassium hydroxide solution to ca. pH 10. The solution pH adjustments lasted until the end of calcium solution additions. The suspension was allowed to age in the mother liquor for 5 days more at 40 °C. Next, the suspension was filtered from 0.22 μm membrane filters, washed with TDW and dried at 60 °C for 48 h. After drying, the solid HAP powder was stored in a desiccator at room temperature. The solid was characterized by X-ray powder diffraction (Siemens D-5000, Gu Kα Radiation) and yielded the characteristic reflections of stoichiometric HAP (ICCD Card 9-432). The specific surface area of the solid was measured by nitrogen adsorption applying the BET isotherm (multiple point) (Micromeritics, Gemini, Model 2371) and was found to be equal to 71 m2/g. Thermogravimetric analysis of dried solid samples weight ca. 10 mg was performed in a nitrogen atmosphere, flowrate 40 mL·min−1, at a heating rate of 10 °C·min−1 (TA Q50 Thermogravimetric analyzer).
2.3. Crystallization of HAP from Supersaturated Solutions
2.3.1. Crystal Growth at Constant Solution Supersaturation
Calcium phosphate solutions, supersaturated with respect to HAP in a double walled pyrex® glass reactor using calcium chloride, and sodium dihydrogen phosphate solutions, prepared fresh for each experiment from respective stock solutions, as detailed elsewhere [9]. The temperature of the supersaturated solutions was maintained at 37.0 ± 0.1 °C by circulating water from a thermostat and the initial solution pH was 7.40. Continuous bubbling through the solutions of pure nitrogen (99.999%, Linde Hellas) pre-saturated with water vapor ensured inert atmosphere to preclude atmospheric carbonate intrusion. The ionic strength of the supersaturated solutions was adjusted to 0.15 M with NaCl from the respective stock solutions. The final concentrations of total calcium, Cat, and total phosphorus, Pt, were at levels corresponding to a driving force for the crystal growth of HAP in the same range as the range corresponding to healthy humans [32,33]. In the experiments performed in the presence of AA, the study concentration in each experiment was attained by the addition of the appropriate volume of AA stock solution prepared from crystalline AA (L(+) Ascorbic Acid, Merck, pro analysi). Following the verification of the stability of the supersaturated solutions, as shown by the stability of the adjusted pH value for at least two hours, accurately weighted quantity of the prepared HAP seed crystals equivalent to ca. 0.35 m2 total surface area was introduced in the supersaturated solutions. The pH of the solutions was monitored. The electrode signal, through the controller unit, was transferred to a computer via a data acquisition system. The addition of a motorized stage system allowed the activation of two mechanically coupled, calibrated borosilicate precision glass syringes for the correction of the solution pH, which became acid due to proton release in the solution concomitant with HAP precipitation, as shown in the general Equation (1), which accounts for solutions with pH between 4 and 9, a range pertinent to most practical applications [34,35]:
drop in the solution pH of the order of the sensitivity limit of measurement of the GCE, i.e., ca. 0.005 pH units, triggered the addition of equal volumes from the two syringes. The two syringes contained solutions, the composition of which was calculated on the basis of the stoichiometry of the precipitating solid, i.e., Ca:P:OH = 5:3:1. Specifically, the composition of the titrant solutions was as follows:
5Ca2+(aq) + xHPO42−(aq) + yH2PO4−(aq)→Ca5(PO4)3OH(s) + zH+(aq)
Syringe 1: Calcium chloride solution and sodium chloride, (2 × CCa,s + m) + (2 × CNaCl,s − 2m) where subscript s denotes the corresponding concentration in the supersaturated solutions (CCa,s and CNaCl,s are the total calcium and total sodium chloride concentrations in the supersaturated solutions) and m is an arbitrary constant determined by preliminary experiments.
Syringe 2: Sodium dihydrogen phosphate, sodium hydroxide, (2 × CNaH2PO4,s + n) + (2 × CNaOH,s + 2m − n), where n is a constant such that . CNaH2PO4,s and CNaOH,s are the total concentrations of NaH2PO4 and NaOH in the supersaturated solutions.
The composition of the titrant solutions 1 and 2 was selected appropriately to maintain the activities of the ion species in the supersaturated solutions throughout the precipitation of HAP. In all experiments, according to series of preliminary experiments, best results were obtained for m = 10 × CCa,s. Titrant solutions reagents replaced ions consumed for the formation of the precipitating solid phase. The rate of titrants addition (mL/s) is directly related to the number of HAP of moles precipitated per unit time. It should be noted that all experiments were performed in stable supersaturated solutions, to ensure that the only process taking place is the growth of the seed crystals introduced. As a consequence, the rates of addition of the titrant solutions were normalized per unit surface area of the seed crystals which initiated the crystal growth process. More details on the experimental setup, in which the methodology of crystal growth at constant supersaturation method was implemented, are provided elsewhere [9]. Another significant advantage of the methodology is the possibility provided to observe morphological or any phase changes taking place on the precipitated solid as a function of the extent of crystallization taking place. Most published work is concerned with precipitates over narrow de-supersaturation breadth of the mineralizing solutions.
In the presence of AA, twice the concentration present in the supersaturated solutions was added in the syringe containing the phosphate and NaOH solutions, to avoid dilution caused by the addition of titrant solutions. Preliminary adsorption studies showed that equilibration of HAP seed crystals with AA, at conditions similar to those corresponding to the crystal growth experiments, did not show any appreciable concentration changes. Without precluding adsorption, if any, it was minimal and did not cause significant changes in the solution speciation.
2.3.2. Dissolution of HAP Crystals at Constant Solution Undersaturation
Calcium phosphate solutions undersaturated with respect to HAP were prepared by mixing equal volumes of calcium chloride and sodium dihydrogen phosphate solutions, prepared and standardized as described in Section 2.3.1, in the thermostatted double-walled, glass reactor at 37.0 ± 0.5 °C by circulating water. The solution pH was adjusted at 7.40 and the ionic strength to 0.15 M by NaCl as in Section 2.3.1. The dissolution of HAP crystals was initiated immediately upon introduction of accurately weighted HAP seed crystals so that the total available surface area was ca. 0.35 m2. The dissolution of HAP was accompanied by an increase in the solution pH, according to Equation (2) (valid to a good approximation over the concentration pH range 4–9):
Ca5(PO4)3OH(s)+ H2O → 5Ca2+(aq) + xHPO42−(aq) + yH2PO4−(aq)+ zOH−(aq)
The composition of the undersaturated solutions was maintained by the addition of titrant solutions, the composition of which was calculated so that the calcium, phosphate, and OH coming from the dissolving solid were appropriately diluted, while pH, the master variable, was maintained. The composition of the titrant solutions in each of the two mechanically coupled syringes was as follows:
Solutions in Syringe 1 (CaCl2 and NaCl solutions):
where CCa,t and CNaCl are the concentrations of total calcium and total sodium chloride in the reactor making up the undersaturated solution. CNaOH was the NaOH concentration in the undersaturated solution, needed to adjust the pH to 7.40. The coefficient 3/5 refers to the molar stoichiometry of Calcium/Phosphate = 5:3, coming from the dissolution of HAP, assuming that it dissolves congruently over a broad pH range and ionic strength values [36]. md is an arbitrary constant determined by preliminary experiments.
CCaCl2 = 2 × CCa,t − md and CNaCl = 2 × CNaCl + 2CNaOH + 3/5 × CCa,t
Solutions in Syringe 2 (NaH2PO4 and HCl):
in Equation (4), CNaH2PO4, t is the total phosphate concentration and md, an arbitrary constant, determined for preliminary experiments equal to 1.7 × CCa,t.
CNaH2PO4 = 2 × CNaH2PO4, t − 3/5 × md, CHCl = 2 × CHCl +7/5 × md − 2 × CNaOH
The rates of dissolution, Rd, were calculated from the slope of the titrants added as a function of time, dV/dt, by Equation (5) [9]:
calcium and phosphorus concentrations during the course of dissolution remained constant to within 2%.
2.3.3. Adsorption Measurements
To investigate deeper the interaction between AA and HAP, adsorption experiments were performed, using different AA concentrations in suspensions of HAP seed crystals in electrolyte solutions (0.15 M NaCl) saturated with respect to HAP. The surface concentration of the adsorbed AA, Γ, was calculated from Equation (6):
where C0, Ceq are the initial and equilibrium AA concentrations, respectively, V the volume of suspension, m the mass of the suspended HAP crystals and S their specific surface area.
2.3.4. X-Ray Photoelectron Spectroscopy
The surface analysis studies were performed in a UHV chamber (P < 10−9 mbar) equipped with a SPECS LHS-10 (EA10) hemispherical electron analyzer. The XPS measurements were carried out at room temperature using un-monochromatized AlKa radiation under conditions optimized for maximum signal (constant ΔΕ mode with pass energy of 36 eV giving a full width at half maximum (FWHM) of 0.9 eV for the Au 4f7/2 peak). The analyzed area was an ellipsoid with dimensions 2.5 × 4.5 mm2. The XPS core level spectra were analyzed using a fitting routine, which allows the decomposition of each spectrum into individual mixed Gaussian–Lorentzian components after a Shirley background subtraction. The samples were in powder form and pressed into pellets. Wide Scans were recorded for all samples, while the core level peaks that were recorded were C1s, Ca2p, O2s, and P2p. The wide scans were recorded with pass energy of 97 eV. Errors in quantitative data are found in the range of ∼10% (peak areas), while the accuracy for BEs assignments is ∼0.1 eV. The binding energy reference for the electrostatic charging due to X-ray irradiation was the C1 s at 284.8 eV from the superficial carbon contamination. The surface charging in all samples was ∼1 eV.
2.3.5. Zeta Potential Measurements
The zeta potential of the HAP particles in their suspensions was calculated from measurements of their electrophoretic mobility, in a Nanosize S analyzer (Malvern). Suspensions of HAP particles were prepared in 10 mM NaCl electrolyte solution with density ca. 0.02% w/w. The suspensions to be measured were equilibrated at 37 °C, under stirring for a period of one week in the absence and in the presence of AA, concentrations in the range between 0 and 10 mM (0, 1 × 10−6, 1 × 10−3, 5 × 10−3 and 10 × 10−3). The pH of the suspensions was adjusted to 7.40 by the addition of standard NaOH solution and remained constant up to before the measurements.
3. Results
3.1. Crystal Growth of HAP
Kinetics Measurements
The rates of crystal growth of HAP seeds used to inoculate the supersaturated solutions, both in the absence and in the presence of AA, were found to vary linearly as a function of the relative solution supersaturation. It should be noted that the volume of titrant–time plots from which the rates of crystal growth were calculated were linear over the extent of crystal growth recorded, which corresponded to extents of growth exceeding 200% of the inoculating HAP seeds. The experimental conditions and the results obtained are summarized in Table 1.

Table 1.
Crystal growth experiments of HAP in supersaturated calcium phosphate solutions, in the absence and in the presence of AA at constant supersaturation; pH 7.40, 37 °C, 0.15 M NaCl. Total calcium, Cat/Total Phosphate, Pt = 1.667.
The plot of the measured rates, RCG, as a function of the relative supersaturation with respect to HAP is shown in Figure 1. The results were fitted in a linear equation in the form of Equation (7) for the range of supersaturations investigated in the present work:
in Equation (7) kCG and n′ are the apparent rate constant and the apparent order of the crystal growth of HAP, respectively. The apparent order is indicative of the underlying mechanism. For n′ ≥ 1, the mechanism is surface diffusion-controlled [9,37]. The apparent rate constant for HAP growth on HAP seeds was found equal to (1.3 ± 0.1) × 10−7 mol·min−1·m−2, while in the presence of AA kCG = (9.3 ± 0.9) × 10−7 mol·min−1·m−2. As shown by the measurements summarized in Table 1, the increase in the rates of crystal growth depended on the supersaturation with respect to HAP. At the lowest supersaturation the rate increased by 460% while for the highest supersaturation the increase was just 20%.
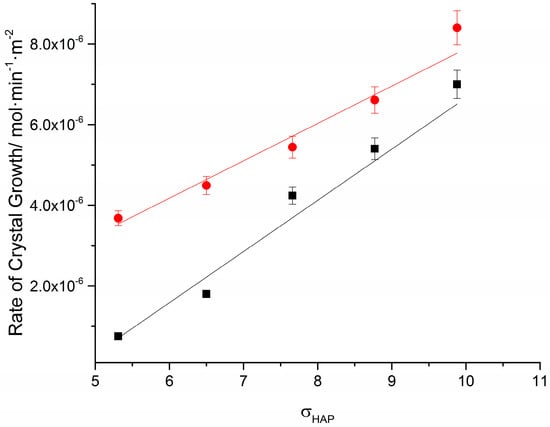
Figure 1.
Crystal growth rates of HAP on HAP seed crystals as a function of the relative supersaturation of the solutions with respect to HAP; 37 °C, pH 7.40, 150 mM NaCl; (■): in the absence of ascorbic acid; (●): in the presence of 0.1 mM ascorbic acid; the error bars are 5% of the values (mean of at least three repetitions) plotted.
It is interesting to note that the morphology of the HAP seed crystals was prismatic with sizes in the range 30–150 nm, while at the end of crystal growth when extensive crystal growth took place (>200%) HAP consisted mostly of platelets, as may be seen in Figure 2. Similar morphology has been reported for HAP both in biological systems [38,39] but also at high pH and large extents of crystallization [40].

Figure 2.
Morphology of HAP crystals shown in scanning electron microscope (SEM) pictures. (a) prismatic HAP seed crystals prepared for this work; bar 300 nm (b) plate-like HAP crystals grown on prismatic HAP seed crystals at constant supersaturation; σHAP = 9.88, pH 7.40, 0.15 M NaCl; Bar 300 nm.
In Figure 3 the morphology of the crystals grown on HAP seed crystals in the presence of 0.1 mM AA is presented. As may be seen there is no change in the grown crystals’ morphology because of the presence of AA (Figure 3a,b). It should be noted however that the growth of crystals with the prismatic habit proceeded as well, despite the fact that the growth was extensive, exceeding 200% of the mass of the inoculating seed crystals. In the absence of AA, hardly any prismatic crystals were detected in the sampled crystals.
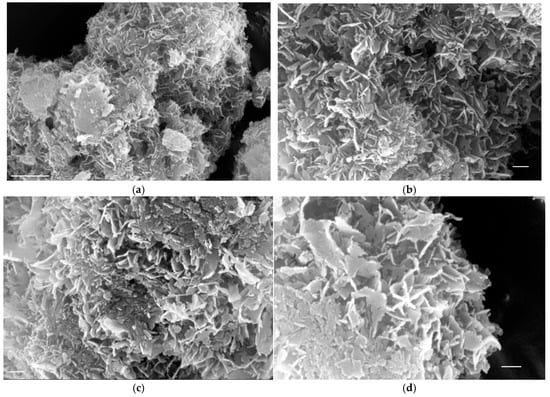
Figure 3.
SEM pictures showing HAP crystals grown in the presence of 0.1 mM AA, 37 °C, 0.15 M NaCl; (a) bar 1 μm; (b) bar 200 nm; (c) bar 200 nm; (d) bar 200 nm.
However, as may be seen in Figure 3c,d, in the core of plate-like crystallites there are prismatic HAP crystallites of the original seed crystals. This observation precluded the possibility of morphology change in the inoculating seeds. The change in morphology from prisms to nanoplates is characteristic of the overgrown HAP on the seed crystals and is most probably not related to the presence of AA in the supersaturated solutions.
The effect of the presence of AA in the supersaturated solutions at concentrations below one order of magnitude in comparison with the respective calcium concentrations in the supersaturated solutions, as shown by the significant increase in the apparent constant for crystal growth, suggested the interaction of AA with HAP crystal surface. Measurements of the adsorption of AA on HAP suspensions revealed limited but significant adsorption, as may be seen in Figure 4.
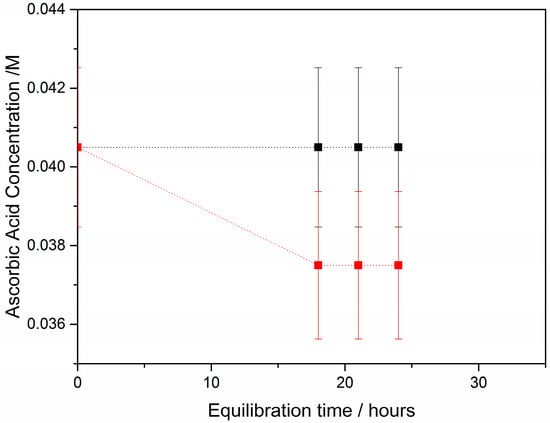
Figure 4.
Adsorption kinetics of AA on HAP crystals; 25 °C, pH 7.40, 0.15 M NaCl; (■) Blank: calcium phosphate solution saturated with respect to HAP, containing 40.5 mM AA without HAP crystals; (■) as before, but in the presence of 80 mg HAP seed crystallites.
From a large literature body and for different adsorbent/adsorbate systems it is the most common observation that small molecules and ions reach equilibrium (at least 80% or more of the total adsorption). For the purposes of the present paper, we were more interested in equilibrium adsorption and not so much in the kinetics of adsorption. Moreover, the very small differences in concentration for equilibration times between time 0 and 18 h were within the experimental error. As expected, therefore, because of the small size of the AA molecule, the equilibrium was attained before 18 h. The measurements showed (see Equation (6)) that the adsorption of AA on HAP was 26.9 μmol·m−2. Assuming that the projected on the x-y plane area of an AA molecule is 104 Å2, 1 m2 area can accommodate 1.6 μmol of AA. The surface area assumed for the AA molecule is a rough estimate based on the bond distances and projection on a flat surface. Since the 104 Å2 per AA molecule is overestimated, a proportionally higher mass of AA can be accommodated per m2. However, it seems that in our conditions the surface coverage exceeds AA needed for one monolayer. At lower concentrations it was not possible to accurately measure concentrations of AA in the solutions, and we did not proceed further for the complete adsorption investigation, a task of ongoing work.
AA uptake on HAP surface would affect the surface charge and/or the respective surface potential of HAP crystals through the interaction of the charged species of AA and the potential determining ions of HAP, which are Ca2+, PO43−, and OH− ions arranged properly in the different crystal faces of HAP. This was confirmed by zeta potential measurements, the results of which are shown in Figure 5:
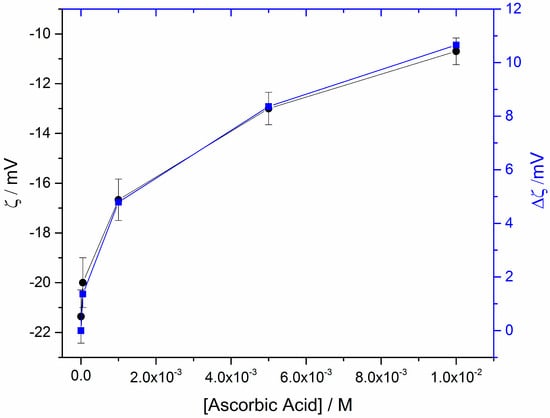
Figure 5.
Zeta potential of HAP particles suspensions in 10 mM NaCl electrolyte solutions as a function of the (initial) AA concentration in the equilibrium solutions; pH 7.40, 25 °C, 10 mM NaCl. Right axis Δζ = ζ(in the presence of AA) − ζ(without AA).
As may be seen in Figure 5, there is a tendency to reach a plateau of the surface potential for AA concentrations in the HAP-AA solutions; equilibrated suspensions at concentrations >10 mM suggested a tendency to reach saturation of the surface corresponding to the HAP particles of the suspension for AA concentrations higher than ca. 10 mM. Measurements beyond the 10 mM AA concentration were not possible, to avoid altering the ionic strength of the suspensions and give false measurements which do not correspond to surface coverage alone. The Δζ plot as a function of the solution concentration of AA in the HAP particles suspension is similar to systems in which adsorption of additives on inorganic particles showed a Langmuir-type adsorption isotherm [41]. Further work of the dependence of zeta potential of HAP in the presence of AA is ongoing.
Further evidence of the presence of AA on the surface of HAP crystallites was obtained by XPS measurements of HAP samples equilibrated with AA in solutions (0.15 M NaCl) saturated with respect to HAP. It should be noted that all samples collected for the analysis following filtration were filtered exhaustively with triply distilled water to avoid artifacts. The XPS spectrum obtained is presented in Figure 6.
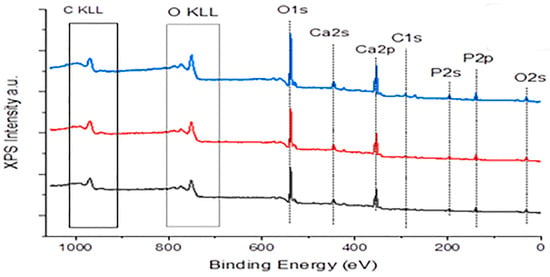
Figure 6.
XPS spectrum of HAP crystals (blue line), equilibrated with 0.05 mM AA (red line) and with 10 mM AA (black line); pH 7.40, 37 °C.
The results of XPS analysis are summarized in Table 2.

Table 2.
XPS analysis of HAP crystals equilibrated with AA: 0.05 mM and 10 mM. pH 7.40; 37 °C, 0.15 M NaCl.
As may be seen in the spectra presented in Figure 6, there is no difference in the patterns for the three samples presented (blue line reference HAP sample, red line 0.05 mM and black line 10 mM AA (very low and very high concentrations)). The differences are small but quantitatively significant for XPS analysis, as may be seen from the calculations on the peaks corresponding to C1s and O2s (framed in Figure 6) the results of the respective intensities are shown in Table 2.
Additional evidence for the presence of AA on the HAP crystals was obtained from the thermogravimetric analysis of the samples. Both reference and samples of HAP grown in the presence of AA were examined and the results are shown in Figure 7.
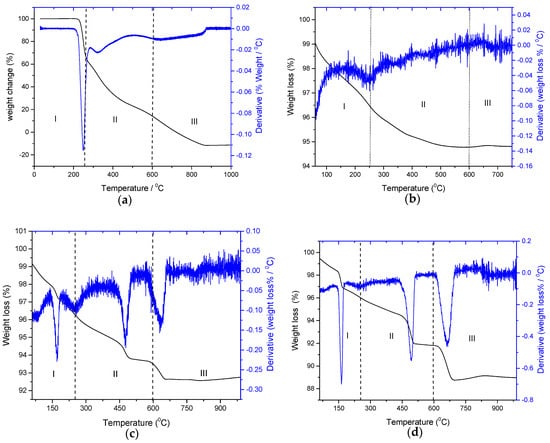
Figure 7.
Thermogravimetric (TG) and differential thermogravimetric (DTG) plots for: (a) crystalline ascorbic acid; (b) HAP seed crystals; (c) HAP crystals equilibrated with 10 mM AA; (d) HAP crystals equilibrated with 40 mM AA.
The TG/DTG profile of pure crystalline AA, shown in Figure 7a, showed a sharp peak at ca. 250 °C corresponding to the oxidation of AA to oxidized carbon species [42]. For pure HAP, shown in Figure 7b, three domains (I, II and III), not sharply defined, may be seen, (35–250 °C) corresponding to adsorbed and structural water (I), stage II (250–600 °C) corresponding to the conversion of surface HPO42− to pyrophosphate and stage III (>600 °C) corresponding to the formation of CaO and P2O5 [43]. The TG/DTG profiles of HAP equilibrated with 10 and 40 mM solutions of AA are shown in Figure 7c and Figure 7d, respectively.
Since the results of the study of the crystallization of HAP in the presence of AA clearly showed effects of the interaction of HAP with the AA present in the supersaturated solutions, we have next investigated the effect of the presence of AA on the dissolution of HAP in calcium phosphate solutions undersaturated with respect to HAP. The experimental conditions and the results obtained are summarized in Table 3. The experimental conditions were selected on the basis of simulation of body fluids, allowing for the variation in the solutions saturation, the master variable.

Table 3.
Dissolution of HAP crystals in calcium phosphate solutions undersaturated with respect to HAP in the absence and in the presence of 0.1 mM AA. 37 °C, pH 7.40, 0.15 M NaCl; Total calcium, Cat/Total phosphate, Pt = 1.667.
The negative sign for the rates of dissolution refers to the mass loss from the seeds, the opposite process of mass increase in the case of crystal growth. As may be seen from the acceleration of dissolution in the presence of AA, contrary to the acceleration of crystal growth, it did not show dependence on the solution undersaturation with respect to HAP and it was 330 ± 60% of the rate in the absence of AA.
Plot of the rates of dissolution, Rdiss, as a function of the relative undersaturation with respect to HAP, is shown in Figure 8.
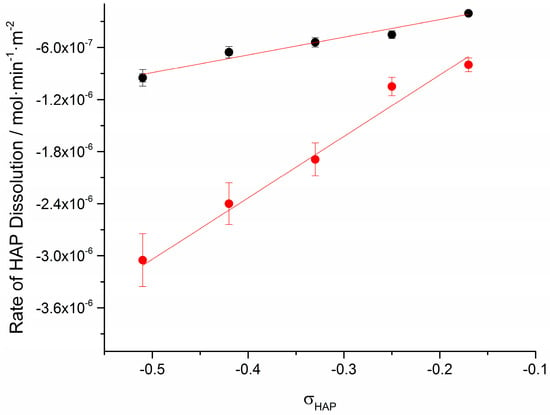
Figure 8.
Plot of the rate of dissolution of HAP crystals in calcium phosphate solutions undersaturated with respect to HAP in the absence (●) and in the presence of 0.1 mM AA (●); 37 °C, pH 7.40, 0.15 M NaCl.
Linear fitting of the data in Equation (8), which implies that m′ = 1, which is similar to Equation (7) for crystal growth, was satisfactory:
where kdiss is the apparent rate constant for dissolution and m′ the apparent order of dissolution. The values for the apparent dissolution rate constants obtained from the slope of the linear fitting of data in Equation (8) were as follows: kdiss was (2.0 ± 0.2) × 10−6 and (7.1 ± 1.3) × 10−6 in the absence and in the presence of 0.1 mM AA in the undersaturated solutions, respectively. As in the case of crystal growth, the presence of AA in the solutions in which the respective process took place, the rates were more than three times higher. In Figure 9, SEM pictures of HAP crystals past dissolution both in the absence and in the presence of AA.

Figure 9.
Morphology of HAP crystals past dissolution at constant undersaturation; σHAP = 0.42, pH 7.40, 37 °C, 0.15 M NaCl. (a): HAP seed crystals; bar 300 nm (b) HAP past dissolution; bar 300 nm (c) HAP past dissolution; bar 200 nm (d), (e) HAP after dissolution in the presence of 0.1 mM AA.
In Figure 9a the HAP reference material morphology is shown. As may be seen, it consisted of prismatic nanocrystals of a mean size of ca. 200–250 nm. Following dissolution at constant undersaturation, in the absence of AA, the mean size was below 150 nm (Figure 9b,c). In the presence of AA, in the undersaturated solutions the faster dissolution resulted in HAP crystallites with mean size below 100 nm (Figure 9d,e).
4. Discussion
The driving force for phase changes (crystal growth and dissolution) in calcium phosphate solutions is the Gibbs free energy change for going from unstable solutions to equilibrium with respect to the phase, which either forms or dissolves in the respective solutions. In the case of HAP, the free energy change for a phase change in thermodynamically unstable calcium phosphate solutions is ΔGHAP [9]:
where Rg is the gas constant, T the absolute temperature, α, the ion activity of the subscripted ion, and the thermodynamic solubility product of HAP. The logarithmic term is defined as the saturation ratio with respect to HAP, SHAP.
in case SHAP > 1 the solution is supersaturated with respect to HAP and is thermodynamically unstable. It is stabilized by the formation of HAP from the respective solution. In this case, SHAP is termed as the supersaturation ratio with respect to HAP. If SHAP = 1, the solution is at equilibrium and is stable, i.e., HAP neither forms nor is dissolved, in case HAP crystals are introduced in the solution. Finally, if SHAP < 1 the solution is undersaturated with respect to HAP and SHAP, in this case, is the undersaturation ratio with respect to HAP. In any case, numerically, SHAP is the measure of deviation from equilibrium.
The relative saturation with respect to HAP, σHAP is
for solutions supersaturated with respect to HAP in which crystal growth takes place, SHAP > 1 and > 0. For solutions undersaturated with respect to HAP in which the HAP crystals introduced dissolve, SHAP < 1 and < 0.
In this work, all measurements of crystal growth and dissolution were performed at constant driving force (supersaturation and undersaturation with respect to HAP, respectively). The experimental methodology adopted in the present work allows for the precise spotting and measurement of induction time (if any) preceding the onset of precipitation. This is essential, especially in cases in which materials other than crystallized material are used for the inoculation of the supersaturated solutions or if solids are poisoned by additive compounds capable of adsorbing onto the solids, which results in the de-activation of the active sites for crystal growth. The application of the constant supersaturation method is important for the improvement of the accuracy of the measurement of the rates of crystal growth, because measurements are performed at the same driving force, allowing us to work over narrow ranges of solution supersaturation and to extend studies at low levels of supersaturation, which simulate closer biological conditions, in which free ions are sequestered through complex formation.
The rates of crystal growth and dissolution depend on the saturation ratio with respect to HAP, according to Equations (7) and (8). As shown in Figure 1, both in the absence and in the presence of AA, from the dependence of the rate of crystal growth on the supersaturation ratio, the value of the apparent order of the process was n = 1. The value of the exponent is indicative of the underlying mechanism. For n ≥ 1 the mechanism is surface diffusion-controlled, while for n < 1 the mechanism is mass-transport-controlled [9,37,44].
In the present case, where n = 1 we have examined the case that the first order dependence of the rate of crystal growth on the relative supersaturation may mean that the mechanism of crystal growth is determined by mass transport of the growth units between the bulk solution and the crystals’ surface. If it were the case, the apparent rate constant would be given by Equation (12):
where D is the diffusion coefficient (of the order of magnitude of 10−9 m2·s−1 [45]), Vm the molecular volume of the growing HAP (=9.8 × 10−5 m3·mol−1), Cs the solubility of HAP (ca. 2.5 × 10−7 M), and δ the diffusion layer thickness. For stirred suspensions of particles in solutions in general, δ may be calculated from Equation (13) [46]:
where <r> is the mean crystal radius of the suspended particles (for HAP crystallites in this work ca. 50 nm) and Δρ is the density difference between the crystalline particle (for HAP–aqueous electrolyte solution suspensions, ρHAP = 5.1 g·cm−3) and the continuous suspension medium (in the present work aqueous solution, ρH2O·= 1.0 g·cm−3 and ρHAP − ρH2O= 4.1 g·cm−3). According to Equation (13), δ was calculated equal to 0.91 μm. Substituting the values in Equation (12), a value of 4.16 × 10−4 m2·s−1 was calculated for the diffusion coefficient. This value is five orders of magnitude larger than the anticipated for ions constituting the HAP crystal growth units. This means that the apparent constant of the rate of crystal growth cannot be the corresponding Equation (12). Hence, it was concluded that the crystal growth of HAP is controlled by surface diffusion of the growth units on the surface of HAP crystals.
In a similar manner, it was found that for the case of dissolution of HAP, both in the absence and in the presence of AA, the respective apparent rate constant for dissolution, kdiss (Equation (8)) is consistent only with the surface diffusion-controlled model. This in turn means that kinetics of both growth and dissolution of HAP are sensitive to surface modifications, due either to specific treatments or even to the adsorption of ionic or molecular species of the HAP crystallites surface.
As may be seen from Equations (9) and (10), the thermodynamic driving force, and the saturation ratio with respect to HAP, depend on the activities of the free Ca2+, PO43−, and OH− ions. Since equilibria between various species make the supersaturated solutions quite complex, it is necessary that all species are considered. The calculations of the saturation ratio were performed using PHREEQC® software, Version 3.8.6.17100 [47]. PHREEQC is a computer program developed by the U.S. Geological Survey for simulating chemical reactions and transport processes in aqueous media. In the present work the software was used for all speciation and saturation-index calculations in the present work. The program uses thermodynamic databases to calculate equilibrium distributions of aqueous species.
Additional equilibria involving L-ascorbic acid (dibasic) were used to modify the database of the software and are shown in Table 4 [48].

Table 4.
Equilibria involving AA considered in calculations of the saturation ratio with respect to HA.
Combination of the crystal growth and dissolution kinetics data yielded Figure 10:
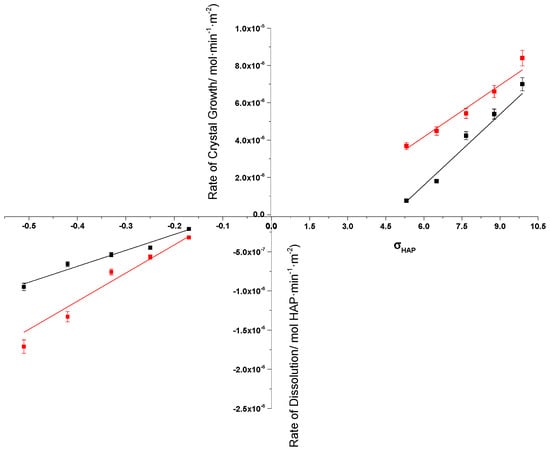
Figure 10.
Crystal growth and dissolution of HAP in the absence and in the presence of AA in supersaturated and undersaturated calcium phosphate solutions, respectively; 37 °C, pH 7.40, 0.15 M NaCl. (■) in the absence of AA; (■) in the presence of 0.1 mM AA.
As may be seen in Figure 10, there is no symmetry between crystal growth and dissolution, despite the fact that the mechanism underlying both processes is the same. A common feature of crystal growth and dissolution is that the rates of both are accelerated in the presence of AA, which as it is apparent from the direct measurements (Figure 4) and indirect evidence from zeta potential, XPS, and TG/DTG measurements (Figure 5, Figure 6 and Figure 7), AA is adsorbed on HAP surfaces in electrolyte solutions. Adsorption is expected to reduce the surface energy of the solid facilitating the incorporation and the release of the growth units from the crystal surface. The adsorption measurements of the present work were extended over very long periods of time (up to one week) to avoid ascorbic acid oxidation or decomposition. These processes are faster, the higher the temperature. Thus, we preferred adsorption measurements at 25 °C. Any changes at 37 °C would be quantitative and not qualitative, their extent depending on the activation energy of adsorption.
It should be noted that the increase in the rates of crystal growth varied with the solution supersaturation with respect to HAP. The increase was the least (ca. 20%) for the highest supersaturation (ca. 460% of the rate in the absence of AA). This is probably due to the extent of interaction of AA with the HAP, which becomes weaker as the driving force for crystal growth increases and the tendency of the crystal growth units to incorporate into the HAP lattice is higher than the blocking capacity of AA on the surface of HAP, at the electrolyte interface. On the contrary, the dissolution rates increase did not depend on the solution undersaturation, suggesting that the interaction of HAP surface with AA was sufficiently strong, and it only catalyzed the HAP crystal building block transfer to the aqueous phase.
Moreover, from the variation in the ζ potential as a function of the concentration of AA, as may be seen in the uptake of AA on the surface of HAP crystals, it results in more positive potential values, suggesting perhaps that there is significant interaction of HAP with the positively charged species of AA in the supersaturated solutions (Table 4). Alternatively, AA may interact with orthophosphate ions in the crystal lattice of HAP, thus reducing the respective negative potential contribution. It is particularly interesting that the higher the concentrations of AA in the solutions the more intense was the peak of AA at the DTG (Figure 7, cf. Figure 7c corresponding to 10 mM of AA in solution and Figure 7d corresponding to 40 mM of AA), suggesting higher adsorption. Moreover, the higher the AA concentration the more the DTG peak shifted to a lower temperature (cf. 250 °C for pure crystalline AA, to 170 °C for 10 mM AA, and 162 °C for 40 mM AA). This may reflect stronger interactions at higher concentrations between the adsorbent and the adsorbate. From the XPS data (Figure 6) it can be seen that the ratios of Ca/P on the surface of HAP are constant and the apparent change is shown in the C1s peak, which is progressively increasing with the increase in AA in the electrolyte solution in contact with HAP. The presence of the same peak even in the control HAP sample is probably due to contamination from the air or from the intrusion of atmospheric carbon dioxide during the equilibration stage.
The present investigation has shown for the first time, unambiguously, that AA does interact with HAP mineral surfaces, by adsorption from electrolyte solutions, which in fact activates in a way the surface of HAP, increasing the rate of crystal growth from supersaturated solutions and the rate of dissolution from undersaturated solutions, as may be seen in Figure 11. The acceleration effects, in both cases, however, decreased with increasing respective driving force.
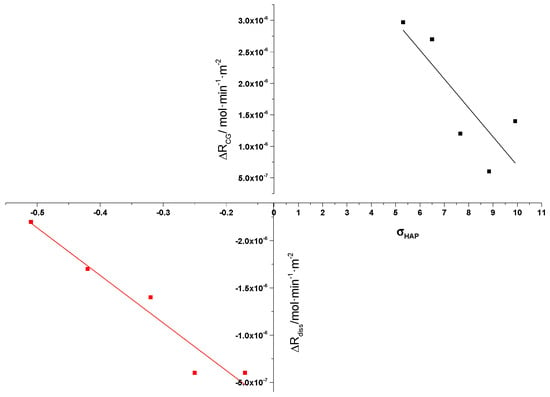
Figure 11.
Change in the crystal dissolution (■) and crystal growth (■) rates of HAP from undersaturated and supersaturated solutions, respectively, in the presence of 0.1 mM AA; 37 °C, pH 7.40, 0.15 M NaCl.
It should be noted that in the case of dissolution, the difference in the rate of dissolution of HAP between measurements in the absence of 0.1 mM AA compared to those in the presence of AA is a negative number but in the graph, for the sake of comparison, the absolute values of the differences between the rates were obtained. As may be seen, there is similarity in the trend, suggesting similar action of the AA in both crystal growth and dissolution. As already shown, in the case of crystal growth of HAP, the acceleration was highest at the lowest supersaturation, with the rate difference decreasing with increasing supersaturation. A similar trend was found for the dissolution, but the domain of relative undersaturations investigated was much narrower and the rate changes due to the presence of 0.1 mM of AA, although large (more than 300% increase), the percentage difference in the rates of dissolution was not as regular as in the case of crystal growth. Apparently, the range of relative undersaturations can only vary between 0 and −1.
The morphology of the crystals did not change in the presence of AA, suggesting that there is no preferential adsorption of the AA molecule to a specific crystal face of HAP. The prismatic crystals’ shape was preserved during dissolution. At the higher rates of dissolution in the presence of the AA (Figure 9d,e) the significant size decrease was visible.
5. Conclusions
The present study investigated the effect of the presence of a most interesting biomolecule during the crystal growth and of the dissolution of HAP, a biomineral of utmost importance for the hard tissues of higher mammals and a basis for many biomaterials. Both crystal growth and dissolution rates increased in the presence of AA. The present study focused on a typical concentration of 0.1 mM, sufficiently high to observe kinetics effects and to study adsorption phenomena, and at the same time sufficiently low to affect saturation of solutions with respect to HAP. Depending on the solution supersaturation, rates of crystal growth 360% higher were measured at constant supersaturation in the presence of 0.1 mM AA. Similar results were obtained for the rates of dissolution. Increasing the driving force of crystal growth or dissolution decreased the difference between the rates in the absence and in the presence of AA. The effect on the kinetics of crystal growth and dissolution was found to be due to the adsorption of AA on HAP. Evidence was obtained from direct adsorption measurements, measurements of the ζ potential, XPS, and TG/DTG. The surface potential shifted to more positive values and XPS analysis showed increasing C1s peaks with increasing AA concentrations in the solutions equilibrated with HAP suspensions. The DTG analysis also yielded evidence of higher amounts of AA taken up by the AA surfaces at physiological conditions and suggested stronger interactions with increasing concentration. The morphology of the HAP crystals was not affected by the presence of AA both in the super and the undersaturated solutions. Extensive crystal growth of HAP-on-HAP seed crystals, both in the presence and in the absence of AA in the respective solutions, favored the formation of plate-like crystallites. The faster dissolution in the presence of AA resulted in drastic reduction in the crystallites size.
Author Contributions
In this work, P.G.K. and P.D.N. contributed to the conceptualization; I.K. and P.D.N. worked on the methodology and validation including formal analysis; I.K., P.D.N. and P.G.K. worked on data curation; I.K. prepared the original draft; and P.G.K. carried out review and editing, visualization, supervision, and project administration. All authors have read and agreed to the published version of the manuscript.
Funding
IK was awarded for this research, scholarship funded by A. MENTZELOPOULOS FOUNDATION, Patras, GREECE, project No33720000, which is gratefully acknowledged.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors wish to express sincere thanks and appreciation to Lambrini Syggelou (FORTH-ICEHT) for the XPS analyses and useful discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HAP | Hydroxyapatite (Ca5(PO4)3OH |
| AA | Ascorbic Acid (C9H12O6) |
| XPS | X-Ray Photoelectron Sectroscopy |
| TG | Thermo Gravimetric |
| DTG | Differential Thermogravinmetric |
| SEM | Scanning Electron Microscopy |
References
- D′Alessandro, C.C.; Komninou, M.A.; Badria, A.F.; Korossis, S.; Koutsoukos, P.; Mavrilas, D. Calcification Assessment of Bioprosthetic Heart Valve Tissues Using an Improved In Vitro Model. IEEE Trans. Biomed. Eng. 2020, 67, 2453–2461. [Google Scholar] [CrossRef] [PubMed]
- Wen, S.; Zhou, Y.; Yim, W.Y.; Wang, S.; Xu, L.; Shi, J.; Qiao, W.; Dong, N. Mechanisms and Drug Therapies of Bioprosthetic Heart Valve Calcification. Front. Pharmacol. 2022, 13, 909801. [Google Scholar] [CrossRef]
- D’Alessandro, C.C.; Dimopoulos, A.; Andriopoulou, S.; Messaris, G.A.; Korossis, S.; Koutsoukos, P.G.; Mavrilas, D. In vitro calcification studies on bioprosthetic and decellularized heart valves under quasi-physiological flow conditions. In Bio-Design and Manufacturing; Springer: Berlin/Heidelberg, Germany, 2021; Volume 4, pp. 10–21. [Google Scholar] [CrossRef]
- Onnis, C.; Virmani, R.; Kawai, K.; Nardi, V.; Lerman, A.; Cademartiri, F.; Scicolone, R.; Boi, A.; Congiu, T.; Faa, G.; et al. Coronary Artery Calcification: Current Concepts and Clinical Implications. Circulation 2024, 149, 251–266. [Google Scholar] [CrossRef] [PubMed]
- Onea, H.-L.; Olinic, M.; Lazar, F.-L.; Homorodean, C.; Ober, M.C.; Spinu, M.; Achim, A.; Tataru, D.A.; Olinic, D.M. A Review Paper on Optical Coherence Tomography Evaluation of Coronary Calcification Pattern: Is It Relevant Today? J. Cardiovasc. Dev. Dis. 2024, 11, 231. [Google Scholar] [CrossRef] [PubMed]
- Apple, D.J.; Werner, L.; Escobar-Gomez, M.; Pandey, S.K. Deposits on the Optical Surfaces of Hydroview Intraocular Lenses. J. Cataract. Refract. Surg. 2000, 26, 796–797. [Google Scholar] [CrossRef] [PubMed]
- Bopp, S.; Özdemir, H.B.; Aktaş, Z.; Khoramnia, R.; Yildirim, T.M.; Schickhardt, S.; Auffarth, G.U.; Özdek, Ş. Clinical Characteristics of Patients with Intraocular Lens Calcification after Pars Plana Vitrectomy. Diagnostics 2023, 13, 1943. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Katsimpris, J.M.; Theoulakis, P.E.; Kouzi-Koliakos, K.; Pavlidou, E.; Petropoulos, I.K.; Koliakos, G.; Vouroutzis, N.; Konstas, A.G. Late Postoperative Opacification of Hydrogel Intraocular Lenses: Analysis of 13 Explanted Lenses. Klin. Monbl. Augenheilkd. 2009, 226, 264–271. [Google Scholar] [CrossRef]
- Koutsoukos, P.G.; Natsi, P.D.; Gartaganis, S.P.; Gartaganis, P.S. Biological Mineralization of Hydrophilic Intraocular Lenses. Crystals 2022, 12, 1418. [Google Scholar] [CrossRef]
- Dalas, E.; Kallitsis, J.K.; Koutsoukos, P.G. Crystallization of Hydroxyaatite on Polymers. Langmuir 1991, 7, 1822–1826. [Google Scholar] [CrossRef]
- Bonucci, E. Biological Calcification; Springer: Berlin/Heidelberg, Germany, 2007; 592p. [Google Scholar]
- Söhnel, O.; Grases, F. Supersaturation of body fluids, plasma and urine, with respect to biological hydroxyapatite. Urol. Res. 2011, 39, 429–436. [Google Scholar] [CrossRef] [PubMed]
- Di Costanzo, L.F. Atomic Details of Biomineralization Proteins Inspiring Protein Design and Reengineering for Functional Biominerals. Chemistry 2022, 4, 827–847. [Google Scholar] [CrossRef]
- Gómez-Morales, J.; Falini, G.; García-Ruiz, J.M. Biological Crystallization. Crystals 2019, 9, 409. [Google Scholar] [CrossRef]
- Tavafoghi, M.; Cerruti, M. The role of amino acids in hydroxyapatite mineralization. J. R. Soc. Interface 2016, 13, 20160462. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Nancollas, G.H. The involvement of calcium phosphates in biological mineralization and demineralization processes. Pure Appl. Chern. 1992, 64, 1673–1678. [Google Scholar] [CrossRef]
- Ehrlich, H.; Koutsoukos, P.G.; Demadis, K.D.; Pokrovsky, O.S. Principles of demineralization: Modern strategies for the isolation of organic frameworks Part I. Common definitions and history. Micron 2008, 39, 1062–1091. [Google Scholar] [CrossRef] [PubMed]
- Habraken, W.; Habibovic, P.; Epple, M.; Bohner, M. Calcium phosphates in biomedical applications: Materials for the future? Mater. Today 2016, 19, 69–87. [Google Scholar] [CrossRef]
- Dorozhkin, S.V. Calcium Orthophosphates as Bioceramics: State of the Art. J. Funct. Biomater. 2010, 1, 22–107. [Google Scholar] [CrossRef]
- Spanos, N.; Misirlis, D.Y.; Kanellopoulou, D.G.; Koutsoukos, P.G. Seeded growth of hydroxyapatite in simulated body fluid. J. Mater. Sci. 2006, 41, 1805–1812. [Google Scholar] [CrossRef]
- Levine, M.; Conry-Cantilena, C.; Wang, Y.; Welch, R.W.; Washko, P.W.; Dhariwal, K.R.; Park, J.B.; Lazarev, A.; Graumlich, J.F.; King, J.; et al. Vitamin C pharmacokinetics in healthy volunteers: Evidence for a recommended dietary allowance. Proc. Natl. Acad. Sci. USA 1996, 93, 3704–3709. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Rose, R.C.; Bode, A.M. Biology of Free Radical Scavengers: An Evaluation of Ascorbate. FASEB J. 1993, 7, 1135–1142. [Google Scholar] [CrossRef]
- Frei, B.; England, L.; Ames, B.N. Ascorbate is an outstanding antioxidant in human blood plasma. Proc. Natl. Acad. Sci. USA 1989, 86, 6377–6381. [Google Scholar] [CrossRef]
- Boskey, A.L.; Stiner, D.; Doty, S.B.; Binderman, I. Requirement of Vitamin C for Cartilage Calcification in a Differentiating Chick Limb-Bud Mesenchymal Cell Culture. Bone 1991, 12, 277–282. [Google Scholar] [CrossRef]
- Ivanov, V.; Ivanova, S.; Niedzwiecki, A.; Rath, M. Vitamin C inhibits the calcification process in human vascular smooth muscle cells. Am. J. Cardiovasc. Dis. 2020, 10, 108–116. [Google Scholar] [PubMed]
- Ciceri, P.; Volpi, E.; Brenna, I.; Arnaboldi, L.; Neri, L.; Brancaccio, D.; Cozzolino, M. Combined effects of ascorbic acid and phosphate on rat VSMC osteoblastic differentiation. Nephrol. Dial. Transpl. 2012, 27, 122–127. [Google Scholar] [CrossRef] [PubMed]
- Singh, P.P.; Kiran, R.; Pendse, A.K.; Ghosh, R.; Surana, S.S. Ascorbic Acid is an Abettor in Calcium Urolithiasis: An Experimental Study. Scanning Microsc. 1993, 7, 28. [Google Scholar]
- Bahal, P.; Djemal, S. Dental Erosion from an Excess of Vitamin, C. Case Rep. Dent. 2014, 2014, 485387. [Google Scholar] [CrossRef]
- Sousa, S.M.G.; Silva, T.L. Demineralization effect of EDTA, EGTA, CDTA and citric acid on root dentin: A comparative study. Braz. Oral. Res. 2005, 19, 188–192. [Google Scholar] [CrossRef]
- Amin, R.M.; Elfeky, S.A.; Verwanger, T.; Krammer, B. A new biocompatible nanocomposite as a promising constituent of sunscreens. Mater. Sci. Eng. C 2016, 63, 46–51. [Google Scholar] [CrossRef]
- Muñoz, E.M.R. Hydroxyapatite-Based Materials: Synthesis and Characterization, Chapter 4. In Biomedical Engineering–Frontiers and Challenges; Fazel-Rezai, R., Ed.; IntechOpen: Rijeka, Croatia, 2011; pp. 75–98. [Google Scholar]
- Drimtzias, E.G.; Rokidi, S.G.; Gartaganis, S.P.; Koutsoukos, P.G. Experimental investigation on mechanism of hydrophilic acrylic intraocular lens calcification. Am. J. Ophthalmol. 2011, 152, 824–833.e1. [Google Scholar] [CrossRef]
- Kinsey, V.E. Comparative chemistry of aqueous humor in posterior and anterior chambers of rabbit eye. Its physiologic significance. A.M.A. Arch. Opthalmol. 1953, 50, 401–417. [Google Scholar]
- Christoffersen, J.; Christoffersen, M.R.; Kibalczyc, W.; Andersen, F.A. A contribution to the understanding of the formation of calcium phosphates. J. Cryst. Growth 1989, 94, 767–777. [Google Scholar] [CrossRef]
- Ding, H.; Pan, H.; Xu, X.; Tang, R. Towards a Detailed Understanding of Magnesium ions on Hydroxyapatite Crystallization Inhibition. Cryst. Growth Des. 2014, 14, 763–769. [Google Scholar] [CrossRef]
- Bell, L.C.; Mika, H.; Kruger, B.J. Synthetic hydroxyapatite-solubility product and stoichiometry of dissolution. Arch. Oral. Biol. 1978, 23, 329–336. [Google Scholar] [CrossRef] [PubMed]
- Tang, R.; Henneman, Z.J.; Nancollas, G.H. Constant composition kinetics study of carbonatedapatite dissolution. J. Cryst. Growth 2003, 249, 614–624. [Google Scholar] [CrossRef]
- Chauhan, N.; Singh, Y. L-histidine controls the hydroxyapatite mineralization with plate-like morphology: Effect of concentration and media. Mater. Sci. Eng. C Mater. Biol. Appl. 2021, 120, 111669. [Google Scholar] [CrossRef] [PubMed]
- Takallu, S.; Mirzaei, E.; Azadi, A.; Karimizade, A.; Tavakol, S. Plate-shape carbonated hydroxyapatite/collagen nanocomposite hydrogel via in situ mineralization of hydroxyapatite concurrent with gelation of collagen at pH = 7.4 and 37 °C. J. Biomed. Mater. Res. B Appl. Biomater. 2019, 107, 1920–1929. [Google Scholar] [CrossRef] [PubMed]
- Koutsoukos, P.G.; Nancollas, G.H. The morphology of hydroxyapatite crystals grown in aqueous solutions at 37 °C. J. Cryst. Growth 1981, 55, 369–375. [Google Scholar] [CrossRef]
- Spanos, N.; Koutsoukos, P.G. Model studies on the effect of orthophospho-L-serine on biological mineralization. Langmuir 2001, 17, 866–872. [Google Scholar] [CrossRef]
- Lerdkanchanaporn, S.; Dollimore, D.; Alexander, K.S. A thermogravimetric study of ascorbic acid and its excipients in pharmaceutical formulations. Thermochim. Acta 1996, 284, 115–126. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Lv, G.; Zuo, Y.; Mu, Y. Thermal and crystallization studies of nano-hydroxyapatite reinforced polyamide 66 biocomposites. Polym. Degrad. Stab. 2006, 91, 1202–1207. [Google Scholar] [CrossRef]
- Wang, L.; Nancollas, G.H. Calcium Orthophosphates: Crystallization and Dissolution. Chem. Rev. 2008, 108, 4628–4669. [Google Scholar] [CrossRef]
- Robinson, R.A.; Chia, C.L. The Diffusion Coefficient of Calcium Chloride in Aqueous Solution at 25 °C. J. Am. Chem. Soc. 1952, 74, 2776–2777. [Google Scholar] [CrossRef]
- Nancollas, G.H. In vitro studies of calcium phosphate crystallization. In Biomineralization; Mann, S., Webb, J., Williams, R.J.P., Eds.; VCJ: Cambridge, NY, USA, 1989; p. 166. [Google Scholar]
- Parkhurst, D.L.; Appelo, C.A.J. Description of input and examples for PHREEQC version 3—A computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations. In Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2013; Volume 6, p. 497. Available online: https://pubs.usgs.gov/tm/06/a43 (accessed on 25 February 2015).
- Martel, A.E.; Smith, R.M. Critical Stability Constants Volume 3: Other Organic Ligands; Plenum Press: New York, NY, USA, 1977; p. 264. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).