Field-Effect Crystal Engineering in Proton–π-Electron Correlated Systems
Abstract
1. Introduction
1.1. Polarization Configurations and Crystal Polymorphs
1.2. Hydrogen Bonds for Strong Polarizations
1.3. Hydrogen-Bonded Antiferroelectric Crystals in Earlier Studies
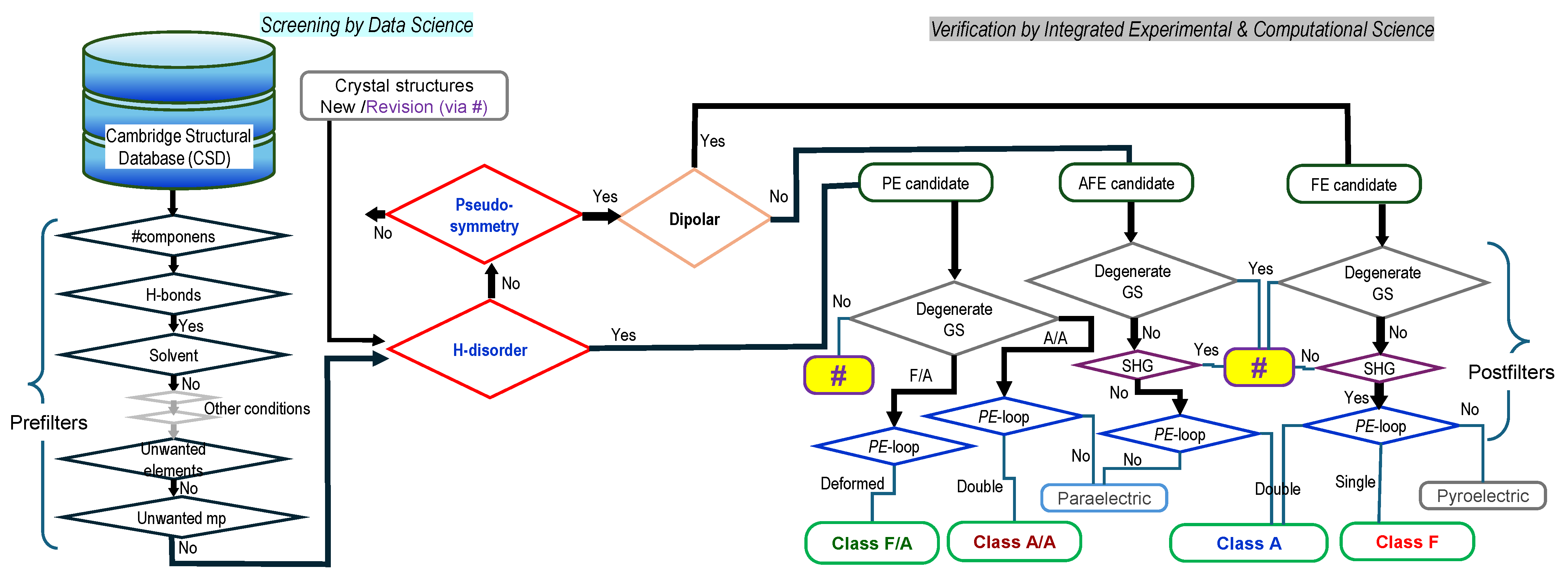
2. Material Explorations Using the Crystal Structural Database
2.1. Pseudo-Symmetry Assessment
2.2. Hydrogen Disorder Assessment
2.3. Additional Issues on Screening
2.4. Hydrogen-Bonded Dielectrics Extracted
3. Preparation and Property Evaluations
3.1. Experimental Procedure
3.2. Macroscopic Switching
3.3. Effects of Microscopic Switching Mechanisms
4. Functional Prediction Using Computational Science
4.1. Computational Methods
4.2. Evaluations of Electric Polarizations
4.3. Simulations of Crystal Structure and Piezoelectricity
5. Integrated Experimental and Computational Approaches for Systematic Understanding
5.1. Assessments of Switching Mechanisms from Polarizations
5.2. Assignments of Switching Mechanisms from Piezoelectricity
5.3. Identification of Field-Induced Crystal Forms
5.4. PT Mode Switching on Ladder Architectures
5.5. Amphoteric Switching on Dipole-Canted Systems
5.6. Two-Dimensional Switching System
5.7. Energy Storage
5.8. Electromechanical Properties
5.9. Analysis of Relative Phase Stability
5.10. Case Studies with Applied Integrated Approach
6. Outlook and Perspective
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PE | paraelectric |
| FE | ferroelectric |
| AFE | antiferroelectric |
| P–E | polarization–electric field |
| SHG | second harmonic generation |
| CSD | Cambridge Structural Database |
| IUCr | International Union of Crystallography |
| FF | flip-flop |
| PT | proton transfer |
| DFT | density functional theory |
| LDA | local density approximation |
| GGA-PBE | Perdew–Burke–Ernzerhof version of the generalized gradient approximation |
| vdW | van der Waals |
| DF-cx | density-functional consistent-exchange |
| rVV | revised Vydrov–van Voorhis |
| CRCA | croconic acid |
| SQA | squaric acid |
| KDP | potassium dihydrogen phosphate (KH2PO4) |
| ADP | ammonium dihydrogen phosphate (NH4H2PO4) |
| 9HPLN | 9-hydroxyphenalenone |
| MeHPLN | 5-methyl-9-hydroxyphenalenone |
| BHPLN | 5-bromo-9-hydroxyphenalenone |
| IHPLN | 5-iodo-9-hydroxyphenalenone |
| dabco | diazabicyclo[2.2.2]octane |
| Phz | phenazine |
| H2ca | chloranilic acid |
| H2ba | bromanilic acid |
| H2ia | iodanilic acid |
| 55dmbp | 5,5′-dimethyl-2,2′-bipyridine |
| 66dmbp | 6,6′-dimethyl-2,2′-bipyridine |
| npd | 1,5-naphthyridine |
| PhMDA | 2-phenylmalondialdehyde |
| CBDC | cyclobutene-1,2-dicarboxylic acid |
| HPLN | 3-hydroxyphenalenone |
| MBI | 2-methylbenzimidazole |
| DCMBI | 5,6-dichloro-2-methylbenzimidazole |
| ALAA | 3-anilinoacrolein anil |
| ATA | anthranilic acid |
| APHTZ | 5-(4-aminophenyl)-1H-tetrazole |
| PDPLA | 1,2-phenylenedipropiolic acid |
| CPHTZ | 5-(4-chlorophenyl)-1H-tetrazole |
| FPHTZ | 5-(4-fluorophenyl)-1H-tetrazole |
| TFMBI | 2-trifluoromethylbenzimidazole |
| DFMBI | 2-difluoromethylbenzimidazole |
| TCMBI | 2-trichloromethylbenzimidazole |
| TFMNI | 2-trifluoromethylnaphthimidazole |
| MPHTZ | 5-(4-methylphenyl)-1H-tetrazole |
| CPPLA | 3-(4-chlorophenyl)propiolic acid |
| FDC | 3,4-furandicarboxylic acid |
| BI2C | bis-(1H-benzimidazol-2-yl)methane |
| PHTZ | 5-phenyl-1H-tetrazole |
| BI2P | 2,2′-(1,2-phenylene)bis-1H-benzimidazole |
| DHBA | 2,5-dihydroxybenzoic acid |
| DHIB | α,α’-dihydroxy-1,3-diisopyopylbenzene |
| NPTL | 2-naphthol |
| LTTL | L-threitol |
| MNTL | DL-mannitol |
| THMCHO | 2,2,6,6-tetrakis(hydroxymethyl)cyclohexanol |
| BHEOB | 1,3-bis(2-hydroxyethoxy)benzen |
| TCHM | tricyclohexylmethanol |
References
- Lines, M.E.; Glass, A.M. Principles and Applications of Ferroelectrics and Related Materials; Oxford University Press: New York, NY, USA, 1977. [Google Scholar]
- Uchino, K. Ferroelectric Devices; Marcel Dekker: New York, NY, USA, 2000. [Google Scholar]
- Merz, W.J. Double Hysteresis Loop of BaTiO3 at the Curie Point. Phys. Rev. 1953, 91, 513–517. [Google Scholar] [CrossRef]
- Sawaguchi, E.; Maniwa, H.; Hoshino, S. Antiferroelectric Structure of Lead Zirconate. Phys. Rev. 1951, 83, 1078. [Google Scholar] [CrossRef]
- Shirane, G.; Sawaguchi, E.; Takagi, Y. Dielectric Properties of Lead Zirconate. Phys. Rev. 1951, 84, 476–481. [Google Scholar] [CrossRef]
- Kittel, C. Theory of Antiferroelectric Crystals. Phys. Rev. 1951, 82, 729–732. [Google Scholar] [CrossRef]
- Randall, C.A.; Fan, Z.; Reaney, I.; Chen, L.-Q.; Trolier-McKinstry, S. Antiferroelectrics: History, fundamentals, crystal chemistry, crystal structures, size effects, and applications. J. Am. Ceram. Soc. 2021, 104, 3775–3810. [Google Scholar] [CrossRef]
- Koch, C.C. Experimental evidence for magnetic or electric field effects on phase transformations. Mater. Sci. Eng. 2000, A281, 213–218. [Google Scholar] [CrossRef]
- Lai, A.; Schuh, C.A. Direct Electric-Field Induced Phase Transformation in Paraelectric Zirconia via Electrical Susceptibility Mismatch. Phys. Rev. Lett. 2021, 126, 015701. [Google Scholar] [CrossRef]
- Asadi, K. (Ed.) Woodhead Publishing Series in Electronic and Optical Materials; Organic Ferroelectric Materials and Applications; Woodhead Publishing: Duxford, UK, 2022. [Google Scholar]
- Furukawa, T. Ferroelectric properties of vinylidene fluoride copolymers. Phase Trans. 1989, 18, 143–211. [Google Scholar] [CrossRef]
- Nalwa, H.S. (Ed.) Ferroelectric Polymers; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Park, C.; Lee, K.; Koo, M.; Park, C. Soft Ferroelectrics Enabling High-Performance Intelligent Photo Electronics. Adv. Mater. 2020, 33, 2004999. [Google Scholar] [CrossRef]
- Horiuchi, S.; Tokura, Y. Organic ferroelectrics. Nat. Mater. 2008, 7, 357–366. [Google Scholar] [CrossRef] [PubMed]
- Tayi, A.S.; Kaeser, A.; Matsumoto, M.; Aida, T.; Stupp, S.I. Supramolecular ferroelectrics. Nat. Chem. 2015, 7, 281–294. [Google Scholar] [CrossRef] [PubMed]
- Harada, J. Plastic/ferroelectric molecular crystals: Ferroelectric performance in bulk polycrystalline forms. APL Mater. 2021, 9, 020901. [Google Scholar] [CrossRef]
- Zhang, W.; Xiong, R.G. Ferroelectric Metal-Organic Frameworks. Chem. Rev. 2012, 112, 1163–1195. [Google Scholar] [CrossRef]
- Liu, H.Y.; Zhang, H.Y.; Chen, X.G.; Xiong, R.G. Molecular Design Principles for Ferroelectrics: Ferroelectrochemistry. J. Am. Chem. Soc. 2020, 142, 15205–15218. [Google Scholar] [CrossRef]
- Akutagawa, T. Chemical Design and Physical Properties of Dynamic Molecular Assemblies. Bull. Chem. Soc. Jpn. 2021, 94, 1400–1420. [Google Scholar] [CrossRef]
- Horiuchi, S.; Ishibashi, S. Hydrogen-Bonded Small-Molecular Crystals Yielding Strong Ferroelectric and Antiferroelectric Polarizations. J. Phys. Soc. Jpn. 2020, 89, 051009. [Google Scholar] [CrossRef]
- Gilli, G.; Bertolasi, V.; Ferretti, V.; Gilli, P. Resonance-assisted hydrogen bonding. III. Formation of intermolecular hydrogen-bonded chains in crystals of β-diketone enols and its relevance to molecular association. Acta Crystallogr. Sect. B 1993, 49, 564–576. [Google Scholar] [CrossRef]
- Horiuchi, S.; Tokunaga, Y.; Giovannetti, G.; Picozzi, S.; Itoh, H.; Shimano, R.; Kumai, R.; Tokura, Y. Above-room-temperature ferroelectricity in a single-component molecular crystal. Nature 2010, 463, 789–792. [Google Scholar] [CrossRef]
- Horiuchi, S.; Kobayashi, K.; Kumai, R.; Ishibashi, S. Proton tautomerism for strong polarization switching. Nat. Commun. 2017, 8, 14426. [Google Scholar] [CrossRef]
- Horiuchi, S.; Kumai, R.; Ishibashi, S. Strong Polarization Switching with Low-Energy Loss in Hydrogen-Bonded Organic Antiferroelectrics. Chem. Sci. 2018, 9, 425–432. [Google Scholar] [CrossRef] [PubMed]
- Horiuchi, S.; Ishibashi, S. Large Polarization and Record-High Performance of Energy-Storage Induced by a Phase Change in Organic Molecular Crystals. Chem. Sci. 2021, 12, 14198–14206. [Google Scholar] [CrossRef]
- Sugawara, T.; Takasu, I. Tautomerism in the Solid State. Adv. Phys. Org. Chem. 1999, 32, 219–265. [Google Scholar]
- Hadjoudis, E.; Mavridis, I.M. Photochromism and thermochromism of Schiff bases in the solid state: Structural aspects. Chem. Soc. Rev. 2004, 33, 579–588. [Google Scholar] [CrossRef]
- Horiuchi, S.; Kumai, R.; Tokura, Y. Hydrogen Bonding Molecular Chains for High-Temperature Ferroelectricity. Adv. Mater. 2011, 23, 2098–2103. [Google Scholar] [CrossRef] [PubMed]
- Horiuchi, S.; Kagawa, F.; Hatahara, K.; Kobayashi, K.; Kumai, R.; Murakami, Y.; Tokura, Y. Above-room-temperature ferroelectricity and antiferroelectricity in benzimidazoles. Nat. Commun. 2012, 3, 1308. [Google Scholar] [CrossRef] [PubMed]
- Horiuchi, S.; Noda, Y.; Hasegawa, T.; Kagawa, F.; Ishibashi, S. Correlated proton transfer and ferroelectricity along alternating zwitterionic and nonzwitterionic anthranilic acid molecules. Chem. Mater. 2015, 27, 6193–6197. [Google Scholar] [CrossRef]
- Horiuchi, S.; Minemawari, H.; Ishibashi, S. Competition of Polar and Antipolar States Hidden Behind a Variety of Polarization Switching Modes in Hydrogen-Bonded Molecular Chains. Mater. Horiz. 2023, 10, 2149–2159. [Google Scholar] [CrossRef]
- Zou, Y.; Hong, S.; Park, M.; Chun, H.; Lah, M.S. Selective gas sorption property of an interdigitated 3-D metal–organic framework with 1-D channels. Chem. Commun. 2007, 5182–5184. [Google Scholar] [CrossRef]
- Saravanakumar, R.; Varghese, B.; Sankararaman, S. Hydrogen-bond network in isomeric phenylenedipropynoic acids and their DABCO salts. Water mediated helical hydrogen bond motifs. CrystEngComm 2009, 11, 337–346. [Google Scholar] [CrossRef]
- Hasegawa, T.; Inoue, S.; Tsuzuki, S.; Horiuchi, S.; Matsui, H.; Okada, T.; Kumai, R.; Yonekura, K.; Maki-Yonekura, S. Exploration and development of molecule-based printed electronics materials: An integrated approach using experimental, computational, and data sciences. Sci. Technol. Adv. Mater. 2024, 25, 2418282. [Google Scholar] [CrossRef]
- Xu, L.; Gu, L.-Y.; Zhao, D.-Y.; Wang, B.; Kang, T.-G. 5-(4-Chlorophenyl)-1H-tetrazole. Acta Crystallogr. Sect. E Struct. Rep. Online 2010, 66, o742. [Google Scholar] [CrossRef]
- Semmingsen, D.; Hollander, F.J.; Koetzle, T.F. A neutron diffraction study of squaric acid (3,4-dihydroxy-3-cyclobutene-1,2-dione). J. Chem. Phys. 1977, 66, 4405–4412. [Google Scholar] [CrossRef]
- Kobayashi, K.; Horiuchi, S.; Ishibashi, S.; Murakami, Y.; Kumai, R. Field-induced antipolar-polar structural transformation and giant electrostriction in organic crystal. J. Am. Chem. Soc. 2018, 140, 3842–3845. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.-Y.; Chu, X.-W.; Qu, Z.-R. 5-p-Tolyl-1H-tetrazole. Acta Crystallogr. Sect. E Struct. Rep. Online 2009, 65, o2463. [Google Scholar] [CrossRef] [PubMed]
- Desiraju, G.R.; Murty, B.N.; Kishan, K.V.R. Unexpected Hydrogen Bonding in the Crystal Structure of (4-Chlorophenyl)propiolic Acid. Role of C–H···O Hydrogen Bonds in Determining O–H···O Networks. Chem. Mater. 1990, 2, 447–449. [Google Scholar] [CrossRef]
- Das, D.; Jetti, R.K.R.; Boese, R.; Desiraju, G.R. Stereoelectronic Effects on Substituent Groups in the Solid State. Crystal Chemistry of Some Cubanecarboxylic and Phenylpropiolic Acids. Cryst. Growth Des. 2003, 3, 675–681. [Google Scholar] [CrossRef]
- Duan, G.-Y.; Sun, Y.-W.; Liu, J.-Z.; Wang, J.-W. Bis(benzimidazol-2-yl)methane. Acta Crystallogr. Sect. E Struct. Rep. Online 2005, 61, o3476–o3477. [Google Scholar] [CrossRef]
- Horiuchi, S.; Ishibashi, S.; Haruki, R.; Kumai, R.; Inada, S.; Aoyagi, S. Metaelectric Multiphase Transitions in a Highly Polarizable Molecular Crystal. Chem. Sci. 2020, 11, 6183–6192. [Google Scholar] [CrossRef]
- Williams, D.E.; Rundle, R.E. Crystal Structure of 3,4-Furandicarboxylic Acid. J. Am. Chem. Soc. 1964, 86, 1660–1666. [Google Scholar] [CrossRef]
- Semmingsen, D.; Nordenson, S.; Aasen, A. The molecular and Crystal Structure of 3,4-Furandicarboxylic Acid. Acta Chem. Scand. A 1986, 40, 559–565. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Cyranski, M. Separation of the energetic and geometric contributions to the aromaticity. Part IV. A general model for the π-electron systems. Tetrahedron 1996, 52, 10255–10264. [Google Scholar] [CrossRef]
- Bei, F.; Jian, F.; Yang, X.; Lu, L.; Wang, X.; Raj, S.S.S.; Fun, H.-K. 1,4-Bis(2-benzimidazolyl)benzene. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 2000, 56, 718–719. [Google Scholar] [CrossRef] [PubMed]
- Horiuchi, S.; Ishibashi, S.; Inada, S.; Aoyagi, S. Hydrogen-Bonded Architectures and Field-Induced Polarization Switching in Bridged Bis(benzimidazole) Crystals. Cryst. Growth Des. 2019, 19, 328–335. [Google Scholar] [CrossRef]
- Haisa, M.; Kashino, S.; Hanada, S.I.; Tanaka, K.; Okazaki, S.; Shibagaki, M. The structures of 2-hydroxy-5-methylbenzoic acid and dimorphs of 2,5-dihydroxybenzoic acid. Acta Crystallogr. Sect. B 1982, 38, 1480–1485. [Google Scholar] [CrossRef]
- Shimoi, Y.; Tsuzuki, S.; Kumai, R.; Sotome, M.; Horiuchi, S. Competing Ferroelectric Polarization: Hydroxyl Flip-Flop versus Proton-Transfer Mechanisms. J. Mater. Chem. C 2022, 10, 10099–10105. [Google Scholar] [CrossRef]
- Dahlenburg, L.; Treffert, H.; Heinemann, F.W. 1,3-Bis(α-aminoisopropyl)benzene, meta-C6H4(CMe2NH2)2: An N,N-bridging and N,C,N-cyclometalating ligand. Inorg. Chim. Acta 2008, 361, 1311–1318. [Google Scholar] [CrossRef]
- Kopf, J.; Morf, M.; Zimmer, B.; Haupt, E.T.K.; Jarchow, O.; Koll, P. The crystal and molecular structure of threitol. Carbohydr. Res. 1993, 247, 119–128. [Google Scholar] [CrossRef]
- Kanters, J.A.; Roelofsen, G.; Smits, D. The crystal and molecular structure of DL-mannitol at −150 °C. Acta Crystallogr. Sect. B 1977, 33, 3635–3640. [Google Scholar] [CrossRef]
- Hua, C.; Li, X.G.; Xu, S.M. 2,2,6,6-Tetrakis(hydroxymethyl)cyclohexanol. Acta Crystallogr. Sect. E Struct. Rep. Online 2007, 63, o547–o548. [Google Scholar] [CrossRef]
- Gibadullina, E.M.; Kayupov, A.R.; Voronina, Y.K.; Syakaev, V.V.; Pudovik, M.A.; Burilov, A.R. Phosphorylation of oxyethylated resorcinol and calix[4]resorcinarene with P(III) acid amides. Phosphorus Sulfur Silicon Relat. Elem. 2018, 193, 787–795. [Google Scholar] [CrossRef]
- Semmingsen, D.; Feder, J. A structural phase transition in squaric acid. Solid State Commun. 1974, 15, 1369–1372. [Google Scholar] [CrossRef]
- Mochida, T.; Izuoka, A.; Sugawara, T.; Moritomo, Y.; Tokura, Y. Organic hydrogen-bonded dielectrics: Quantum paraelectricity based on tautomerization of 9-hydroxyphenalenone derivatives. J. Chem. Phys. 1994, 101, 7971–7974. [Google Scholar] [CrossRef]
- Abrahams, S.C.; Bair, H.E.; Haddon, R.C.; Stillinger, F.H.; Svenseon, C. Order–disorder phase transitions in 9-hydroxyphenalenone. J. Chem. Phys. 1981, 74, 644–646. [Google Scholar] [CrossRef]
- Mochida, T.; Izuoka, A.; Sugawara, T.; Moritomo, Y.; Tokura, Y. Dielectric relaxation derived from collective molecular reorientation of 9-hydroxyphenalenone in the solid state. J. Chem. Phys. 1994, 100, 6646–6648. [Google Scholar] [CrossRef]
- Mochida, T.; Suzuki, S.; Takasu, I.; Sugawara, T. Synthesis, crystal structure, and dielectric constants of 9-hydroxy-5-iodophenalen-1-one and its deuteroxy analogue. J. Phys. Chem. Solids 2003, 64, 1257–1260. [Google Scholar] [CrossRef]
- Kiyanagi, R.; Kojima, A.; Kimura, H.; Watanabe, M.; Noda, Y.; Mochida, T.; Sugawara, T. Phase Transition Scheme of Isolated Hydrogen-bonded Material h-MeHPLN Studied by Neutron and X-ray Diffraction. J. Phys. Soc. Jpn. 2005, 74, 613–620. [Google Scholar] [CrossRef]
- Matsuo, T.; Kohno, K.; Inaba, A.; Mochida, T.; Izuoka, A.; Sugawara, T. Calorimetric study of proton tunneling in solid 5-bromo-9-hydroxyphenalenone and deuteration-induced phase transitions in its deuteroxy analog. J. Chem. Phys. 1998, 108, 9809–9816. [Google Scholar] [CrossRef]
- Kiyanagi, R.; Kimura, H.; Watanabe, M.; Noda, Y.; Mochida, T.; Sugawara, T. Indication of Tunneling State of Hydrogen Atom in Hydrogen-Bonded Material 5-Bromo-9-hydroxyphenalenon Studied by X-ray and Neutron Diffractions. J. Phys. Soc. Jpn. 2008, 77, 064602. [Google Scholar] [CrossRef]
- Szafrański, M.; Czarnecki, P.; Katrusiak, A.; Habrylo, S. DTA Investigation of Phase Transitions in 1,3-Cyclohexanedione under High Pressures. Solid State Commun. 1992, 82, 277–281. [Google Scholar] [CrossRef]
- Szafrański, M.; Katrusiak, A.; McIntyre, G.J. Ferroelectric order of parallel bistable hydrogen bonds. Phys. Rev. Lett. 2002, 89, 215507. [Google Scholar] [CrossRef] [PubMed]
- Horiuchi, S.; Ishii, F.; Kumai, R.; Okimoto, Y.; Tachibana, H.; Nagaosa, N.; Tokura, Y. Ferroelectricity near room-temperature in co-crystals of nonpolar organic molecules. Nat. Mater. 2005, 4, 163–166. [Google Scholar] [CrossRef]
- Kumai, R.; Horiuchi, S.; Okimoto, Y.; Tokura, Y. Large Dielectric Susceptibility Associated with Proton Transfer in a Supramolecular Structure of Chloranilic Acid and 5,5’-Dimethyl-2,2’-Bipyridine. J. Chem. Phys. 2006, 125, 084715. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, K.; Horiuchi, S.; Ishibashi, S.; Kagawa, F.; Murakami, Y.; Kumai, R. Structure–property relationship of supramolecular ferroelectric 6,6’-dimethyl-2,2’-bipyridinium chloranilate accompanied by high polarization, competing structural phases, and polymorphs. Chem.–Eur. J. 2014, 20, 17515. [Google Scholar] [CrossRef]
- Hollander, F.J.; Semmingsen, D.; Koetzle, T.F. The molecular and crystal structure of squaric acid (3,4-dihydroxy-3-cyclobutene-1,2-dione) at 121 °C: A neutron diffraction study. J. Chem. Phys. 1977, 67, 4825–4831. [Google Scholar] [CrossRef]
- Maier, H.-D.; Müller, D.; Petersson, J. Temperature and Frequency Dependence of the Dielectric Constant and Proton NMR near the Structural Phase Transition of Squaric Acid. Phys. Status Solidi B 1978, 89, 587–593. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Michel, K.H. Bond Geometry and Phase Transition Mechanism of H-Bonded Ferroelectrics. Phys. Rev. Lett. 1998, 80, 2173–2176. [Google Scholar] [CrossRef]
- Feder, J. Two dimensional ferroelectricity. Ferroelectrics 1976, 12, 71–83. [Google Scholar] [CrossRef]
- Moritomo, Y.; Tokura, Y.; Takahashi, H.; Mōri, N. Quantum paraelectricity and subsequent disappearance of bond alternation of molecule caused by proton dynamics in squaric acid crystal. Phys. Rev. Lett. 1991, 67, 2041–2044. [Google Scholar] [CrossRef]
- Dalal, N.; Klymachyov, A.; Bussmann-Holder, A. Coexistence of Order-Disorder and Displacive Features at the Phase Transitions in Hydrogen-Bonded Solids: Squaric Acid and its Analogs. Phys. Rev. Lett. 1998, 81, 5924–5927. [Google Scholar] [CrossRef]
- Palomar, J.; Klymachyov, A.N.; Panizian, D.; Dalal, N.S. Bisquaric Acid: Unusual Solid State NMR, Electronic Structure, and a Predicted Order−Disorder Transition. J. Phys. Chem. A 2001, 105, 8926–8930. [Google Scholar] [CrossRef]
- Takasu, I.; Sugawara, T.; Mochida, T. Dielectric Response in Bisquaric Acid Crystal: Possible Generation of Protonic Soliton in a Quasi-One-Dimensional Hydrogen-Bonded System. J. Phys. Chem. B 2004, 108, 18495–18499. [Google Scholar] [CrossRef]
- Hong, S.; Liow, C.H.; Yuk, J.M.; Byon, H.R.; Yang, Y.; Cho, E.; Yeom, J.; Park, G.; Kang, H.; Kim, S.; et al. Reducing Time to Discovery: Materials and Molecular Modeling, Imaging, Informatics, and Integration. ACS Nano 2021, 15, 3971–3995. [Google Scholar] [CrossRef] [PubMed]
- Spek, A.L. Single-crystal structure validation with the program PLATON. J. Appl. Cryst. 2003, 36, 7–13. [Google Scholar] [CrossRef]
- Abrahams, S.C. Structurally based prediction of ferroelectricity in inorganic materials with point group 6 mm. Acta Crystallogr. B 1988, 44, 585–595. [Google Scholar] [CrossRef]
- Abrahams, S.C. Systematic prediction of new ferroelectrics on the basis of structure. Ferroelectrics 2011, 104, 37–51. [Google Scholar] [CrossRef]
- Capillas, C.; Tasci, E.S.; de la Flor, G.; Orobengoa, D.; Perez-Mato, J.M.; Aroyo, M.I. A new computer tool at the Bilbao Crystallographic Server to detect and characterize pseudosymmetry. Z. Kristallogr. Cryst. Mater. 2011, 226, 186–196. [Google Scholar] [CrossRef]
- Ricci, F.; Reyes-Lillo, S.E.; Mack, S.A.; Neaton, J.B. Candidate ferroelectrics via ab initio high-throughput screening of polar materials. Npj Comp. Mater. 2024, 10, 15. [Google Scholar] [CrossRef]
- Thompson, S.Y.; Stokes, H.T.; Campbell, B.J.; Goldberg, E.D.; Evans, J.S.O. Exploitation of pseudo-symmetry in the Cambridge Structural Database for molecular ferroelectric discovery. CrystEngComm 2025. Advance Article. [Google Scholar] [CrossRef]
- Seyedraoufi, S.; Sødahl, E.D.; Görbitz, C.H.; Berland, K. Database mining and first-principles assessment of organic proton-transfer ferroelectrics. Phys. Rev. Mater. 2024, 8, 054413. [Google Scholar] [CrossRef]
- Tolédano, P.; Guennou, M. Theory of antiferroelectric phase transitions. Phys. Rev. B 2016, 94, 014107. [Google Scholar] [CrossRef]
- Marsh, R.E. The perils of Cc revisited. Acta Crystallogr. Sect. B 1997, 53, 317–322. [Google Scholar] [CrossRef]
- Taylor, R.; Wood, P.A. A Million Crystal Structures: The Whole Is Greater than the Sum of Its Parts. Chem. Rev. 2019, 119, 9427–9477. [Google Scholar] [CrossRef]
- Kurtz, S.K.; Perry, T.T. A powder technique for evaluation of nonlinear optical materials. J. Appl. Phys. 1968, 39, 3798–3813. [Google Scholar] [CrossRef]
- Sawada, R.; Uemura, H.; Sotome, M.; Yada, H.; Kida, N.; Iwano, K.; Shimoi, Y.; Horiuchi, S.; Okamoto, H. Large second-order optical nonlinearity in a ferroelectric molecular crystal of croconic acid with strong intermolecular hydrogen bonds. Appl. Phys. Lett. 2013, 102, 162901. [Google Scholar] [CrossRef]
- Sunami, K.; Horiuchi, S.; Ishibashi, S.; Tsutsumi, J. Unveiling High Electro-Optic Performance in a Proton–π-Electron-Coupled Ferroelectric Crystal. Adv. Electron. Mater. 2024, 2024, 2400346. [Google Scholar] [CrossRef]
- Szklarz, P.; Bator, G. Pyroelectric properties of tricyclohexylmethanol (TCHM) single crystal. J. Phys. Chem. Solids 2005, 66, 121–125. [Google Scholar] [CrossRef]
- Zelenovskii, P.S.; Vasileva, D.S.; Vasilev, S.G.; Kopyl, S.; Kholkin, A. Ferroelectricity in glycine: A mini-review. Front. Mater. 2022, 9, 918890. [Google Scholar] [CrossRef]
- Ishibashi, S.; Tamura, T.; Tanaka, S.; Kohyama, M.; Terakura, K. Ab Initio Calculations of Electric-Field-Induced Stress Profiles for Diamond/c−BN (110) Superlattices. Phys. Rev. B 2007, 76, 153310. [Google Scholar] [CrossRef]
- Available online: http://www.qmas.jp/ (accessed on 18 August 2025).
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground State of the Electron Gas by a Stochastic Method. Phys. Rev. Lett. 1980, 45, 566–569. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Dion, M.; Rydberg, H.; Schröder, E.; Langreth, D.C.; Lundqvist, B.I. Van der Waals Density Functional for General Geometries. Phys. Rev. Lett. 2004, 92, 246401. [Google Scholar] [CrossRef]
- King-Smith, R.D.; Vanderbilt, D. Theory of Polarization of Crystalline Solids. Phys. Rev. B 1993, 47, 1651–1654. [Google Scholar] [CrossRef] [PubMed]
- Resta, R. Macroscopic Polarization in Crystalline Dielectrics: The Geometric Phase Approach. Rev. Mod. Phys. 1994, 66, 899–915. [Google Scholar] [CrossRef]
- Spaldin, N.A. A beginner’s guide to the modern theory of polarization. J. Solid State Chem. 2012, 195, 2–10. [Google Scholar] [CrossRef]
- Ishibashi, S.; Terakura, K.J. Exotic Ferroelectricity in Tetrathiafulvalene-p-Chloranil: Anomalous Effective Charges and a Picture in the Framework of Maximally Localized Wannier Orbitals. J. Phys. Soc. Jpn. 2014, 83, 073702. [Google Scholar] [CrossRef]
- Terakura, K.; Ishibashi, S. Mechanism of covalency-induced electric polarization within the framework of maximally localized Wannier orbitals. Phys. Rev. B 2015, 91, 195120. [Google Scholar] [CrossRef]
- Horiuchi, S.; Kumai, R.; Ishibashi, S. Single-component organic molecular ferroelectrics based on disk- or wheel-like rotation. J. Mater. Chem. C 2021, 9, 13739–13747. [Google Scholar] [CrossRef]
- Ishibashi, S.; Horiuchi, S.; Kumai, R. Hydrogen-bonded single-component organic ferroelectrics revisited by van der Waals density-functional theory calculations. Phys. Rev. Mater. 2021, 5, 094409. [Google Scholar] [CrossRef]
- Berland, K.; Hyldgaard, P. Exchange functional that tests the robustness of the plasmon description of the van der Waals density functional. Phys. Rev. B 2014, 89, 035412. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Van Voorhis, T. Nonlocal van der Waals density functional: The simpler the better. J. Chem. Phys. 2010, 133, 244103. [Google Scholar] [CrossRef]
- Sabatini, R.; Gorni, T.; de Gironcoli, S. Nonlocal van der Waals density functional made simple and efficient. Phys. Rev. B 2013, 87, 041108. [Google Scholar] [CrossRef]
- Saenger, W.; Betzel, C.; Hingerty, B.; Brown, G.M. Flip-flop hydrogen bonding in a partially disordered system. Nature 1982, 296, 581–583. [Google Scholar] [CrossRef]
- Chen, P.; Marianski, M.; Baldauf, C. H-Bond Isomerization in Crystalline Cellulose III: Proton Hopping versus Hydroxyl Flip-Flop. ACS Macro Lett. 2016, 5, 50–54. [Google Scholar] [CrossRef] [PubMed]
- Ishibashi, S.; Kumai, R.; Horiuchi, S. A straightforward method using the sign of the piezoelectric coefficient to identify the ferroelectric switching mechanism. Sci. Rep. 2023, 13, 8810. [Google Scholar] [CrossRef] [PubMed]
- Horiuchi, S.; Tsutsumi, J.; Kobayashi, K.; Kumai, R.; Ishibashi, S. Piezoelectricity of Strongly Polarized Ferroelectrics in Prototropic Organic Crystals. J. Mater. Chem. C 2018, 6, 4714–4719. [Google Scholar] [CrossRef]
- Liu, S.; Chen, R.E. Origin of Negative Longitudinal Piezoelectric Effect. Phys. Rev. Lett. 2017, 119, 207601. [Google Scholar] [CrossRef]
- You, L.; Zhang, Y.; Zhou, S.; Chaturvedi, A.; Morris, S.A.; Liu, F.; Chang, L.; Ichinose, D.; Funakubo, H.; Hu, W.; et al. Origin of giant negative piezoelectricity in a layered van der Waals ferroelectric. Sci. Adv. 2019, 5, eaav3780. [Google Scholar] [CrossRef]
- Ghosh, P.S.; Lisenkov, S.; Ponomareva, I. Negative longitudinal piezoelectricity coexisting with both negative and positive transverse piezoelectricity in a hybrid formate perovskite. ACS Appl. Mater. Interfaces 2022, 14, 46449–46456. [Google Scholar] [CrossRef]
- Furukawa, T.; Wen, J.X. Electrostriction and Piezoelectricity in Ferroelectric Polymers. Jpn. J. Appl. Phys. 1984, 23, L677–L679. [Google Scholar] [CrossRef]
- Katsoureas, I.; Asadi, K.; Li, M.; Van Dreil, T.B.; Kjaer, K.S.; Zhao, D.; Lenz, T.; Gu, Y.; Blom, P.W.M.; Damjanovic, D.; et al. The negative piezoelectric effect of the ferroelectric polymer poly(vinylidene fluoride). Nat. Commun. 2016, 15, 78–84. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q. Ferroelectric Polymers Exhibiting Negative Longitudinal Piezoelectric Coefficient: Progress and Prospects. Adv. Sci. 2020, 7, 1902468. [Google Scholar] [CrossRef]
- Liu, S.; Cui, Z.; Fu, P.; Liu, M.; Zhang, Y.; Jia, R.; Zhao, Q. Piezoelectricity and ferroelectricity in odd-odd nylons with long alkane segments. Appl. Phys. Lett. 2014, 104, 172906. [Google Scholar]
- Urbanaviciute, I.; Meng, X.; Biler, M.; Wei, Y.; Cornelissen, T.D.; Bhattacharjee, S.; Linares, M.; Kemerink, M. Negative piezoelectric effect in an organic supramolecular ferroelectric. Mater. Horiz. 2019, 6, 1688–1698. [Google Scholar] [CrossRef]
- Lu, H.; Kim, D.-J.; Aramberri, H.; Holzer, M.; Buragohain, P.; Dutta, S.; Schroeder, U.; Deshpande, V.; Íñiguez, J.; Gruverman, A.; et al. Electrically induced cancellation and inversion of piezoelectricity in ferroelectric Hf0.5Zr0.5O2. Nature Commun. 2024, 15, 860. [Google Scholar] [CrossRef]
- Dutta, S.; Buragohain, P.; Glinsek, S.; Richter, C.; Aramberri, H.; Lu, H.; Schroeder, U.; Defay, E.; Gruverman, A.; Íñiguez, J. Piezoelectricity in hafnia. Nat. Commun. 2021, 12, 7301. [Google Scholar] [CrossRef]
- Qi, Y.; Reyes-Lillo, S.E.; Rabe, K.M. Sign of the piezoelectric response in double-rath ferroelectrics. Phys. Rev. B 2025, 111, L180101. [Google Scholar] [CrossRef]
- Ishii, F.; Nagaosa, N.; Tokura, Y.; Terakura, K. Covalent ferroelectricity in hydrogen-bonded organic molecular systems. Phys. Rev. B 2006, 73, 212105. [Google Scholar] [CrossRef]
- Ishibashi, S.; Horiuchi, S.; Kumai, R. Computational finding of metastable ferroelectric phases of squaric acid. Phys. Rev. B 2018, 97, 184102, Erratum in: Phys. Rev. B 2023, 108, 059903. [Google Scholar] [CrossRef]
- Moina, A.P. Polarization rotation by external electric field in the two-dimensional antiferroelectric squaric acid H2C4O4. Phys. Rev. B 2021, 103, 214104. [Google Scholar] [CrossRef]
- Moina, A.P. Negative/positive electrocaloric effect in antiferroelectric squaric acid. J. Appl. Phys. 2023, 133, 094101. [Google Scholar] [CrossRef]
- Grünebohm, A.; Ma, Y.-.B.; Marathe, M.; Xu, B.-X.; Able, K.; Kalcher, C.; Meyer, K.-C.; Shvartsman, V.V.; Lupascu, D.C.; Ederer, C. Origins of the Inverse Electrocaloric Effect. Energy Technol. 2018, 6, 1491–1511. [Google Scholar] [CrossRef]
- Wang, G.; Lu, Z.; Li, Y.; Li, L.; Ji, H.; Feteira, A.; Zhou, D.; Wang, D.; Zhang, S.; Reaney, I.M. Electroceramics for High-Energy Density Capacitors: Current Status and Future Perspectives. Chem. Rev. 2021, 121, 6124–6172. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, T.; Ye, J.; Wang, G.; Dong, X.; Withers, R.; Liu, Y. Antiferroelectrics for Energy Storage Applications: A Review. Adv. Mater. Technol. 2018, 3, 1800111. [Google Scholar] [CrossRef]
- Yang, L.; Kong, X.; Li, F.; Hao, H.; Cheng, Z.; Liu, H.; Li, J.F.; Zhang, S. Perovskite lead-free dielectrics for energy storage applications. Prog. Mater. Sci. 2019, 102, 72–108. [Google Scholar] [CrossRef]
- Hao, X.; Zhai, J.; Kong, L.B.; Xu, Z. A comprehensive review on the progress of lead zirconate-based antiferroelectric materials. Prog. Mater. Sci. 2014, 63, 1–57. [Google Scholar] [CrossRef]
- Yan, F.; Qian, J.; Wang, S.; Zhai, J. Progress and outlook on lead-free ceramics for energy storage applications. Nano Energy 2024, 123, 109394. [Google Scholar] [CrossRef]
- Park, M.H.; Hwang, C.S. Fluorite-structure antiferroelectrics. Rep. Prog. Phys. 2019, 82, 124502. [Google Scholar] [CrossRef]
- Berlincourt, D. Transducers using forced transition between ferroelectric and antiferroelectric states. IEEE Trans. Sonics Ultrason. 1966, 13, 116–124. [Google Scholar] [CrossRef]
- Uchino, K. Antiferroelectric Shape Memory Ceramics. Actuators 2016, 5, 11. [Google Scholar] [CrossRef]
- Narayan, B.; Malhotra, J.S.; Pandey, R.; Yaddanapudi, K.; Nukala, P.; Dkhil, B.; Senyshyn, A.; Ranjan, R. Electrostrain in excess of 1% in polycrystalline piezoelectrics. Nat. Mater. 2018, 17, 427–431. [Google Scholar] [CrossRef]
- Park, S.; Shrout, T.R. Ultrahigh Strain and piezoelectric behavior in relaxor based ferroelectric single crystals. J. Appl. Phys. 1997, 82, 1804–1811. [Google Scholar] [CrossRef]
- Zhuo, F.; Li, Q.; Zhou, Y.; Ji, Y.; Yan, Q.; Zhang, Y.; Xi, X.; Chu, X.; Cao, W. Large field-induced strain, giant strain memory effect, and high thermal stability energy storage in (Pb,La)(Zr,Sn,Ti)O3 antiferroelectric single crystal. Acta Mater. 2018, 148, 28–37. [Google Scholar] [CrossRef]
- Pan, H.; Zhu, M.; Banyas, E.; Alaerts, L.; Acharya, M.; Zhang, H.; Kim, J.; Chen, X.; Huang, X.; Xu, M.; et al. Clamping enables enhabnces electromechanical responses in antiferroelectric thin films. Nat. Mater. 2024, 23, 944–950. [Google Scholar] [CrossRef]
- Piezoelectric Materials Data Book; Ferroperm Ltd.: Kvistgard, Denmark, 1996.
- Lasave, J.; Koval, S.; Dalal, N.S.; Migoni, R.L. Origin of Antiferroelectricity in NH4H2PO4 from First Principles. Phys. Rev. Lett. 2007, 98, 267601. [Google Scholar] [CrossRef]
- Moriwake, H.; Konishi, A.; Ogawa, T.; Fisher, C.A.J.; Kuwabara, A.; Fu, D. The electric field induced ferroelectric phase transition of AgNbO3. J. Appl. Phys. 2016, 119, 064102. [Google Scholar] [CrossRef]
- Li, P.F.; Liao, W.Q.; Tang, Y.Y.; Ye, H.Y.; Zhang, Y.; Xiong, R.G. Unprecedented Ferroelectric–Antiferroelectric–Paraelectric Phase Transitions Discovered in an Organic–Inorganic Hybrid Perovskite. J. Am. Chem. Soc. 2017, 139, 8752–8757. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, X.; Ji, C.; Li, L.; Wang, S.; Peng, Y.; Tao, K.; Sun, Z.; Hong, M.; Luo, J. Discovery of an Above-Room-Temperature Antiferroelectric in Two-Dimensional Hybrid Perovskite. J. Am. Chem. Soc. 2019, 141, 3812–3816. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, Y.; Zeng, X.; Xu, H.; Guo, W.; Wang, B.; Hua, L.; Tang, L.; Luo, J.; Sun, Z. A high-temperature double perovskite molecule-based antiferroelectric with excellent anti-breakdown capacity for energy storage. Nat. Commun. 2023, 14, 2420. [Google Scholar] [CrossRef]
- Kagawa, F.; Horiuchi, S.; Minami, N.; Ishibashi, S.; Kobayashi, K.; Kumai, R.; Murakami, Y.; Tokura, Y. Polarization switching ability dependent on multidomain topology in a uniaxial organic ferroelectric. Nano Lett. 2014, 14, 239–243. [Google Scholar] [CrossRef] [PubMed]

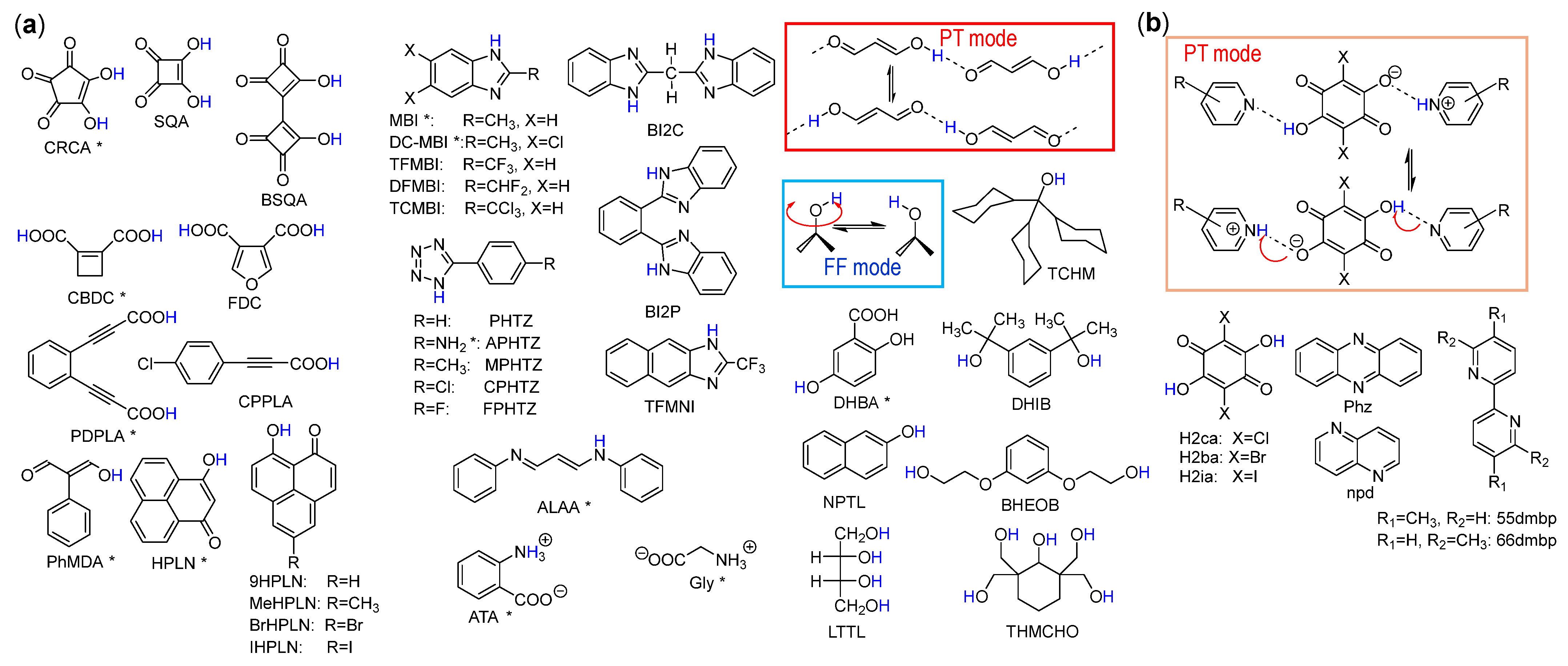
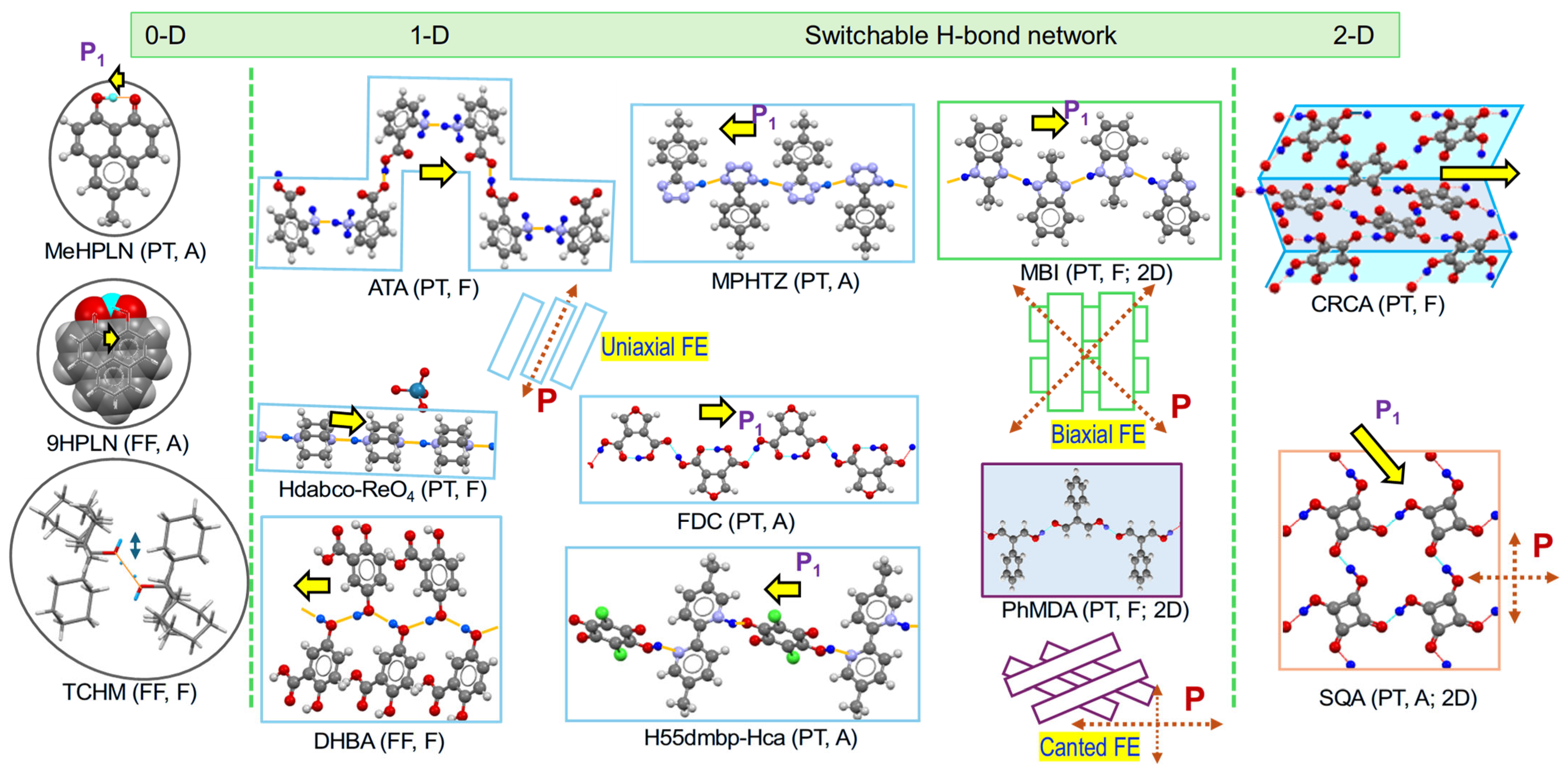
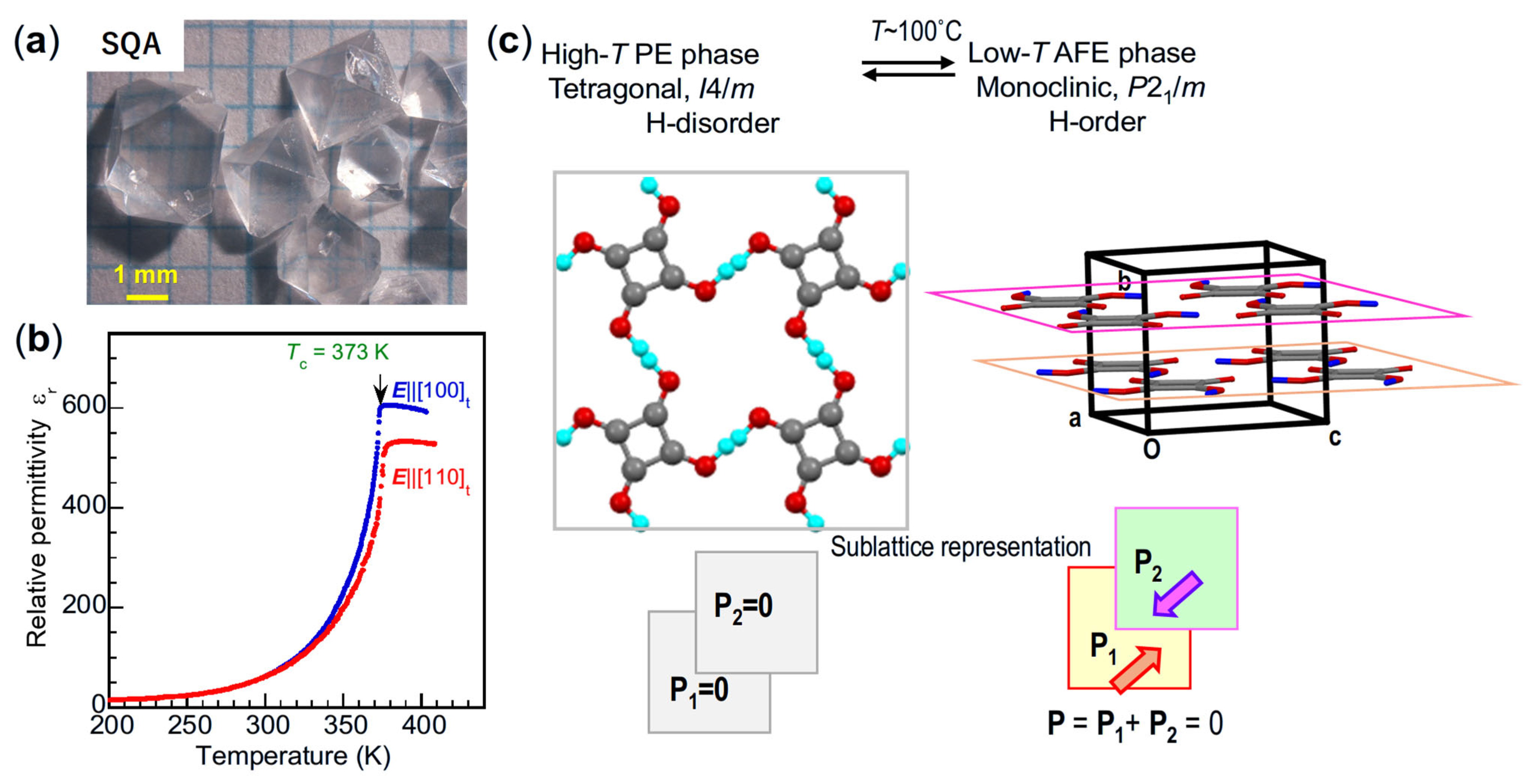
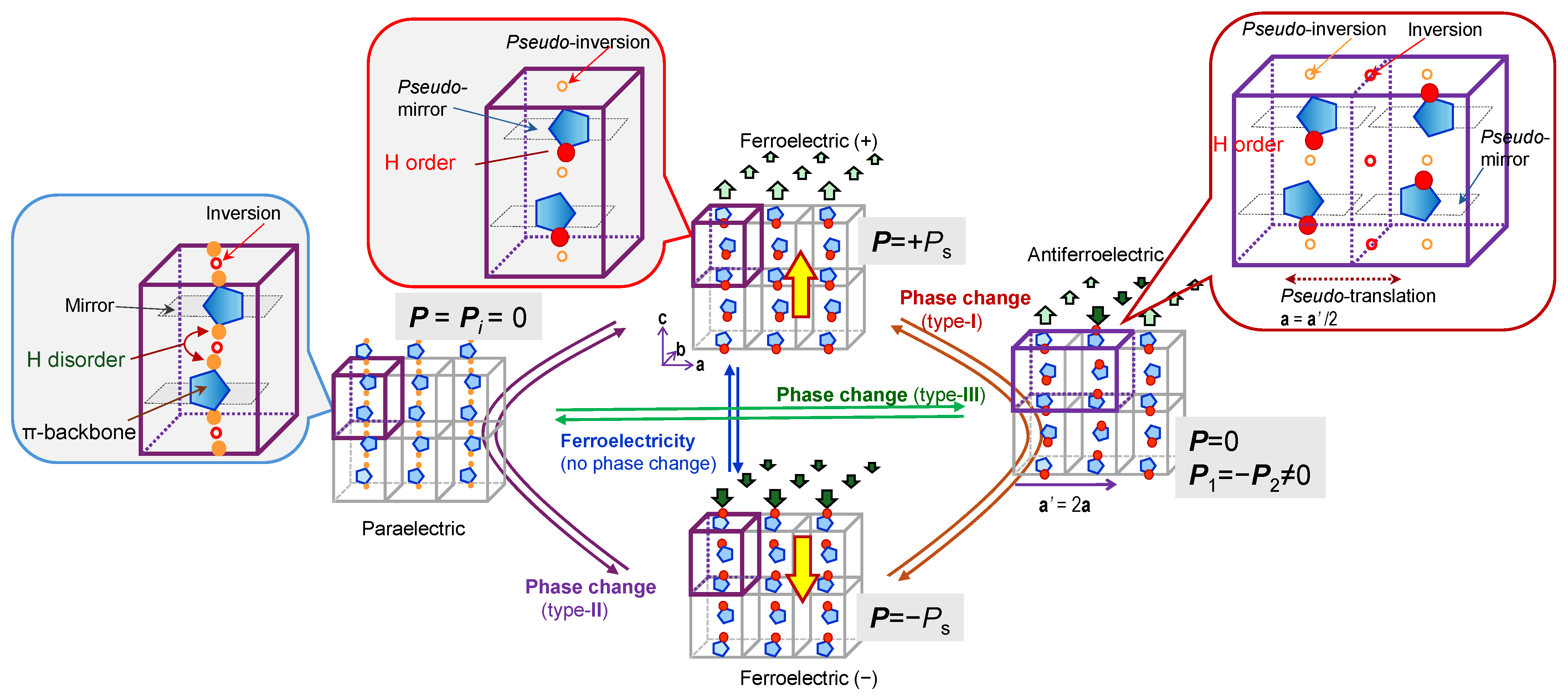
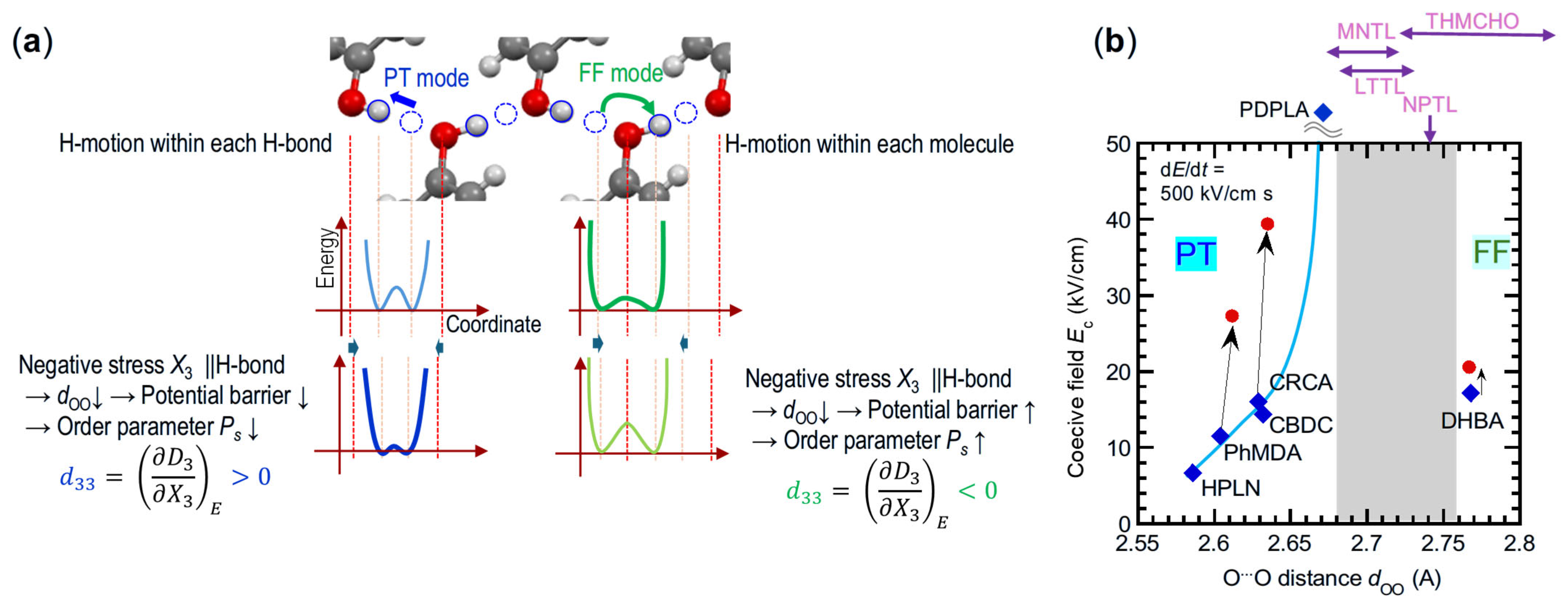
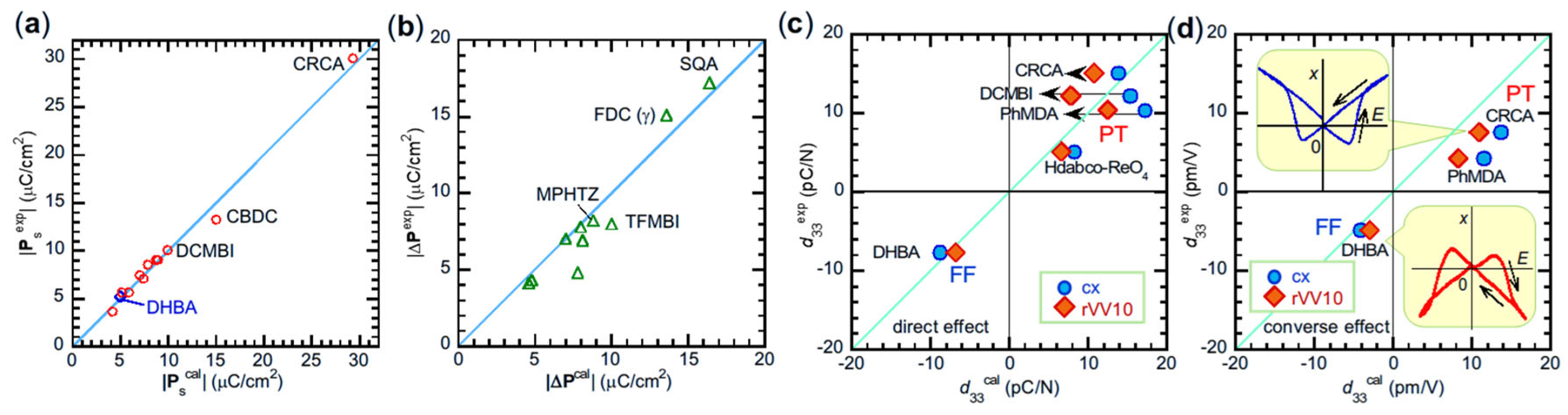
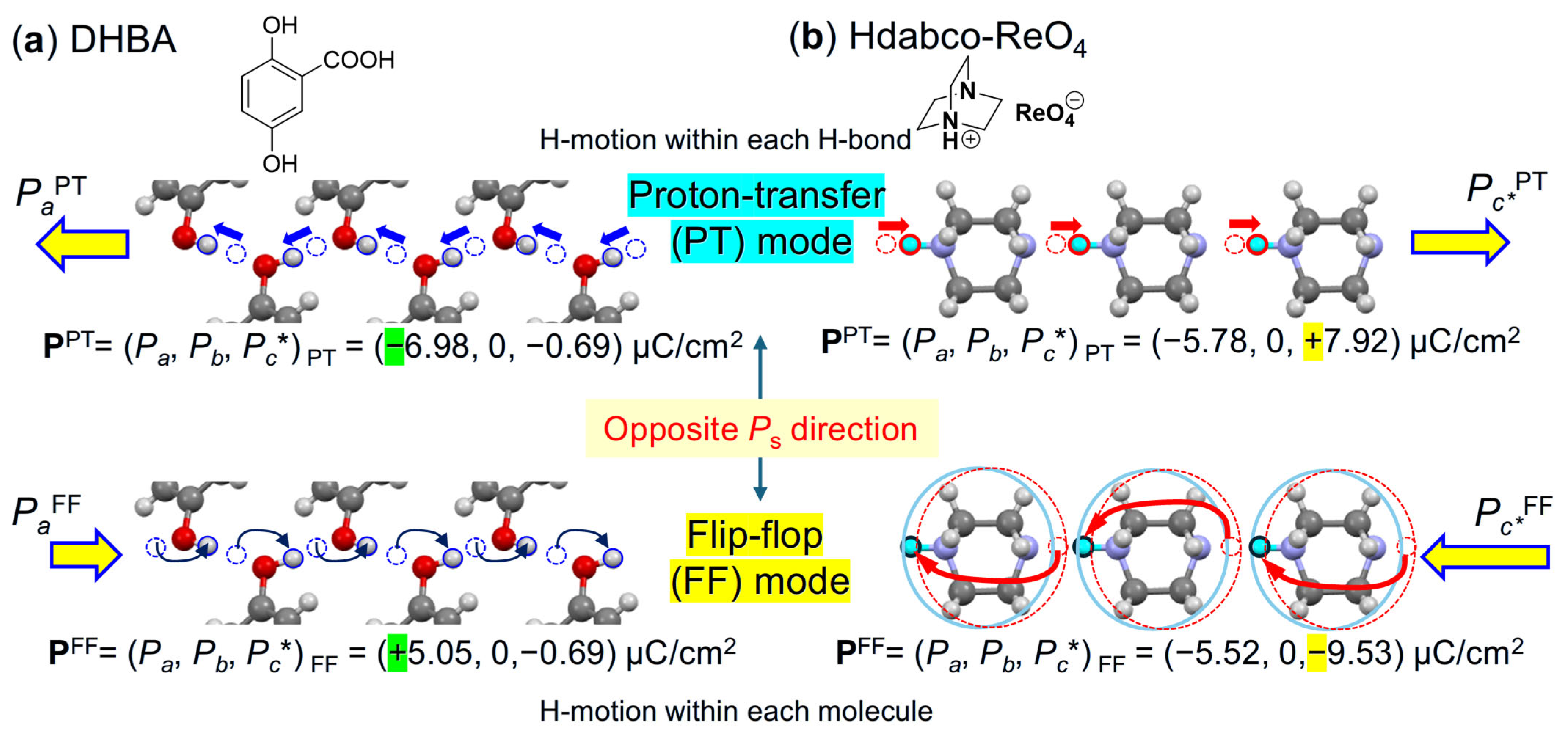
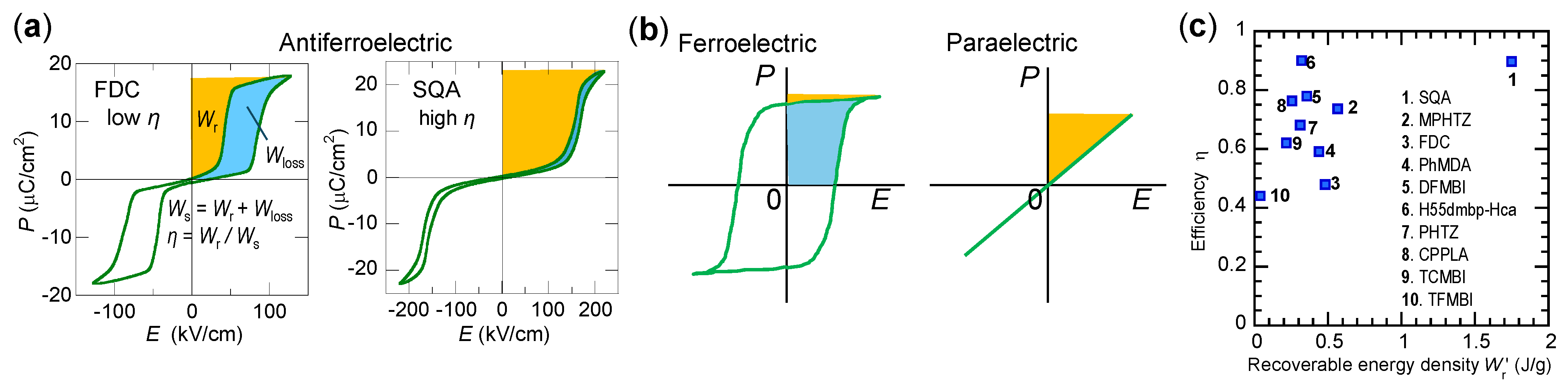
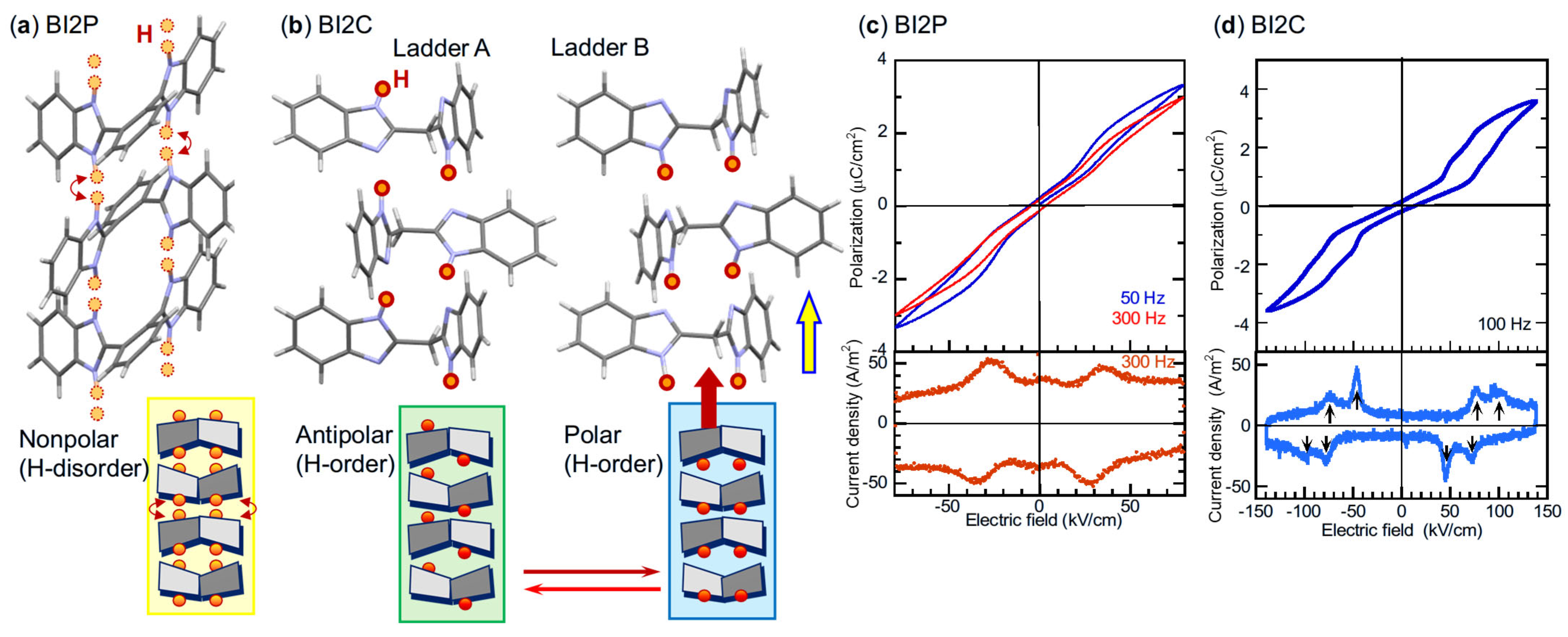
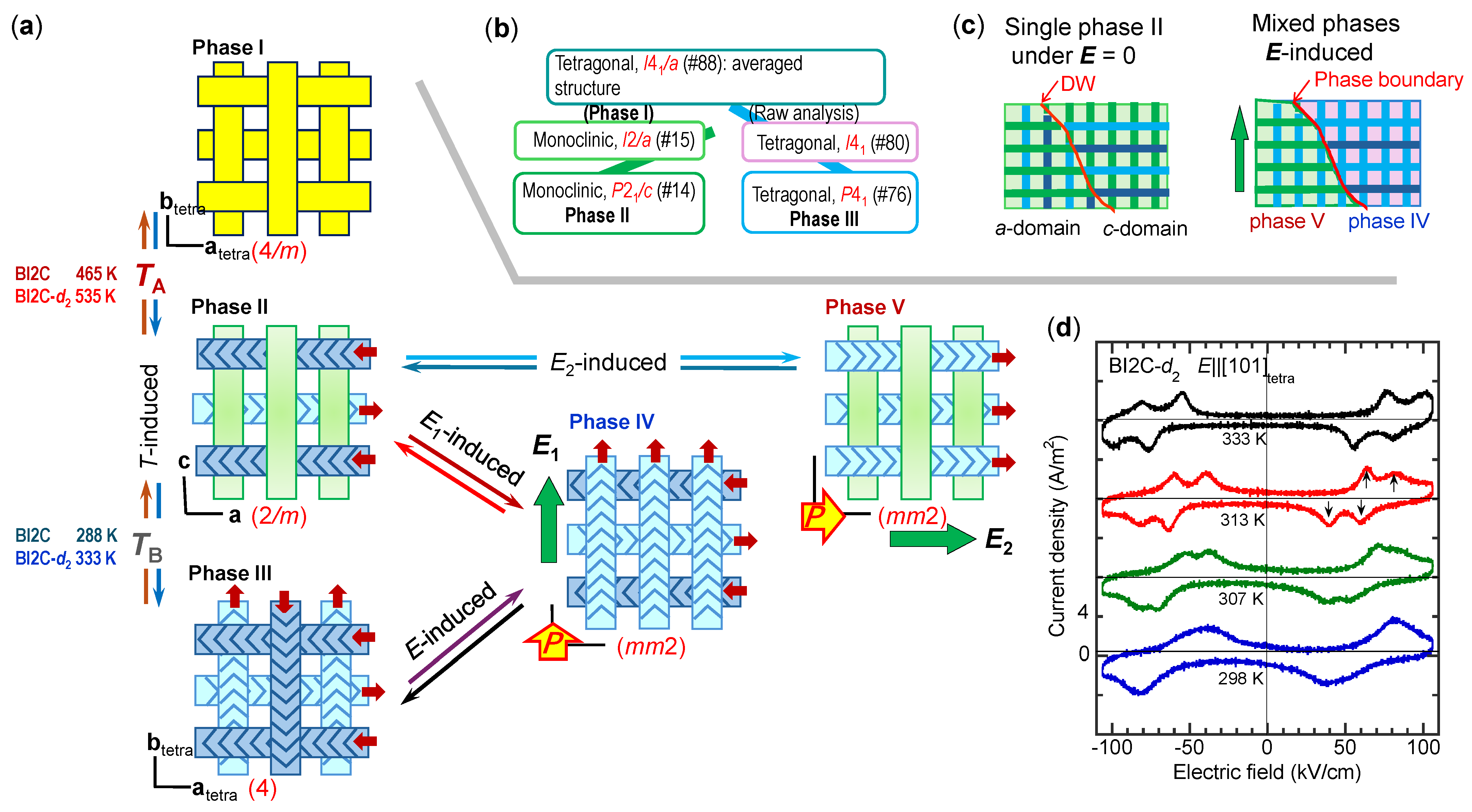
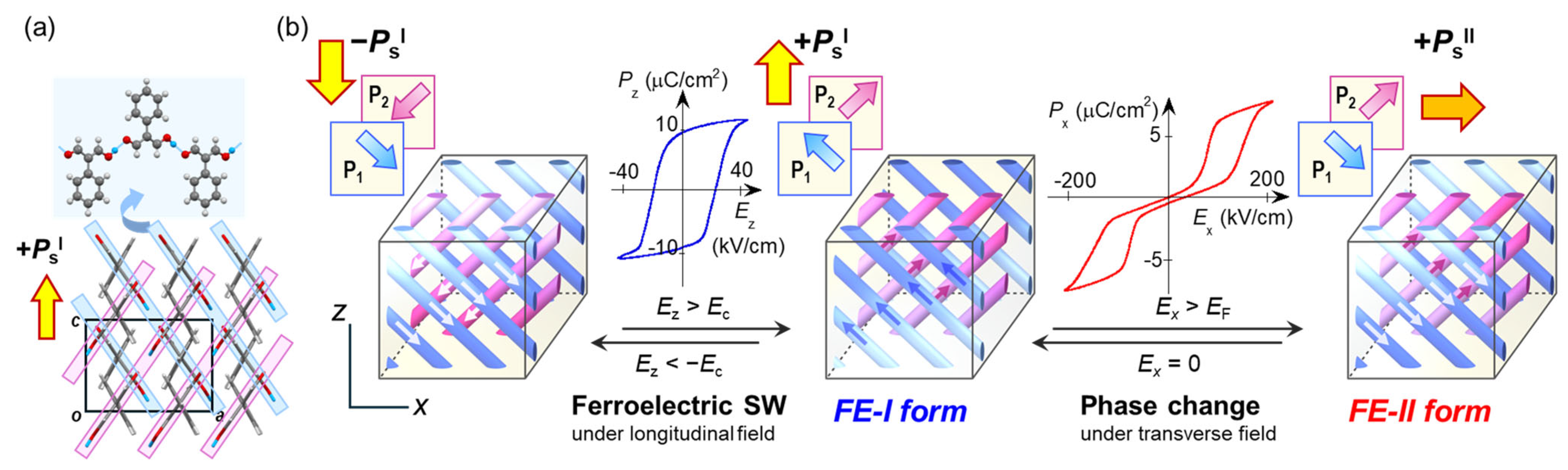
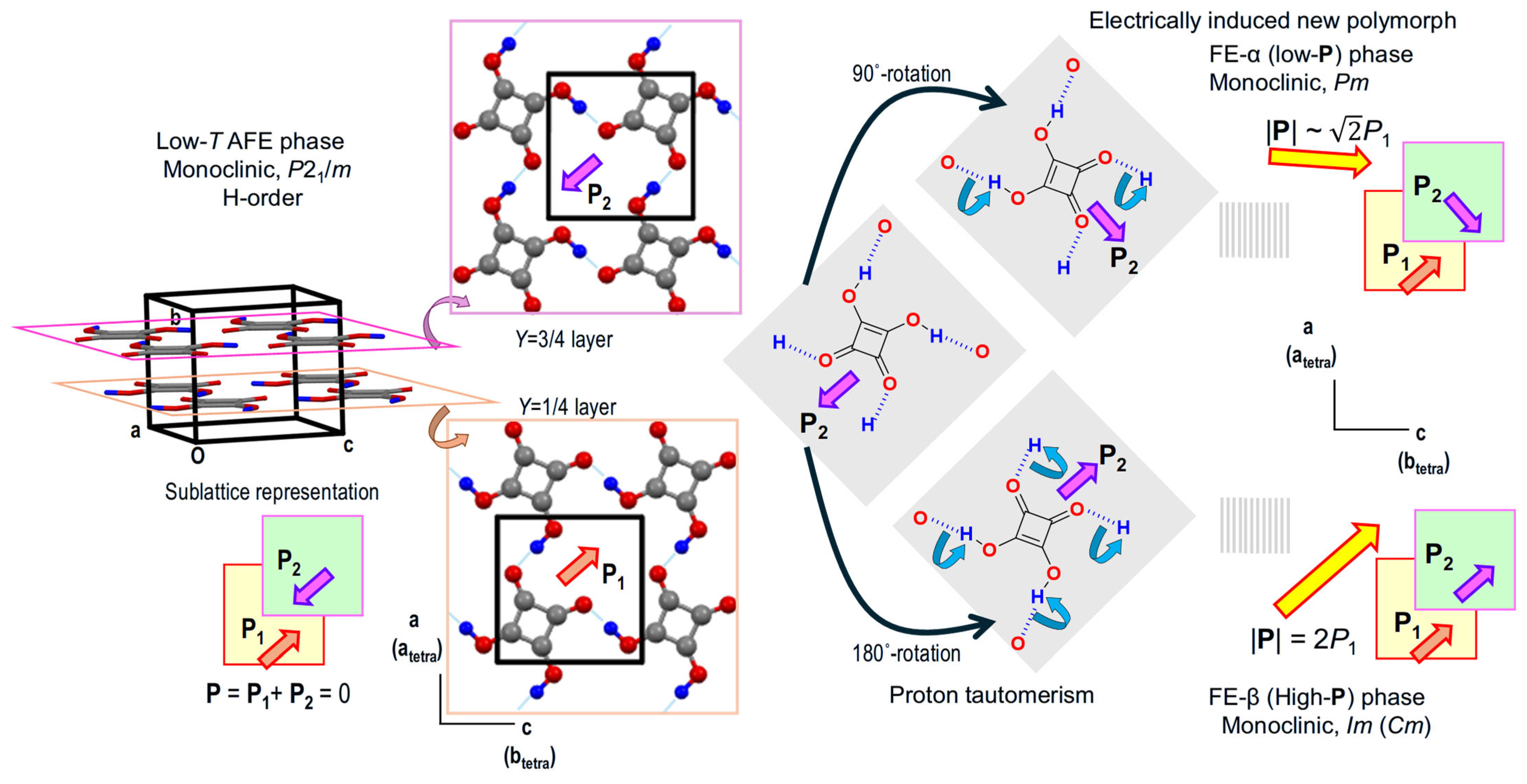
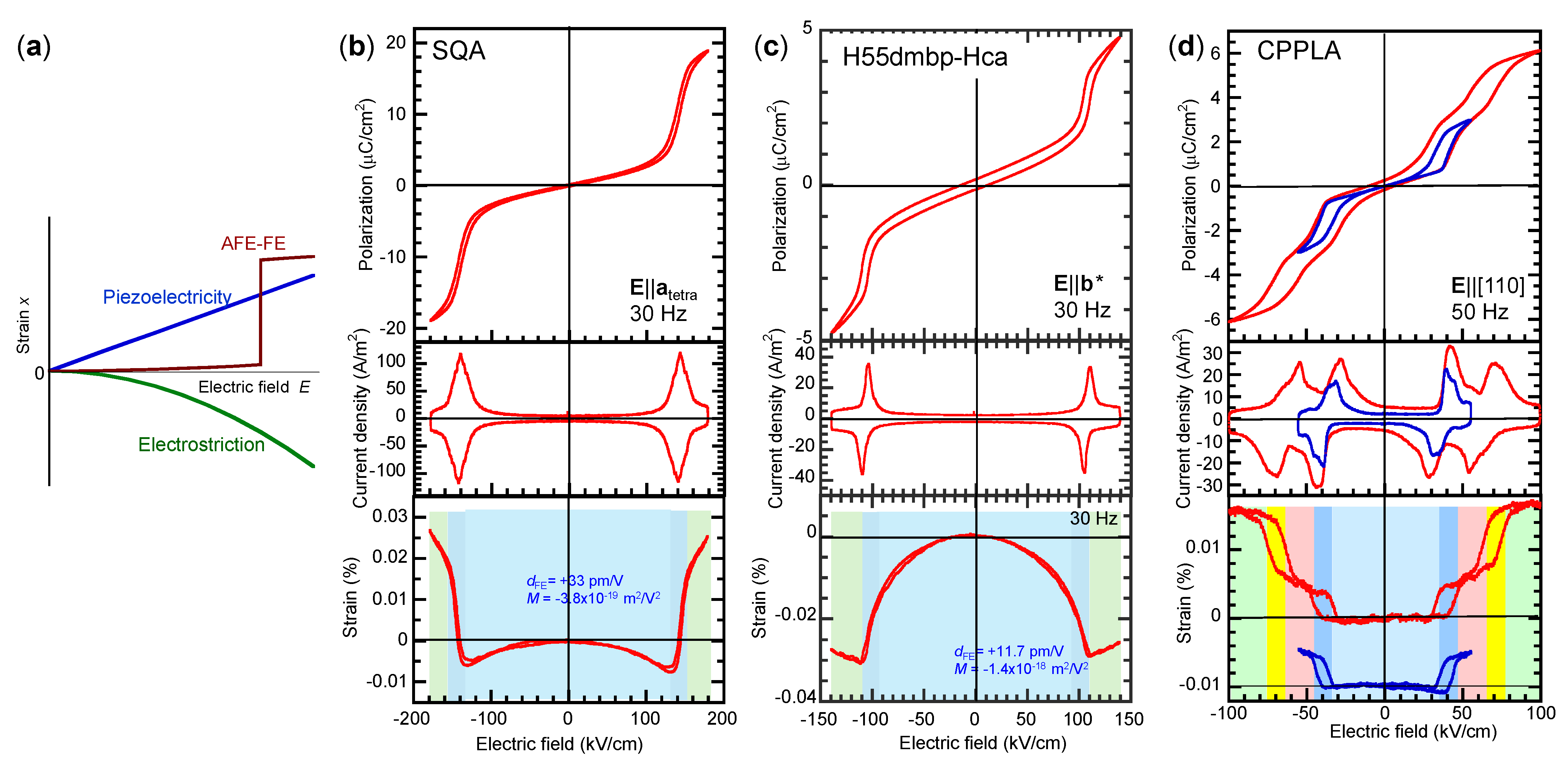
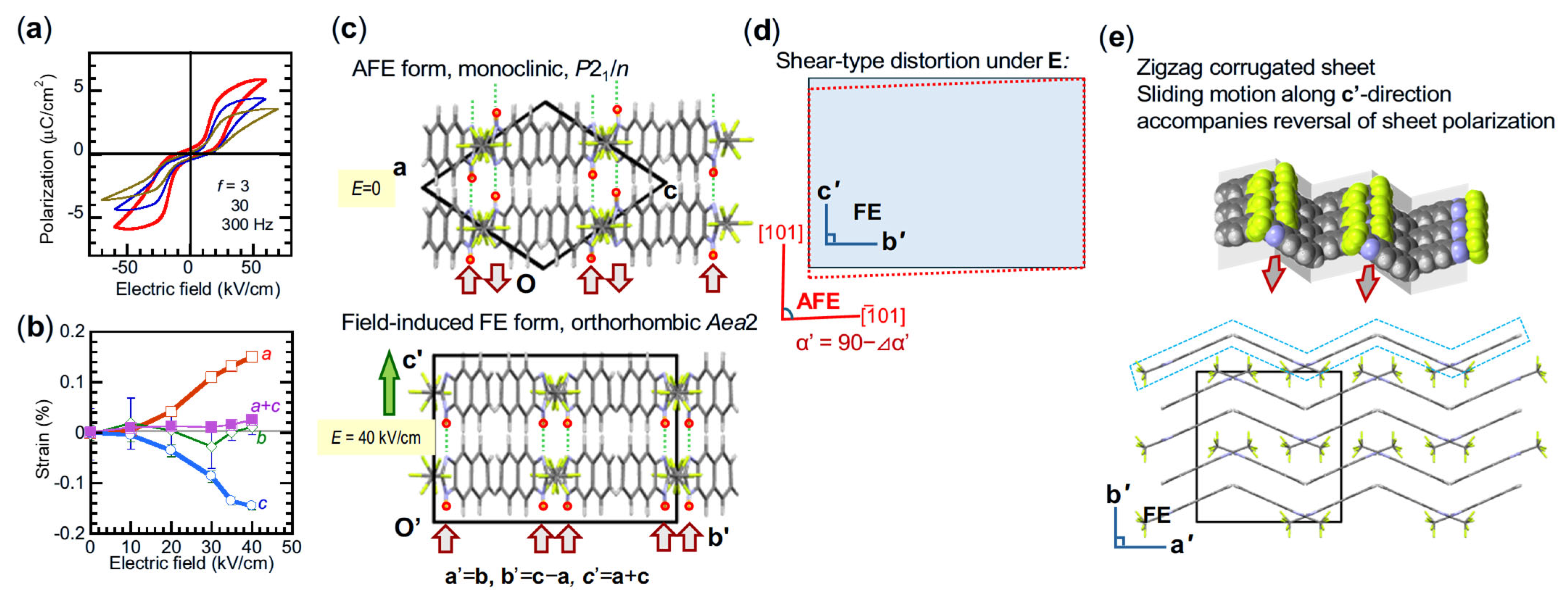
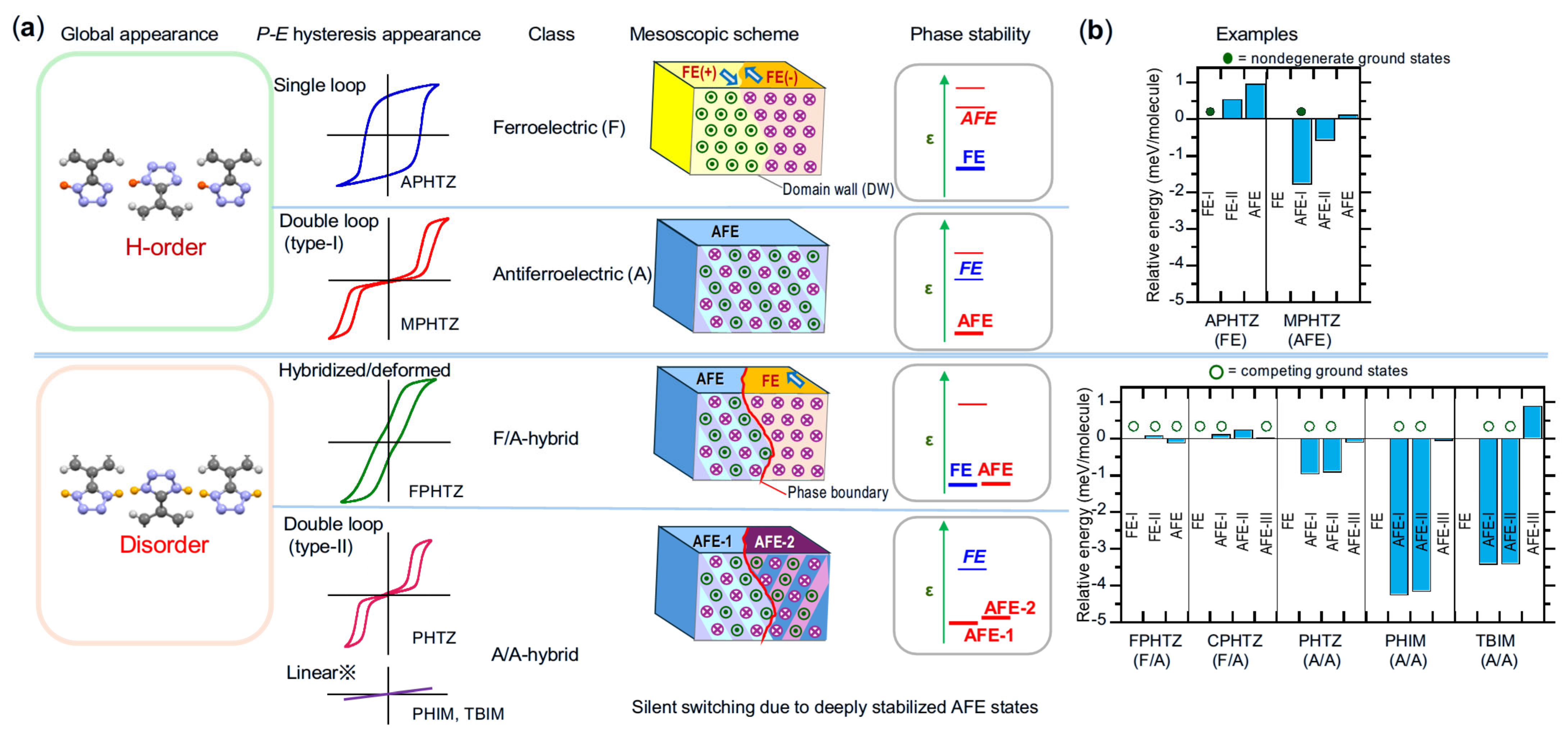
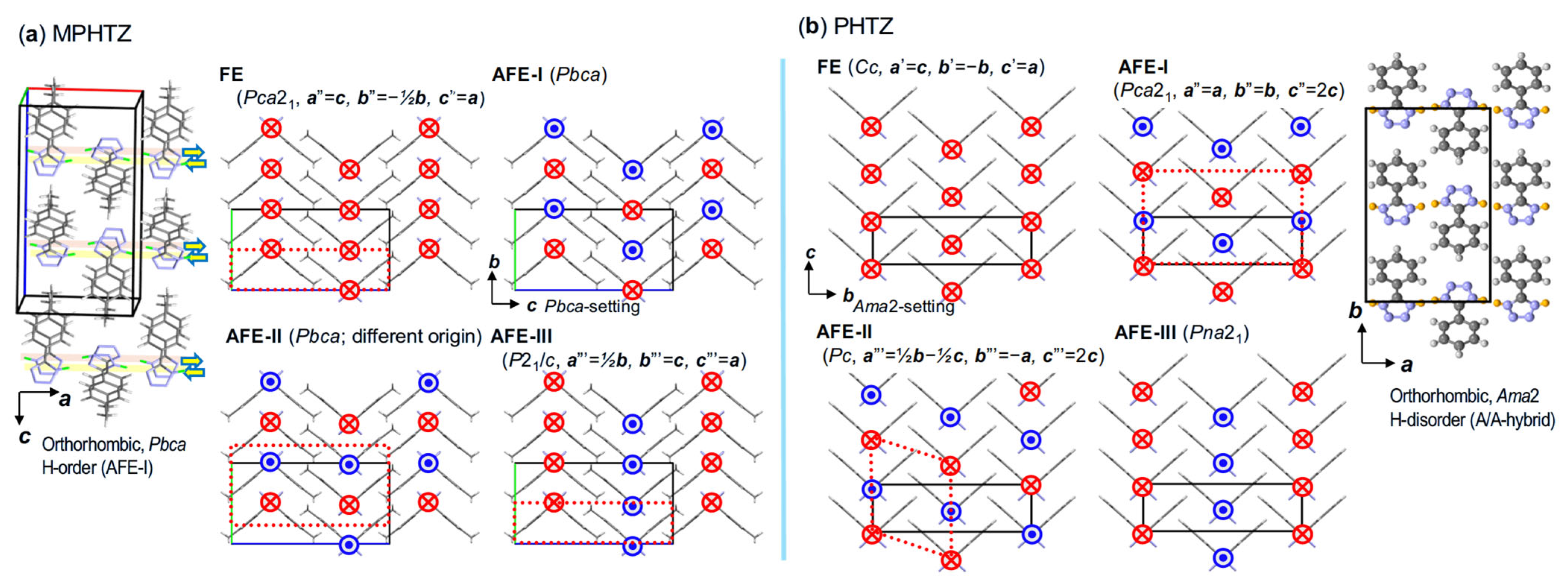
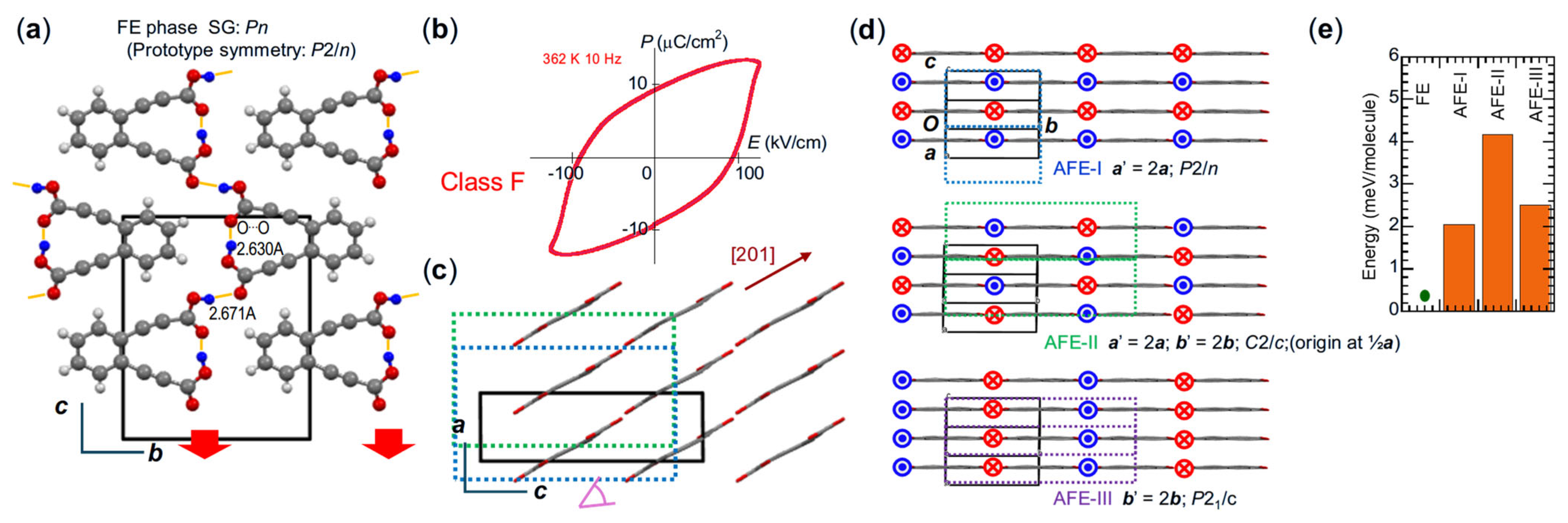

| Compound | Class | Polarization (μC/cm2) | SHG a (×urea) | Space Gr@RT b Proper {psd-sym} | Pseudo-Symmetry Elements | CSD Refcode | Refs. | Hydrogen Bond | sw. Field (kV/cm) d | ΔU (meV/molecule) e | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |Ps| | |ΔP| | Axis | dOO (Å) | dNN (Å) | Ec c | EFA (ΔEFA) {f (Hz)} | ||||||||
| Proton-transfer type | ||||||||||||||
| CRCA | F | 30 (29.4) | c | 47 ± 13 | Pca21 {Pcam} | −1, m | GUMMUW | [22,23] | 2.62–2.63 | 16.0/39.3 | ||||
| CBDC | F | 13.2 (15.1) | [] | 0.23 | Cc {C2/c} | −1, 2 | CBUDCX | [23,28] | 2.63–2.64 | 14.3 | ||||
| PhMDA | F | 9 (9.0) | 5.8 (6.1) | c; a | 17.2 | Pna21 {Pnab} | −1, b | PROLON | [25,28] | 2.60 | 11.5/27.2 | 110 (59) {100} | 0.79 † | |
| HPLN | F | 5.6 (5.2) | a | 1.4 | Pn {P21/n} | −1, 21 | TAPZIT | [28] | 2.55–2.59 | 6.7 | ||||
| MBI | F | 7.4 (7.1) | atetra | 0.14 | Pn {P42/n} | −1, 42 | KOWYEA | [29] | 2.86–2.97 | 15.4 | ||||
| DCMBI | F | 10 (10.0) | c | 0.56 | Pca21 {Pcam} | −1, m | REZBOP | [29] | 2.98 | |||||
| ALAA | F | 3.6 (4.2) | c | - | Iba2 {Ibca} | −1, a | ANPHPR | [23] | 2.97 | 26 | ||||
| ATA | F | 5.6 (5.97) | a | 0.25 | P21cn {Pccn} | −1, c | AMBACO | [30] | 2.54 | 2.87 | ||||
| APHTZ | F | 7.0 (7.5) | a | 0.09 | Pn {P21/n} | −1, 21 | CITVIL | [31,32] | 2.90–2.91 | 34.4 | ||||
| PDPLA | F | 9 (8.8) | [201] | 0.28 | Pc {P2/c} | −1, 2 | HOQMEG | [33,34] | 2.63–2.67 | |||||
| CPHTZ | F/A | (9.2) | [101] | ND | P2/c (*) | KUSLUG | [31,35] | 2.89 | ||||||
| FPHTZ | F/A | (7.9) | a | 0.01 | P21/n (*) | VIHLUX | [31] | 2.91 | ||||||
| SQA | A | 17.2 (16.4) | atetra | ND | P21/m {I4/m} | I, 4 | KECYBU | [24,25,36] | 2.55 | 166 (6) {50} | 1.27 | |||
| TFMBI | A | 7.8 (8.0) | c | ND | P21/c {Pbcm} | b, m | ZAQRIU | [29] | 2.87 | 13 (8) {0.2} | ||||
| DFMBI | A | 8.0 (10.0) | c | ND | P21/c {Pbcm} | b, m | REZBIJ | [29] | 2.85 | 67 (12) {2} | ||||
| TCMBI | A | 7.0 (7.0) | a | 2.4 | P21 {Pmc21} # | c, m | REZBAB | [29] | 2.80–2.81 | 49 (22) {10} | ||||
| TFMNI | A | 4.8 (7.8) | [101] | ND | P21/n {Cmce} | C, m, 2 | NIBCAF | [37] | 2.97 | 24 (11) {100} | 1.01 | |||
| MPHTZ | A | 8.2 (8.8) | a | ND | Pbca {Pbcm} | T, m | QUCJII | [31,38] | 2.80 | 88 (24) {100} | 1.78 | |||
| CPPLA | A | 4.3 (4.8) | b | ND | P-1 {1/2c} | T, −1 | SUHSET | [25,39,40] | 2.61–2.65 | 55 {100} | 0.19 | |||
| BI2C | A | 4.1 (4.6) | atetra | ND | P21/c {I41/a} | I, 41 | XAVFEG | [41,42] | 2.77–2.85 | 75 (32) {100} | ||||
| FDC (γ) | A | 15.1 (13.6) | [] | ND | P-1 {1/2a; P21/c} | T, d | FURDCB | [25] | 2.54–2.65 | 62 (40) {50} | 0.62 | |||
| FDC (α) | (A) | (13.7) | b | - | P21/c {1/2c; P21/m} | T, m | FURDCB | [25,43,44] | 2.54–2.65 | 2.98 | ||||
| PHTZ | A/A | 6.9 (8.1) | a | - | Ama2 (*) # | TOSJOA | [31,45] | 2.83 | 65 (21) {100} | 0.96 | ||||
| BI2P | F/A | (8.8) | c | 0.02 | Pccn (*) | AWEHAL | [46,47] | 2.86 | 31 (8) {300} | |||||
| Hydrogen flip-flop type | ||||||||||||||
| DHBA | F | 5.2 (5.0) | a | 0.02 | Pc {P21/c} | −1, 21 | BESKAL | [48,49] | 2.77 | 17.1/20.5 | ||||
| DHIB | F/A | (4.6) | c | ND | P2/c (*) | SIXNAP | [34,50] | 2.90–2.91 | 24 (26) {100} | |||||
| NPTL | (F) | ND | c | 0.09 | Cc {C2/c} | −1, 2 | NAPHOB | [49] | 2.74 | >180 | ||||
| LTTL | (F) | ND | c | 0.01 | P32 {P3212} | 2, 2 | LEDPUF | [34,51] | 2.68–2.73 | >100 | ||||
| MNTL | (F) | ND | c | 0.07 | Pna21 {Pnam} | −1, m | DLMANT | [34,52] | 2.67–2.72 | >360 | ||||
| THMCHO | (F) | ND | c | 0.01 | Pna21 {Pnam} | −1, m | YEYLUK | [34,53] | 2.72–2.83 | >300 | ||||
| BHEOB | (A/A) | >1 | c | ND | C2/c (*) | XAHBOB | [34,54] | 2.75–2.83 | >130 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horiuchi, S.; Minemawari, H.; Tsutsumi, J.; Ishibashi, S. Field-Effect Crystal Engineering in Proton–π-Electron Correlated Systems. Crystals 2025, 15, 736. https://doi.org/10.3390/cryst15080736
Horiuchi S, Minemawari H, Tsutsumi J, Ishibashi S. Field-Effect Crystal Engineering in Proton–π-Electron Correlated Systems. Crystals. 2025; 15(8):736. https://doi.org/10.3390/cryst15080736
Chicago/Turabian StyleHoriuchi, Sachio, Hiromi Minemawari, Jun’ya Tsutsumi, and Shoji Ishibashi. 2025. "Field-Effect Crystal Engineering in Proton–π-Electron Correlated Systems" Crystals 15, no. 8: 736. https://doi.org/10.3390/cryst15080736
APA StyleHoriuchi, S., Minemawari, H., Tsutsumi, J., & Ishibashi, S. (2025). Field-Effect Crystal Engineering in Proton–π-Electron Correlated Systems. Crystals, 15(8), 736. https://doi.org/10.3390/cryst15080736






