Molecular Dynamics Simulations on the Deformation Behaviors and Mechanical Properties of the γ/γ′ Superalloy with Different Phase Volume Fractions
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Models
2.2. Simulation Method
2.3. Atomic Interactions
2.4. Microstructure and Strain Distribution Analysis Method
3. Results and Analysis
3.1. The Stress–Strain Responses and Associated Mechanical Properties
3.2. The Microstructure Evolution Analysis
3.3. The Atomic Strain Distribution Analysis
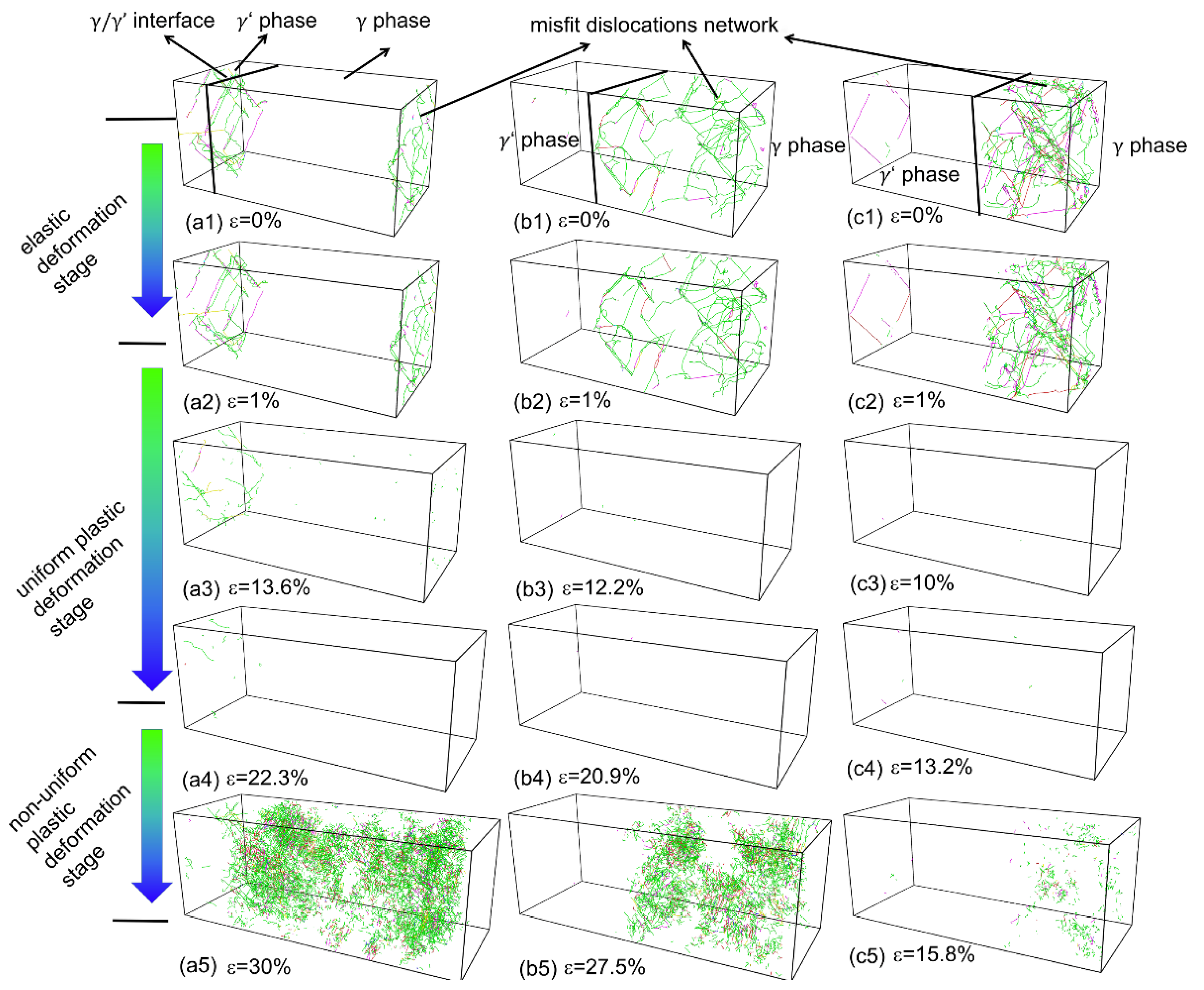
3.4. The Dislocation Configuration Evolution Analysis
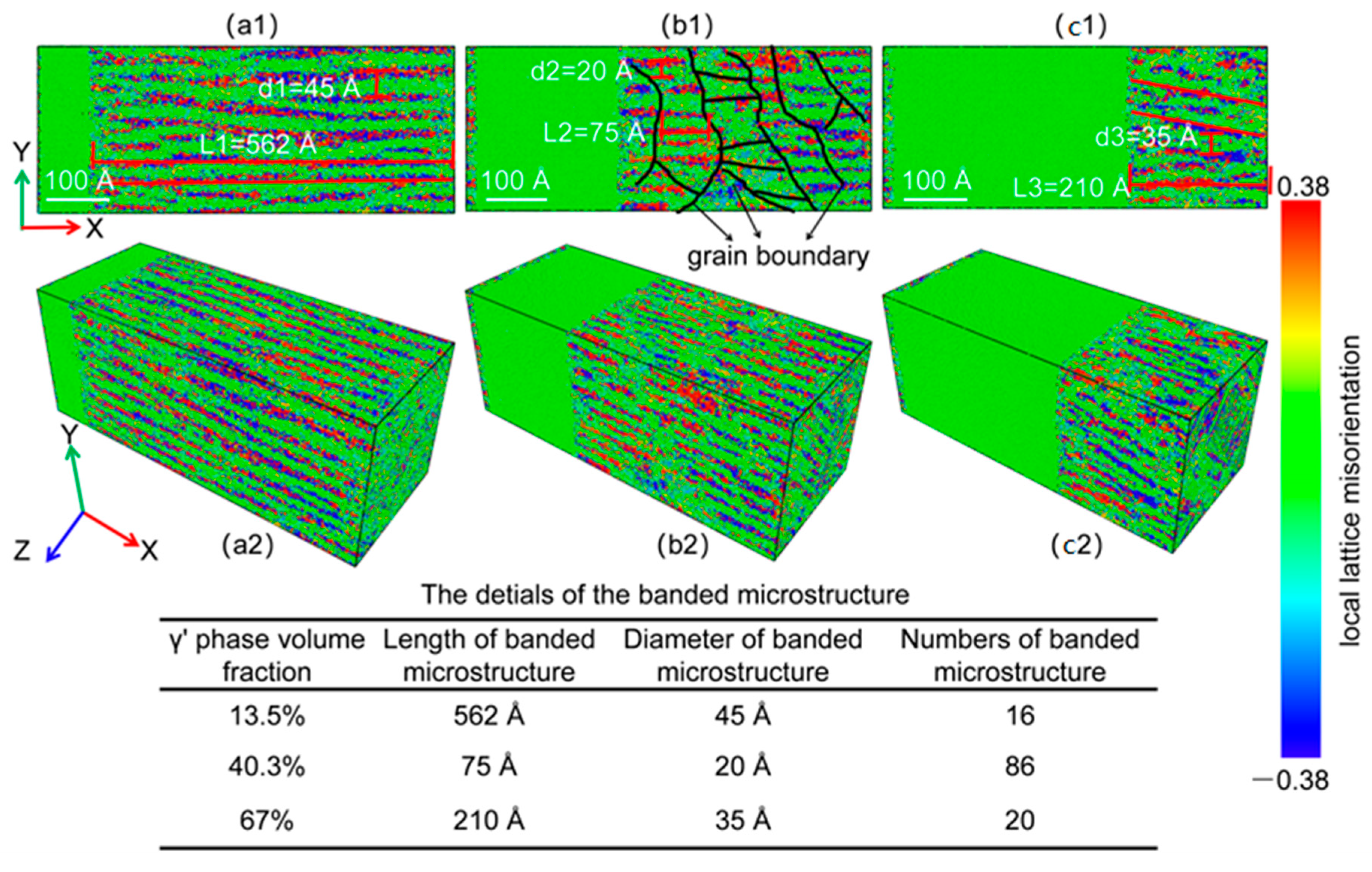
3.5. The Local Lattice Misorientation Analysis
4. Discussion
4.1. Deformation Behaviors
4.2. Mechanical Properties
5. Conclusions
- For a system with low phase volume fraction, the deformation process involved the decomposition of stacking faults (misfit dislocation network) of the phase and the uniform phase transformation of the local atom structure of the phase. Thus, we obtained a lamellar microstructure of uniformly distributed mixed BCC/HCP microstructures in the phase. The atomic stress concentration (strain localization) occurred only at the / phase interface, leading to the initiation of nanopore at the phase interface.
- For the system with a high phase volume fraction, the deformation process was mainly related to the decomposition of stacking faults and the phase transformation of the local atoms’ structure of the phase. Because of the interaction between the stacking faults and the mixed BCC/HCP microstructure, the long-lamellar microstructure of mixed BCC/HCP atoms was broken down into many short-lamellar microstructures, which could be regarded as fine grains. The atomic stress concentration (strain localization) emerged at the interaction region of the stacking faults and mixed BCC/HCP microstructure, resulting in the initiation of nanopore at this area.
- As the phase volume fraction increased from 13.5 to 67%, the tensile strength () of the system first increased to its maximum value and then gradually decreased. The maximum uniform plastic strain () decreased linearly and significantly with an increase in the phase volume fraction. Based on our calculation, we obtained the functional relationship between the tensile strength (), maximum uniform plastic strain () and the phase volume fraction of / superalloy under this severe service condition.
- The deformation system with phase volume fractions ( had excellent comprehensive mechanical properties.
- The results of this study offered a theoretical framework to explain the difference in the mechanical properties for the / superalloy with different phase volume fractions. It also provided a theoretical basis for the composition and microstructure design of / superalloys.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, W.-P.; Guo, Y.-F.; Wang, Y.-S.; Mueller, R.; Gross, D. Molecular dynamics simulation of the structural evolution of misfit dislocation networks at γ/γ′ phase interfaces in Ni-based superalloys. Philos. Mag. 2011, 91, 357–372. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, Q.; Liu, R.; Yue, Z.; Tang, M.; Li, X. Molecular dynamics simulation of crack propagation behaviors at the Ni/Ni3Al grain boundary. RSC Adv. 2014, 4, 32749. [Google Scholar] [CrossRef]
- Li, H.; Du, W.; Liu, Y. Molecular Dynamics Study of Tension Process of Ni-Based Superalloy. Acta Metall. Sin. (Engl. Lett.) 2020, 33, 741–750. [Google Scholar] [CrossRef]
- Pollock, T.M.; Tin, S. Nickel-Based Superalloys for Advanced Turbine Engines: Chemistry, Microstructure and Properties. J. Propuls. Power 2006, 22, 361–374. [Google Scholar] [CrossRef]
- Chamanfar, A.; Sarrat, L.; Jahazi, M.; Asadi, M.; Weck, A.; Koul, A.K. Microstructural characteristics of forged and heat treated Inconel-718 disks. Mater. Des. 2013, 52, 791–800. [Google Scholar] [CrossRef]
- McAllister, D.; Lv, D.; Peterson, B.; Deutchman, H.; Wang, Y.; Mills, M.J. Lower temperature deformation mechanisms in a γ″-strengthened Ni-base superalloy. Scr. Mater. 2016, 115, 108–112. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, Y.; Yu, Y. Revealing mechanical property–strengthening micro-mechanism of Ni/Ni3Al-based alloys by molecular dynamics simulation. J. Mol. Model. 2022, 28, 371. [Google Scholar] [CrossRef]
- Lapin, J. Effect of ageing on the microstructure and mechanical behaviour of a directionally solidified Ni3Al-based alloy. Intermet. 1997, 5, 615–624. [Google Scholar] [CrossRef]
- Wu, J.; Li, C.; Liu, Y.; Xia, X.; Wu, Y.; Li, Y.; Wang, H. Formation and widening mechanisms of envelope structure and its effect on creep behavior of a multiphase Ni3Al-based intermetallic alloy. Mater. Sci. Eng. A 2019, 763, 138158. [Google Scholar] [CrossRef]
- Pope, D.P.; Ezz, S.S. Mechanical properties of Ni3AI and nickel-base alloys with high volume fraction of γ′. Int. Met. Rev. 1984, 29, 136–167. [Google Scholar] [CrossRef]
- Kawahara, K.; Kaneno, Y.; Kakitsuji, A.; Takasugi, T. Microstructural factors affecting hardness property of dual two-phase intermetallic alloys based on Ni3Al–Ni3V pseudo-binary alloy system. Intermetallics 2009, 17, 938–944. [Google Scholar] [CrossRef]
- Yun-Jiang, W.; Chong-Yu, W. First-principles calculations for the elastic properties of Ni-base model superalloys: Ni_Ni3Al multilayers. Chin. Phys. B 2009, 18, 4339–4348. [Google Scholar] [CrossRef]
- Qin, X.; Liang, Y.; Gu, J.; Peng, G. The Effect of Interatomic Potentials on the Nature of Nanohole Propagation in Single-Crystal Nickel: A Molecular Dynamics Simulation Study. Crystals 2023, 13, 585. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, X.; Yang, X.-S.; He, W.; Shi, S.-Q.; Ma, X. Atomistic simulation of martensitic transformations induced by deformation of α-Fe single crystal during the mode-I fracture. J. Mater. Sci. 2020, 56, 2275–2295. [Google Scholar] [CrossRef]
- Li, J.; Dong, L.; Zang, X.; Zhang, X.; Zhao, W.; Wang, F. Study on micro-crack propagation behavior of single-crystal α-Ti under shear stress based on molecular dynamics. Mater. Today Commun. 2020, 25, 101622. [Google Scholar] [CrossRef]
- Yashiroa, K.; Naitob, M.; Tomitac, Y. Molecular dynamics simulation of dislocation nucleation and motion at γ/γ′ interface in Ni-based superalloy. Int. J. Mech. Sci. 2002, 44, 1845–1860. [Google Scholar] [CrossRef]
- Li, N.-L.; Wu, W.-P.; Nie, K. Molecular dynamics study on the evolution of interfacial dislocation network and mechanical properties of Ni-based single crystal superalloys. Phys. Lett. A 2018, 382, 1361–1367. [Google Scholar] [CrossRef]
- Yang, H.; Zhu, L.; Zhang, R.; Zhou, J.; Sun, Z. Influence of high stacking-fault energy on the dissociation mechanisms of misfit dislocations at semi-coherent interfaces. Int. J. Plast. 2020, 126, 102610. [Google Scholar] [CrossRef]
- Li, B.; Dong, C.; Yu, J.; Zhang, Q.; Zhou, H.; Liu, R. Mechanical behaviour and microstructural evolution of Ni-based single crystal alloys under shock loading. RSC Adv. 2018, 8, 22127–22135. [Google Scholar] [CrossRef]
- Chen, B.; Wu, W.-P. Molecular dynamics simulations of dynamics mechanical behavior and interfacial microstructure evolution of Ni-based single crystal superalloys under shock loading. J. Mater. Res. Technol. 2021, 15, 6786–6796. [Google Scholar] [CrossRef]
- Qin, X.; Yan, W.; Liang, Y.; Li, F. Effects of the temperature, strain rate, and loading conditions on the deformation behaviors and mechanical properties of the Ni/Ni3Al superalloy. RSC Adv. 2024, 14, 21821–21831. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Ackland, G.J.; Tichy, G.; Vitek, V.; Finnis, M.W. Simple N-body potentials for the noble metals and nickel. Philos. Mag. A 1987, 56, 735–756. [Google Scholar] [CrossRef]
- Purja Pun, G.P.; Mishin, Y. Development of an interatomic potential for the Ni-Al system. Philos. Mag. 2009, 89, 3245–3267. [Google Scholar] [CrossRef]
- Ben, L.; Shiming, Z.; Essa, F.A.; Chao, D.; Jingui, Y.; Qiaoxin, Z. Crack Propagation and Microstructural Evolution of Ni-based Single Crystal Alloy Under Shear Loads. Rare Metal. Mater. Eng. 2018, 47, 1370–1376. [Google Scholar] [CrossRef]
- Chen, B.; Wu, W.-P.; Chen, M.-X. Orientation-Dependent Morphology and Evolution of Interfacial Dislocation Networks in Ni-Based Single-Crystal Superalloys: A Molecular Dynamics Simulation. Acta Mech. Solida Sin. 2020, 34, 79–90. [Google Scholar] [CrossRef]
- Larsen, P.M.; Schmidt, S.; Schiøtz, J. Robust structural identification via polyhedral template matching. Model. Simul. Mater. Sci. Eng. 2016, 24, 055007. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sci. Eng. 2012, 20, 085007. [Google Scholar] [CrossRef]
- Shimizu, F.; Ogata, S.; Li, J. Theory of Shear Banding in Metallic Glasses and Molecular Dynamics Calculations. Mater. Trans. 2007, 48, 2923–2927. [Google Scholar] [CrossRef]
- Falk, M.L.; Langer, J.S. Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E 1998, 57, 7192–7205. [Google Scholar] [CrossRef]
- Park, M.H.; Shibata, A.; Harjo, S.; Tsuji, N. Grain refinement of dual phase steel maximizes deformation ability of martensite, leading to simultaneous enhancement of strength and ductility. Acta Mater. 2025, 292, 121061. [Google Scholar] [CrossRef]
- Cautaerts, N.; Crout, P.; Ånes, H.W.; Prestat, E.; Jeong, J.; Dehm, G.; Liebscher, C.H. Free, flexible and fast: Orientation mapping using the multi-core and GPU-accelerated template matching capabilities in the Python-based open source 4D-STEM analysis toolbox Pyxem. Ultramicroscopy 2022, 237, 113517. [Google Scholar] [CrossRef] [PubMed]
- Jariwala, S.; Sun, H.; Adhyaksa, G.W.; Lof, A.; Muscarella, L.A.; Ehrler, B.; Garnett, E.C.; Ginger, D.S. Local crystal misorientation influences non-radiative recombination in halide perovskites. Joule 2019, 3, 3048–3060. [Google Scholar] [CrossRef]
- Park, J.-U.; Jun, S.-Y.; Lee, B.H.; Jang, J.H.; Lee, B.-S.; Lee, H.-J.; Lee, J.-H.; Hong, H.-U. Alloy design of Ni-based superalloy with high γ′ volume fraction suitable for additive manufacturing and its deformation behavior. Addit. Manuf. 2022, 52, 102680. [Google Scholar] [CrossRef]
- Feng, L.; Gencang, Y.; Xuefeng, G. Research of grain refinement in undercooled DD3 single crystal superalloy. Mater. Sci. Eng. A 2001, 311, 54–63. [Google Scholar] [CrossRef]
- Liu, F.; Gencang, Y. Stress-induced recrystallization mechanism for grain refinement in highly undercooled superalloy. J. Cryst. Growth 2001, 231, 295–305. [Google Scholar] [CrossRef]
- Zhang, W.W.; Yang, Y.; Tan, Y.B.; Zeng, M.T.; Ma, M.; Xiang, S.; Zhao, F. Microstructure evolution and strengthening mechanisms of MP159 superalloy during room temperature rolling and cryorolling. J. Alloys Compd. 2022, 908, 164667. [Google Scholar] [CrossRef]
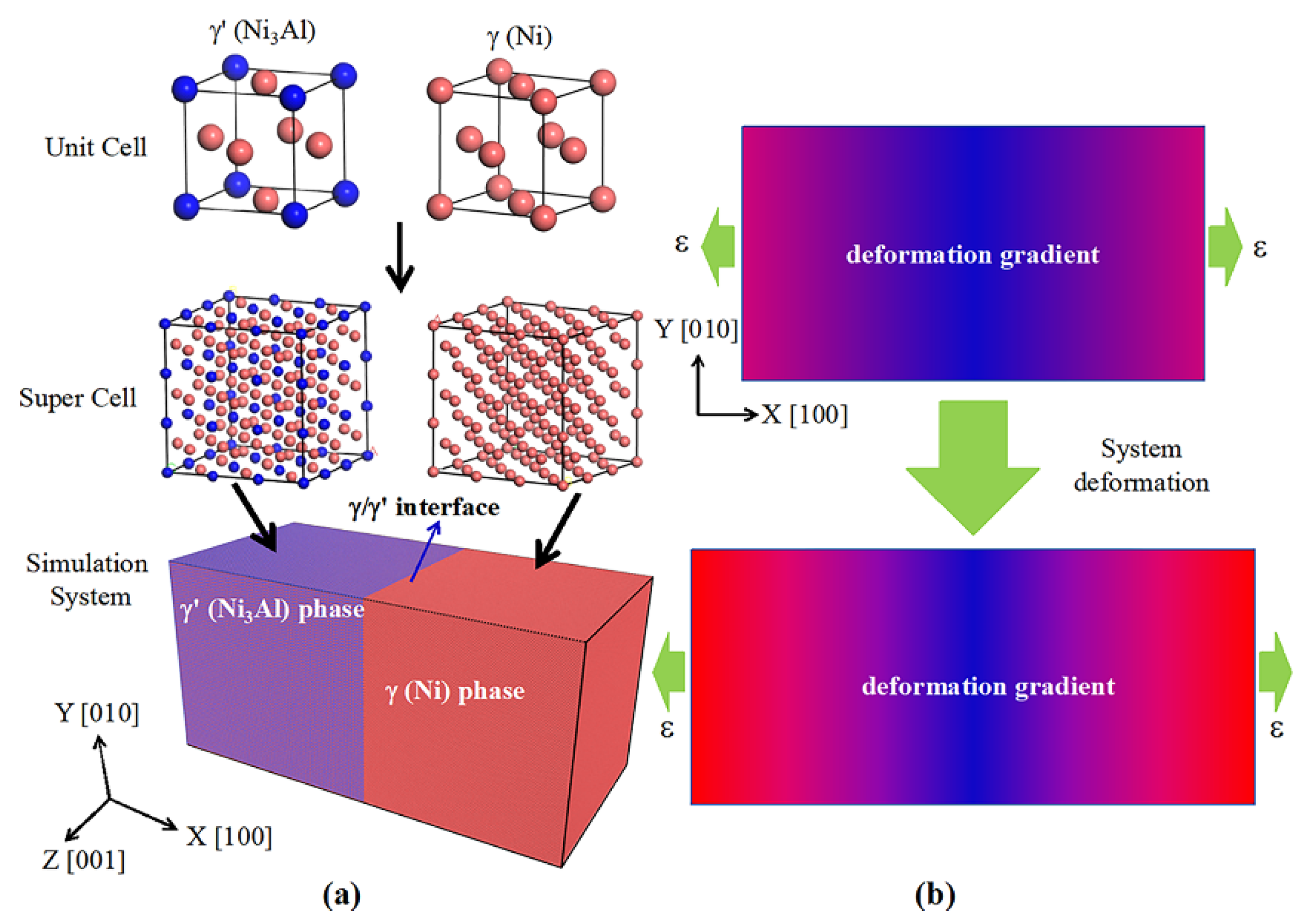





| Phase Volume Fraction | Model Size (X-, Y-, and Z-Direction)/nm | Atomic Percent (at%) | Weight Percent (wt%) | ||
|---|---|---|---|---|---|
| Nickel | Aluminum | Nickel | Aluminum | ||
| 13.5% | 52.9 × 25.7 × 25.7 | 96.75% | 3.25% | 98.48% | 1.52% |
| 26.9% | 53.0 × 25.7 × 25.7 | 93.47% | 6.53% | 96.83% | 3.17% |
| 40.3% | 53.1 × 25.7 × 2.57 | 90.17% | 9.83% | 95.05% | 4.95% |
| 53.7% | 53.2 × 25.7 × 25.7 | 86.84% | 13.16% | 93.14% | 6.86% |
| 67% | 53.3 × 25.7 × 25.7 | 83.49% | 16.51% | 91.10% | 8.90% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, X.; Yan, W.; Liang, Y.; Li, F. Molecular Dynamics Simulations on the Deformation Behaviors and Mechanical Properties of the γ/γ′ Superalloy with Different Phase Volume Fractions. Crystals 2025, 15, 706. https://doi.org/10.3390/cryst15080706
Qin X, Yan W, Liang Y, Li F. Molecular Dynamics Simulations on the Deformation Behaviors and Mechanical Properties of the γ/γ′ Superalloy with Different Phase Volume Fractions. Crystals. 2025; 15(8):706. https://doi.org/10.3390/cryst15080706
Chicago/Turabian StyleQin, Xinmao, Wanjun Yan, Yilong Liang, and Fei Li. 2025. "Molecular Dynamics Simulations on the Deformation Behaviors and Mechanical Properties of the γ/γ′ Superalloy with Different Phase Volume Fractions" Crystals 15, no. 8: 706. https://doi.org/10.3390/cryst15080706
APA StyleQin, X., Yan, W., Liang, Y., & Li, F. (2025). Molecular Dynamics Simulations on the Deformation Behaviors and Mechanical Properties of the γ/γ′ Superalloy with Different Phase Volume Fractions. Crystals, 15(8), 706. https://doi.org/10.3390/cryst15080706






