1. Introduction
Superlattices are a class of artificially engineered metamaterials that enable precise control over phonon band structures, resulting in thermal and acoustic properties that deviate significantly from those of their constituent materials. These engineered characteristics make superlattices highly attractive for thermoelectric applications, where their ability to substantially suppress lattice thermal conductivity via interfacial phonon scattering enhances energy conversion efficiency [
1,
2,
3,
4]. In addition, superlattices are integral components in nanophotonic devices such as quantum cascade lasers, where they critically influence optical and electronic performance. However, real-world imperfections—such as variations in layer thickness, interfacial defects, and complex thermodynamic environments—introduce intricate thermal transport phenomena. These complexities necessitate a deeper understanding of phonon dynamics in order to optimize heat dissipation and improve the thermal performance of superlattice-based devices.
Phonon transport in superlattices can be broadly categorized into two regimes: coherent and incoherent transport [
5,
6,
7,
8,
9]. In the coherent regime, phonons maintain their wave-like nature across multiple interfaces, leading to transport behaviors that deviate from classical particle-like predictions such as those described by the Boltzmann transport equation. Intriguingly, experimental and simulation studies have shown that reducing the superlattice period length can paradoxically increase thermal conductivity [
10,
11,
12,
13], while increasing the number of superlattice periods can result in a roughly linear rise in thermal conductivity [
5,
6,
14,
15]. These observations challenge the classical view, in which denser interfaces should increase phonon interface scattering and suppress thermal conductivity, which should be saturated once the phonon mean free paths are limited by interface density.
When phonon coherence is significant, the superlattice behaves as a periodic medium whose unit cell corresponds to one superlattice period [
16,
17]. In this case, the group velocity of coherent phonon modes can increase as the period length decreases, leading to a rise in thermal conductivity—a trend opposite to that expected under incoherent transport. This non-monotonic dependence of thermal conductivity on layer thickness has been observed across a variety of material systems, both experimentally and numerically [
10,
11,
12,
13]. Additionally, short-period superlattices often exhibit a reduced anharmonic phonon scattering phase space, which further contributes to the increase in thermal conductivity. Despite these well-established indicators of phonon coherence, most studies to date have primarily focused on macroscopic trends in thermal conductivity. A more fundamental understanding of coherence requires mode-resolved investigations of phonon behavior under varying thermal and structural conditions.
Despite decades of intensive research on superlattice structures [
7,
8,
18,
19], since the 1990s in particular, the study of coherent phonon transport and its manipulation in superlattices has emerged as a rapidly growing area of interest. Since 2014, several landmark experimental studies have uncovered distinct and significant coherent phonon behaviors. Notable examples include the seminal work by Ravichandran et al. (2014), which demonstrated a crossover from coherent to incoherent phonon transport in (SrTiO
3)
m/(CaTiO
3)
n superlattices [
12]; the study by Luckyanova et al. (2018) on the Anderson localization of coherent phonons in GaAs/AlAs superlattices [
20]; and experiments performed by Hu et al. (2020), which showed that aperiodic GaAs/AlAs superlattices exhibit lower thermal conductivity than their periodic counterparts.
Recent advances in computational and experimental methodologies have enabled more nuanced investigations into the transition between coherent and incoherent phonon transport in superlattices. Molecular dynamics simulations have clarified how key parameters—including temperature [
15], superlattice period length [
6,
11,
13], the number of periods [
21], interfacial defects [
22,
23], and aperiodicity in layer thicknesses [
6,
16,
24,
25]—govern this transition. Anharmonic phonon scattering, in particular, has been identified as a key mechanism that disrupts coherence by breaking the phase relationships between phonon modes [
15,
17]. Wavepacket simulations further demonstrate that phonons entering a superlattice from a homogeneous medium can form new, spatially extended coherent modes governed by modified phonon dispersion relations. These modes traverse the superlattice with minimal interface scattering, effectively perceiving the entire structure as a homogeneous medium [
10,
12,
16,
25].
Such coherent phonon modes provide new opportunities for researchers to tailor thermal conductivity through structural modifications. Strategies such as introducing random variations in layer thickness [
6,
24,
26] or embedding nanoscale obstacles [
20] have been shown to induce phonon localization and reduce thermal conductivity. Notably, our recent work demonstrated that by optimizing the thicknesses of Lennard-Jones superlattice layers and incorporating alloying, it is possible to achieve thermal conductivities even lower than those of the binary alloys formed by the base materials [
22]. Experimental results from Si/Ge superlattices demonstrate similar effects [
27].
A particularly informative approach to examining the coherent–incoherent transition involves analyzing phonon behavior in reciprocal space. Wavepacket simulations show that as phonons traverse into a superlattice, their spectral content evolves, forming superlattice-specific coherent modes [
16,
25]. However, most such simulations assume a background temperature of zero, raising questions about how these coherent modes persist under realistic thermal conditions. To address this, recent analyses of local heat flux spectra in conceptual “m40–m90” superlattices have provided direct evidence of phonon coherence and its degradation with increasing temperature or period length [
17]. In short-period superlattices at low temperatures, the nearly identical spectra across both material regions indicate strong coherence. As the temperature or period length increases, these spectra diverge, signaling the emergence of incoherent transport.
In our recent work [
15], we employed nonequilibrium molecular dynamics simulations to study periodic and aperiodic Lennard-Jones superlattices. By fitting the results to a two-mode coherent–incoherent phonon model, we uncovered a significant disappearance of coherent phonon modes, i.e., decoherence. This effect was attributed to the conversion of coherent modes to incoherent modes, driven by phase-breaking anharmonic scattering processes that become increasingly dominant at elevated temperatures.
Despite significant progress in the field, a comprehensive understanding of how key phonon properties—particularly the population and lifetimes of coherent phonon modes—evolve with temperature and structural parameters remains incomplete. Most previous investigations [
28,
29] have concentrated on low-temperature regimes and short superlattice periods, where phonon coherence dominates. In this study, we extend the scope to higher temperatures and longer period lengths to capture the full transition from predominantly coherent to incoherent phonon transport. Through this work, we aim to uncover the fundamental mechanisms that govern heat conduction in superlattices and provide guidance for the rational design of thermally optimized superlattice structures.
This paper is organized as follows:
Section 2 outlines the computational methodologies used in this study.
Section 3 presents and discusses our results, focusing on the evolution of spectral phonon properties as a function of temperature and superlattice period length. Finally,
Section 4 summarizes our key findings and their implications for phonon transport engineering in superlattices.
3. Results and Discussion
In this section, we present key results from the phonon SED analysis of Lennard-Jones superlattices across a broad range of temperatures and period lengths. Both factors have been identified in previous studies as critical in determining the phonon coherence and thermal transport behavior of superlattice structures, but it remains largely unexplored how individual coherent phonon modes, i.e., the superlattice modes, are affected by these factors.
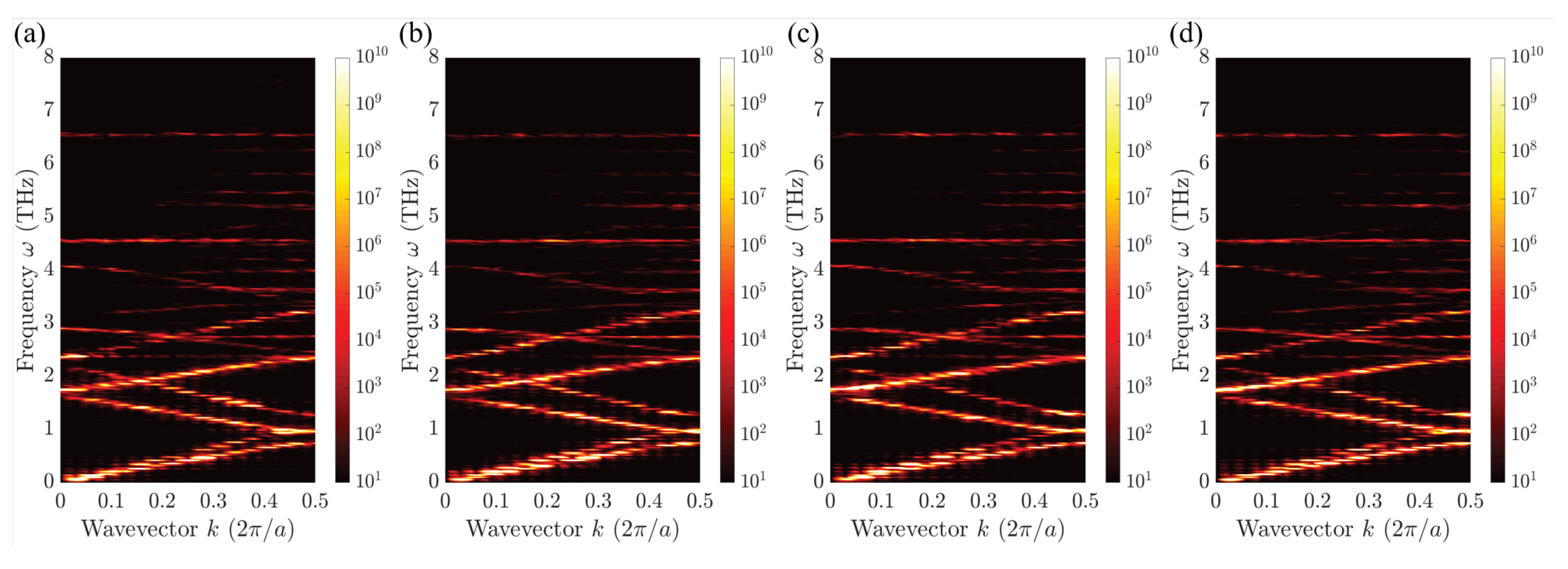
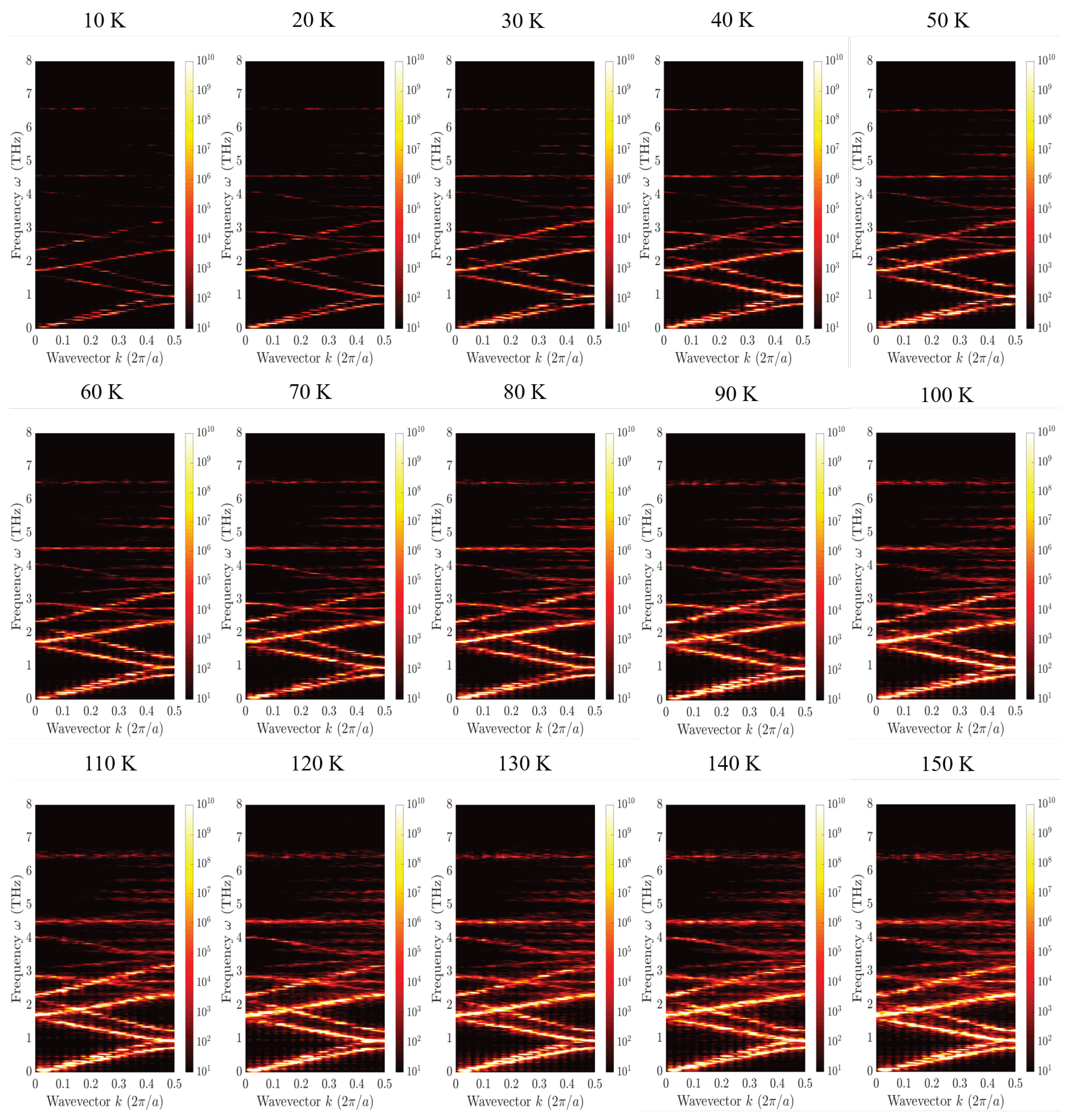
3.1. Temperature Dependence of SED Heat Map
Figure 3 presents the SED heat map of a 32-period 2UC-2UC superlattice across a temperature range of 10 K to 150 K. In all cases, the SED heat map reveals distinct acoustic branches alongside multiple optical branches. When comparing the low-temperature cases (e.g., 10 K and 20 K) with high-temperature cases (e.g., 140 K and 150 K), we observe that the increasing temperature enhances the density of the energy carried by each phonon mode. This behavior aligns with phonon theory, which predicts greater energy storage in phonon modes at elevated temperatures.
Furthermore, the SED heat maps qualitatively illustrate the significant broadening of prominent phonon branches—particularly low-lying acoustic modes and intermediate-frequency optical modes—both in the frequency and wavevector domains. The frequency-domain broadening of phonon linewidths indicates a reduction in phonon lifetime, primarily due to intensified anharmonic phonon–phonon scattering at higher temperatures. However, the slopes of the phonon branches, which correspond to phonon group velocities, remain largely unchanged with temperature. Consequently, the phonon mean free path, given by the product of the phonon group velocity and phonon lifetime, decreases as the temperature rises. These trends are consistent with previous studies on simpler material systems [
35,
36].
Additionally, the observed broadening along the wavevector axis suggests a reduction in phonon coherence length [
37,
38]. While the phonon mean free path is frequently discussed in thermal transport studies, the phonon coherence length is less explored, yet it plays a crucial role in determining phonon coherence in superlattice structures [
33,
39].
It is important to note that our classical molecular dynamics simulations correspond to the classical limit of phonon distribution, where phonon occupation follows the Maxwell–Boltzmann distribution rather than the Bose–Einstein distribution. As a result, even at 10 K, we still observe significant optical phonon branches extending to high frequencies near 6.5 THz. Nevertheless, the SED analysis presented here provides key insights into the temperature-dependent variations in phonon lifetime and population. A more detailed examination of these effects, along with their structural influences, will be discussed later in this manuscript.
3.2. Spectral Energy Density as a Function of Superlattice Period Length
The influence of the period length
p on the phonon properties of superlattices has been extensively studied [
1,
10,
11,
12,
13]. The general consensus is that when thermal transport is dominated by incoherent, particle-like phonons, thermal conductivity increases with the increasing period length due to reduced interface density and, consequently, decreased phonon interface scattering. Conversely, when coherent phonons dominate, thermal conductivity decreases as the period length increases. This behavior arises because the phonon group velocity typically decreases in superlattices with longer periods (or unit cells), as explained by the Brillouin zone folding mechanism [
10], which was proposed in the 2000s to describe period-dependent lattice thermal transport in superlattices. More recently, it has also been shown that a longer period length is associated with an increased phonon scattering rate due to changes in the phonon scattering phase space [
29]. This phenomenon is analogous to that observed in simpler materials, such as diamond and boron nitride [
40], and in nanomesh structures (also known as phononic crystals) [
33], where a larger unit cell complicates the phonon band structure, significantly increasing the number of three-phonon scattering processes allowed.
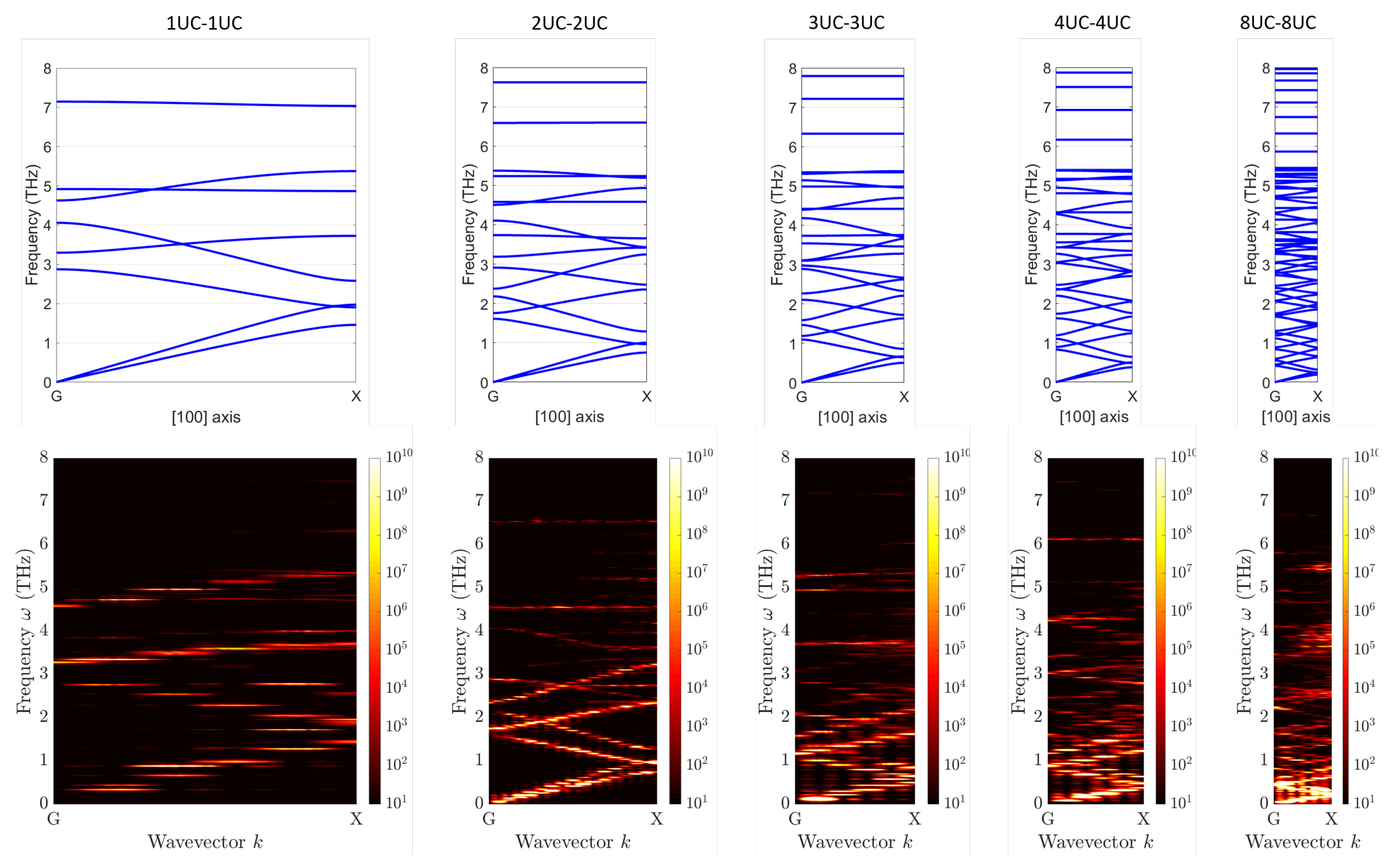
Here, we examine the evolution of phonon SED as a function of the period length. As shown in
Figure 4, the upper row presents the phonon dispersion relations of m40-m90 superlattices with varying period lengths, ranging from the smallest possible period of 1UC-1UC (composed of one unit cell of m40 material and one unit cell of m90 material) to an 8UC-8UC superlattice, which represents the upper limit of the unit cell size that can be handled by our computational resources for lattice dynamics calculations. The width of the horizontal axis in each panel corresponds to the size of the first Brillouin zone, meaning that superlattices with longer period lengths in real space exhibit smaller first Brillouin zones, resulting in narrower phonon dispersion plots.
A comparison of the five phonon dispersion panels in
Figure 4 shows that although the overall structure of the phonon branches remains similar, the slopes of the acoustic branches systematically decrease with the increasing period length. This reduction in slope is most pronounced near the Brillouin zone boundary (close to the X point), where the acoustic branches progressively flatten, approaching a slope of zero. This reduction in slope indicates a decrease in phonon group velocity, a behavior well understood within the framework of Brillouin zone folding [
10]. The SED heat maps in the lower row of
Figure 4 confirm this trend, as they exhibit phonon dispersion curves that are in good agreement with the lattice dynamics calculations presented in the upper row. These heat maps also show a significant flattening of the acoustic branches. Furthermore, the phonon branches appear increasingly broadened along the vertical (frequency) axis, indicating an increased phonon scattering rate. This observation aligns with previous studies, which suggest that increased phonon scattering at longer period lengths contributes to changes in thermal transport behavior. In the following sections, we will provide a more detailed analysis of phonon scattering rates as a function of period length and temperature to establish a more rigorous understanding of these effects.
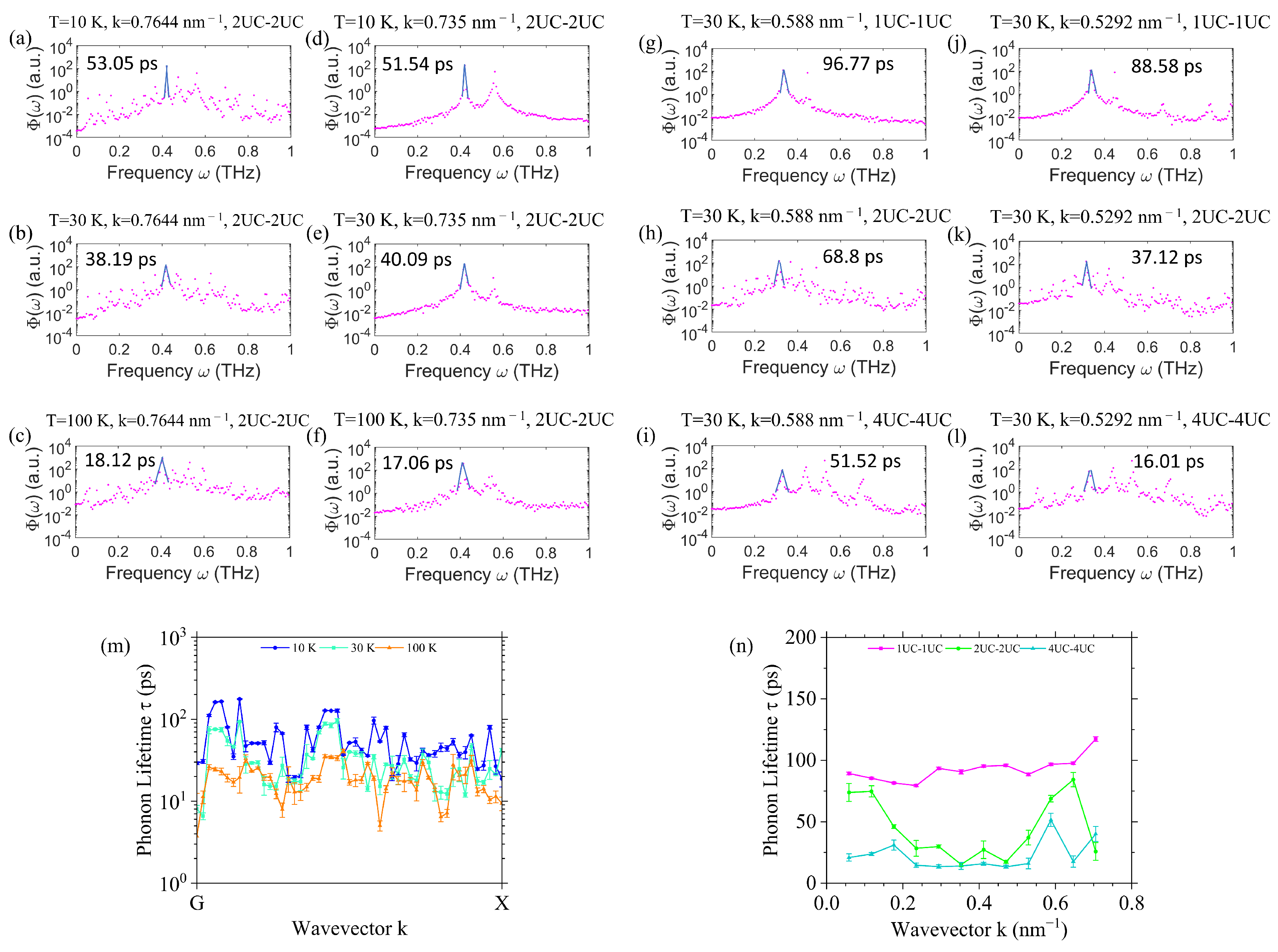
3.3. Detailed Analysis of Superlattice Phonon Lifetimes
The linewidth of a SED peak corresponds directly to the phonon scattering rate, which is the inverse of the phonon lifetime. In this section, we examine how superlattice phonon lifetimes vary with both temperature and period length.
Figure 5a–c show the SED spectra for a transverse acoustic (TA) phonon mode at
along the
–
direction of the 2UC-2UC superlattice. As the temperature increases, the SED peak broadens significantly. By fitting the SED peaks to Lorentzian functions, following the procedure detailed in
Section 2, we extract phonon lifetimes of 53 ps, 38 ps, and 18 ps at 10 K, 30 K, and 100 K, respectively. A similar trend is observed in
Figure 5d–f for another TA mode at
in the same direction, with the phonon lifetimes being 51 ps, 40 ps, and 17 ps at 10 K, 30 K, and 100 K, respectively. This systematic decrease in phonon lifetimes with increasing temperature arises from enhanced anharmonic phonon–phonon scattering, a well-established mechanism in crystalline solids [
39,
41]. This anharmonic effect not only reduces the lattice thermal conductivity of superlattices but also contributes to the loss of phonon coherence, as demonstrated in previous experimental and simulation studies [
5,
6,
17,
22,
33]. A summary of the phonon lifetimes extracted at different temperatures for the TA branch of the 2UC–2UC superlattice is provided in
Figure 5m, clearly illustrating a general trend of decreasing phonon lifetimes at higher temperatures.
To investigate the influence of the period length on phonon lifetimes, we compare the same phonon modes across superlattices with different period lengths.
Figure 5g–i present the SED peaks of a TA phonon mode at
in 1UC-1UC, 2UC-2UC, and 4UC-4UC superlattices. The phonon lifetime decreases systematically with the increasing period length. Specifically, it is 97 ps, 69 ps, and 51 ps in 1UC-1UC, 2UC-2UC, and 4UC-4UC superlattices, respectively, showing a robust decreasing trend. The same trend is shown for another TA mode at
in
Figure 5j–l. These findings are consistent with a recent anharmonic lattice dynamics study, which revealed shorter phonon lifetimes in superlattices with longer period lengths [
29].
However, we emphasize that the reduction in phonon lifetime is not the sole contributor to the decreasing thermal conductivity observed in longer-period superlattices. As illustrated in
Figure 4, the phonon dispersion relations undergo significant modifications due to the Brillouin zone folding (BZF) mechanism [
10]. As a result, even phonon modes with identical reciprocal wavevectors in different superlattices exhibit differing frequencies. In superlattices with longer period lengths, these modes shift toward lower frequencies, reflecting the flattening of acoustic branches, which is an outcome predicted by early theoretical studies on BZF [
6,
9,
10]. This flattening reduces the phonon group’s velocity and, in combination with shorter lifetimes, leads to diminished thermal conductivity.
Figure 5n summarizes the extracted phonon lifetimes for the TA branch across the 1UC, 2UC, and 4UC superlattices. The trend confirms that increasing the superlattice period length leads to reduced phonon lifetimes. This behavior is expected, as longer period lengths enlarge the size of the superlattice unit cell and thus complicate the phonon dispersion landscape. This increased complexity enhances the available phase space for phonon–phonon scattering, which in turn elevates the scattering rate and reduces the phonons’ lifetime.
3.4. Decoherence of Coherent Superlattice Phonons at Higher Temperatures
We emphasize that the phonon dispersion relations shown in this work correspond to the large unit cell of the superlattice, which represents one period of the superlattice. As is well established, these phonon dispersion relations can be understood as resulting from the folding of the original phonon dispersion curves of the base materials of the superlattice—namely, the m40 and m90 Lennard-Jones crystals, in this work. This phenomenon is known as the Brillouin zone folding mechanism [
10]. Consequently, the phonon modes represented by the dispersion relations computed from the large unit cell are typically referred to as coherent phonons, since they are synchronized with the superlattice structure. Notably, these phonons do not perceive the interfaces within the superlattice as discontinuities, and, as a result, they are not scattered at the interfaces [
16].
In contrast, incoherent phonons, which are associated with the respective base materials of the superlattice (m40 and m90), experience scattering at each interface. These incoherent phonons follow the dispersion relations of the pure m40 or m90 crystals. The distinction between coherent and incoherent phonons has important implications for the thermal transport properties of the superlattice [
6,
15,
16,
25]. Specifically, when thermal transport is dominated by coherent phonons, the thermal conductivity of the superlattice increases almost linearly with the number of periods (or equivalently, the total length of the structure). This behavior has been well documented in recent studies and is attributed to the ballistic transport of coherent phonons [
6], which obey the dispersion relations of the superlattice rather than those of the individual base materials. On the other hand, when the thermal transport is dominated by incoherent phonons, the thermal conductivity of the superlattice remains nearly constant as more periods are added. This is because the incoherent, particle-like phonons are scattered at each interface, and the dense interfaces significantly limit the mean free path of the phonons. As a result, the thermal conductivity remains essentially constant with the increasing structure length.
In this work, we investigate a fundamental aspect of coherent superlattice phonons: how they maintain their coherence. Previous studies have indirectly observed the transition from coherent to incoherent phonon transport using nonequilibrium molecular dynamics simulations [
15], as well as the coherent–incoherent two-phonon model proposed for superlattice structures [
6]. These studies concluded that coherent phonons transition into incoherent modes at higher temperatures or when the superlattice period length increases. This conclusion was derived by extracting the overall thermal conductance from the thermal conductivity of periodic and aperiodic superlattices and fitting the results to the two-phonon model. In 2024 and 2025, we further used the atomistic phonon wavepacket method to directly demonstrate the conversion of incoherent phonons—those that follow the phonon dispersion relations of the base materials comprising the m40-m90 superlattice (similar to the superlattices studied in the present work)—into coherent phonon modes that follow the phonon dispersion relations of the superlattice [
16,
25]. Our results directly reveal that this conversion arises from coherent interference between phonon modes.
While these previous studies provided valuable insights into the mechanisms of coherent-to-incoherent phonon conversion, they were either inferred indirectly through molecular dynamics simulations or conducted at a background temperature of zero, where anharmonic phonon–phonon scattering is absent. In this work, we employ SED analysis to directly examine the energy stored in the superlattice’s coherent modes, enabling us to determine whether these modes disappear at elevated temperatures.
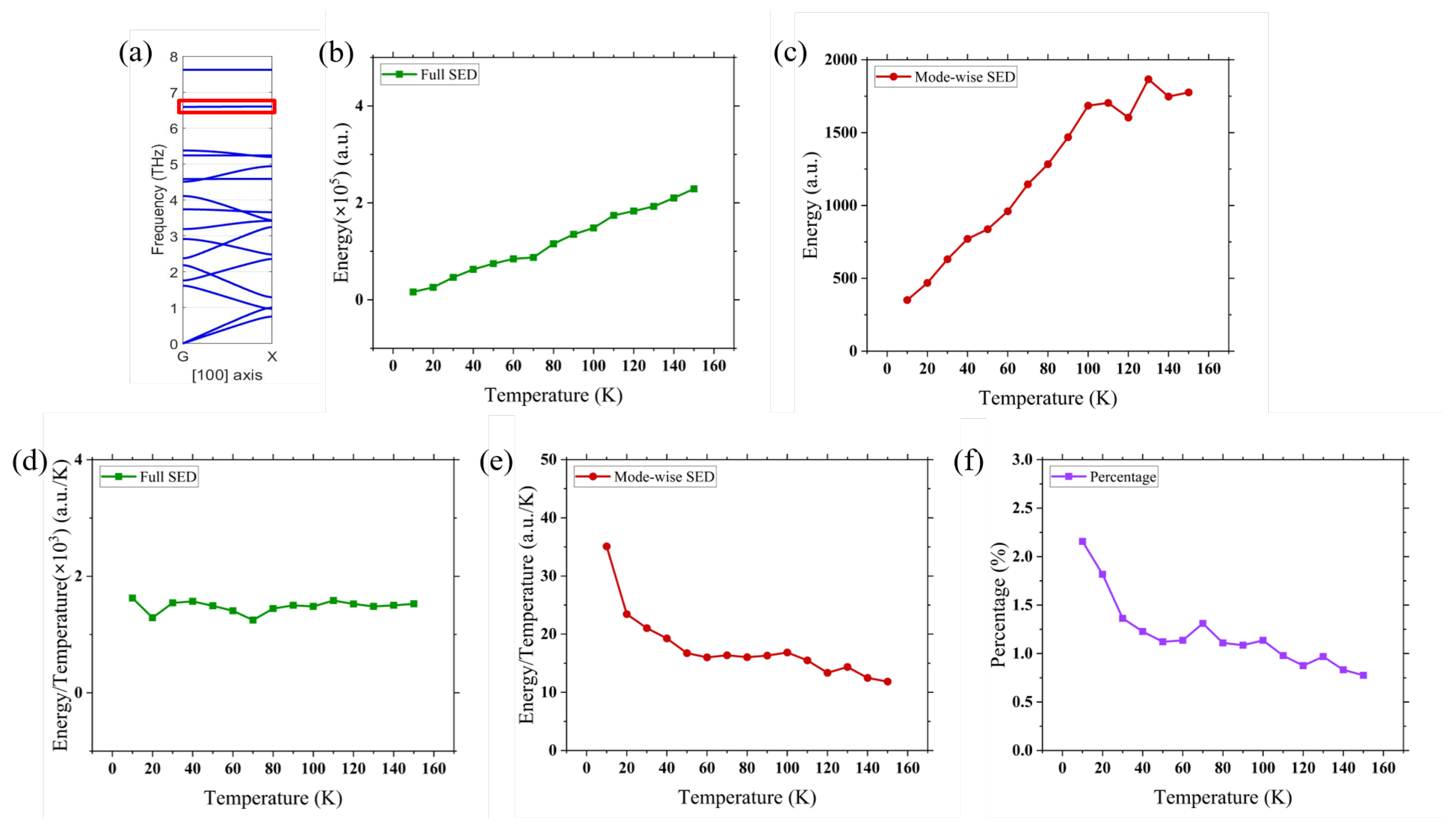
As shown in
Figure 6a, we select a high-frequency optical branch from the superlattice phonon dispersion relations to examine the decoherence of the coherent mode. Although this phonon branch is not expected to contribute significantly to heat transport in the superlattice, it resides in a distinct frequency range that lacks the degeneracy of other phonon modes. This allows us to unambiguously quantify the energy stored in this branch and, correspondingly, the phonon population.
Figure 6b presents the total spectral energy density of all phonon modes across the entire phonon spectrum of the 2UC-2UC superlattice studied in this work. As expected, the total energy density increases monotonically with temperature.
Figure 6c displays the total SED of the selected high-frequency optical branch in
Figure 6a, which also exhibits an overall increasing trend with temperature. These results indicate that both the total thermal energy stored in the superlattice and that stored in the selected phonon branch increase with temperature.
In contrast,
Figure 6d,e present the total spectral energy density normalized by temperature, which corresponds to the mode-wise heat capacity. This quantity serves as an indicator of the number of phonon modes available at a given temperature, which we will refer to as the total spectral heat capacity in subsequent discussions.
As shown in
Figure 6d, the total spectral heat capacity of the entire phonon spectrum remains nearly constant with increasing temperature, with minor fluctuations arising from noise in the molecular dynamics simulations. This is expected, as the heat capacity remains at its classical limit (
per atom, where
is the Boltzmann constant) in classical molecular dynamics simulations.
Interestingly,
Figure 6e shows that the total spectral heat capacity of the selected optical phonon branch in
Figure 6a exhibits a pronounced decreasing trend with temperature. To further illustrate this behavior, we plotted the ratio of the total SED of the selected phonon branch to the total SED of the entire phonon spectrum in
Figure 6f. This ratio also shows a significant decrease, indicating a loss of phonon modes in the selected phonon branch. This observation is critical, as it suggests that the optical phonon branch is losing phonon modes that store thermal energy. Since this branch belongs to the superlattice phonon dispersion relation, we infer that these superlattice phonon modes, or coherent modes, are converting into non-superlattice modes—specifically, incoherent modes that follow the phonon dispersion relations of the base materials. The reason for this is that at higher temperatures, the intensified anharmonic phonon scatterings, which break the phase and thus the coherence of phonons, hinder the formation of coherent phonon modes; instead, the vibration energy remains in the incoherent modes, which tend to follow the phonon dispersion relations of the local material, m40 or m90 in the m40-m90 superlattice studied in this work. This finding agrees with our recent study based on the two-phonon model, which suggests the conversion of coherent phonons into incoherent phonons at higher temperatures [
15]. It also complements our recent atomistic phonon wavepacket study, which directly revealed the conversion of incoherent phonons into coherent phonons [
16].
4. Conclusions
In this work, we conducted extensive molecular dynamics simulations to investigate the behavior of coherent superlattice phonon modes in multi-period superlattices composed of conceptual Lennard-Jones materials. By employing a phonon SED analysis, we elucidated the evolution of phonon modes associated with the superlattice phonon dispersion relation—commonly referred to as coherent phonons—as being a function of the temperature and superlattice period length. The SED method, which extracts detailed phonon properties from atomic trajectories, provides a realistic assessment of phonon dispersions and lifetimes. Our findings reveal that elevated temperatures significantly reduce the lifetimes of most superlattice phonon modes due to enhanced anharmonic phonon–phonon scattering. Notably, we observed a pronounced decrease in the spectral heat capacity of a high-frequency optical phonon branch at higher temperatures. This unambiguously indicates the decoherence of coherent phonon modes (consistent with our prior work that indirectly suggested the conversion of coherent modes), which obey the superlattice dispersion relations, into incoherent modes, which follow the dispersion relations of the constituent base materials. The intensified anharmonicity disrupts the phase coherence of the phonons, effectively destroying their coherent nature. While the complex structure of the superlattice phonon dispersion relation limits an unambiguous spectral heat capacity analysis of all phonon branches, our results offer strong support for the coherent-to-incoherent mode conversion mechanism existing under thermal excitation.
Furthermore, we examined the impact of the superlattice period length on phonon dispersions and lifetimes. In agreement with the Brillouin zone folding theory, the SED analysis revealed a significant flattening of acoustic branches with increasing period length, implying reduced phonon group velocities. This directly correlates with the observed reduction in lattice thermal conductivity in longer-period superlattices when coherent transport dominates. Interestingly, we also found that the lifetimes of many coherent phonon modes decrease as the superlattice period length increases, likely due to an expanded phase space for phonon–phonon scattering, further contributing to the suppression of thermal transport.
This study provides a comprehensive analysis of the temperature- and geometry-dependent behavior of coherent phonons in superlattices. Unlike previous investigations, which inferred the loss of phonon coherence indirectly through changes in thermal conductivity, our work presents direct evidence of the disappearance of coherent phonon modes, i.e., decoherence, at elevated temperatures. Using SED analysis, we demonstrate that this phenomenon arises from enhanced anharmonic scattering and coherence degradation. These results deepen our fundamental understanding of phonon transport in nanoscale periodic structures and offer valuable insights for the development of thermally tunable materials and devices.