Design and Processing of Metamaterials

Abstract

Metamaterials represent artificially structured materials that exhibit unusual properties, such as a negative refractive index, negative permeability and permittivity, negative cloaking by Poisson ratios and optical effects, etc., which are inaccessible in natural materials. According to recent developments, novel devices and tools based on metamaterials are attracting great interest as they offer improved performance, functionality, sensitivity, biocompatibility, complex structures, and design freedom. Leveraging numerical design approaches, such as finite element analysis and finite difference time domain methods, researchers have tailored metamaterials to meet specific requirements in various areas through a range of manufacturing techniques. These materials can be broadly classified into optical, mechanical, thermal, electromagnetic, and acoustic categories based on their properties and intended use. The choice of fabrication method depends heavily on the specific application, the desired scale, and the complexity of the metamaterial design. These manufacturing methods can be broadly divided into top-down and bottom-up approaches, while each of them has advantages and limitations and offers valuable pathways for the development of the final product. This review offers a basic overview of metamaterials, covering their fundamental principles, fabrication and characterization techniques, and current design methodologies. It also explores their diverse applications, including specific case studies in medicine, while addressing existing limitations and challenges. Finally, this review highlights future perspectives, emphasizing the need for continued innovation in fabrication and characterization to unlock the full potential of metamaterials.

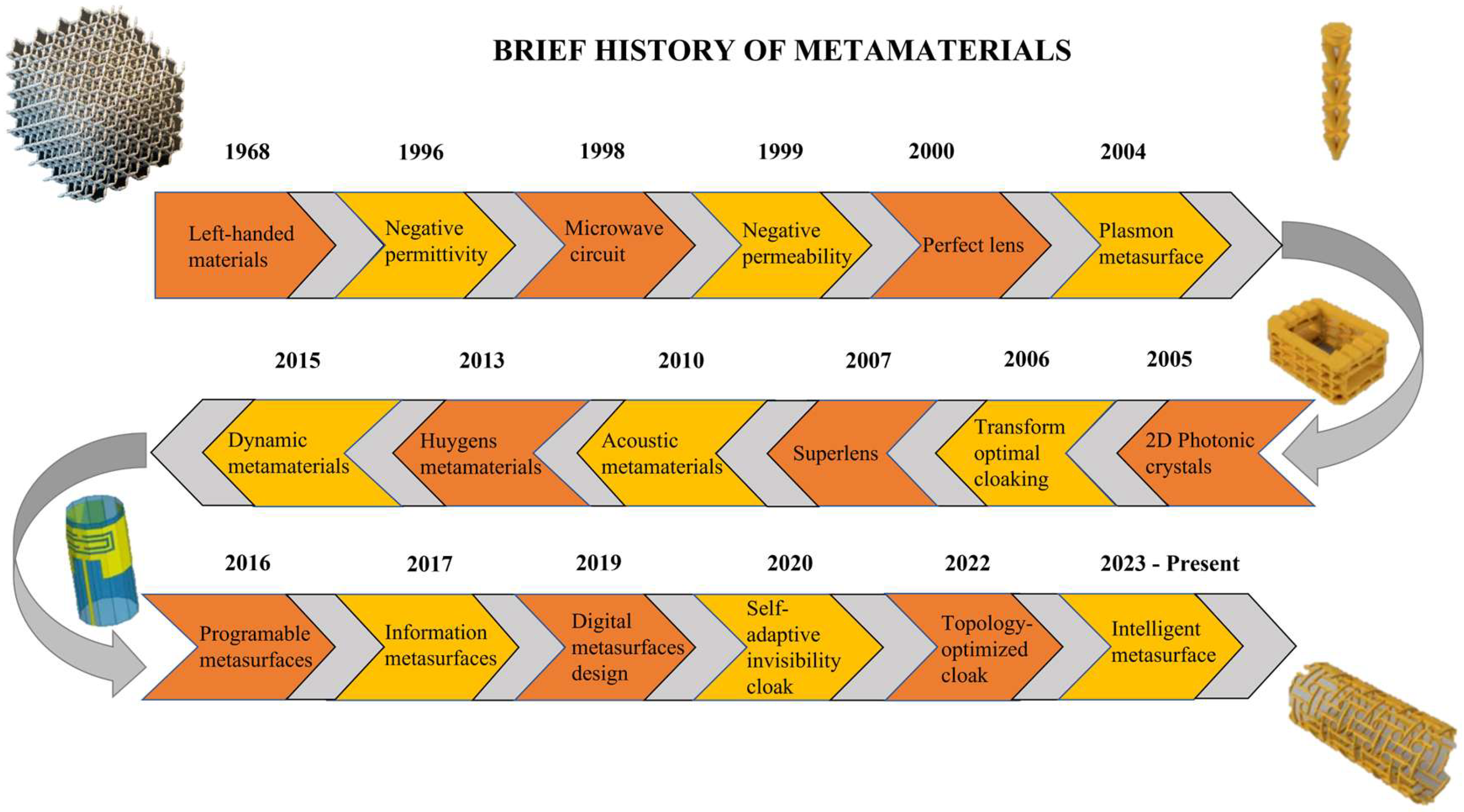
1. Introduction

Metamaterials, whose properties rely more on structure than chemical composition, have emerged in the last two decades as a significant area of research due to their unique properties not typically associated with other classes of materials [1]. Metamaterials, through their carefully engineered subwavelength structure (i.e., structural features smaller than the wavelength of interacting waves), differ from conventional materials by exhibiting unconventional electromagnetic properties—such as negative refractive indices, negative electrical permittivity, and negative magnetic permeability [2]. While these properties are often achieved through artificial design, analogous phenomena are observed within biological systems. For example, the intricate nanostructures present in butterfly wings [3] and reptile skin [4] produce structural coloration and optical effects that resemble those of engineered metamaterials. In both cases, the observed properties stem not from the chemical composition alone but from the precise organization of substructures at subwavelength scales [5,6,7].

In the Greek language, the prefix “meta” translates to “beyond”. Metamaterials represent a novel class of engineered materials that exhibit electromagnetic properties not found in natural substances. Typically, natural materials, such as diamond and glass, possess positive values for the refractive index, magnetic permeability, and electrical permittivity. In contrast, metamaterials can demonstrate negative refractive indices [8,9] negative electrical permittivities [10,11], and negative magnetic susceptibilities [12,13]. Metamaterials encompass a range of engineered materials, including those with a negative refractive index along with simultaneously negative permittivity and permeability, as well as materials with large negative thermal expansion or near-zero in-plane thermal expansion, large Poisson ratios, or reversed macroscopic magnetization [14]. These materials are often referred to by various terminologies, including left-handed (LH) materials [15,16] backward-wave (BW) media [17], negative-index materials (NIMs) [8], and double-negative (DNG) media [6,18].

Metamaterials exhibit unique features, such as perfect lensing [17], classical electromagnetically induced transparency [19,20,21] cloaking abilities [22], high-frequency magnetism [23] and dynamic modulation of terahertz (THz) radiation [24], and phenomena, like the reverse Doppler effect and the reverse Cerenkov effect [25]. These exceptional properties facilitate the creation of functional devices capable of switching and tuning [26,27,28,29]. Based on their permittivity and permeability, metamaterials can be classified as mu-negative materials (MNG), epsilon-negative materials (ENG), double-positive materials (DPS), and DNG materials [30]. MNG and ENG are considered single-negative materials, while double-negative and double-positive materials can be engineered for specific frequency bands.

The applications of metamaterials are far-reaching, impacting various fields, including optics, acoustics, and electromagnetics. In optics, they enable groundbreaking technologies, such as superlenses that exceed the diffraction limit [5,31]. In acoustics, metamaterials offer innovative solutions for sound insulation and noise control, highlighting their versatility [32]. Furthermore, the development of electromagnetics is a key driver in enhancing wireless communication technologies by improving antenna performance and enabling new functionalities in wireless devices [5,33].

Also, metamaterials hold transformative potential in medicine, particularly in enhancing wireless telemetry systems for early disease diagnosis and continuous physiological monitoring, as exemplified by their use in wireless endoscopes and advanced cancer detection devices that leverage changes in tissue permittivity and conductivity [34,35,36]. Furthermore, metamaterials improve medical imaging techniques, such as MRI, by significantly reducing scan times and enhancing signal-to-noise ratios [37], while their applications in microwave hyperthermia and wireless strain sensing contribute to more effective cancer treatments and patient monitoring [38,39].

The study of metamaterials is not a recent development; rather, it has a rich historical foundation. The fundamental idea of developing materials with tailored properties through microstructural design dates back nearly a century [5,31].

The concept of metamaterials, artificial materials engineered to exhibit properties not found in nature, has its roots in the pioneering work of Russian physicist Victor G. Veselago in the 1960s. Veselago first theorized the existence of materials with a negative refractive index, proposing that such materials could exhibit unique electromagnetic properties, including reversed-phase velocity and energy flow [15]. His groundbreaking work laid the theoretical foundation for metamaterials, although the practical realization of these materials remained elusive for decades [40].

Veselago’s theoretical predictions were based on Maxwell’s equations, which describe the behavior of electromagnetic waves. He demonstrated that in a hypothetical material with simultaneously negative permittivity and permeability, the phase velocity of light would be antiparallel to the direction of energy flow, a phenomenon not observed in natural materials. Despite the elegance of his theory, Veselago’s ideas were initially met with skepticism, as no known materials exhibited the required negative refractive index at the time [41].

The field of metamaterials gained traction in the late 20th century, thanks to advances in materials science and nanotechnology. In 1968, Leonard introduced parallel plate wave transmission structures, which provided a practical framework for exploring wave behavior in engineered materials [42]. That work marked an early step toward the experimental realization of metamaterials, as it demonstrated the potential for manipulating electromagnetic waves using structured materials.

The true breakthrough in metamaterials research came in the early 2000s when scientists successfully fabricated materials with negative refractive indices. This achievement was made possible by the development of split-ring resonators (SRRs) and other nanostructured components, which allowed for precise control over electromagnetic properties [30]. These advances were documented in several key studies, including a comprehensive review by Pendry and Smith [43], which highlighted the potential of metamaterials for applications such as superlenses, cloaking devices, and advanced antennas.

Since then, the field of metamaterials has expanded rapidly, with research focusing on both fundamental principles and practical applications. A review by Engheta and Ziolkowski [28] explored the theoretical and experimental progress in metamaterials, emphasizing their potential to revolutionize photonics, telecommunications, and sensing technologies. The history of metamaterials (Figure 1) is a testament to the power of theoretical insight and technological innovation. From Veselago’s initial proposal to the cutting-edge applications of today, metamaterials have evolved from a theoretical curiosity to a cornerstone of modern materials science.

Figure 1. Brief history of metamaterials (readapted from [44,45,46]).

Figure 1. Brief history of metamaterials (readapted from [44,45,46]).

As research continues, the potential for metamaterials to enable new technologies and deepen our understanding of wave–matter interactions remains vast.

While initial cloaks were narrowband, recent work on dielectric metamaterials [47] and quasi-conformal mappings [48] addresses losses and scalability, paving the way for clinical applications.

This review summarizes the state-of-the-art design and processing of metal, ceramic, and semiconductor metamaterials while outlining promising avenues for future fruitful research.

1.1. Fundamental Principles of Metamaterials

A thorough understanding of natural materials enhances the design of metamaterials, enabling the development of new, controllable materials [49]. Metamaterials are known for the specially designed unit cells or atoms (periodic or nonperiodic subwavelength “meta-atoms” [49]) that work together to exhibit unconventional properties not found in natural materials, making their field inherently interdisciplinary by bridging areas such as electromagnetics, optics, solid-state physics, and acoustics [50,51]. Thus, three distinct categories of metamaterials, i.e., homogeneous (periodic), random, and inhomogeneous, have been developed at microwave frequencies, each exhibiting unique structural arrangements of meta-atoms and facilitating the exploration of novel physical phenomena and the advancement of practical devices [49,52].

Due to the availability of extreme medium parameters, early studies of homogeneous metamaterials revealed their potential to realize unusual physical phenomena such as negative permittivity, negative permeability, and zero index of refraction [49,53].

A highly homogeneous zero-index metamaterial (ZIM) in the microwave regime based on a SrTiO₃ ceramic was proposed, engineered, and characterized by Liu et al. Their study introduced and experimentally validated a novel antenna design that incorporated the developed ZIM within a metallic waveguide, achieving enhanced directivity. The fabricated prototype achieved a peak directivity of 11.2 dB, despite its compact aperture dimensions of 1.2λ₀ × 1.2λ₀. Furthermore, the antenna demonstrated sustained high directivity across a broad range of aperture sizes, from 0.5λ₀ × 0.5λ₀ to significantly larger scales, effectively approaching the theoretical directivity limit over this extended range [54].

On the other hand, NIMs are applied in superlenses to achieve resolutions below the diffraction limit, making them invaluable for medical diagnostics [55].

The integration of NIMs in imaging systems has shown promising results in visualizing nanoscale structures, which traditional lenses cannot achieve [56]. Wang Y. et al. proposed the integration of a NIM lens with a microstrip antenna, enhancing its directional radiation capability, relative bandwidth, and average gain by 7.54 dB, with a maximum gain of 10.24 dB in the 18.38–20.66 GHz frequency range [56].

Random metamaterials, with randomly packed meta-atoms, are composed of conductive and insulating phases, where negative permittivity is achieved through an interconnected conductive network, allowing for enhanced control over electromagnetic properties, including radiation, reflection, and scattering. The generation of electromagnetic diffusion or Lambertian reflection is a key application of this approach, where varying the geometrical parameters of meta-atoms across space leads to spatially random distributions of effective medium parameters such as permittivity, permeability, the refractive index, and wave impedance [49,57]. The ability to fabricate custom-made magneto-dielectric materials has led to the development of transformation optics, inspired by Einstein’s theory of general relativity.

Gholipur and Bahari demonstrated that silver nanowires, randomly dispersed within a Zr_0.9Ni_0.1O_γ dielectric matrix, exhibited both negative permittivity and negative magnetic permeability within the microwave spectral range. The selection of silver as the metallic component was based on its minimal loss factor, a crucial consideration for metamaterials operating in the microwave to infrared frequency range. Furthermore, the use of a dielectric host with a high permittivity was deemed advantageous for this composite material [58].

Another study was conducted on iron/epoxy random metamaterials, synthesized through a simple mixing and pressure-forming technique, to investigate the influence of iron content on their electrical properties. The composites demonstrated a percolation threshold at an iron volume fraction of 0.425. Below this threshold, conductivity was governed by hopping conduction due to the isolated nature of the iron particles, while above, a conductive network formed, leading to metal-like conduction and negative permittivity [59].

This approach maps theoretical spatial distortions onto real-world inhomogeneous and anisotropic metamaterials, offering precise control over electromagnetic wave propagation. Inhomogeneous metamaterials, characterized by nonperiodic meta-atom distributions, provide enhanced flexibility in manipulating electromagnetic fields.

The design of inhomogeneous electromagnetic metamaterials (IEMMMs) for wireless power transfer systems shows how varying effective permeability can enhance efficiency by up to 28%. IEMMMs are tailored for specific applications, such as improving magnetic field modulation in power transfer systems. In An et al.’s paper, an inhomogeneous EMMM (IEMM) with three kinds of effective permeability was proposed to improve the range and efficiency of a wireless power transfer system (WPTS). Their study examined the effective permeability of circular, square, and “8”-shaped coil unit cells and investigated the magnetic field control achieved by negative permeability mediums. Based on the analysis, a two-dimensional Impedance-Enhanced Magnetic Metamaterial (IEMMM), composed of square and “8”-shaped coil unit cell combinations, was developed. Finite element simulations confirmed that the IEMMM effectively modulated the magnetic field and reduced flux leakage in a Wireless Power Transfer System (WPTS). Notably, the designed IEMMM enhanced the power transmission efficiency of the WPTS by as much as 28% [60].

This design freedom, combined with subwavelength geometries and gradient variations, allows for the creation of novel devices, such as invisibility cloaks and advanced optical lenses, driving innovation in electromagnetic wave control and engineering applications [49,59,61].

The world of electromagnetic waves, including light, displays many peculiar effects compared with Newton’s mechanics, particularly due to their wave-like nature, finite wave speeds, and dependence on parameters like electric permittivity and magnetic permeability [62,63].

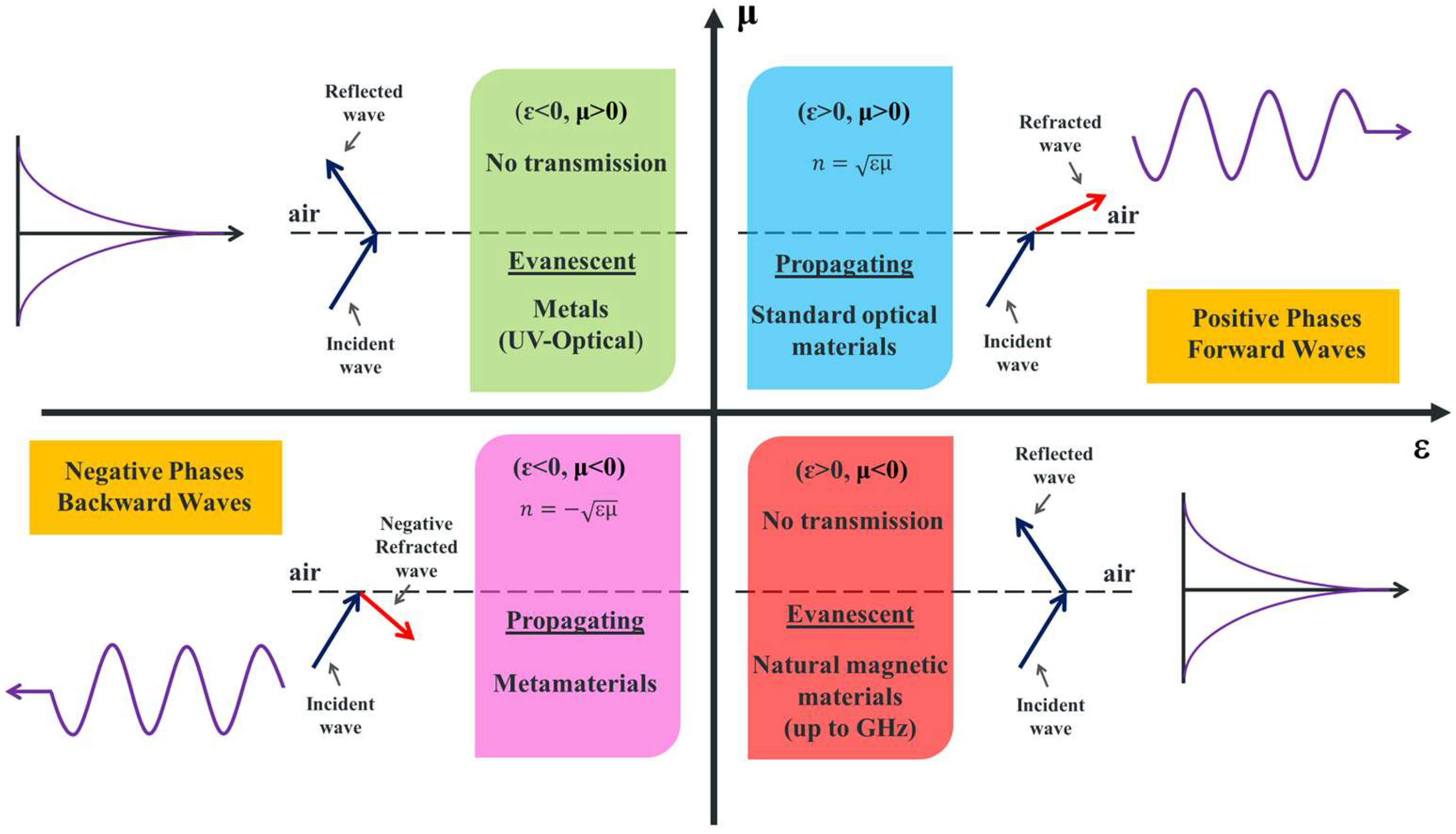
1.2. Electromagnetic Theory

Electromagnetic phenomena are primarily governed by Maxwell’s equations that describe the relationships between electric and magnetic fields, their sources, and the properties of materials [64]. The electromagnetic properties of metamaterials are intricately linked to their ability to alter the propagation of electromagnetic waves through engineered structures [64]. This manipulation is often described in terms of permittivity (ε) and permeability (μ), which characterize a material’s response to electric and magnetic fields, respectively. The refractive index (n = √με) and impedance (Z = √μ/ε), considered macroscopic effective parameters, are derived quantities, directly dependent on permittivity and permeability. Consequently, alterations in either ε or μ will induce corresponding changes in n and Z in a coupled manner, as these relationships are fundamentally linked through Maxwell’s equations [30,64]. In metamaterials, these parameters can be designed to achieve negative values, leading to a negative refractive index. The capacity to control this parameter leads to novel wave interactions, such as reversed Doppler effects and negative refraction, which have significant implications for optical imaging and cloaking technologies [65,66].

Furthermore, it is crucial to recognize that non-classical permittivity and permeability are usually frequency-dependent, often occurring within narrow spectral ranges [67]. These properties are particularly relevant in regions such as visible light or nearby frequencies, where the manipulation of electromagnetic waves is most impactful [68].

The theoretical framework for understanding metamaterials is often based on transformation optics, which provides a mathematical approach to designing materials that can control the flow of electromagnetic waves in desired ways. Thus, from a coordinate transformation, researchers can create a perfect invisibility cloak, similar to a “mirror” that projects the originally flat electromagnetic space into physical space [69,70,71].

Metamaterials can be classified using various schemes based on their electromagnetic properties and applications [72].

The practical impact of transformation optics was first demonstrated in 2006 with a microwave invisibility cloak. By spatially varying ε and μ using an SRR, the cloak bent microwaves around a hidden object, validating Veselago’s theoretical predictions and Pendry’s superlens concept [73].

Figure 2 represents the primary classification of metamaterials based on their permittivity and permeability [1]. Integrating topology optimization into the design can lead to a better configuration of metamaterials that fits in the area of permittivity and permeability. The unit cell geometry (e.g., split-ring resonators or wire arrays) determines these effective medium properties, allowing tailored wave manipulation for applications such as cloaking and antennas.

The figure illustrates a quadrant-based graphical representation, where each quadrant delineates a specific combination of ε and μ values, highlighting the unique electromagnetic properties of each class, as follows:

-

Double-Positive (DPS): both ε and μ are positive (top-right quadrant), typical of conventional materials like dielectrics.

-

Epsilon-Negative (ENG): ε < 0, μ > 0 (top-left quadrant); found in plasmonic materials (e.g., metals at optical frequencies).

-

Mu-Negative (MNG): ε > 0, μ < 0 (bottom-right quadrant); exhibited by certain magnetic resonators.

-

Double-Negative (DNG): both ε and μ are negative (bottom-left quadrant), enabling negative refraction and superlensing.

Recent advancements in the field have also highlighted the role of plasmonic effects in enhancing the performance of metamaterials. Plasmonic metamaterials leverage the interaction between light and free electrons in metals to achieve strong field localization and enhanced nonlinear optical responses [74]. This has opened new avenues for applications in sensing, imaging, and information processing, where the ability to control light at the nanoscale is crucial [75]. Moreover, the integration of metamaterials with microelectromechanical systems (MEMSs) has emerged as a promising strategy for creating reconfigurable devices. This integration allows for dynamic control over metamaterial properties, enabling applications that require adaptability to changing conditions [75].

The development of plasmonic biosensors for early disease detection represents a significant advancement in nanotechnology, particularly through the application of plasmonic metamaterials. These biosensors utilize gold or silver nanostructures to support localized surface plasmon resonances (LSPRs), thereby enhancing both sensitivity and specificity in disease biomarkers detection. The interaction of light with these nanostructures generates intense electromagnetic fields that enable the detection of biomolecules at extremely low concentrations [76] making them suitable for applications in cancer diagnostics (detecting HER2 for breast cancer) and infectious disease screening (identifying pathogens like SARS-CoV-2) [77] or point-of-care testing when their miniaturized design allows for use in resource-limited settings [78].

The excitation of surface plasmons at the metal–dielectric interface leads to a measurable shift in resonance wavelength or intensity when target biomolecules are present [76].

These sensors can detect biomolecules down to picomolar levels, enabling the real-time monitoring of interactions [79].

While plasmonic biosensors show great promise, challenges such as reproducibility and scalability remain, which could hinder their widespread clinical adoption.

As the field continues to evolve, the interplay between electromagnetic theory and practical applications of metamaterials will undoubtedly lead to further innovations and discoveries.

1.3. Justification of Review Importance

This review is primarily intended for researchers, engineers, and academics within the fields of materials science, physics, and engineering. A comprehensive overview of this rapidly evolving field is crucial because it synthesizes the extensive and rapidly evolving body of knowledge surrounding metamaterials, which possess unique properties that can be leveraged for groundbreaking applications in medicine, optics, telecommunications, and energy harvesting. By critically analyzing the current literature in the field, this review will shed light on prevailing trends, pinpoint existing gaps, and highlight challenges that need to be addressed in the field. Such insights will offer valuable guidance for future research initiatives and foster meaningful collaborations. Moreover, this work will serve as a valuable resource for professors and students, enhance academic discourse, and stimulate technological advancements across various industries.

Recent advancements in artificial intelligence (AI) and additive manufacturing (AM) have significantly impacted the design and fabrication of metamaterials. AI-driven techniques, particularly machine learning (ML) and deep learning (DL), facilitate the inverse design of metamaterials by predicting optimal geometries and configurations tailored to specific performance criteria. This overview discusses significant methodologies and their implications in the field. This review explores how AI techniques, including Generative Adversarial Networks (GANs), Variational Autoencoders (VAEs), and deep learning, work alongside additive manufacturing to streamline and enhance the design and prototyping of metamaterials. While the integration of AI and AM in metamaterial design presents numerous advantages, challenges remain, such as the need for more interpretable models and the handling of complex loading scenarios in practical applications. Overcoming these issues is essential for the ongoing development of metamaterials. Moreover, this review also highlights the critical advancements and challenges in utilizing additive manufacturing techniques, including fused deposition modeling (FDM), stereolithography (SLA), and selective laser sintering (SLS), in producing intricate metamaterials, particularly for medical applications. It underscores the importance of addressing issues related to scalability and quality consistency to ensure the broader adoption of these technologies. These innovations pave the way for metamaterials to transition from experimental concepts to commercially viable solutions. By encompassing these advancements, this review not only provides a snapshot of the current state of metamaterials but also highlights the transformative potential of AI and AM in pushing the boundaries of material performance. Future research directions include the development of self-learning metamaterial systems that autonomously adapt to operational conditions, as well as the exploration of hybrid fabrication techniques that integrate both top-down and bottom-up approaches for enhanced functionality. As the field continues to evolve, this review serves as a fundamental resource for guiding interdisciplinary efforts and unlocking the full potential of metamaterials in real-world applications.

2. Principles of Metamaterial Design

The design of metamaterials serves as a crucial bridge between theoretical concepts and practical applications. Functionally, metamaterials include electromagnetic metamaterials (manipulating electromagnetic waves, e.g., cloaking devices [72], acoustic metamaterials (controlling sound waves, e.g., acoustic cloaking) [80], mechanical metamaterials (exhibiting unusual mechanical properties like negative Poisson’s ratios or tunable stiffness) [81,82] thermal metamaterials (managing heat flow, e.g., thermal cloaking) [83], and optical metamaterials (manipulating light, e.g., superlenses) [8]. Based on scale, they range from macroscopic (visible structures for engineering applications) to microscopic/nanoscopic (used in photonics or nanomedicine [84]. Design-wise, they can be periodic (repeating unit cells) or aperiodic/random (irregular structures for specialized uses) [85]. Mechanical metamaterials, in particular, derive their unique properties—such as auxetic behavior (expanding when stretched), negative compressibility, or programmable deformation—from their carefully designed internal architectures rather than their chemical composition. Their design relies on unit cell geometry, multiunit cell arrangements, and material selection, enabling applications in lightweight structures, energy absorption, and advanced robotics [84].

Traditionally, the design process involves extensive full-wave electromagnetic simulations and the retrieval of scattering (S) parameters, in which numerical simulations are iteratively conducted to fine-tune the constitutive parameters of individual metamaterial elements [50]. The design of metamaterials is grounded in several fundamental concepts, including NIMs, anisotropic materials, and resonant structures. Negative-index materials lead to a modified Snell’s law (the refracted angle becomes “negative”, altering the traditional calculation of the light’s refraction when it passes between two media with different refractive indices) [28,64], enabling applications such as cloaking, superlensing, and sensors [5,86]. These NIMs are typically regarded as artificially engineered materials exhibiting unique optical properties as a result of combining two or more elemental materials [87]. Anisotropic materials exhibit direction-dependent properties (manipulation of wave propagation), which can be tailored for specific applications in optics [88] and acoustics [89]. Furthermore, anisotropic acoustic metamaterials can convert evanescent waves onto propagating waves (by effectively coupling large wave vector components), allowing high-resolution imaging even in the far field [5,31,80]. Subwavelength resonant structures are the key components of metamaterials (can respond, as a homogenous material, to the electric and magnetic field), giving them unique properties [49,90]. A typical highly conductive metamaterial structure is the SRR, which exhibits a balance between its capacitance and inductance and can be engineered to be very compact, having dual band features [91,92]. Based on the resonant properties of the structure and when applying a time-varying magnetic field perpendicular to the surface (generates currents), an SRR creates a magnetic field that can either counteract or reinforce the original field, leading to either positive or negative permeability (μ) [5,86,93]. Resonators can be classified as internal and external depending on their position towards the structure. Internal resonators are an integral part of the material and, as a matter of fact, do not require additional space. On the other hand, external resonators are placed externally, which protects the main structure and is an accessible way to be repaired [94]. Metamaterials can provide various types of resonances depending on other compositions and interactions with other waves: band-gap resonance, acoustic resonance [94], plasmonic resonance [95], and Fano resonance [96]. Dispersion is a fundamental characteristic of electromagnetic systems originating from the interaction between light and materials. Metamaterials exhibit design flexibility due to their artificial structures, enabling precise manipulation of electromagnetic properties at subwavelength scales [97]. This unique characteristic enables the intrinsic resonance of subwavelength structural elements to generate significant dispersion in their effective material parameters. Metamaterials can overcome the inherent limitations of classic diffraction, reflection, and refraction theory, paving the way for advanced dispersion engineering in a wide range of applications [98]. Design methodologies for metamaterials encompass analytical approaches, numerical methods, such as the finite-difference time-domain (FDTD) and the finite element method (FEM), and experimental validation techniques [71,99]. Numerical simulations are particularly valuable for modeling complex interactions within metamaterials, allowing for optimization prior to physical fabrication [71]. The FDTD method, a simple and versatile technique, has been widely used to simulate electromagnetic wave propagation (by directly implementing Maxwell’s time-dependent curl equations [100] in metamaterials by treating them as dispersive media) [78,95,99,101].

An alternative numerical method for solving the time-domain Maxwell’s equations in the presence of metamaterials is the FEM, which is used for modeling complex geometries [102]. This approach is suitable for settling heat conduction problems, especially for thermal metamaterials, and allows us to understand the damages caused in the matrix of a composite material that is exposed to extreme conditions, including different temperatures, pressures, and static or dynamic loading [103,104]. While FDTD and the FEM are the main methods for electromagnetic analysis, other numerical techniques, including Rigorous Coupled Waveguide Analysis [105], Method of Moments [106,107], and the Boundary Element Method [108], are also employed in certain situations. Design optimization strategies for metamaterials should be flexible enough to integrate with any of these numerical modeling methods. Different experimental validation techniques are used to provide theoretical or calculated predictions about the behavior and properties of metamaterials. These techniques can be classified depending on the type of response that they are designed to measure, e.g., electromagnetic [109], mechanical [110], or acoustic [111], and are essential for validating metamaterial designs.

2.1. Metamaterials Design and Fabrication Techniques

Metamaterials research has expanded significantly in the last decade, spanning from the basic pursuit of designing new materials to the investigation of the unique properties emerging from their subwavelength structure. A range of capabilities is required to design and analyze these complex material archetypes. This section presents a brief overview of several design and fabrication methods currently in use or under development. The subwavelength nature of single metamaterial spacings offers the possibility of tailored responses, with the potential for significant effects on properties in electromagnetic and other functions. Hybrid structures that allow for foreshadowing of system properties are also considered.

Figure 3 illustrates the design space of mechanical metamaterials, emphasizing the key parameters that influence their design and performance. These parameters are derived from three main categories: (1) materials and fabrication techniques, which determine the physical and structural properties of the metamaterials; (2) unit cell design, which defines the individual behavior of each repeating structural element; and (3) multiunit cell architecture, which governs the overall arrangement and interaction of multiple unit cells to achieve desired mechanical properties at a larger scale. This comprehensive framework provides a structured methodology for designing mechanical metamaterials, allowing researchers to tailor their properties for specific applications, such as lightweight structures, energy absorption, or tunable stiffness. By understanding and optimizing these parameters, it becomes possible to push the boundaries of material performance and explore new functionalities in engineering and technology.

A major class of well-known properties is the permittivity and permeability of electrical materials, often expressed in tensor form. From these properties, Maxwell’s equations are expressed in a form with material properties. A second class is the scattering parameters, which relate either to the tensor properties or to transfer matrices that represent the boundaries of the material. Additional tool sets that enable the optimization of specific response properties provide methods that could also exploit constitutive requirements, such as those derived from transformative electromagnetic techniques. Additionally, targeted manufacturing options, such as lithography, etching, and screen printing, can be employed. These techniques can be broadly categorized into computational methods, fabrication approaches, and hybrid systems that integrate multiple functionalities.

Top-down methods like lithography enabled early transformation optics devices, such as the Duke microwave cloak [48]. However, bottom-up approaches (e.g., 3D printing) [113] now allow more complex gradient-index designs for broadband applications.

The advent of computational methods has significantly transformed the design landscape of metamaterials. Techniques such as topology optimization, evolutionary algorithms, and deep learning have emerged as powerful tools for the inverse design of metamaterials. For instance, deep generative models, like Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs), streamline the design process by predicting and generating metamaterial structures that meet specific performance criteria, thus reducing the reliance on trial-and-error approaches [114]. These methods allow for the exploration of complex design spaces, enabling the discovery of novel configurations that exhibit desired electromagnetic responses.

Employed to streamline the design process, GANs reduce reliance on trial-and-error methods, enabling rapid exploration of design spaces [115].

These models assist in generating new metamaterial designs by learning from existing data, thus enhancing the efficiency of the design process [116].

Techniques such as image-based deep learning networks minimize preprocessing steps, allowing for direct generation of metamaterial designs from input parameters [117].

On the other hand, additive manufacturing techniques, including 3D printing, have revolutionized the fabrication of metamaterials by allowing for the creation of intricate geometries that were previously unattainable through traditional methods. This approach enables the production of metamaterials with tailored properties, such as customizable thermal expansion and mechanical responses [118]. Furthermore, the integration of stimuli-responsive materials with 4D printing techniques facilitates the development of metamaterials that can adapt their properties in real time based on environmental changes [118].

The flexibility and precision of additive manufacturing also support the fabrication of complex multimaterial structures, enhancing the functional capabilities of metamaterials [119].

The exploration of hybrid systems that combine different types of metamaterials or integrate active components into passive structures is gaining traction. For example, the incorporation of digital logic gates into soft, conductive mechanical metamaterials allows for the creation of multifunctional devices that can perform computational tasks while also exhibiting mechanical properties [120]. This modular approach not only enhances the versatility of metamaterials but also paves the way for the development of intelligent systems capable of self-powered information processing [121].

Advanced simulation techniques, such as discrete dipole approximation and finite element analysis, play a crucial role in predicting the behavior of metamaterials under various conditions. These methods enable researchers to model complex interactions within metamaterials and optimize their designs before fabrication [122]. Additionally, the use of machine learning algorithms to analyze simulation data can further refine design parameters and improve the accuracy of predictions regarding metamaterial performance [123].

As the field of metamaterials continues to evolve, new design techniques are emerging that leverage advancements in materials science and engineering. For instance, the development of programmable granular metamaterials allows for the tuning of mechanical properties through structural design, offering a vast design space for energy absorption applications [124]. Furthermore, the integration of artificial intelligence in the design process is expected to enhance computational efficiency and accelerate the discovery of novel metamaterials with tailored functionalities [123]. The design techniques for metamaterials are diverse and continually advancing, driven by the need for innovative solutions across various applications. The combination of computational methods, advanced fabrication techniques, and hybrid systems is paving the way for the next generation of metamaterials with unprecedented capabilities. The most comprehensive coverage of the design and fabrication of metamaterials would include elements from all of these classes.

2.2. Unit Cell Design

The unit cell in metamaterials is fundamental as it encapsulates essential information about the crystal structure, including geometric attributes, material characteristics, and lattice spacing. These elements are pivotal in establishing the periodicity of the crystal and influencing the position and extent of the band gap [125]. The repeating unit cell establishes the crystal periodicity and controls the position and extent of the band gap [125]. Choosing the appropriate unit cell shape is fundamental in metamaterial design, as it directly influences the resonant bandwidth, incident-angle stability, and cross-polarization level. Given their structures, these shapes can be broadly classified as centrally connected N-poles, rings, internal solids, and composites [126]. The foundational unit cell supports the design of a reconfigurable metamaterial device and determines the fundamental behavior of the structure. Typically, the design process begins with a static configuration, which is then enhanced by incorporating tunable elements, materials, or structures [127]. The unit cell’s physical geometry controls the electromagnetic coupling within the metamaterial, introducing frequency selectivity with either desired or undesired effects, and can facilitate the suppression of either electric or magnetic excitations. Moreover, the unit cell geometry can be engineered to couple electric and magnetic responses strongly [127].

The design of metamaterial unit cells is a multifaceted challenge that includes considerations of geometry, material selection, and operational context. For example, any changes to the physical dimensions of an SRR that affect either inductance (L) or capacitance (C) will directly impact its resonant frequency [128]. Thus, a narrower gap increases capacitance, which lowers the resonant frequency. Conversely, a wider gap decreases capacitance, raising the resonant frequency. The overall size and shape of the rings influence the inductance. Larger rings generally result in higher inductance. Using nested or multiple rings introduces more complex interactions, affecting both L and C and allowing for the creation of multiband resonances [129].

Asymmetric designs, such as L-shaped or zigzag wires, introduce anisotropy, enabling polarization-dependent responses. In contrast, stacked nanowire unit cells in hyperbolic metamaterials create extreme anisotropy, where the permittivity tensor has opposite signs for different components, enabling subdiffractional imaging. Asymmetric unit cell designs disrupt the symmetry of the metamaterial, resulting in its electromagnetic response varying depending on the polarization of the incident light. Specifically, symmetric unit cell designs disrupt the symmetry of the metamaterial, resulting in its electromagnetic response varying depending on the polarization of the incident light [130]. This is crucial for applications requiring precise control over polarization, such as optical isolators, polarization converters, and chiral metamaterials. Asymmetric electromagnetic wave transmission of linear polarization is possible via polarization conversion through chiral metamaterial structures [131].

Coupling electric LC resonators with magnetic SRRs enables the creation of double-negative media. All-dielectric unit cells, such as spheres or disks of high-index dielectrics, support Mie resonances with spectral positions that depend on the particle diameter and aspect ratio [132]. Reconfigurable unit cells, like MEMS-actuated SRRs or liquid crystal-filled gaps, enable dynamic switching of EM properties, though complex geometries often require advanced lithography and present fabrication trade-offs [28].

Effective manipulation of the unit cell can lead to significant advances in the performance and applicability of metamaterials in various fields, including medicine [133], telecommunications [134], and even sensing technologies [135]. The unit cell is the basic “building block” of metamaterials [119], and its design can significantly influence the overall electromagnetic properties of the material. Therefore, it is necessary to first define what a unit cell is in the context of metamaterials. Although in many practical implementations of metamaterials, this takes the form of a volume of material with certain exceptional properties within a dielectric, the term “building block” is generally not useful or instructive for the design process of metamaterials [119]. In traditional crystalline materials, translational invariance to symmetry is the fundamental requirement of the unit cell. In other words, there are an infinite number of unit cells that are translated away from each other, so that the crystal is invariant when translated through each of these units. Theoretically, the same requirement applies to three-dimensional periodic materials as to metamaterials. However, for a practical realization of a metamaterial, the unit cell size is always limited by the size of the system to be realized [136].

In this sense, the unit cell is an imposed limitation, and its design generally lacks complete translational invariance to symmetry. The attainment of perfect translational invariance in practical metamaterials is significantly impeded by several key challenges, including spatial disorder arising from fabrication imperfections like nanoscale misalignments [130] and finite size effects, which cause edge effects [78,133]. Finite metamaterial samples exhibit mode truncation effects that are absent in infinite-lattice theories, while dispersive and lossy resonant elements challenge homogenization due to spatial dispersion and frequency-dependent losses [137], near-field coupling between unit cells at subwavelength scales leads to unintended interactions and “hotspots”, and scalability versus performance trade-offs force compromises between large-area fabrication precision and throughput [8]. Researchers mitigate these issues through statistical homogenization to model disorder, edge optimization to minimize reflections, and active tuning to correct inhomogeneities using technologies like MEMS or liquid crystals dynamically [138,139].

The design of unit cells in practical metamaterials is, therefore, different from that in traditional materials, and it is often difficult to determine the symmetry of the material from a simple examination of the underlying configuration of basic elements [136]. This viewpoint is useful across all scales of metamaterial design, from simple wires on a printed circuit board that defines frequency-selective surface to subwavelength skin depth thickness penetration limits within the unit cells of acoustical metamaterials [140]. However, most designs are formed from an arrangement of a small number of basic building blocks, with the liquid crystal (LC) used in the design frequency for dimensional simplicity. The most common building blocks used to form electrical/magnetic and chiral topologies within metamaterials are the split-ring resonator and the square split-ring resonator, the Jerusalem or cross resonator, thin wires for electrically shorted reactions, split Cube geometries, and fishnets metamaterials and arrays of these topologies that impart an anisotropic response to the medium [127].

Khansanami et al. showed that the shape and thickness of the unit cell are critical for defining a metamaterial’s mechanical and vibrational properties [136]. In another example, a square-shaped unit cell with specific dimensions was analyzed to optimize its metamaterial properties [141].

One of the primary considerations in unit cell design is the method of homogenization, which is essential for predicting the effective properties of metamaterials. The predictive accuracy of conventional homogenization methods, such as volumetric averaging, encounters significant limitations when predicting metamaterial effective properties. These include mismatches when the unit cell size approaches operating wavelengths [137], the failure to account for localized field discontinuities and enhancements at inclusion boundaries [49], inadequate representation of strong anisotropy and frequency dispersion [63], inability to model dynamic changes in nonlinear or tunable metamaterials [16], and neglect of near-field interactions and coupling between unit cells [30], especially in complex subwavelength structures or those with thin metallic inclusions [44,63,137,142]. Such considerations are crucial for ensuring accurate predictions of the metamaterial’s optical properties. The choice of unit cell geometry significantly determines the operational bandwidth and resonant frequencies of metamaterials. For instance, an SRR unit cell design can significantly alter the current path, leading to new resonant frequencies, particularly favorable for multiband antenna applications [143]. Similarly, nested U-ring resonators have been shown to facilitate miniaturization while achieving multiband behavior, demonstrating that more complex geometries can enhance performance beyond traditional designs [144]. In contrast to metallic metamaterial unit cells, which are often complex, particularly when a magnetic response is essential, all-dielectric metamaterials (ADMs) can be employed with much simpler geometries (spheres and cubes) [127]. These findings underscore the necessity of innovative geometrical configurations in unit cell design to achieve desired electromagnetic properties. Thus, the integration of materials, such as LCs, into metamaterial designs has opened new opportunities for tuning and dynamic control of electromagnetic responses. Savo et al. presented an LC metamaterial absorber that can be electronically controlled to shape the spatial distribution of terahertz radiation, highlighting the potential of combining different materials within the unit cell to improve functionality [145]. This approach aligns with the trend towards reconfigurable metamaterials, where MEMSs are employed for independent tuning of multiple resonances at terahertz [146,147].

Integration of LCs into metamaterials enables dynamic control and adaptive properties [145] through real-time reconfigurability, enhanced tunability, and multifunctionality. Specifically, LCs’ anisotropic refractive indices facilitate electrically tunable optical and THz metamaterials with dynamic switching capabilities [148]. Their dielectric property variations allow for the development of reconfigurable microwave [149] and radio frequency (RF) devices for beam-steering and frequency-agile sensing. Furthermore, LCs amplify nonlinear effects for ultrafast optical switches and dynamic light focusing, and their thermotropic phase changes allow for thermal and mechanical adaptability in applications like self-regulating thermal cloaks and soft robotics [150]. While response time limitations exist, innovations in hybrid LC–polymer composites and future integration with AI-driven design and nanoscale LC patterning hold promise for enhancing metamaterial functionality, thereby transforming static metamaterials into adaptive systems for diverse applications [146].

Such advancements highlight the importance of the geometric design of unit cells and the materials used in their construction.

2.3. Topology Optimization

Topology optimization (TO) is an effective and versatile design method developed decades ago, as a mathematical approach for optimizing structural shapes and material distribution in components, to maximize performance according to relevant design specifications [151,152,153,154]. Originally developed for structural mechanics problems [155], TO offers a systematic and performance-driven framework for designing metamaterials by iteratively optimizing the structural layout to achieve a specific objective (e.g., maximum stiffness, thermal dissipation, or minimum weight/cost) under defined constraints [156]. In the design of metamaterials, optimization is used to identify the optimal topology of the periodic unit cell microstructure [157]. Topology optimization, applicable to diverse physical phenomena including heat transfer and wave propagation (e.g., sound and electromagnetic wave), is now being employed to design metamaterials with a wide range of tailored properties, such as elasticity, viscoelasticity, extreme thermal expansion, photonic and phononic bandgaps, thermal exchange, and even negative permeability [157,158].

In the context of microstructure topology optimization, determining the effective properties of unit cells typically requires the application of numerical homogenization, which involves solving linear equilibrium equations. This process, however, is computationally intensive. To mitigate this, reduced-order modeling techniques that utilize Krylov subspaces have been proposed, enhancing computational efficiency. These methods employ an iterative solver to address large linear systems, leveraging a search space based on previous solutions. The approach assumes that the numerical stiffness matrices between successive iterations change only incrementally, reflecting small modifications in the structure’s topology or shape [159].

Topology optimization methods like SIMP and SKB significantly influence metamaterial unit cell design [152]. SIMP, through penalizing intermediate densities, produces clear, high-contrast geometries ideal for static, high-stiffness applications like mechanical metamaterials, with computational efficiency but potential numerical artifacts [160], while SKB, using gradual stiffness reduction, creates smoother, more manufacturable structures suitable for complex, multimaterial designs like thermal or acoustic metamaterials, albeit with higher computational costs [161]. Hybrid approaches combining SIMP and SKB [162] leverage both clarity and smoothness, and the choice between them depends on the target application, with SIMP favored for precision [163] and SKB for adaptability in multi-physics designs. This impacts performance, manufacturability, and functionality uniquely [163] and provides ongoing advances in computational tools, expanding optimization possibilities [155].

Among the various methods available, the Solid Isotropic Material with Penalization (SIMP) method and the Soft-Kill Binary (SKB) method have gained significant attention due to their unique capabilities in generating optimal topologies [154,164]. The SIMP method excels in generating clear and distinct topologies, making it a popular choice for various engineering applications. On the other hand, the Soft-Kill Binary method offers smoother transitions and more robust optimization results, particularly in complex and multimaterial structures [154,164].

The SIMP method is one of the most widely used methods in topology optimization. It works by introducing a material model that penalizes intermediate densities, encouraging the material distribution to approach either 0 (void) or 1 (solid) [161]. This penalization is achieved through a power-law relationship between the material density and stiffness, which helps in reducing the presence of gray elements (intermediate densities) in the final design. The SIMP method is known for its simplicity and computational efficiency, making it a popular choice for various engineering applications [165].

One of the key advantages of the SIMP method is its ability to generate clear and distinct topologies. By penalizing intermediate densities, SIMP ensures that the final design is predominantly composed of solid and void regions, which is often more manufacturable and easier to interpret [161]. This is particularly useful in industrial applications where clear boundaries between materials and voids are crucial. For instance, in the topology optimization of functionally graded materials (FGMs), the SIMP method has been successfully used to maximize fracture resistance by optimizing the distribution of the second phase [165].

However, the SIMP method is not without its limitations. One of the main drawbacks is the potential for numerical instabilities, such as checkerboard patterns and mesh dependency, which can lead to less smooth and less meaningful topologies. These issues can be addressed through the use of filtering schemes and other numerical stabilization techniques, as demonstrated in several studies [161,166].

The SKB method, on the other hand, is a variant of the Bi-directional Evolutionary Structural Optimization (BESO) method. Unlike the hard-kill approach, which abruptly removes elements from the design domain, the soft-kill method gradually reduces the stiffness of elements that are deemed unnecessary. This gradual approach enables smoother transitions between solid and void regions, resulting in more realistic and smooth topologies [154,164].

The SKB method is particularly useful in cases where smooth transitions are critical, such as in the design of structures with multiple material phases or in applications where manufacturability is a key concern. The soft-kill approach also helps to avoid the convergence issues often associated with hard-kill methods, making it more robust for large-scale structures [154,164]. For example, in the context of multimaterial topology optimization, the SKB method has been shown to effectively handle the distribution of multiple material phases while maintaining smooth boundaries [163].

Despite its advantages, the SKB method can be computationally more expensive than the SIMP method, especially for large-scale structures. This is because the soft-kill approach requires iterative updates to the material properties, which can increase the computational burden. However, recent advancements in computational techniques, such as GPU-based algorithms, have helped mitigate these issues, making the SKB method more feasible for practical applications [162].

Given the strengths and weaknesses of each method, researchers have explored hybrid approaches that combine the SIMP and SKB methods. These hybrid methods aim to leverage the computational efficiency and clarity of SIMP while incorporating the smoothness and robustness of the SKB method. For example, one study proposed a hybrid BESO method that combines the soft-kill and hard-kill approaches for large-scale structures, achieving reduced execution time, decreased memory consumption, and improved FEA convergence [162].

Similarly, other studies have integrated SIMP with evolutionary algorithms, such as genetic algorithms (GAs), to enhance the optimization process. These hybrid methods have shown promising results, with improved convergence speed and better optimization effects compared to traditional methods [154,164].

While the focus on topology optimization presents significant advantages in material design, it is essential to consider the potential for failure due to defects and high void fractions. Balancing optimization with structural integrity remains a critical challenge in the field of metamaterials. For a metamaterial sample that consists of semi-interactively different materials, the void fraction after topology optimization is probably very high, given the mechanical properties of the sample system [167]. There could be one or more cracking locations that, combined with high stresses, lead to the splitting failure of the material. In this case, if the desired mechanical properties of the metamaterial sample are described at the micro-level, it is possible to realize the actual design requirements. In the process of topology optimization, to complete the solution of the topology, the volume elements connected to the kth need to be determined [167]. Topology optimization enhances the mechanical properties of metamaterials by allowing for tailored designs that can achieve desired stiffness and energy absorption characteristics [168].

The optimization process can lead to the emergence of complex structures that exhibit unique mechanical behaviors, such as increased stiffness and improved energy absorption under deformation [168].

The presence of topological defects can significantly influence the mechanical response of metamaterials, potentially leading to failure modes like cracking under high stress [169].

Understanding these defects is essential, as they can alter the material’s properties and overall performance, emphasizing the need for careful design and optimization [169].

The design of functionally graded metamaterials allows for varying mechanical properties across the material, which can be optimized for specific applications, enhancing performance and durability [151].

Advanced optimization techniques, including genetic algorithms, can facilitate the design of energy-absorbing structures that meet specific stress–strain requirements, further mitigating failure risks [170].

Integrating topology optimization into metamaterial design not only improves performance but also facilitates the creation of structures with complex geometries that cannot be achieved using traditional methods. This integration utilizes advanced computational techniques, enabling the design of structures that optimize material distribution to achieve desired properties, such as sound absorption and mechanical strength [171]. Topology optimization improves the acoustic performance of metamaterials, as demonstrated in studies where optimized structures achieved superior sound absorption capabilities compared to conventional designs [172].

The mechanical properties of metamaterials can be tailored through optimization, leading to lightweight yet strong structures, which are crucial in applications like the aerospace and automotive industries [173].

The use of additive manufacturing in conjunction with topology optimization allows for the fabrication of intricate designs that traditional manufacturing methods cannot produce. This includes self-supporting structures that eliminate the need for additional support during production [173].

Anisotropic properties of materials can be effectively incorporated into the design process, further enhancing the complexity and functionality of the resulting metamaterials [173].

While the benefits of integrating topology optimization into metamaterial design are substantial, challenges remain, including the computational cost and time associated with the optimization process. These factors can limit the practical application of such advanced techniques in real-world scenarios [174]. Topology optimization has proven valuable in designing metamaterials with specific mechanical properties, such as negative Poisson’s ratios. Qin et al. introduced an advanced topology optimization method that enables the design of lightweight metamaterials with tuned Poisson ratios and demonstrated the method’s ability to automatically determine optimal configurations rather than relying on predefined shapes [175]. This capability was further supported by the work of Vogiatzis et al., who used a refined level set method to optimize negative-Poisson-ratio metamaterials (including both single- and multiple-material), highlighting the flexibility and effectiveness of topology optimization in achieving desired material distributions [172].

Furthermore, the applicability of topology optimization extends beyond mechanical properties to thermal and acoustic metamaterials. Sha et al. explored the potential of extending 2D thermal metamaterials to 3D configurations through tailored mathematical models, emphasizing the role of topology optimization in improving thermal management capabilities [176]. Similarly, Mendez et al. examined computational material design for acoustic cloaking, where the introduction of topological derivatives enabled the design of metamaterials across multiple length scales, demonstrating the versatility of topology optimization in metamaterial applications [177].

Integrating topology optimization with other design methods, such as shape optimization, has proven to offer significant advantages. Stankiewicz’s research on auxetic piezoelectric metamaterials showed that combining topology and shape optimization can leverage the strengths of both approaches and lead to improved design results [178]. This hybrid approach was further validated by Han et al., who demonstrated the practicality of combining topology and shape optimization methods for bifunctional metamaterials by the obtained experimental results that closely matched the optimization predictions [179]. Zeng et al. highlighted the need to consider large geometric deformations in the topology optimization of energy-absorbing structures, suggesting that traditional small deformation assumptions may be insufficient for advanced metamaterial designs [170]. This finding underscores the importance of adapting and refining optimization techniques to address the unique challenges posed by the dynamic and complex behavior exhibited by metamaterials.

3. Metamaterial Fabrication Techniques

Various fabrication methods are required to precisely control the structure at different levels (micro, nano) and to obtain materials with unique properties that differ from those of naturally occurring materials. Metamaterials can be fabricated using both top-down and bottom-up approaches (Figure 4).

The top-down technique (applicable for large-scale manufacturing) involves the fabrication of metamaterials from bulk to micro/nanoscale, while bottom-up approaches facilitate the growth and self-assembly of atoms and molecules to produce micro/nanoscale structures.

Top-down techniques, such as photolithography, electron beam lithography, and etching processes, imply a gradual process of reducing and constructing the metamaterial structure, from macroscopic dimensions to precise nanoscale features [97,159,180]. These methods, however, can be limited by scalability and cost [71,180].

Photolithography, a microfabrication technique, is used to manipulate single- and multilayer metamaterials designed to operate at terahertz frequencies. This method is based on the photopolymerization of monomers and enables the achievement of high-resolution subwavelength structures [1]. Light-sensitive photoresists, which undergo chemical changes when exposed to light, enable patterning at the nanoscale. Photolithography, a low-cost method with high efficiency, as described in ref. [181], is restricted due to limited diffraction. Therefore, derived techniques (from traditional photolithography), such as shift mask lithography [182] deep ultraviolet immersion lithography [183], and electron beam lithography [184], have been proposed to overcome this restriction. Despite these advancements, photolithography still faces challenges in effective manufacturing and must be adapted to enhance functionality and precision. Electron beam lithography (EBL) represents a powerful tool for the rapid prototyping of metasurfaces [185]. This method involves generating a pattern by focusing a Gaussian electron beam onto a resistant material to break chemical bonds. Despite its long time processing and high operating costs [181,185], EBL is used for manufacturing large-area surfaces and provides high-resolution patterning for nanoscale structures [181]. It builds upon the principles of traditional photolithography, incorporating enhancements to processing and patterning while reducing the diffraction limitation. Etching processes have evolved over the past years, leading to the development of various technologies, including chemical etching [171] (involving the reaction between species), physical etching (incorporating removal of the material) [186], and ion beam etching [182]. The substrate etching approach is suitable for metamaterials as it improves sensitivity and reduces the effective refractive index [183]. Regarding the ion beam etching technique, an ion beam interacts with the material’s surface without altering the internal structure, which can contribute to the fabrication of metamaterials with complex geometries [1,182]. However, this method is often limited to several structures, and the used equipment is expensive [1].

Bottom-up approaches, such as self-assembly [187], chemical vapor deposition (CVD) [188], and 3D printing [189], ensure promising alternatives for producing complex structures at lower costs [190,191,192]. The self-assembly process involves the organization of individual components into ordered or unconventional patterns or structures [193,194]. This process can occur with either active materials that interact according to predetermined programs or passive materials that interact in line with intermolecular forces, geometry, or surface chemistry [189]. This method is used to synthesize different types of nanoparticles for surface functionalization, along with a variety of metamaterials, with potential applications in the optical field, electromagnetic domain, or other fields [189,194,195]. The self-assembly process holds significant potential for synthesizing large-dimension metamaterials with homogenous properties, making them ideal substrates for energy materials [193,196]. It is also an effective approach for assembling plasmonic metamaterials and fabricating sensor-based metamaterials. However, the self-assembly technique is usually limited regarding system phase distribution and the templates used. Single-phase system metamaterials are usually determined, while multi-phase systems or complex systems have not been widely explored [196]. As for templates, they are also limited to certain types of particles [197]. An alternative method for fabricating metamaterials is chemical vapor deposition (CVD), often combined with physical vapor deposition (PVD) to create complex and controlled structures over large uniform areas [198]. Compared to other techniques, CVD is remarkable for its versatility in depositing a wide range of materials for various fields (e.g., material science [199], medicine [200] or engineering), thus achieving conformal layers with high production efficiency and low-cost fabrication. Unlike PVD, which uses the vaporization of solid precursors for deposition, the CVD process deposits solid materials onto a substrate by introducing gaseous precursors, often in combination with carrier gases, which react to form thin films or coatings [201]. The disadvantages of this method include the production of chemical compounds and limited low-pressure and high-temperature depositions [199,202]. Three-dimensional printing or additive manufacturing (AM) expands the possibilities of creating metamaterials with unique electrical and transmission properties that cannot be obtained by conventional approaches [203]. Advanced metamaterials can be fabricated using AM by controlling the structure of patterns and topology, offering high design freedom for achieving negative stiffness and a negative Poisson’s ratio [204]. Three-dimensional printing technologies include different methods such as inkjet printing [203] selective laser sintering (SLS) [204], fused deposition modeling (FDM) [205], and stereolithography (SLA) [206], each with specific advantages and disadvantages but following similar fundamental working principles while providing a fast, convenient, and efficient route for the fabrication of metamaterials with a low production cost [74]. AM has certain limitations. For example, the extrusion temperature is limited, resulting in poor surface quality, and, consequently, the final product exhibits weak mechanical properties [207].

Such techniques facilitate the production of intricate geometries, including multimaterial and functionally graded metamaterials, which are essential for applications requiring tailored thermal, mechanical, or optical properties [208].

Thus, 3D-printed mechanical metamaterials with unique properties, such as negative Poisson’s ratios, have been developed for lightweight aerospace components and energy-absorbing structures [208]. Furthermore, 4D printing, which incorporates stimuli-responsive materials, allows for the creation of dynamic metamaterials that adapt their properties in real time to environmental changes [209].

In summary, top-down methods offer high precision but can be expensive and time-consuming, while bottom-up methods, particularly additive manufacturing, allow greater design flexibility and scalability [71,190]. The choice of a manufacturing technique often depends on the specific application and required material properties [71].

Table 1. Main fabrication techniques of metamaterials.

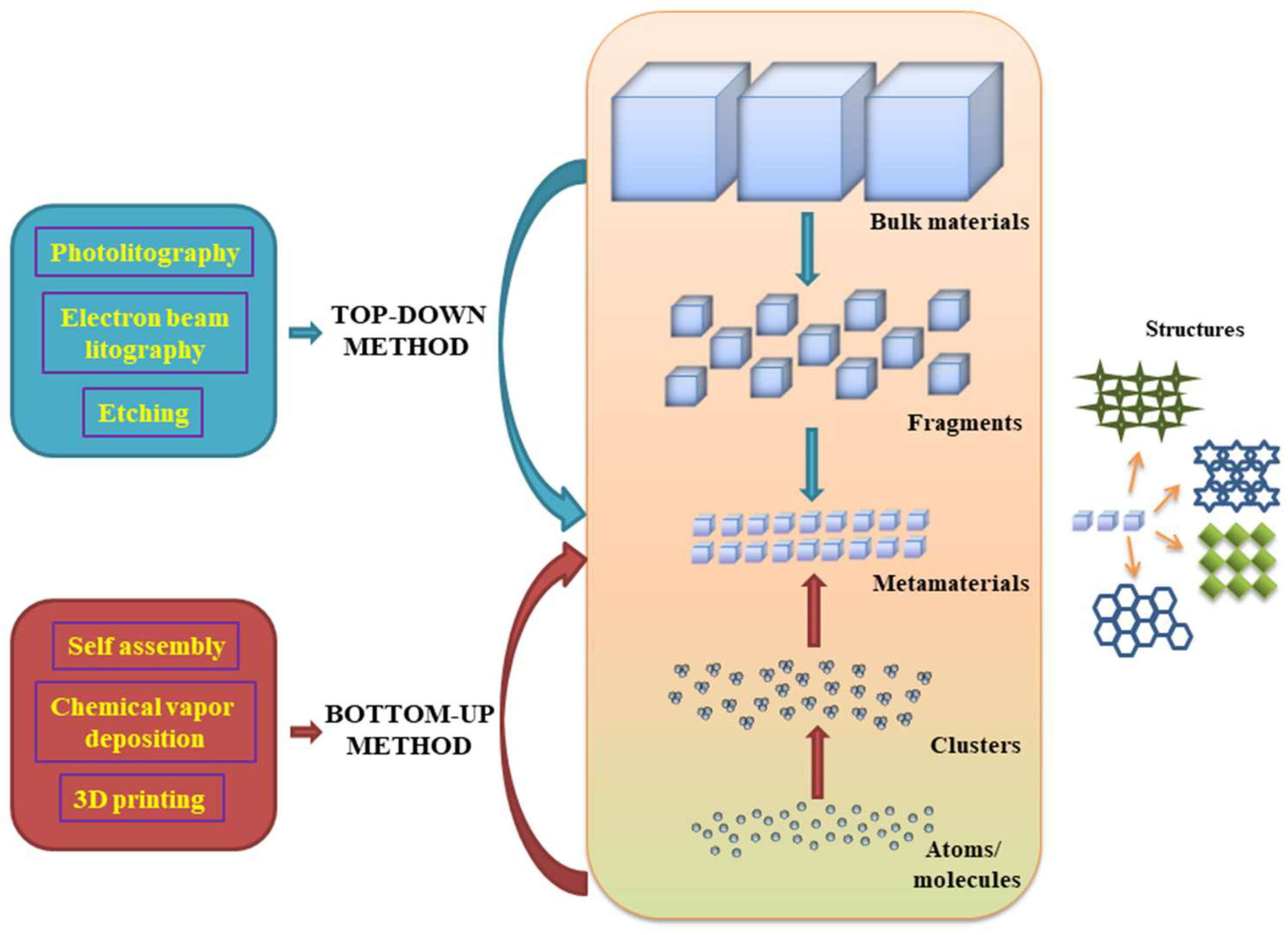
Approach	Technique	Advantages	Disadvantages	References
Top-down	Photolithography	High-resolution structures, low-cost	Restricted due to limit diffraction, low effective manufacturing	[1,181,210]
	Electron beam lithography	High resolution pattering for nanoscale structures, rapid prototyping	High operating costs, time intensive for large areas	[181,185]
	Etching	High sensitivity, low refractive index	Limited structure, high-cost equipment	[1,182,183]
Bottom-up	Self-assembly	Low-cost, suitable for different types of nanoparticles, homogenous structures	Restricted template types, limited by phase distribution	[193,194,195,196,210]
	Chemical vapor deposition	Complex and controlled structure, high production efficiency, conformal layer deposition, low-cost fabrication	Low pressure and high temperature limitations, production of chemical compounds waste	[198,211]
	3D printing	Design freedom, suitable for developing advanced metamaterials, low-cost production	Limited extrusion temperature, weak mechanical properties, poor quality surface	[203,204,205]

summarizes the main metamaterial fabrication techniques and highlights the advantages and disadvantages of each method.

Furthermore, the design and fabrication of metamaterials are inherently tailored to their intended functions, with each application demanding specific structural and material properties [212]. Consequently, metamaterial fabrication techniques must be carefully selected based on the specific functional requirements of each application. For instance, electromagnetic applications, such as cloaking devices, demand nanoscale precision fabrication, achievable through EBL or photolithography, to precisely control permittivity and permeability [181,185] AM offers a distinct advantage in the fabrication of metamaterials for energy absorption, enabling the creation of complex auxetic geometries [119,204]. Similarly, thermal management applications require the CVD technique for controlled thermal conductivity gradients [213,214], while acoustic metamaterials utilize self-assembly techniques to achieve specific resonant properties that manipulate sound waves [189,194].

Fundamentally, the choice of a fabrication method, whether top-down (e.g., etching for optical metasurfaces [182,183]) or bottom-up (e.g., 3D printing for tissue scaffolds [215,216]), is guided by the intended metamaterial function and operational requirements, including scale and desired anisotropy [190]. The implementation of a function-specific approach ensures optimal performance by addressing the distinct demands of each application, ranging from medical biosensors requiring nanoscale precision, through EBL [148,217,218], to large-scale structural applications where scalability is paramount, through AM [154,173]. Thus, the interplay between function-driven design and targeted fabrication is critical to realizing the unique properties of metamaterials across diverse applications [14].

4. Metamaterials in Medicine

Metamaterials present unique properties and features that have found a lot of applications in various domains [49], with a remarkable continuous development of metamaterials in optical [219], imaging [220], and medical fields. One of the most attractive applications in optics and imaging based on metamaterials is represented by superlenses [49,220]. A superlens is a metamaterial-based optical device that manipulates and controls the near-field interactions and enhances the evanescent waves typically associated with nanoscale sources. By exciting magnetic and electric surface modes, it couples with these near fields and focuses them on the opposite side, enabling the imaging of nanoscale objects that traditional lenses cannot resolve [213,221]. Due to the naturally occurring negative permittivity (ε < 0) in materials, such as silver and other metals at visible wavelengths, a thin metallic film can function as an optical superlens [222]. Other types of lenses, including beam steering lenses and antenna lenses, have been proposed, analyzed, and realized using the gradient refractive index of metamaterials, which can convert the generated wave into a quasi-plane wave [149]. Recent developments have shown a great interest in metamaterials in medicine and bio/medicine. Driven by the need for diagnosis and continuous monitoring of vital parameters, even outside the clinical environment, metamaterials with various structures tailored for different purposes have found applications in medicine [201,223]. Excellent results have been achieved using, for instance, negative-index media that refract light in the opposite direction of conventional materials, chiral materials that change the polarization state of light, and thin films with strong dispersion, which work as a resonant atomic system with electromagnetically induced transparency. These results produced a boost for the use of novel metamaterials in the biomedical field [223]. Metamaterials have been developed for different medical applications, encompassing mechanical metamaterials, auxetic metamaterials [45,224], optical metamaterials [225], and acoustic metamaterials [46]. For instance, mechanical metamaterials with zero or negative Poisson ratios and unique constitutive behaviors offer innovative solutions for tissue engineering and functional implants [203,226]. These materials possess specific properties suitable for the medical domain, including a low modulus of elasticity, high and negative stiffness, high strength, and ultra-low weight. A prosthesis or implant fabricated from a metamaterial with a modulus of elasticity close to bone, while ensuring toughness and high stiffness, will behave like a natural bone. Moreover, by modulating their structure, specific properties can be obtained in specific areas to meet the needs of particular medical applications. Thus, mechanical metamaterials will behave more naturally because they can overcome the challenge of preventing bone sclerosis and resorption by creating favorable mechanical junctions and angles [201,226]. Auxetic metamaterials, another type with excellent mechanical properties, exhibit the uncommon properties of lateral expansion when stretched and densification when compressed. These materials, comprising a special group of metamaterials with varied geometrical structures, shapes, and auxetic foams, have found application in biomedical devices involving prostheses, tissue engineering, orthopedics, in vitro devices, and advanced clinical devices [45]. For example, auxetic films show huge potential in the biomedical field as they can control the normal function of different organs of the body, providing the necessary mechanical properties for a wide range of biomaterials or medical devices, such as bone screws, intervertebral discs, or skull implants [224,227]. Optical metamaterials in the medical field are commonly used as biosensors. These devices are highlighted for several advantages, providing a fast method to identify specific objects and to detect different chemical compounds in real-time and cost-effectively. They operate across a broad spectrum, from visible to infrared (IR) light, and are non-invasive with high sensitivity [228]. Nevertheless, acoustic metamaterials are widely used in medicine for drug delivery [229] and noise imaging reduction [230] in signal acquisition equipment. Their artificial design structures that break through sound waves are capable of manipulating and controlling sound waves at different wavelength scales.

Several studies have explored the metamaterials previously mentioned, each offering unique properties that enhance their potential applications in the medical/biomedical field. Medical antennas represent a crucial part of medical systems that facilitate communications between the patient and the monitoring stations [201,225,231]. In recent years, the demand for antennas providing wireless telemetry systems in medicine has grown significantly, driven by the need for early diagnosis and continuous monitoring of different parameters [225]. Designing these metamaterial-based antennas often involves periodic SRRs, which are known for their negative permeability and dielectric constant of less than 1, in conjunction with metallic posts [225,231]. Saban’s research focused on developing an antenna using printed metamaterials, thus demonstrating a greater efficiency compared to a regular antenna. By incorporating SRRs and metallic strips, the antenna achieved an improved bandwidth, with a Voltage Standing Wave Ratio (VSWR) better than 2:3:1, shifting the resonant frequency on the human body by 3% [231]. Saban continued his research by optimizing small antennas for integration into communication systems for receiving and transmitting signals. This resulted in an improved bandwidth, from 50% up to 100%, while the resonant frequency was enhanced by up to 5% when the antenna was placed on the human body [225]. Hosseinzadeh et al. mentioned that one of the most significant applications of medical antennas is the wireless endoscope, which is a capsule-shaped system used for gastrointestinal monitoring or treatment [201]. Further, Yue et al. designed a miniaturized and ultra-thin midfield wireless energy transmission antenna utilizing metamaterial structures [218]. Metamaterials have also found promising applications in radio bands used for medical purposes. Raghavan and Rajeshkumar explored the use of metamaterial antennas for Industrial, Scientific, and Medical (ISM) radio bands, a part of the radio spectrum reserved for the use of radio frequency. The designed antenna was suitable for dual-frequency bands within the MHz range, being an excellent candidate for medical applications within the ISM spectrum [223]. Cancer is characterized by the uncontrolled proliferation of malignant cells, which can grow in nearly all body parts. Thus, early detection and localization are critical for effective treatment. In this respect, Vafapour et al. studied a metamaterial sensor antenna for detecting breast cancer cell lines. They placed an SRR atop a substrate, while a third iteration of the Minkowski fractal curve was used as a Defected Ground Structure, in the ground plane. This design proved effective in investigating the electrical characteristics of the cancer cell lines, and the simulated results determined resonant frequencies corresponding to different constants of breast cancer cell lines [148,217].

The Minkowski fractal antenna, designed for breast cancer detection, demonstrated resonant frequencies of 2.35, 2.42, and 2.52 GHz when tested with various breast cancer cell lines, including MDA-MB-231 and MCF-7 [217].

A novel graphene buzzle metamaterial refractometer achieved high sensitivity, with an average sensitivity of 495 GHz/RIU, effectively distinguishing between different cancer cell types based on their dielectric properties [214].

Hosseinzadeh et al. also highlighted the potential for developing microwave devices combined with metamaterial structures, which can lead to a cost-effective device, more specifically, a biosensor with high precision for localizing malignant cells [232]. Hamza et al.’s study aimed to develop an innovative multiband biosensor design for the early detection of cervical cancer, operating across the frequency range of 0 to 6 THz.

The development of metamaterial-based biosensors represents a significant technological advancement in early cancer detection, offering unprecedented sensitivity and real-time monitoring capabilities [109,148] through the engineered enhancement of light–matter interactions via subwavelength structures [92]. These sensors demonstrate a detection sensitivity 100–1000 times greater than conventional electrochemical or optical biosensors [35], with a designed split-ring resonator (SRR) that can achieve attomolar (10⁻¹⁸ M) detection limits for cancer biomarkers [148].

The sensor architecture, consisting of a patterned aluminum layer on a polyimide substrate, is carefully optimized to achieve near-perfect absorption. Full-wave electromagnetic simulations were crucial in the design process, enabling a thorough analysis of the sensor’s absorption characteristics and the impact of material properties [223].

The corona-shaped metamaterial biosensor exhibited high sensitivity and selectivity, confirming its capability to detect cancer markers in real time [233]. Yang et al. confirmed that mechanical metamaterials improve the sensitivity of sensors, which is crucial for monitoring physiological changes in real time. These materials enhance the sensitivity of biomolecule detection, facilitating precise diagnostics through their high penetrability in biological tissues [189].

These sensors also facilitate real-time monitoring, with wireless designs demonstrating continuous tracking of tumor progression through frequency shifts of 183.2 GHz per growth stage [233] and microfluidic-integrated designs achieving rapid response times of less than 5 min, exceeding traditional methods performance like ELISA [35].

Compared to conventional biosensors, metamaterial biosensors offer significantly lower detection limits (attomolar vs. picomolar), faster response times (minutes vs. hours), greater multiplexing capabilities (5–10 biomarkers vs. 1–2), smaller size (sub-mm vs. cm-scale), and reduced cost per test (USD 10−50 vs. USD 100–500) [92,216]. These attributes render them a promising alternative for early and accurate cancer diagnosis [109].

A flexible terahertz metamaterial biosensor recorded a maximum resonance peak frequency shift of 183.2 GHz when monitoring breast cancer cell growth, indicating its potential for non-destructive detection [233].

In the field of tissue engineering, mechanical metamaterials are the most suitable type of medical metamaterial due to their ability to manufacture scaffolds that support cell attachment and direct their functions.

Mechanical metamaterials offer a revolutionary approach to tissue engineering by providing unprecedented control over mechanical properties through their designed internal architectures. This enables the creation of scaffolds that more accurately mimic the complex mechanical environment of native tissues compared to traditional scaffold materials [46,234]. These metamaterials exhibit enhanced mechanical compatibility by precisely tuning the elastic modulus, Poisson’s ratio, and energy absorption [140,235]. Furthermore, they offer improved biocompatibility through structural design that promotes cell attachment and mechanotransduction, controlled degradation rates, and interconnected pore networks for vascularization [189,236]. Their capacity to achieve functional gradation, characterized by spatially varying and dynamically responsive properties, addresses the limitations of homogeneous traditional scaffolds [237]. While fabrication complexity and scalability are ongoing concerns [234], the current applications in bone, cartilage, and skin regeneration [123,238], along with future directions in bioactive coatings, biodegradable materials, and sensing capabilities [239] highlight the significant potential of mechanical metamaterials in advancing tissue engineering.

Techniques like bioprinting allow for the creation of bioactive bone implants and artificial tissues, utilizing diverse materials such as biodegradable polymers and metals [240].

Structures inspired by nature, such as triply periodic minimal surfaces, enhance mechanical compatibility and functionality in tissue scaffolds [234].

Mahmud et al. demonstrated that metamaterials optimize wireless power transfer systems, addressing challenges like tissue absorption and coupling efficiency, thus enabling longer-lasting implantable medical devices [241].

Moreover, they can be used to fabricate advanced scaffolds, expand the forms of mechanical signals, and enhance the cellular response towards tissue regeneration [140,189]. Dogan et al. conducted a comprehensive review of various tissues (e.g., cartilage, bone, skin, and vascularized tissues) that can be regenerated using mechanical metamaterials, with a particular focus on those fabricated by 3D printing, and suggested various guidelines for fabricating metamaterials in the field of medicine [58]. Three-dimensional-formed hydrogels are often used as a scaffold for regenerating tissue [189,215].

Hydrogel-based scaffolds offer unique physicochemical properties that closely resemble the natural extracellular matrix (ECM) [189,215]. Their superior biocompatibility and bioactivity distinguish them from alternative materials, such as ceramics, metals, and synthetic polymers. Notably, hydrogels derived from natural polymers (e.g., alginate, hyaluronic acid), exhibit excellent biocompatibility, minimizing immunogenic responses and promoting cellular adhesion, proliferation, and differentiation [215,236]. Their high water content (80–99%) replicates the native tissue environment, facilitating efficient nutrient diffusion and waste removal, which is crucial for cell survival [189].

Furthermore, hydrogels offer tunable mechanical and degradation properties. Unlike rigid ceramic- or metal-based scaffolds, they can be engineered to match the mechanical properties of soft tissues (e.g., cartilage, skin) through crosslinking density and polymer composition [215].

Hong et al. [242] emphasized the importance of mechanical stability against the physical impact of hydrogels for effective tissue regeneration. They explored how the mechanical properties of hydrogels could be regulated by adjusting the molecular weight, thus affecting the mobility of polymer chains. According to their research, the tunability allows for the creation of a hydrogel-based cell matrix with biodegradable support, playing a crucial role in the stem cell proliferation process [215]. Metamaterials also hold promise for bone regeneration, where they can be integrated into implants to promote bone tissue growth once they interact with the tissue.

Degradation kinetics can also be modulated to synchronize with tissue regeneration, preventing premature structural failure [236]. The porous, hydrated structure of hydrogels further facilitates enhanced drug and growth factor delivery, enabling the controlled release of bioactive molecules (e.g., growth factors) and reducing systemic side effects [189,243].

Bone tissue, a hierarchical structure with both mineralized and non-mineralized components, requires extreme compressive strength and superior toughness. The use of light-assisted 3D technology could provide a wide range of options for creating advanced structures to meet these requirements [189]. Lecina-Tejero et al. examined different studies on auxetic materials for skin regeneration and revealed that human skin is a complex and large organ with three heterogeneous layers, populated by different cell types with different functional, mechanical, and biological characteristics [189,238]. These layers, the epidermis, the dermis, and the hypodermis, are also different in terms of structure or composition. For example, the dermis consists of a collagen network with elastic fibers that provide tissue toughness and hyperelasticity [58]. N. Li et al. proposed a novel electronic skin (e-skin) that combines the unique properties of mechanical metamaterials with self-powering capabilities, multimodal fusion perception, and shape memory reconfigurability. The e-skin incorporates multimodal sensory capabilities, effectively replicating a biomimetic sensory system’s auditory, tactile, and visual perception [244]. In another study, Kirillova et al. presented a novel 4D biofabrication method capable of producing hollow self-folding hydrogel tubes, employing alginate and hyaluronic acid hydrogels as representative models. This technique combines polymer–cell bioinks in a simultaneous printing process, creating shape-morphing biopolymer hydrogels that facilitate the precise fabrication of these advanced structures, with applications in tissue engineering and regenerative medicine [236]. Zeenat et al. summarized major bioprinting techniques, highlighting two main approaches for forming vasculature within 3D printed structures. The first one involves the release of angiogenic factors to stimulate the growth of vasculature, while the second focuses on the direct printing of the vascular network to target the tissue cell. Both approaches provide precision and control over the internal and external structure of 3D-printed constructs [243]. Medical imaging techniques represent non-invasive methods to diagnose or treat different medical conditions. Kasban et al. conducted a detailed comparison of medical imaging techniques, covering their current concepts, risks, challenges, advantages, and applications. Among these, they considered Magnetic Resonance Imaging (MRI), a radiation-free imaging technique used to visualize the morphological changes in diseased tissues [232]. Wang et al. discussed future challenges and opportunities for nanomaterials as MRI agents, emphasizing key applications such as tissue necrosis, clinical diagnosis, and local ischemia [33].

MRI image generation is predicated on the detection of spatial variations in the phase and frequency of radiofrequency (RF) waves, which are absorbed and subsequently emitted by the nuclear spins of the imaged object. Standard MRI detectors, utilizing conventional coils, operate within the near-field regime of the RF magnetic field. Metamaterials offer the potential for improved coil performance by enabling precise control over this magnetic near field [245].

B. Li et al. further explored the potential of MRI, suggesting that the recent advancements in metamaterials could significantly enhance imaging capabilities. They proved that metamaterial-based lenses can enhance the signal-to-noise ratio (SNR) even during accelerating scans because of their capabilities to enable interaction with radiofrequency (RF) and to amplify it [246]. Moreover, integrating nano-metamaterials can contribute to MRI contrast agents due to their complex microhierarchical structure [33].

In contrast to the resonant operation of conventional MR coils, the µ_r = −1 metamaterial lens, based on split-ring resonators, functions at a frequency distinct from the individual resonance of its constituent elements. This operational deviation, arising from the collective response of the split rings, which yields the desired effective permeability, contributes to a reduction in both losses and noise [247].

Several metamaterial designs have been developed to boost the SNR. For instance, Duan et al. reported a magnetic metamaterial composed of an array of unit cells featuring metallic helices to improve the SNR by enabling field enhancement around a specific resonant mode. Their study confirmed the suitability of magnetic metamaterials for SNR improvement, increasing image resolution and scan efficiency. Also, it was concluded that the resonant mode, when applied to MRI, could be excited by the radiofrequency magnetic field and highly boost the SNR [248]. For preclinical imaging, a dual-nuclei radiofrequency coil was developed and assessed by Hurshkainen et al., leveraging the resonant excitation of eigenmodes within a pair of multimode wire metamaterial-inspired resonators. Numerical and experimental analyses demonstrated that the strategic selection of excited eigenmodes enables precise control over the penetration depth within a subject, facilitating either whole-body excitation or targeted surface excitation in small animals. For multi-nuclei MRI applications, the proposed coil design offers compatibility through the tunable nature of its short and long-wire resonators. Larmor frequency tuning is facilitated by manipulating resonator length and patch parameters, with the patches providing distributed load capacitance for the short-wire resonator [249]. Overall, recent advancements in metamaterials have significantly enhanced MRI performance, offering higher-resolution images with improved SNRs.

Furthermore, Jiang et al. conducted extensive research on stretchable strain sensors. In their two reviews, they emphasized that strain sensors that convert mechanical stimuli into electrical signals [250] or optical signals [251] play an important role in medical applications. They concluded that the sensitivity of stretchable strain sensors is an important parameter that can be improved by using specific metamaterials. The integration of auxetic metamaterials into strain sensor design has proven to increase their sensitivity by reducing the structural Poisson’s ratio and strain concentration [251]. In addition, the incorporation of wireless force sensing within intelligent implantable devices facilitates real-time, in situ monitoring of mechanical stress, thereby enabling dynamic parametric modulation for optimized functional performance. Luo et al. developed proof-of-concept metamaterial orthopedic implants designed to extract energy from natural body movements. The resulting electrical signal was utilized for direct, wireless, and electronics-free transmission of sensor data, eliminating the need for traditional electronic components. These implants allow for real-time wireless communication over moderate distances, with power outputs measured in the picowatt (pW) range [252]. Various studies have explored additional applications of metamaterials in medicine, including microwave hyperthermia [253,254], radiation shields [254], and hearing aids [160]. An overview of these applications can be found in

Table 2. Various applications of metamaterials in medicine.

Application	Specific Use	Benefits	Metamaterial Properties	References
Optical antennas	Provides effective communication in medical systems	High efficiency	Negative permeability, subunit dielectric constant	[26,223,225,231]
Cancer detection	Detects early signs of cancer by localizing malignant cells with biosensors	High precision, cost-effective	High sensitivity, negative values of relative permittivity, electromagnetic properties	[148,201,223]
Tissue engineering	Scaffolds for regenerating different tissues such as bone, skin, cartilage, or vascular	Enhanced stem cell proliferation, enhanced biocompatibility, natural-tissue-like behavior	Mechanical stability, high strength and toughness, precise control over structure	[104,189,215,243]
Medical imaging	MRI enhancement for accelerated scans and better SNRs	High-resolution images, simple installation	Magnetic, resonant, and dielectric properties	[201,232,248]
Strain sensors	Monitories healing of fractured bones, mechanical stimuli detection	Enhanced sensitivity, non-invasive	Auxetic properties, distinctive resonance frequency, reduced Poisson’s ratio	[201,250]
Microwave hyperthermia	Superficial cancer treatment in specific locations by focusing resolution	Environmentally friendly, non-invasive, enhanced distribution field	Electromagnetic convergence, thermal and heat properties	[253,255,256]
Radiation shields	Protection against extreme electromagnetic radiation of medical equipment	High indicators of transparency, enhanced performance of the system	Absorption properties, tunable and low-profile features	[35,254,257]
Hearing aids	Rehabilitates higher cortical functions	High bandwidth, miniaturization, low mutual coupling	Filtration and dielectrics properties, resistance to mechanical properties	[160,240,258]

.

5. Conclusions, Challenges, and Future Directions

This review provides an overview of the latest advancements in the design and processing of the key controlled-structure metamaterials, underscoring their potential to enhance performance in various fields. The discussion highlights the challenges faced by metamaterials in achieving high performance and efficiency, the complexity of developing novel and unique designs, and the potential future directions for the field. While significant progress has been made in characterizing and optimizing metamaterials and metadevices, with notable successes over time, we have concluded that further improvement in this area is necessary to address the current challenges and overcome limitations. The various fabrication techniques available for producing metamaterials offer a wide range of approaches and different perspectives for the development of innovative devices. However, despite their promising potential, their performance and characteristics have some limitations and challenges. Metamaterials are frequency-dependent on the applied electromagnetic wave, which can impact their efficiency in specific applications. In addition, the negative permittivity and permeability of certain metamaterials often lead to material and energy losses due to high absorption and scattering. The fundamental limitations of these manufacturing approaches make it challenging to determine the ideal method, one that not only meets the stringent efficiency requirements but also delivers good performance across various parameters for different aspects. Costly equipment, expensive operating systems, and time-consuming process maintenance are among the primary hurdles in producing metamaterials. Although metamaterials can achieve complex structures and geometries compared to traditional materials, their validation requires advanced computer simulations, including numerical methods and experimental techniques, which are often time-consuming and require specialized expertise.

The integration of practical fabrication techniques for efficient and rapid prototyping of complex metamaterials design with quality control methods can ensure the uniformity and reproducibility of metamaterials. Advanced techniques, such as EBL, photolithography, or AM, enable the achievement of complex nanoscale patterns, with quality and uniformity assessed through characterization techniques like scanning electron microscopy (SEM) or atomic force microscopy (AFM). Nevertheless, scalability and cost-effectiveness remain pivotal factors for the commercial viability of metamaterials. AM technology offers a pathway to the large-area production of metamaterials without compromising the quality of the final product. On the other hand, techniques such as photolithography or self-assembly propose low manufacturing costs, prioritizing high production rates over expensive devices with complex parts that require costly maintenance. Integrating these methods into the manufacturing process of metamaterials ensures good scalability at an affordable price, facilitating their use in various fields, including telecommunications, electronics, and medicine.

This comprehensive examination of the current status of metamaterials reveals their ability to exhibit unique properties through complex design. We have explored the historical evolution of metamaterials, their theoretical principles, various manufacturing methods, and their applications, particularly in the medical field. Future developments in manufacturing efficiency, as well as advancements in computational tools, will create new opportunities for the design of innovative and specialized metamaterials that will surpass current limitations and play a crucial role in various areas in the years to come.