Temperature-Controlled Defective Phononic Crystals with Shape Memory Alloys for Tunable Ultrasonic Sensors
Abstract
1. Introduction
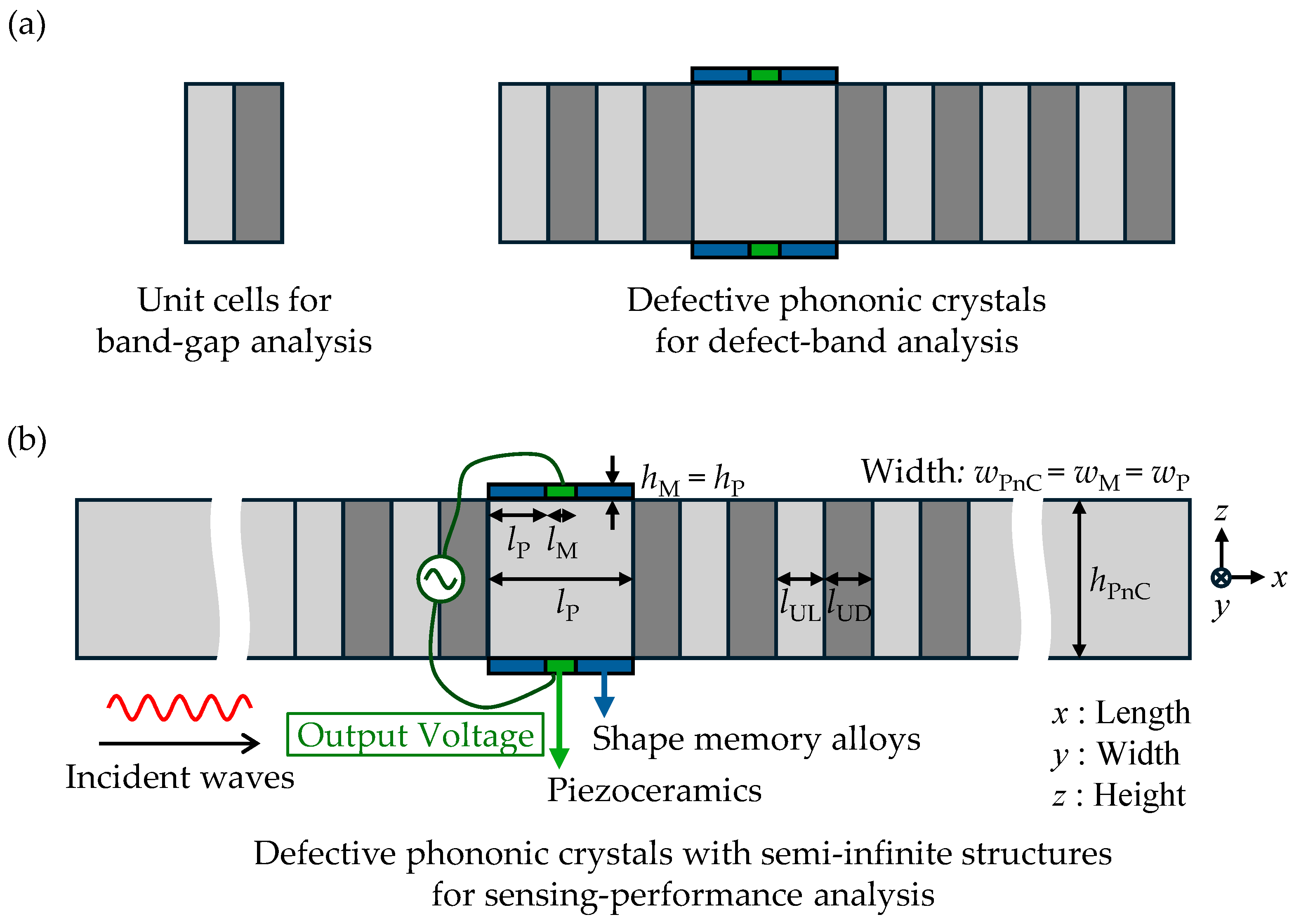
2. Target System Description
3. Analytical Modeling
3.1. Temperature-Dependent Material Properties of Shape Memory Alloys
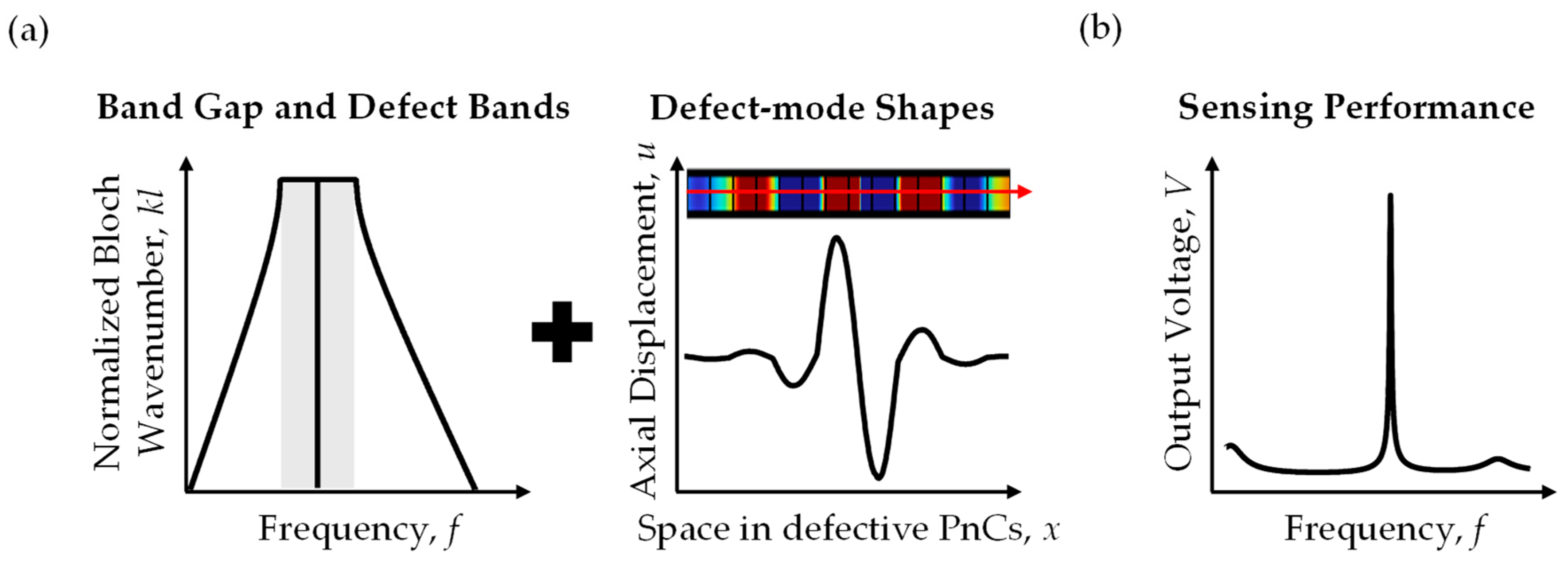
3.2. Band-Structure Analysis
3.3. Sensing-Performance Analysis
4. Numerical Validation
4.1. Evaluation Plan
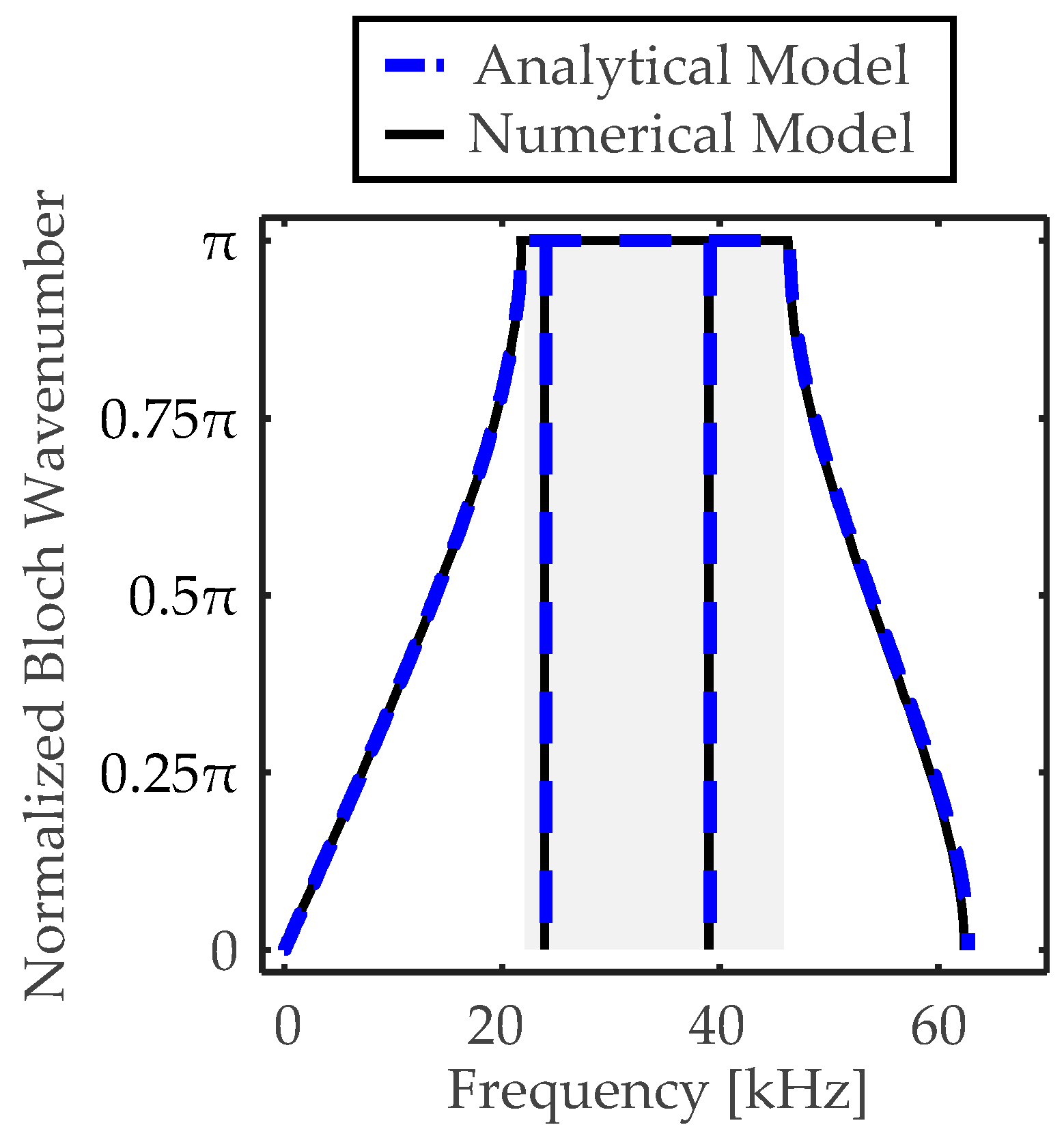
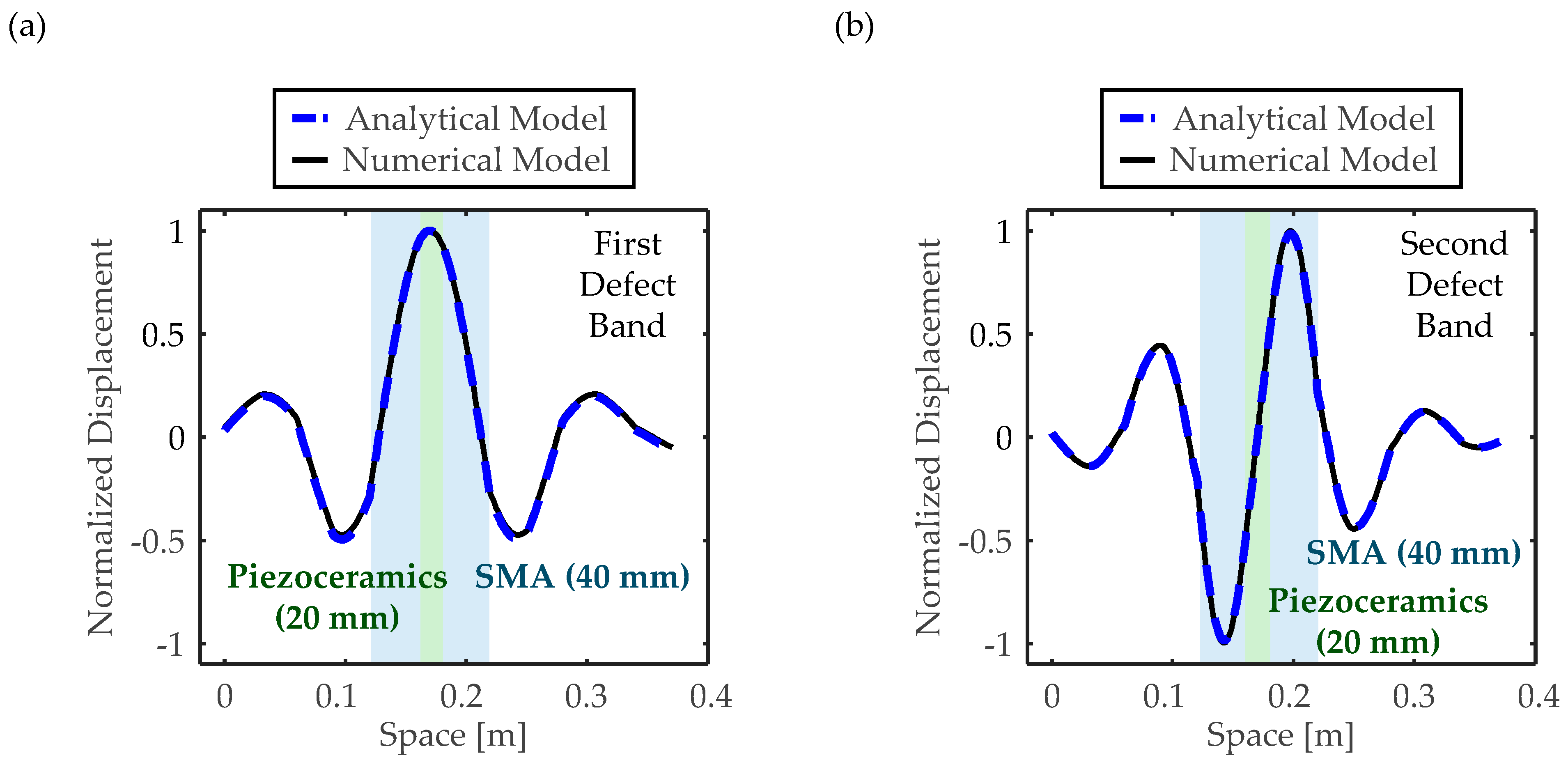
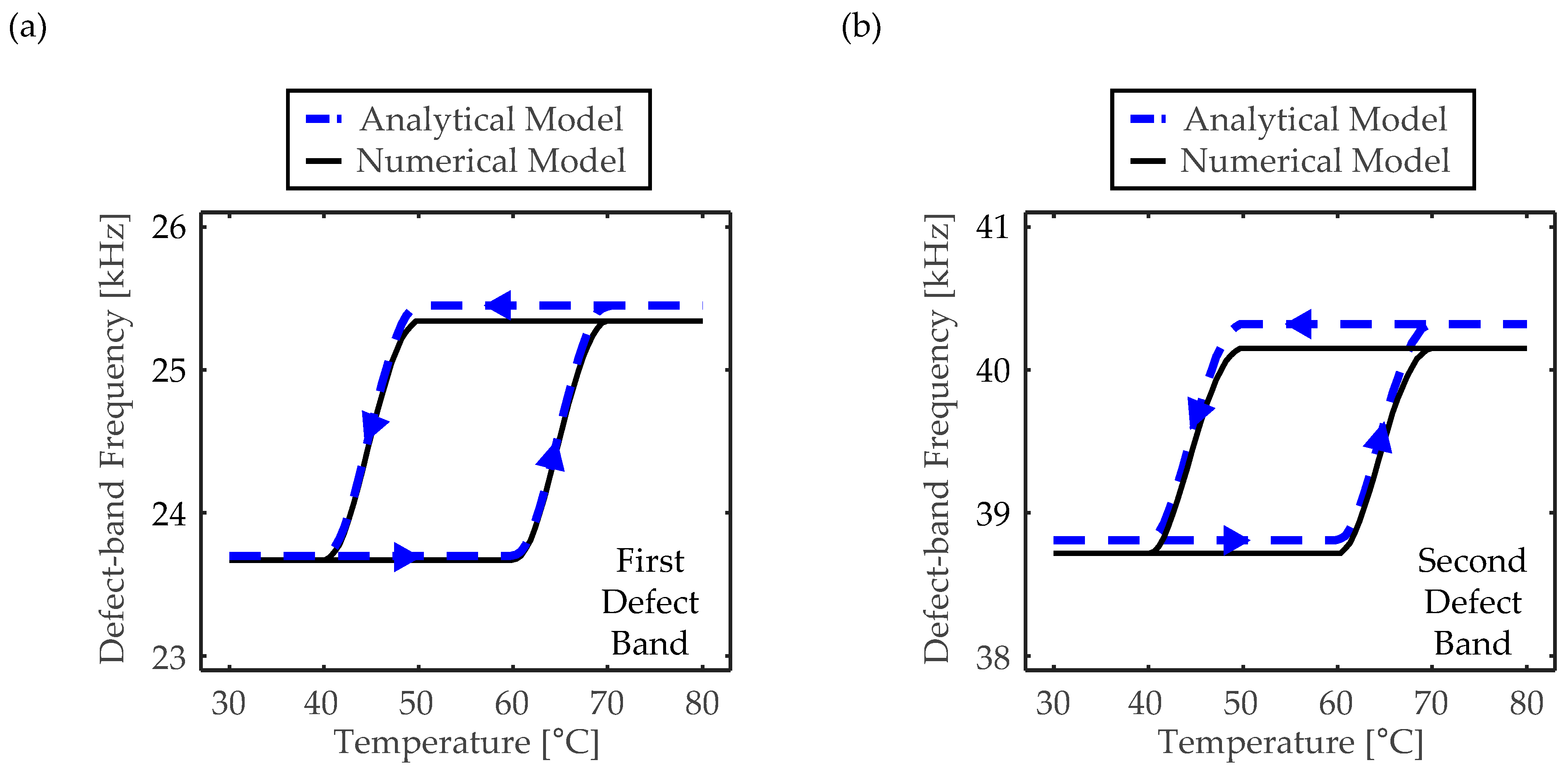
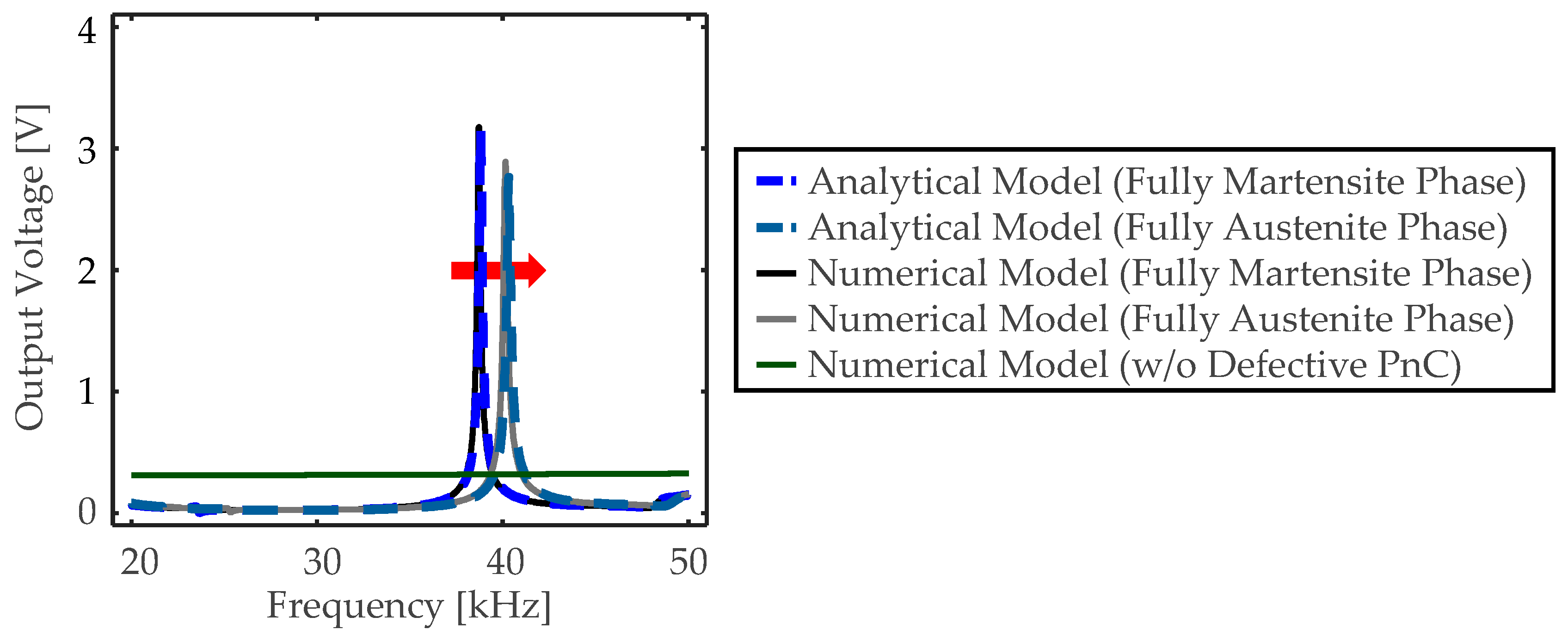
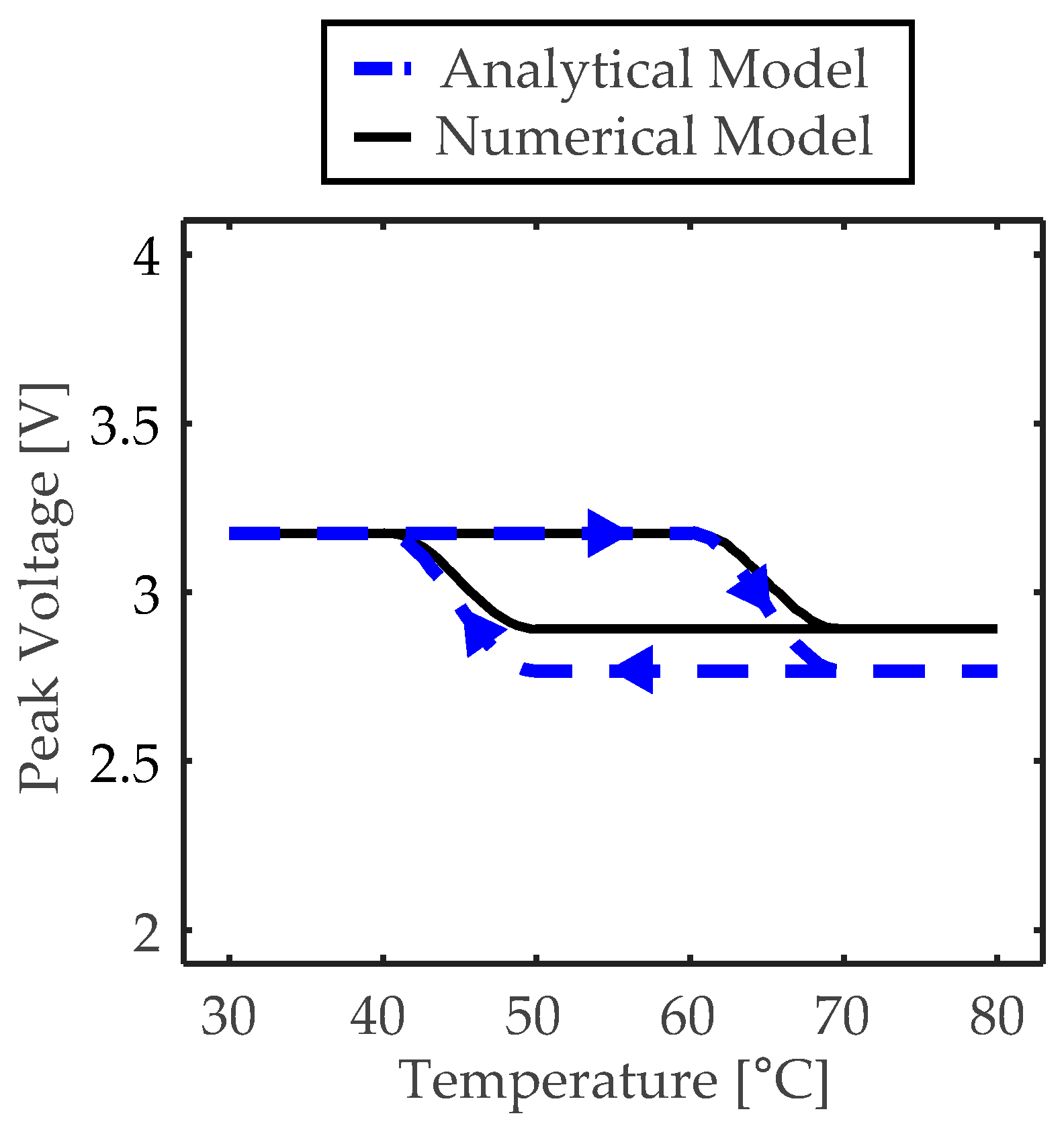
4.2. Validation Study in Analyses of Band Structure and Sensing Performance
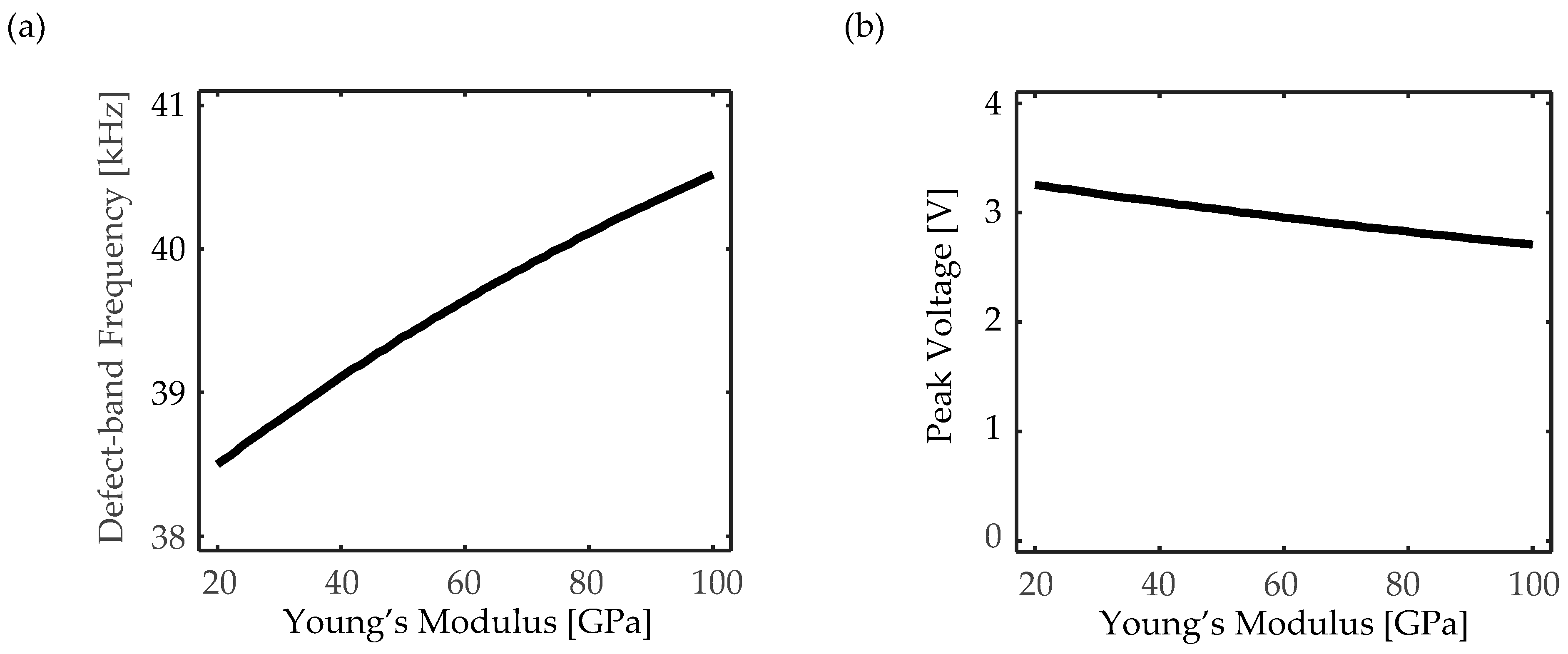
4.3. Parametric Study
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Settings in COMSOL Simulations
References
- Vasileiadis, T.; Varghese, J.; Babacic, V.; Gomis-Bresco, J.; Navarro Urrios, D.; Graczykowski, B. Progress and perspectives on phononic crystals. J. Appl. Phys. 2021, 129, 160901. [Google Scholar] [CrossRef]
- Dong, H.-W.; Shen, C.; Liu, Z.; Zhao, S.-D.; Ren, Z.; Liu, C.-X.; He, X.; Cummer, S.A.; Wang, Y.-S.; Fang, D. Inverse design of phononic meta-structured materials. Mater. Today 2024, 80, 824–855. [Google Scholar] [CrossRef]
- Lee, J.; Kim, Y.Y. Elastic metamaterials for guided waves: From fundamentals to applications. Smart Mater. Struct. 2023, 32, 123001. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, Y.; Yang, S.; Bian, Z. Band gap manipulation on P-wave propagating in functionally graded phononic crystal by periodical thermal field. Int. J. Mech. Sci. 2021, 212, 106817. [Google Scholar] [CrossRef]
- Wu, Q.; He, J.; Chen, W.; Li, Q.; Liu, S. Topology optimization of phononic crystal with prescribed band gaps. Comput. Methods Appl. Mech. Eng. 2023, 412, 116071. [Google Scholar] [CrossRef]
- Akbari-Farahani, F.; Ebrahimi-Nejad, S. From defect mode to topological metamaterials: A state-of-the-art review of phononic crystals & acoustic metamaterials for energy harvesting. Sens. Actuators A Phys. 2024, 365, 114871. [Google Scholar]
- Zhang, S.; Zhang, Z. Magnetically tunable band gaps and defect states of longitudinal waves in hard magnetic soft phononic crystal beams. Eur. J. Mech.-A/Solids 2025, 111, 105575. [Google Scholar] [CrossRef]
- Gao, X.; Qin, J.; Hong, J.; Wang, S.; Zhang, G. Wave propagation characteristics and energy harvesting of magnetically tunable defective phononic crystal microbeams. Acta Mech. 2025, 236, 1579–1597. [Google Scholar] [CrossRef]
- Yao, B.; Wang, S.; Hong, J.; Gu, S. Size and temperature effects on band gap analysis of a defective phononic crystal beam. Crystals 2024, 14, 163. [Google Scholar] [CrossRef]
- Jo, S.-H.; Lee, D. An improved analytical model of a thick defective phononic crystal for bending wave excitation. Int. J. Mech. Sci. 2024, 264, 108822. [Google Scholar] [CrossRef]
- Jo, S.-H. Electroelastically coupled stiffness matrix method for phononic crystals with piezoelectric defects and its applications to filters, sensors, and energy harvesters. Mech. Mater. 2025, 203, 105262. [Google Scholar] [CrossRef]
- Zhang, G.; Gao, X.; Wang, S.; Hong, J. Bandgap and its defect band analysis of flexoelectric effect in phononic crystal plates. Eur. J. Mech.-A/Solids 2024, 104, 105192. [Google Scholar] [CrossRef]
- Biçer, A.; Cicek, A. Liquid concentration sensing via weakly coupled point defects in a phononic crystal. J. Mol. Liq. 2024, 409, 125487. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, K.; Wang, B. Energy harvesting performance of acoustic energy harvesters consisting of flexoelectric plates and defect-state phononic crystals. J. Vib. Eng. Technol. 2024, 12, 5101–5117. [Google Scholar] [CrossRef]
- Katch, L.; Moghaddaszadeh, M.; Willey, C.; Juhl, A.; Nouh, M.; Argüelles, A. Analysis of geometric defects in square locally resonant phononic crystals: A comparative study of modeling approaches. J. Acoust. Soc. Am. 2023, 154, 3052–3061. [Google Scholar] [CrossRef]
- Zhang, L.-Y.; Yin, X.; Yang, J.; Li, A.; Xu, G.-K. Multilevel structural defects-induced elastic wave tunability and localization of a tensegrity metamaterial. Compos. Sci. Technol. 2021, 207, 108740. [Google Scholar] [CrossRef]
- Hosseinkhani, A.; Ebrahimian, F.; Younesian, D.; Moayedizadeh, A. Defected meta-lattice structures for the enhanced localized vibrational energy harvesting. Nano Energy 2022, 100, 107488. [Google Scholar] [CrossRef]
- Zhong, J.; Xiang, J. Designing a phononic crystal with a large defect to enhance elastic wave energy localization and harvesting. Jpn. J. Appl. Phys. 2022, 61, 017002. [Google Scholar]
- Zhang, X.; Li, Y.; Wang, Y.; Jia, Z.; Luo, Y. Narrow-band filter design of phononic crystals with periodic point defects via topology optimization. Int. J. Mech. Sci. 2021, 212, 106829. [Google Scholar] [CrossRef]
- He, J.; Sun, J.; Fan, J.; Jia, Z.; Zhang, X. Optimal designs of phononic crystal microstructures considering point and line defects. Symmetry 2021, 13, 1993. [Google Scholar] [CrossRef]
- Xiao, J.; Ding, X.; Wang, Y.; Huang, W.; He, Q.; Shao, Y. Gear fault detection via directional enhancement of phononic crystal resonators. Int. J. Mech. Sci. 2024, 278, 109453. [Google Scholar] [CrossRef]
- Xiao, J.; Ding, X.; Huang, W.; He, Q.; Shao, Y. Rotating machinery weak fault features enhancement via line-defect phononic crystal sensing. Mech. Syst. Signal Process. 2024, 220, 111657. [Google Scholar] [CrossRef]
- Na, K.; Kim, K.; Yoo, J.; Lee, J.; Youn, B.D. Optimized relative entropy for robust fault detection in excavator traveling gearboxes via smeared envelope spectrum analysis of cyclo-non-stationary signals. Expert Syst. Appl. 2025, 266, 126110. [Google Scholar] [CrossRef]
- Na, K.; Kim, Y.; Yoon, H.; Youn, B.D. FASER: Fault-affected signal energy ratio for fault diagnosis of gearboxes under repetitive operating conditions. Expert Syst. Appl. 2024, 238, 122078. [Google Scholar] [CrossRef]
- Zhang, G.; He, Z.; Wang, S.; Hong, J.; Cong, Y.; Gu, S. Elastic foundation-introduced defective phononic crystals for tunable energy harvesting. Mech. Mater. 2024, 191, 104909. [Google Scholar] [CrossRef]
- Yang, J.; Jo, S.-H. Experimental validation for mechanically tunable defect bands of a reconfigurable phononic crystal with permanent magnets. Crystals 2024, 14, 701. [Google Scholar] [CrossRef]
- Jo, S.-H. Electrically controllable behaviors in defective phononic crystals with inductive-resistive circuits. Int. J. Mech. Sci. 2024, 278, 109485. [Google Scholar] [CrossRef]
- Jo, S.-H.; Park, M.; Kim, M.; Yang, J. Tunable bandpass filters using a defective phononic crystal shunted to synthetic negative capacitance for longitudinal waves. J. Appl. Phys. 2024, 135, 164502. [Google Scholar] [CrossRef]
- Kim, M.S.; Heo, J.K.; Rodrigue, H.; Lee, H.T.; Pané, S.; Han, M.W.; Ahn, S.H. Shape memory alloy (SMA) actuators: The role of material, form, and scaling effects. Adv. Mater. 2023, 35, 2208517. [Google Scholar] [CrossRef]
- Tabrizikahou, A.; Kuczma, M.; Łasecka-Plura, M.; Farsangi, E.N.; Noori, M.; Gardoni, P.; Li, S. Application and modelling of Shape memory alloys for structural vibration control: State-of-the-art review. Constr. Build. Mater. 2022, 342, 127975. [Google Scholar] [CrossRef]
- Miyabuchi, H.; Yoshimura, T.; Murakami, S.; Fujimura, N. Characterization of direct piezoelectric effect in 31 and 33 modes for application to vibration energy harvester. Jpn. J. Appl. Phys. 2011, 50, 09ND17. [Google Scholar] [CrossRef]
- Kim, D.; Hewa-Kasakarage, N.N.; Hall, N.A. A theoretical and experimental comparison of 3-3 and 3-1 mode piezoelectric microelectromechanical systems (MEMS). Sens. Actuators A Phys. 2014, 219, 112–122. [Google Scholar] [CrossRef]
- Kim, S.-B.; Park, H.; Kim, S.-H.; Wikle, H.C.; Park, J.-H.; Kim, D.-J. Comparison of MEMS PZT cantilevers based on d33 and d31 modes for vibration energy harvesting. J. Microelectromechanical Syst. 2012, 22, 26–33. [Google Scholar] [CrossRef]
- Candido de Sousa, V.; Tan, D.; De Marqui, C.; Erturk, A. Tunable metamaterial beam with shape memory alloy resonators: Theory and experiment. Appl. Phys. Lett. 2018, 113, 143502. [Google Scholar] [CrossRef]
- Chuang, K.-C.; Lv, X.-F.; Wang, Y.-H. A bandgap switchable elastic metamaterial using shape memory alloys. J. Appl. Phys. 2019, 125, 055101. [Google Scholar] [CrossRef]
- Lv, X.-F.; Xu, S.-F.; Huang, Z.-L.; Chuang, K.-C. A shape memory alloy-based tunable phononic crystal beam attached with concentrated masses. Phys. Lett. A 2020, 384, 126056. [Google Scholar] [CrossRef]
- van den Boom, S.; van Keulen, F.; Aragón, A. Fully decoupling geometry from discretization in the Bloch–Floquet finite element analysis of phononic crystals. Comput. Methods Appl. Mech. Eng. 2021, 382, 113848. [Google Scholar] [CrossRef]
- Chin, E.B.; Mokhtari, A.A.; Srivastava, A.; Sukumar, N. Spectral extended finite element method for band structure calculations in phononic crystals. J. Comput. Phys. 2021, 427, 110066. [Google Scholar] [CrossRef]
- Schalcher, L.; Dos Santos, J.; Miranda, E., Jr. Extended plane wave expansion formulation for 1-D viscoelastic phononic crystals. Partial Differ. Equ. Appl. Math. 2023, 7, 100489. [Google Scholar] [CrossRef]
- Shen, W.; Cong, Y.; Gu, S.; Yin, H.; Zhang, G. A rasterized plane wave expansion method for complex 2-D phononic crystals. Mech. Syst. Signal Process. 2024, 212, 111324. [Google Scholar] [CrossRef]
- Jo, S.-H.; Lee, D.; Yoon, H.; Youn, B.D. Double piezoelectric defects in phononic crystals for ultrasonic transducers. J. Phys. D Appl. Phys. 2023, 56, 074002. [Google Scholar] [CrossRef]
- Manktelow, K.; Leamy, M.J.; Ruzzene, M. Comparison of asymptotic and transfer matrix approaches for evaluating intensity-dependent dispersion in nonlinear photonic and phononic crystals. Wave Motion 2013, 50, 494–508. [Google Scholar] [CrossRef]
- Han, L.; Zhang, Y.; Ni, Z.-Q.; Zhang, Z.-M.; Jiang, L.-H. A modified transfer matrix method for the study of the bending vibration band structure in phononic crystal Euler beams. Phys. B Condens. Matter 2012, 407, 4579–4583. [Google Scholar] [CrossRef]
- Jo, S.-H.; Youn, B.D. An explicit solution for the design of a target-frequency-customized, piezoelectric-defect-introduced phononic crystal for elastic wave energy harvesting. J. Appl. Phys. 2021, 130, 184902. [Google Scholar] [CrossRef]
- Jo, S.-H.; Yoon, H.; Shin, Y.C.; Youn, B.D. An analytical model of a phononic crystal with a piezoelectric defect for energy harvesting using an electroelastically coupled transfer matrix. Int. J. Mech. Sci. 2021, 193, 106160. [Google Scholar] [CrossRef]
- Jo, S.-H.; Yoon, H.; Shin, Y.C.; Youn, B.D. Revealing defect-mode-enabled energy localization mechanisms of a one-dimensional phononic crystal. Int. J. Mech. Sci. 2022, 215, 106950. [Google Scholar] [CrossRef]
- Billah, T.; Aquib, T.I.; Dey, K. A review on surface modification of NiTinol for biomedical applications. J. Mater. Sci. 2024, 59, 19340–19379. [Google Scholar] [CrossRef]
- Wadood, A. Brief overview on nitinol as biomaterial. Adv. Mater. Sci. Eng. 2016, 2016, 4173138. [Google Scholar] [CrossRef]
- Jo, S.-H.; Youn, B.D. Longitudinal wave localization using a one-dimensional phononic crystal with differently patterned double defects. Int. J. Mech. Sci. 2023, 237, 107783. [Google Scholar] [CrossRef]
- Zhang, G.-Y.; Liu, Z.-J.; Guo, Y.; Dou, X.-L.; Zhang, C.-R.; Sun, X.-W. Effect of incomplete line defect size on energy localization and harvesting in phononic crystals. J. Acoust. Soc. Am. 2024, 156, 3921–3929. [Google Scholar] [CrossRef]
- Deng, T.; Zhao, L.; Jin, F. Dual-functional perforated metamaterial plate for amplified energy harvesting of both acoustic and flexural waves. Thin-Walled Struct. 2024, 197, 111615. [Google Scholar] [CrossRef]
- Lima, S.E.; Frazão, O.; Farias, R.G.; Araujo, F.M.; Ferreira, L.A.; Santos, J.L.; Miranda, V. Mandrel-based fiber-optic sensors for acoustic detection of partial discharges—A proof of concept. IEEE Trans. Power Deliv. 2010, 25, 2526–2534. [Google Scholar] [CrossRef]
- Kim, S.J.; Kim, K.; Hwang, T.; Park, J.; Jeong, H.; Kim, T.; Youn, B.D. Motor-current-based electromagnetic interference de-noising method for rolling element bearing diagnosis using acoustic emission sensors. Measurement 2022, 193, 110912. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jo, S.-H. Temperature-Controlled Defective Phononic Crystals with Shape Memory Alloys for Tunable Ultrasonic Sensors. Crystals 2025, 15, 412. https://doi.org/10.3390/cryst15050412
Jo S-H. Temperature-Controlled Defective Phononic Crystals with Shape Memory Alloys for Tunable Ultrasonic Sensors. Crystals. 2025; 15(5):412. https://doi.org/10.3390/cryst15050412
Chicago/Turabian StyleJo, Soo-Ho. 2025. "Temperature-Controlled Defective Phononic Crystals with Shape Memory Alloys for Tunable Ultrasonic Sensors" Crystals 15, no. 5: 412. https://doi.org/10.3390/cryst15050412
APA StyleJo, S.-H. (2025). Temperature-Controlled Defective Phononic Crystals with Shape Memory Alloys for Tunable Ultrasonic Sensors. Crystals, 15(5), 412. https://doi.org/10.3390/cryst15050412





