Procedures for X-Ray Diffraction Phase Analysis: The Case of Fine Sediments from Peña Blanca, Chihuahua, Mexico
Abstract
1. Introduction
2. Materials and Methods
2.1. Sampling
2.2. Procedures for Dating with 210Pb and 137Cs
2.3. General Characterization of Samples
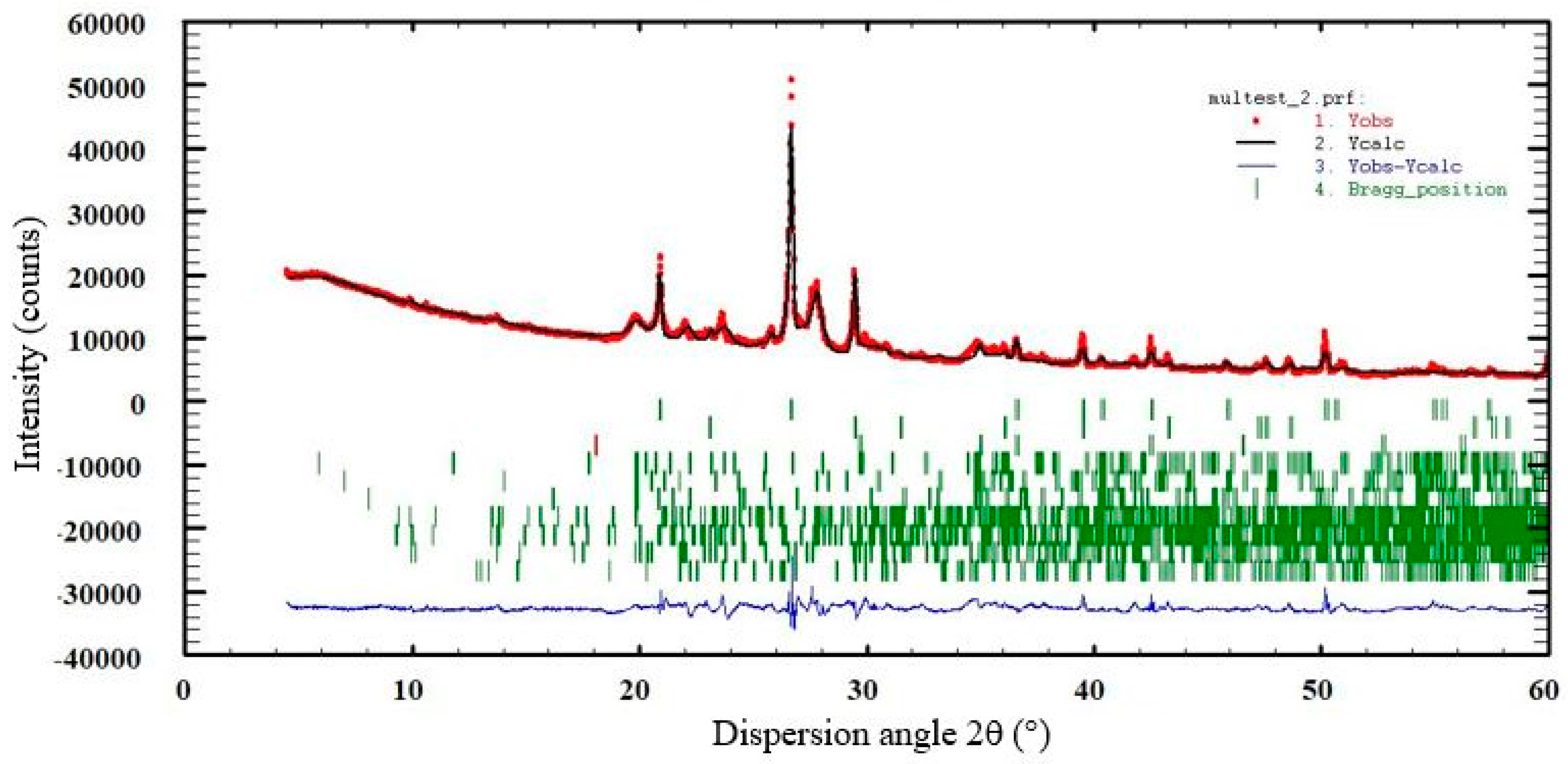
2.4. XRD Characterization of Samples
3. Results
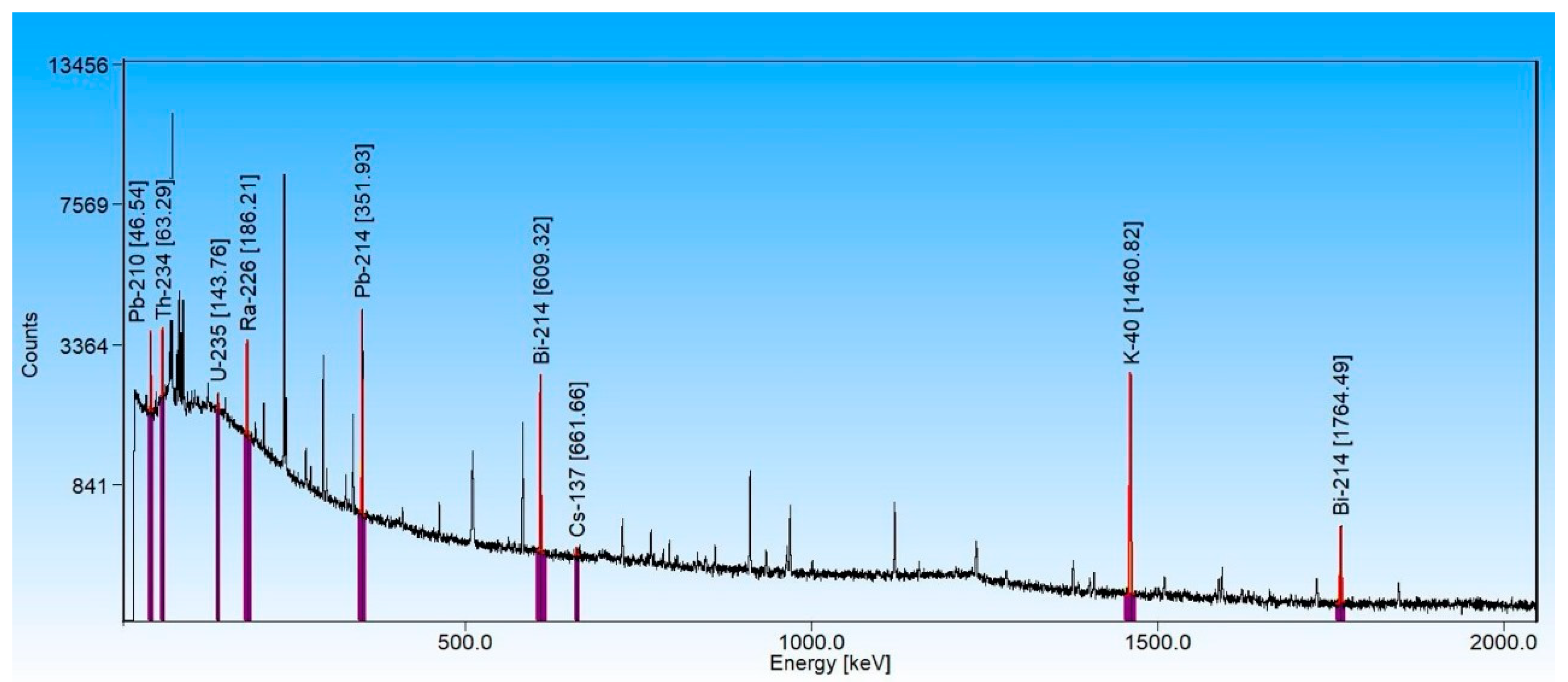
3.1. High-Resolution Gamma Spectrometry of the Sediments
3.2. General Characterization of Study Samples
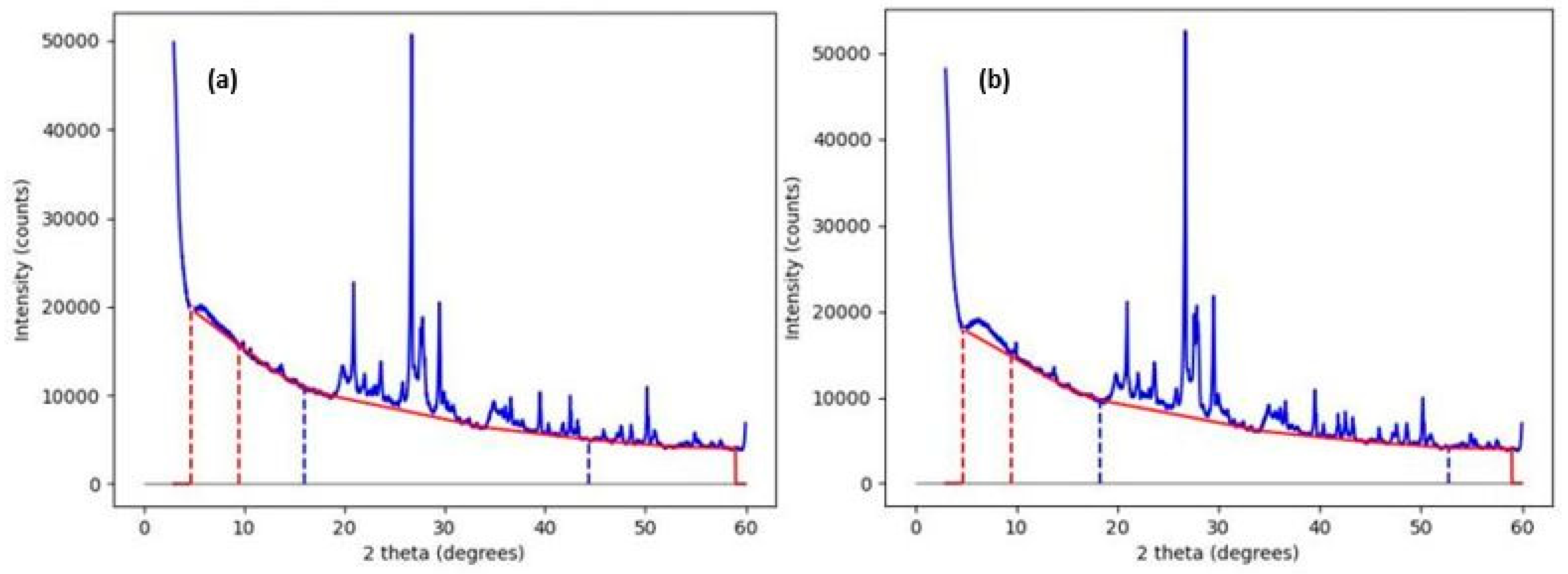
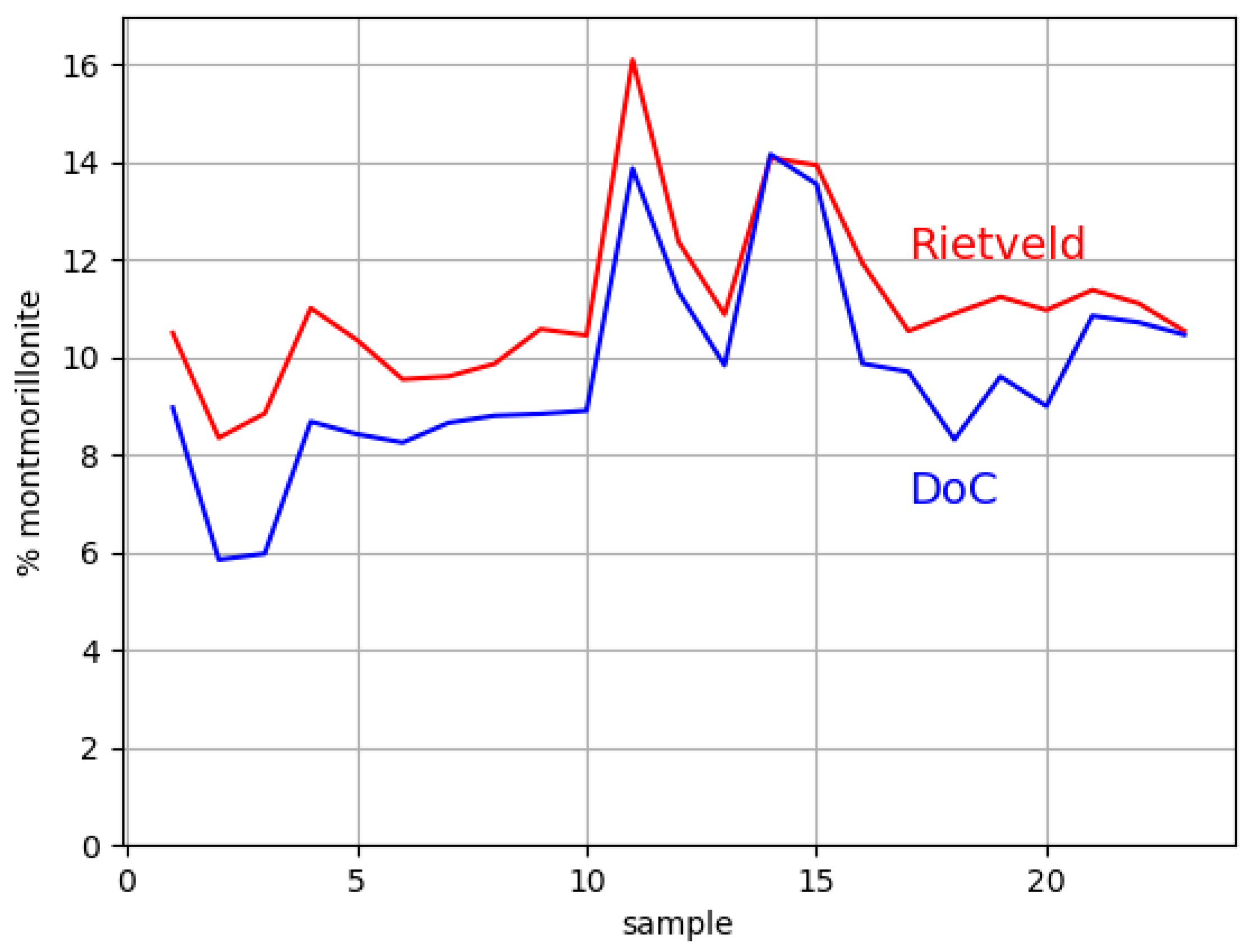
3.3. Reliability of the Proposed XRD Phase Analysis
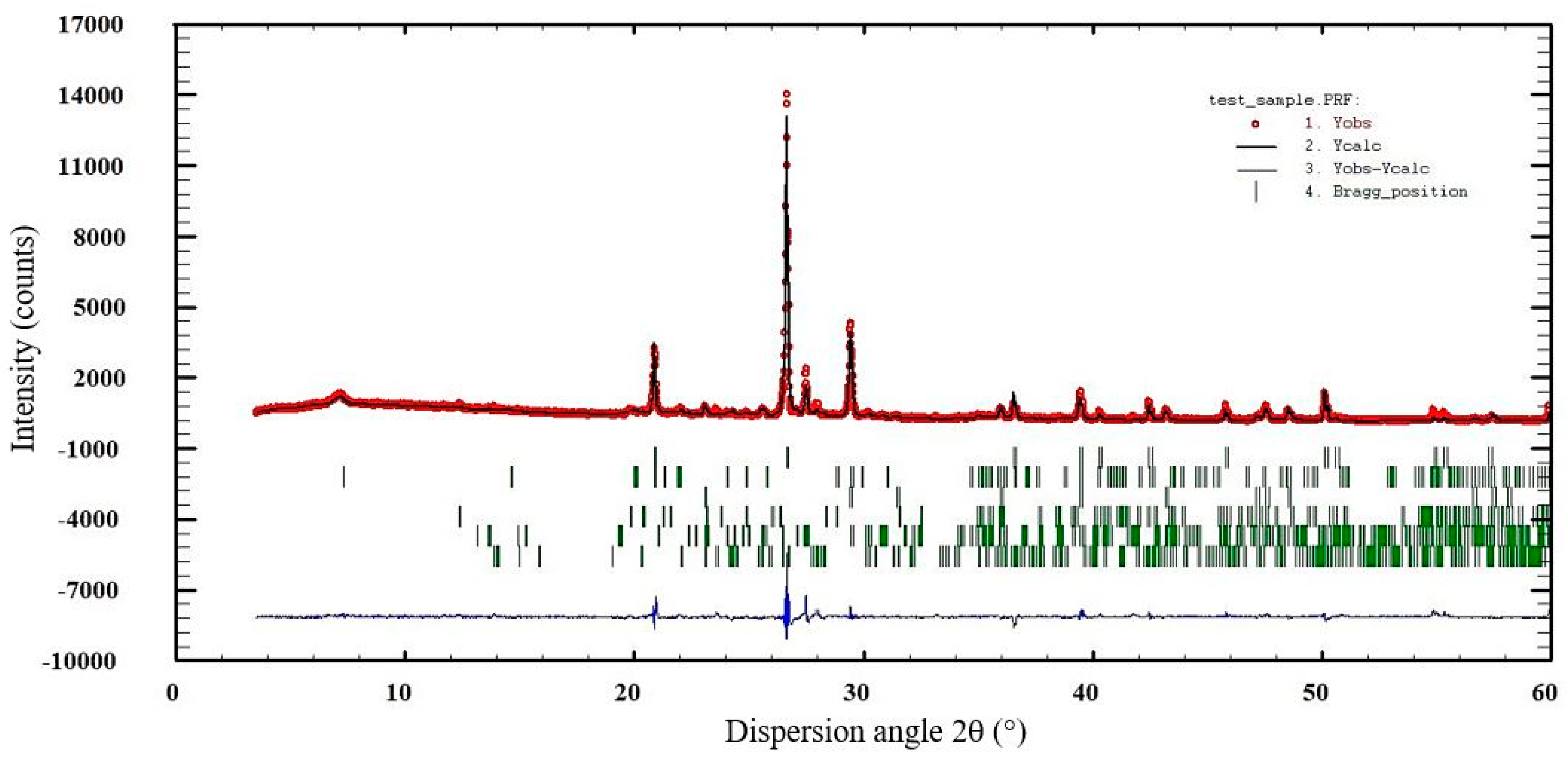
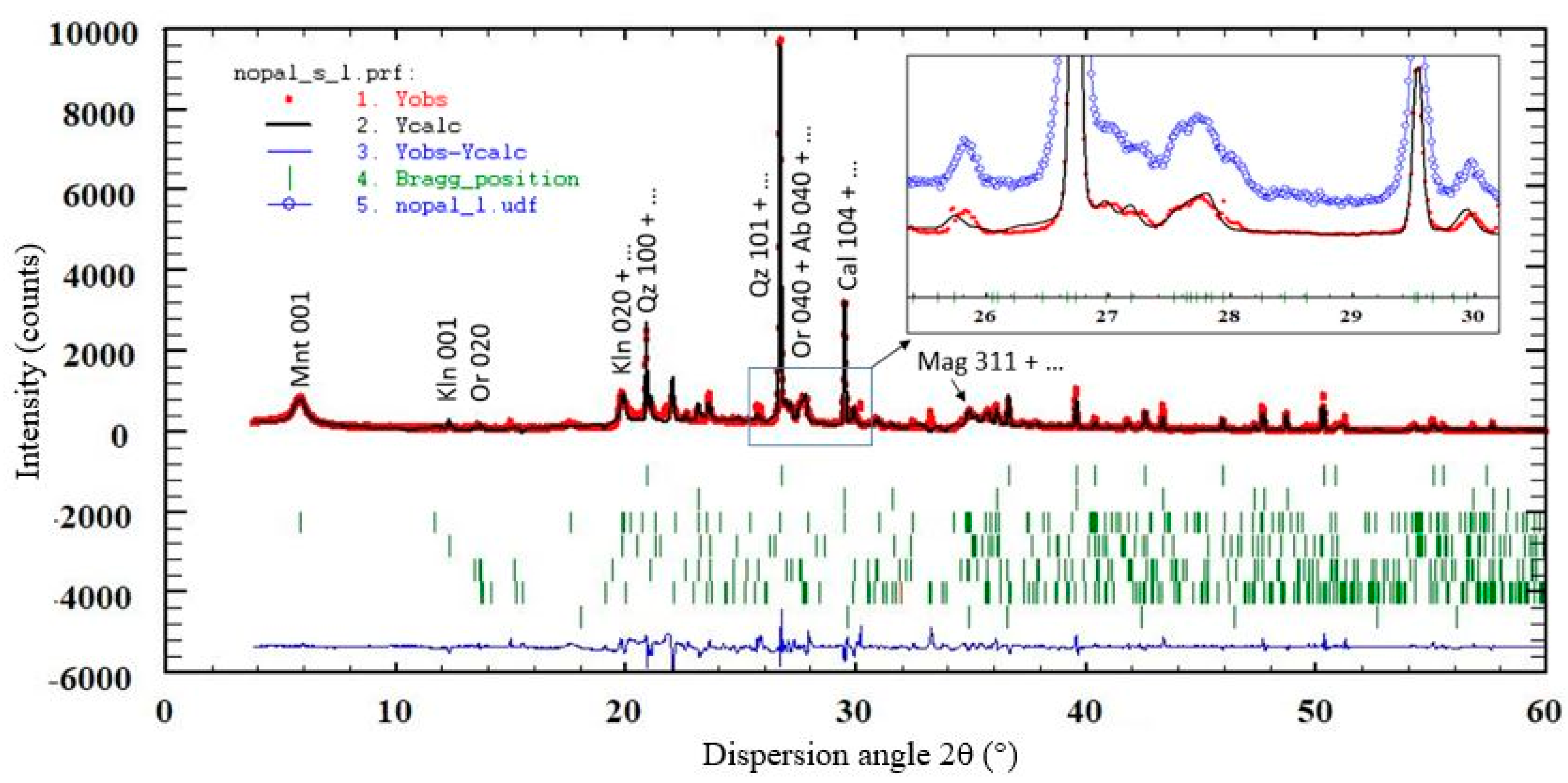
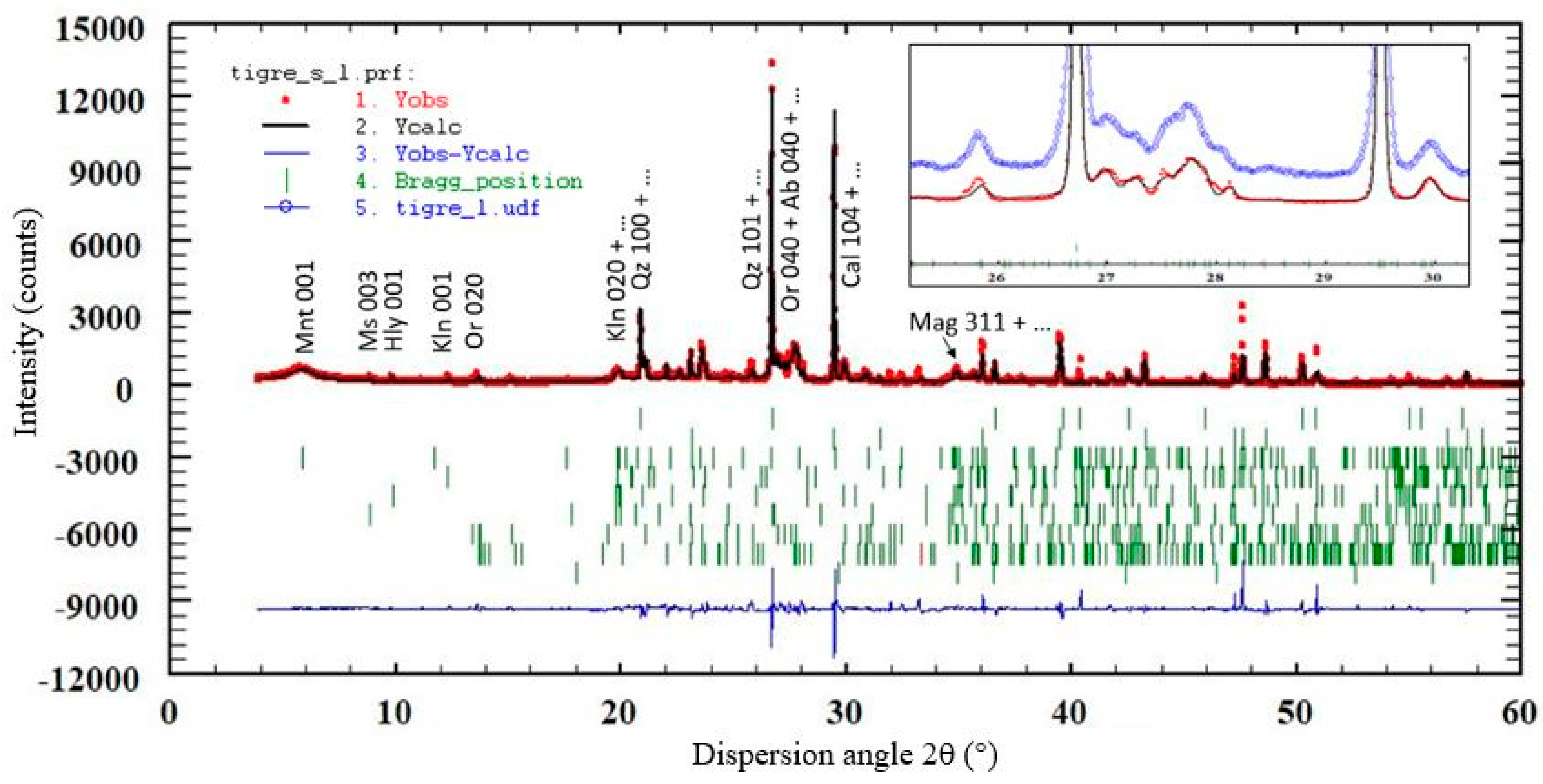
3.4. XRD Results
- Smooth and represent a suitable background;
- Calculate the net areas corresponding to poorly and well-crystallized phases;
- Estimate the cryptocrystalline concentration rapid via DoC;
- Present diffraction and analytical results;
- Apply the Rietveld multi-pattern refinement with the program Fullprof;
- Compare the DoC and Rietveld results.
4. Discussion
- −
- The modeled crystal structure may differ from that of the phase to be represented. This is not serious in quartz, as natural quartz is close to stoichiometric. But in other minerals that are solid solutions, for example feldspars, the difference between the experimental sample and the accessible models can be significant. In our research, we have selected the models chemically and structurally closest to our samples from the information available in databases.
- −
- Microabsorption: This has a significant effect when the absorption coefficients of the present phases differ considerably. The phases clearly detected in our samples are quartz, montmorillonite, calcite, kaolinite, and various feldspars. The mass absorption coefficients for all these phases (examined with CuKα radiation) are 50~80 cm2/g. Magnetite (for CuKα) has a mass absorption coefficient of 205 cm2/g, quite different from our aluminosilicates. Fortunately, in our samples, magnetite (or other iron compounds) is not present in any significant amount. Our experiments do not suffer from inaccuracies due to microabsorption.
- −
- Texture: One of the main disadvantages of traditional one-peak-per-phase XRD methods is the effect of the preferred orientation (texture). It is advisable to reduce the particle size to eliminate the shape anisotropy of the crystallites. If the presence of texture is unavoidable, careful Rietveld processing can help. (Here is an example of possible difficulties caused by texture. In the Fullprof program, representing the texture by an inverse pole figure modeled as a Gaussian bell curve (NOR parameter = 0) leads to physically incorrect results. The March–Dollase distribution (NOR = 1) must be used). In our work with fine powders, using the Fullprof program, we systematically used the March–Dollase algorithm. The results (Pref1 ≈ 1.0) indicated non-intense textures.
- −
- Microstrain of chemical origin (microheterogeneity of the atomic content and unit cell dimensions): Our XRD peaks, especially those produced by montmorillonite, show broadening due to the small crystallite size and microstrain. Due to the complexity of the diffractograms, we have not attempted to separate these effects (say, by the well-known Thomson–Cox–Hastings method). In our Rietveld analyses, we represent the variations in composition and cell dimensions by superimposing intensity bells associated with slightly different crystals.
- −
- Extinction, non-validity of the kinematic theory of XRD: This problem is notably recognized in quartz-containing rocks. Our quartz powders are made of small crystals, and so this difficulty does not affect us.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SPB | Sierra Peña Blanca |
| XRD | X-ray diffraction |
| ICP-OES | Inductively coupled plasma atomic emission spectroscopy |
| CIMAV | Centro de Investigación en Materiales Avanzados |
| DoC | Degree of crystallinity |
| PONKCS | Partial or No Known Crystal Structure |
| SEM | Scanning electron microscopy |
| EDS | Energy dispersive X-ray spectroscopy |
| RM | Rietveld method |
| Ab | Albite |
| An | Anorthite |
| Cal | Calcite |
| Hly | Halloysite |
| Kln | Kaolinite |
| Mag | Magnetite |
| Mnt | Montmorillonite |
| Ms | Muscovite |
| Or | Orthoclase |
| Qz | Quartz |
| Sa | Sanidine |
| DL | Detection limit |
Appendix A
| Sample | Al | Ca | Fe | K | Mg | Na | Si | Ti |
|---|---|---|---|---|---|---|---|---|
| 1 | 7.39 | 3.94 | 2.44 | 2.96 | 1.15 | 1.18 | 20.72 | 0.16 |
| 2 | 6.91 | 3.65 | 2.23 | 2.86 | 1.03 | 1.14 | 20.48 | 0.15 |
| 3 | 7.07 | 3.73 | 2.30 | 2.91 | 1.08 | 1.20 | 19.74 | 0.15 |
| 4 | 7.14 | 3.83 | 2.34 | 2.98 | 1.06 | 1.24 | 20.97 | 0.16 |
| 5 | 6.90 | 3.77 | 2.37 | 2.83 | 1.03 | 1.28 | 18.93 | 0.16 |
| 6 | 5.07 | 2.82 | 2.18 | 2.72 | 0.66 | 1.07 | 23.34 | 0.21 |
| 7 | 6.23 | 3.71 | 2.33 | 2.93 | 0.88 | 1.49 | 23.26 | 0.18 |
| 8 | 6.45 | 3.74 | 2.37 | 2.96 | 0.93 | 1.37 | 23.50 | 0.18 |
| 9 | 5.54 | 6.33 | 2.63 | 2.49 | 1.29 | 1.48 | 18.92 | 0.19 |
| 10 | 6.32 | 3.77 | 2.38 | 2.96 | 0.86 | 1.34 | 23.22 | 0.18 |
| 11 | 6.34 | 3.93 | 2.28 | 2.96 | 0.86 | 1.41 | 22.89 | 0.18 |
| 12 | 4.65 | 2.74 | 2.27 | 2.92 | 0.63 | 1.21 | 23.51 | 0.21 |
| 13 | 6.22 | 3.60 | 2.18 | 2.93 | 0.88 | 1.40 | 23.39 | 0.17 |
| 14 | 6.62 | 4.17 | 2.26 | 2.89 | 0.86 | 1.37 | 23.79 | 0.17 |
| 15 | 5.95 | 3.68 | 2.16 | 2.88 | 0.79 | 1.38 | 23.43 | 0.15 |
| 16 | 6.72 | 4.23 | 2.21 | 2.93 | 0.96 | 1.48 | 23.01 | 0.14 |
| 17 | 7.14 | 4.37 | 2.30 | 3.06 | 0.96 | 1.53 | 24.05 | 0.16 |
| 18 | 5.15 | 2.74 | 2.12 | 2.83 | 0.88 | 1.36 | 22.96 | 0.15 |
| 19 | 4.92 | 2.78 | 2.16 | 2.80 | 0.85 | 1.29 | 23.30 | 0.16 |
| 20 | 6.58 | 4.30 | 2.25 | 2.94 | 0.91 | 1.46 | 24.11 | 0.15 |
| 21 | 6.57 | 4.37 | 2.18 | 2.85 | 0.86 | 1.45 | 24.45 | 0.16 |
| 22 | 6.25 | 3.90 | 2.07 | 2.84 | 0.81 | 1.47 | 23.64 | 0.16 |
| 23 | 6.32 | 3.83 | 2.11 | 2.85 | 0.85 | 1.51 | 24.12 | 0.17 |
| Sample | Mnt-DoC | Qz | Cal | Mag | Mnt-1 | Mnt-2 | Mnt-3 | Mnt-Total | An | Kln | Sa |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 9.0 | 33.42 | 10.35 | 0.59 | 1.51 | 7.77 | 1.22 | 10.5 | 41.49 | 3.12 | 0.53 |
| 2 | 5.9 | 31.91 | 11.46 | 0.67 | 2.67 | 5 | 0.68 | 8.35 | 42.61 | 4.43 | 0.57 |
| 3 | 6.0 | 32.01 | 10.92 | 0.61 | 4.26 | 1.26 | 3.33 | 8.85 | 42.31 | 4.76 | 0.54 |
| 4 | 8.7 | 31.1 | 11.16 | 0.63 | 2.39 | 6.34 | 2.28 | 11.01 | 40.63 | 4.93 | 0.55 |
| 5 | 8.4 | 32.59 | 10.62 | 0.63 | 1.76 | 6.26 | 2.34 | 10.36 | 41.78 | 3.37 | 0.66 |
| 6 | 8.3 | 32.15 | 11.24 | 0.7 | 1.86 | 6.28 | 1.41 | 9.55 | 41.55 | 4.21 | 0.6 |
| 7 | 8.7 | 30.63 | 10.22 | 0.94 | 1.92 | 6.7 | 0.99 | 9.61 | 44.5 | 3.69 | 0.42 |
| 8 | 8.8 | 30.14 | 10.79 | 0.77 | 1.63 | 7.36 | 0.88 | 9.87 | 44.34 | 3.66 | 0.43 |
| 9 | 8.8 | 30.12 | 11.41 | 0.65 | 1.43 | 9.15 | 0 | 10.58 | 42.96 | 3.8 | 0.49 |
| 10 | 8.9 | 29.18 | 11.28 | 0.43 | 0.74 | 9.13 | 0.58 | 10.45 | 44.91 | 3.28 | 0.46 |
| 11 | 13.9 | 27.24 | 9.87 | 0.71 | 1.37 | 11.95 | 2.78 | 16.1 | 41.85 | 3.77 | 0.45 |
| 12 | 11.3 | 27.96 | 11.79 | 0.64 | 1.36 | 9.85 | 1.16 | 12.37 | 43.05 | 3.6 | 0.59 |
| 13 | 9.8 | 34.4 | 12.3 | 0.5 | 1.09 | 9.08 | 0.71 | 10.88 | 37.94 | 3.4 | 0.58 |
| 14 | 14.2 | 32.65 | 12.56 | 0.73 | 1.7 | 11.07 | 1.32 | 14.09 | 35.88 | 3.64 | 0.45 |
| 15 | 13.6 | 28.81 | 12.37 | 0.57 | 1.48 | 10.39 | 2.07 | 13.94 | 40.23 | 3.6 | 0.48 |
| 16 | 9.9 | 28.23 | 12.5 | 0.5 | 1.24 | 9.98 | 0.71 | 11.93 | 42.39 | 3.86 | 0.59 |
| 17 | 9.7 | 30.41 | 11.58 | 0.42 | 1.02 | 9.13 | 0.39 | 10.54 | 43.05 | 3.46 | 0.54 |
| 18 | 8.3 | 29.05 | 12.67 | 0.49 | 1.5 | 9.13 | 0.27 | 10.9 | 42.26 | 4.17 | 0.47 |
| 19 | 9.6 | 29.7 | 12.81 | 0.48 | 1.27 | 9.04 | 0.93 | 11.24 | 41.21 | 4.08 | 0.49 |
| 20 | 9.0 | 27.09 | 13.4 | 0.52 | 1.88 | 8.95 | 0.14 | 10.97 | 43.56 | 3.91 | 0.54 |
| 21 | 10.9 | 27.22 | 13.36 | 0.48 | 1.28 | 9.88 | 0.22 | 11.38 | 43.77 | 3.24 | 0.56 |
| 22 | 10.7 | 27.93 | 11.91 | 0.48 | 1.53 | 9.3 | 0.28 | 11.11 | 45.02 | 3.14 | 0.42 |
| 23 | 10.5 | 29.37 | 11.61 | 0.35 | 1.06 | 9.1 | 0.38 | 10.54 | 45.12 | 2.58 | 0.44 |
Appendix B

References
- Schmidt, R.H. A climatic delineation of the ‘real’ Chihuahuan Desert. J. Arid. Environ. 1979, 2, 243–250. [Google Scholar] [CrossRef]
- Goodell, P.C. Chihuahua city uranium province, Chihuahua Mex. In Proceedings of the Technical Committee Meeting on Uranium Deposits in Volcanic Rocks, El Paso, TX, USA, 2–5 April 1984; pp. 97–124. [Google Scholar]
- Reyes Cortes, M. Deposito de molibdeno asociado con uranio en Peña Blanca, Mexico. In Proceedings of the Technical Committee Meeting on Uranium Deposits in Volcanic Rocks, El Paso, TX, USA, 2–5 April 1984; pp. 161–174. [Google Scholar]
- Allen, P.A. From landscapes into geological history. Nature 2008, 451, 274–276. [Google Scholar] [CrossRef]
- Tuli, J.K. Nuclear Wallet Cards; Brookhaven National Laboratory: Upton, NY, USA, 2011. [Google Scholar]
- Appleby, P.G.; Oldfield, F. The calculation of lead-210 dates assuming a constant rate of supply of unsupported 210Pb to the sediment. CATENA 1978, 5, 1–8. [Google Scholar] [CrossRef]
- Sanchez-Cabeza, J.A.; Ruiz-Fernández, A.C. 210Pb sediment radiochronology: An integrated formulation and classification of dating models. Geochim. Cosmochim. Acta 2012, 82, 183–200. [Google Scholar] [CrossRef]
- Appleby, P.G.; Oldfieldz, F. The assessment of 210Pb data from sites with varying sediment accumulation rates. Hydrobiologia 1983, 103, 29–35. [Google Scholar] [CrossRef]
- Atkins, P.; De Paula, J. Physical Chemistry; Macmillan: New York, NY, USA, 2006; Volume 1. [Google Scholar]
- Shang, J.; Liu, C.; Wang, Z.; Zachara, J.M. Effect of Grain Size on Uranium (VI) Surface Complexation Kinetics and Adsorption Additivity. Environ. Sci. Technol. 2011, 45, 6025–6031. [Google Scholar] [CrossRef]
- Baqer, Y.; Thornton, S.; Stewart, D.I.; Norris, S.; Chen, X. Analysis of Uranium Sorption in a Laboratory Column Experiment Using a Reactive Transport and Surface Complexation Model. Transport Porous Media 2023, 149, 423–452. [Google Scholar] [CrossRef]
- McKinley, J.P.; Zachara, J.M.; Smith, S.C.; Turner, G.D. The influence of uranyl hydrolysis and multiple site-binding reactions on adsorption of U (VI) to montmorillonite. Clays Clay Miner. 1995, 43, 586–598. [Google Scholar] [CrossRef]
- Singleton, A.A.; Schmidt, A.H.; Bierman, P.R.; Rood, D.H.; Neilson, T.B.; Greene, E.S.; Bower, J.A.; Perdrial, N. Effects of grain size, mineralogy, and acid-extractable grain coatings on the distribution of the fallout radionuclides 7Be, 10Be, 137Cs, and 210Pb in river sediment. Geochim. Cosmochim. Acta 2017, 197, 71–86. [Google Scholar] [CrossRef]
- Bobos, I.; Madruga, M.J.; Reis, M.; Esteves, J.; Guimarães, V. Clay mineralogy insights and assessment of the natural (228Ra, 226Ra, 210Pb, 40K) and anthropogenic (137Cs) radionuclides dispersion in the estuarine and lagoon systems along the Atlantic coast of Portugal. CATENA 2021, 206, 105532. [Google Scholar] [CrossRef]
- Muñoz-Arcos, E.G.; Millward, G.E.; Clason, C.C.; Bravo-Linares, C.M.; Blake, W.H. Fine sediment-associated contaminants in gravel bed rivers: Evaluating storage times and turnover using fallout radionuclides (FRNs). Sci. Total Environ. 2025, 959, 178177. [Google Scholar] [CrossRef]
- Singh, B.K.; Um, W. Application of clay materials for sorption of radionuclides from waste solutions. Minerals 2023, 13, 239. [Google Scholar] [CrossRef]
- Zhang, B.; Gao, B.; Ma, W.; Wang, S.; Qi, W.; Wu, J.; Wang, R.; Zhou, Y.; Liu, Y. Different behavior of uranium (VI) on two clay minerals: Montmorillonite and kaolinite. J. Radioanal. Nucl. Chem. 2023, 332, 4029–4046. [Google Scholar] [CrossRef]
- Zhang, Y. Progress and perspectives on hexavalent uranium waste forms for the immobilization of uranium-rich radioactive wastes. Mater. Chem. Phys. 2024, 324, 129714. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, B. Fidelity of the 210Pb dating method, a subaquatic sediment perspective. Sci. Total Environ. 2023, 871, 161972. [Google Scholar] [CrossRef] [PubMed]
- Aba, A.; Al-Dousari, A.M.; Ismaeel, A. Depositional characteristics of 7Be and 210Pb in Kuwaiti dust. J. Radioanal. Nucl. Chem. 2016, 307, 15–23. [Google Scholar] [CrossRef]
- Sun, X.; Fan, D.; Liao, H.; Liu, M.; Tian, Y.; Zhang, X.; Yang, Z. Variation in sedimentary 210Pb over the last 60 years in the Yangtze River Estuary: New insight to the sedimentary processes. Mar. Geol. 2020, 427, 106240. [Google Scholar] [CrossRef]
- Baskaran, M. Applications of Radon Progeny in Atmospheric Studies. In Radon: A Tracer for Geological, Geophysical and Geochemical Studies; Springer International Publishing: Cham, Switzerland, 2016; pp. 85–117. [Google Scholar] [CrossRef]
- Barsanti, M.; Garcia-Tenorio, R.; Schirone, A.; Rozmaric, M.; Ruiz-Fernández, A.C.; Sanchez-Cabeza, J.A.; Delbono, I.; Conte, F.; De Oliveira Godoy, J.M.; Heijnis, H.; et al. Challenges and limitations of the 210Pb sediment dating method: Results from an IAEA modelling interlaboratory comparison exercise. Quat. Geochronol. 2020, 59, 101093. [Google Scholar] [CrossRef]
- Cullity, B.D.; Stock, S.R. Elements of X-Ray Diffraction; Prentice Hall: Upper Saddle River, NJ, USA, 2001; p. 664. [Google Scholar]
- Rietveld, H. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- McCusker, L.; Von Dreele, R.; Cox, D.; Louër, D.; Scardi, P. Rietveld refinement guidelines. J. Appl. Crystallogr. 1999, 32, 36–50. [Google Scholar] [CrossRef]
- Gražulis, S.; Merkys, A.; Vaitkus, A. Crystallography Open Database (COD). In Handbook of Materials Modeling: Methods: Theory and Modeling; Andreoni, W., Yip, S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 1863–1881. [Google Scholar] [CrossRef]
- Kabekkodu, S.N.; Dosen, A.; Blanton, T.N. PDF-5+: A comprehensive powder diffraction file™ for materials characterization. Powder Diffr. 2024, 39, 47–59. [Google Scholar] [CrossRef]
- Zagorac, D.; Müller, H.; Ruehl, S.; Zagorac, J.; Rehme, S. Recent developments in the Inorganic Crystal Structure Database: Theoretical crystal structure data and related features. J. Appl. Crystallogr. 2019, 52, 918–925. [Google Scholar] [CrossRef]
- Downs, R.T.; Hall-Wallace, M. The American Mineralogist crystal structure database. Am. Mineral. 2003, 88, 247–250. [Google Scholar]
- Putz, H.; Brandenburg, K. Match!-Phase Analysis Using Powder Diffraction; Crystal Impact: Bonn, Germany, 2024. [Google Scholar]
- Suzuki, Y. Automated Data Analysis for Powder X-Ray Diffraction Using Machine Learning. Synchrotron Radiat. News 2022, 35, 9–15. [Google Scholar] [CrossRef]
- Lee, J.-W.; Park, W.B.; Lee, J.H.; Singh, S.P.; Sohn, K.-S. A deep-learning technique for phase identification in multiphase inorganic compounds using synthetic XRD powder patterns. Nat. Commun. 2020, 11, 86. [Google Scholar] [CrossRef] [PubMed]
- Surdu, V.-A.; Győrgy, R. X-ray Diffraction Data Analysis by Machine Learning Methods—A Review. Appl. Sci. 2023, 13, 9992. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent developments of the program FULLPROF. Comm. Powder Diffr. Newsl. 2001, 26, 12–19. [Google Scholar]
- Lutterotti, L.; Pilliere, H.; Fontugne, C.; Boullay, P.; Chateigner, D. Full-profile search-match by the Rietveld method. J. Appl. Crystallogr. 2019, 52, 587–598. [Google Scholar] [CrossRef] [PubMed]
- Coelho, A. TOPAS and TOPAS-Academic: An optimization program integrating computer algebra and crystallographic objects written in C++. J. Appl. Crystallogr. 2018, 51, 210–218. [Google Scholar] [CrossRef]
- Bergmann, J.; Friedel, P.; Kleeberg, R. BGMN-a New Fundamental Parameters Based Rietveld Program for Laboratory X-ray Sources, it’s Use in Quantitative Analysis and Structure Investigations. IUCr Comm. Powder Diffr. Newsl. 1998, 20, 5–8. [Google Scholar]
- Toby, B.H.; Von Dreele, R.B. GSAS-II: The genesis of a modern open-source all purpose crystallography software package. J. Appl. Crystallogr. 2013, 46, 544–549. [Google Scholar] [CrossRef]
- Madsen, I.C.; Scarlett, N.V.; Kern, A. Description and survey of methodologies for the determination of amorphous content via X-ray powder diffraction. ZKri 2011, 226, 944–955. [Google Scholar] [CrossRef]
- Clark, G.L.; Reynolds, D.H. Quantitative analysis of mine dusts: An X-Ray diffraction method. Ind. Eng. Chem. Anal. Ed. 1936, 8, 36–40. [Google Scholar] [CrossRef]
- Butler, B.M.; Hillier, S. Automated Full-Pattern Summation of X-Ray Powder Diffraction Data for High-Throughput Quantification of Clay-Bearing Mixtures. Clays Clay Miner. 2021, 69, 38–51. [Google Scholar] [CrossRef]
- O’Connor, B.H.; Raven, M.D. Application of the Rietveld refinement procedure in assaying powdered mixtures. Powder Diffr. 1988, 3, 2–6. [Google Scholar] [CrossRef]
- Klug, H.P.; Alexander, L.E. X-Ray Diffraction Procedures: For Polycrystalline and Amorphous Materials; Wiley: Hoboken, NJ, USA, 1974; p. 966. [Google Scholar]
- Scarlett, N.V.; Madsen, I.C. Quantification of phases with partial or no known crystal structures. Powder Diffr. 2006, 21, 278–284. [Google Scholar] [CrossRef]
- Riello, P. Quantitative analysis of amorphous fraction in the study of the microstructure of semi-crystalline materials. In Diffraction Analysis of the Microstructure of Materials; Springer: Berlin, Germany, 2004; pp. 167–184. [Google Scholar] [CrossRef]
- Mejdi, M.; Wilson, W.; Saillio, M.; Chaussadent, T.; Divet, L.; Tagnit-Hamou, A. Quantifying glass powder reaction in blended-cement pastes with the Rietveld-PONKCS method. Cem. Concr. Res. 2020, 130, 105999. [Google Scholar] [CrossRef]
- Kanzari, A.; Gérard, M.; Boekhout, F.; Galoisy, L.; Calas, G.; Descostes, M. Impact of incipient weathering on uranium migration in granitic waste rock piles from former U mines (Limousin, France). J. Geochem. Explor. 2017, 183, 114–126. [Google Scholar] [CrossRef]
- Maestracci, B.; Delchini, S.; Chateigner, D.; Pilliere, H.; Lutterotti, L.; Borovin, E. Simultaneous combined XRF-XRD analysis of geological sample: New methodological approach for on-site analysis on New-Caledonian Ni-rich harzburgite. J. Geochem. Explor. 2023, 252, 107250. [Google Scholar] [CrossRef]
- ISO-18400-102; Soil Quality- Sampling-Part 102: Selection and Application of Sampling Techniques. International Organization for Standardization: Geneva, Switzerland, 2017; p. 71.
- Switzer, A.D. Measuring and Analyzing Particle Size in a Geomorphic Context. Treatise Geomorphol. 2013, 14, 224–242. [Google Scholar]
- Sanchez-Cabeza, J.-A.; Díaz-Asencio, M.; Ruiz-Fernández, A.C. (Eds.) Radiocronología de Sedimentos Costeros Utilizando 210Pb: Modelos, Validación y Aplicaciones; IAEA: Vienna, Austria, 2012. [Google Scholar]
- Kawrakow, I.; Mainegra-Hing, E.; Rogers, D. EGSnrcMP: The Multi-Platform Environment for EGSnrc; National Research Council of Canada: Ottawa, ON, Canada, 2006. [Google Scholar]
- Rogers, D.W.; Kawrakow, I.; Seuntjens, J.; Walters, B.; Mainegra-Hing, E. NRC User Codes for EGSnrc; NRCC Report PIRS-702 (Rev. B); NRC: Ottawa, ON, Canada, 2003. [Google Scholar]
- Venegas-Argumedo, Y.; Montero-Cabrera, M. True coincidence summing corrections for an extended energy range HPGe detector. In Proceedings of the AIP Conference Proceedings, Ciudad Juárez, Mexico, 4–6 March 2015. [Google Scholar]
- Strachnov, V.; LaRosa, J.; Dekner, R.; Zeisler, R.; Fajgelj, A. Report on the Intercomparison Run IAEA-375: Determination of Radionuclides in Soil Sample IAEA-375; International Atomic Energy Agency, Agency’s Laboratories: Vienna, Austria, 1996. [Google Scholar]
- IAEA. Reference Sheet–Reference Material IAEA-375, Radionuclides and Trace Elements in Soil; Analytical Quality Control Services (AQCS); Agency’s Laboratories, International Atomic Energy Agency: Seibersdorf, Austria, 2000; p. 4. [Google Scholar]
- Currie, L.A. Limits for qualitative detection and quantitative determination. Application to radiochemistry. Anal. Chem. 1968, 40, 586–593. [Google Scholar] [CrossRef]
- Nacional, S.M. Información Estadística Climatológica. Available online: https://smn.conagua.gob.mx/es/climatologia/informacion-climatologica/informacion-estadistica-climatologica (accessed on 10 October 2024).
- Warr, L.N. IMA–CNMNC approved mineral symbols. MinM 2021, 85, 291–320. [Google Scholar] [CrossRef]
- Aniel, B.; Leroy, J.M. The reduced uraniferous mineralizations associated with the volcanic rocks of the Sierra Pena Blanca (Chihuahua, Mexico). Am. Mineral. 1985, 70, 1290–1297. [Google Scholar]
- George-Aniel, B.; Poty, B.; Leroy, J. Uranium deposits of the Sierra Peña Blanca: Three examples of mechanisms of ore deposit formation in a volcanic environment. In Proceedings of the Technical Committee Meeting on Uranium Deposits in Volcanic Rocks, El Paso, TX, USA, 2–5 April 1984; pp. 490–498. [Google Scholar]
- Barré, P.; Montagnier, C.; Chenu, C.; Abbadie, L.; Velde, B. Clay minerals as a soil potassium reservoir: Observation and quantification through X-ray diffraction. Plant Soil 2008, 302, 213–220. [Google Scholar] [CrossRef]
- Meteoblue. Simulated Historical Climate & Weather Data for 29.25° N, 105.9° W. Available online: https://www.meteoblue.com/en/weather/historyclimate/climatemodelled/29.25N-105.9E1179_America%2FChihuahua (accessed on 18 December 2024).
- Caraveo-Castro, C.d.R.; Montero-Cabrera, M.E.; Méndez-García, C.G.; Cabral-Lares, R.M.; Castillo-Sandoval, I. Mineralogical characterization and uranium radioactivity of recent sediments from the Laguna del Cuervo, Chihuahua. In Proceedings of the 1st National Congress of the Mexican Society of Synchrotron Light & 1st International Congress of Synchrotron Light Techniques, Leon, Guanajuato, Mexico, 21–26 June 2021. [Google Scholar]
- Ma, L.; Wu, J.; Abuduwaili, J.; Liu, W. Aeolian particle transport inferred using a ~150-year sediment record from Sayram Lake, arid northwest China. J. Limnol. 2015, 74, 584–593. [Google Scholar] [CrossRef]
- Vandenberghe, J.; Sun, Y.; Wang, X.; Abels, H.A.; Liu, X. Grain-size characterization of reworked fine-grained aeolian deposits. Earth-Sci. Rev. 2018, 177, 43–52. [Google Scholar] [CrossRef]
- Vandenberghe, J. Grain size of fine-grained windblown sediment: A powerful proxy for process identification. Earth-Sci. Rev. 2013, 121, 18–30. [Google Scholar] [CrossRef]
- Shi, H.; Yue, D.; Zhao, J.; Wang, X. Research on flood sediments and rainstorm events in Huangtuwa, Northern Shaanxi. Front. Environ. Sci. 2023, 11, 1180730. [Google Scholar] [CrossRef]
- Wennrich, V.; Böhm, C.; Brill, D.; Carballeira, R.; Hoffmeister, D.; Jaeschke, A.; Kerber, F.; Maldonado, A.; May, S.M.; Olivares, L.; et al. Late Pleistocene to modern precipitation changes at the Paranal clay pan, central Atacama Desert. Glob. Planet. Change 2024, 233, 104349. [Google Scholar] [CrossRef]
- Núñez-López, D.; Muñoz-Robles, C.A.; Reyes-Gómez, V.M.; Velasco-Velasco, I.; Gadsden-Esparza, H. Characterization of drought at different time scales in Chihuahua, México. Agrociencia 2007, 41, 253–262. [Google Scholar]
- Esquivel, E. Lluvia y sequía en el norte de México. Un. Análisis Precipitación Histórica En. Chihuahua. Gac. Ecológica 2002, 65, 43–52. [Google Scholar]
- Renteria-Villalobos, M.; Hanson, R.T.; Eastoe, C. Evaluation of climate variability on sustainability for transboundary water supply in Chihuahua, Mexico. J. Hydrol. Reg. Stud. 2022, 44, 101207. [Google Scholar] [CrossRef]
- Ortega-Gaucin, D. Hydrological drought characterization in the Rio Grande basin, Mexico. Terra Latinoam. 2013, 31, 167–180. [Google Scholar]
- Perez-Reyes, V.; Cabral Lares, R.M.; Canche Tello, J.G.; Faudoa Gómez, F.G.; Rodríguez Guerra, Y.; Hernández Herrera, C.; Reyes Cortés, I.A.; Loredo Portales, R.; Hernández Cruz, D.; Esparza Ponce, H.E.; et al. Experimental Modeling and Synchrotron Light analysis of uranium transport by surface water in sediments of Peña Blanca-Laguna del Cuervo, Chihuahua. Supl. Rev. Mex. Física 2024, 5, 011203. [Google Scholar] [CrossRef]
- Pérez-Reyes, V.; Cabral-Lares, R.M.; Canche-Tello, J.G.; Rentería-Villalobos, M.; González-Sánchez, G.; Carmona-Lara, B.P.; Hernández-Herrera, C.; Faudoa-Gómez, F.; Rodríguez-Guerra, Y.; Vázquez-Olvera, G.; et al. Uranium Mineral Transport in the Peña Blanca Desert: Dissolution or Fragmentation? Simulation in Sediment Column Systems. Appl. Sci. 2025, 15, 609. [Google Scholar] [CrossRef]
- Pérez-Reyes, V.; Cabral-Lares, R.M.; Méndez-García, C.G.; Caraveo-Castro, C.d.R.; Reyes-Cortés, I.A.; Carrillo-Flores, J.; Montero-Cabrera, M.E. Transport and concentration of uranium isotopes in the Laguna del Cuervo, Chihuahua, Mexico. Supl. Rev. Mex. Física 2022, 3, 010606. [Google Scholar] [CrossRef]
- Akçay, H. Aqueous speciation and pH effect on the sorption behavior of uranium by montmorillonite. J. Radioanal. Nucl. Chem. 1998, 237, 133–137. [Google Scholar] [CrossRef]
- Bachmaf, S.; Merkel, B.J. Sorption of uranium (VI) at the clay mineral–water interface. Environ. Earth Sci. 2011, 63, 925–934. [Google Scholar] [CrossRef]
- Catalano, J.G.; Brown, G.E. Uranyl adsorption onto montmorillonite: Evaluation of binding sites and carbonate complexation. Geochim. Cosmochim. Acta 2005, 69, 2995–3005. [Google Scholar] [CrossRef]
- Dent, A.J.; Ramsay, J.D.F.; Swanton, S.W. An EXAFS study of uranyl ion in solution and sorbed onto silica and montmorillonite clay colloids. J. Colloid Interface Sci. 1992, 150, 45–60. [Google Scholar] [CrossRef]
- Hennig, C.; Reich, T.; Dähn, R.; Scheidegger, A.M. Structure of uranium sorption complexes at montmorillonite edge sites. Radiochim. Acta 2002, 90, 653–657. [Google Scholar] [CrossRef]
- Schindler, M.; Legrand, C.A.; Hochella, M.F. Alteration, adsorption and nucleation processes on clay–water interfaces: Mechanisms for the retention of uranium by altered clay surfaces on the nanometer scale. Geochim. Cosmochim. Acta 2015, 153, 15–36. [Google Scholar] [CrossRef]
- Sylwester, E.R.; Hudson, E.A.; Allen, P.G. The structure of uranium (VI) sorption complexes on silica, alumina, and montmorillonite. Geochim. Cosmochim. Acta 2000, 64, 2431–2438. [Google Scholar] [CrossRef]
- Yu, S.; Ma, J.; Shi, Y.; Du, Z.; Zhao, Y.; Tuo, X.; Leng, Y. Uranium (VI) adsorption on montmorillonite colloid. J. Radioanal. Nucl. Chem. 2020, 324, 541–549. [Google Scholar] [CrossRef]

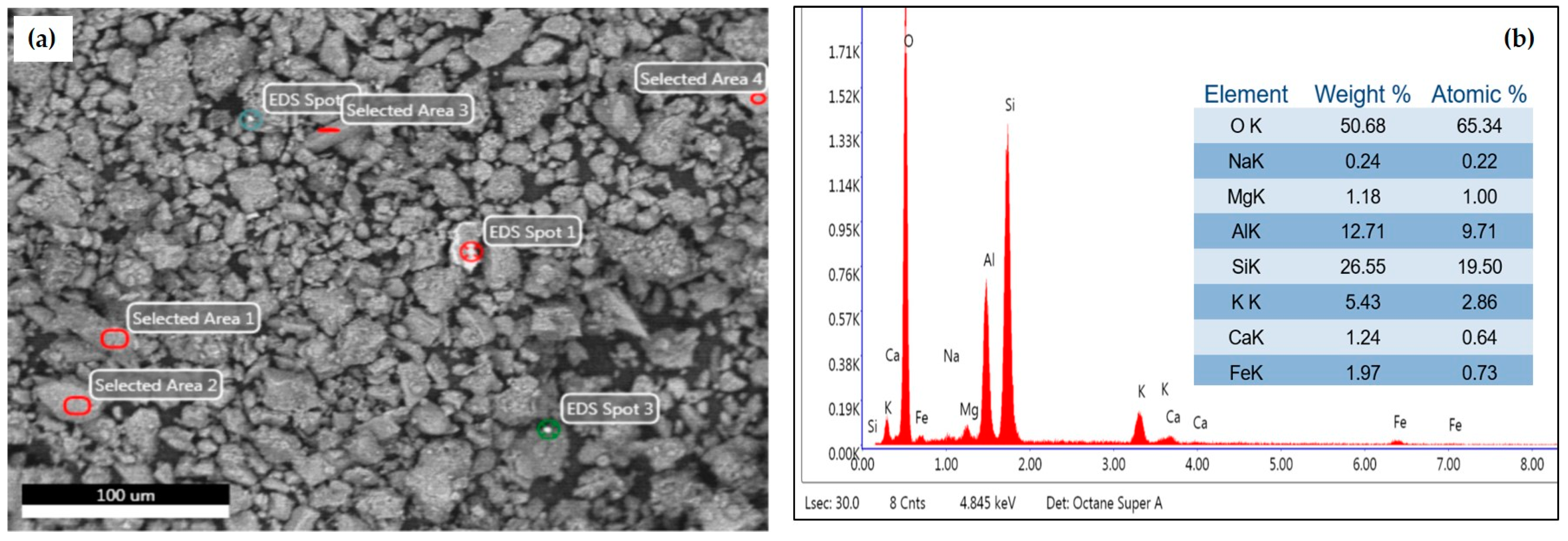
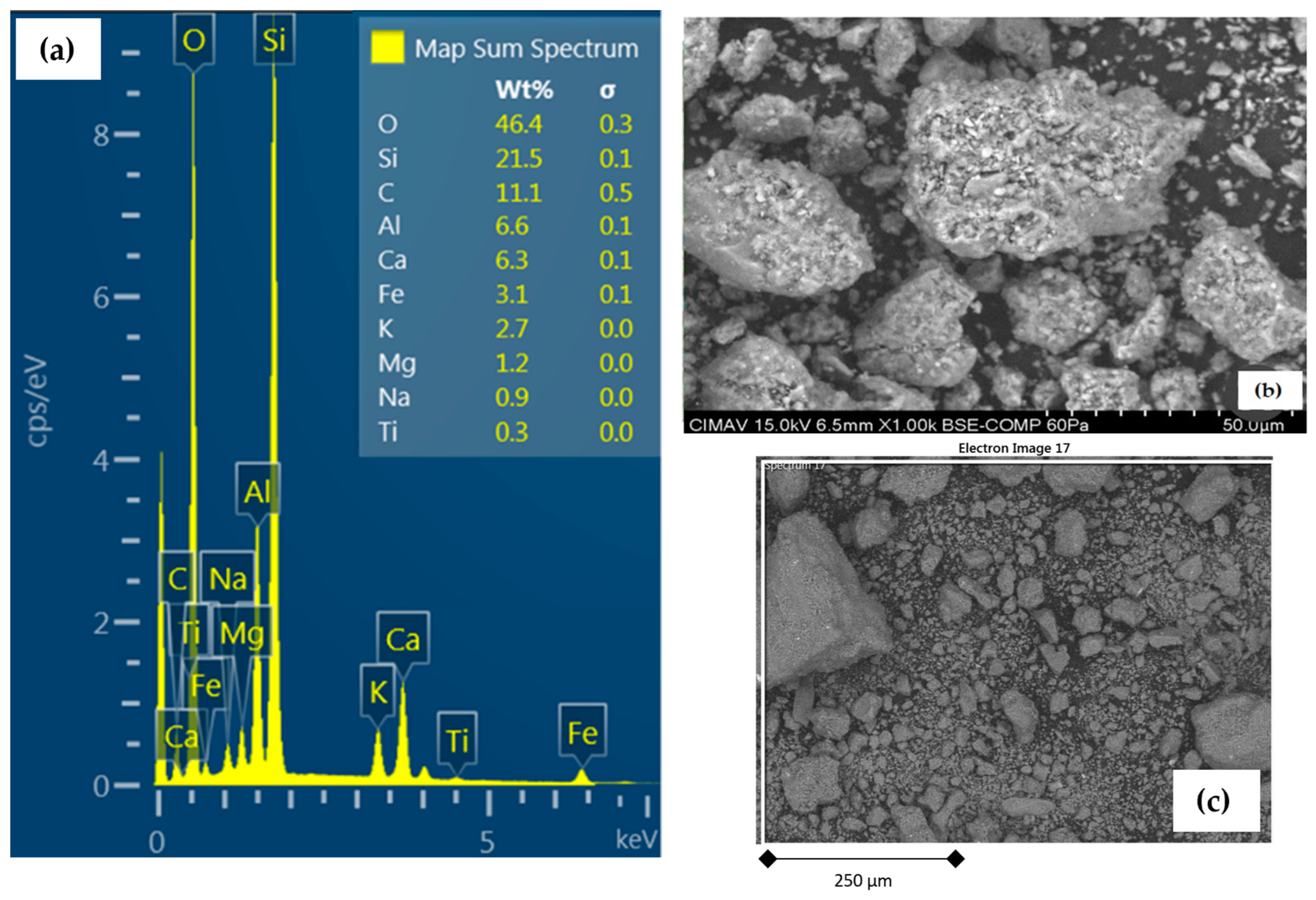
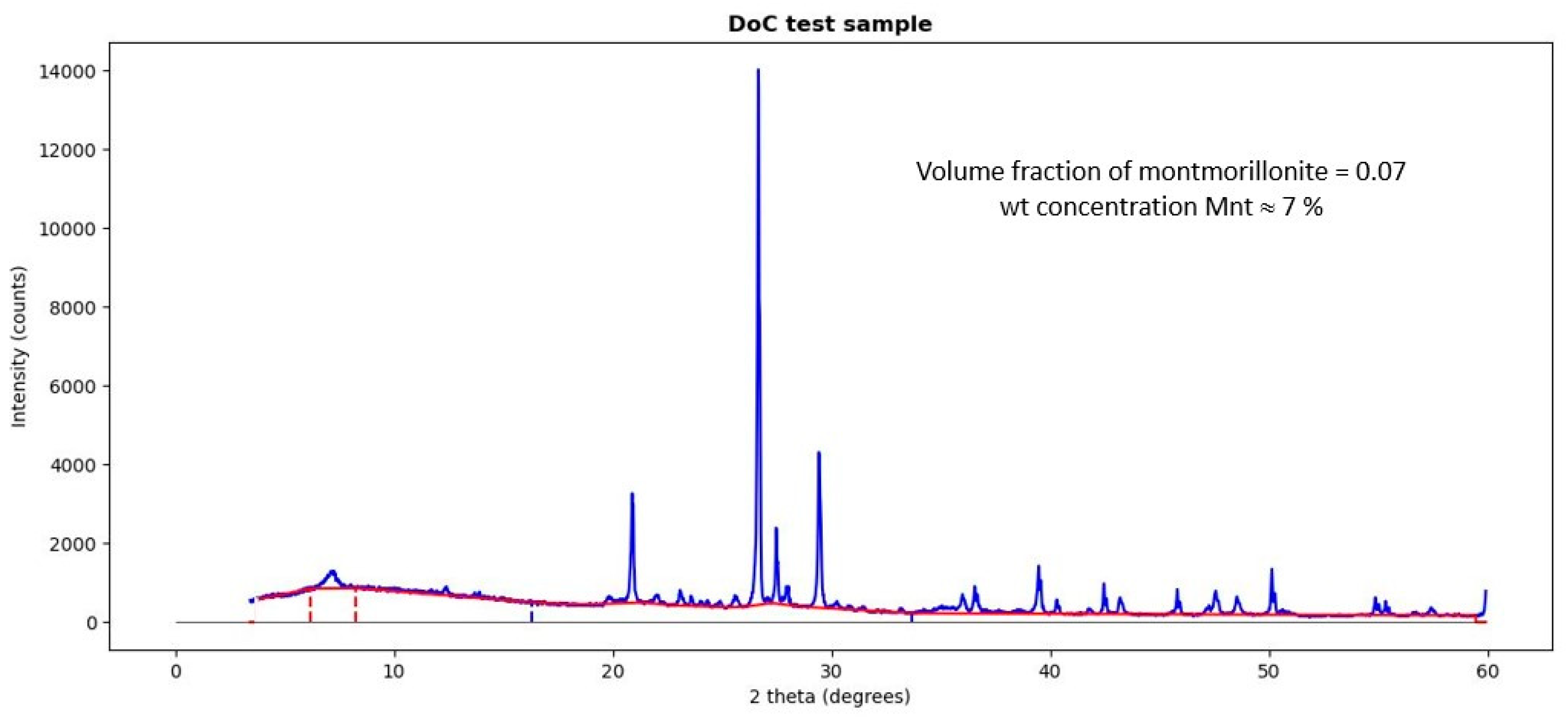

| Al | Ca | Fe | K | Mg | Na | Si | Ti |
|---|---|---|---|---|---|---|---|
| 6.3 (0.8) | 3.9 (0.7) | 2.27 (0.12) | 2.88 (0.11) | 0.9 (0.1) | 1.35 (0.13) | 23 (2) | 0.17 (0.02) |
| Phase | Experimentally Mixed | XRD Rietveld |
|---|---|---|
| Quartz | 34.4 | 36.6 (0.6) |
| Calcite | 16.5 | 15.6 (0.3) |
| Montmorillonite | 9.2 | 8.5 + (0.3) |
| Kaolinite | 8.4 | 9.1 (0.3) |
| Microcline | 16.0 | 17.1 (0.3) |
| Albite | 13.8 | 13.0 (0.3) |
| Analbite | 1.4 | DL |
| Cristobalite | 0.3 (DL) | 0 |
| Phase | Nopal | Tigre |
|---|---|---|
| Quartz (Qz) | 35.13 (1.74) | 24.87 (1.32) |
| Calcite (Cal) | 14.81 (1.24) | 25.56 (1.63) |
| Montmorillonite (Mnt) | 10.89 (0.55) | 9.37 (0.42) |
| Kaolinite (Kln) | 13.88 (0.83) | 2.92 (0.55) |
| Halloysite (Hly) | - | 4.57 (0.54) |
| Muscovite (Ms) | - | 2.6 (0.1) |
| Orthoclase (Or) | 13.76 (0.83) | 24.89 (0.88) |
| Albite (Ab) | 10.45 (0.78) | 4.81 (0.46) |
| Magnetite (Mag) | ~1 (DL) | ~1 (DL) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caraveo-Castro, C.d.R.; Rodríguez-Guerra, Y.; Fuentes-Montero, L.; González-Jacquez, A.I.; Fuentes-Cobas, L.E.; Montero-Cabrera, M.E. Procedures for X-Ray Diffraction Phase Analysis: The Case of Fine Sediments from Peña Blanca, Chihuahua, Mexico. Crystals 2025, 15, 169. https://doi.org/10.3390/cryst15020169
Caraveo-Castro CdR, Rodríguez-Guerra Y, Fuentes-Montero L, González-Jacquez AI, Fuentes-Cobas LE, Montero-Cabrera ME. Procedures for X-Ray Diffraction Phase Analysis: The Case of Fine Sediments from Peña Blanca, Chihuahua, Mexico. Crystals. 2025; 15(2):169. https://doi.org/10.3390/cryst15020169
Chicago/Turabian StyleCaraveo-Castro, Carmen del Rocio, Yair Rodríguez-Guerra, Luis Fuentes-Montero, Andrés Isaak González-Jacquez, Luis E. Fuentes-Cobas, and María Elena Montero-Cabrera. 2025. "Procedures for X-Ray Diffraction Phase Analysis: The Case of Fine Sediments from Peña Blanca, Chihuahua, Mexico" Crystals 15, no. 2: 169. https://doi.org/10.3390/cryst15020169
APA StyleCaraveo-Castro, C. d. R., Rodríguez-Guerra, Y., Fuentes-Montero, L., González-Jacquez, A. I., Fuentes-Cobas, L. E., & Montero-Cabrera, M. E. (2025). Procedures for X-Ray Diffraction Phase Analysis: The Case of Fine Sediments from Peña Blanca, Chihuahua, Mexico. Crystals, 15(2), 169. https://doi.org/10.3390/cryst15020169






