Spectroscopic Ellipsometry and Wave Optics: A Dual Approach to Characterizing TiN/AlN Composite Dielectrics
Abstract
1. Introduction
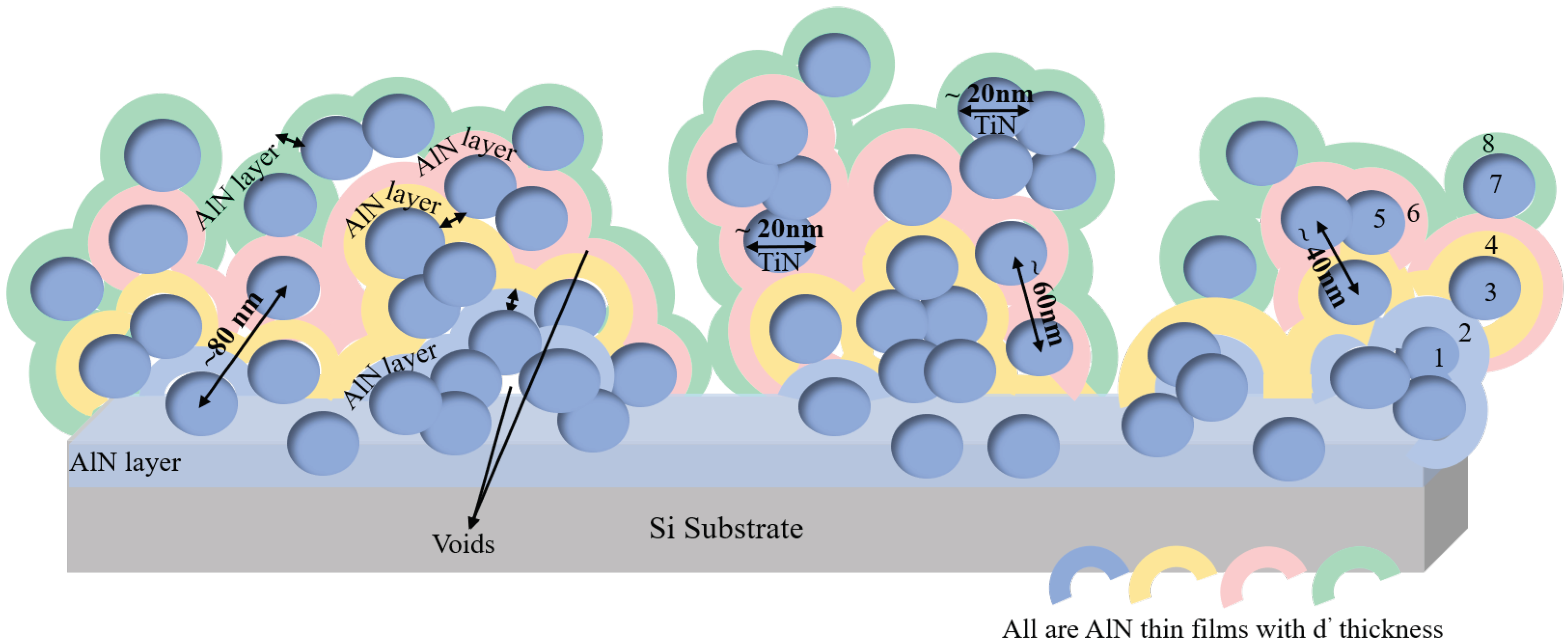
2. Structure of the Composite
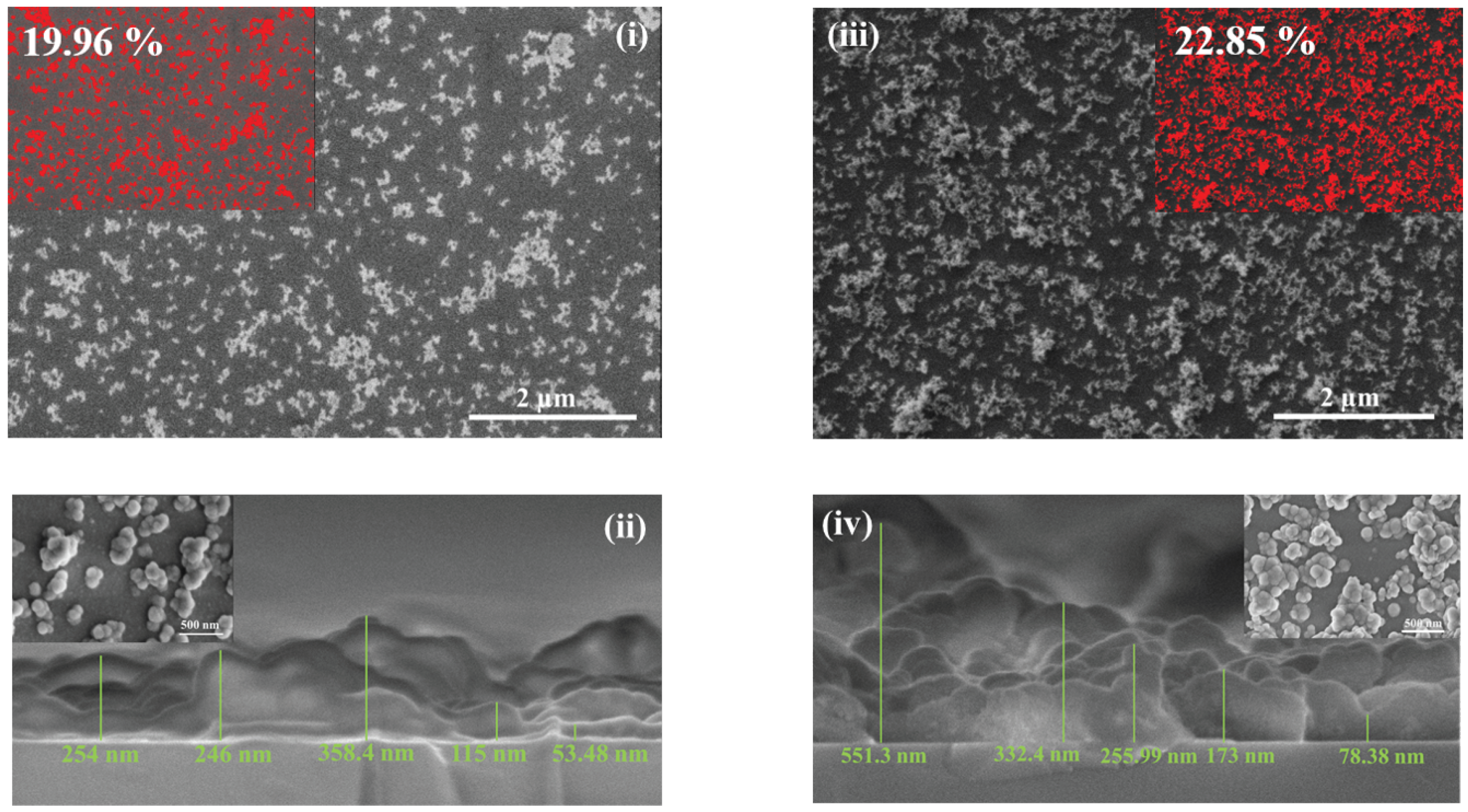
2.1. SEM Characterization
2.2. XPS Characterization
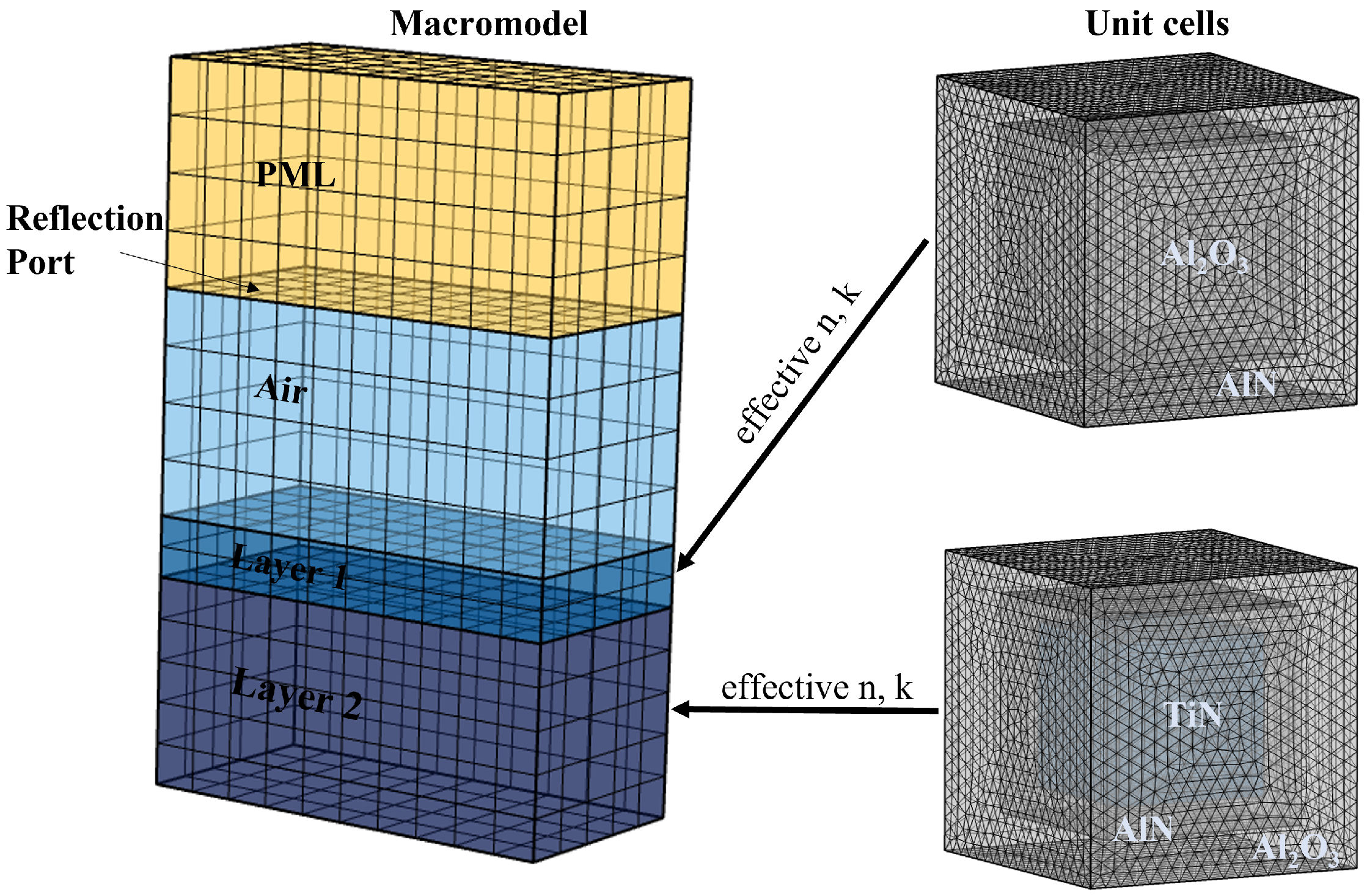
3. Numerical Modelling
3.1. Numerical Acquisition of
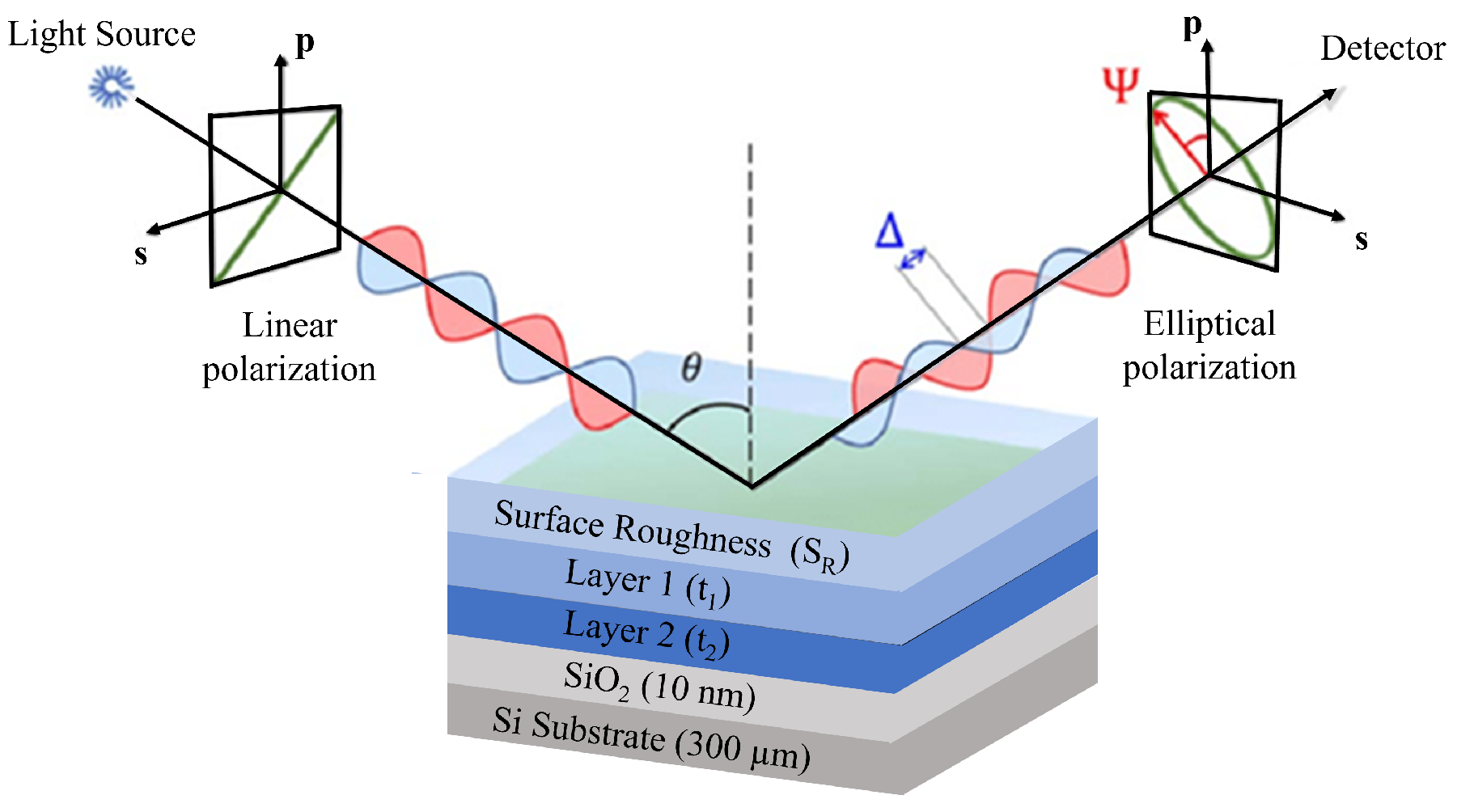
3.2. Acquisition of from SE Measurements
4. Results and Discussion
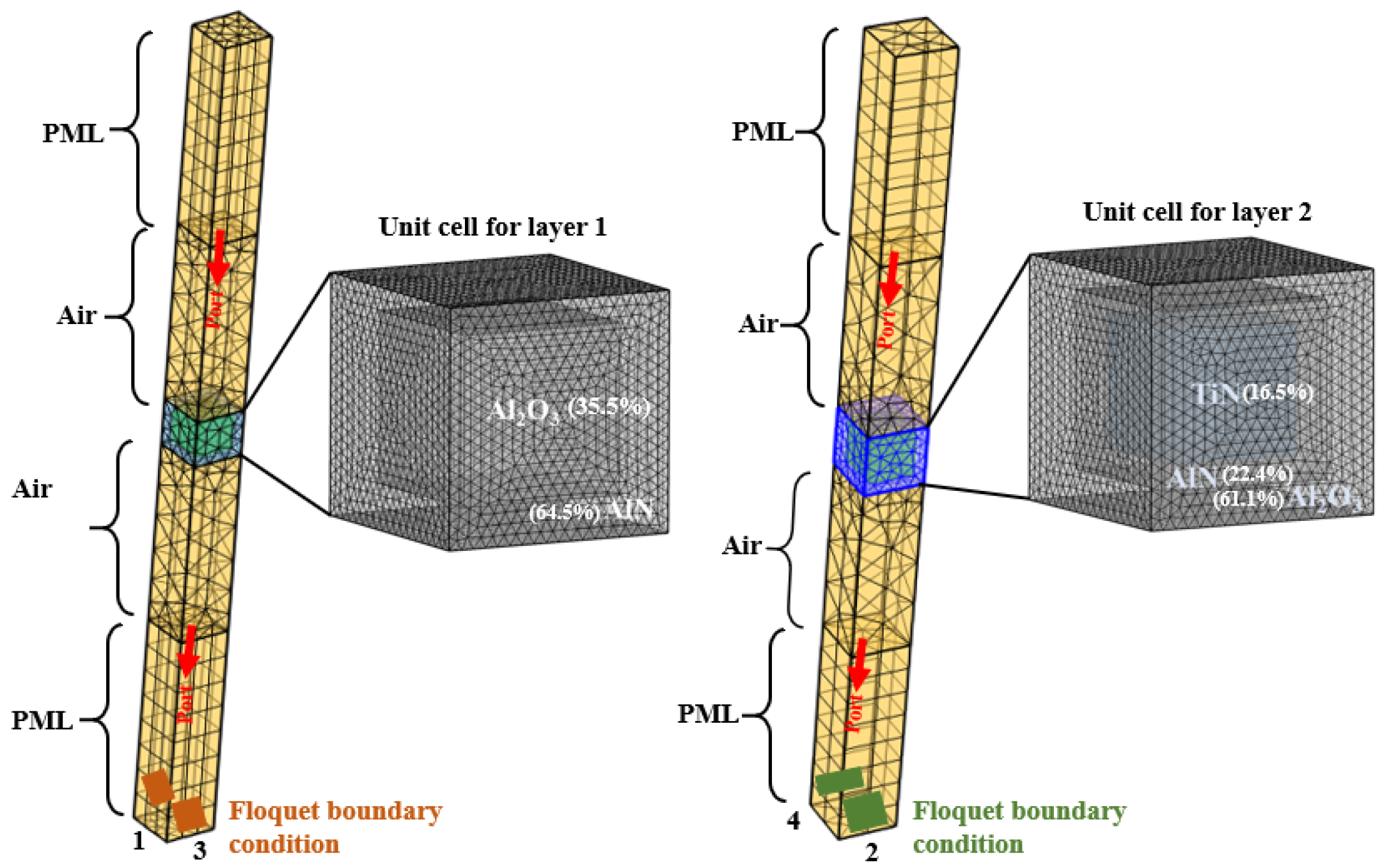
4.1. Numerical Simulation
- Perfectly Matched Layers (PMLs) were applied to the top and bottom domains of the computational domain to simulate an infinite space. Both the PMLs and air regions were assigned a thickness equal to each.
- The boundary surfaces between the PML domain and the air spacing serve as ports for initiating the incident wave illumination and for post-process calculation of the scattering coefficients .
- Floquet periodic boundary conditions are implemented on the transverse sides of the computational domain to emulate an infinitely extensive film.
4.2. Optical Measurements by Spectroscopic Ellipsometer
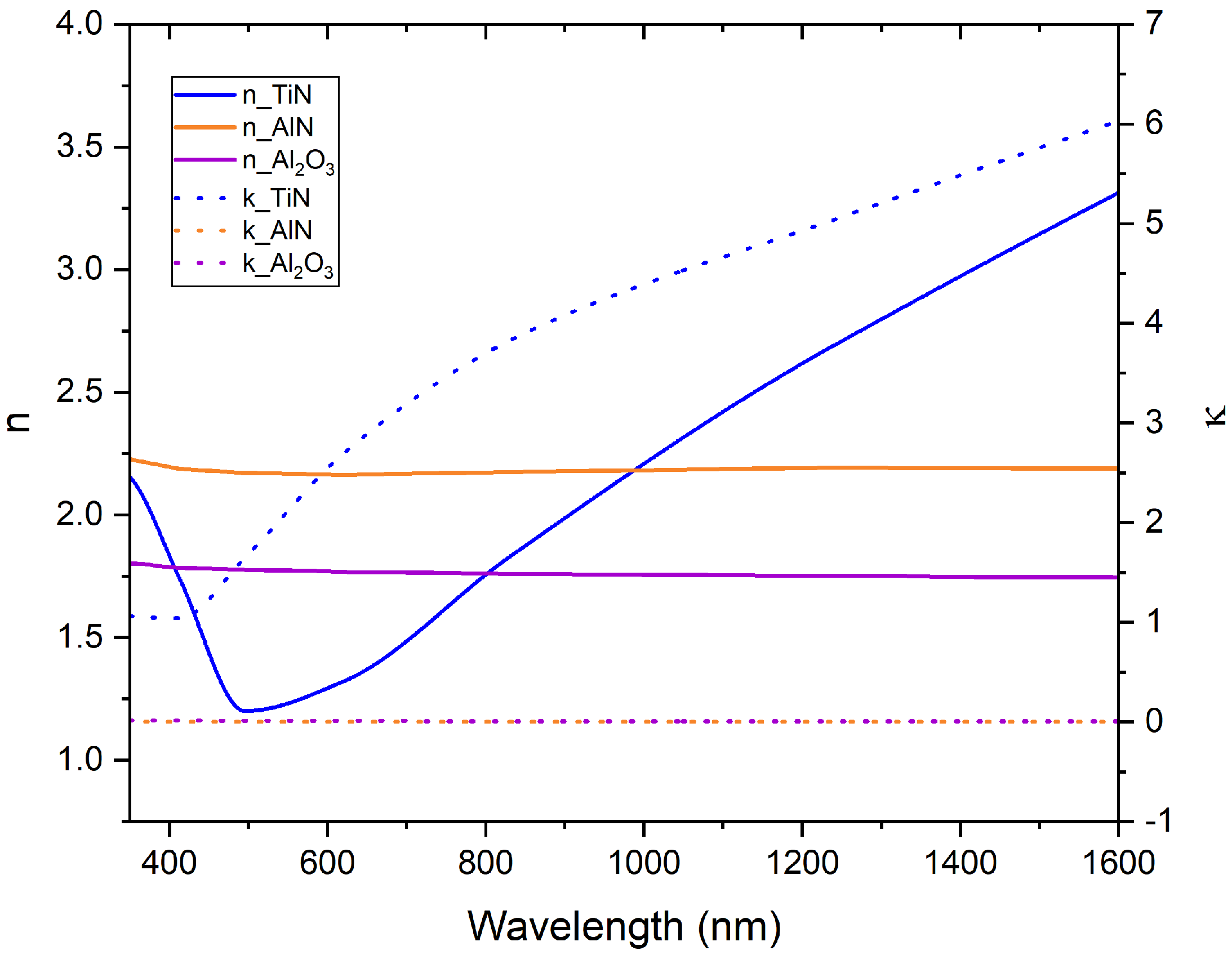
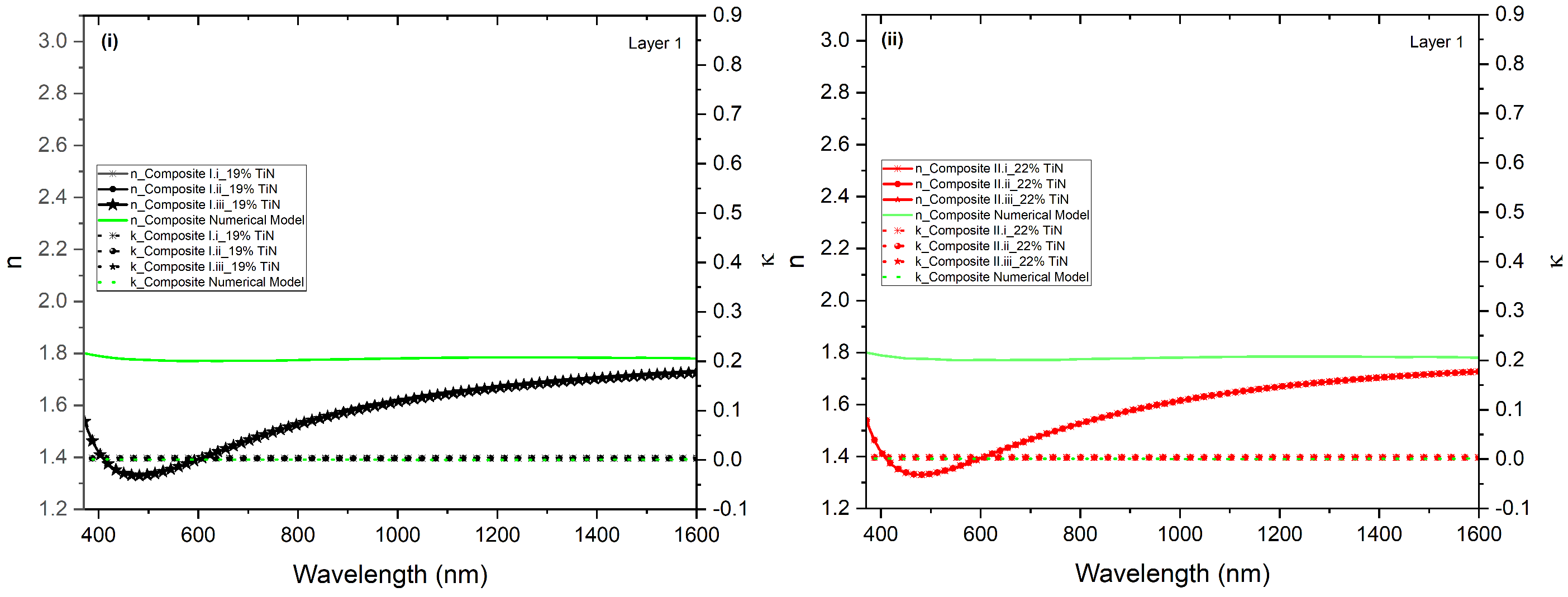
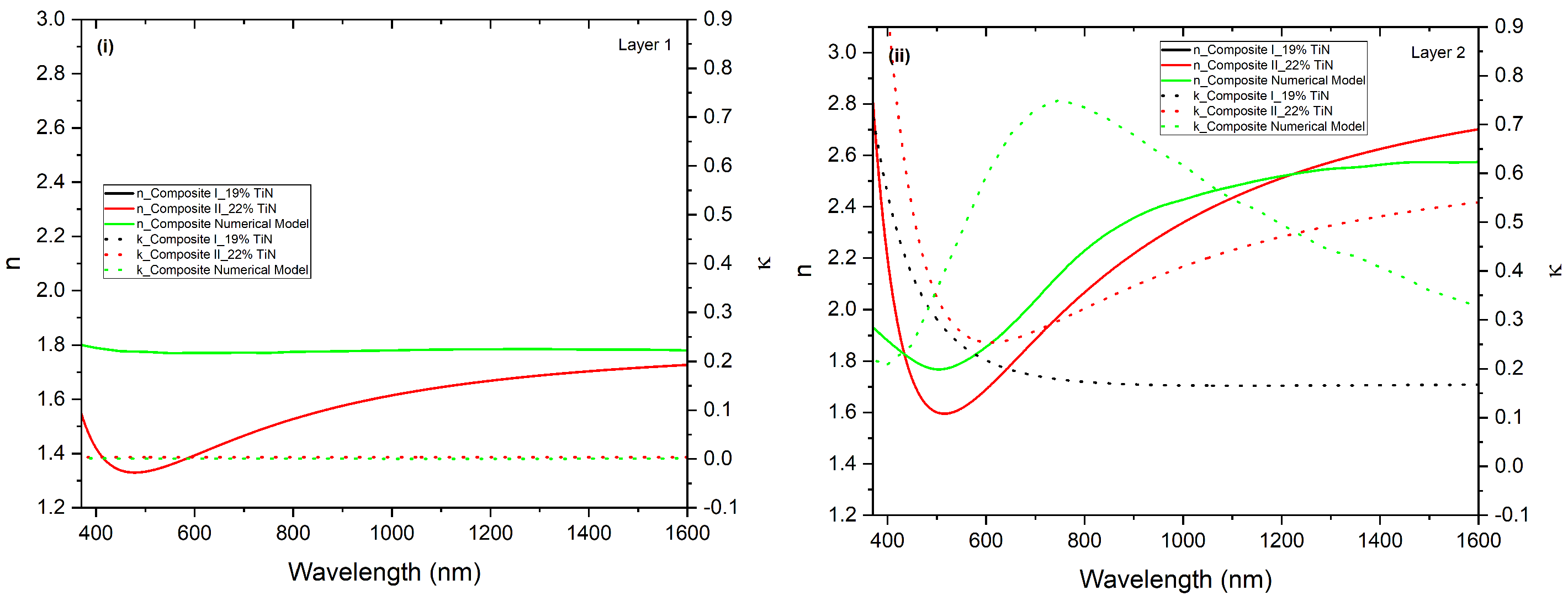
4.3. Analysis of the Retrieved Refractive Index for Composites I and II
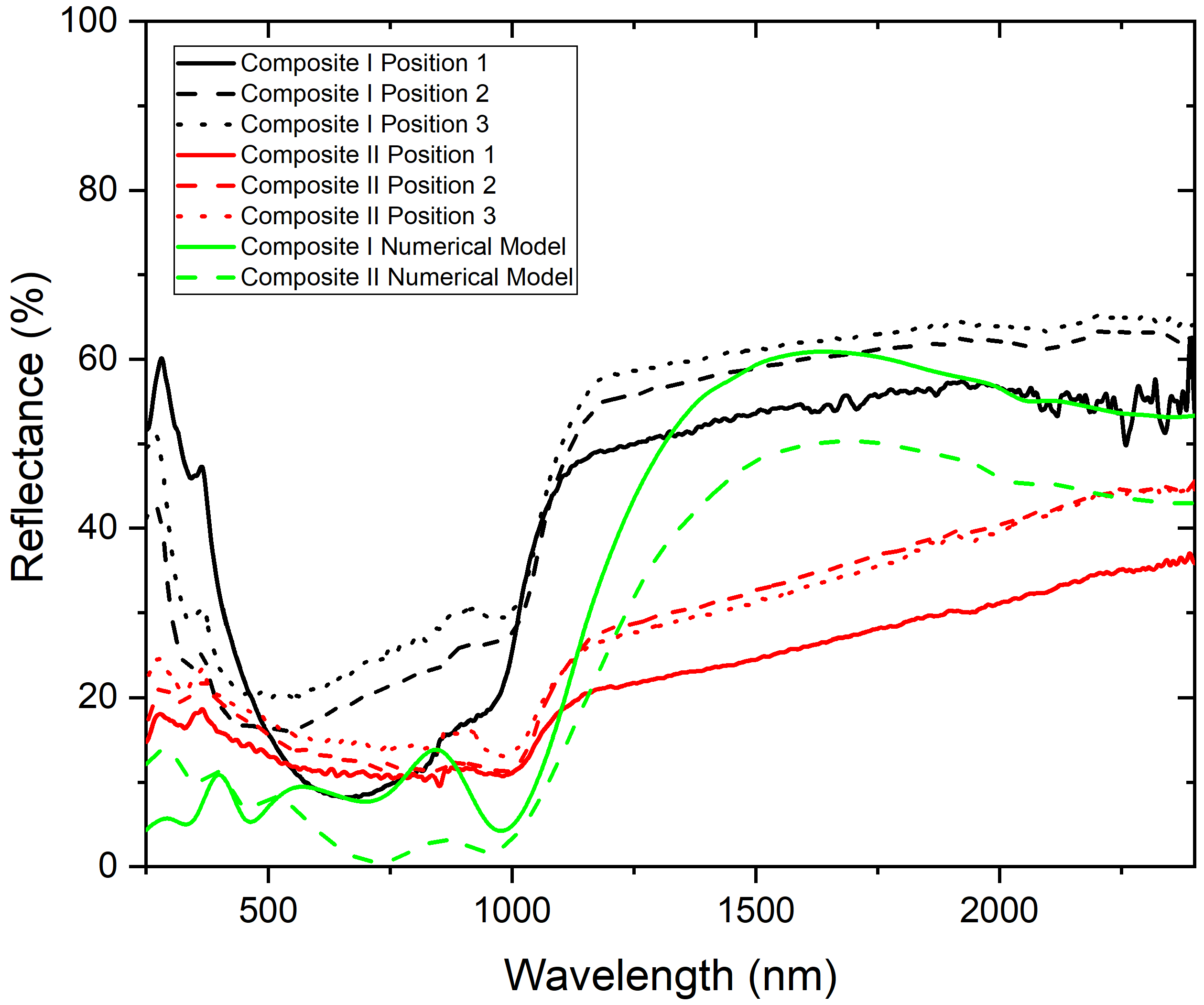
4.4. Analysis of the Reflectance Properties of Composites I and II
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Knöner, G.; Parkin, S.; Nieminen, T.A.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Measurement of the Index of Refraction of Single Microparticles. Phys. Rev. Lett. 2006, 97, 157402. [Google Scholar] [CrossRef]
- Brown, R. Absorption and Scattering of Light by Small Particles. Opt. Acta Int. J. Opt. 1984, 31, 3. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar] [CrossRef]
- Righini, M.; Ghenuche, P.; Cherukulappurath, S.; Myroshnychenko, V.; de Abajo, F.J.G.; Quidant, R. Nano-optical Trapping of Rayleigh Particles and Escherichia coli Bacteria with Resonant Optical Antennas. Nano Lett. 2009, 9, 3387–3391. [Google Scholar] [CrossRef]
- Bendix, P.M.; Oddershede, L.B. Expanding the Optical Trapping Range of Lipid Vesicles to the Nanoscale. Nano Lett. 2011, 11, 5431–5437. [Google Scholar] [CrossRef]
- Khanna, N.; Hachemi, M.E.; Sevilla, R.; Hassan, O.; Morgan, K.; Barborini, E.; Belouettar, S. Multi-physical modelling, design optimisation and manufacturing of a composite dielectric solar absorber. Compos. Part C Open Access 2022, 8, 100282. [Google Scholar] [CrossRef]
- Bilokur, M.; Gentle, A.R.; Arnold, M.D.; Cortie, M.B.; Smith, G.B. High temperature optically stable spectrally-selective Ti1xAlxN-based multilayer coating for concentrated solar thermal applications. Sol. Energy Mater. Sol. Cells 2019, 200, 109964. [Google Scholar] [CrossRef]
- Du, M.; Liu, X.; Hao, L.; Wang, X.; Mi, J.; Jiang, L.; Yu, Q. Microstructure and thermal stability of Al/Ti0.5Al0.5N/Ti0.25Al0.75N/AlN solar selective coating. Sol. Energy Mater. Sol. Cells 2013, 111, 49–56. [Google Scholar] [CrossRef]
- Khanna, N. Metamaterial Design and Elaborative Approach for Efficient Selective Solar Absorber. Ph.D. Thesis, Unilu-University of Luxembourg, Belval, Luxembourg, 2022. [Google Scholar]
- Liao, H.M.; Sodhi, R.N.S.; Coyle, T.W. Surface composition of AlN powders studied by x-ray photoelectron spectroscopy and bremsstrahlung-excited Auger electron spectroscopy. J. Vac. Sci. Technol. A Vac. Surfaces Film. 1993, 11, 2681–2686. [Google Scholar] [CrossRef]
- Méndez, M.G.; Rodríguez, S.M.; Shaji, S.; Krishnan, B.; Pérez, P.B. Structural Properties of AlN Films with Oxygen Content Deposited by Reactive Magnetron Sputtering: XRD and XPS Characterisation. Surf. Rev. Lett. 2011, 18, 23–31. [Google Scholar] [CrossRef]
- Jose, F.; Ramaseshan, R.; Dash, S.; Bera, S.; Tyagi, A.K.; Raj, B. Response of magnetron sputtered AlN films to controlled atmosphere annealing. J. Phys. D Appl. Phys. 2010, 43, 075304. [Google Scholar] [CrossRef]
- Zhang, Y. Characterization of as-received hydrophobic treated AlN powder using XPS. J. Mater. Sci. Lett. 2002, 21, 1603–1605. [Google Scholar] [CrossRef]
- Rohmer, M.M.; Bénard, M.; Poblet, J.M. Structure, Reactivity, and Growth Pathways of Metallocarbohedrenes M8C12 and Transition Metal/Carbon Clusters and Nanocrystals: A Challenge to Computational Chemistry. Chem. Rev. 2000, 100, 495–542. [Google Scholar] [CrossRef]
- Chang, Y.H.; Chiu, C.W.; Chen, Y.C.; Wu, C.C.; Tsai, C.P.; Wang, J.L.; Chiu, H.T. Syntheses of nano-sized cubic phase early transition metal carbides from metal chlorides and n-butyllithium. J. Mater. Chem. 2002, 12, 2189–2191. [Google Scholar] [CrossRef]
- Nelson, J.A.; Wagner, M.J. High Surface Area Mo2C and WC Prepared by Alkalide Reduction. Chem. Mater. 2002, 14, 1639–1642. [Google Scholar] [CrossRef]
- Dobrzański, L.A. Significance of materials science for the future development of societies. J. Mater. Process. Technol. 2006, 175, 133–148. [Google Scholar] [CrossRef]
- Siegenfeld, A.F.; Bar-Yam, Y. An Introduction to Complex Systems Science and Its Applications. Complexity 2020, 2020, 1–16. [Google Scholar] [CrossRef]
- Körkel, S.; Kostina, E.; Bock, H.G.; Schlöder, J.P. Numerical methods for optimal control problems in design of robust optimal experiments for nonlinear dynamic processes. Optim. Methods Softw. 2004, 19, 327–338. [Google Scholar] [CrossRef]
- Tan, G.; Lehmann, A.; Teo, Y.M.; Cai, W. Methods and Applications for Modeling and Simulation of Complex Systems; Springer Nature: Singapore, 2019. [Google Scholar]
- Batsanov, S.S.; Ruchkin, E.D.; Poroshina, I.A. Refractive Indices of Solids; Springer: Berlin/Heidelberg, Germany, 2016; Available online: https://www.ebook.de/de/product/26683914/stepan_s_batsanov_evgeny_d_ruchkin_inga_a_poroshina_refractive_indices_of_solids.html (accessed on 19 January 2025).
- Bahaa, E.A.; Saleh, M.C.T. Fundamentals of Photonics; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Mayerhöfer, T.G.; Pahlow, S.; Popp, J. The Bouguer-Beer-Lambert Law: Shining Light on the Obscure. ChemPhysChem 2020, 21, 2029–2046. [Google Scholar] [CrossRef]
- Zhang, K.; Hao, L.; Du, M.; Mi, J.; Wang, J.; Meng, J. A review on thermal stability and high temperature induced ageing mechanisms of solar absorber coatings. Renew. Sustain. Energy Rev. 2017, 67, 1282–1299. [Google Scholar] [CrossRef]
- Pérez, I.H. Multilayer Selective Coatings for High Temperature Solar Applications; Editions Universitaires Européennes: Londonm UK, 2017; Available online: https://www.ebook.de/de/product/29245585/irene_heras_perez_multilayer_selective_coatings_for_high_temperature_solar_applications.html (accessed on 19 January 2025).
- Chen, Z.; Boström, T. Electrophoretically deposited carbon nanotube spectrally selective solar absorbers. Sol. Energy Mater. Sol. Cells 2016, 144, 678–683. [Google Scholar] [CrossRef]
- Striebel, M.; Wrachtrup, J.; Gerhardt, I. Absorption and Extinction Cross Sections and Photon Streamlines in the Optical Near-field. Sci. Rep. 2017, 7, 15420. [Google Scholar] [CrossRef] [PubMed]
- Garnett, J.C.M. Colours in metal glasses and in metallic films. Philos. Trans. R. Soc 1904, 203, 385–420. [Google Scholar] [CrossRef]
- Doyle, W.T. Optical properties of a suspension of metal spheres. Phys. Rev. B 1989, 39, 9852–9858. [Google Scholar] [CrossRef]
- Markel, V.A. ntroduction to the Maxwell Garnett approximation tutorial. J. Opt. Soc. Am. A 2016, 33, 1244. [Google Scholar] [CrossRef]
- Nayak, J.K.; Chaudhuri, P.R.; Ratha, S.; Sahoo, M.R. A comprehensive review on effective medium theories to find effective dielectric constant of composites. J. Electromagn. Waves Appl. 2022, 37, 1–41. [Google Scholar] [CrossRef]
- Orfanidis, S.J. Electromagnetic Waves and Antennas. 2016. Available online: https://eceweb1.rutgers.edu/~orfanidi/ewa/ (accessed on 19 January 2025).
- Nicolson, A.M.; Ross, G.F. Measurement of the Intrinsic Properties of Materials by Time-Domain Techniques. IEEE Trans. Instrum. Meas. 1970, 19, 377–382. [Google Scholar] [CrossRef]
- Smith, D.R.; Vier, D.C.; Koschny, T.; Soukoulis, C.M. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys. Rev. E 2005, 71, 036617. [Google Scholar] [CrossRef]
- Lissberger, P.H. Ellipsometry and polarised light. Nature 1977, 269, 270. [Google Scholar] [CrossRef]
- Bakker, J.; Bryntse, G.; Arwin, H. Determination of refractive index of printed and unprinted paper using spectroscopic ellipsometry. Thin Solid Film. 2004, 455-456, 361–365. [Google Scholar] [CrossRef]
- Yusoh, R.; Horprathum, M.; Eiamchai, P.; Chindaudom, P.; Aiempanakit, K. Determination of Optical and Physical Properties of ZrO2 Films by Spectroscopic Ellipsometry. Procedia Eng. 2012, 32, 745–751. [Google Scholar] [CrossRef]


| Etching Time(s) | (at.%) | (at.%) | (at.%) | (at.%) | (at.%) | (at.%) | |
|---|---|---|---|---|---|---|---|
| 0 | 30.89 | 24.06 | 19.32 | 25.72 | 0 | 0 | Rows ignored-Presence of Carbon. |
| 60 | 43.74 | 1.87 | 31.77 | 22.60 | 0 | 0 | |
| 120 | 45.63 | 0 | 33.04 | 21.31 | 0 | 0 | Layer 1: , |
| 180 | 45.91 | 0 | 33.25 | 20.82 | 0 | 0 | |
| 240 | 45.68 | 0 | 33.24 | 21.39 | 0 | 0 | |
| 300 | 45.68 | 0 | 32.74 | 21.39 | 0 | 0 | |
| 600 | 44.12 | 0 | 25.66 | 30.21 | 0 | 0 | |
| 900 | 41.36 | 0 | 13.42 | 45.21 | 0 | 0 | |
| 1200 | 36.11 | 0 | 11.05 | 44.01 | 6.80 | 2.00 | Layer 2: , , |
| 1800 | 23.85 | 0 | 10.25 | 30.32 | 31.13 | 4.42 | |
| 2400 | 14.99 | 0 | 7.10 | 18.65 | 55.61 | 3.63 | |
| 3000 | 8.27 | 0 | 3.78 | 10.30 | 75.13 | 2.49 | |
| 3600 | 4.47 | 0 | 2.94 | 5.36 | 85.89 | 1.23 | |
| 4200 | 2.00 | 0 | 1.28 | 2.55 | 93.47 | 0.67 | |
| 4800 | 1.29 | 0 | 0.30 | 0.83 | 97.56 | 0 | Subtracted: and content |
| 5400 | 0.77 | 0 | 0 | 0.49 | 98.73 | 0 | |
| 6000 | 0 | 0 | 0 | 0.19 | 99.80 | 0 | |
| 6600 | 0 | 0 | 0 | 0 | 100 | 0 | Rows ignored-Silicon substrate. |
| 7200 | 0 | 0 | 0 | 0 | 100 | 0 | |
| 9000 | 0 | 0 | 0 | 0 | 100 | 0 |
| Spectroscopic Ellipsometer Model | Composite I | Composite II | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample i | Sample ii | Sample iii | Sample i | Sample ii | Sample iii | |||||||
| Surface Roughness | 68.5 nm | 80 nm | 64.5 nm | 115.5 nm | 79.2 nm | 71.5 nm | ||||||
| Layer 1 Cauchy Transparent | 48.3 nm | 55 nm | 55 nm | 44 nm | 84.8 nm | 91.4 nm | ||||||
| Layer 2 Cauchy Absorbent | 192.5 nm | 180 nm | 198 nm | 281.8 nm | 294.6 nm | 296.4 nm | ||||||
| 10 nm | ||||||||||||
| Si Substrate | 300 | |||||||||||
| Fitting parameter | layer1 | layer2 | layer1 | layer2 | layer1 | layer2 | layer1 | layer2 | layer1 | layer2 | layer1 | layer2 |
| A (1) | 1.809 | 2.973 | 1.809 | 2.973 | 1.809 | 2.973 | 1.809 | 2.973 | 1.809 | 2.973 | 1.809 | 296.43 |
| B () | −0.219 | −0.732 | −0.219 | −0.732 | −0.219 | −0.732 | −0.219 | −0.732 | −0.219 | −0.732 | −0.219 | −0.732 |
| C () | 0.025 | 0.097 | 0.025 | 0.097 | 0.025 | 0.097 | 0.025 | 0.097 | 0.025 | 0.097 | 0.025 | 0.097 |
| D (1) | 0.003 | 0.0003 | 0.003 | 0.288 | 0.003 | 0.376 | 0.003 | 0.686 | 0.003 | 0.704 | 0.003 | 0.667 |
| E () | 0 | 0.092 | 0 | −0.02 | 0 | −0.167 | 0 | −0.314 | 0 | −0.316 | 0 | −0.4 |
| F () | 0 | −0.002 | 0 | 0.006 | 0 | 0.027 | 0 | 0.057 | 0 | 0.064 | 0 | 0.095 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Hachemi, M.; Khanna, N.; Barborini, E. Spectroscopic Ellipsometry and Wave Optics: A Dual Approach to Characterizing TiN/AlN Composite Dielectrics. Crystals 2025, 15, 143. https://doi.org/10.3390/cryst15020143
El Hachemi M, Khanna N, Barborini E. Spectroscopic Ellipsometry and Wave Optics: A Dual Approach to Characterizing TiN/AlN Composite Dielectrics. Crystals. 2025; 15(2):143. https://doi.org/10.3390/cryst15020143
Chicago/Turabian StyleEl Hachemi, Mohamed, Nikhar Khanna, and Emanuele Barborini. 2025. "Spectroscopic Ellipsometry and Wave Optics: A Dual Approach to Characterizing TiN/AlN Composite Dielectrics" Crystals 15, no. 2: 143. https://doi.org/10.3390/cryst15020143
APA StyleEl Hachemi, M., Khanna, N., & Barborini, E. (2025). Spectroscopic Ellipsometry and Wave Optics: A Dual Approach to Characterizing TiN/AlN Composite Dielectrics. Crystals, 15(2), 143. https://doi.org/10.3390/cryst15020143







