Mathematical Modeling to Predict the Formation of Micrometer-Scale Crystals Using Reverse Anti-Solvent Crystallization
Abstract
1. Introduction
2. The Establishment of Mathematical Models
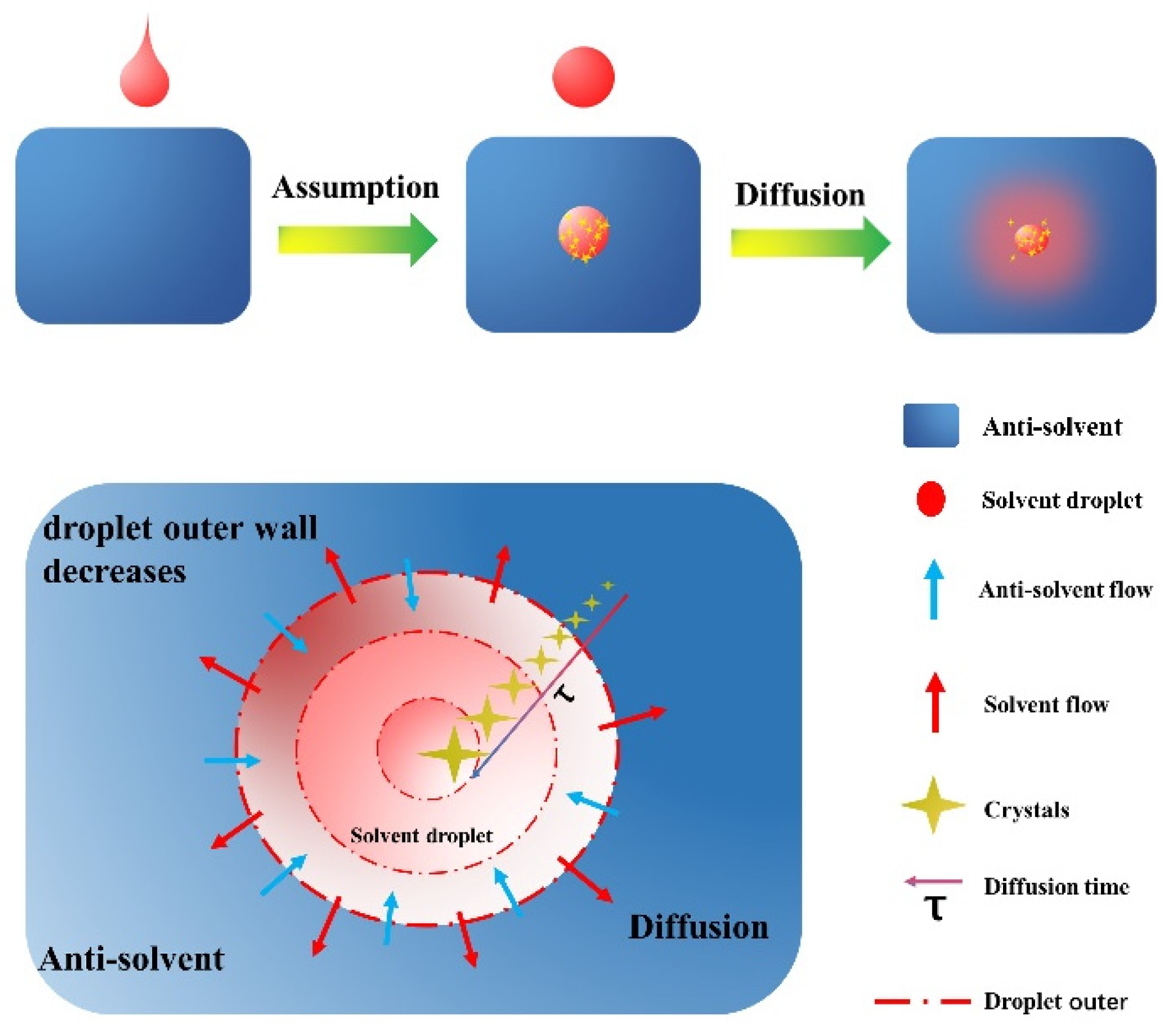
2.1. Prelude to the Mathematical Model
2.2. Mechanism Analysis and Mathematical Model Establishment
- (1)
- Each dripping droplet is spherical. When the spherical droplet completely enters the anti-solvent, the solvent could diffuse. At this time, crystallization begins to occur.
- (2)
- The solvent diffusion time in each droplet is the same as the time used for crystal growth, and the crystal nucleus growth time is ignored.
- (3)
- No secondary nucleation occurred in each drop of solution.
- (4)
- The supersaturation as the driving force for crystal growth keeps a constant value when crystal will occur in each solvent droplet.
- (5)
- The crystal growth rate is only related to the temperature and supersaturation.
2.3. Experiment
2.3.1. Materials
- (1)
- The main materials include a φ3 mm silicone tube, a peristaltic pump, a beaker, a Buchner funnel and vacuum filtration device, a small reactor, a set of stirring devices, and two sets of heating devices (ovens);
- (2)
- The test instruments include a scanning electron microscope (Nano SEM 450, Nova) and a laser particle size analyzer (MS2000, Malvern);
- (3)
- The experiment reagents include deionized water, anhydrous ethanol (analytically pure 99.9%), and NaCl (analytically pure).
2.3.2. Experiment Methods
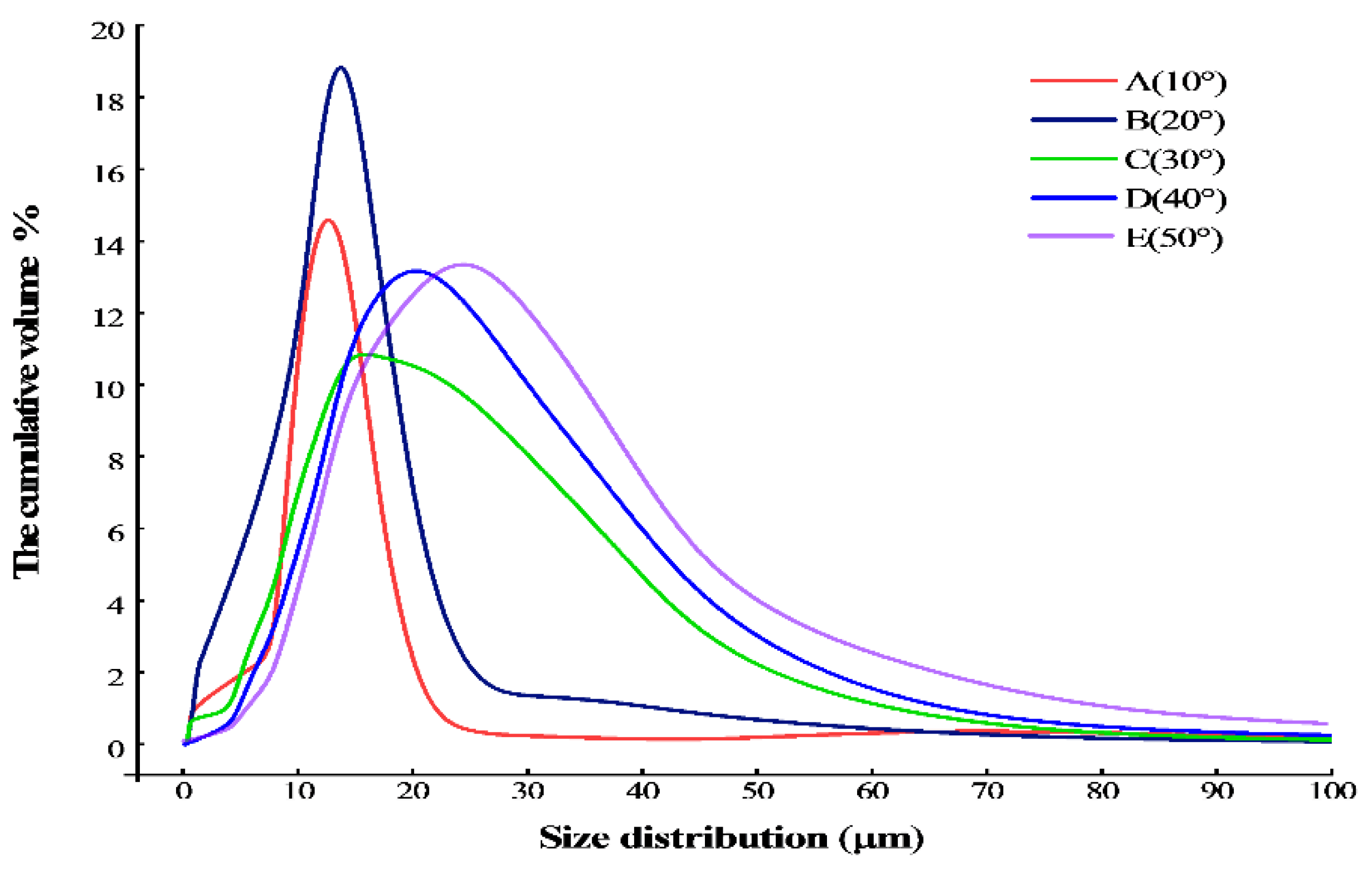
3. Result
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, L.; Song, Y.; Li, B.; Guan, G.; Jiang, Y. A modified method for modelling, optimization and control of an anti-solvent crystallization process. Chem. Eng. Sci. 2020, 211, 115253. [Google Scholar] [CrossRef]
- Power, G.; Hou, G.; Kamaraju, V.K.; Morris, G.; Zhao, Y.; Glennon, B. Design and optimization of a multistage continuous cooling mixed suspension, mixed product removal crystallizer. Chem. Eng. Sci. 2015, 133, 125–139. [Google Scholar] [CrossRef]
- Nayhouse, M.; Tran, A.; Kwon, J.S.-I.; Crose, M.; Orkoulas, G.; Christofides, P.D. Modeling and control of ibuprofen crystal growth and size distribution. Chem. Eng. Sci. 2015, 134, 414–422. [Google Scholar] [CrossRef]
- Ghadipasha, N.; Romagnoli, J.A.; Tronci, S.; Baratti, R. A model-based approach for controlling particle size distribution in combined cooling-antisolvent crystallization processes. Chem. Eng. Sci. 2018, 190, 260–272. [Google Scholar] [CrossRef]
- Liu, Y.C.; Acevedo, D.; Yang, X.; Naimi, S.; Wu, W.-L.; Pavurala, N.; Nagy, Z.K.; O’Connor, T.F. Population Balance Model Development Verification and Validation of Cooling Crystallization of Carbamazepine. Cryst. Growth Des. 2020, 20, 5235–5250. [Google Scholar] [CrossRef]
- Galán, O.; Grosso, M.; Baratti, R.; Romagnoli, J.A. Stochastic approach for the calculation of anti-solvent addition policies in crystallization operations: An application to a bench-scale semi-batch crystallizer. Chem. Eng. Sci. 2010, 65, 1797–1810. [Google Scholar] [CrossRef]
- Prasad, R.; Dalvi, S.V. Sonocrystallization: Monitoring and controlling crystallization using ultrasound. Chem. Eng. Sci. 2020, 226, 115911. [Google Scholar] [CrossRef]
- Cogoni, G.; de Souza, B.P.; Frawley, P.J. Particle Size Distribution and yield control in continuous Plug Flow Crystallizers with recycle. Chem. Eng. Sci. 2015, 138, 592–599. [Google Scholar] [CrossRef]
- Jiang, X.; Shao, Y.; Sheng, L.; Li, P.; He, G. Membrane Crystallization for Process Intensification and Control: A Review. Engineering 2021, 7, 50–62. [Google Scholar] [CrossRef]
- Kovacic, B.; Vrecer, F.; Planinsek, O. Spherical crystallization of drugs. Acta Pharm. 2012, 62, 1–14. [Google Scholar] [CrossRef]
- Toldy, A.I.; Badruddoza, A.Z.M.; Zheng, L.; Hatton, T.A.; Gunawan, R.; Rajagopalan, R.; Khan, S.A. Spherical Crystallization of Glycine from Monodisperse Microfluidic Emulsions. Cryst. Growth Des. 2012, 12, 3977–3982. [Google Scholar] [CrossRef]
- Chen, M.; Liu, X.; Yu, C.; Yao, M.; Xu, S.; Tang, W.; Song, X.; Dong, W.; Wang, G.; Gong, J. Strategy of selecting solvent systems for spherical agglomeration by the Lifshitz-van der Waals acid-base approach. Chem. Eng. Sci. 2020, 220, 115613. [Google Scholar] [CrossRef]
- Li, L.; Zhao, S.; Xin, Z. Three-solvent spherical crystallization method with a model drug: Clopidogrel hydrogen sulfate. Chem. Eng. Sci. 2020, 212, 115001. [Google Scholar] [CrossRef]
- Wu, B.; Li, J.; Li, C.; He, J.; Luo, P. Antisolvent crystallization intensified by a jet crystallizer and a method for investigating crystallization kinetics. Chem. Eng. Sci. 2020, 211, 115259. [Google Scholar] [CrossRef]
- Holaň, J.; Ridvan, L.; Billot, P.; Štěpánek, F. Design of co-crystallization processes about particle size distribution. Chem. Eng. Sci. 2015, 128, 36–43. [Google Scholar] [CrossRef]
- Unno, J.; Hirasawa, I. Partial Seeding Policy for Controlling the Crystal Quality in Batch Cooling Crystallization. Chem. Eng. Technol. 2020, 43, 1065–1071. [Google Scholar] [CrossRef]
- Ferguson, S.; Morris, G.; Hao, H.; Barrett, M.; Glennon, B. Characterization of the anti-solvent batch, plug flow and MSMPR crystallization of benzoic acid. Chem. Eng. Sci. 2013, 104, 44–54. [Google Scholar] [CrossRef]
- Park, Y.; Hong, M.; Koo, J.Y.; Lee, M.; Lee, J.; Moon, D.J.; Sohn, S.H.; Joo, T.; Lim, W.T.; Lim, H.; et al. Reverse Anti-solvent Crystallization Process for the Facile Synthesis of Zinc Tetra(4-pyridyl)porphyrin Single Crystalline Cubes. Sci. Rep. 2017, 7, 2582. [Google Scholar] [CrossRef]
- Maghsoodi, M.; Nokhodchi, A. Agglomeration of Celecoxib by Quasi Emulsion Solvent Diffusion Method: Effect of Stabilizer. Adv. Pharm. Bull. 2016, 6, 607–616. [Google Scholar] [CrossRef]
- Khurshid, M.F.; Hussain, T.; Masood, R.; Hussain, N. Development and evaluation of a controlled drug delivery wound dressing based on polymeric porous microspheres. J. Ind. Text. 2016, 46, 986–999. [Google Scholar] [CrossRef]
- Nagula, R.L.; Wairkar, S. Cellulose microsponges based gel of naringenin for atopic dermatitis: Design, optimization, in vitro and in vivo investigation. Int. J. Biol. Macromol. 2020, 164, 717–725. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Wang, J. Preparation and characterization of spherical submicron ε-CL-20 via green mechanical demulsification. J. Energetic Mater. 2019, 37, 475–483. [Google Scholar] [CrossRef]
- Chen, H.; Paul, S.; Xu, H.; Wang, K.; Mahanthappa, M.K.; Sun, C.C. Reduction of Punch-Sticking Propensity of Celecoxib by Spherical Crystallization via Polymer Assisted Quasi-Emulsion Solvent Diffusion. Mol. Pharm. 2020, 17, 1387–1396. [Google Scholar] [CrossRef]
- Wang, J.; Cao, W.; Zhu, L.; Wang, J.; Lakerveld, R. Emulsion-assisted cooling crystallization of ibuprofen. Chem. Eng. Sci. 2020, 226, 115861. [Google Scholar] [CrossRef]
- Garg, N.; Tona, R.; Martin, P.; Martin-Soladana, P.M.; Ward, G.; Douillet, N.; Lai, D. Seeded droplet microfluidic system for small molecule crystallization. Lab Chip 2020, 20, 1815–1826. [Google Scholar] [CrossRef]
- Vicent, V.; Ndoye, F.-T.; Verboven, P.; Nicolaï, B.; Alvarez, G. Modeling ice recrystallization in frozen carrot tissue during storage under dynamic temperature conditions. J. Food Eng. 2020, 278, 109911. [Google Scholar] [CrossRef]
- Bhoi, S.; Sarkar, D. Hybrid finite volume and Monte Carlo method for solving multi-dimensional population balance equations in crystallization processes. Chem. Eng. Sci. 2020, 217, 115511. [Google Scholar] [CrossRef]
- Tatsukawa, S.; Kadota, K.; Yoshida, M.; Shirakawa, Y. Development of quantifying supersaturation to determine the effect of the anti-solvent on precipitation in liquid-liquid interfacial crystallization. J. Mol. Liq. 2020, 309, 113097. [Google Scholar] [CrossRef]
- Peña, R.; Burcham, C.L.; Jarmer, D.J.; Ramkrishna, D.; Nagy, Z.K. Modeling and optimization of spherical agglomeration in suspension through a coupled population balance model. Chem. Eng. Sci. 2017, 167, 66–77. [Google Scholar] [CrossRef]






| NO. | Concentration g/g (Water) | Dripping Droplet Velocity μL/min | Agitation Rate rpm/min | Temperature °C |
|---|---|---|---|---|
| 1 | 0.36 | 100 | 500 | 10 |
| 2 | 0.36 | 100 | 500 | 20 |
| 3 | 0.36 | 100 | 500 | 30 |
| 4 | 0.36 | 100 | 500 | 40 |
| 5 | 0.36 | 100 | 500 | 50 |
| 1 | 1.257 | 7.279 | 14.012 | 3.738 | 1.752 |
| 2 | 1.651 | 8.745 | 20.601 | 4.220 | 2.161 |
| 3 | 1.687 | 11.517 | 24.690 | 4.745 | 1.997 |
| 4 | 4.822 | 15.637 | 32.965 | 6.814 | 1.799 |
| 5 | 7.495 | 19.480 | 39.669 | 9.131 | 1.653 |
| Parameter [units] | Description | Value |
|---|---|---|
| [m3/mol] | The molar volume of liquid | 1.8 × 10−5 |
| [mol/m3] | Droplet concentration | 55.6 × 103 |
| [m2/s] | Diffusion coefficient | 2 × 10−9 |
| [m/s] | Growth rate constant | 7.1150 × 10−5 |
| [-] | Growth rate order | 1.079 |
| [kJ/mol] | Activation energy for growth | 1.9023 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, F.; Wen, X.; Zhang, Y.; Wang, J.; Liu, Y. Mathematical Modeling to Predict the Formation of Micrometer-Scale Crystals Using Reverse Anti-Solvent Crystallization. Crystals 2025, 15, 145. https://doi.org/10.3390/cryst15020145
Wang J, Wang F, Wen X, Zhang Y, Wang J, Liu Y. Mathematical Modeling to Predict the Formation of Micrometer-Scale Crystals Using Reverse Anti-Solvent Crystallization. Crystals. 2025; 15(2):145. https://doi.org/10.3390/cryst15020145
Chicago/Turabian StyleWang, Jianhua, Fawei Wang, Xu Wen, Yankang Zhang, Jiapeng Wang, and Yucun Liu. 2025. "Mathematical Modeling to Predict the Formation of Micrometer-Scale Crystals Using Reverse Anti-Solvent Crystallization" Crystals 15, no. 2: 145. https://doi.org/10.3390/cryst15020145
APA StyleWang, J., Wang, F., Wen, X., Zhang, Y., Wang, J., & Liu, Y. (2025). Mathematical Modeling to Predict the Formation of Micrometer-Scale Crystals Using Reverse Anti-Solvent Crystallization. Crystals, 15(2), 145. https://doi.org/10.3390/cryst15020145






