Reconfiguration of Nematic Disclinations in Plane-Parallel Confinements
Abstract
1. Introduction
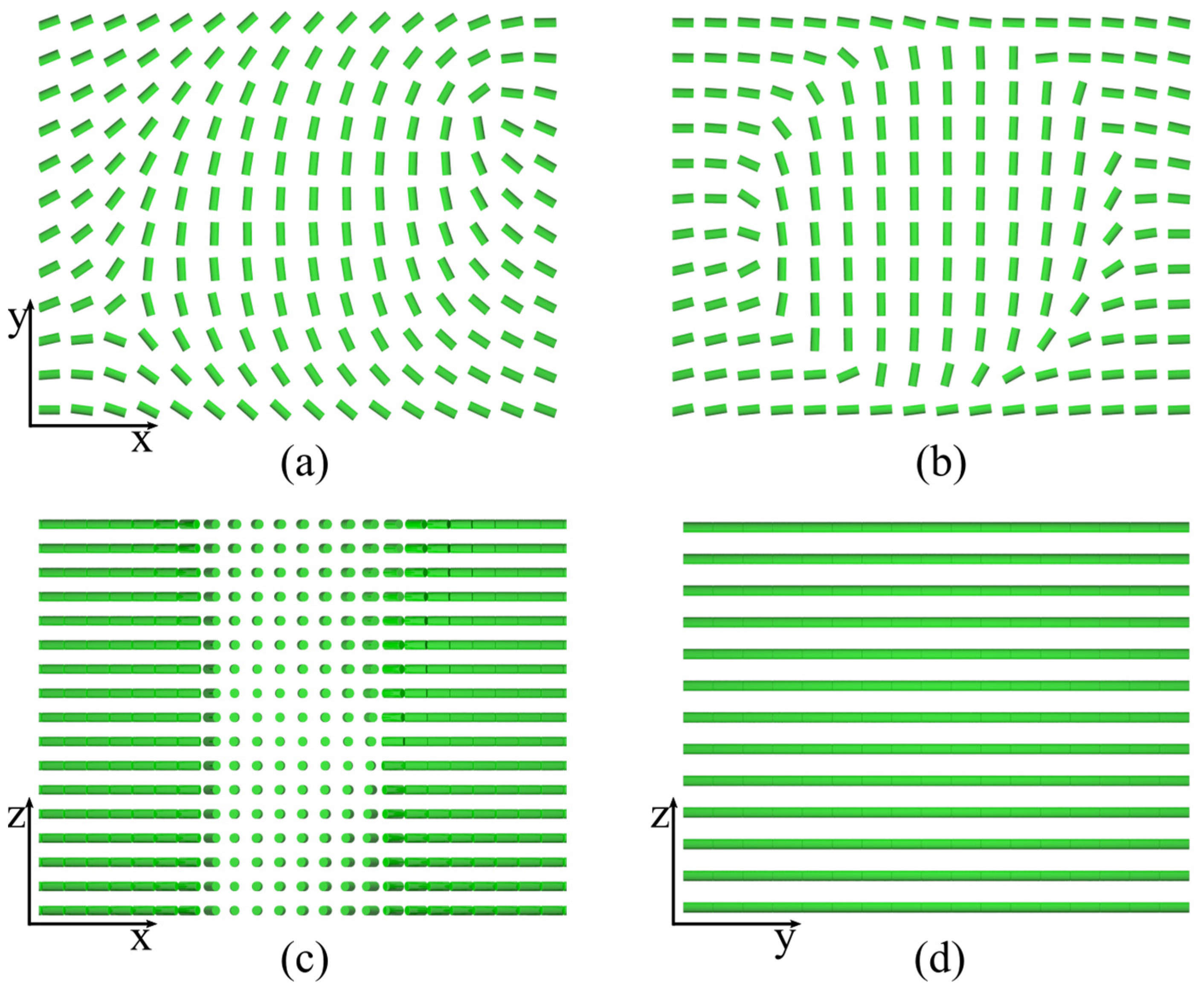
2. Methods
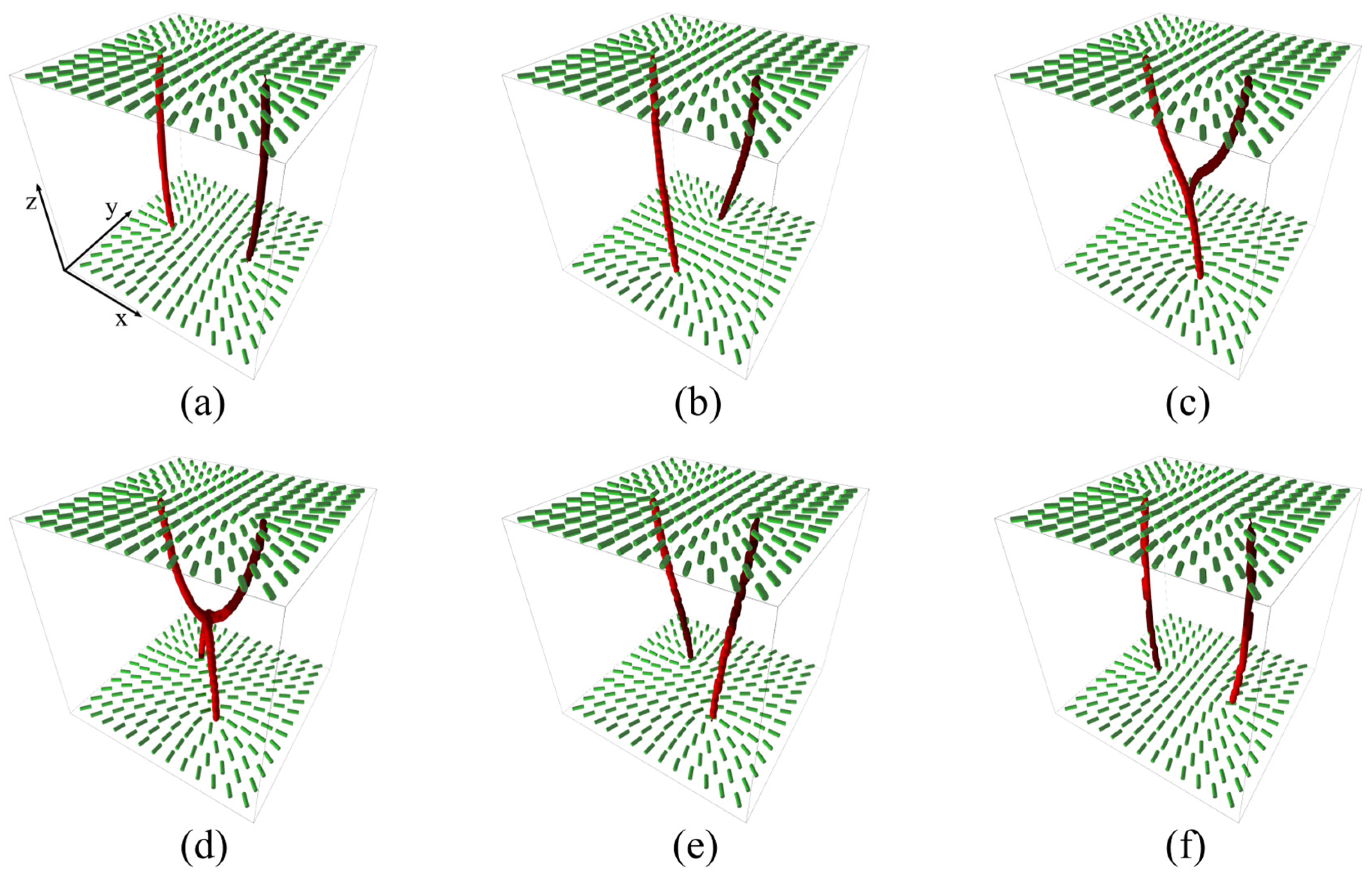
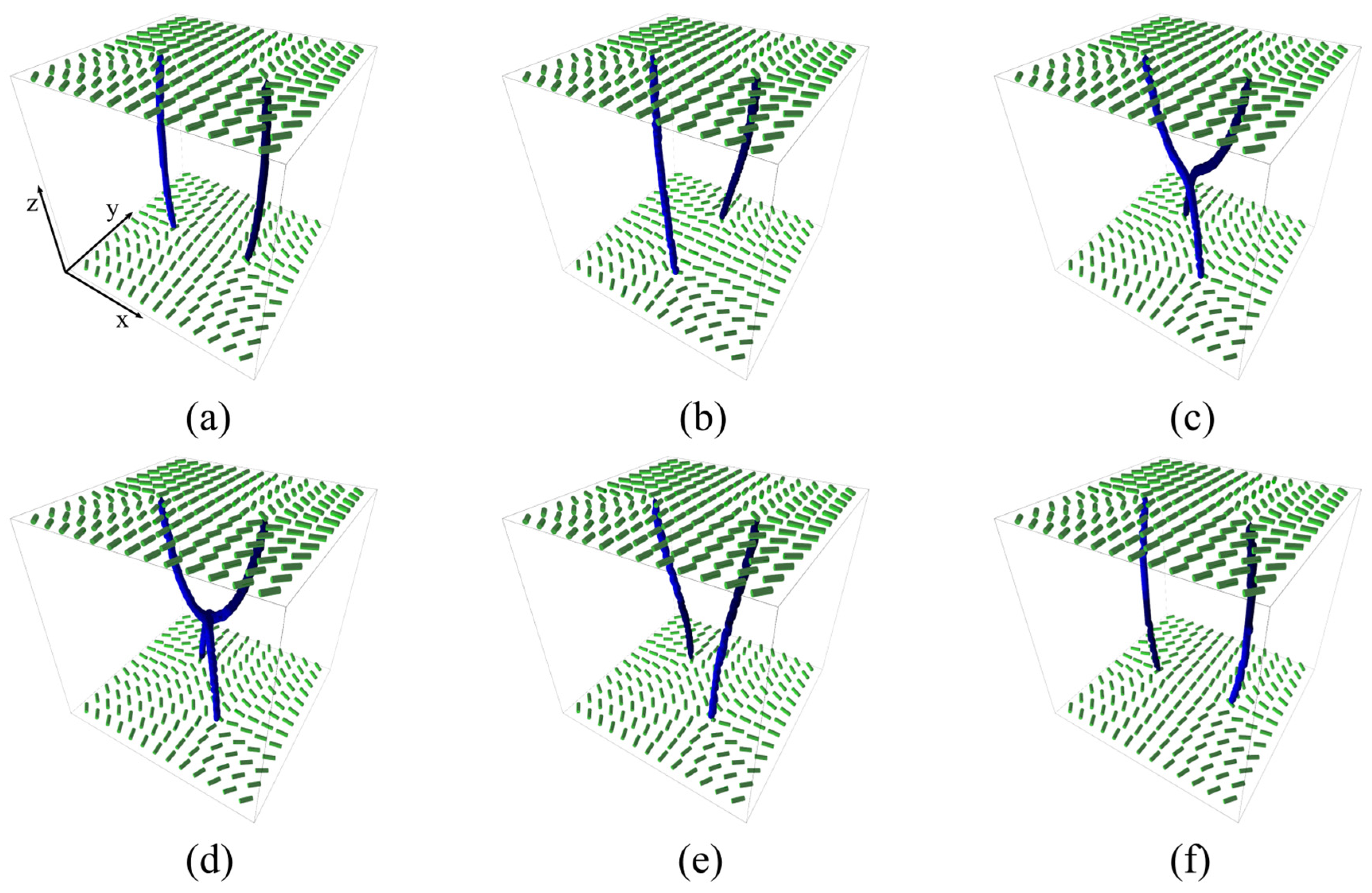
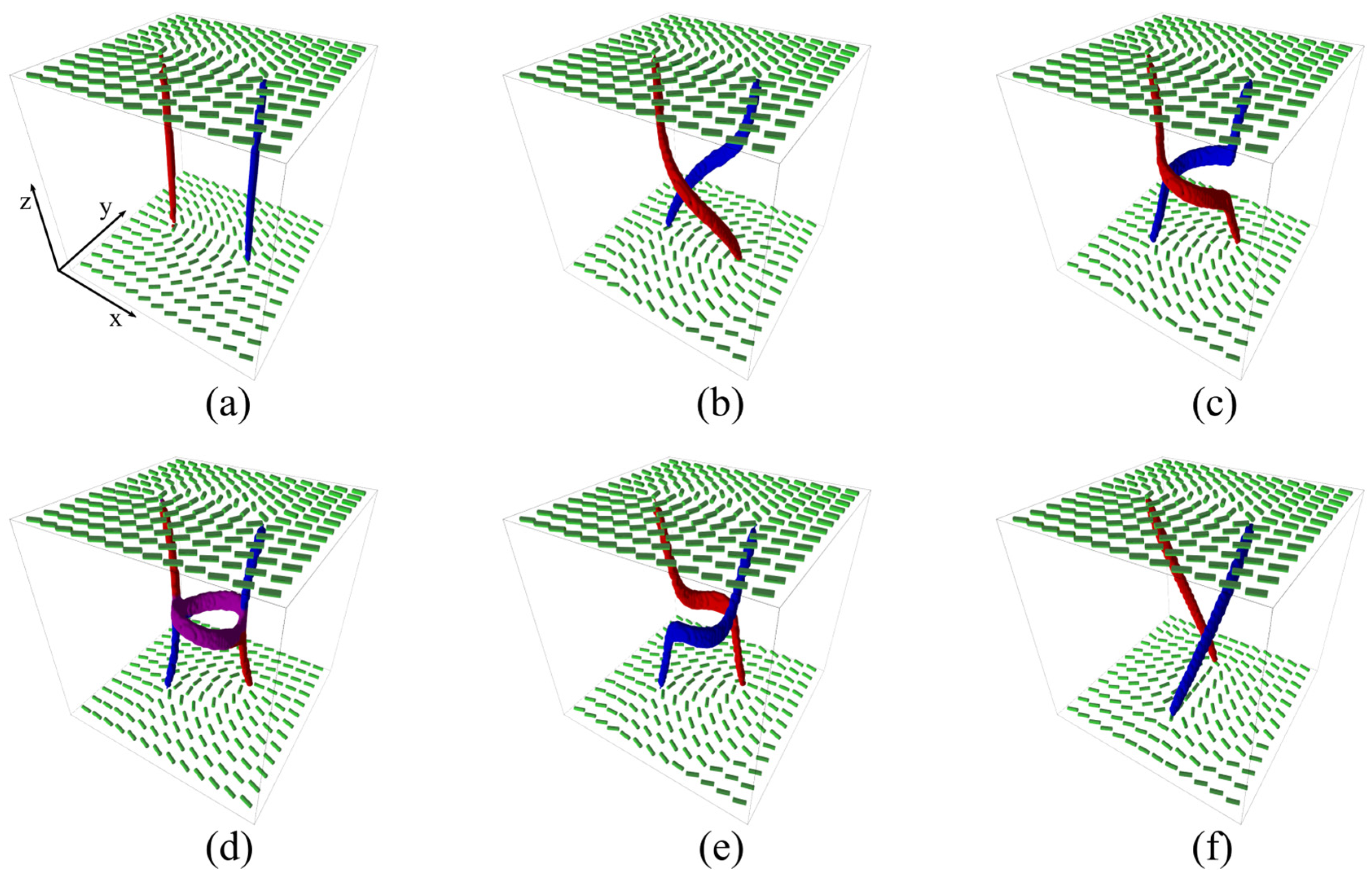
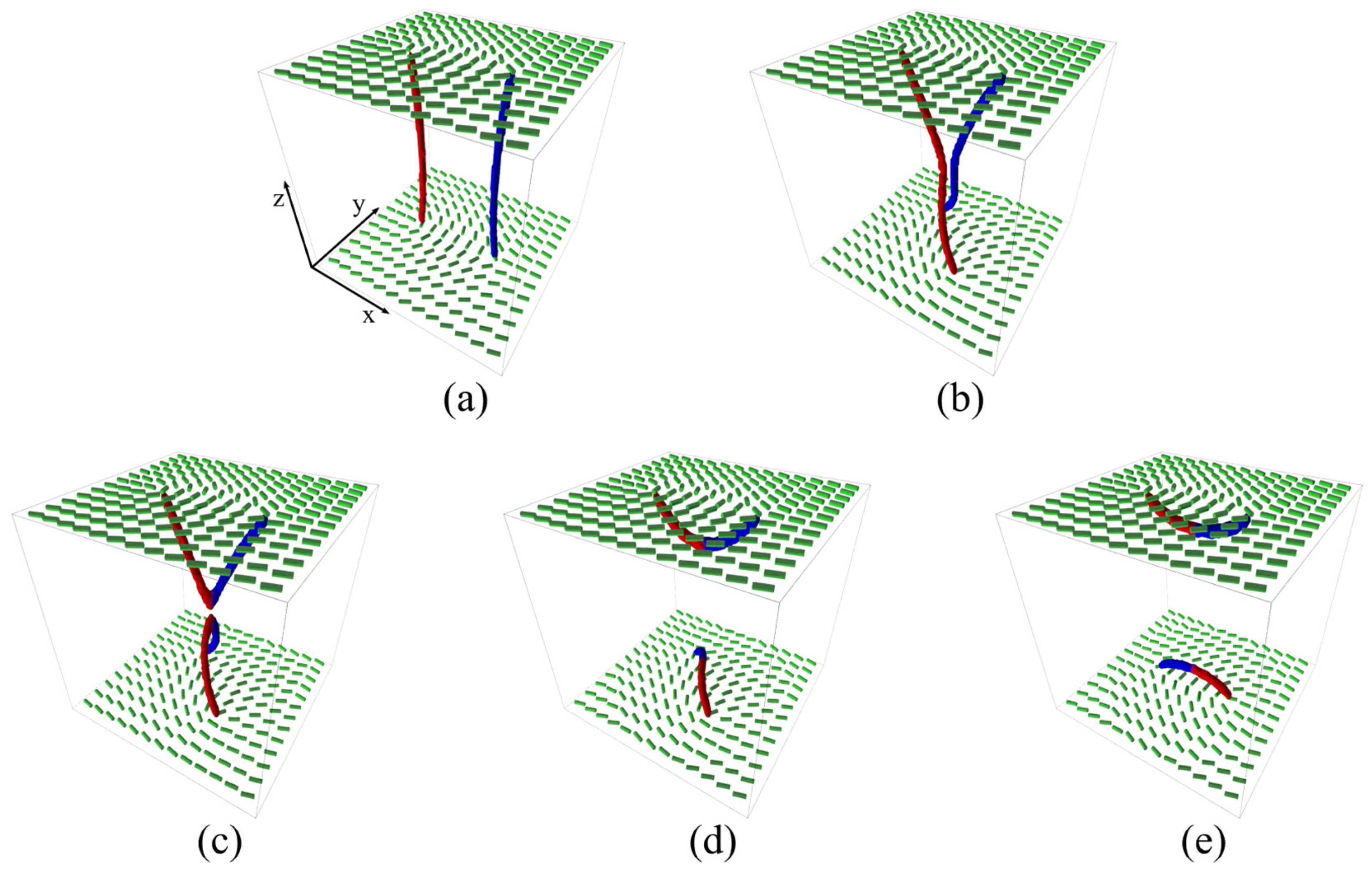
3. Results
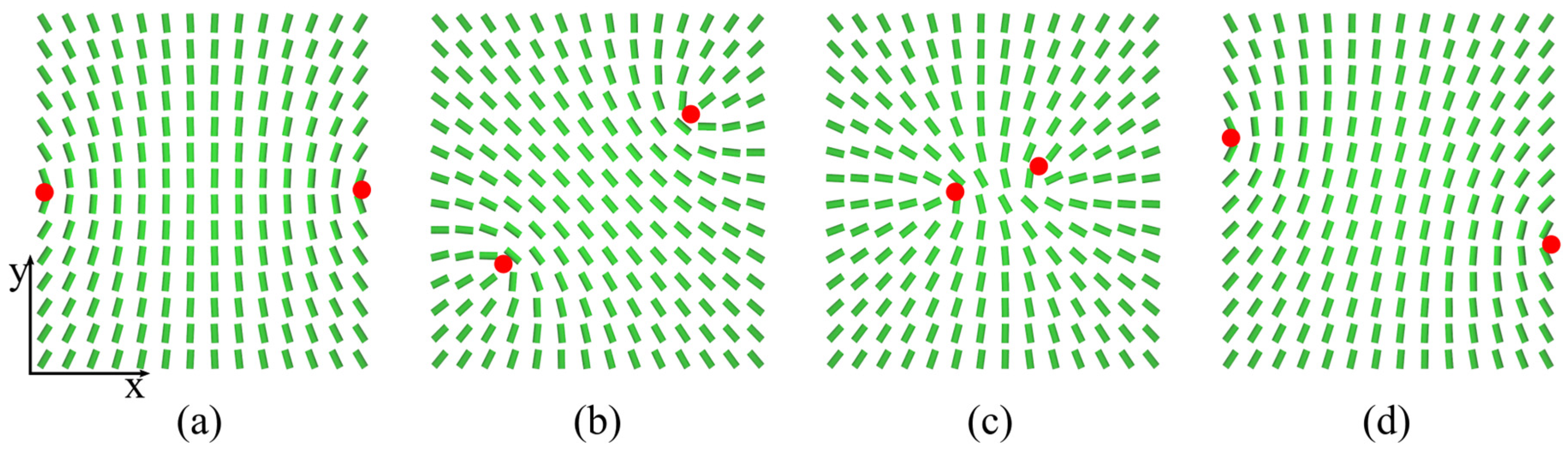
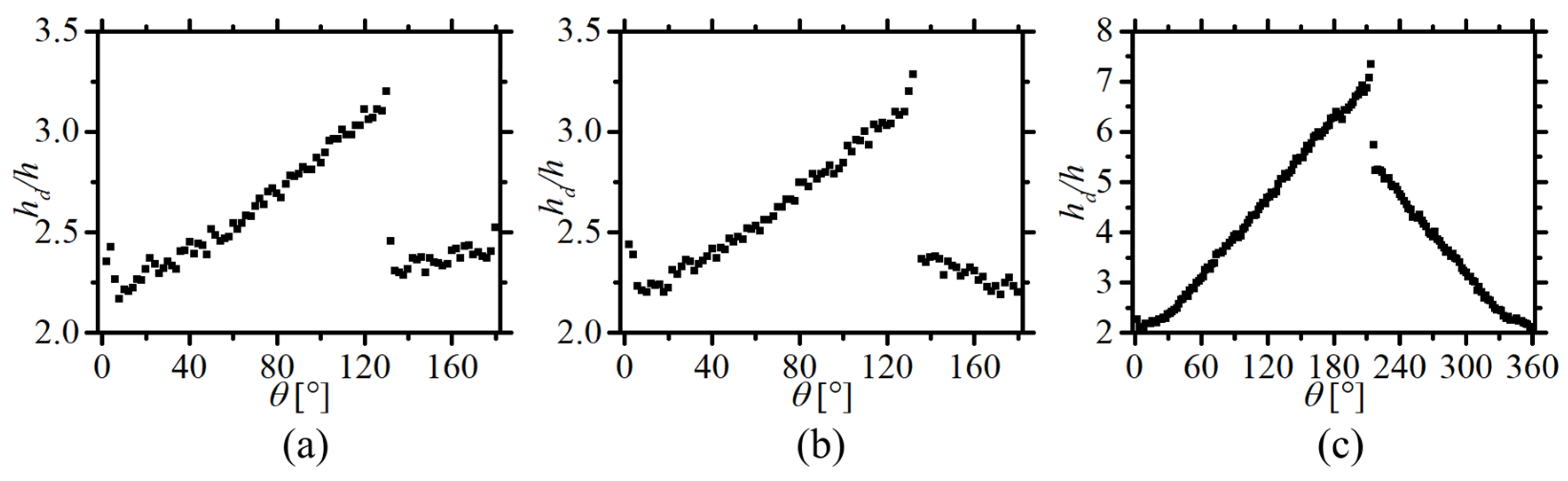
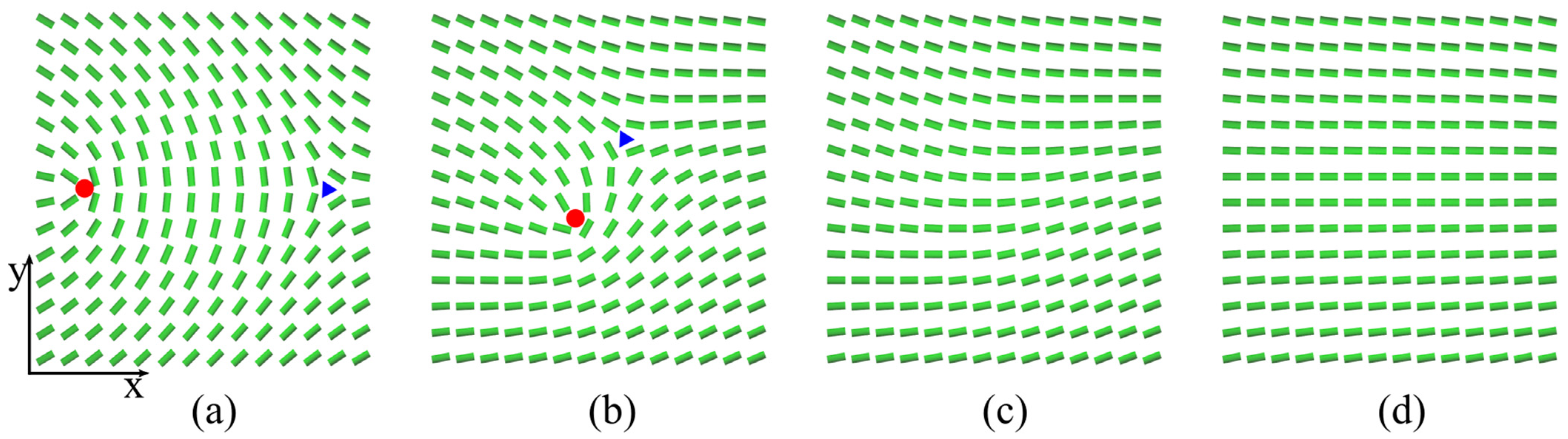
3.1. Pairs {1/2,1/2} and {−1/2,−1/2}
3.2. Pairs {−1/2,1/2}
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zurek, W.H. Cosmological experiments in superfluid helium? Nature 1985, 317, 505–508. [Google Scholar] [CrossRef]
- Kleman, D.; Michel, L.; Toulouse, G. Classification of topologically stable defects in ordered media. J. Phys. Lett. 1977, 38, 195–197. [Google Scholar] [CrossRef]
- Kleman, M.; Lavrentovich, O.D. Soft Matter Physics: An Introduction; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Schopohl, N.; Sluckin, T.J. Defect Core Structure in Nematic Liquid Crystals. Phys. Rev. Lett. 1987, 59, 2582–2584. [Google Scholar] [CrossRef] [PubMed]
- Kralj, S.; Virga, E.G.; Žumer, S. Biaxial torus around nematic point defects. Phys. Rev. E 1999, 60, 1858. [Google Scholar] [CrossRef]
- Zhou, S.; Shiyanovskii, S.V.; Park, H.S.; Lavrentovich, O.D. Fine Structure of the Topological Defect Cores Studied for Disclinations in Lyotropic Chromonic Liquid Crystals. Nat. Commun. 2017, 8, 14974. [Google Scholar] [CrossRef]
- Lavrentovich, O.D. Topological defects in dispersed liquid crystals, or words and worlds around liquid crystal drops. Liq. Cryst. 1998, 24, 117–126. [Google Scholar] [CrossRef]
- Ferris, A.J.; Afghah, S.; Selinger, R.L.B.; Selinger, J.V.; Rosenblatt, C. Electric field-induced crossover from 3D to 2D topological defects in a nematic liquid crystal: Experimental verification. Soft Matter. 2020, 16, 642–650. [Google Scholar] [CrossRef]
- Nikkhou, M.; Škarabot, M.; Čopar, S.; Ravnik, M.; Žumer, S.; Muševič, I. Light-controlled topological charge in a nematic liquid crystal. Nat. Phys. 2015, 11, 183. [Google Scholar] [CrossRef]
- Harkai, S.; Murray, B.S.; Rosenblatt, C.; Kralj, S. Electric field driven reconfigurable multistable topological defect patterns. Phys. Rev. Res. 2020, 2, 013176. [Google Scholar] [CrossRef]
- Chuang, I.; Durrer, R.; Turok, N.; Yurke, B. Cosmology in the Laboratory: Defect Dynamics in Liquid Crystals. Science 1991, 251, 1336. [Google Scholar] [CrossRef]
- Backer, A.S.; Callan-Jones, A.C.; Pelcovits, R.A. Nematic cells with defect-patterned alignment layers. Phys. Rev. E 2008, 77, 021701. [Google Scholar] [CrossRef] [PubMed]
- Murray, B.S.; Pelcovits, R.A.; Rosenblatt, C. Creating arbitrary arrays of two-dimensional topological defects. Phys. Rev. E 2014, 90, 052501. [Google Scholar] [CrossRef]
- Culbreath, C.; Glazar, N.; Yokoyama, H. Note: Automated maskless micro-multidomain photoalignment. Rev. Sci. Instr. 2011, 82, 126107. [Google Scholar] [CrossRef] [PubMed]
- Glazar, N.; Culbreath, C.; Li, Y.; Yokoyama, H. Switchable liquid-crystal phase-shift mask for super-resolution photolithography based on Pancharatnam–Berry phase. Appl. Phys. Expr. 2015, 8, 116501. [Google Scholar] [CrossRef]
- Wang, M.; Li, Y.; Yokoyama, H. Artificial web of disclination lines in nematic liquid crystals. Nat. Comm. 2017, 8, 388. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, M.; Chehui, P.; Sun, K.; Yaroshchuk, O.; Lavrentovich, O.D.; Wei, Q.-H. High-Resolution and High-Throughput Plasmonic Photopatterning of Complex Molecular Orientations in Liquid Crystal. Adv. Mater. 2016, 28, 2353–2358. [Google Scholar] [CrossRef]
- Yu, H.; Jiang, M.; Guo, Y.; Turiv, T.; Lu, W.; Ray, V.; Lavrentovich, O.D.; Wei, Q.-H. Plasmonic Metasurfaces with High UV–Vis Transmittance for Photopatterning of Designer Molecular Orientations. Adv. Opt. Mater. 2019, 7, 1900117. [Google Scholar] [CrossRef]
- Guo, Y.; Jiang, M.; Afghah, S.; Peng, C.; Selinger, R.L.B.; Lavrentovich, O.D.; Wei, Q.-H. Photopatterned Designer Disclination Networks in Nematic Liquid Crystals. Adv. Opt. Mater. 2021, 9, 2100181. [Google Scholar] [CrossRef]
- Peng, C.; Guo, Y.; Turiv, T.; Jiang, M.; Wei, Q.-H.; Lavrentovich, O.D. Patterning of Lyotropic Chromonic Liquid Crystals by Photoalignment with Photonic Metamasks. Adv. Mater. 2017, 29, 1606112. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Kralj, S.; Virga, E.G. Universal Fine Structure of Nematic Hedgehogs. J. Phys. A Math. Gen. 2001, 34, 829. [Google Scholar] [CrossRef]
- Bisi, F.; Gartland, E.C.; Rosso, R.; Virga, E.G. Order reconstruction in frustrated nematic twist cells. Phys. Rev. E 2003, 68, 021707. [Google Scholar] [CrossRef]
- Hamdi, R.; Lombardo, G.; de Santo, M.P.; Barberi, R. Biaxial coherence length in a nematic π-cell. Eur. Phys. J. E 2013, 36, 115. [Google Scholar] [CrossRef] [PubMed]
- Kralj, S.; Žumer, S. The saddle-splay surface elasticity of nematic structures confined to a cylindrical capillary. Phys. Rev. E 1995, 51, 366–379. [Google Scholar] [CrossRef]
- Kurik, M.V.; Lavrentovich, O.D. Defects in Liquid Crystals: Homotopy Theory and Experimental Studies. Sov. Phys. Usp. 1988, 31, 196. [Google Scholar] [CrossRef]
- Singer, I.M. Differential geometry, fiber bundles and physical theories. Physics Today 1982, 35, 41. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. A unified field theory of mesons and baryons. Nucl. Phys. 1962, 31, 556. [Google Scholar] [CrossRef]
- Hobson, A. There are no particles, there are only fields. Am. J. Phys. 2013, 81, 211. [Google Scholar] [CrossRef]
- Rößler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797. [Google Scholar] [CrossRef]
- Fukuda, J.; Žumer, S. Quasi-two-dimensional Skyrmion lattices in a chiral nematic liquid crystal. Nat. Commun. 2011, 2, 246. [Google Scholar] [CrossRef]
- Smalyukh, I.I. Review: Knots and other new topological effects in liquid crystals and colloids. Rep. Prog. Phys. 2020, 83, 106601. [Google Scholar] [CrossRef]
- Sutcliffe, P. Skyrmion Knots in Frustrated Magnets. Phys. Rev. Lett. 2017, 118, 247203. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Yu, B.; Wu, H.; Li, C.; Zhu, Z.; Zayats, A.V. Topological transformation and free-space transport of photonic hopfions. Adv. Photon. 2023, 5, 015001. [Google Scholar] [CrossRef]
- Muševič, I.; Škarabot, M.; Tkalec, U.; Ravnik, M.; Žumer, S. Two-dimensional nematic colloidal crystals self-assembled by topological defects. Science 2006, 313, 5789. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harkai, S.; Rosenblatt, C.; Kralj, S. Reconfiguration of Nematic Disclinations in Plane-Parallel Confinements. Crystals 2023, 13, 904. https://doi.org/10.3390/cryst13060904
Harkai S, Rosenblatt C, Kralj S. Reconfiguration of Nematic Disclinations in Plane-Parallel Confinements. Crystals. 2023; 13(6):904. https://doi.org/10.3390/cryst13060904
Chicago/Turabian StyleHarkai, Saša, Charles Rosenblatt, and Samo Kralj. 2023. "Reconfiguration of Nematic Disclinations in Plane-Parallel Confinements" Crystals 13, no. 6: 904. https://doi.org/10.3390/cryst13060904
APA StyleHarkai, S., Rosenblatt, C., & Kralj, S. (2023). Reconfiguration of Nematic Disclinations in Plane-Parallel Confinements. Crystals, 13(6), 904. https://doi.org/10.3390/cryst13060904







