1. Introduction
The importance of spray properties in terms of efficient NO
x reduction in urea–selective catalytic reduction (SCR) systems is growing. This is caused by stricter emission limits directly, and indirectly, through the development of compact SCR units located close to the engine, so-called close-coupled SCRs. Close-coupled to the engine SCRs, due to higher exhaust gas temperatures, offer a huge potential of NO
x reduction [
1], especially in terms of catalyst warm-up time; but at the same time, decrease the available distance for mixing the urea–water solution (UWS) with the exhaust gases. When the space for mixing is limited, then the spray properties become the key factor in determining the quality of the SCR system. Therefore, besides investigating alternative solutions [
2], the urea–water sprays are more often studied than in the past—when the inline underfloor SCR systems were a standard solution.
The experimental studies on UWS injection related to SCR systems’ development are usually aimed at spray characterization for proper injector selection, or determining the spray properties for further computational fluid dynamics (CFD) simulations, where full SCR system designs are optimized. These include both spray formation as well as spray-wall interaction. In many studies available in the literature, UWS is replaced with pure water [
3,
4,
5,
6,
7,
8,
9]. For preliminary studies, such an approach seems to be justified since the physical properties influencing spray behaviour, specifically surface tension and viscosity, are similar for these two liquids. In certain cases, however, even small differences between the liquids can lead to different spray characteristics. Different spray characteristics in turn, may be crucial when highly accurate results are required. Moreover, some parameters differ more (e.g., specific heat). Different values of specific heat may lead to different droplet sizes at higher distances from the injector outlet, especially in hot flow conditions. Nevertheless, even in cold-flow studies on injector characterization, small differences in surface tension and viscosity together may have an influence on measured spray parameters. When spray characterization optical methods are applied a different refractive index may lead to different results as well, especially in the case of Mie scattering. A comparison of selected physical properties of water and UWS is shown in
Table 1.
If more precise studies are required, then before replacing UWS with water one needs to ensure that these two liquids produce similar sprays. However, detailed information on differences in spray parameters for the same conditions is very limited. Spiteri et al. [
3], based on his earlier findings [
20], stated that water and UWS sprays behave similarly. On the other hand, Birkhold et al. [
21] noticed that the evaporation dynamics of UWS differ from pure water. They stated that the decrease in vapour pressure due to an increasing concentration of urea in the droplet results in a continuous increase of the droplet temperature and a slower evaporation, compared to pure water [
21]. The model proposed by Ebrahiman et al. [
17] confirmed that during vaporization urea concentration increases, which in turn leads to a decrease in vapour pressure. However, their calculations of droplet evaporation indicated the low influence of the presence of urea on water evaporation, even though it had a huge effect on the droplet temperature. If the evaporation is slower, as reported by Birkhold et al. [
21], this may have an effect on droplet sizes at further distances.
The crucial element in the SCR system’s development is fine adjustment of the spray pattern and droplet size distribution to a specific SCR unit’s design. Thus, a fast and reliable method for spray characterization is very important for proper injector selection and spray pattern optimization.
Many of the studies available in the literature regarding sprays in SCR systems were based on a UWS injection. However, most of them were specifically aimed at the properties of the UWS, and no comparison with water was made. Grout et al. [
22], based on the diameter change of individual droplets, calculated the evaporation rate of the UWS according to the D-square evaporation law. Postrioti et al. [
23] observed urea–water sprays in order to determine the liquid mass distribution over the visualized area. They also used phase doppler anemometry (PDA) to determine droplet diameters. They determined the Sauter mean diameter at 16 locations at distances of 90 mm and 140 mm from the injector outlet. They made 5 additional measurements in order to compare the results with backlight imaging. Payri et al. [
24] studied the atomization of UWS sprays in hot co-flow to simulate exhaust system conditions. They used a diffused back illumination technique at high imaging speed. They observed that droplet diameter and velocity are affected by injection pressure. Moreover, the differences were seen depending on the measurement position of the spray, which indicated the role of the evaporative conditions.
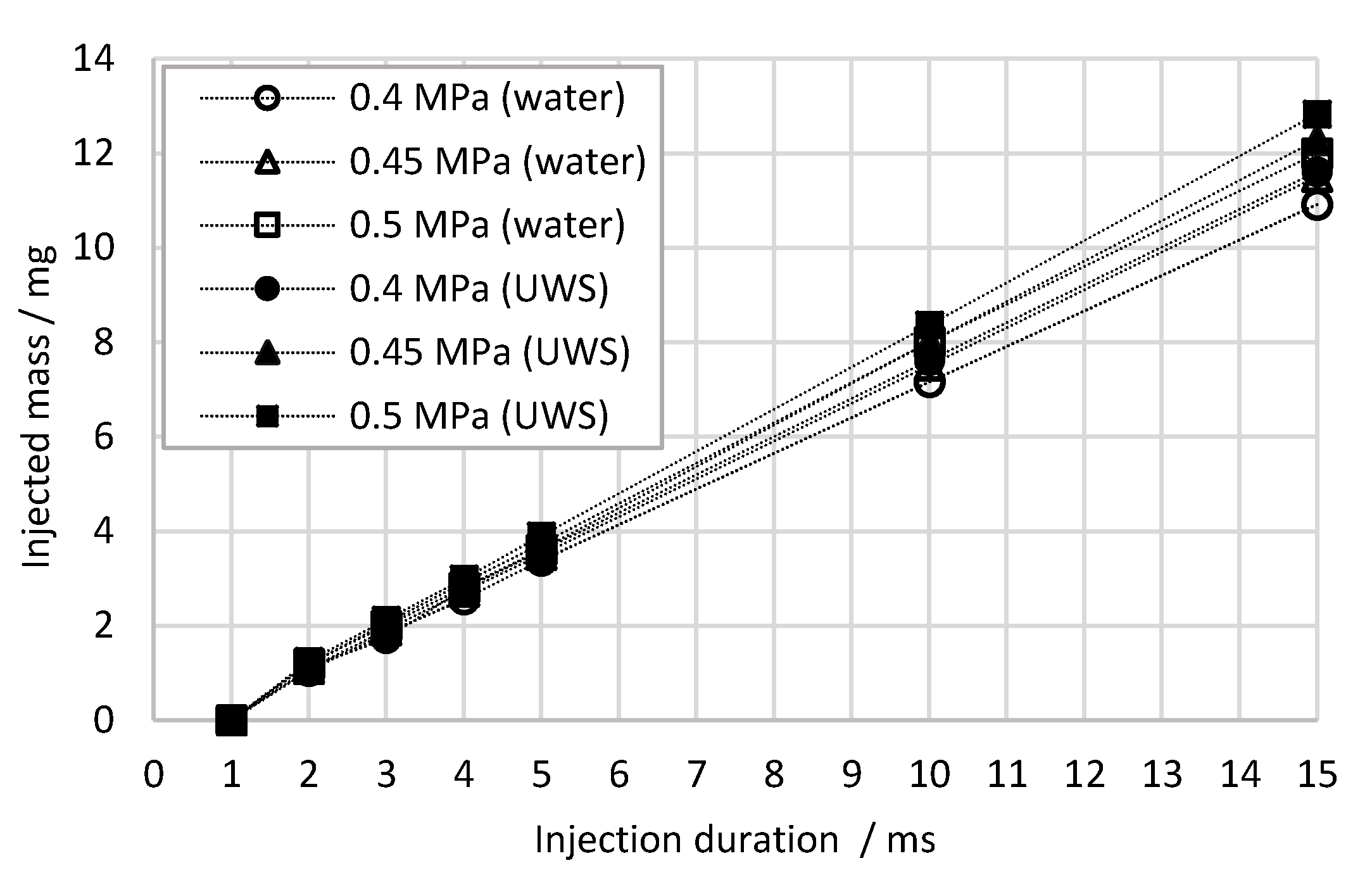
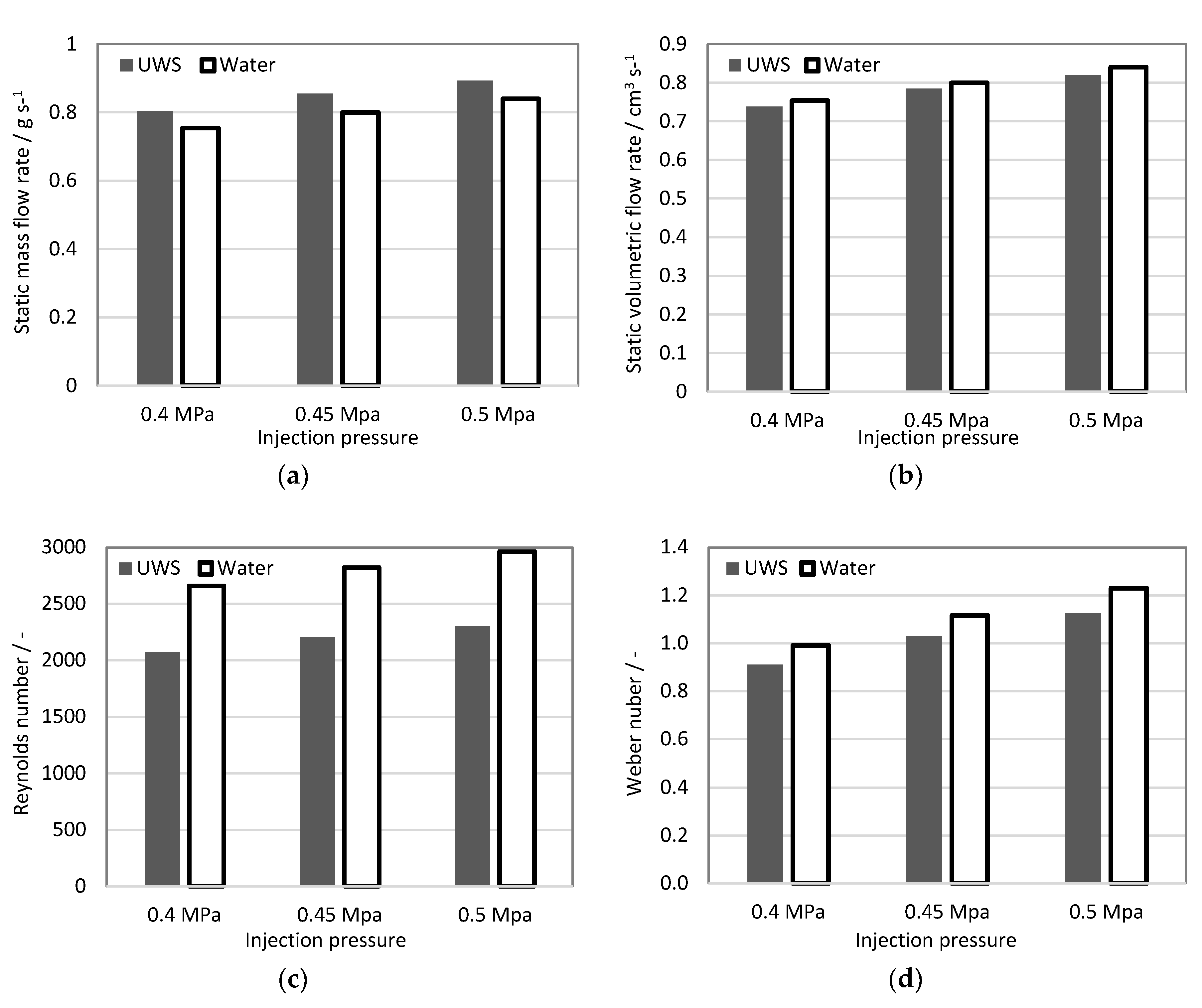
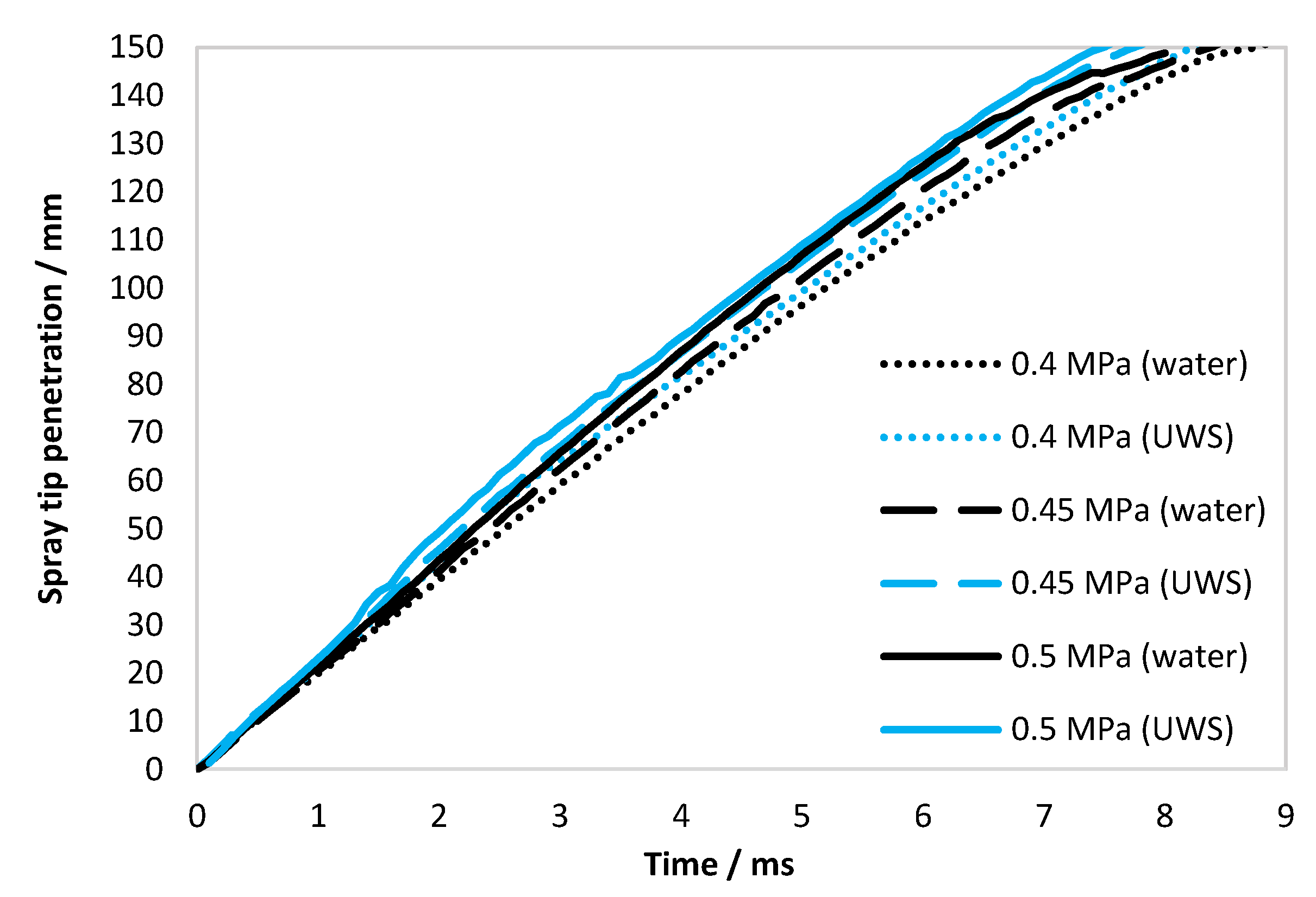
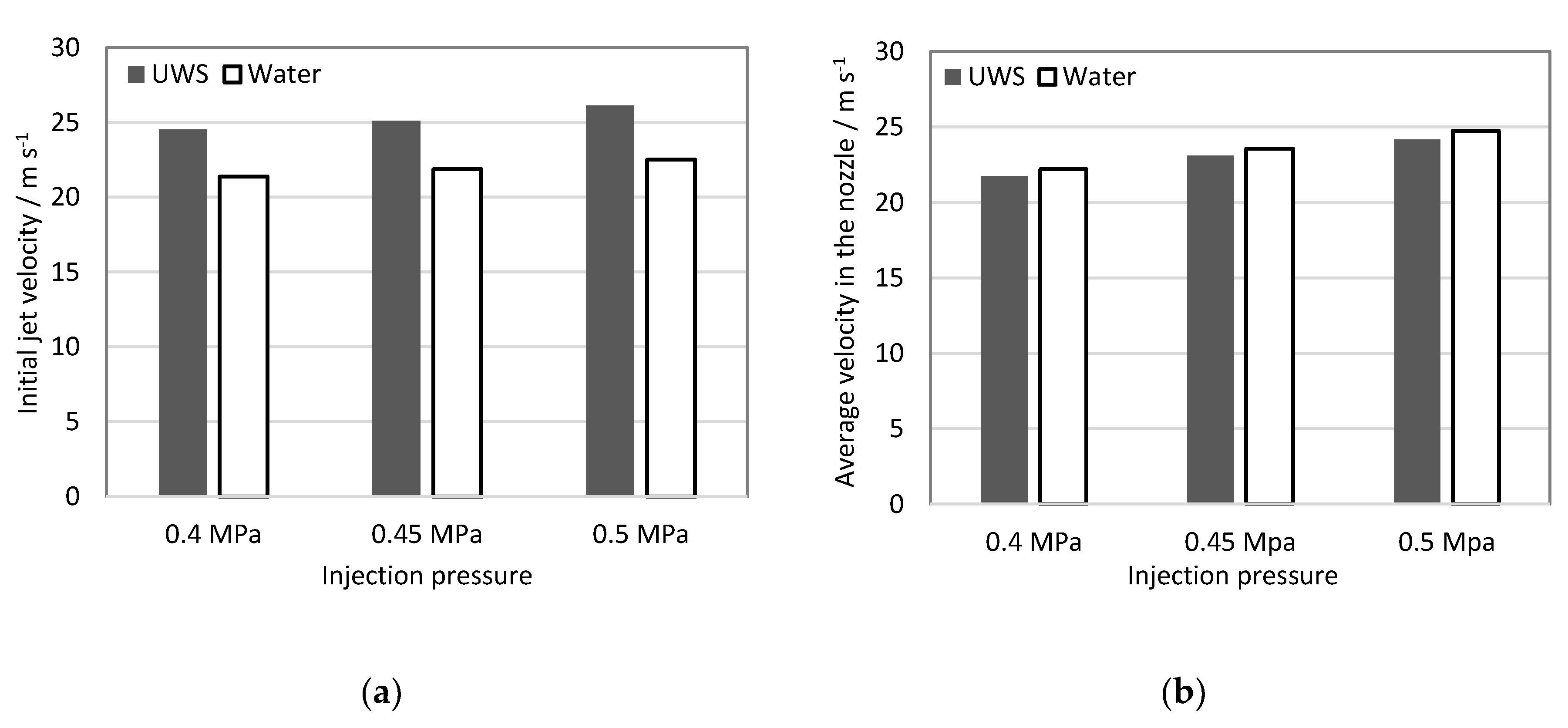
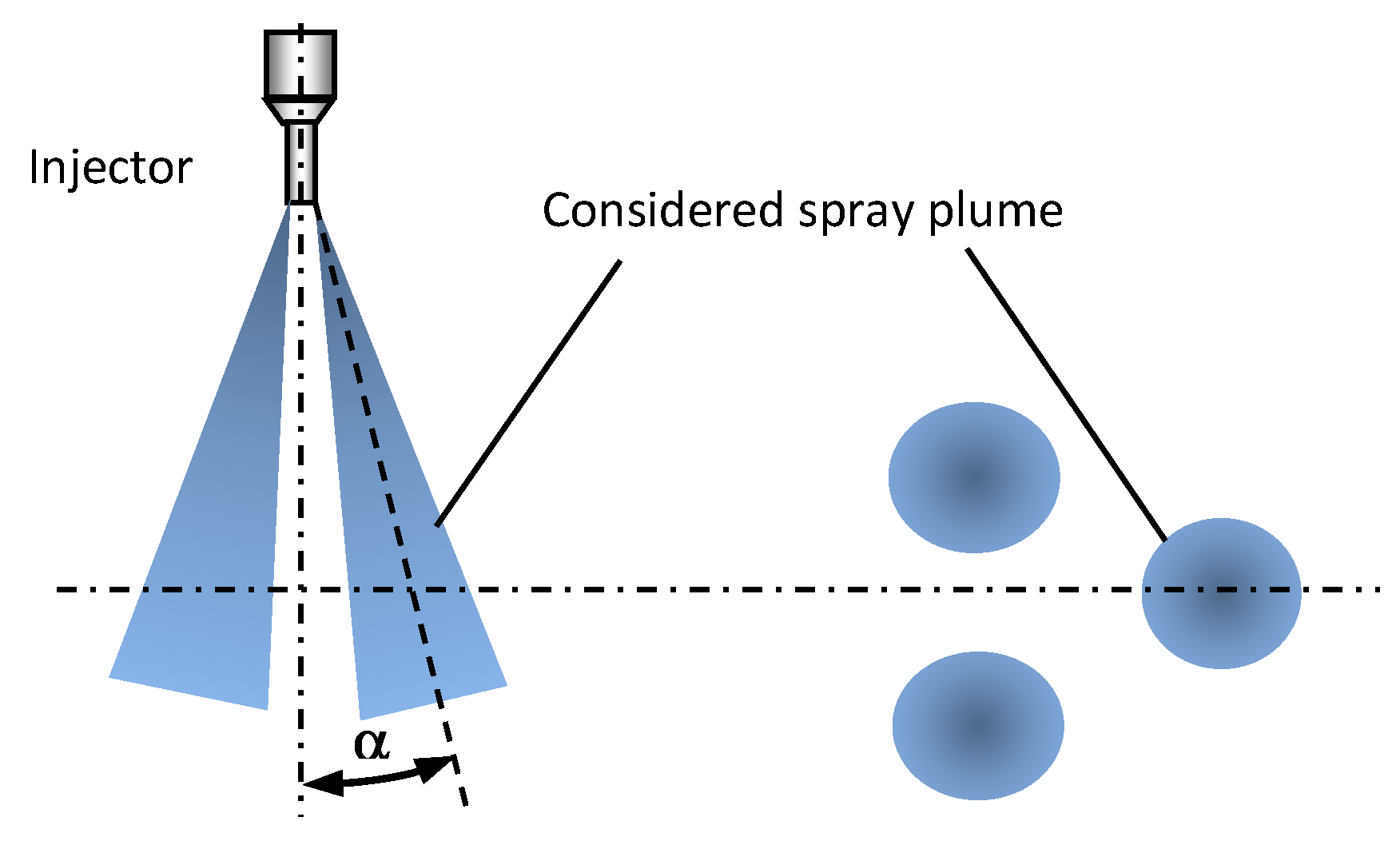
In this study, we combine global and local spray properties’ determination using optical techniques with flow characteristics’ measurements, in order to provide comprehensive data on the difference between UWS and water sprays. The parameters under consideration are: Droplet size distribution and statistical droplet parameters; spray angle (visualization angle, spray plume inclination angle); spray tip penetration; unbroken liquid length; initial jet velocity; static flow properties such as static flow rate (mass, volumetric and average velocity), Reynolds number, Weber number (referred to gas); and finally, Ohnesorge number.
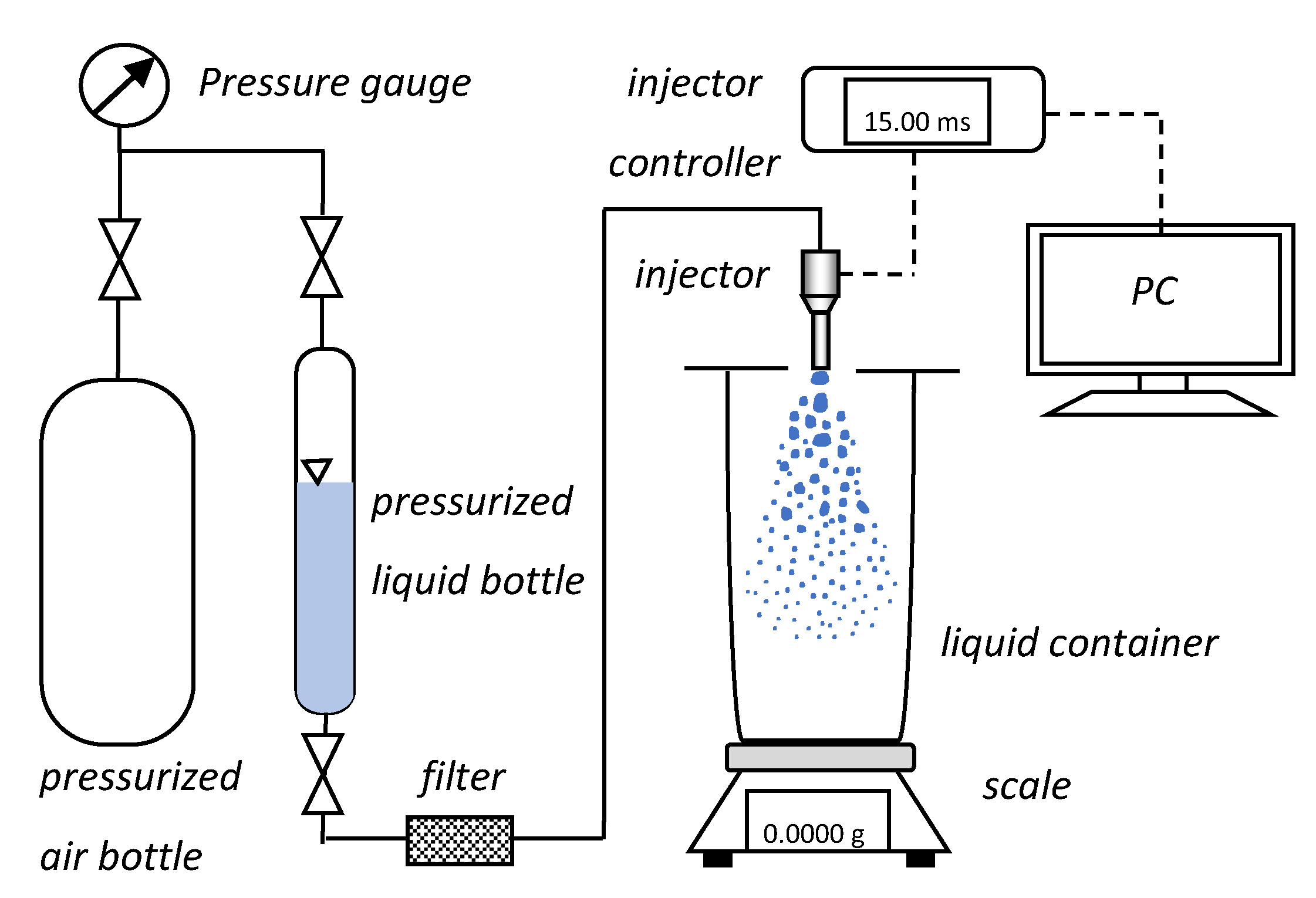
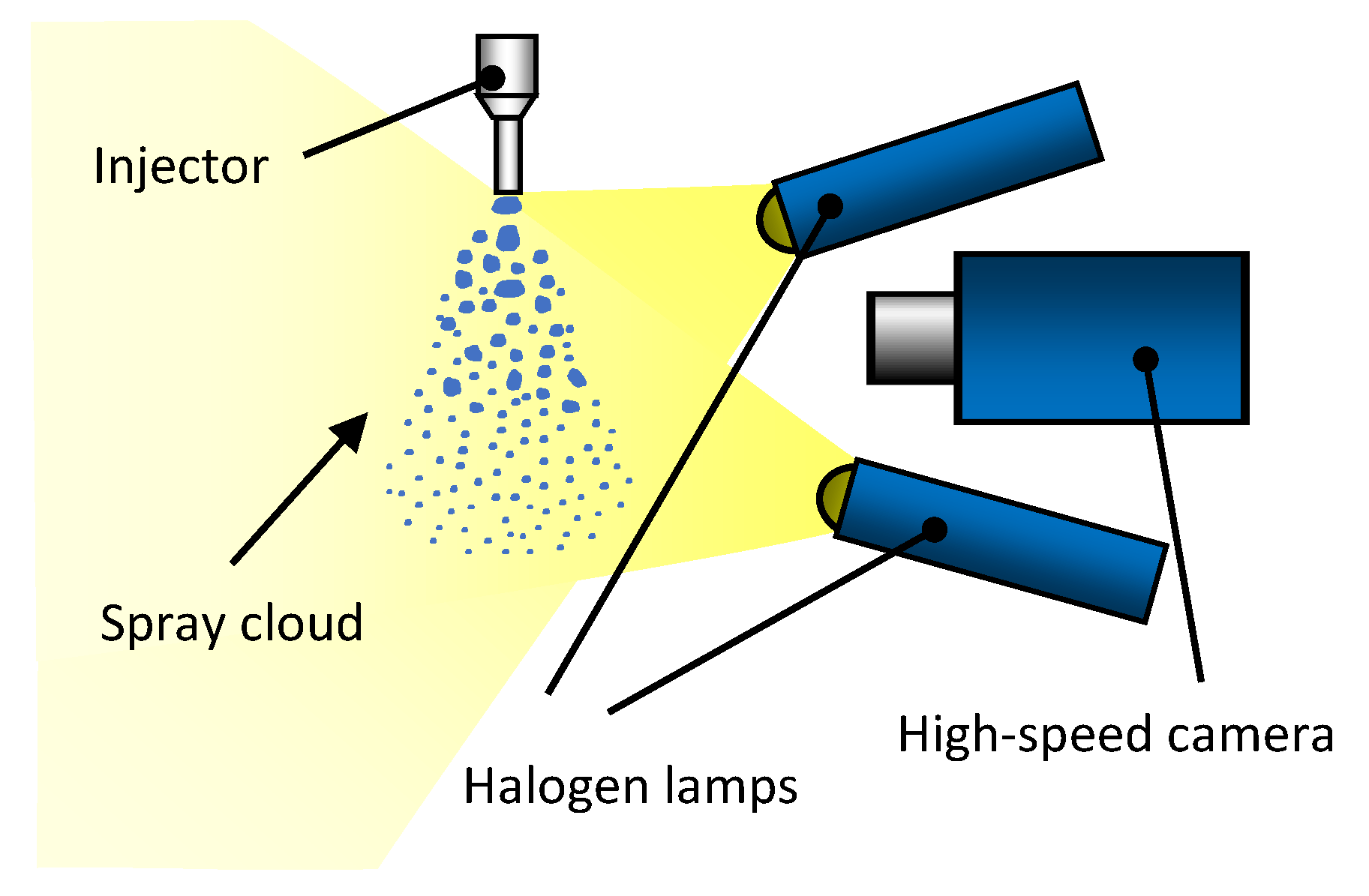
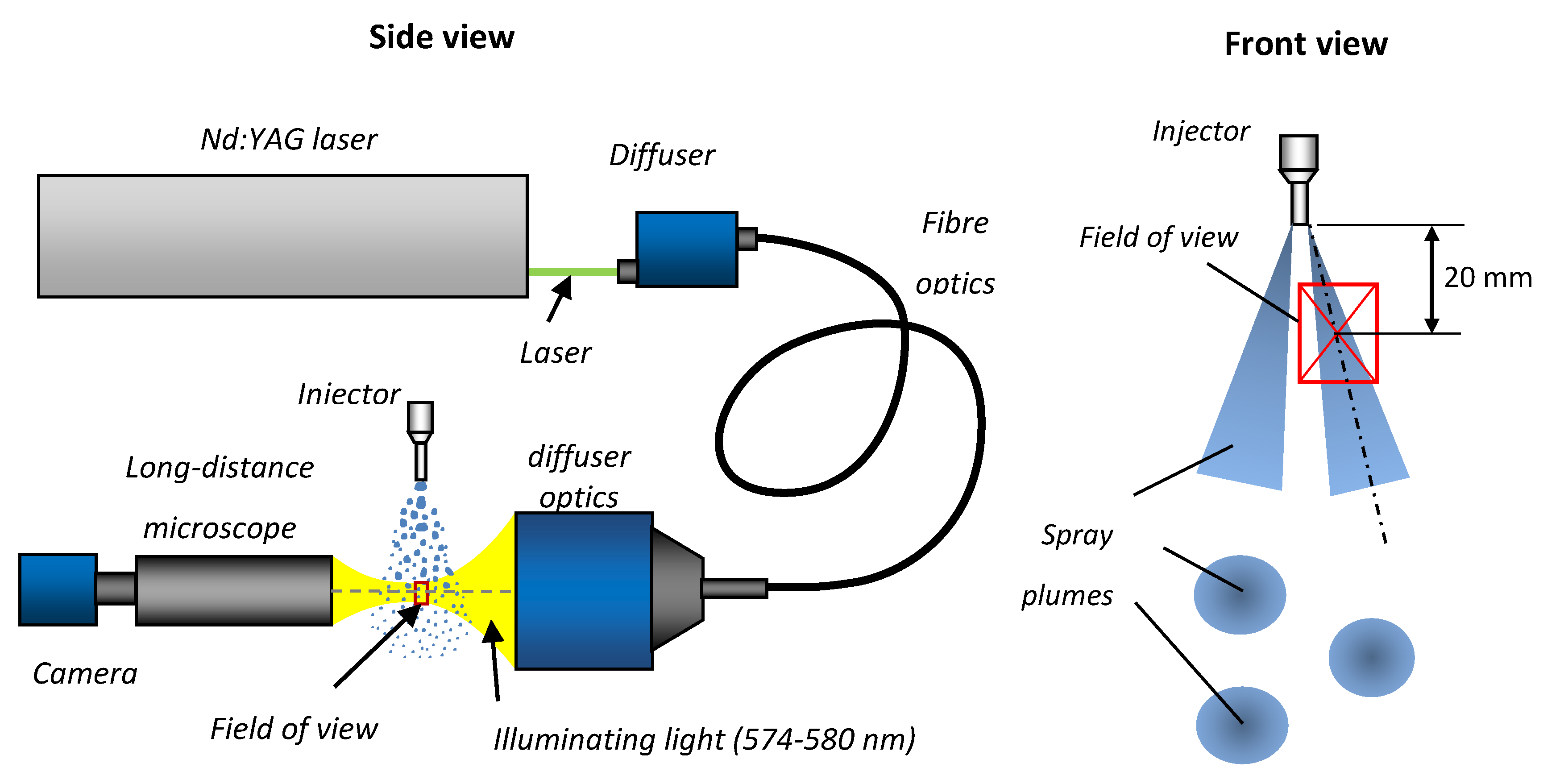
To our knowledge, this is the first study which examines the influence on the injection process of replacing UWS with water over such a wide range. Both liquids were injected by the same commercial SCR system injector into ambient air under the same pressure and temperature. Long-distance microscopy with backlight illumination (shadowgraphy) was used to determine the droplet size distribution 20 mm from the injector’s outlet. It was also used to determine the unbroken liquid length and spray inclination angle. The spray visualization angle, spray tip penetration and initial jet velocity were determined by high-speed Mie scattering imaging. The static flow parameters were calculated based on the measurements of the injected mass over different injection durations.
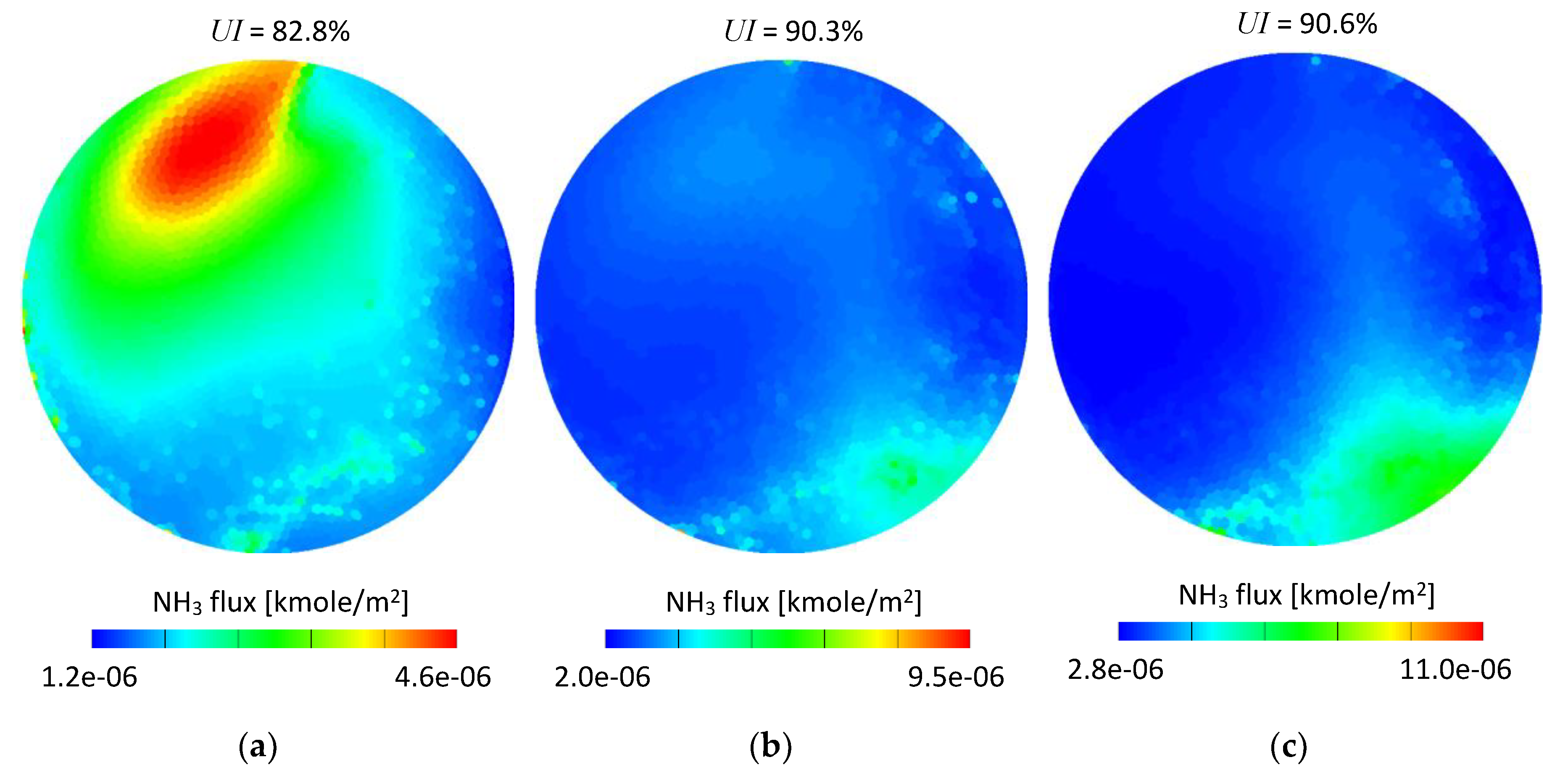
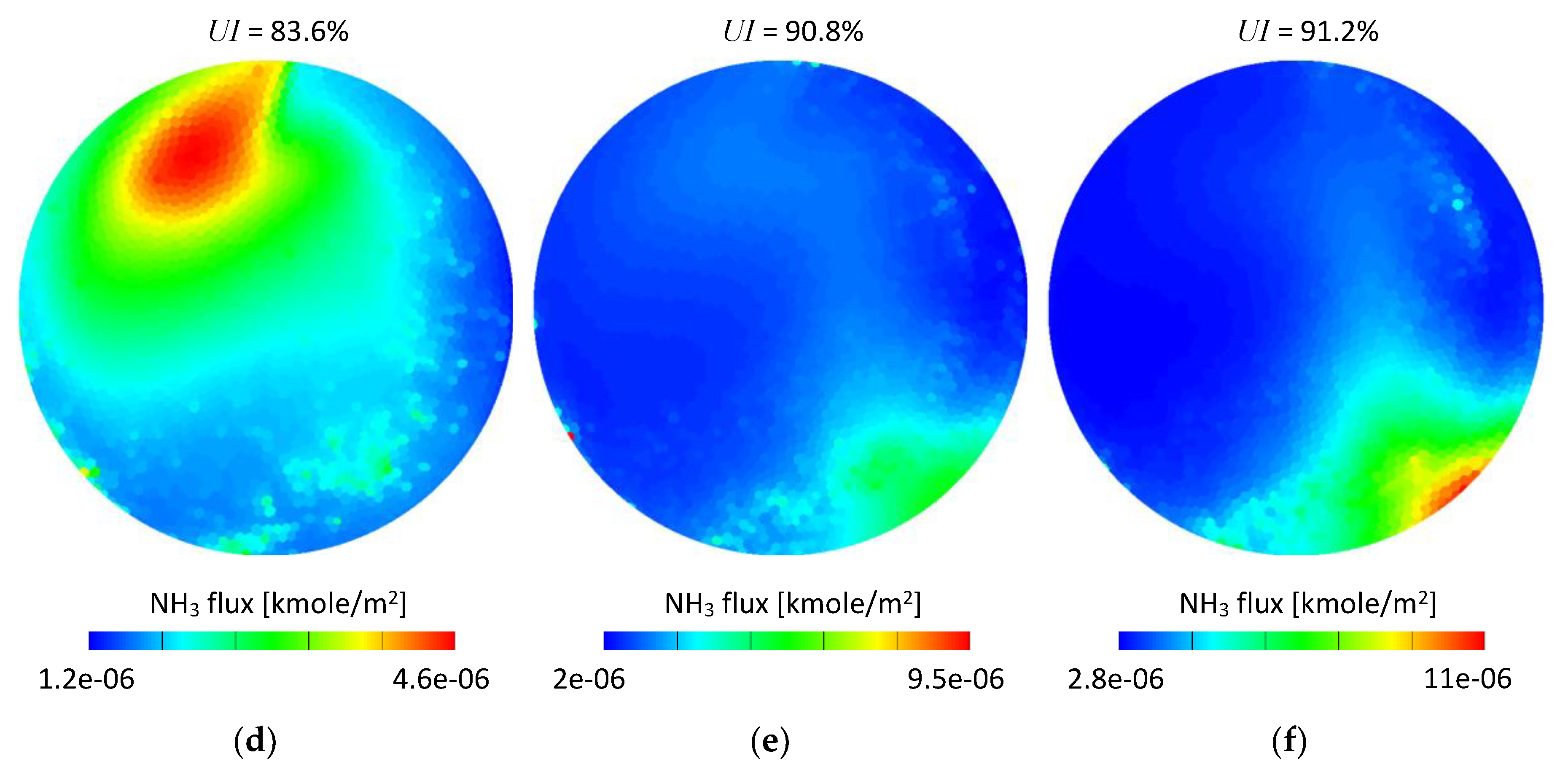
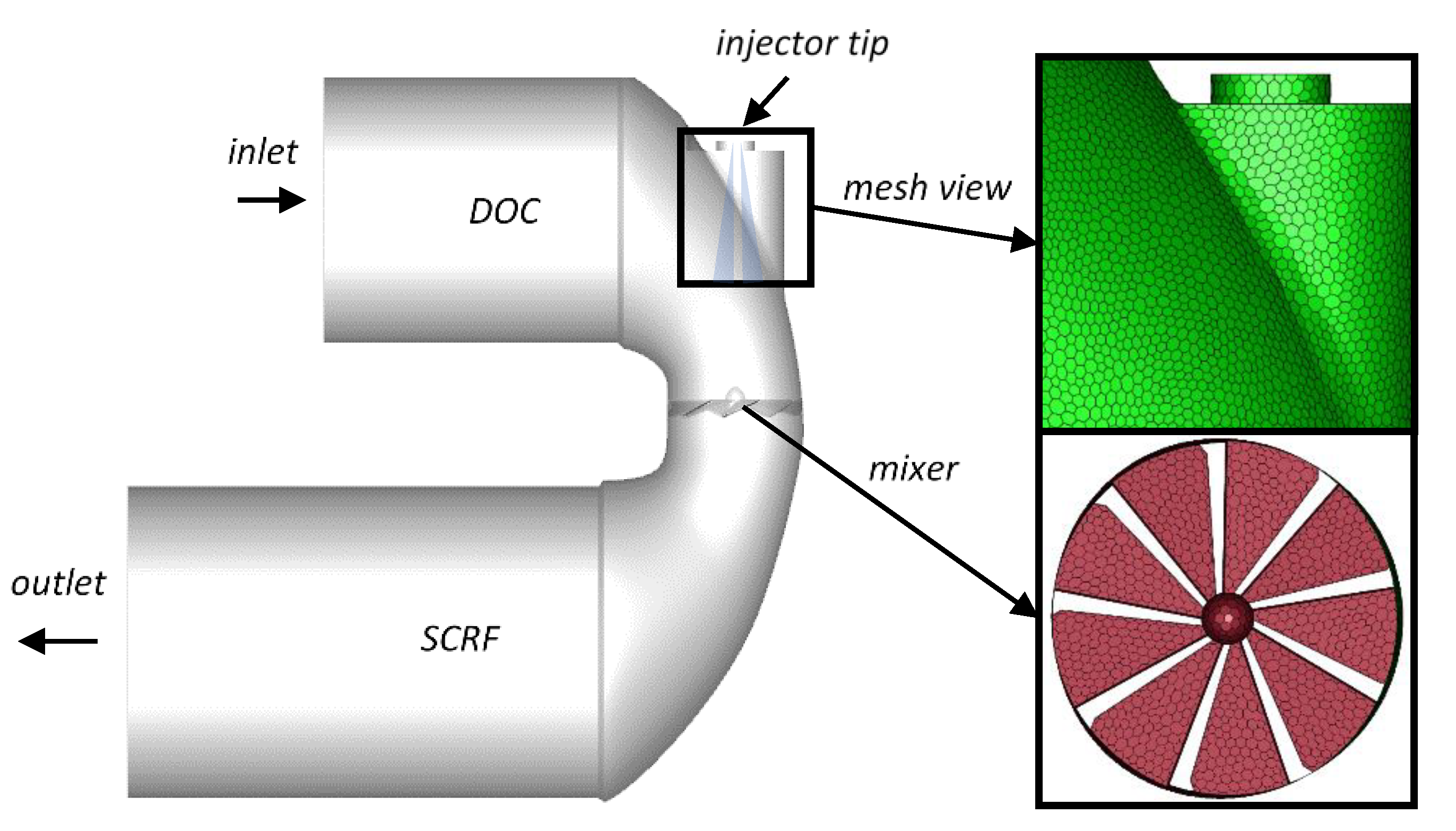
Further, since CFD is extensively used for SCR systems’ development, the determined spray parameters were used in simulations of an exhaust system in order to examine the effect of using spray data obtained for water instead of UWS on the simulations’ results. Crucial parameters influencing the overall SCR system performance were compared, specifically wall film formation and ammonia homogenization. The simulations were performed for a light-duty close-coupled SCR system under various conditions relevant to an automotive diesel engine.
4. Conclusions
In this study, UWS and pure water were compared in terms of spray properties generated from the same set-up under the same conditions. The parameters under consideration were: Droplet size distribution and statistical droplet parameters; spray angle (visualization angle, spray plume inclination angle); spray tip penetration; unbroken liquid length; initial jet velocity; static flow properties such as static flow rate (mass, volumetric and average velocity), Reynolds number, Weber number (referred to gas); and finally, Ohnesorge number. Moreover, the influence of different spray properties on CFD simulations was also studied.
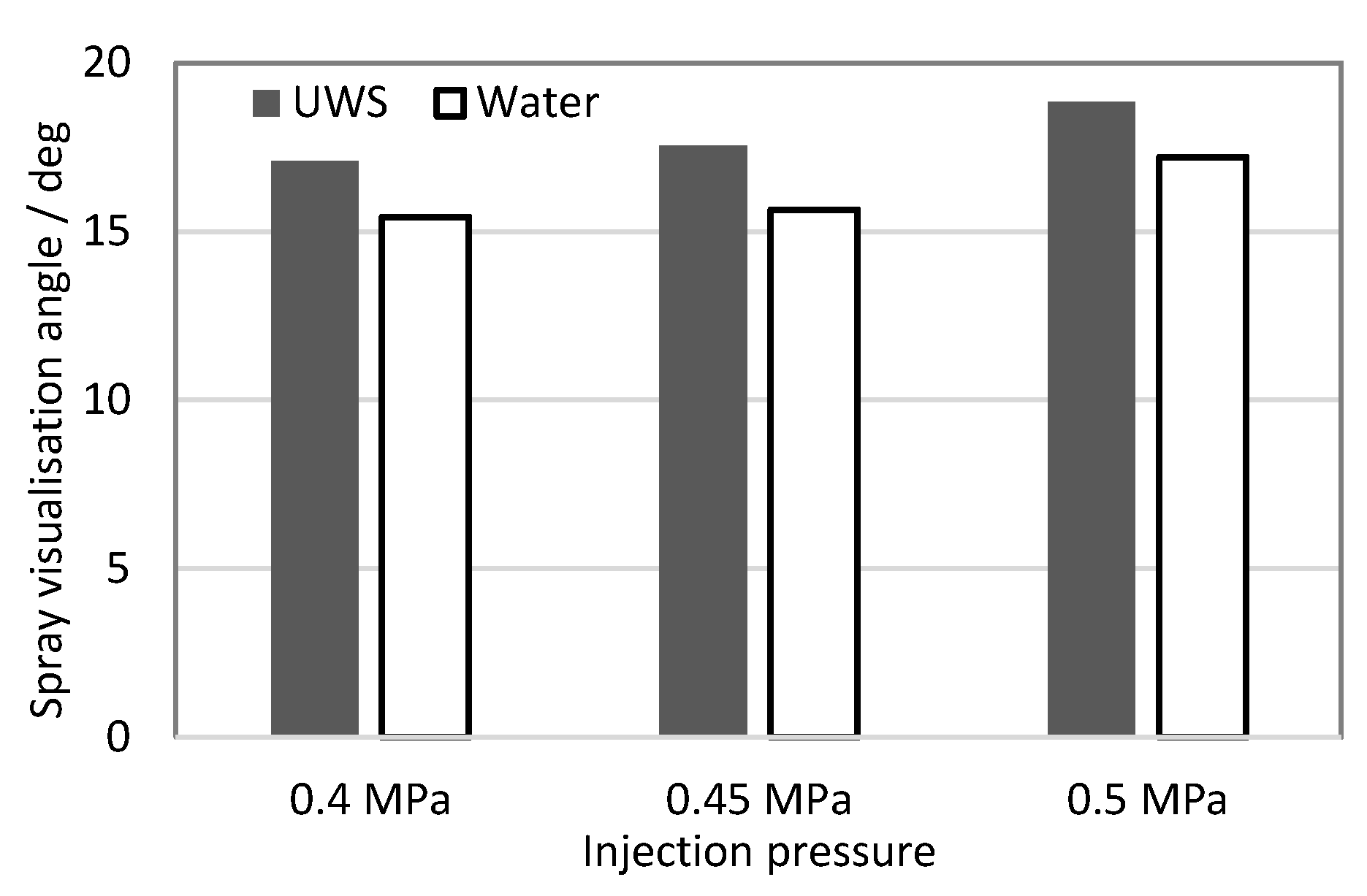
The experimental studies showed differences in almost all considered spray parameters. The jet inclination angle was the only parameter unaffected by replacing UWS with water. The Reynolds number, Weber number (referred to gas) and Ohnesorge number in all considered cases were higher for water. The static volumetric flow rate and, thus, average velocity in the nozzle was higher for water; while the initial jet velocity and the spray tip penetration were higher for UWS. It is supposed that the higher initial jet velocity in the case of UWS was caused by higher UWS density (and as a result inertia), and viscosity leading to a longer delay and consequently, higher pressure build-up before the exit of the first liquid from the nozzle. In turn, higher initial jet velocity together with higher density and thus momentum, explain the higher spray tip penetration for all UWS cases. The spray angle was also dependent on the fluid type—the visualization angle for UWS was higher than for water for all considered injection pressures—even though the number of observed droplets and the injected volume was higher for water. It is presumed that the decreased spray angle for water resulted mainly from the different refractive index, making the water sprays less visible and more difficult to separate from the background. This feature also needs to be taken into account when UWS is replaced with water.
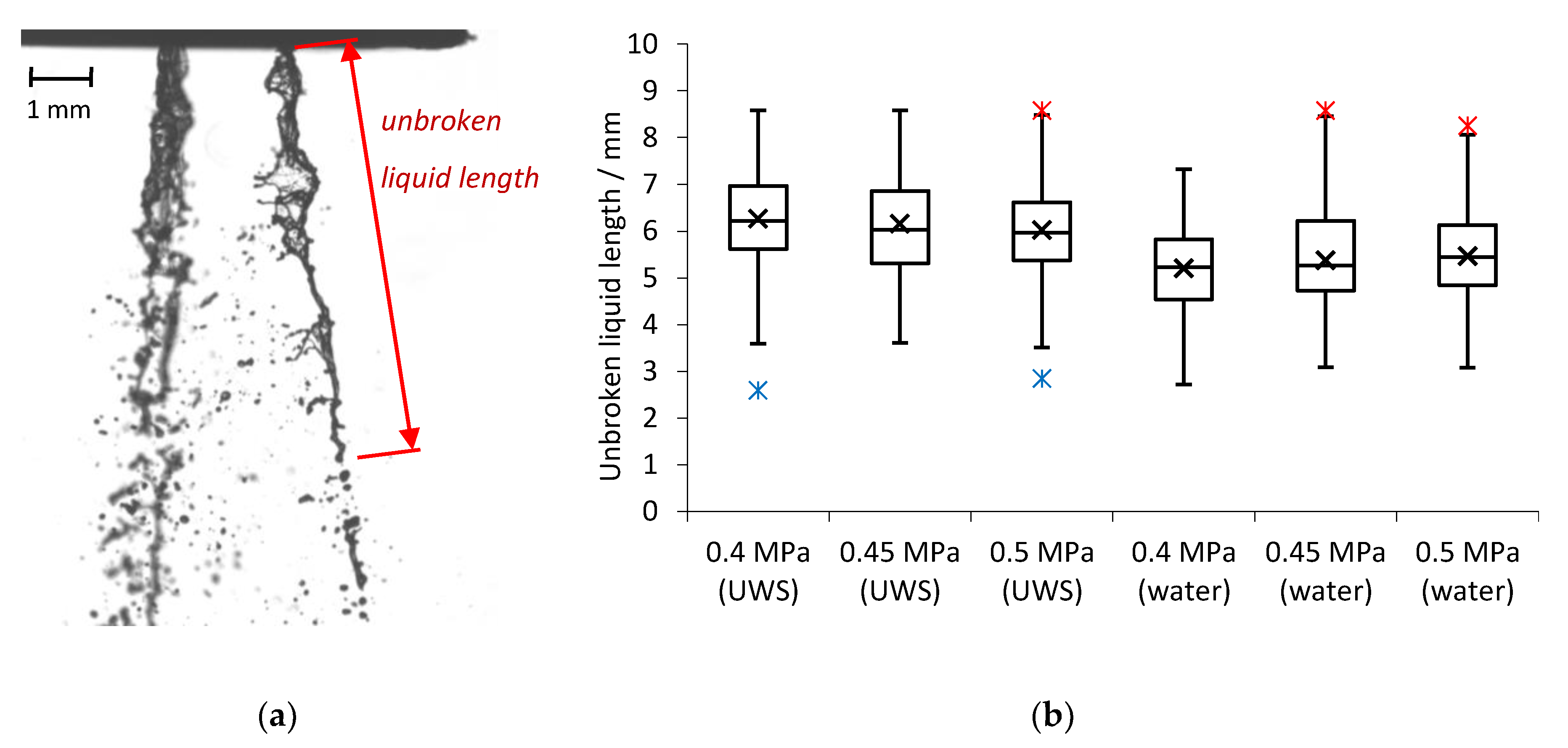
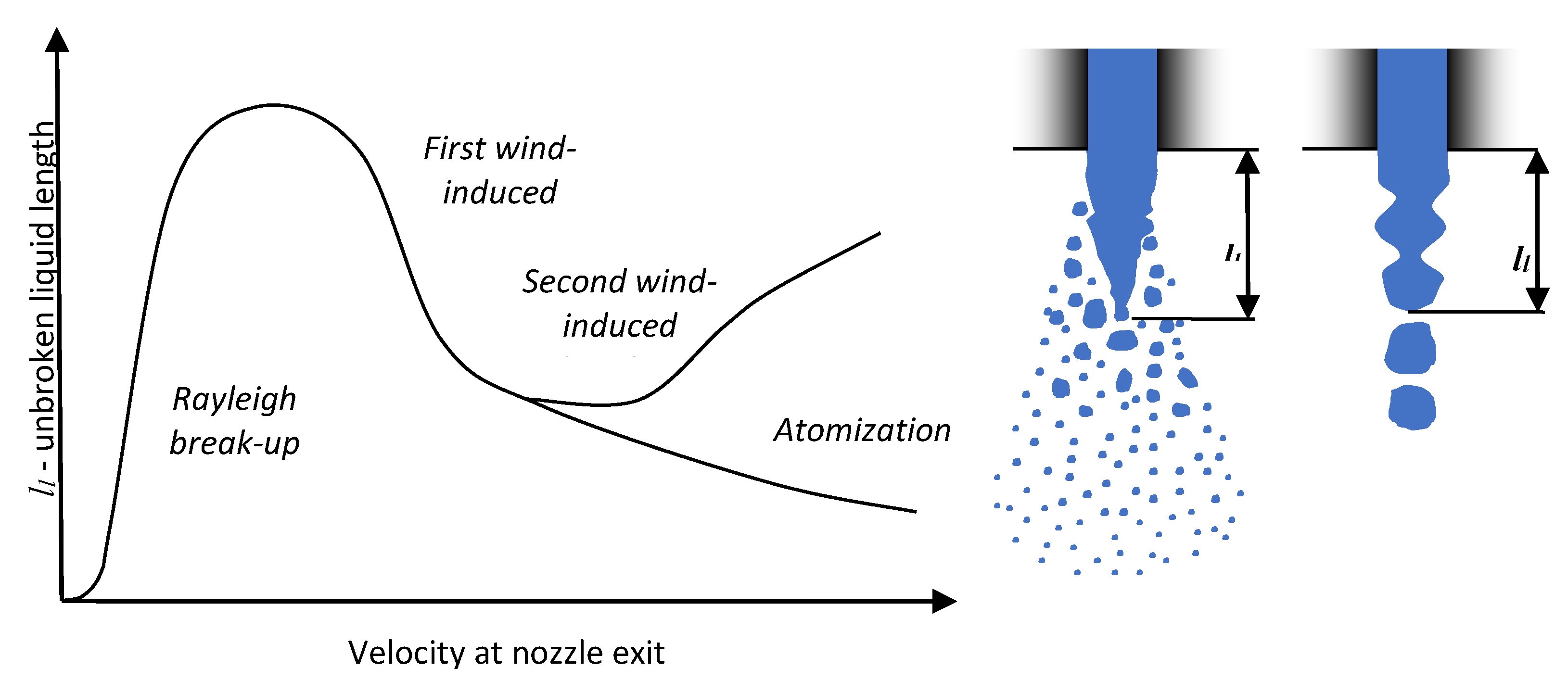
Moreover, different spray behaviour was noticed in terms of primary break-up. The unbroken liquid length for UWS tended to decrease with the increased injection pressure (and flow velocity); while for water, the effect was opposite. This suggests that the replacement of UWS with water caused the change in the break-up regime from the first wind-induced regime into the second wind-induced regime. It needs to be emphasized that in the case of different injection set-ups (injection pressure, nozzle diameter) the same jet break-up regime can be maintained. Nevertheless, it can be generally concluded that replacing UWS with water (by increased Ohnesorge number and Reynolds number) moves the jet droplet break-up process towards the next break-up regime.
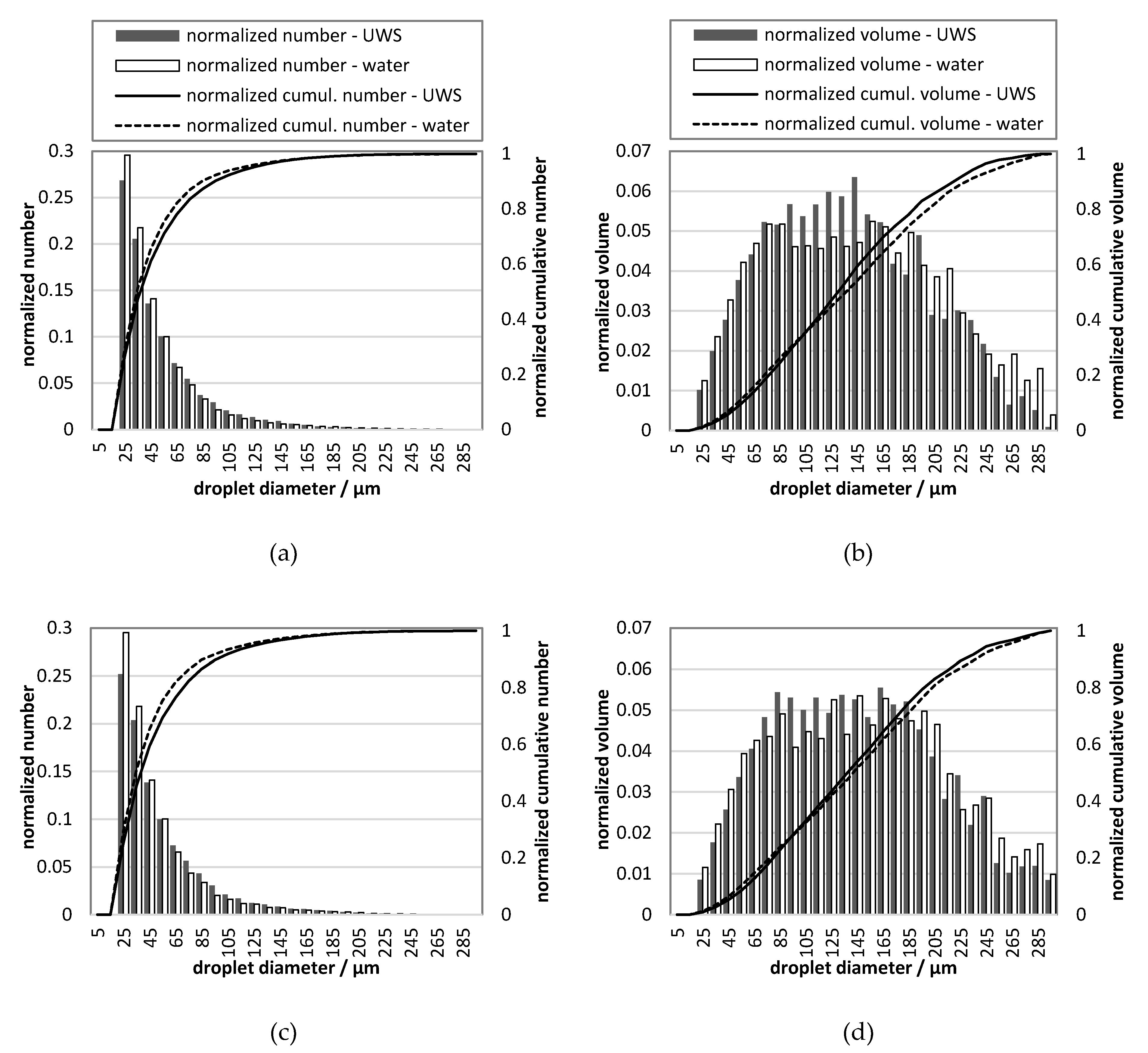
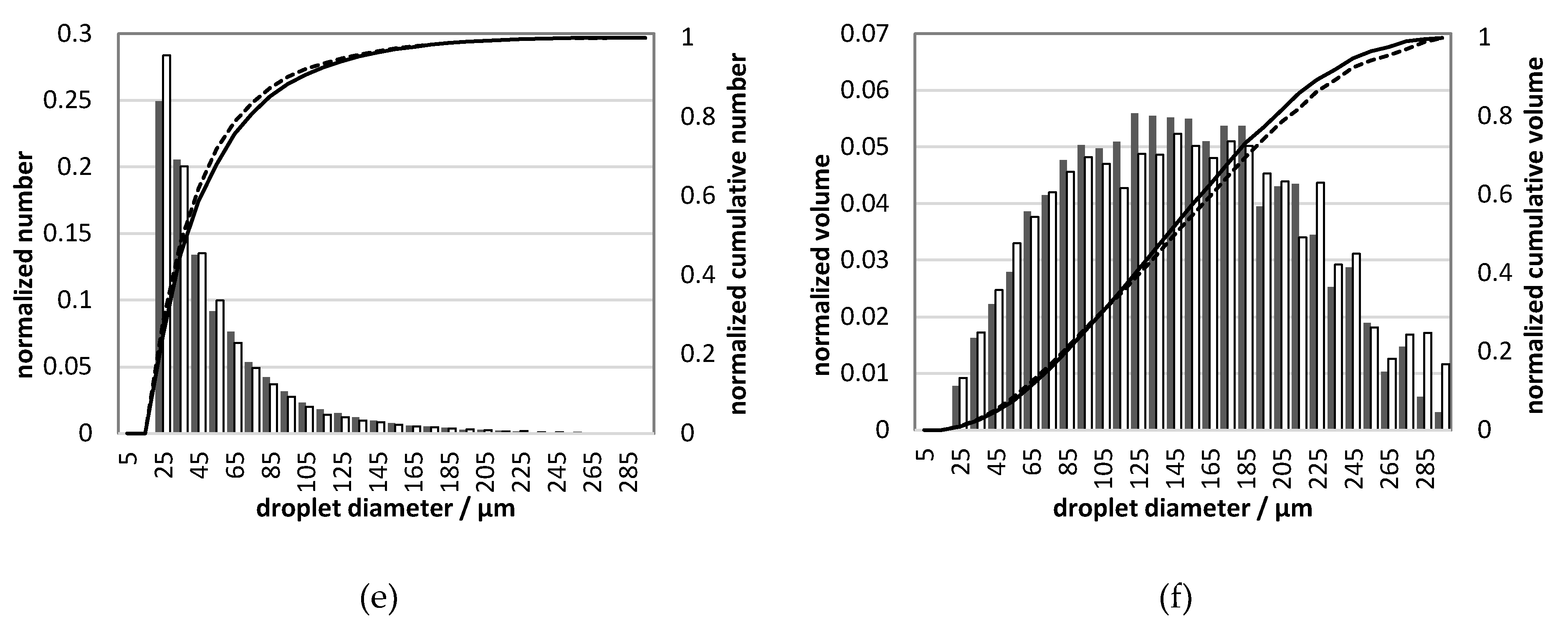
An important finding was shown in that water and UWS sprays do have a similar Sauter mean diameter, but at the same time the droplet size distributions are considerably different. The normalized number and normalized volume of the smallest and the biggest droplets for water were higher than for UWS.
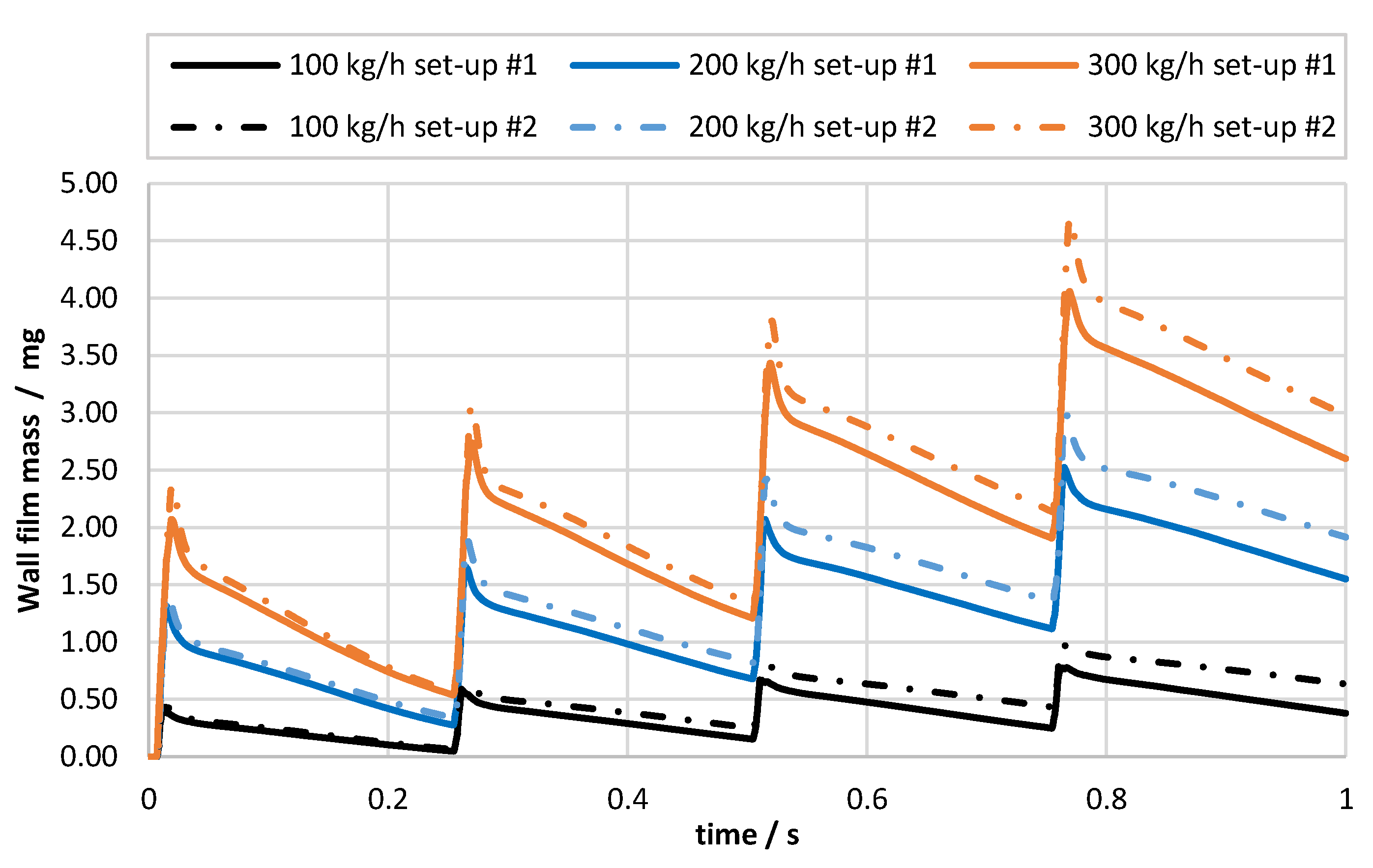
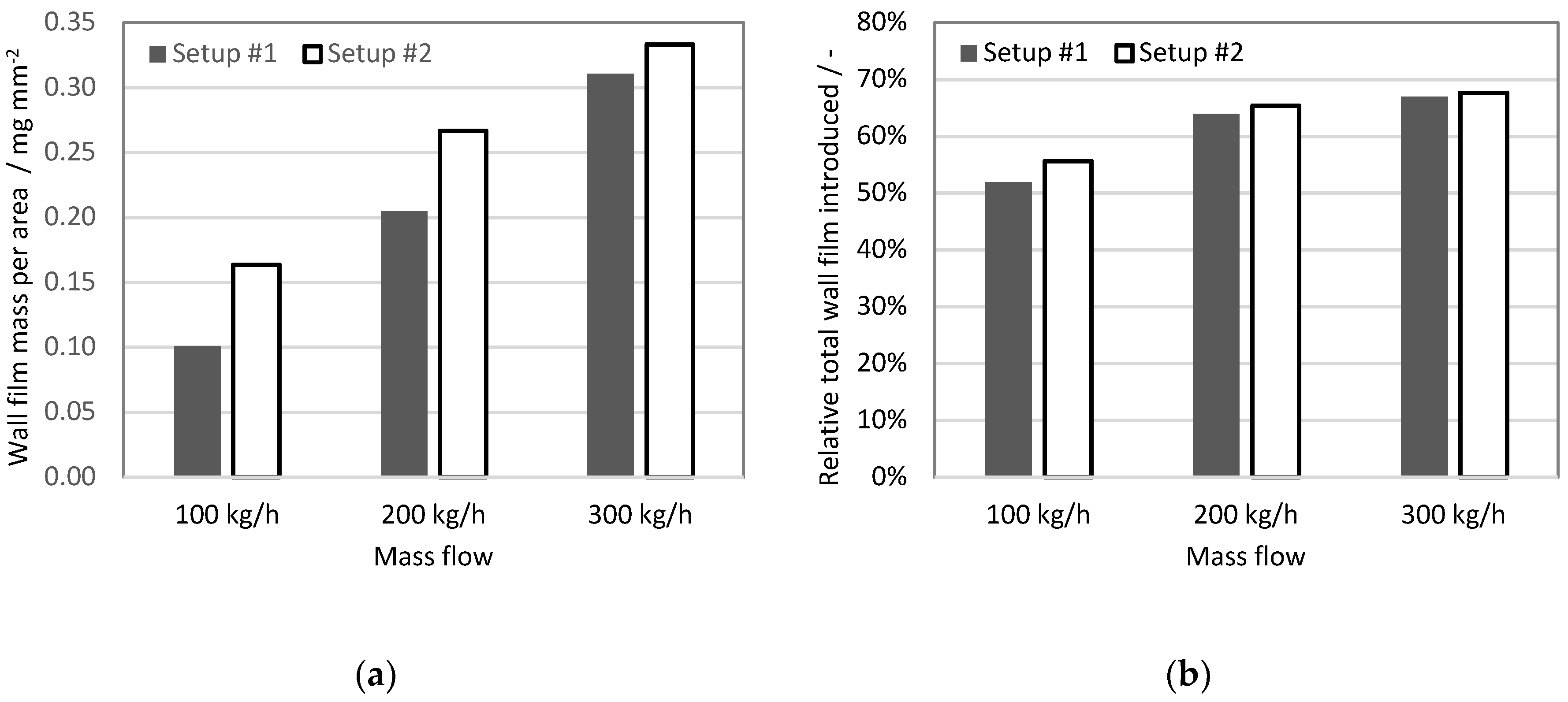
The differences between the measured spray parameters for UWS and water affected the simulations’ results. The simulation set-up based on spray data obtained for water resulted in higher wall film accumulation at the end of each injection event, and at the end of the simulations. This leads to an important conclusion that using experimental data obtained for water instead of UWS did not cause an underestimation of the wall film formation. As far as the ammonia uniformity index is concerned, the differences between the simulations based on the UWS spray data and the water spray data were very low. However, unlike the case of the wall film, the effect was opposite as the simulations based on the water spray data led to more optimistic results for all considered exhaust gas mass flows. This shall be taken into consideration when developing an SCR system using CFD simulations.