Deciphering the Effect of Microbead Size Distribution on the Kinetics of Heterogeneous Biocatalysts through Single-Particle Analysis Based on Fluorescence Microscopy
Abstract
1. Introduction
2. Results and Discussion
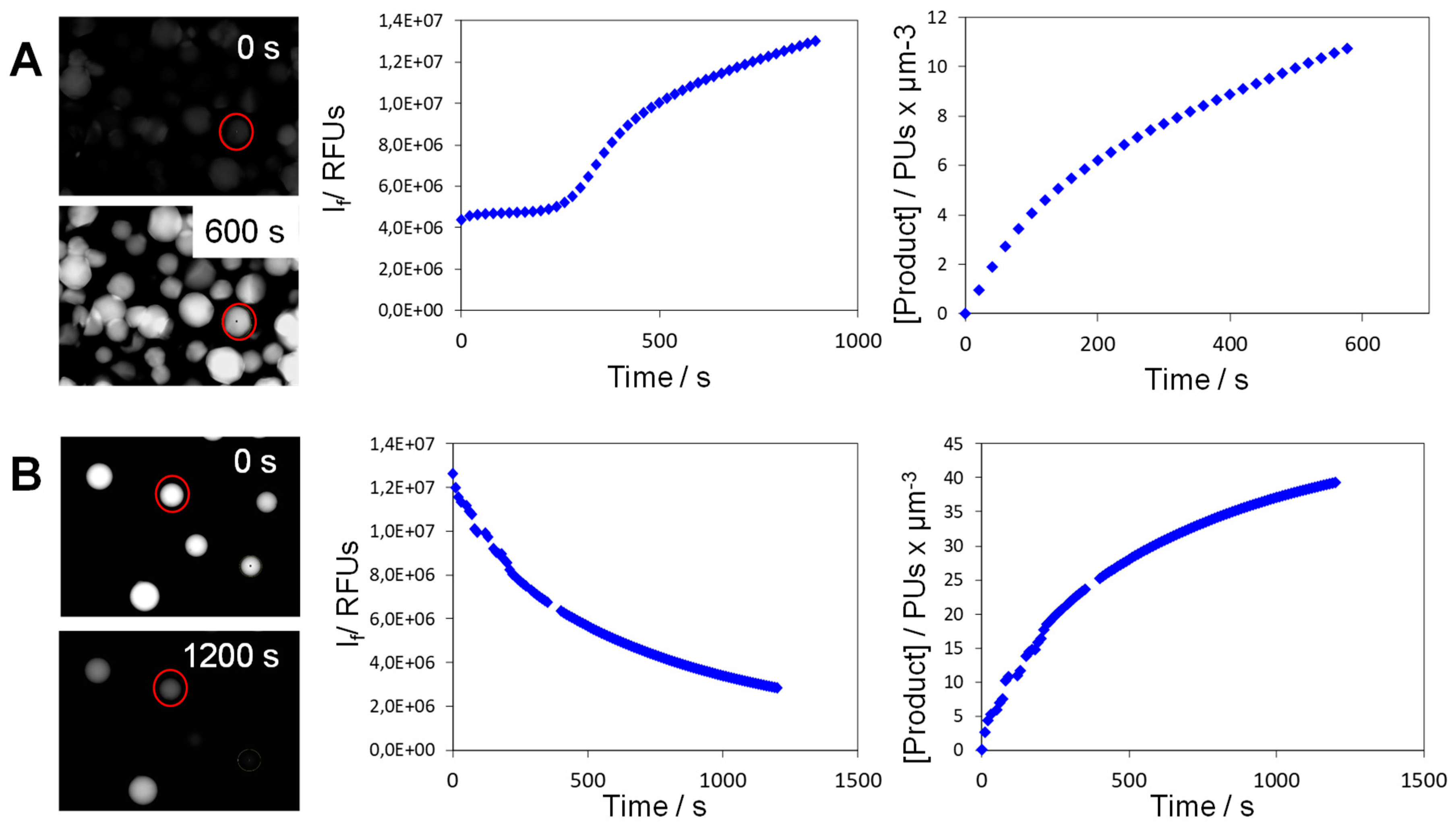
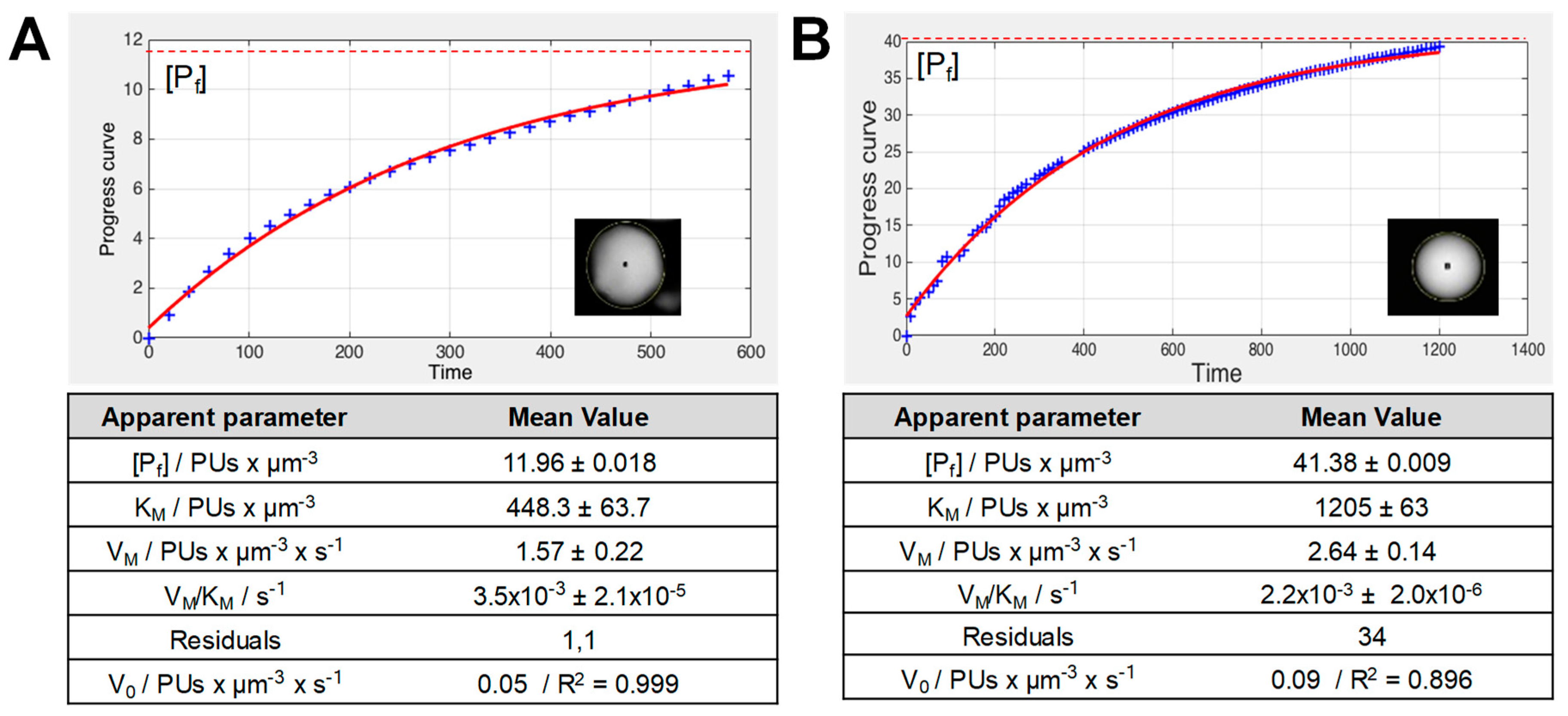
2.1. Validation of Image Analytics
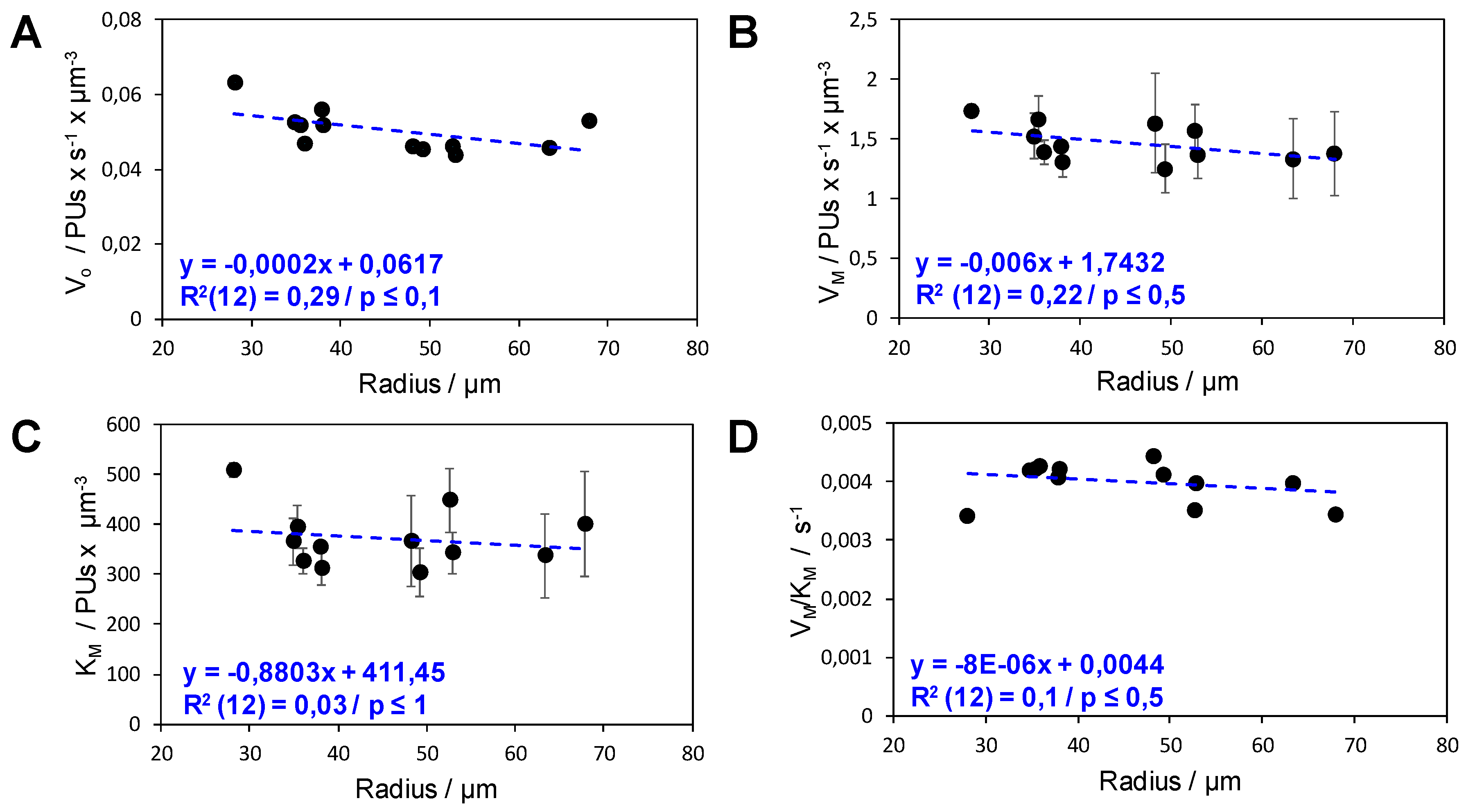
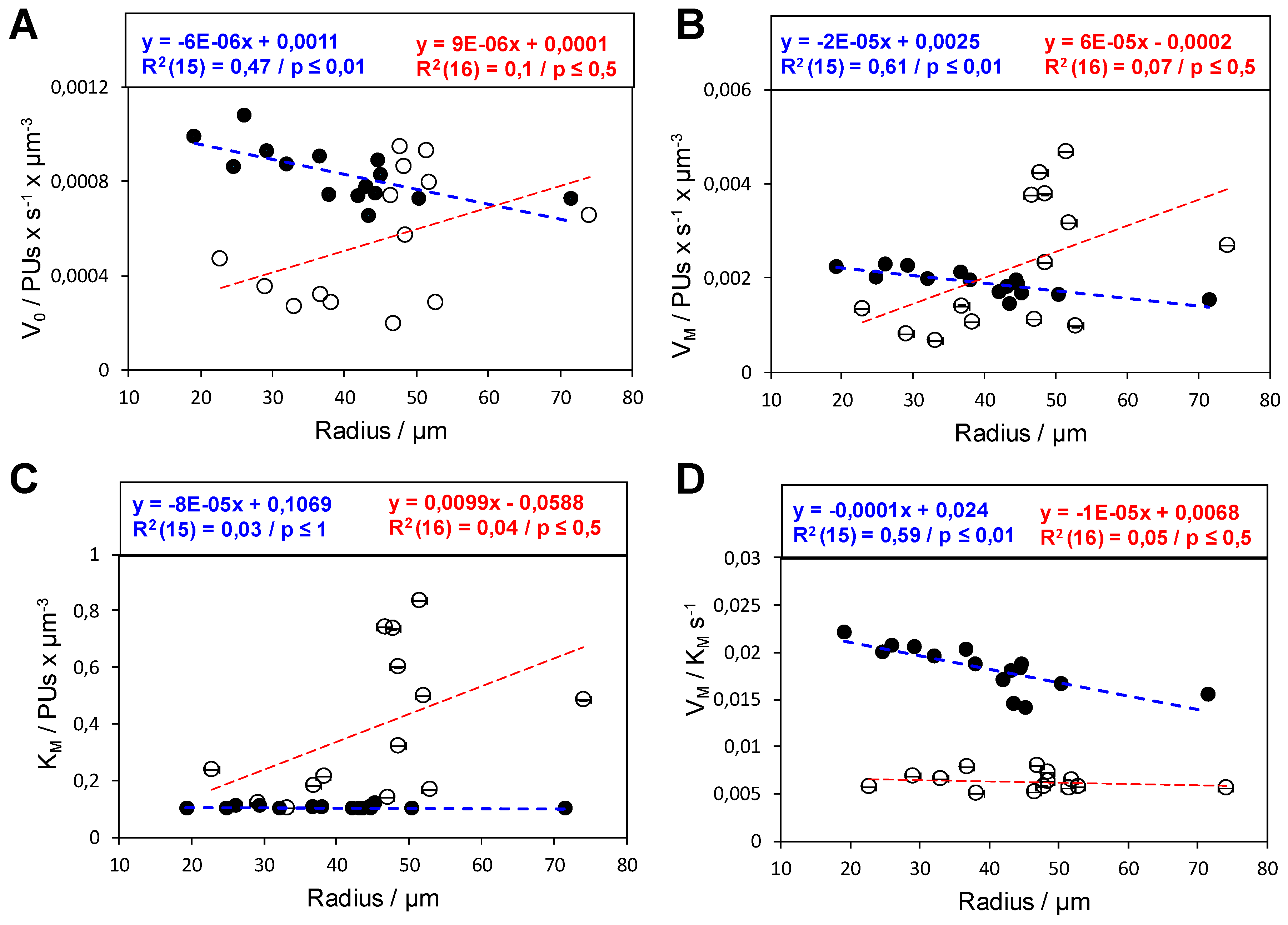
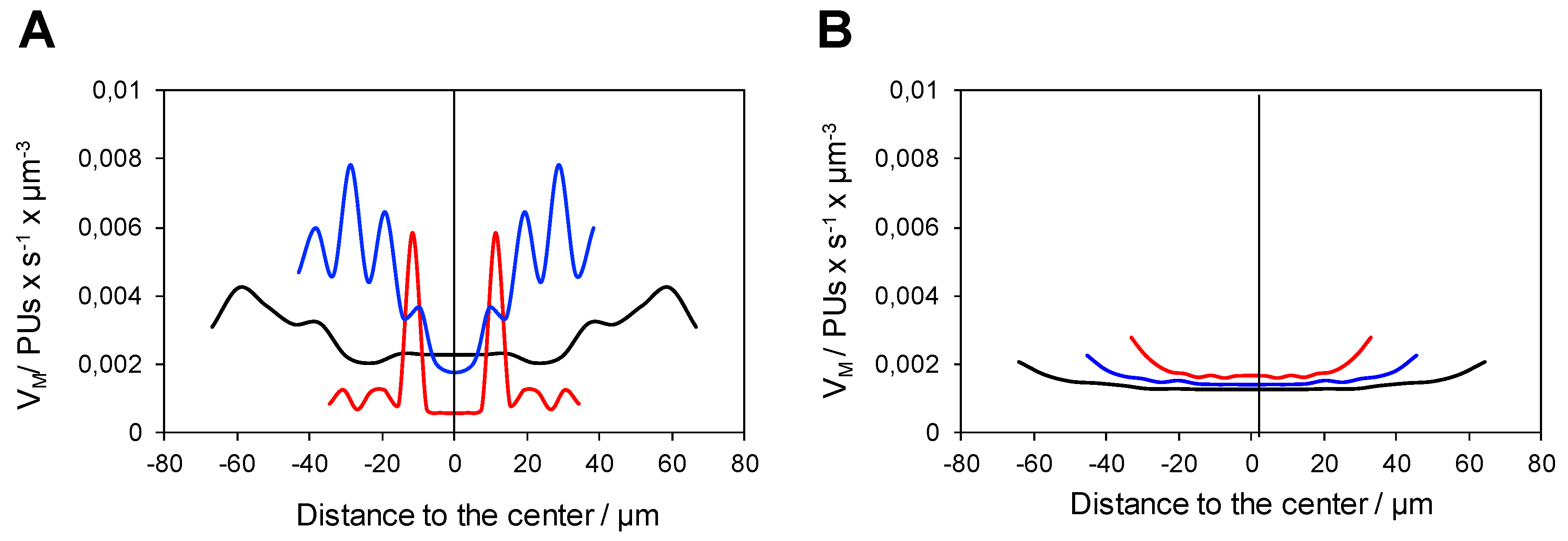
2.2. Analysis of the Functional Heterogeneity within Samples of Immobilized Enzymes
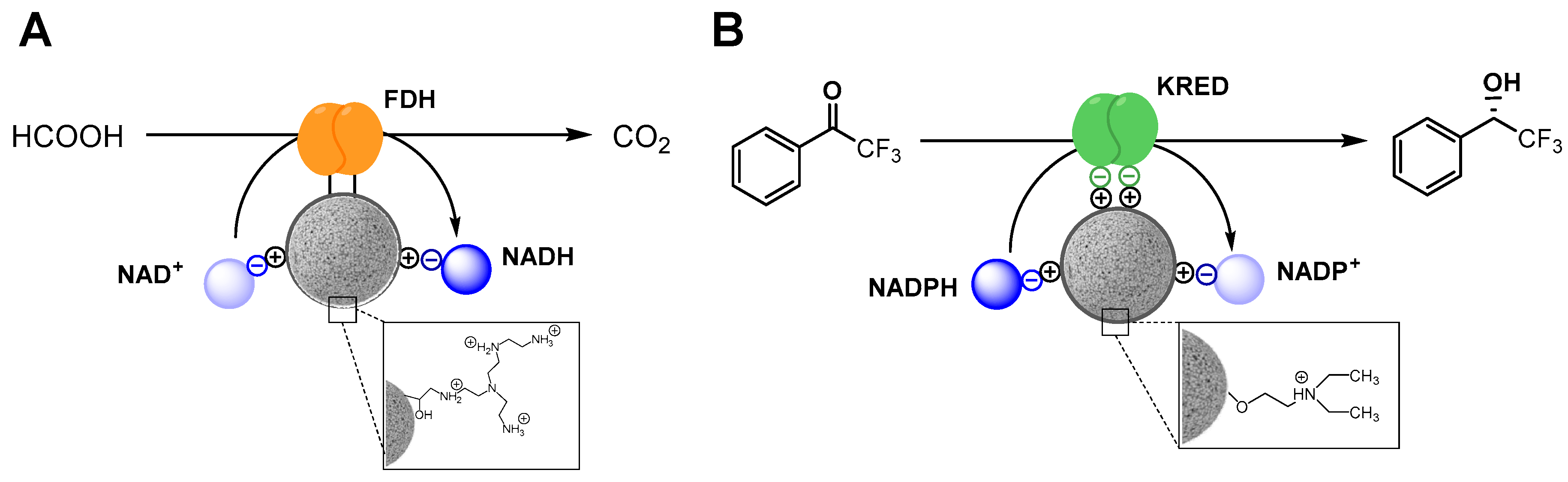
2.3. Functional Heterogeneity of a Co-Immobilized His-BsADH/NADH Pair Using Different Carbonylic Substrates
3. Materials and Methods
3.1. Materials
3.2. Expression and Immobilization of His-BsADH
3.3. Coating of Immobilized His-BsADH with PEI
3.4. Ionic Adsorption of NAD on His-BsADH Immobilized on Ag-Co2+ and Coated with PEI (NAD/PEI/His-BsADH@AG-Co2+)
3.5. Spectrophotometric Enzyme Assay
3.6. In Operando Activity Assays through Time-Lapse Fluorescence Microscopy
3.7. Image Processing and Analytics
3.7.1. Identification of Regions of Interest (ROIs) through Image Segmentation
3.7.2. Obtaining Reaction Progress Curves of Single Particles
3.8. Fitting of Normalized Time Courses to Determine the Kinetic Parameters of the Immobilized Enzymes
3.9. Initial Rate Analysis
3.10. Statistical Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- DiCosimo, R.; McAuliffe, J.; Poulose, A.J.; Bohlmann, G. Industrial use of immobilized enzymes. Chem. Soc. Rev. 2013, 42, 6437–6474. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, R.C.; Ortiz, C.; Berenguer-Murcia, A.; Torres, R.; Fernandez-Lafuente, R. Modifying enzyme activity and selectivity by immobilization. Chem. Soc. Rev. 2013, 42, 6290–6307. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Li, J.; Zhang, T. Heterogeneous single-atom catalysis. Nat. Rev. Chem. 2018, 2, 65–81. [Google Scholar] [CrossRef]
- Gao, W.Y.; Cardenal, A.D.; Wang, C.H.; Powers, D.C. In Operando Analysis of Diffusion in Porous Metal-Organic Framework Catalysts. Chemistry (Weinheim an der Bergstrasse, Germany) 2019, 25, 3465–3476. [Google Scholar] [CrossRef]
- Secundo, F. Conformational changes of enzymes upon immobilisation. Chem. Soc. Rev. 2013, 42, 6250–6261. [Google Scholar] [CrossRef]
- Bolivar, J.M.; Eisl, I.; Nidetzky, B. Advanced characterization of immobilized enzymes as heterogeneous biocatalysts. Catal. Today 2016, 259, 66–80. [Google Scholar] [CrossRef]
- Benítez-Mateos, A.I.; Nidetzky, B.; Bolivar, J.M.; López-Gallego, F. Single-Particle Studies to Advance the Characterization of Heterogeneous Biocatalysts. ChemCatChem 2018, 10, 654–665. [Google Scholar] [CrossRef]
- Weltz, J.S.; Schwartz, D.K.; Kaar, J.L. Surface-Mediated Protein Unfolding as a Search Process for Denaturing Sites. ACS Nano 2016, 10, 730–738. [Google Scholar] [CrossRef]
- Uemura, S.; Iizuka, R.; Ueno, T.; Shimizu, Y.; Taguchi, H.; Ueda, T.; Puglisi, J.D.; Funatsu, T. Single-molecule imaging of full protein synthesis by immobilized ribosomes. Nucleic Acids Res. 2008, 36, e70. [Google Scholar] [CrossRef][Green Version]
- Dorywalska, M.; Blanchard, S.C.; Gonzalez, R.L.; Kim, H.D.; Chu, S.; Puglisi, J.D. Site-specific labeling of the ribosome for single-molecule spectroscopy. Nucleic Acids Res. 2005, 33, 182–189. [Google Scholar] [CrossRef]
- Blanchard, S.C.; Kim, H.D.; Gonzalez, R.L., Jr.; Puglisi, J.D.; Chu, S. tRNA dynamics on the ribosome during translation. Proc. Natl. Acad. Sci. USA 2004, 101, 12893–12898. [Google Scholar] [CrossRef] [PubMed]
- Chirico, G.; Cannone, F.; Beretta, S.; Diaspro, A.; Campanini, B.; Bettati, S.; Ruotolo, R.; Mozzarelli, A. Dynamics of green fluorescent protein mutant2 in solution, on spin-coated glasses, and encapsulated in wet silica gels. Protein Sci. 2002, 11, 1152–1161. [Google Scholar] [CrossRef] [PubMed]
- Faulón Marruecos, D.; Schwartz, D.K.; Kaar, J.L. Impact of surface interactions on protein conformation. Curr. Opin. Colloid Interface Sci. 2018, 38, 45–55. [Google Scholar] [CrossRef]
- Cantone, S.; Ferrario, V.; Corici, L.; Ebert, C.; Fattor, D.; Spizzo, P.; Gardossi, L. Efficient immobilisation of industrial biocatalysts: Criteria and constraints for the selection of organic polymeric carriers and immobilisation methods. Chem. Soc. Rev. 2013, 42, 6262–6276. [Google Scholar] [CrossRef] [PubMed]
- Size Polydispersity of Agarose Microbeads ABTTM. Available online: https://www.abtbeads.es/size-exclusion-chromatography/plain-agarose-beads (accessed on 1 October 2019).
- Size Polydispersity of Metacrylate Microbeads PUROLITETM. Available online: https://www.purolite.com/ls-product-type/enzyme-immobilization-resins (accessed on 1 October 2019).
- Size Polydispersity of Metacrylate Microbeads RELIZYMETM. Available online: https://www.resindion.com/index.php?option=com_virtuemart&page=shop.browse&category_id=30&Itemid=53&TreeId=46 (accessed on 1 October 2019).
- Size Polydispersity of Silica-Based Porous Microparticle. Available online: https://www.sigmaaldrich.com/catalog/search?term=MFCD00163370&interface=MDL%20No.&N=0+&mode=partialmax&lang=es®ion=ES&focus=product (accessed on 1 October 2019).
- Size Polydispersity of Silica-Based Porous Microparticles EziGTM. Available online: http://enginzyme.com/wp-content/uploads/2017/03/EziG%E2%84%A2-Product-Data-Sheet.pdf (accessed on 1 October 2019).
- Suárez, S.; Guerrero, C.; Vera, C.; Illanes, A. Effect of particle size and enzyme load on the simultaneous reactions of lactose hydrolysis and transgalactosylation with glyoxyl-agarose immobilized β-galactosidase from Aspergillus oryzae. Process Biochem. 2018, 73, 56–64. [Google Scholar] [CrossRef]
- Bahamondes, C.; Illanes, A. Effect of internal diffusional restrictions on the selectivity of α-chymotrypsin in a series-parallel reaction of peptide synthesis. Process Biochem. 2018, 68, 117–120. [Google Scholar] [CrossRef]
- Valencia, P.; Wilson, L.; Aguirre, C.; Illanes, A. Evaluation of the incidence of diffusional restrictions on the enzymatic reactions of hydrolysis of penicillin G and synthesis of cephalexin. Enzyme Microb. Technol. 2010, 47, 268–276. [Google Scholar] [CrossRef]
- Bolivar, J.M.; Schelch, S.; Mayr, T.; Nidetzky, B. Mesoporous Silica Materials Labeled for Optical Oxygen Sensing and Their Application to Development of a Silica-Supported Oxidoreductase Biocatalyst. ACS Catal. 2015, 5, 5984–5993. [Google Scholar] [CrossRef]
- Consolati, T.; Bolivar, J.M.; Petrasek, Z.; Berenguer, J.; Hidalgo, A.; Guisan, J.M.; Nidetzky, B. Biobased, Internally pH-Sensitive Materials: Immobilized Yellow Fluorescent Protein as an Optical Sensor for Spatiotemporal Mapping of pH Inside Porous Matrices. ACS Appl. Mater. Interfaces 2018, 10, 6858–6868. [Google Scholar] [CrossRef]
- Kovarik, M.L.; Allbritton, N.L. Measuring enzyme activity in single cells. Trends Biotechnol. 2011, 29, 222–230. [Google Scholar] [CrossRef][Green Version]
- Muzzey, D.; van Oudenaarden, A. Quantitative time-lapse fluorescence microscopy in single cells. Annu. Rev. Cell. Dev. Biol. 2009, 25, 301–327. [Google Scholar] [CrossRef] [PubMed]
- Velasco-Lozano, S.; Benítez-Mateos, A.I.; López-Gallego, F. Co-immobilized Phosphorylated Cofactors and Enzymes as Self-Sufficient Heterogeneous Biocatalysts for Chemical Processes. Angew. Chem. Int. Ed. 2017, 56, 771–775. [Google Scholar] [CrossRef] [PubMed]
- Benítez-Mateos, A.I.; San Sebastian, E.; Ríos-Lombardía, N.; Morís, F.; González-Sabín, J.; López-Gallego, F. Asymmetric Reduction of Prochiral Ketones by Using Self-Sufficient Heterogeneous Biocatalysts Based on NADPH-Dependent Ketoreductases. Chem. Eur. J. 2017, 23, 16843–16852. [Google Scholar] [CrossRef] [PubMed]
- Illanes, A.; González, J.M.; Gómez, J.M.; Valencia, P.; Wilson, L. Diffusional restrictions in glyoxyl-agarose immobilized penicillin G acylase of different particle size and protein loading. Electron. J. Biotechnol. 2010, 13, 2–3. [Google Scholar] [CrossRef]
- Bäuerle, F.; Zotter, A.; Schreiber, G. Direct determination of enzyme kinetic parameters from single reactions using a new progress curve analysis tool. Protein Eng. Des. Sel. 2016, 30, 151–158. [Google Scholar] [CrossRef][Green Version]
- Illanes, A.; Fernandez-Lafuente, R.; Guisan, J.M.; Wilson, L. Heterogeneous Enzyme Kinetics. In Enzyme Biocatalysis; Illanes, A., Ed.; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar]
- Sigurdardóttir, S.B.; Lehmann, J.; Grivel, J.C.; Zhang, W.; Kaiser, A.; Pinelo, M. Alcohol dehydrogenase on inorganic powders: Zeta potential and particle agglomeration as main factors determining activity during immobilization. Colloids Surf. B Biointerfaces 2019, 175, 136–142. [Google Scholar] [CrossRef]
- Wang, C.; Lin, W. Diffusion-controlled luminescence quenching in metal-organic frameworks. J. Am. Chem. Soc. 2011, 133, 4232–4235. [Google Scholar] [CrossRef]
- Zotter, A.; Bauerle, F.; Dey, D.; Kiss, V.; Schreiber, G. Quantifying enzyme activity in living cells. J. Biol. Chem. 2017, 292, 15838–15848. [Google Scholar] [CrossRef]
- Lopez-Gallego, F.; Yate, L. Selective biomineralization of Co3(PO4)2-sponges triggered by His-tagged proteins: Efficient heterogeneous biocatalysts for redox processes. Chem. Commun. (Camb.) 2015, 51, 8753–8756. [Google Scholar] [CrossRef]
- Zimmerman, S.B.; Trach, S.O. Estimation of macromolecule concentrations and excluded volume effects for the cytoplasm of Escherichia coli. J. Mol. Biol. 1991, 222, 599–620. [Google Scholar] [CrossRef]
- Kienle, D.F.; Falatach, R.M.; Kaar, J.L.; Schwartz, D.K. Correlating Structural and Functional Heterogeneity of Immobilized Enzymes. ACS Nano 2018, 12, 8091–8103. [Google Scholar] [CrossRef] [PubMed]

| Carrier | Bead Size (µm) | Refs | |||
|---|---|---|---|---|---|
| Standard | Large | Small | Wide Range | ||
| ABTTM | 50–150 | n.a | 20–50 | n.a | [15] |
| PuroliteTM | 150–300 | 300–710 | n.a | 300–1200 | [16] |
| RelizymeTM | 100–300 | 200–500 | n.a | n.a | [17] |
| CPG-Silica | 120–200 | n.a | 20–80 | n.a | [18] |
| EziGTM | 75–125 | n.a | n.a | n.a | [19] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñoz-Morales, E.; Velasco-Lozano, S.; Benítez-Mateos, A.I.; Marín, M.J.; Ramos-Cabrer, P.; López-Gallego, F. Deciphering the Effect of Microbead Size Distribution on the Kinetics of Heterogeneous Biocatalysts through Single-Particle Analysis Based on Fluorescence Microscopy. Catalysts 2019, 9, 896. https://doi.org/10.3390/catal9110896
Muñoz-Morales E, Velasco-Lozano S, Benítez-Mateos AI, Marín MJ, Ramos-Cabrer P, López-Gallego F. Deciphering the Effect of Microbead Size Distribution on the Kinetics of Heterogeneous Biocatalysts through Single-Particle Analysis Based on Fluorescence Microscopy. Catalysts. 2019; 9(11):896. https://doi.org/10.3390/catal9110896
Chicago/Turabian StyleMuñoz-Morales, Emilio, Susana Velasco-Lozano, Ana I. Benítez-Mateos, María J. Marín, Pedro Ramos-Cabrer, and Fernando López-Gallego. 2019. "Deciphering the Effect of Microbead Size Distribution on the Kinetics of Heterogeneous Biocatalysts through Single-Particle Analysis Based on Fluorescence Microscopy" Catalysts 9, no. 11: 896. https://doi.org/10.3390/catal9110896
APA StyleMuñoz-Morales, E., Velasco-Lozano, S., Benítez-Mateos, A. I., Marín, M. J., Ramos-Cabrer, P., & López-Gallego, F. (2019). Deciphering the Effect of Microbead Size Distribution on the Kinetics of Heterogeneous Biocatalysts through Single-Particle Analysis Based on Fluorescence Microscopy. Catalysts, 9(11), 896. https://doi.org/10.3390/catal9110896








