RETRACTED: Catalytic Combustion Characteristics of Methane-Air Mixtures in Small-Scale Systems at Elevated Temperatures
Abstract
1. Introduction
2. Physical System and Modeling Approach
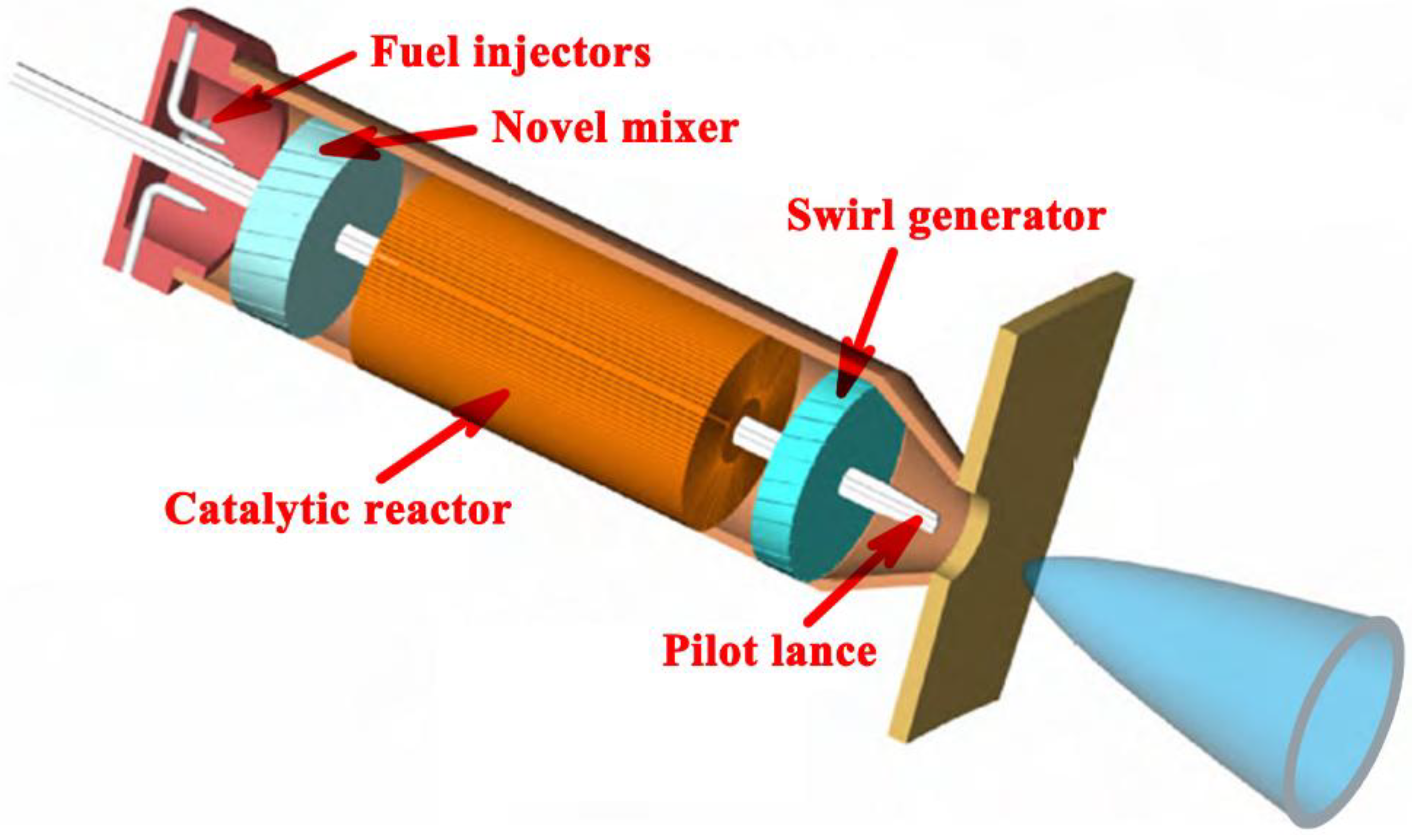
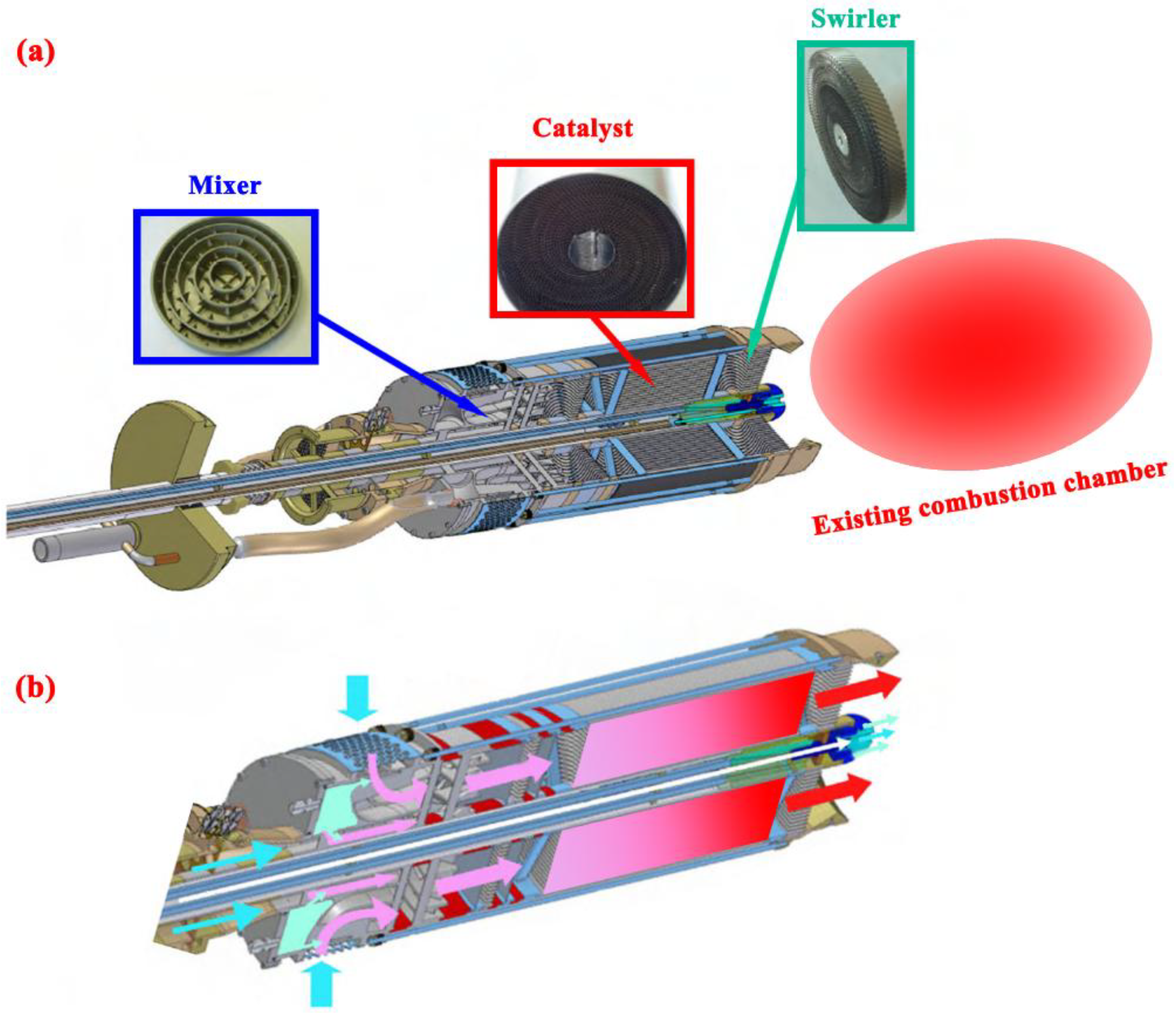
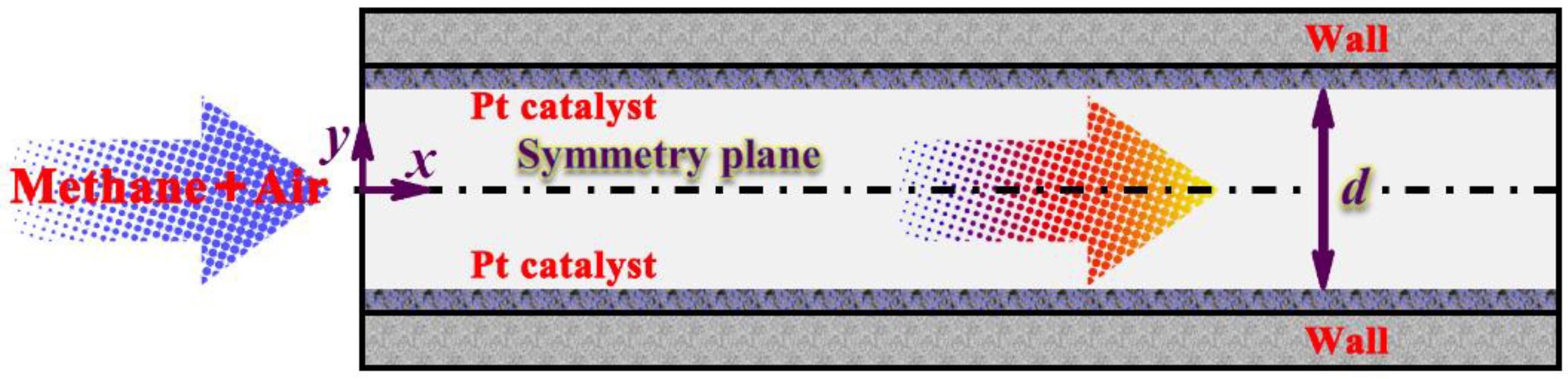
2.1. Physical Description of the Small-scale System
2.2. Mathematical Model
- The thermodynamic system operates under steady-state conditions.
- The gaseous mixture is assumed to behave qualitatively as an ideal gas.
- The flow distribution at the inlet of the channel is flat in the transverse direction.
- Pressure drop in the channel is negligible.
- There is a constant gas concentration and temperature at the inlet of the channel.
- The catalyst is uniformly distributed on the surface of the catalytic reactor.
2.3. Detailed Chemical Kinetic Model
2.4. Computation Scheme
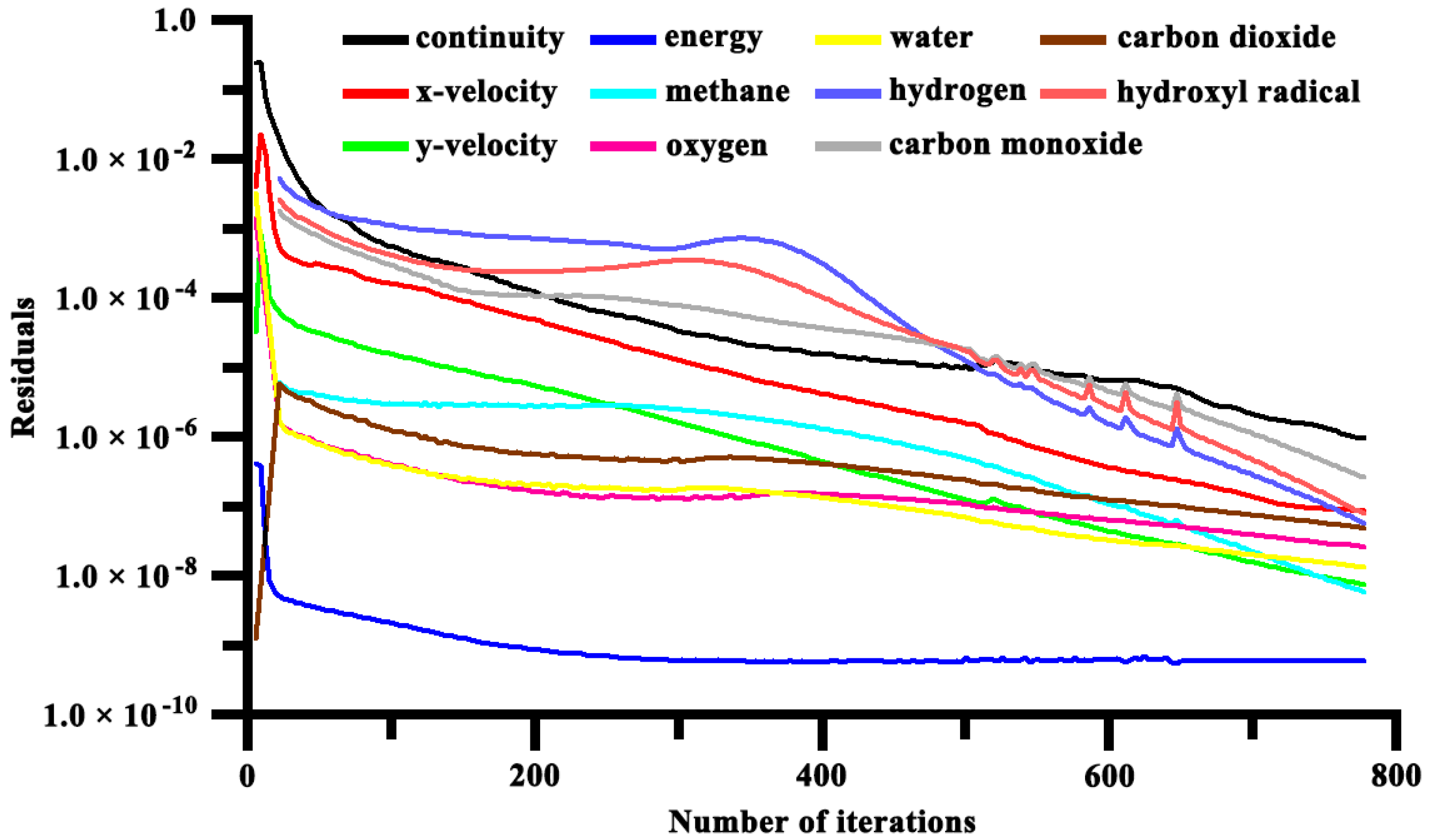
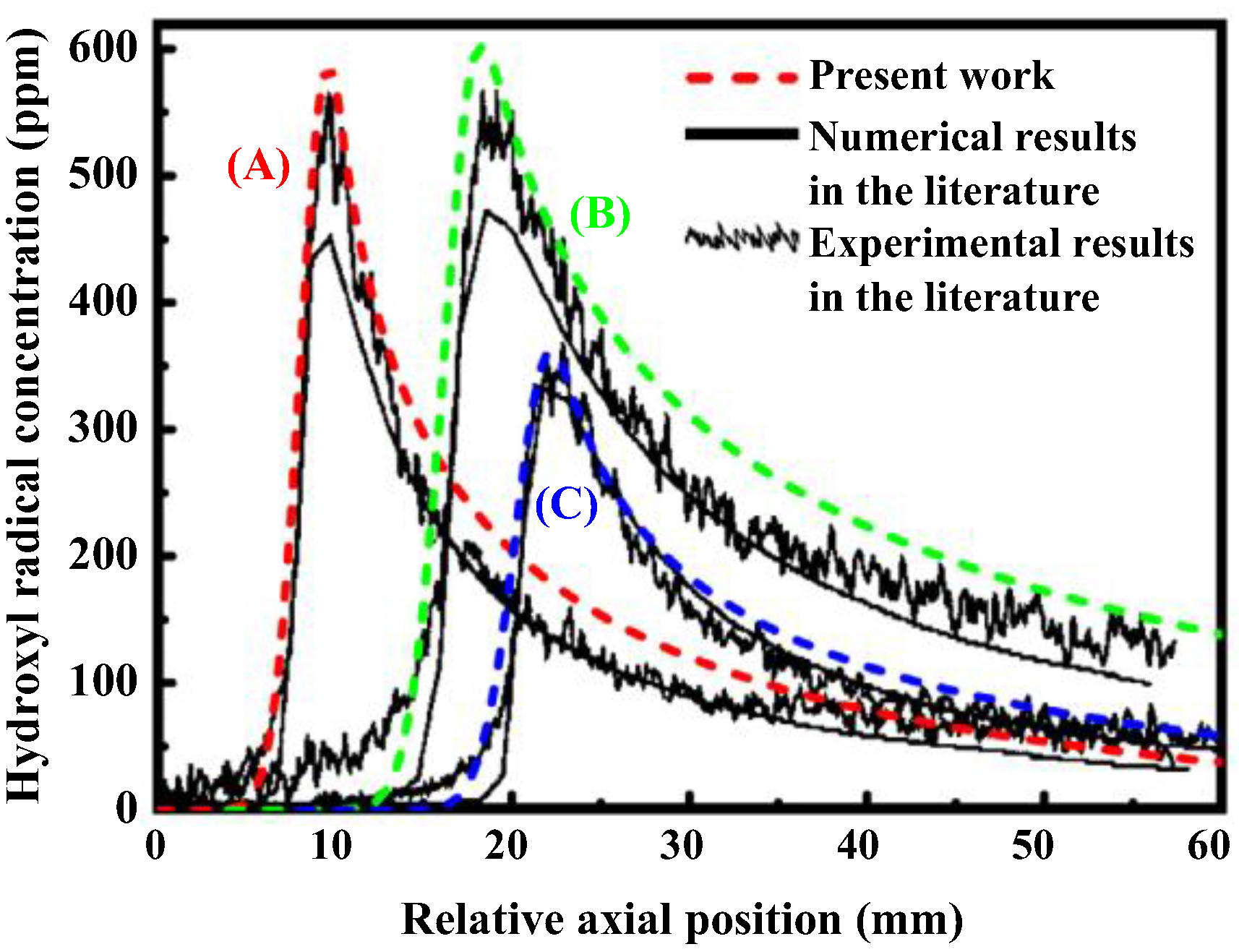
2.5. Numerical Validation
3. Combustion Modes and Major Pollutants
3.1. Combustion Modes
3.2. Major Pollutants
4. Results
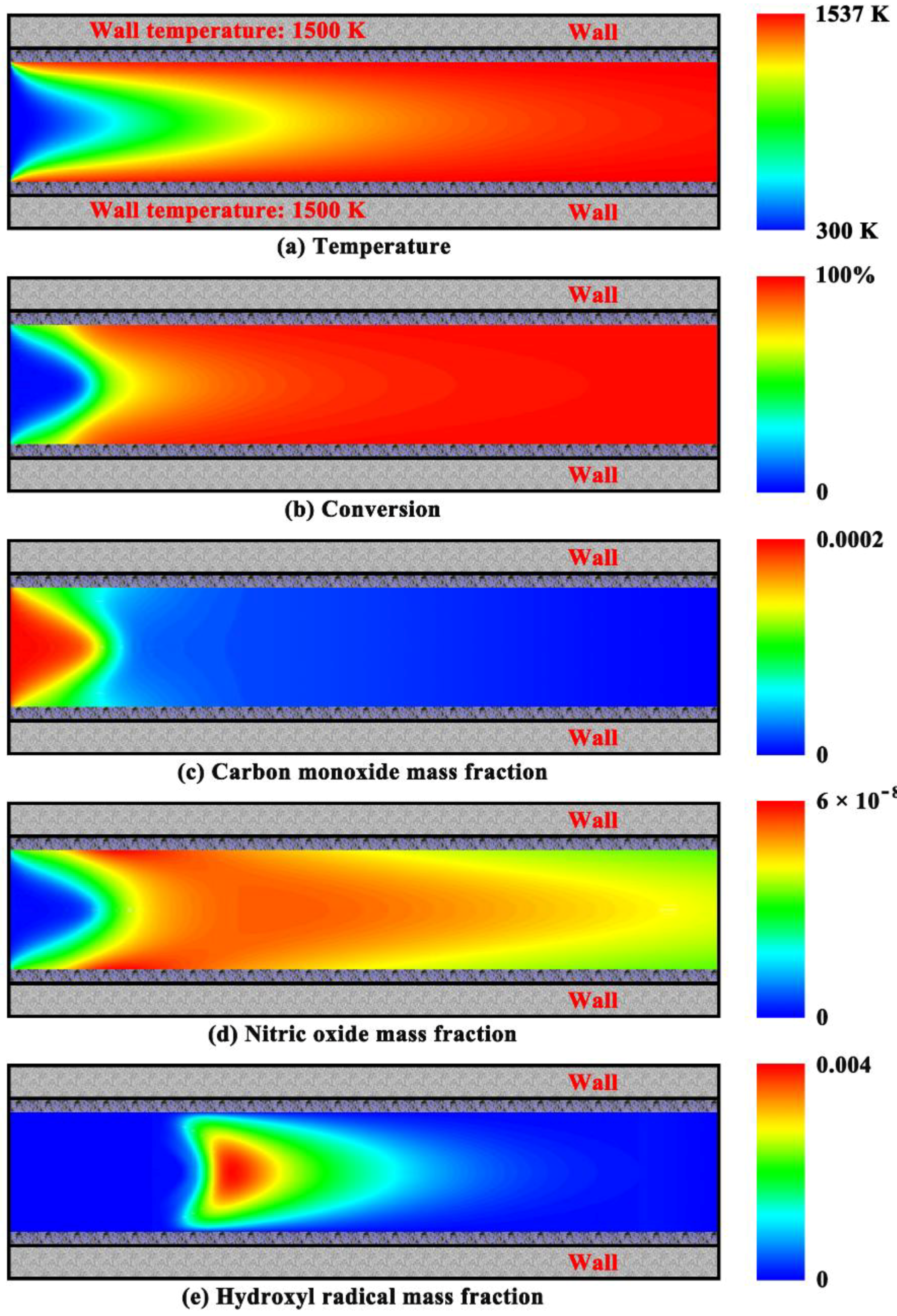
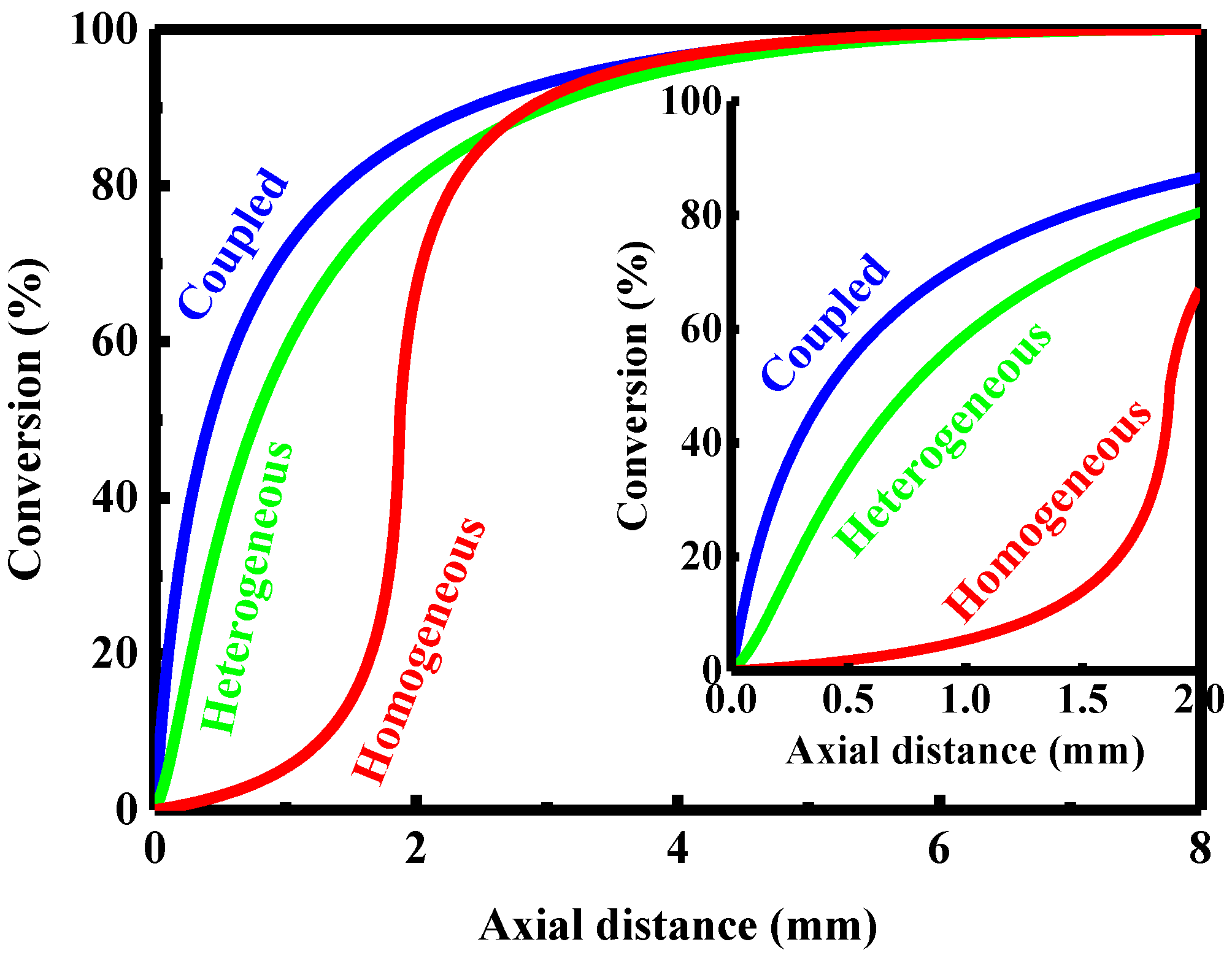
4.1. Coupled Homogeneous-Heterogeneous Combustion Characteristics
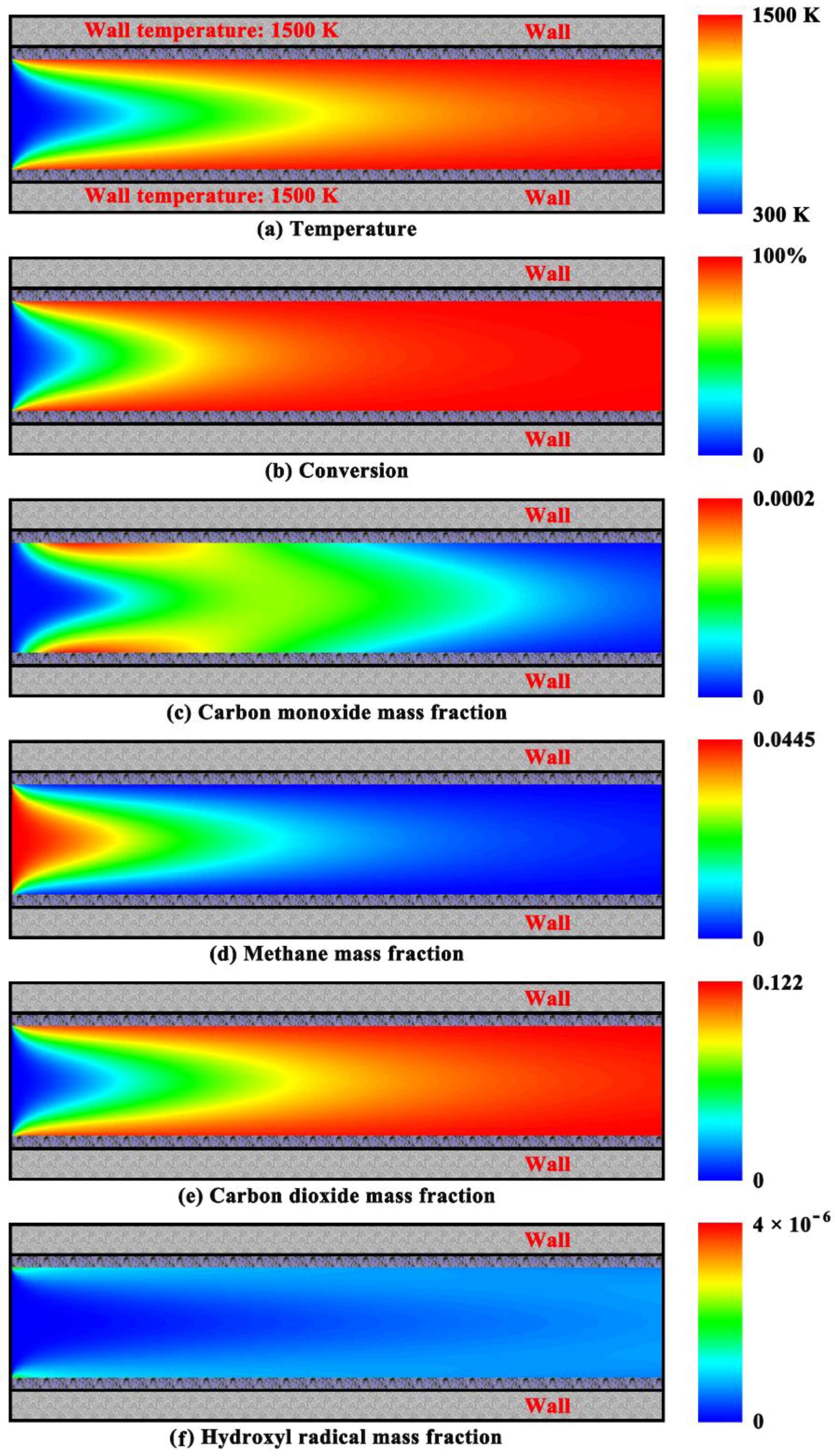
4.2. Purely Heterogeneous Combustion Characteristics
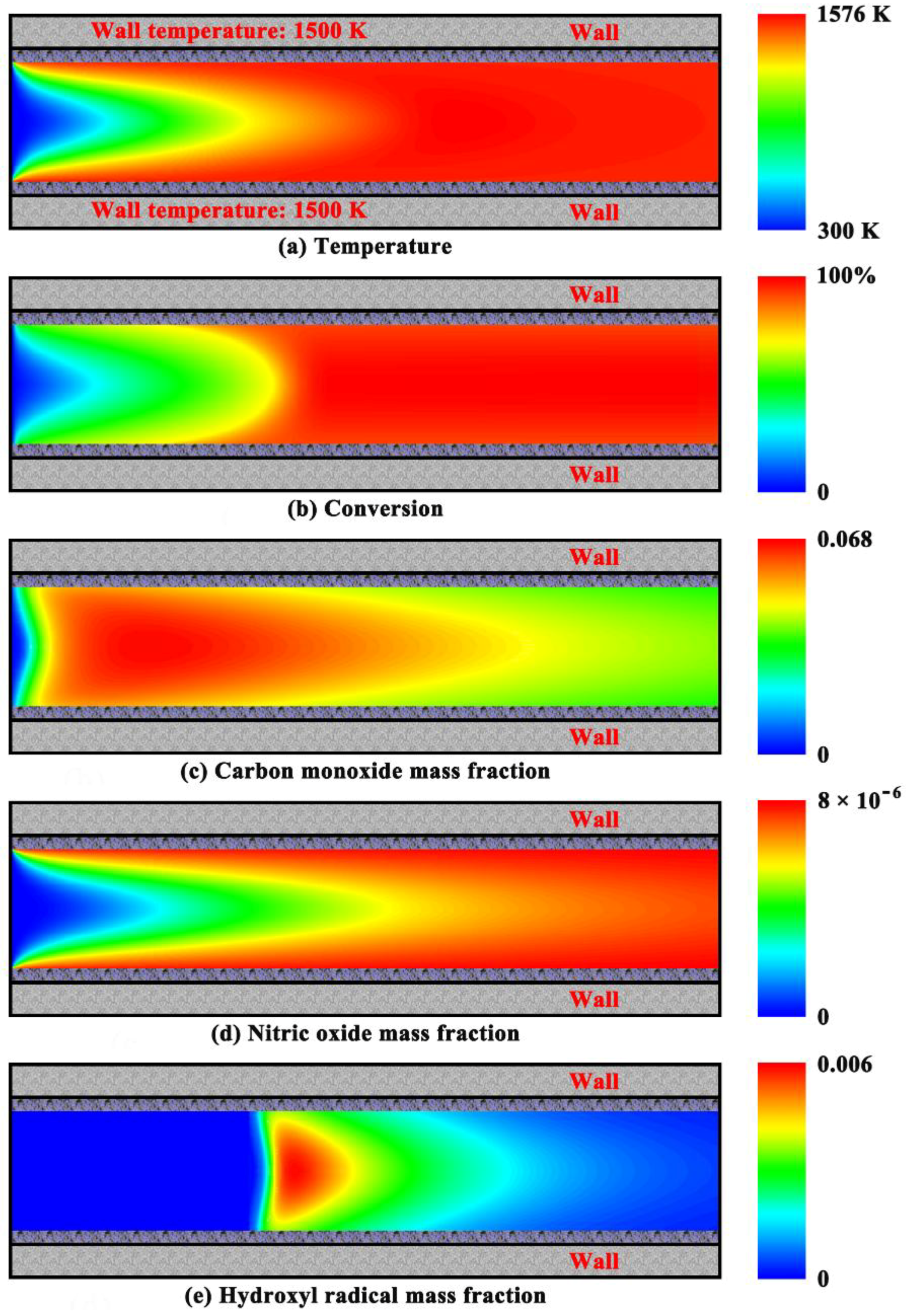
4.3. Purely Homogeneous Combustion Characteristics
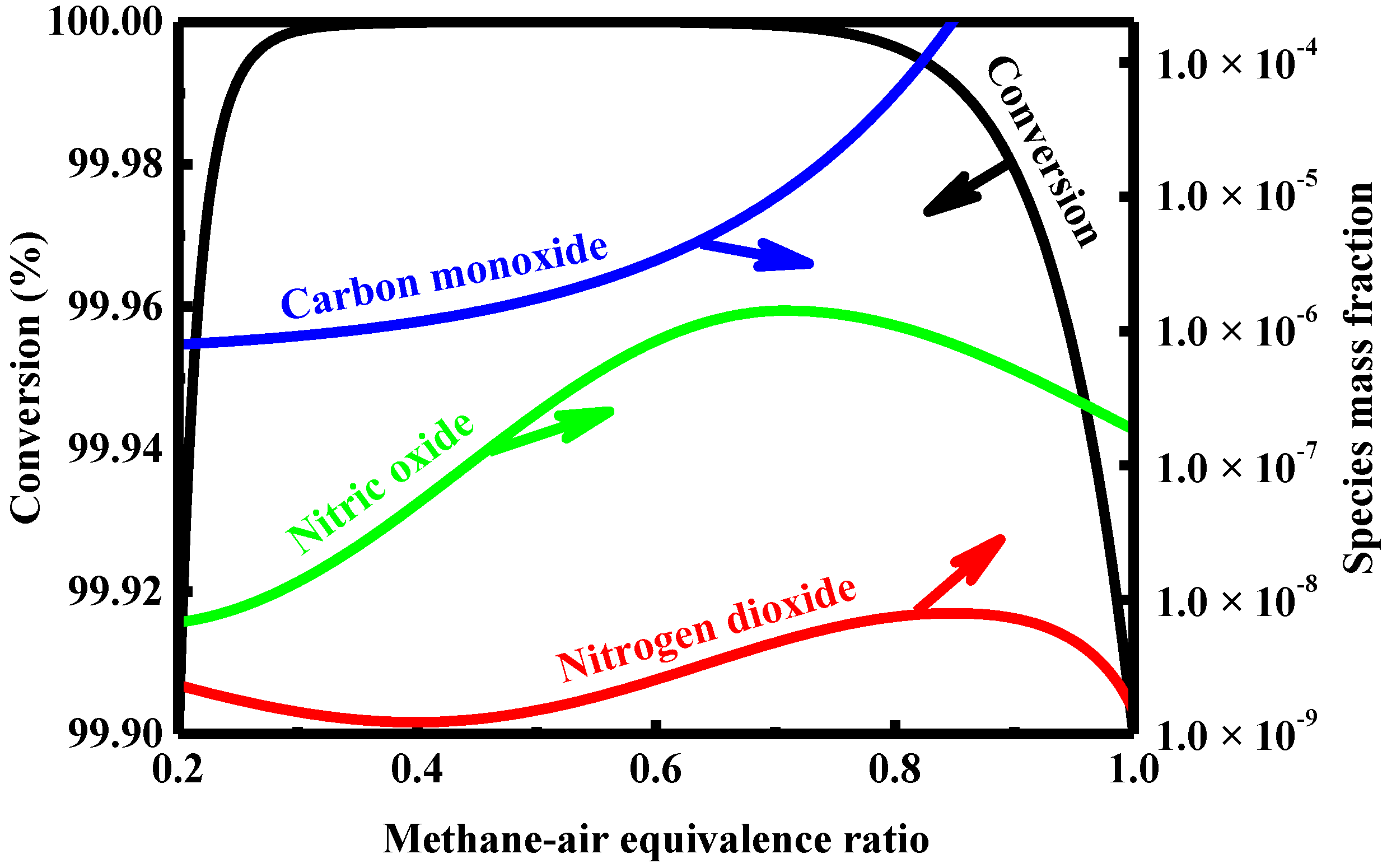
4.4. Effect of Feed Composition
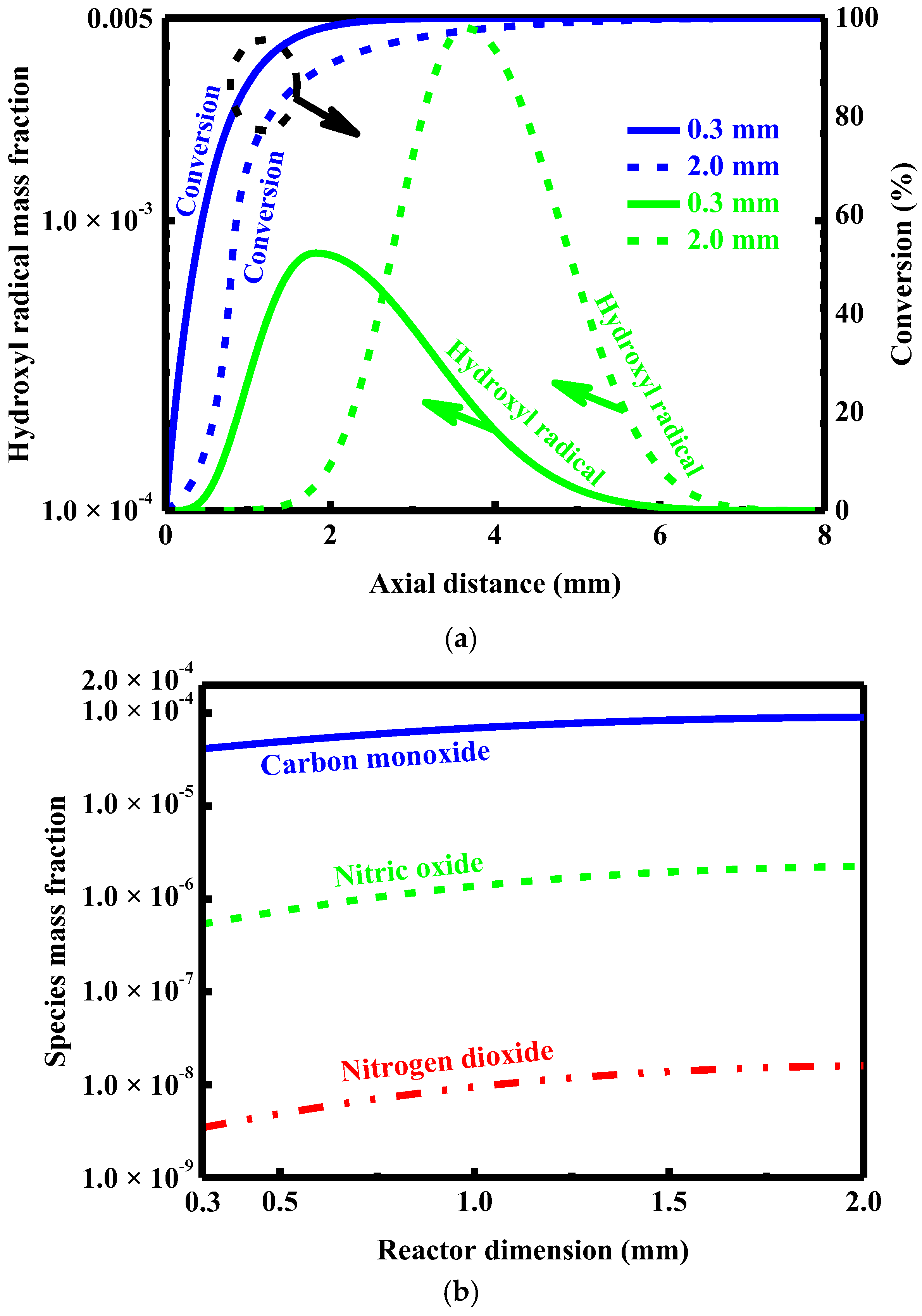
4.5. Effect of Dimension
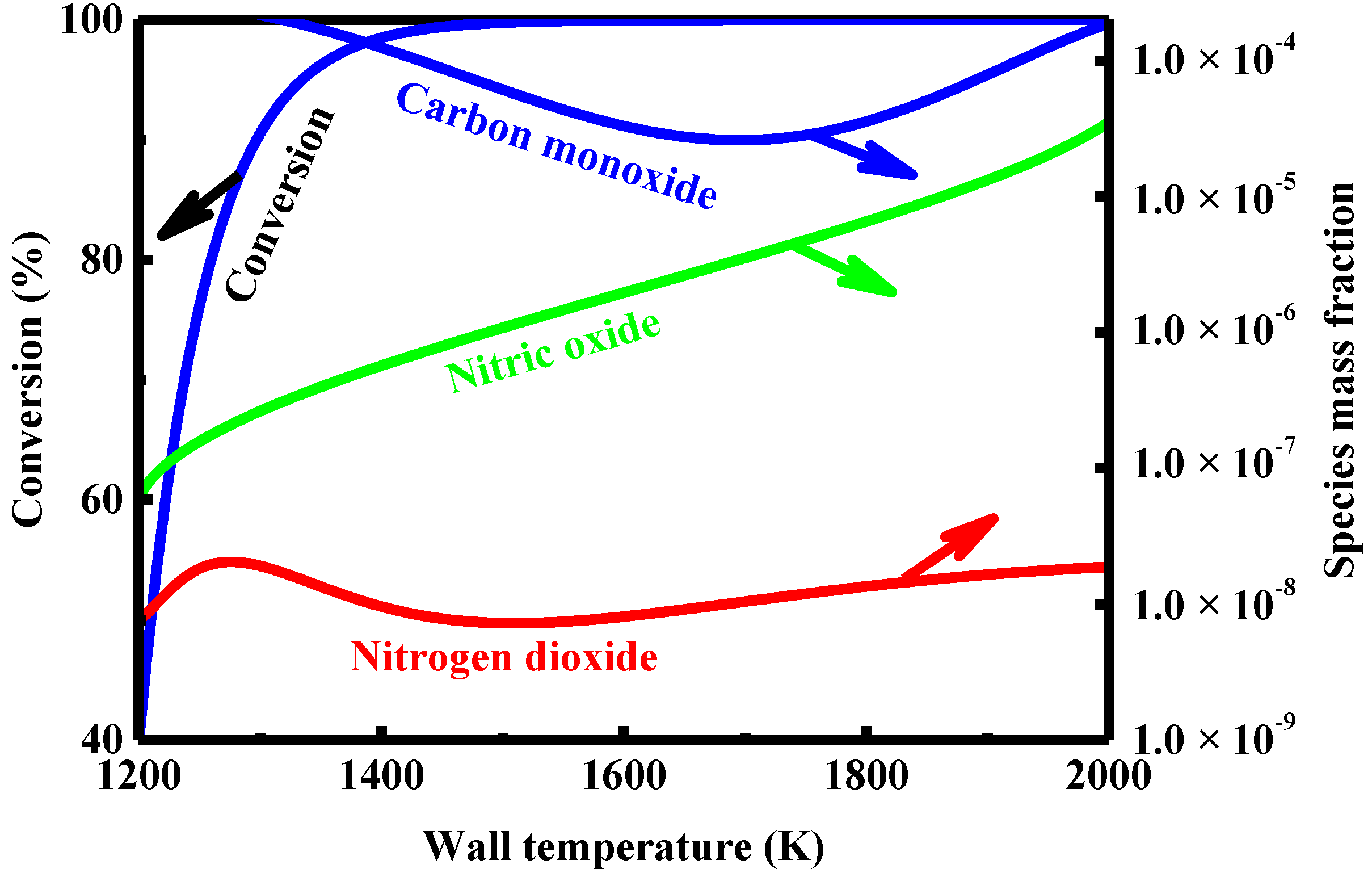
4.6. Effect of Wall Temperature
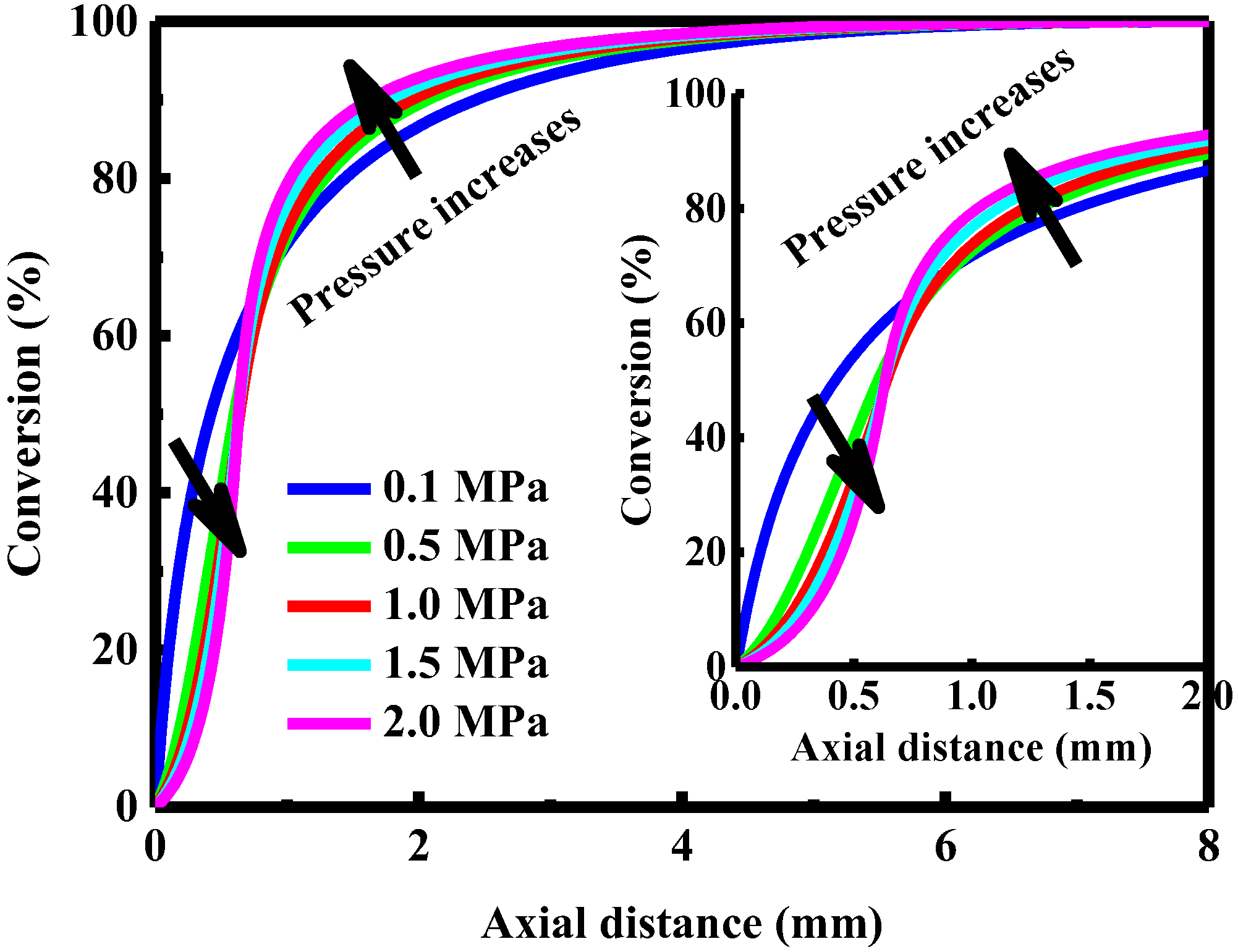
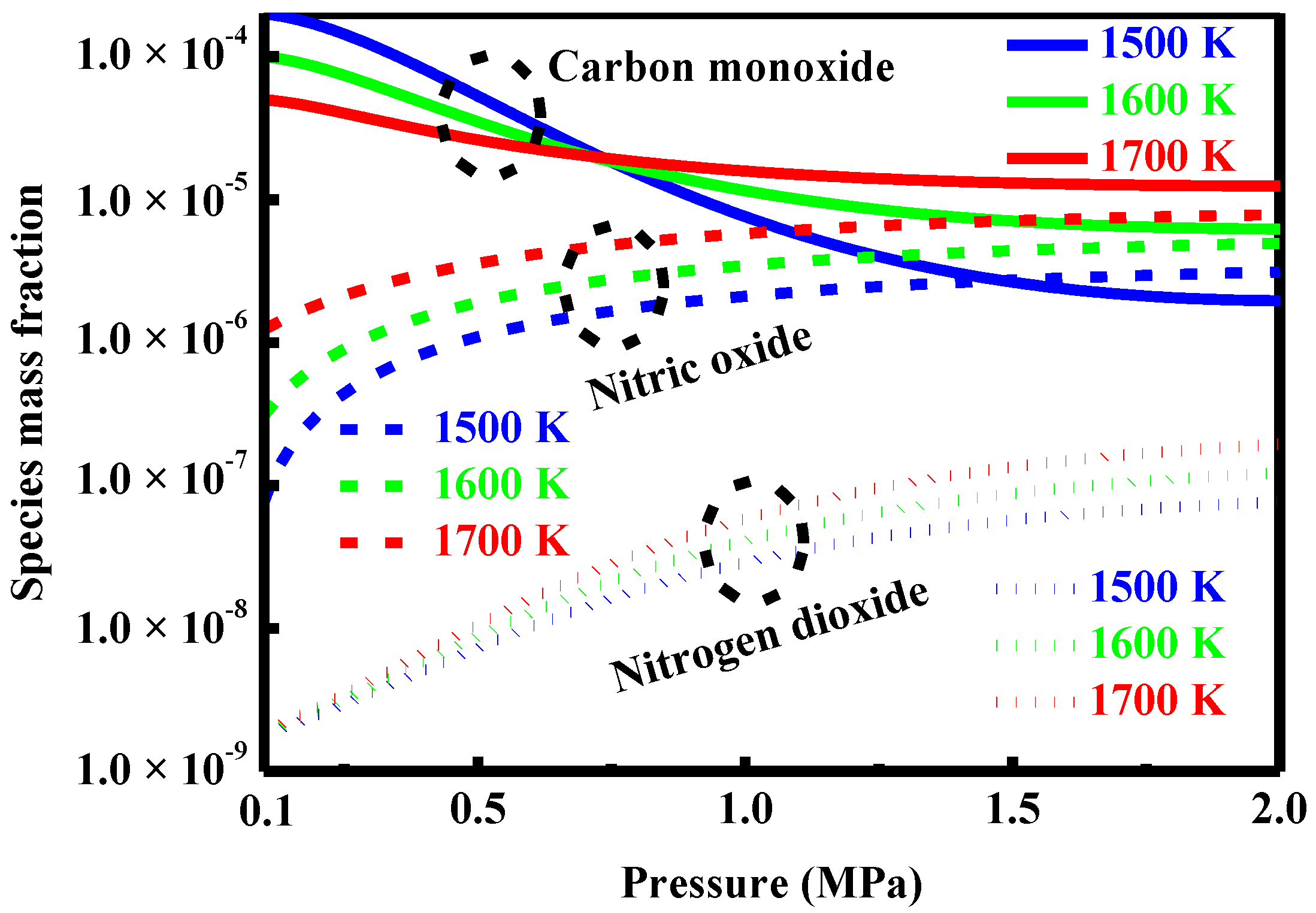
4.7. Effect of Pressure
5. Discussion
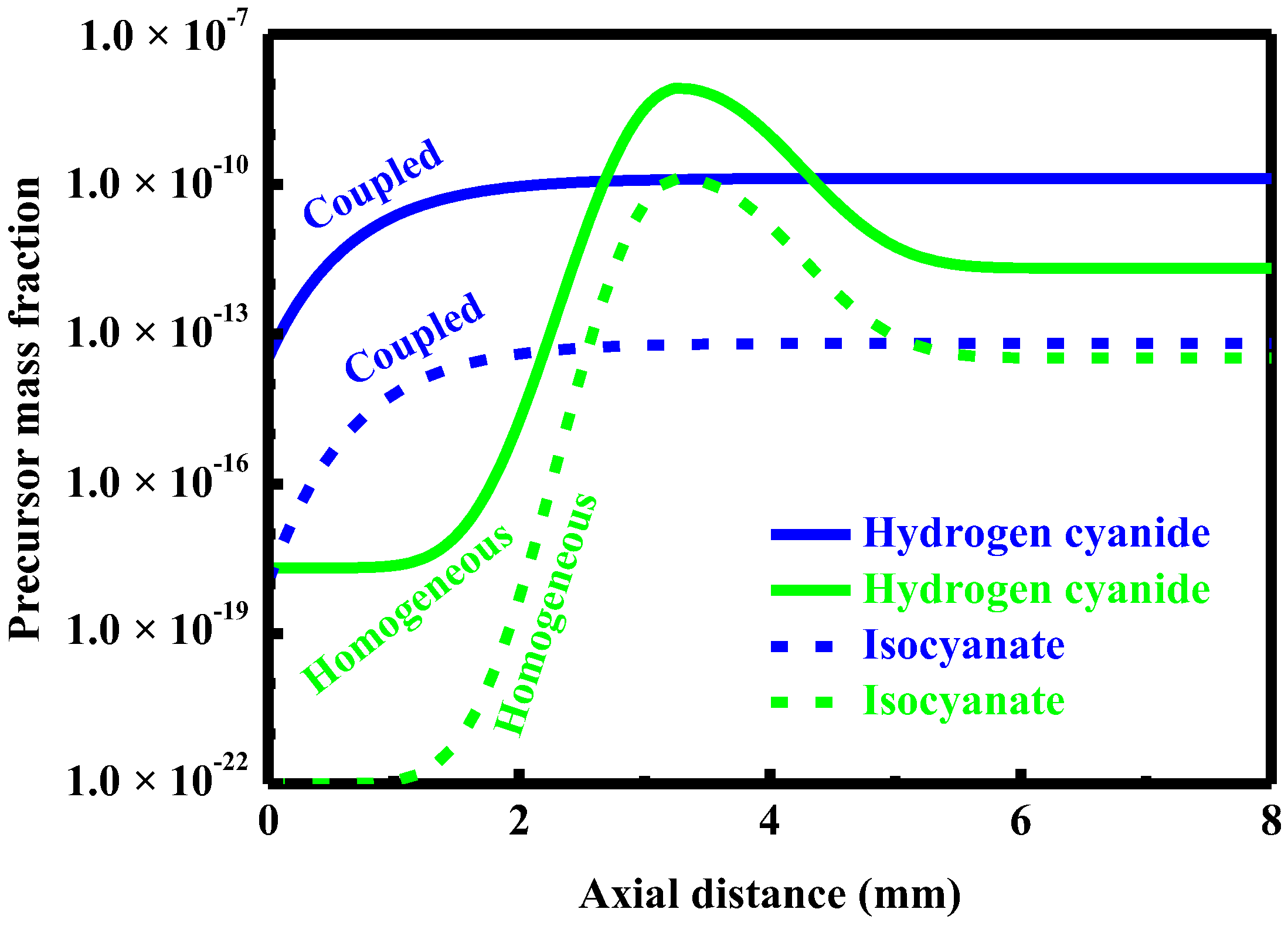
5.1. Competing Pathways of Two Parallel Reactions
5.2. Formation and Control of Carbon Monoxide
5.3. Formation and Control of the Oxides of Nitrogen
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shirsat, V.; Gupta, A.K. A review of progress in heat recirculating meso-scale combustors. Appl. Energy 2011, 88, 4294–4309. [Google Scholar] [CrossRef]
- Walther, D.C.; Ahn, J. Advances and challenges in the development of power-generation systems at small scales. Prog. Energy Combust. Sci. 2011, 37, 583–610. [Google Scholar] [CrossRef]
- Haynes, B.S. Combustion research for chemical processing. Proc. Combust. Inst. 2018, in press. [Google Scholar] [CrossRef]
- Chou, S.K.; Yang, W.M.; Chua, K.J.; Li, J.; Zhang, K.L. Development of micro power generators-A review. Appl. Energy 2011, 88, 1–16. [Google Scholar] [CrossRef]
- Kaisare, N.S.; Vlachos, D.G. A review on microcombustion: Fundamentals, devices and applications. Prog. Energy Combust. Sci. 2012, 38, 321–359. [Google Scholar] [CrossRef]
- Ju, Y.; Maruta, K. Microscale combustion: Technology development and fundamental research. Prog. Energy Combust. Sci. 2011, 37, 669–715. [Google Scholar] [CrossRef]
- Ribeirinha, P.; Abdollahzadeh, M.; Pereira, A.; Relvas, F.; Boaventura, M.; Mendes, A. High temperature PEM fuel cell integrated with a cellular membrane methanol steam reformer: Experimental and modelling. Appl. Energy 2018, 215, 659–669. [Google Scholar] [CrossRef]
- Chen, Y.; Yao, F.; Huang, X. Mass transfer and reaction in methanol steam reforming reactor with fractal tree-like microchannel network. Int. J. Heat Mass Transfer 2015, 87, 279–283. [Google Scholar] [CrossRef]
- Engelbrecht, N.; Chiuta, S.; Bessarabov, D.G. A highly efficient autothermal microchannel reactor for ammonia decomposition: Analysis of hydrogen production in transient and steady-state regimes. J. Power Sources 2018, 386, 47–55. [Google Scholar] [CrossRef]
- Kim, J.H.; Um, D.H.; Kwon, O.C. Hydrogen production from burning and reforming of ammonia in a microreforming system. Energy Convers. Manage. 2012, 56, 184–191. [Google Scholar] [CrossRef]
- Hockett, A.; Hampson, G.; Marchese, A.J. Development and validation of a reduced chemical kinetic mechanism for computational fluid dynamics simulations of natural gas/diesel dual-fuel engines. Energy Fuels 2016, 30, 2414–2427. [Google Scholar] [CrossRef]
- Tyagi, A.; Boxx, I.; Peluso, S.; O’Connor, J. The role of flow interaction in flame-flame interaction events in a dual burner experiment. Proc. Combust. Inst. 2018, in press. [Google Scholar] [CrossRef]
- Yehia, O.R.; Reuter, C.B.; Ju, Y. Low-temperature multistage warm diffusion flames. Combust. Flame 2018, 195, 63–74. [Google Scholar] [CrossRef]
- Burrell, R.R.; Lee, D.J.; Egolfopoulos, F.N. Propagation and extinction of subatmospheric counterflow methane flames. Combust. Flame 2018, 195, 117–127. [Google Scholar] [CrossRef]
- Smyth, S.A.; Kyritsis, D.C. Experimental determination of the structure of catalytic micro-combustion flows over small-scale flat plates for methane and propane fuel. Combust. Flame 2012, 159, 802–816. [Google Scholar] [CrossRef]
- Lyubovsky, M.; Smith, L.L.; Castaldi, M.; Karim, H.; Nentwick, B.; Etemad, S.; LaPierre, R.; Pfefferle, W.C. Catalytic combustion over platinum group catalysts: Fuel-lean versus fuel-rich operation. Catal. Today 2003, 83, 71–84. [Google Scholar] [CrossRef]
- Gancarczyk, A.; Iwaniszyn, M.; Piątek, M.; Korpyś, M.; Sindera, K.; Jodłowski, P.J.; Łojewska, J.; Kołodziej, A. Catalytic combustion of low-concentration methane on structured catalyst supports. Ind. Eng. Chem. Res. 2018, 57, 10281–10291. [Google Scholar] [CrossRef]
- Jodłowski, P.J.; Jędrzejczyk, R.J.; Chlebda, D.; Gierada, M.; Łojewska, J. In situ spectroscopic studies of methane catalytic combustion over Co, Ce, and Pd mixed oxides deposited on a steel surface. J. Catal. 2017, 350, 1–12. [Google Scholar] [CrossRef]
- Nguyen, V.N.; Deja, R.; Peters, R.; Blum, L.; Stolten, D. Study of the catalytic combustion of lean hydrogen-air mixtures in a monolith reactor. Int. J. Hydrogen Energy 2018, 43, 17520–17530. [Google Scholar] [CrossRef]
- San José, M.J.; Alvarez, S.; López, R. Catalytic combustion of vineyard pruning waste in a conical spouted bed combustor. Catal. Today 2018, 305, 13–18. [Google Scholar] [CrossRef]
- Carroni, R.; Griffin, T. Catalytic, hybrid lean combustion for gas turbines. Catal. Today 2010, 155, 2–12. [Google Scholar] [CrossRef]
- Forzatti, P. Status and perspectives of catalytic combustion for gas turbines. Catal. Today 2003, 83, 3–18. [Google Scholar] [CrossRef]
- Mundhwa, M.; Thurgood, C.P. Numerical study of methane steam reforming and methane combustion over the segmented and continuously coated layers of catalysts in a plate reactor. Fuel Process. Technol. 2017, 158, 57–72. [Google Scholar] [CrossRef]
- Di Benedetto, A.; Landi, G.; Di Sarli, V.; Barbato, P.S.; Pirone, R.; Russo, G. Methane catalytic combustion under pressure. Catal. Today 2012, 197, 206–213. [Google Scholar] [CrossRef]
- Richardson, J.T.; Shafiei, M.; Cantu, T.; Machiraju, D.; Telleen, S. Low NOx emission combustion catalyst using ceramic foam supports. Stud. Surf. Sci. Catal. 2004, 147, 457–462. [Google Scholar]
- D’Alessandro, F.; Pacchiarotta, G.; Rubino, A.; Sperandio, M.; Villa, P.; Carrera, A.M.; Fakhrai, R.; Marra, G.; Congiu, A. Lean catalytic combustion for ultra-low emissions at high temperature in gas-turbine burners. Energy Fuels 2011, 25, 136–143. [Google Scholar] [CrossRef]
- Runyon, J.; Marsh, R.; Bowen, P.; Pugh, D.; Giles, A.; Morris, S. Lean methane flame stability in a premixed generic swirl burner: Isothermal flow and atmospheric combustion characterization. Exp. Therm. Fluid Sci. 2018, 92, 125–140. [Google Scholar] [CrossRef]
- Jainski, C.; Rißmann, M.; Böhm, B.; Janicka, J.; Dreizler, A. Sidewall quenching of atmospheric laminar premixed flames studied by laser-based diagnostics. Combust. Flame 2017, 183, 271–282. [Google Scholar] [CrossRef]
- James, A.; Brindley, J.; McIntosh, A.C. Classification of behaviour in a steady plug-flow model of catalytic combustion. Chem. Eng. Sci. 2001, 56, 4649–4658. [Google Scholar] [CrossRef]
- James, A.; Brindley, J.; McIntosh, A.C. Stability of multiple steady states of catalytic combustion. Combust. Flame 2002, 130, 137–146. [Google Scholar] [CrossRef]
- Tolmachoff, E.D.; Booth, A.D.; Lee, I.C.; Allmon, W.R.; Waits, C.M. Modeling and experimental analysis of n-dodecane oxidation in platinum-coated channels. Combust. Flame 2015, 162, 3674–3680. [Google Scholar] [CrossRef]
- Richards, G.A.; McMillian, M.M.; Gemmen, R.S.; Rogers, W.A.; Cully, S.R. Issues for low-emission, fuel-flexible power systems. Prog. Energy Combust. Sci. 2001, 27, 141–169. [Google Scholar] [CrossRef]
- Li, Y.-H.; Chen, G.-B.; Wu, F.-H.; Cheng, T.-S.; Chao, Y.-C. Combustion characteristics in a small-scale reactor with catalyst segmentation and cavities. Proc. Combust. Inst. 2013, 34, 2253–2259. [Google Scholar] [CrossRef]
- Li, Y.-H.; Chen, G.-B.; Wu, F.-H.; Cheng, T.-S.; Chao, Y.-C. Effects of catalyst segmentation with cavities on combustion enhancement of blended fuels in a micro channel. Combust. Flame 2012, 159, 1644–1651. [Google Scholar] [CrossRef]
- Shimizu, T.; Abid, A.D.; Poskrebyshev, G.; Wang, H.; Nabity, J.; Engel, J.; Yu, J.; Wickham, D.; Van Devener, B.; Anderson, S.L.; Williams, S. Methane ignition catalyzed by in situ generated palladium nanoparticles. Combust. Flame 2010, 157, 421–435. [Google Scholar] [CrossRef]
- Kommu, M.; Kaisare, N.S. Ignition of homo/hetero combustion of propane in a microreactor with catalyst segmentation. Chem. Eng. Res. Des. 2018, 138, 125–134. [Google Scholar] [CrossRef]
- Jeon, S.W.; Yoon, W.J.; Jeong, M.W.; Kim, Y. Optimization of a counter-flow microchannel reactor using hydrogen assisted catalytic combustion for steam reforming of methane. Int. J. Hydrogen Energy 2014, 39, 6470–6478. [Google Scholar] [CrossRef]
- Mundhwa, M.; Parmar, R.D.; Thurgood, C.P. A comparative parametric study of a catalytic plate methane reformer coated with segmented and continuous layers of combustion catalyst for hydrogen production. J. Power Sources 2017, 344, 85–102. [Google Scholar] [CrossRef]
- Kunte, A.; Raghu, A.K.; Kaisare, N.S. A spiral microreactor for improved stability and performance for catalytic combustion of propane. Chem. Eng. Sci. 2018, 187, 87–97. [Google Scholar] [CrossRef]
- Carroni, R.; Griffin, T.; Kelsall, G. Cathlean: catalytic, hybrid, lean-premixed burner for gas turbines. Appl. Therm. Eng. 2004, 24, 1665–1676. [Google Scholar] [CrossRef]
- Kaisare, N.S.; Deshmukh, S.R.; Vlachos, D.G. Stability and performance of catalytic microreactors: Simulations of propane catalytic combustion on Pt. Chem. Eng. Sci. 2008, 63, 1098–1116. [Google Scholar] [CrossRef]
- Goralski, C.T.; Schmidt, L.D. Modeling heterogeneous and homogeneous reactions in the high-temperature catalytic combustion of methane. Chem. Eng. Sci. 1999, 54, 5791–5807. [Google Scholar] [CrossRef]
- Fumey, B.; Buetler, T.; Vogt, U.F. Ultra-low NOx emissions from catalytic hydrogen combustion. Appl. Energy 2018, 213, 334–342. [Google Scholar] [CrossRef]
- Hinokuma, S.; Kiritoshi, S.; Kawabata, Y.; Araki, K.; Matsuki, S.; Sato, T.; Machida, M. Catalytic ammonia combustion properties and operando characterization of copper oxides supported on aluminum silicates and silicon oxides. J. Catal. 2018, 361, 267–277. [Google Scholar] [CrossRef]
- Pfefferle, L.D. Heterogeneous/homogeneous reactions and transport coupling for catalytic combustion systems: a review of model alternatives. Catal. Today 1995, 26, 255–265. [Google Scholar] [CrossRef]
- Westbrook, C.K.; Mizobuchi, Y.; Poinsot, T.J.; Smith, P.J.; Warnatz, J. Computational combustion. Proc. Combust. Inst. 2005, 30, 125–157. [Google Scholar] [CrossRef]
- Law, C.K. Combustion at a crossroads: Status and prospects. Proc. Combust. Inst. 2007, 31, 1–29. [Google Scholar] [CrossRef]
- Miller, J.A.; Pilling, M.J.; Troe, J. Unravelling combustion mechanisms through a quantitative understanding of elementary reactions. Proc. Combust. Inst. 2005, 301, 43–88. [Google Scholar] [CrossRef]
- Klippenstein, S.J. From theoretical reaction dynamics to chemical modeling of combustion. Proc. Combust. Inst. 2017, 36, 77–111. [Google Scholar] [CrossRef]
- Buckmaster, J.; Clavin, P.; Liñán, A.; Matalon, M.; Peters, N.; Sivashinsky, G.; Williams, F.A. Combustion theory and modeling. Proc. Combust. Inst. 2005, 30, 1–19. [Google Scholar] [CrossRef]
- Kiefer, J.; Ewart, P. Laser diagnostics and minor species detection in combustion using resonant four-wave mixing. Prog. Energy Combust. Sci. 2011, 37, 525–564. [Google Scholar] [CrossRef]
- Michelsen, H.A.; Schulz, C.; Smallwood, G.J.; Will, S. Laser-induced incandescence: Particulate diagnostics for combustion, atmospheric, and industrial applications. Prog. Energy Combust. Sci. 2015, 51, 2–48. [Google Scholar] [CrossRef]
- Choudary, C.; Mazumder, S. Direct numerical simulation of catalytic combustion in a multi-channel monolith reactor using personal computers with emerging architectures. Comput. Chem. Eng. 2014, 61, 175–184. [Google Scholar] [CrossRef]
- Curran, H.J. Developing detailed chemical kinetic mechanisms for fuel combustion. Proc. Combust. Inst. 2018, in press. [Google Scholar] [CrossRef]
- Deutschmann, O.; Maier, L.I.; Riedel, U.; Stroemman, A.H.; Dibble, R.W. Hydrogen assisted catalytic combustion of methane on platinum. Catal. Today 2000, 59, 141–150. [Google Scholar] [CrossRef]
- Williams, J.L. Monolith structures, materials, properties and uses. Catal. Today 2001, 69, 3–9. [Google Scholar] [CrossRef]
- Nijhuis, T.A.; Beers, A.E.W.; Vergunst, T.; Hoek, I.; Kapteijn, F.; Moulijn, J.A. Preparation of monolithic catalysts. Catal. Rev. 2001, 43, 345–380. [Google Scholar] [CrossRef]
- Fichtner, M.; Mayer, J.; Wolf, D.; Schubert, K. Microstructured rhodium catalysts for the partial oxidation of methane to syngas under pressure. Ind. Eng. Chem. Res. 2001, 40, 3475–3483. [Google Scholar] [CrossRef]
- Torniainen, P.M.; Chu, X.; Schmidt, L.D. Comparison of monolith-supported metals for the direct oxidation of methane to syngas. J. Catal. 1994, 146, 1–10. [Google Scholar] [CrossRef]
- Deshmukh, S.R.; Vlachos, D.G. Effect of flow configuration on the operation of coupled combustor/reformer microdevices for hydrogen production. Chem. Eng. Sci. 2005, 60, 5718–5728. [Google Scholar] [CrossRef]
- Stefanidis, G.D.; Vlachos, D.G. Intensification of steam reforming of natural gas: Choosing combustible fuel and reforming catalyst. Chem. Eng. Sci. 2010, 65, 398–404. [Google Scholar] [CrossRef]
- Deshmukh, S.R.; Vlachos, D.G. CFD simulations of coupled, countercurrent combustor/reformer microdevices for hydrogen production. Ind. Eng. Chem. Res. 2005, 44, 4982–4992. [Google Scholar] [CrossRef]
- Stefanidis, G.D.; Kaisare, N.S.; Vlachos, D.G. Modeling ignition in catalytic microreactors. Chem. Eng. Technol. 2008, 31, 1170–1175. [Google Scholar] [CrossRef]
- Miller, J.A.; Bowman, C.T. Mechanism and modeling of nitrogen chemistry in combustion. Prog. Energy Combust. Sci. 1989, 15, 287–338. [Google Scholar] [CrossRef]
- Hill, S.C.; Douglas Smoot, L. Modeling of nitrogen oxides formation and destruction in combustion systems. Prog. Energy Combust. Sci. 2000, 26, 417–458. [Google Scholar] [CrossRef]
- Lipatnikov, A.N. Stratified turbulent flames: Recent advances in understanding the influence of mixture inhomogeneities on premixed combustion and modeling challenges. Prog. Energy Combust. Sci. 2017, 62, 87–132. [Google Scholar] [CrossRef]
- van Oijen, J.A.; Donini, A.; Bastiaans, R.J.M.; ten Thije Boonkkamp, J.H.M.; de Goey, L.P.H. State-of-the-art in premixed combustion modeling using flamelet generated manifolds. Prog. Energy Combust. Sci. 2016, 57, 30–74. [Google Scholar] [CrossRef]
- ANSYS Fluent User’s Guide; Release 16.0; ANSYS Inc.: Canonsburg, PA, USA, 2014.
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method Approach, Second Edition; Pearson Education Limited: London, UK, 2007. [Google Scholar]
- Blasi, J.M.; Weddle, P.J.; Karakaya, C.; Diercks, D.R.; Kee, R.J. Modeling reaction-diffusion processes within catalyst washcoats: II. Macroscale processes informed by microscale simulations. Chem. Eng. Sci. 2016, 145, 308–316. [Google Scholar] [CrossRef]
- Bidabehere, C.M.; García, J.R.; Sedran, U. Transient effectiveness factors in the dynamic analysis of heterogeneous reactors with porous catalyst particles. Chem. Eng. Sci. 2015, 137, 293–300. [Google Scholar] [CrossRef]
- Gonzalez-Juez, E.D.; Kerstein, A.R.; Ranjan, R.; Menon, S. Advances and challenges in modeling high-speed turbulent combustion in propulsion systems. Prog. Energy Combust. Sci. 2017, 60, 26–67. [Google Scholar] [CrossRef]
- Dogwiler, U.; Benz, P.; Mantzaras, J. Two-dimensional modelling for catalytically stabilized combustion of a lean methane-air mixture with elementary homogeneous and heterogeneous chemical reactions. Combust. Flame 1999, 116, 243–258. [Google Scholar] [CrossRef]
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, W.C., Jr.; et al. GRI-Mech Version 3.0; Gas Research Institute: Chicago, IL, USA, 2000. [Google Scholar]
- Simmie, J.M. Detailed chemical kinetic models for the combustion of hydrocarbon fuels. Prog. Energy Combust. Sci. 2003, 29, 599–634. [Google Scholar] [CrossRef]
- Kee, R.J.; Rupley, F.M.; Meeks, E.; Miller, J.A. CHEMKIN-III: A Fortran Chemical Kinetics Package for the Analysis of Gasphase Chemical and Plasma Kinetics; Report No. SAND96-8216; Sandia National Laboratories: Livermore, CA, USA, 1996. [Google Scholar]
- Coltrin, M.E.; Kee, R.J.; Rupley, F.M.; Meeks, E. SURFACE CHEMKIN-III: A Fortran package for analyzing heterogeneous chemical kinetics at a solid-surface- gas-phase interface; Report No. SAND96-8217; Sandia National Laboratories: Livermore, CA, USA, 1996. [Google Scholar]
- Dogwiler, U.; Mantzaras, J.; Benz, P.; Kaeppeli, B.; Bombach, R.; Arnold, A. Homogeneous ignition of methane-air mixtures over platinum: Comparison of measurements and detailed numerical predictions. Symp. (Int.) Comb. 1998, 27, 2275–2282. [Google Scholar] [CrossRef]
- Bensalem, O.; Ernst, W.R. Mathematical modeling of homogeneous-heterogeneous reactions in monolithic catalyst. Combust. Sci. Technol. 1982, 29, 1–13. [Google Scholar] [CrossRef]
- Alam, I.; West, D.H.; Balakotaiah, V. Transport effects on pattern formation and maximum temperature in homogeneous-heterogeneous combustion. Chem. Eng. J. 2016, 288, 99–115. [Google Scholar] [CrossRef]
- Harrison, B.K.; Ernst, W.R. Catalytic combustion in cylindrical channels: a homogeneous-heterogeneous model. Combust. Sci. Technol. 1978, 19, 31–38. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Veser, G. Heterogeneous-homogeneous interactions in catalytic microchannel reactors. AlChE J. 2006, 52, 2217–2229. [Google Scholar] [CrossRef]
- Bucci, M.A.; Robinet, J.-C.; Chibbaro, S. Global stability analysis of 3D micro-combustion model. Combust. Flame 2016, 167, 132–148. [Google Scholar] [CrossRef]
- Gauthier, G.P.; Bergthorson, J.M. Effect of external heat loss on the propagation and quenching of flames in small heat-recirculating tubes. Combust. Flame 2016, 173, 27–38. [Google Scholar] [CrossRef]
- Pfefferle, W.C.; Pfefferle, L.D. Catalytically stabilized combustion. Prog. Energy Combust. Sci. 1986, 12, 25–41. [Google Scholar] [CrossRef]
- Kohse-Höinghaus, K. Clean combustion: Chemistry and diagnostics for a systems approach in transportation and energy conversion. Prog. Energy Combust. Sci. 2018, 65, 1–5. [Google Scholar] [CrossRef]
- Hansen, N.; Cool, T.A.; Westmoreland, P.R.; Kohse-Höinghaus, K. Recent contributions of flame-sampling molecular-beam mass spectrometry to a fundamental understanding of combustion chemistry. Prog. Energy Combust. Sci. 2009, 35, 168–191. [Google Scholar] [CrossRef]
- Egolfopoulos, F.N.; Hansen, N.; Ju, Y.; Kohse-Höinghaus, K.; Law, C.K.; Qi, F. Advances and challenges in laminar flame experiments and implications for combustion chemistry. Prog. Energy Combust. Sci. 2014, 43, 36–67. [Google Scholar] [CrossRef]
- Kaisare, N.S.; Vlachos, D.G. Optimal reactor dimensions for homogeneous combustion in small channels. Catal. Today 2007, 120, 96–106. [Google Scholar] [CrossRef]
- Miesse, C.M.; Masel, R.I.; Jensen, C.D.; Shannon, M.A.; Short, M. Submillimeter-scale combustion. AlChE J. 2004, 50, 3206–3214. [Google Scholar] [CrossRef]
- Carriere, T.; Westmoreland, P.R.; Kazakov, A.; Stein, Y.S.; Dryer, F.L. Modeling ethylene combustion from low to high pressure. Proc. Combust. Inst. 2002, 29, 1257–1266. [Google Scholar] [CrossRef]
- Madane, K.; Kulkarni, A.A. Pressure equalization approach for flow uniformity in microreactor with parallel channels. Chem. Eng. Sci. 2018, 176, 96–106. [Google Scholar] [CrossRef]
- Hunt, G.; Karimi, N.; Torabi, M. Two-dimensional analytical investigation of coupled heat and mass transfer and entropy generation in a porous, catalytic microreactor. Int. J. Heat Mass Transfer 2018, 119, 372–391. [Google Scholar] [CrossRef]
- Sattari-Najafabadi, M.; Nasr Esfahany, M.; Wu, Z.; Sunden, B. Mass transfer between phases in microchannels: A review. Chem. Eng. Process. Process Intensif. 2018, 127, 213–237. [Google Scholar] [CrossRef]
- Basini, L. Fuel rich catalytic combustion: Principles and technological developments in short contact time (SCT) catalytic processes. Catal. Today 2006, 117, 384–393. [Google Scholar] [CrossRef]
- Choudhary, T.V.; Banerjee, S.; Choudhary, V.R. Catalysts for combustion of methane and lower alkanes. Appl. Catal. A 2002, 234, 1–23. [Google Scholar] [CrossRef]
- Glarborg, P.; Miller, J.A.; Ruscic, B.; Klippenstein, S.J. Modeling nitrogen chemistry in combustion. Prog. Energy Combust. Sci. 2018, 67, 31–68. [Google Scholar] [CrossRef]
- Hashemi, H.; Jacobsen, J.G.; Rasmussen, C.T.; Christensen, J.M.; Glarborg, P.; Gersen, S.; van Essen, M.; Levinsky, H.B.; Klippenstein, S.J. High-pressure oxidation of ethane. Combust. Flame 2017, 182, 150–166. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Gao, X.; Xu, D. RETRACTED: Catalytic Combustion Characteristics of Methane-Air Mixtures in Small-Scale Systems at Elevated Temperatures. Catalysts 2018, 8, 439. https://doi.org/10.3390/catal8100439
Chen J, Gao X, Xu D. RETRACTED: Catalytic Combustion Characteristics of Methane-Air Mixtures in Small-Scale Systems at Elevated Temperatures. Catalysts. 2018; 8(10):439. https://doi.org/10.3390/catal8100439
Chicago/Turabian StyleChen, Junjie, Xuhui Gao, and Deguang Xu. 2018. "RETRACTED: Catalytic Combustion Characteristics of Methane-Air Mixtures in Small-Scale Systems at Elevated Temperatures" Catalysts 8, no. 10: 439. https://doi.org/10.3390/catal8100439
APA StyleChen, J., Gao, X., & Xu, D. (2018). RETRACTED: Catalytic Combustion Characteristics of Methane-Air Mixtures in Small-Scale Systems at Elevated Temperatures. Catalysts, 8(10), 439. https://doi.org/10.3390/catal8100439





