Selective Ammoxidation of Methanol to Hydrogen Cyanide over Silica-Supported FeMo Oxide Catalysts: Experiments and Kinetic Modeling
Abstract
1. Introduction
2. Results and Discussion
2.1. Kinetic Experiments
2.1.1. Definition of Conversions and Selectivities
2.1.2. Intrinsic Kinetic Experiment
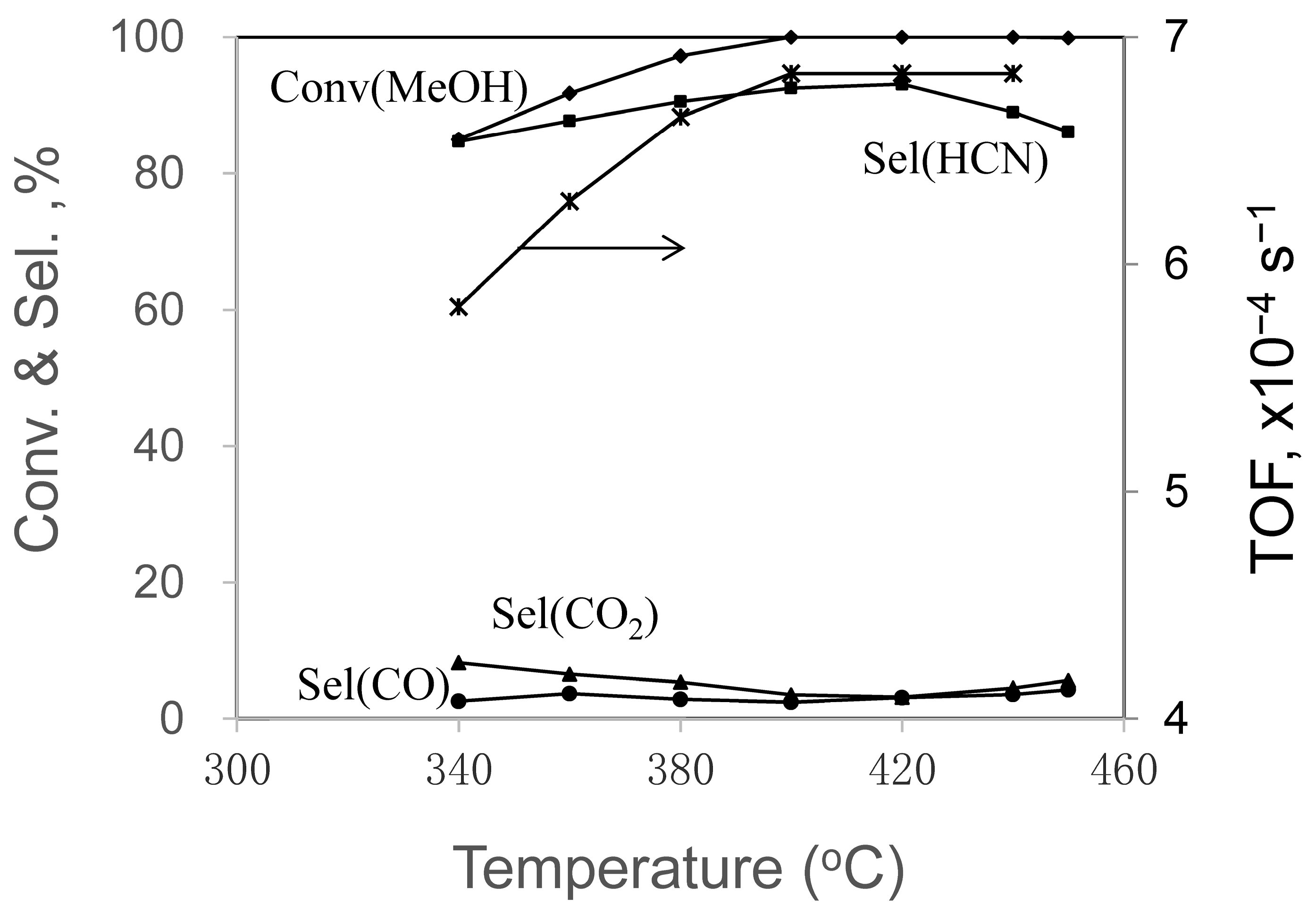
2.1.3. Effect of Temperature
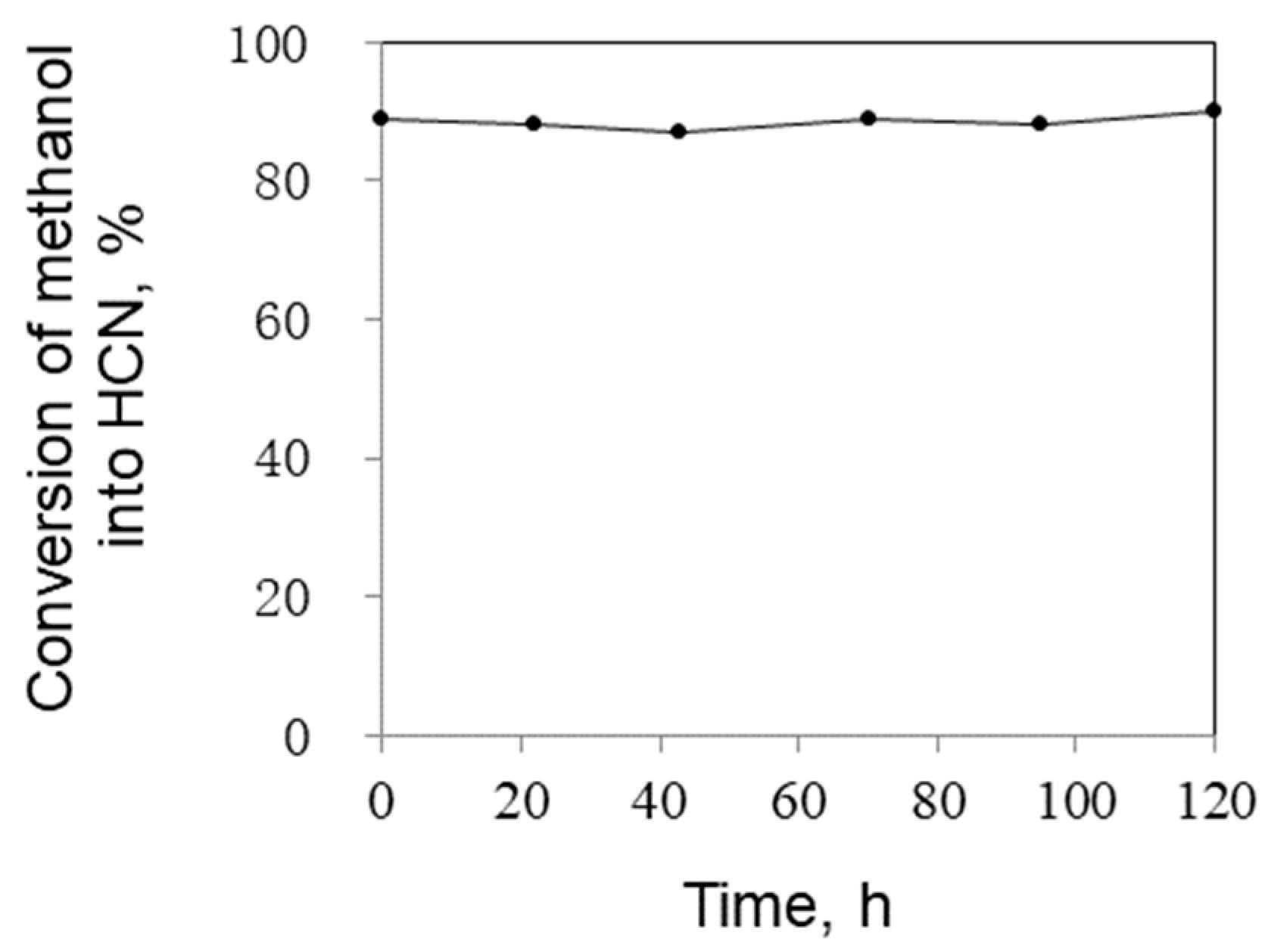
2.1.4. Catalyst Stability
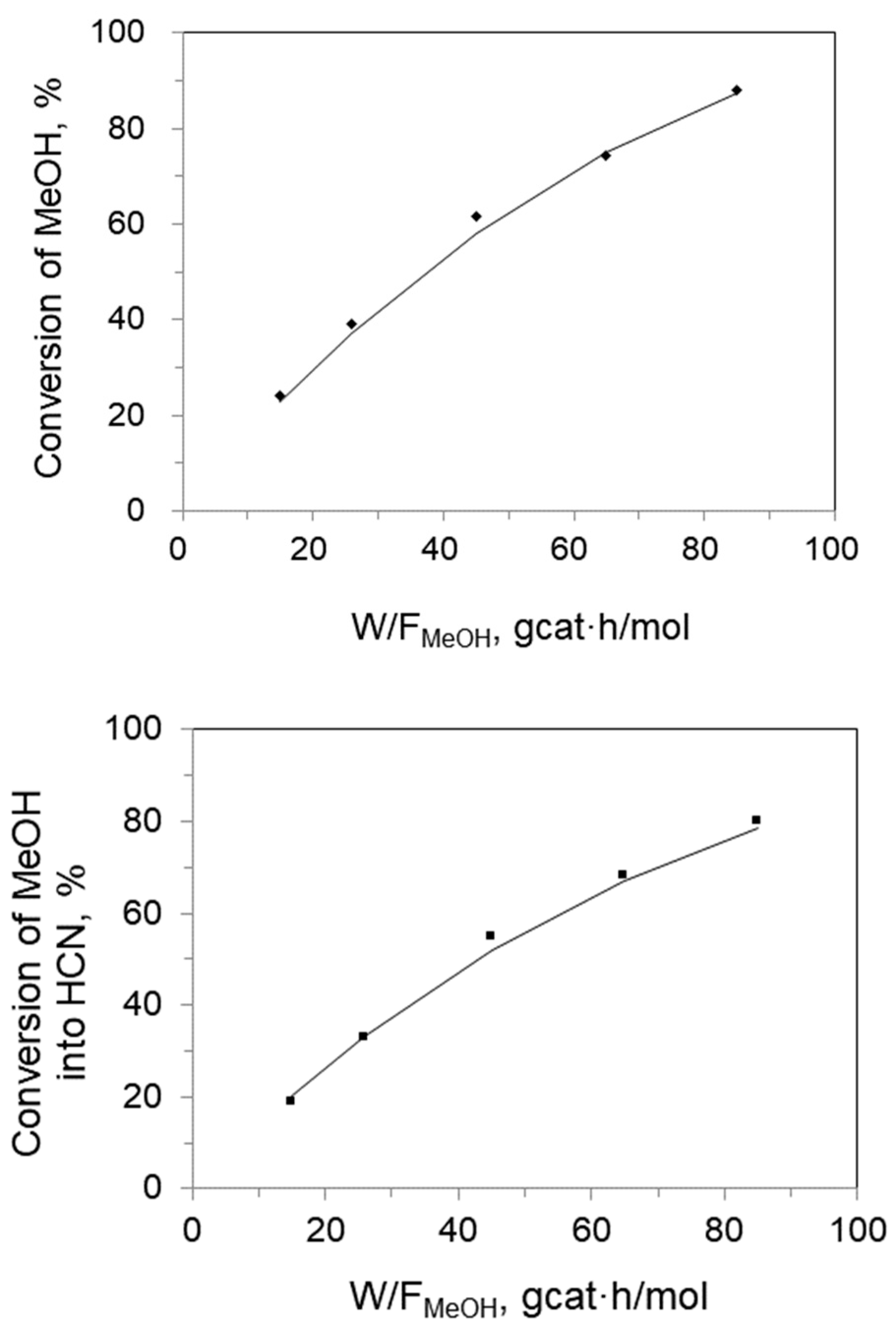
2.1.5. Effect of Space Time
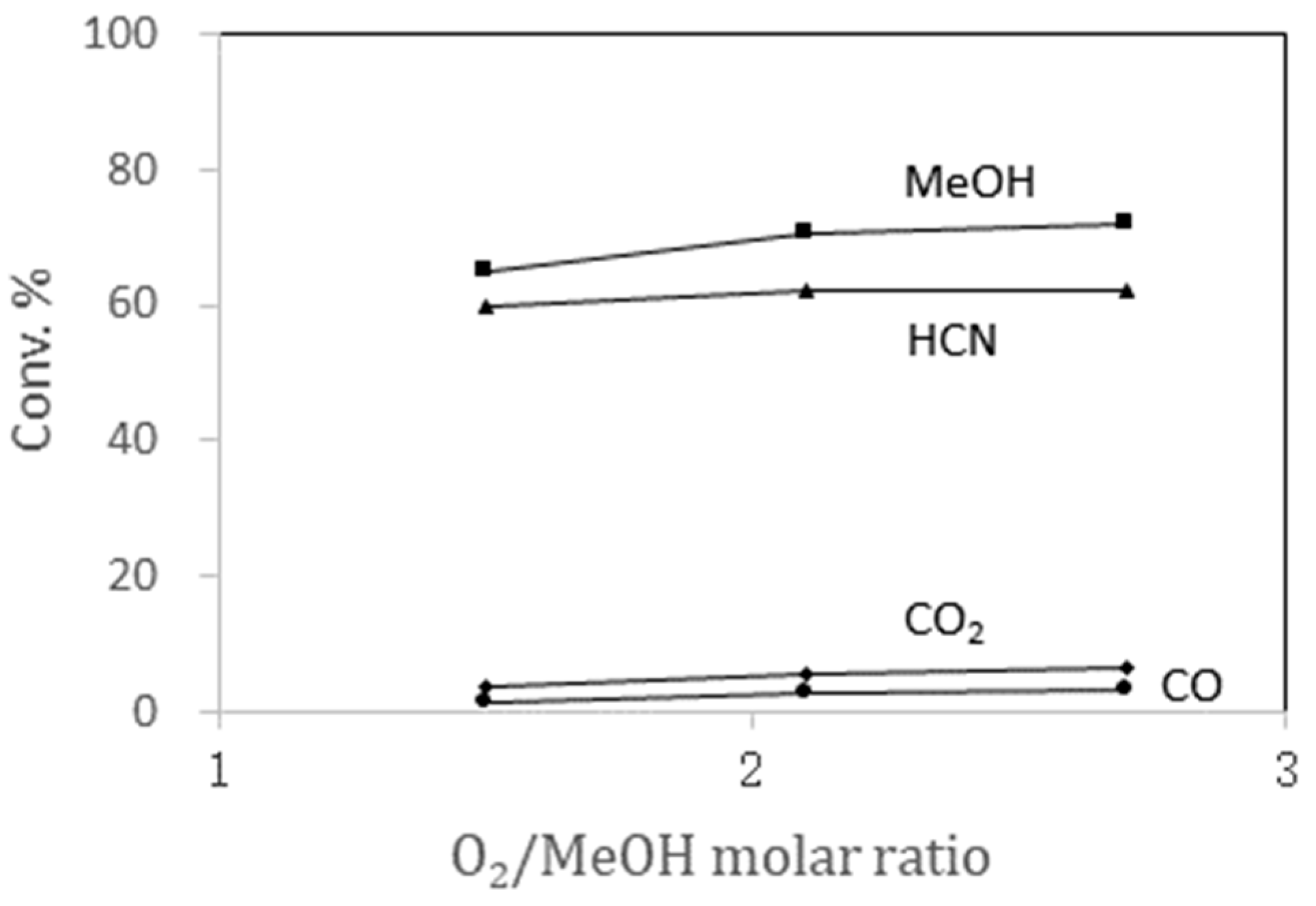
2.1.6. Effect of O2/Methanol Molar Ratios in the Feed
2.2. Kinetic Modeling
2.2.1. Thermodynamic Aspects
2.2.2. Reaction Scheme
2.2.3. Rate Equations
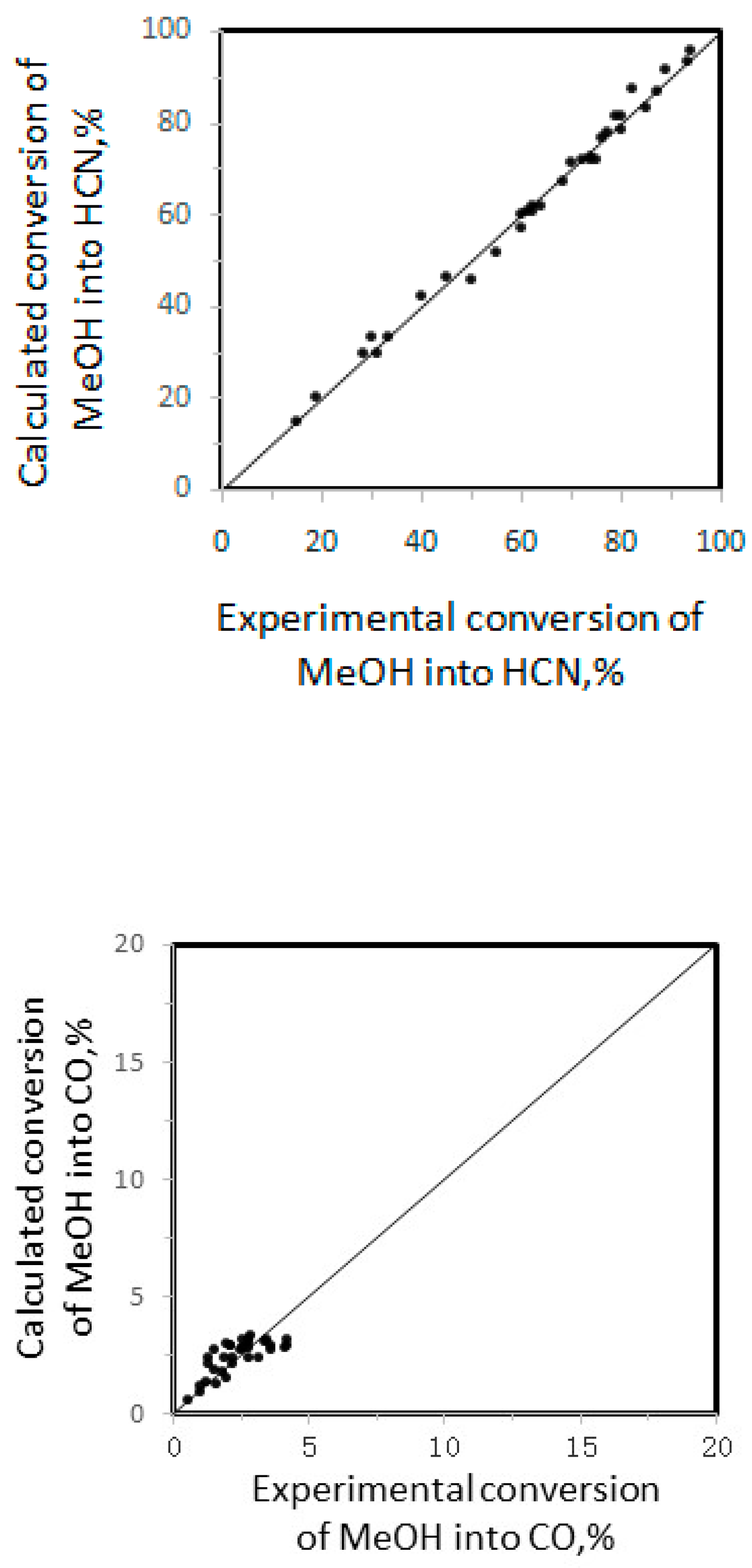
2.2.4. Parameter Estimation
3. Experimental
3.1. Material and Catalyst Preparation
3.2. Reactor Setup
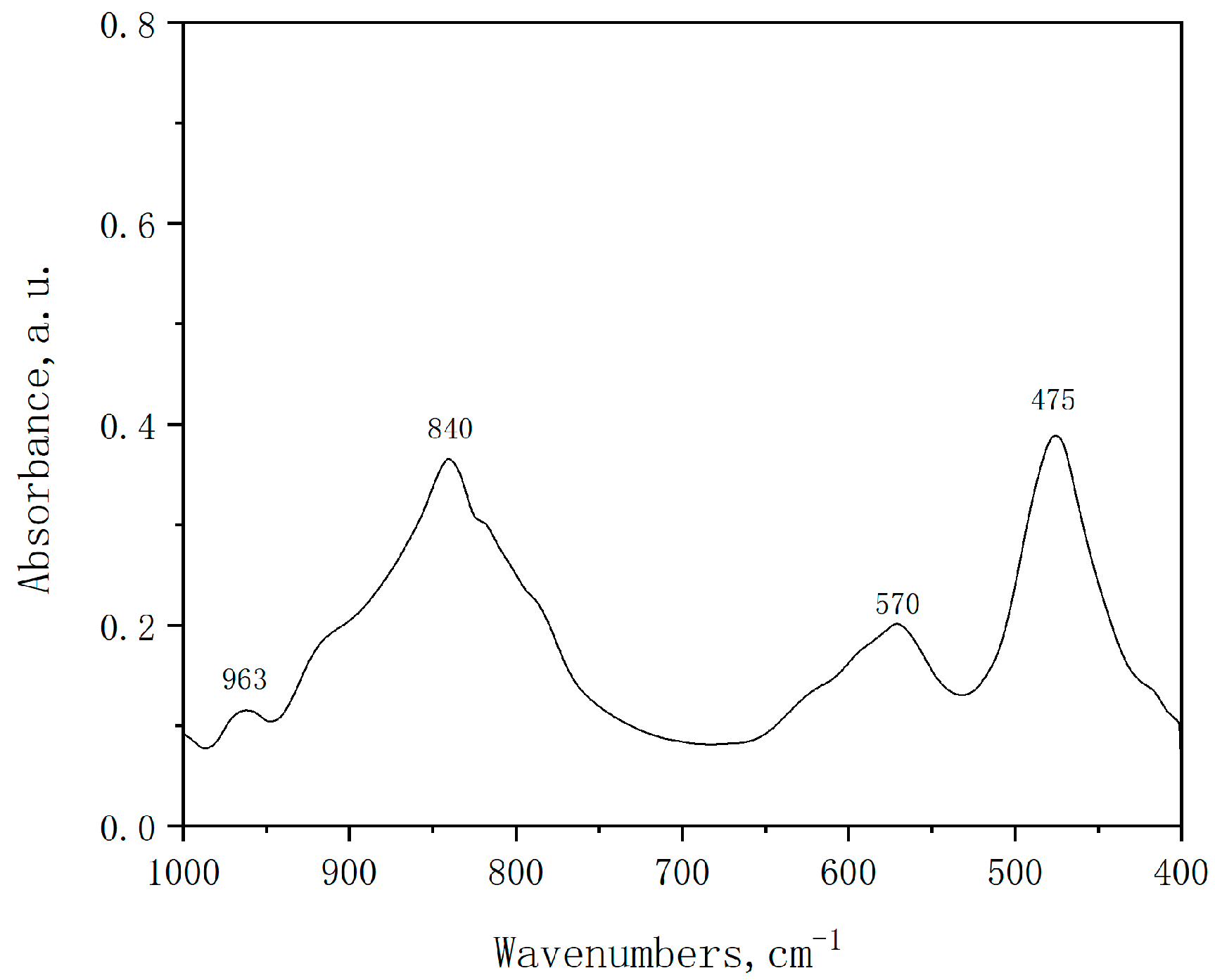
3.3. Material Characterization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
| Ai | Frequency factor for elementary reaction step i, kmol/(kgcat h) |
| Ei | Activation energy for elementary reaction step i, J/mol |
| ri | Rate of reaction step i, kmol/(kgcat h) |
| Fi | Molar feed rate of reactant i, kmol/h |
| W/FMeOH0 | Space time in terms of methanol feed, kgcat h/kmol |
| De | Effective diffusivity, m2/s |
| CAs | Gas concentration of A at the catalyst surface, kmol/m3 |
| CAb | Bulk gas concentration of A, kmol/m3 |
| ρb | Bulk density of catalyst bed, kg/m3 |
| ρc | Solid catalyst density, kg/m3 |
| R | Catalyst particle radius, m |
| −r’A(obs) | Observed reaction rate of reactant A, kmol/kgcat·s |
References
- Horn, R.; Schlogl, R. Methane activation by heterogeneous catalysis. Catal. Lett. 2015, 145, 23–29. [Google Scholar] [CrossRef]
- Dietz, A.G.; Schmidt, L.D. Conditions for HCN synthesis and catalyst activation over Pt–Rh gauzes. Appl. Catal. A Gen. 1999, 180, 287–298. [Google Scholar] [CrossRef]
- Sasaki, U.; Utsumi, H.; Morishita, K.; Miyaki, K. Process for Production of Prussic Acid. U.S. Patent 5,976,482, 2 November 1999. [Google Scholar]
- Wang, Y.F.; Jia, S.X.; Wu, Y.N.; Wu, Y. Catalytic active components of iron-molybdenum catalyst and catalytic ammoxidation. J. Chem. Ind. Eng. 1991, 5, 638–641. [Google Scholar]
- Koryablina, N.; Khramov, M.; Monical, V. Process of Catalytic Ammoxidation for Hydrogen Cyanide Production. U.S. Patent 776,322,5B2, 27 July 2010. [Google Scholar]
- Sasaki, Y.; Utsumi, H.; Otani, M.; Morishita, V. Process for Preparing Iron-Antimony-Phosphorus-Containing Catalyst for Fluidized Bed Process. U.S. Patent 4,981,830, 1 January 1991. [Google Scholar]
- Sasaki, Y.; Utsumi, H.; Otani, M. Process for Production of Hydrogen Cyanide. U.S. Patent 5,158,787, 27 October 1992. [Google Scholar]
- Hassani, H. Synthesis, characterization and catalytic performance of iron molybdate Fe2(MoO4)3 nanoparticles. Catal. Commun. 2015, 60, 19–22. [Google Scholar] [CrossRef]
- Hidalgo, G.; Tonelli, M.; Burel, L.; Millet, J. Microwave-assisted hydrothermal synthesis, characterization and catalytic performance of Fe2(MoO4)3 in the selective oxidation of propene. Catal. Today 2021, 363, 36–44. [Google Scholar] [CrossRef]
- Devendran, P.; Ayyar, M. One-pot synthesis and characterization studies of iron molybdenum mixed metal oxide (Fe2(MoO4)3) nano-photocatalysts. J. Mater. Sci. 2016, 51, 1–10. [Google Scholar]
- Basavaraja, S.; Balaji, D.; Bedre, M.D.; Raghunandan, D.; Swamy, P.M.P.; Venkataraman, A. Solvothermal synthesis and characterization of acicular α-Fe2O3 nanoparticles. Bull. Mater. Sci. 2011, 34, 1313–1317. [Google Scholar] [CrossRef]
- Wiesz, P.B.; Prater, C.D. Interpretation of measurements in experimental catalysis. Adv. Catal. 1954, 6, 143–196. [Google Scholar]
- Oyama, S.; Zhang, X.; Lu, J.; Gu, Y.; Fujitani, T. Epoxidation of propylene with H2 and O2 in the explosive regime in a packed-bed catalytic membrane reactor. J. Catal. 2008, 257, 1–4. [Google Scholar] [CrossRef]
- Mears, D.E. Tests for transport limitations in experimental catalytic reactors. Ind. Eng. Chem. Process. Des. Dev. 1971, 10, 541–547. [Google Scholar] [CrossRef]
- Chuang, K.T.; Zhou, B.; Tong, S. Kinetics and mechanism of catalytic oxidation of formaldehyde over hydrophobic catalysts. Ind. Eng. Chem. Res. 1994, 33, 1680–1686. [Google Scholar] [CrossRef]
- Radheshyam, A.; Reddy, V.S.; Dwivedi, R.; Prasad, R. Kinetic studies and mechanism evolution of the ammoxidation of 3-picoline over V2O5/ZrO2 catalyst. Can. J. Chem. Eng. 2005, 83, 274–280. [Google Scholar] [CrossRef]
- Golodets, G.I.; Ross, J.R.H. Chapter XXIV: The ammoxidation of organic substances, Stud. Surf. Sci. Catal. 1983, 15, 767–792. [Google Scholar]
- Ebner, J.R.; Gleaves, J.T.; Kuechler, T.C.; Li, T.P. Ammoxidation of methanol to hydrogen cyanide binary oxide catalysts and mechanistic aspects. In Industrial Chemicals via C1 Processes; Fahey, D., Ed.; ACS Symposium Series; American Chemical Society: Washington, DC, USA, 1987; pp. 189–205. [Google Scholar]
- Burrington, J.D.; Kartisek, C.; Grasselli, R.K. Surface intermediates in selective propylene oxidation and ammoxidation over heterogeneous molybdate and antimonate catalysts. J. Catal. 1984, 87, 363–380. [Google Scholar] [CrossRef]
- Froment, G.F.; Bischoff, K.B. Chemical Reactor Analysis and Design; Wiley: New York, NY, USA, 1992. [Google Scholar]





| Temp, °C | Conv (MeOH) | Yield of Products, % | C Balance | N Balance | ||
|---|---|---|---|---|---|---|
| % | HCN | CO | CO2 | % | % | |
| 340 | 85.0 | 72.0 | 2.2 | 7.0 | 95.5 | 96.7 |
| 360 | 91.8 | 80.5 | 3.4 | 6.0 | 97.9 | 95.6 |
| 380 | 97.2 | 88.0 | 2.8 | 5.2 | 98.8 | 98.6 |
| 400 | 100.0 | 92.5 | 2.5 | 3.5 | 98.5 | 98.7 |
| 420 | 100.0 | 93.1 | 3.1 | 3.2 | 99.4 | 97.6 |
| 440 | 100.0 | 89.0 | 3.6 | 4.5 | 97.1 | 99.0 |
| Sample | Composition (wt.%) | BET Analysis | ||||
|---|---|---|---|---|---|---|
| Fe | Mo | Si | O | a Surface Area, m2/g | Pore Volume, cm3/g | |
| FeMo/SiO2 | 18.28 | 19.49 | 31.62 | 30.61 | 17.08 | 0.0957 |
| Parameter | Base Value | +10% Change (ΔOutput %) | −10% Change (ΔOutput %) | Sensitivity Level |
|---|---|---|---|---|
| A1 | 6.87401 × 10−1 | 3.9 | –4.7 | Moderate |
| A2 | 6.03154 × 106 | 1.3 | –1.5 | Moderate |
| A3 | 5.72650 × 100 | –0.2 | 0.2 | Low |
| A4 | 2.10023 × 103 | –0.5 | 0.6 | Low |
| E1 | 1.34061 × 104 | –11.4 | 9.5 | High |
| E2 | 6.70289 × 104 | –22.4 | 12.2 | High |
| E3 | 2.57893 × 104 | –1.1 | –1.2 | Moderate |
| E4 | 5.35679 × 104 | 3.6 | –8.2 | Moderate |
| Name of 95% Confidence Limits | ||||
|---|---|---|---|---|
| Parameter | Estimate | Lower | Upper | t-Value |
| A1 | 6.87401 × 10−1 | 6.39988 × 10−1 | 7.34815 × 10−1 | 2.89961 × 101 |
| A2 | 6.03154 × 106 | 5.20929 × 106 | 6.85378 × 106 | 1.46709 × 101 |
| A3 | 5.72650 × 100 | 4.56727 × 100 | 6.88574 × 100 | 9.87979 × 100 |
| A4 | 2.10023 × 103 | 1.87744 × 103 | 2.32302 × 103 | 1.88538 × 101 |
| E1 | 1.34061 × 104 | 1.29879 × 104 | 1.38243 × 104 | 6.41132 × 101 |
| E2 | 6.70289 × 104 | 6.58934 × 104 | 6.81645 × 104 | 1.18054 × 102 |
| E3 | 2.57893 × 104 | 2.42561 × 104 | 2.73224 × 104 | 3.36417 × 101 |
| E4 | 5.35679 × 104 | 5.19286 × 104 | 5.52072 × 104 | 6.53538 × 101 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Zhao, Y. Selective Ammoxidation of Methanol to Hydrogen Cyanide over Silica-Supported FeMo Oxide Catalysts: Experiments and Kinetic Modeling. Catalysts 2025, 15, 1004. https://doi.org/10.3390/catal15111004
Wang B, Zhao Y. Selective Ammoxidation of Methanol to Hydrogen Cyanide over Silica-Supported FeMo Oxide Catalysts: Experiments and Kinetic Modeling. Catalysts. 2025; 15(11):1004. https://doi.org/10.3390/catal15111004
Chicago/Turabian StyleWang, Bo, and Yuhuan Zhao. 2025. "Selective Ammoxidation of Methanol to Hydrogen Cyanide over Silica-Supported FeMo Oxide Catalysts: Experiments and Kinetic Modeling" Catalysts 15, no. 11: 1004. https://doi.org/10.3390/catal15111004
APA StyleWang, B., & Zhao, Y. (2025). Selective Ammoxidation of Methanol to Hydrogen Cyanide over Silica-Supported FeMo Oxide Catalysts: Experiments and Kinetic Modeling. Catalysts, 15(11), 1004. https://doi.org/10.3390/catal15111004





