Property Prediction of Ag-Filled Isotropic Conductive Adhesive through the Analysis of Its Curing and Decomposition Kinetics
Abstract
:1. Introduction
2. Results and Discussions
2.1. Curing Kinetics
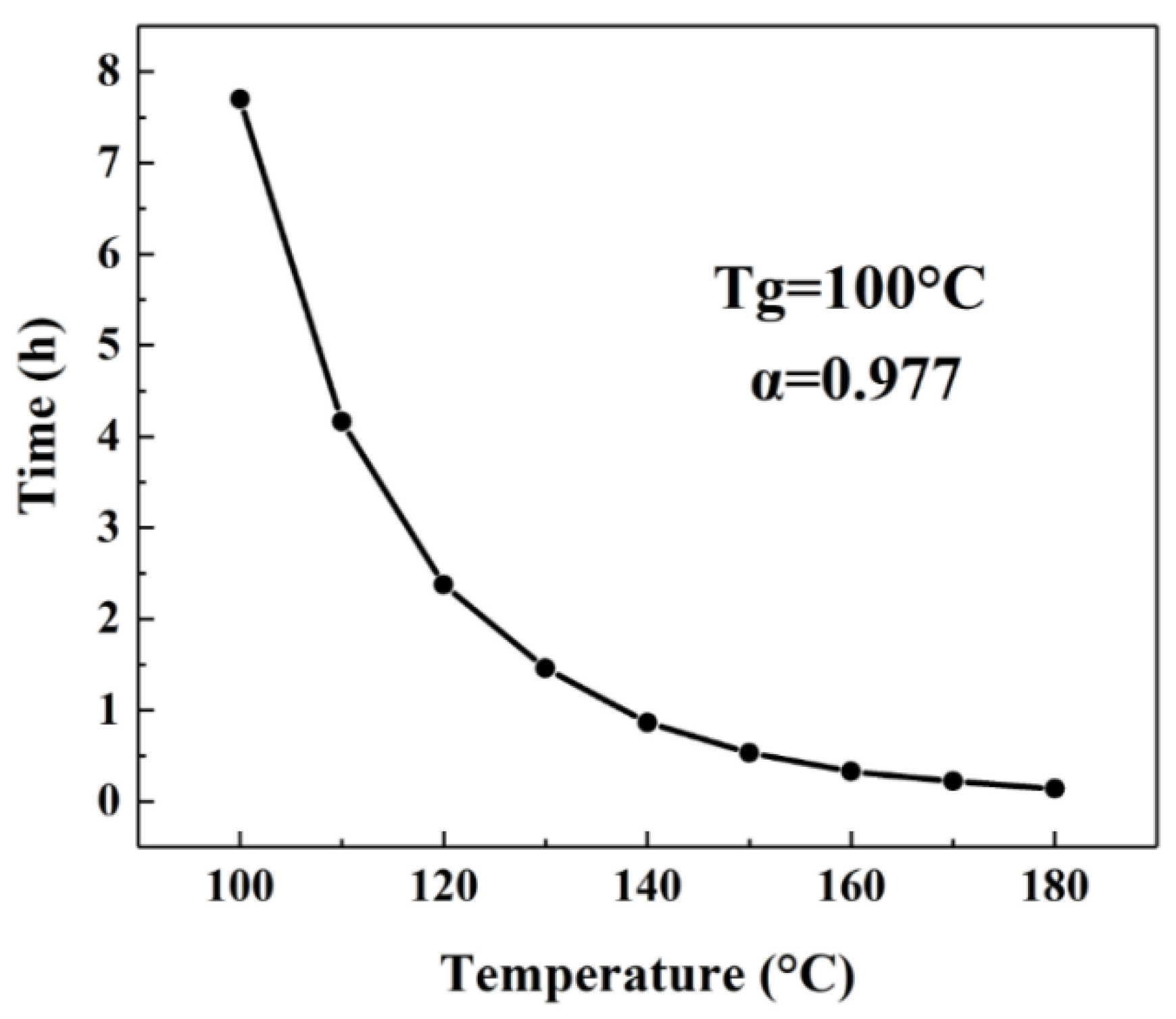
2.2. Relationship between Tg and the Curing Process
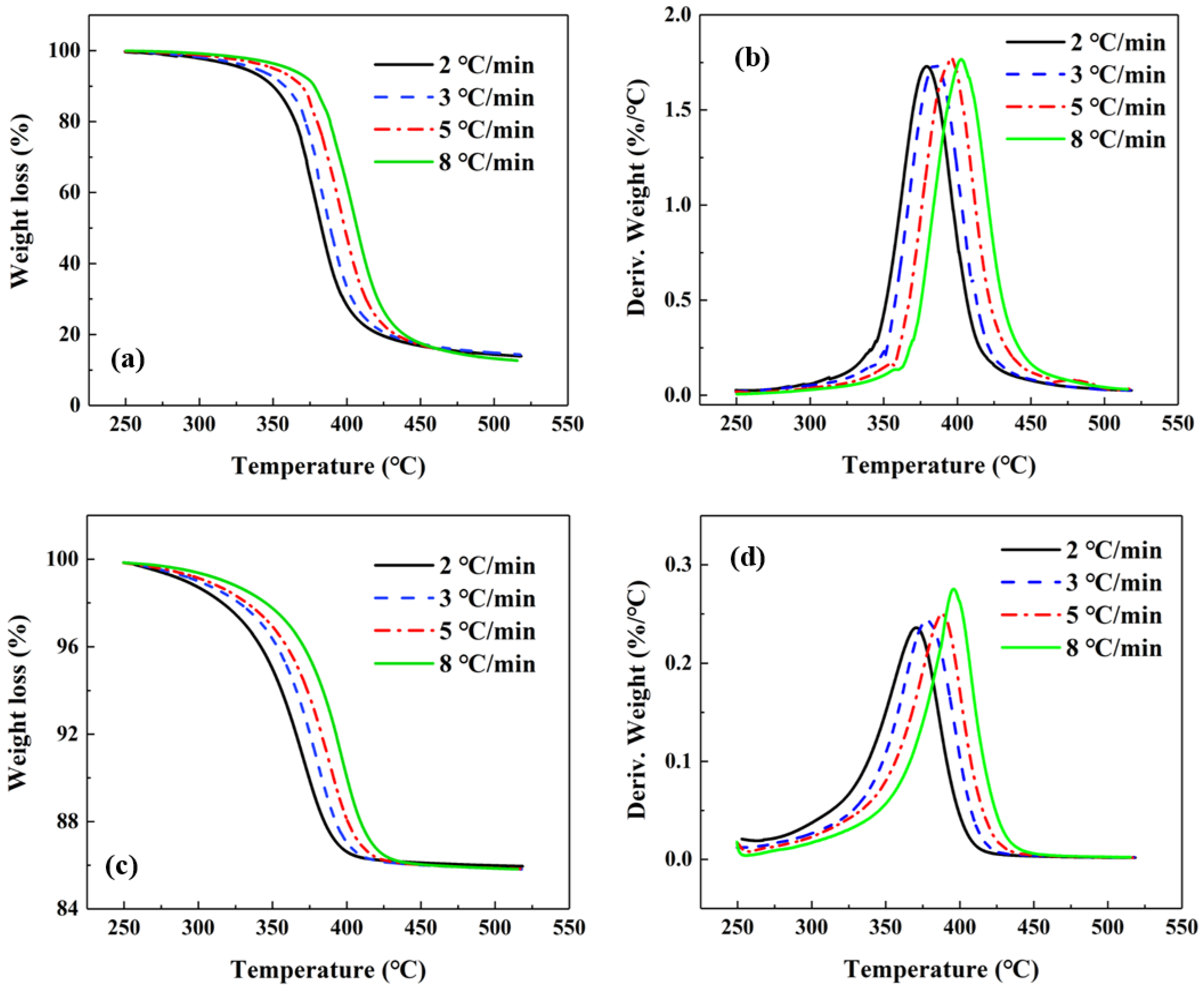
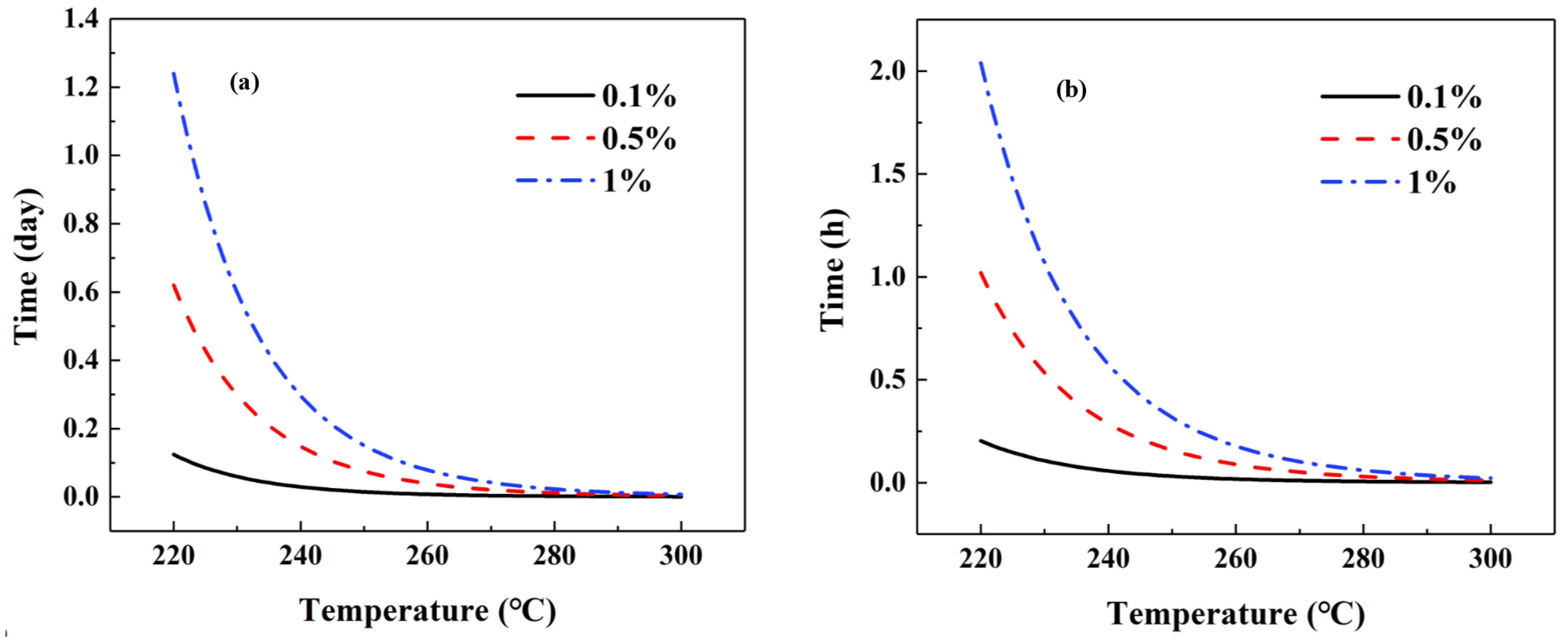
2.3. Decomposition Kinetics and Thermal Endurance
3. Materials and Methods
3.1. Materials and Sample Preparation
3.2. Test Method
4. Conclusions
- (1)
- The curing behaviors of both the Ag-filled ICA and its unfilled matrix resin exhibited the characteristics of a catalytic reaction mechanism, which means the addition of micro-scale silver flakes did not change the curing mechanisms by much. However, the addition of micro-scale silver flakes accelerated the transformation of the reaction mechanism from chemical reaction-controlled to diffusion-controlled.
- (2)
- The curing activation energy of the unfilled matrix resin was 72.9 kJ/mol, higher than that of the Ag-filled ICA (68.1 kJ/mol), which indicates the curing process of Ag-filled ICA was easier to take place. The tested and calculated data were compared to verify the accuracy of the established kinetic equations, which showed a good consistency.
- (3)
- The activation energy for the thermal decomposition of the ICA and the matrix resin were calculated to be 134.1 kJ/mol and 152.7 kJ/mol, respectively, using the Ozawa–Flynn–Wall method, which means the decomposition of the ICA was easier to occur than that of the matrix resin.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yim, M.J.; Li, Y.; Moon, K.-S.; Paik, K.W.; Wong, C.P. Review of Recent Advances in Electrically Conductive Adhesive Materials and Technologies in Electronic Packaging. J. Adhes. Sci. Technol. 2008, 22, 1593–1630. [Google Scholar] [CrossRef]
- Chan, Y.C.; Uddin, M.A.; Alam, M.O.; Han, H.P. Curing kinetics of anisotropic conductive adhesive film. J. Electron. Mater. 2003, 32, 131–136. [Google Scholar] [CrossRef]
- Cui, H.W.; Jiu, J.T.; Sugahara, T.; Nagao, S.; Suganuma, K.; Uchida, H.; Schroder, K.A. Using the Friedman method to study the thermal degradation kinetics of photonically cured electrically conductive adhesives. J. Therm. Anal. Calorim. 2015, 119, 425–433. [Google Scholar] [CrossRef]
- Wang, X.; Wu, J.; Li, Y.; Zhou, C.; Xu, C. Pyrolysis kinetics and pathway of polysiloxane conversion to an amorphous SiOC ceramic. J. Therm. Anal. 2014, 115, 55–62. [Google Scholar] [CrossRef]
- Carmona, V.B.; Campos, A.D.; Marconcini, J.M.; Mattoso, L.H.C. Kinetics of thermal degradation applied to biocomposites with TPS, PCL and sisal fibers by non-isothermal procedures. J. Therm. Anal. Calorim. 2014, 115, 153–160. [Google Scholar] [CrossRef]
- Künzel, M.; Yan, Q.-L.; Šelešovský, J.; Zeman, S.; Matyáš, R. Thermal behavior and decomposition kinetics of ETN and its mixtures with PETN and RDX. J. Therm. Anal. 2014, 115, 289–299. [Google Scholar] [CrossRef]
- Baby, M.; Pal, R.; Francis, N.; Sudhi, S. Novolac epoxy resin from 4,4′-dihydroxybenzophenone: Thermal, thermomechanical, interfacial, and cure kinetics with DGEBA/DICY blend. J. Appl. Polym. Sci. 2018, 135, 46164. [Google Scholar] [CrossRef]
- Qi, Y.; Weng, Z.; Wang, J.; Zhang, S.; Zong, L.; Liu, C.; Jian, X. A novel bio-based phthalonitrile resin derived from catechin: Synthesis and comparison of cur-ing behavior with petroleum-based counterpart. Polym. Int. 2018, 67, 322–329. [Google Scholar] [CrossRef]
- Cui, H.W.; Suganuma, K.; Uchida, H. Using the Ozawa method to study the thermally initiated curing kinetics of vinyl ester resin. RSC Adv. 2014, 5, 2677–2683. [Google Scholar] [CrossRef]
- Pongsa, U.; Samthong, C.; Praserthdam, P.; Somwangthanaroj, A. Influence of diaminobenzoyl-functionalized multiwalled carbon nanotubes on the nonisothermal curing kinetics, dynamic mechanical properties, and thermal conductivity of epoxy-anhydride composites. J. Appl. Polym. Sci. 2016, 133, 43567. [Google Scholar] [CrossRef]
- Li, Q.; Li, X.; Meng, Y. Curing of DGEBA epoxy using a phenol-terminated hyperbranched curing agent: Cure kinetics, gelation, and the TTT cure diagram. Thermochim. Acta 2012, 549, 69–80. [Google Scholar] [CrossRef]
- Jiang, H.; Zhou, M.B.; Zhu, J.F.; Zhang, X.P. Preparation of core-shell structured SiO2@Ag spheres and their role in improving mi-cro-sized Ag flake filled electrically conductive adhesive for LED packaging. In Proceedings of the 18th International Conference on Electronic Packaging Technology, Harbin, China, 16–19 August 2017; pp. 1607–1611. [Google Scholar]
- Hutchinson, J.M.; Moradi, S. Thermal conductivity and cure kinetics of epoxy-boron nitride composites—A Review. Materials 2020, 13, 3634. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Strachan, A. Molecular scale simulations on thermoset polymers: A review. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 103–122. [Google Scholar] [CrossRef]
- Riesen, R. Collected Applications of Thermal Analysis Thermosets; Mettler Toledo: Schwerzenbach, Switzerland, 2006. [Google Scholar]
- Kim, Y.C.; Hong, S.; Sun, H.; Kim, M.G.; Choi, K.; Cho, J.; Choi, H.R.; Koo, J.C.; Moon, H.; Byun, D.; et al. UV-curing kinetics and performance development of in situ curable 3D printing materials. Eur. Polym. J. 2017, 93, 140–147. [Google Scholar] [CrossRef]
- Turi, E.A. Thermal Characterization of Polymeric Materials; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Wang, Q.; Zhang, S.; Liu, G.; Lin, T.; He, P. The mixture of silver nanowires and nanosilver-coated copper micronflakes for electrically conductive adhesives to achieve high electrical conductivity with low percolation threshold. J. Alloys Compd. 2020, 820, 153184. [Google Scholar] [CrossRef]
- DiBenedetto, A.T. Prediction of the glass transition temperature of polymers: A model based on the principle of corresponding states. J. Polym. Sci. Part B Polym. Phys. 1987, 25, 1949–1969. [Google Scholar] [CrossRef]
- Pascault, J.P.; Williams, R.J.J. Glass transition temperature versus conversion relationships for thermosetting polymers. J. Polym. Sci. Part B Polym. Phys. 1990, 28, 85–95. [Google Scholar] [CrossRef]
- Popescu, C. Integral method to analyze the kinetics of heterogeneous reactions under non-isothermal conditions A variant on the Ozawa-Flynn-Wall method. Thermochim. Acta 1996, 285, 309–323. [Google Scholar] [CrossRef]
- Mothé Cheila, G.; Iara, C.M. Study of kinetic parameters of thermal decomposition of bagasse and sugarcane straw using Friedman and Ozawa–Flynn–Wall isoconversional methods. J. Therm. Anal. Calorim. 2013, 113, 497–505. [Google Scholar] [CrossRef]
- ASTM E1877Standard Practice for Calculating Thermal Endurance of Materials from Thermogravimetric Decomposition Data, ASTM International: West Conshohocken, PA, USA, 2000.
- Yamaguchi, M. Thermal Hysteresis Involving Reversible Self-Catalytic Reactions. Accounts Chem. Res. 2021, 54, 2603–2613. [Google Scholar] [CrossRef] [PubMed]
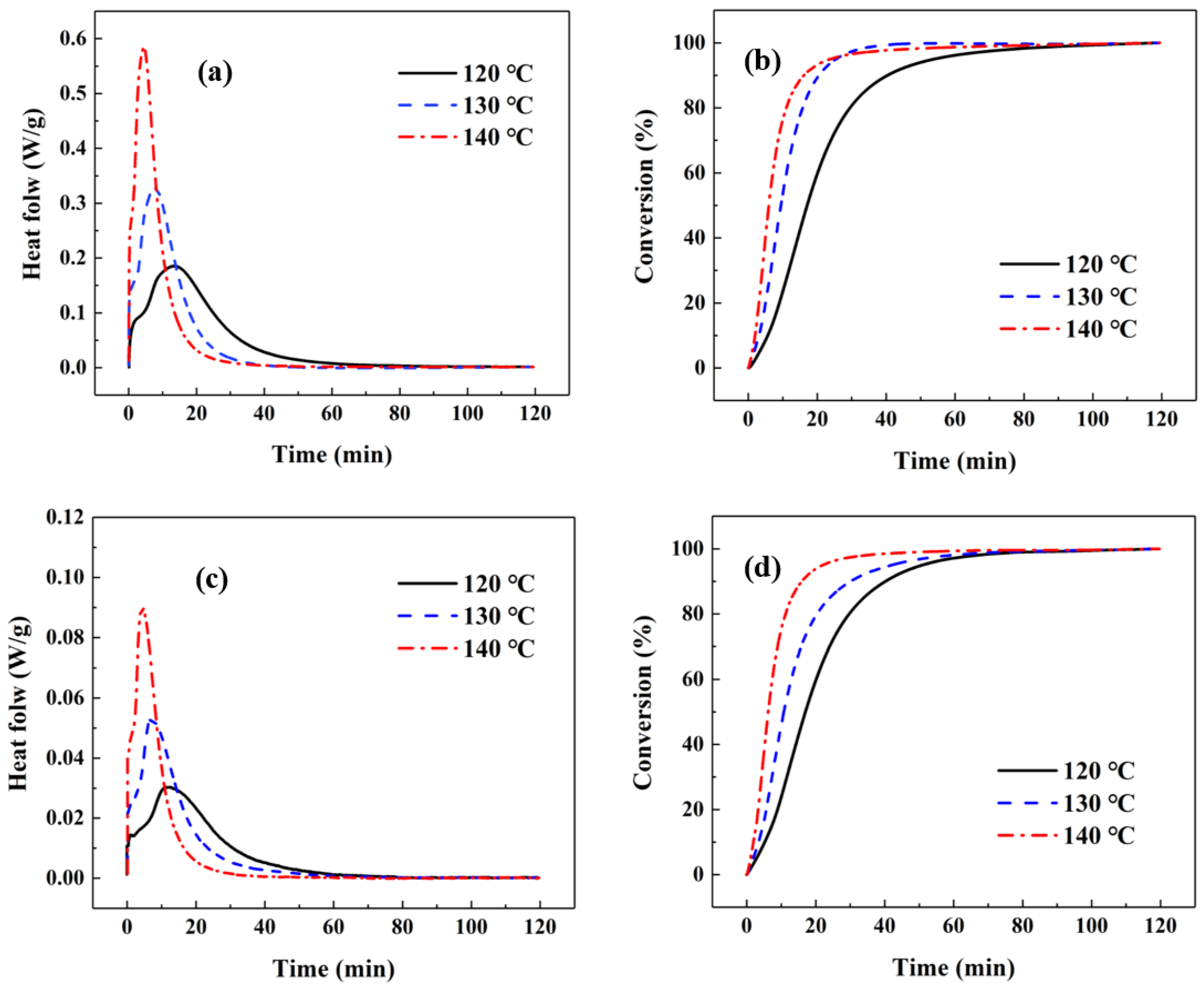
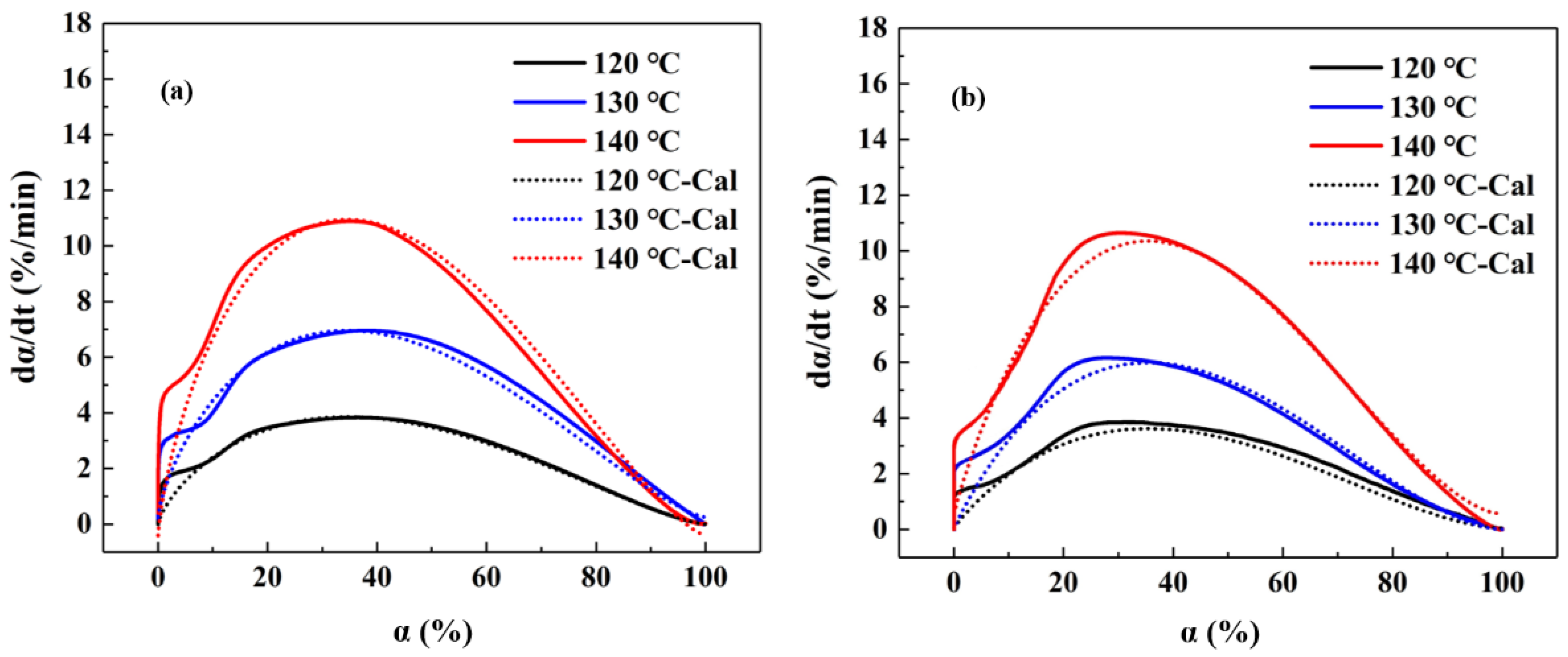
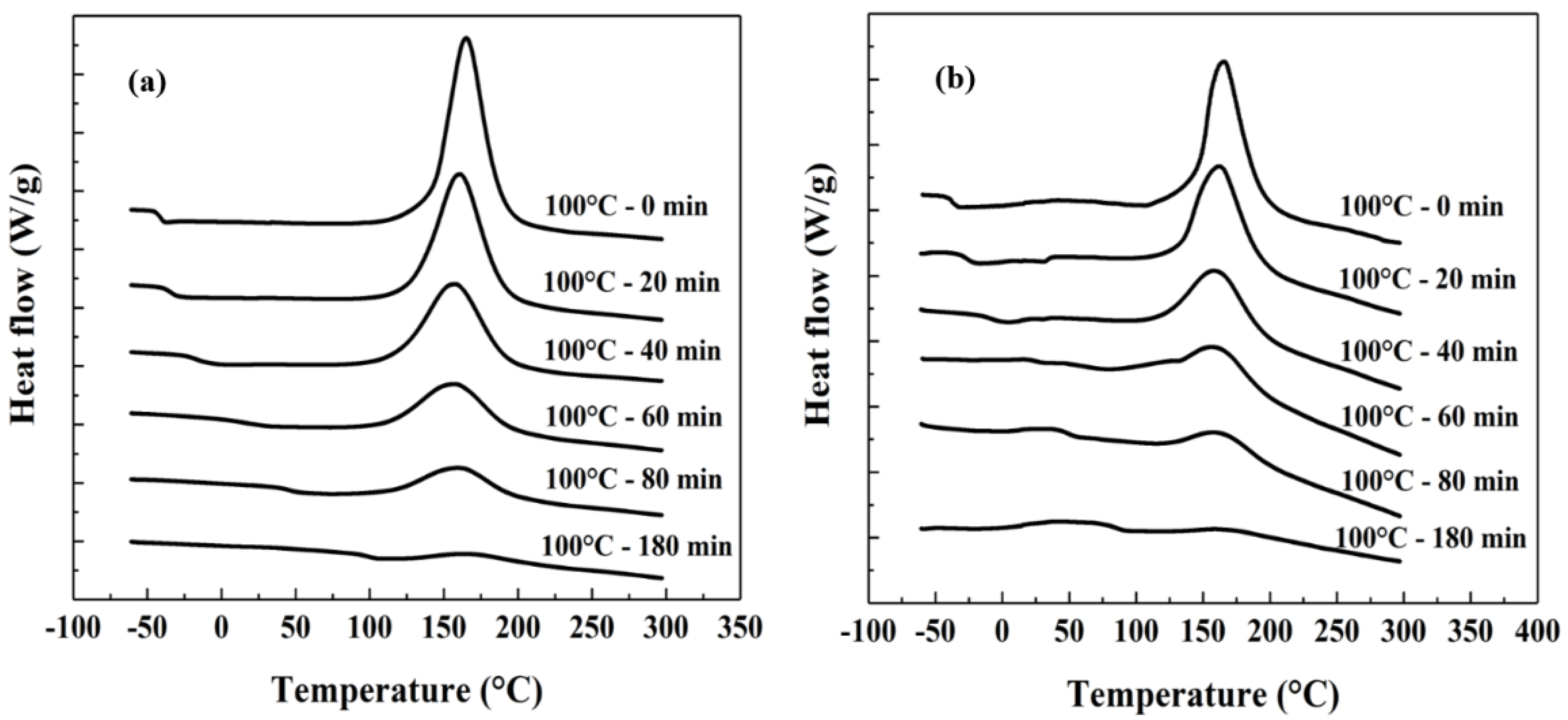
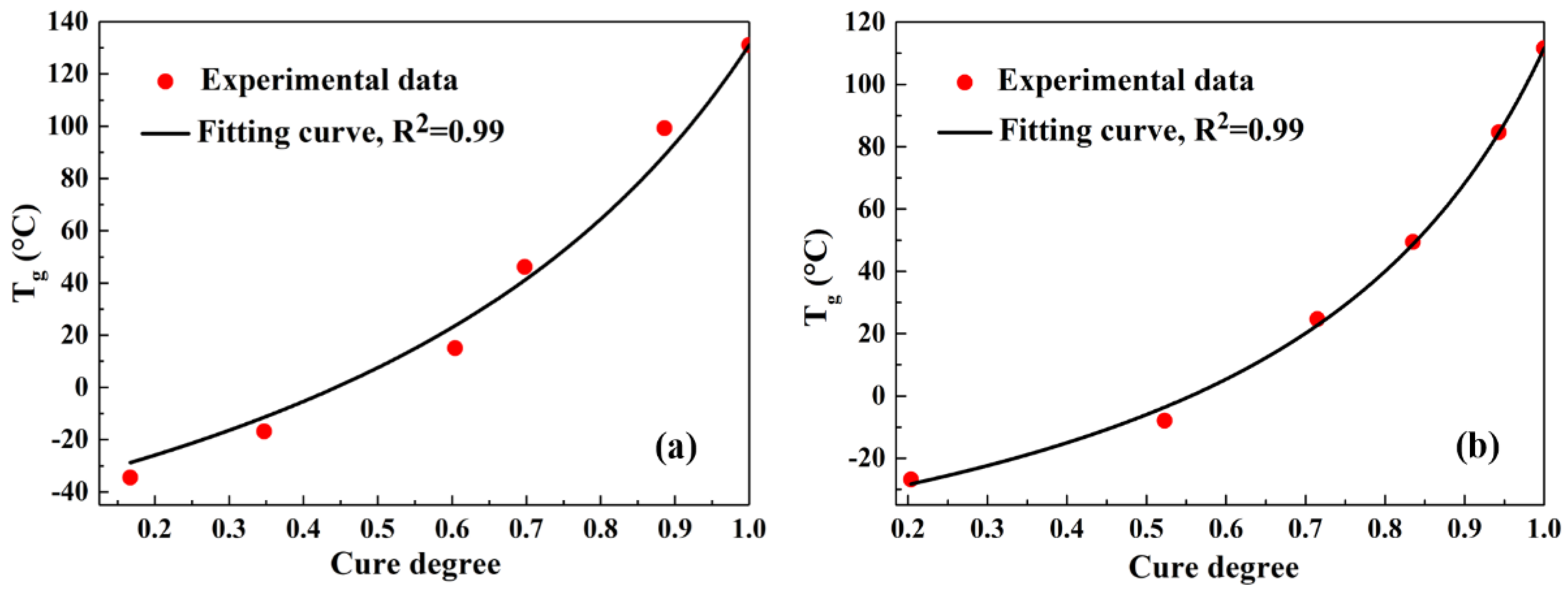
| Sample | T (°C) | tmax (min) | Total Enthalpy (J/g) |
|---|---|---|---|
| Unfilled matrix resin | 120 | 13.5 | 281.1 |
| 130 | 7.7 | 300.1 | |
| 140 | 4.5 | 320.7 | |
| Ag-filled ICA | 120 | 11.9 | 52.3 |
| 130 | 7.1 | 53.4 | |
| 140 | 4.3 | 54.8 |
| Sample | T (°C) | k (T) (min−1) | n | m | EA (kJ/mol) | k0 (s−1) | ||
|---|---|---|---|---|---|---|---|---|
| Matrix resin | 120 | 0.15 | 1.28 | 0.72 | 1.40 | 0.74 | 72.9 | 1.24 × 107 |
| 130 | 0.26 | 1.38 | 0.75 | |||||
| 140 | 0.45 | 1.54 | 0.74 | |||||
| ICA | 120 | 0.20 | 1.54 | 0.91 | 1.71 | 0.94 | 68.1 | 3.73 × 106 |
| 130 | 0.34 | 1.76 | 0.92 | |||||
| 140 | 0.55 | 1.84 | 0.99 |
| Sample | T (°C) | αmax (%) | (dα/dt)max (%/min) |
|---|---|---|---|
| Unfilled matrix resin | 120 | 36.6 | 3.84 |
| 130 | 37.9 | 6.96 | |
| 140 | 35.0 | 10.89 | |
| Ag-filled ICA | 120 | 31.0 | 3.85 |
| 130 | 28.4 | 6.16 | |
| 140 | 30.1 | 10.64 |
| t (min) | ΔHr (J/g) | Tg (°C) | α | |||
|---|---|---|---|---|---|---|
| Unfilled Matrix Resin | Ag-Filled ICA | Unfilled Matrix Resin | Ag-Filled ICA | Unfilled Matrix Resin | Ag-Filled ICA | |
| 0 | 346.8 | 46.6 | −41.5 | −38.0 | 0 | 0 |
| 20 | 288.9 | 37.1 | −34.42 | −26.8 | 0.17 | 0.20 |
| 40 | 226.5 | 22.2 | −16.82 | −7.9 | 0.35 | 0.52 |
| 60 | 137.3 | 13.3 | 15.08 | 24.6 | 0.60 | 0.72 |
| 80 | 104.7 | 7.7 | 46.16 | 49.4 | 0.70 | 0.84 |
| 180 | 39.5 | 2.7 | 99.28 | 84.6 | 0.89 | 0.94 |
| Sample | TM (°C) | Weight Loss (%) | EA (KJ/mol) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 °C/min | 3 °C/min | 5 °C/min | 8 °C/min | 2 °C/min | 3 °C/min | 5 °C/min | 8 °C/min | ||
| Unfilled matrix resin | 379.2 | 384.8 | 395.5 | 402.8 | 85.7 | 85.5 | 87.1 | 87.3 | 152.7 |
| Ag-filled ICA | 370.8 | 378.0 | 388.0 | 396.1 | 13.9 | 14.0 | 14.0 | 14.0 | 134.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Zhou, M.; Zhang, X. Property Prediction of Ag-Filled Isotropic Conductive Adhesive through the Analysis of Its Curing and Decomposition Kinetics. Catalysts 2022, 12, 185. https://doi.org/10.3390/catal12020185
Jiang H, Zhou M, Zhang X. Property Prediction of Ag-Filled Isotropic Conductive Adhesive through the Analysis of Its Curing and Decomposition Kinetics. Catalysts. 2022; 12(2):185. https://doi.org/10.3390/catal12020185
Chicago/Turabian StyleJiang, Han, Minbo Zhou, and Xinping Zhang. 2022. "Property Prediction of Ag-Filled Isotropic Conductive Adhesive through the Analysis of Its Curing and Decomposition Kinetics" Catalysts 12, no. 2: 185. https://doi.org/10.3390/catal12020185
APA StyleJiang, H., Zhou, M., & Zhang, X. (2022). Property Prediction of Ag-Filled Isotropic Conductive Adhesive through the Analysis of Its Curing and Decomposition Kinetics. Catalysts, 12(2), 185. https://doi.org/10.3390/catal12020185






