Instrumental Reciprocity as an Error
Abstract
1. Introduction
2. Experimental Design and Procedures
2.1. Experimental Game
2.2. Treatments
2.3. Procedures
3. Results
3.1. Cooperation and Reciprocation Rates
3.2. Strategies of Second Movers
3.3. Is Instrumental Reciprocity a Simple Mistake?
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Selten, R.; Stoecker, R. End behaviour in sequences of finite prisoner’s dilemma supergames. J. Econ. Behav. Organ. 1986, 3, 47–70. [Google Scholar] [CrossRef]
- Sonnemans, J.; Schram, A.; Offerman, T. Strategic behavior in public good games: When partners drift apart. Econ. Lett. 1999, 62, 35–41. [Google Scholar] [CrossRef]
- Reuben, E.; Suetens, S. Revisiting strategic versus non-strategic cooperation. Exp. Econ. 2012, 15, 24–43. [Google Scholar] [CrossRef]
- Cabral, L.; Ozbay, E.; Schotter, A. Intrinsic and instrumental reciprocity: An experimental study. Games Econ. Behav. 2014, 87, 100–121. [Google Scholar] [CrossRef]
- Embrey, M.; Fréchette, G.R.; Yuksel, S. Cooperation in the Finitely Repeated Prisoner’s Dilemma. Q. J. Econ. 2018, 133, 509–551. [Google Scholar] [CrossRef]
- Zelmer, J. Linear public goods experiments: A meta-analysis. Exp. Econ. 2003, 6, 299–310. [Google Scholar] [CrossRef]
- Andreoni, J.; Croson, R. Partners versus Strangers: Random Rematching in Public Goods Experiments. In Handbook of Experimental Economics Results; Plott, C.R., Smith, V.L., Eds.; North-Holland: Amsterdam, The Netherlands, 2008; Chapter 82; pp. 776–783. [Google Scholar]
- Kreps, D.M.; Milgrom, P.; Roberts, J.; Wilson, R. Rational cooperation in the finitely repeated prisoners’ dilemma. J. Econ. Theory 1982, 27, 245–252. [Google Scholar] [CrossRef]
- Andreoni, J.; Miller, J.H. Rational Cooperation in the Finitely Repeated Prisoner’s Dilemma: Experimental Evidence. Econ. J. 1993, 103, 570–585. [Google Scholar] [CrossRef]
- Camerer, C.F.; Fehr, E. When Does ‘Economic Man’ Dominate Social Behavior? Science 2006, 311, 47–52. [Google Scholar] [CrossRef] [PubMed]
- Cox, C.A.; Jones, M.T.; Pflum, K.E.; Healy, P.J. Revealed reputations in the finitely-repeated prisoners’ dilemma. Econ. Theory 2015, 58, 441–484. [Google Scholar] [CrossRef]
- Palfrey, T.R.; Prisbrey, J.E. Anomalous behavior in public goods experiments: How much and why? Am. Econ. Rev. 1997, 87, 829–846. [Google Scholar]
- Delton, A.W.; Krasnow, M.M.; Cosmides, L.; Tooby, J. Evolution of direct reciprocity under uncertainty can explain human generosity in one-shot encounters. Proc. Natl. Acad. Sci. USA 2011, 108, 13335–13340. [Google Scholar] [CrossRef] [PubMed]
- Muller, L.; Sefton, M.; Steinberg, R.; Vesterlund, L. Strategic Behavior and Learning in Repeated Voluntary-Contribution Experiments. J. Econ. Behav. Organ. 2008, 67, 782–793. [Google Scholar] [CrossRef]
- Brandts, J.; Charness, G. The strategy versus the direct-response method: A first survey of experimental evidence. Exp. Econ. 2011, 14, 375–398. [Google Scholar] [CrossRef]
- Selten, R.; Mitzkewitz, M.; Uhlich, G. Duopoly strategies programmed by experienced players. Econometrica 1997, 65, 517–555. [Google Scholar] [CrossRef]
- Bruttel, L.V.; Kamecke, U. Infinity in the lab: How do people play repeated games? Theory Decis. 2012, 72, 205–219. [Google Scholar] [CrossRef]
- Fischbacher, U. z-Tree: Zurich Toolbox for Ready-made Economic Experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar] [CrossRef]
- Fréchette, G.R. Session-effects in the laboratory. Exp. Econ. 2012, 15, 485–498. [Google Scholar] [CrossRef]
- Dal Bo, P.; Fréchette, G.R. Strategy Choice In The Infinitely Repeated Prisoners’ Dilemma; Working Paper; New York University: New York, NY, USA, 2018. [Google Scholar]
- McKelvey, R.D.; Palfrey, T.R. Quantal Response Equilibria for Normal Form Games. Games Econ. Behav. 1995, 10, 6–38. [Google Scholar] [CrossRef]
- Goeree, J.K.; Holt, C.A.; Palfrey, T.R. Quantal Response Equilibrium A Stochastic Theory of Games; Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar]
- Gintis, H. Strong reciprocity and human sociality. J. Theor. Biol. 2000, 206, 169–179. [Google Scholar] [CrossRef] [PubMed]
- Fehr, E.; Schmidt, K.M. The Economics of Fairness, Reciprocity and Altruism–Experimental Evidence and New Theories. In Handbook on the Economics of Giving, Reciprocity and Altruism; Kolm, S.C., Ythier, J.M., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; pp. 615–691. [Google Scholar]
- Bicchieri, C. The Grammar of Society: The Nature and Dynamics of Social Norms; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Boyd, R.; Richerson, P.J. Solving the Puzzle of Human Cooperation. In Evolution and Culture; Levinson, S.C., Jaisson, P., Eds.; MIT Press: Cambridge, MA, USA, 2005; pp. 105–132. [Google Scholar]
- Axelrod, R. The Evolution of Cooperation; Basic Books: New York, NY, USA, 1984. [Google Scholar]
- Rand, D.G.; Peysakhovich, A.; Kraft-Todd, G.T.; Newman, G.E.; Wurzbacher, O.; Nowak, M.A.; Greene, J.D. Social heuristics shape intuitive cooperation. Nat. Commun. 2014, 5, 3677. [Google Scholar] [CrossRef] [PubMed]
- Todd, P.M.; Gigerenzer, G. Simple Heuristics that Make Us Smart; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition, and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
| 1. | |
| 2. | A general reputation-building argument need not specify why cooperative types choose to cooperate. One of the most common explanations is that some players have social preferences and that is why they cooperate (e.g., as argued by Andreoni and Miller [9] and Camerer and Fehr [10]). However, the same logic applies if cooperative types are cooperating due to other reasons, such as inability to backward induct [1], having naive prior beliefs [11], or because they are prone to make mistakes [12]. |
| 3. | |
| 4. | |
| 5. | In Section A of the Supplementary we show that always defect dominates all the other strategies of second movers. |
| 6. | Throughout the results section, we report p-values from regressions used to test whether the frequency of various strategies and actions significantly differ. In all regressions, we cluster standard errors on sessions since errors may be correlated because participants are randomly re-matched within sessions. Section B of the Supplementary contains the output of all regressions and the precise description of each regression. Given that there is some concern about session effects and clustering in laboratory experiments [19], we checked whether our results hold if instead we cluster standard errors on subjects. We find that they do (see the Supplementary for details). Finally, the Supplementary also contains the results of the equivalent nonparametric tests. |
| 7. | This is well in line with evidence from infinitely repeated prisoner’s dilemmas showing that tit-for-tat is one of the most common cooperative strategies [20]. |
| 8. | The same is true for always reciprocate. It has a lower expected payoff than the strategy ddcd, but it is used considerably more often. |
| 9. | For example, the payoff difference between reciprocate then defect and always reciprocate in a SPD with a continuation probability of 0.50 and a payoff of mutual cooperation of 37 points, as in SPD-High, can also be attained in a SPD with a continuation probability of 0.23 and a payoff of mutual cooperation of 44 points, or a SPD with a continuation probability of 0.77 and a payoff of mutual cooperation of 30 points. |
| 10. | Consider the example where second movers believe that their matched first mover is a reciprocator with certainty (i.e., , and ). Second movers with this belief and with Fehr-Schmidt preference in SPD-High or in SPD-Low, derive a higher expected utility from reciprocate then defect (which gives second movers an expected utility of ) than from both always defect (which gives ) and always reciprocate (which gives ). Second movers with in SPD-High or in SPD-Low derive a higher expected utility from always reciprocate, and second movers with in SPD-High or in SPD-Low derive a higher expected utility from always defect. |
| 11. | Alternatively, one can always assume that second movers hold out-of-equilibrium beliefs, in which case it is not hard to find beliefs for which the three types choose different strategies (e.g., see footnote 10). However, making this assumption makes this explanation quite similar to simply assuming that different individuals use different social heuristics. |
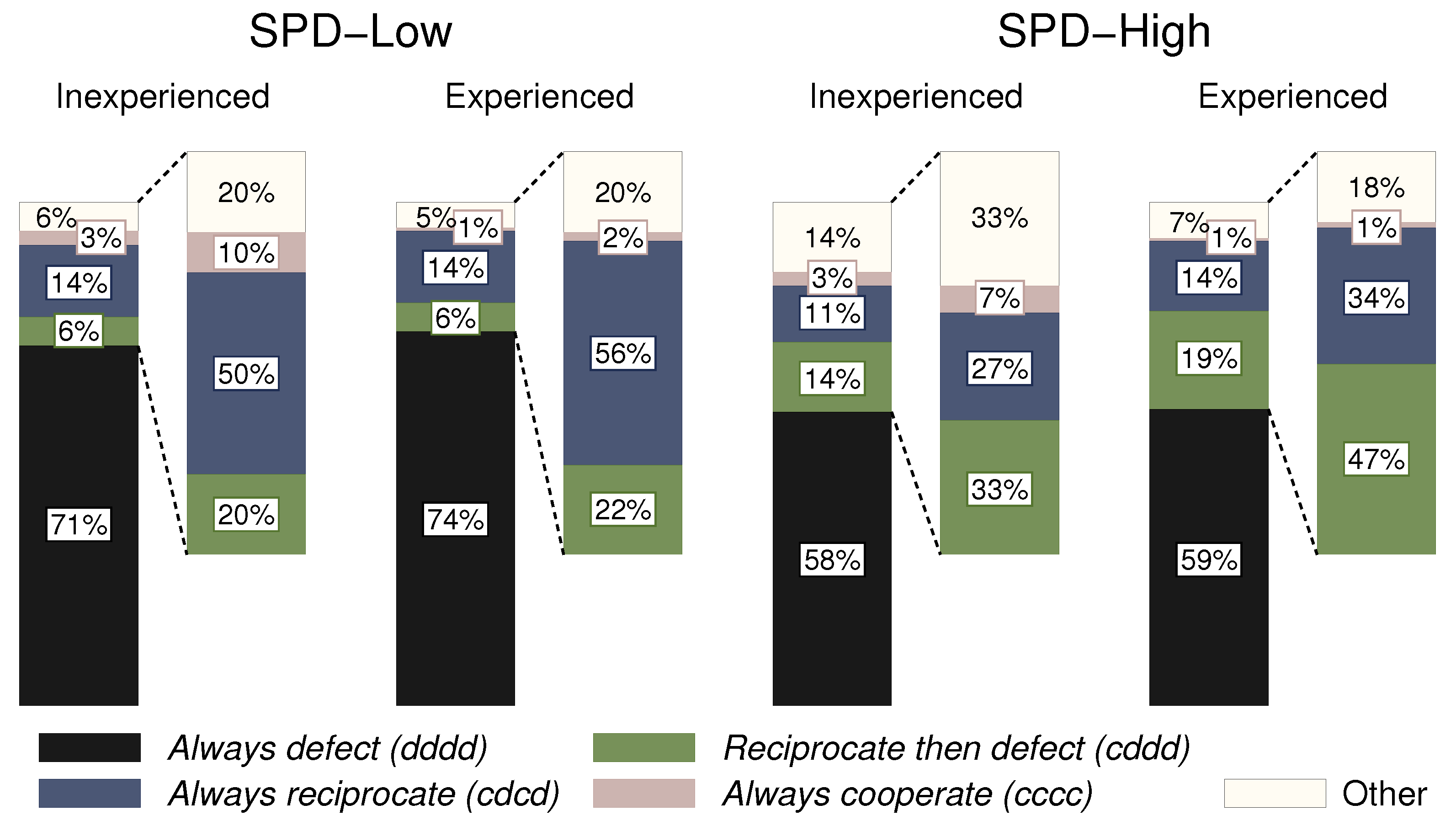
| First Mover’s Action In: | Period 1 | Period 2 | ||
|---|---|---|---|---|
| Second mover’s strategies: | ||||
| always defect | d | d | d | d |
| reciprocate then defect | c | d | d | d |
| d | c | d | d | |
| d | d | c | d | |
| d | d | d | c | |
| c | c | d | d | |
| always reciprocate | c | d | c | d |
| c | d | d | c | |
| d | c | c | d | |
| d | c | d | c | |
| d | d | c | c | |
| c | c | c | d | |
| c | c | d | c | |
| c | d | c | c | |
| d | c | c | c | |
| always cooperate | c | c | c | c |
| Period | SPD-Low | SPD-High | ||||||
|---|---|---|---|---|---|---|---|---|
| Inexperienced | Experienced | Inexperienced | Experienced | |||||
| 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | |
| If first mover cooperates | 23% | 23% | 21% | 19% | 31% | 19% | 35% | 19% |
| If first mover defects | 6% | 9% | 2% | 1% | 11% | 11% | 3% | 3% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reuben, E.; Suetens, S. Instrumental Reciprocity as an Error. Games 2018, 9, 66. https://doi.org/10.3390/g9030066
Reuben E, Suetens S. Instrumental Reciprocity as an Error. Games. 2018; 9(3):66. https://doi.org/10.3390/g9030066
Chicago/Turabian StyleReuben, Ernesto, and Sigrid Suetens. 2018. "Instrumental Reciprocity as an Error" Games 9, no. 3: 66. https://doi.org/10.3390/g9030066
APA StyleReuben, E., & Suetens, S. (2018). Instrumental Reciprocity as an Error. Games, 9(3), 66. https://doi.org/10.3390/g9030066





