The Effect of Competition on Risk Taking in Contests
Abstract
1. Introduction
2. Related Literature
3. Theoretical Analysis
4. Experimental Analysis
4.1. Design and Procedures
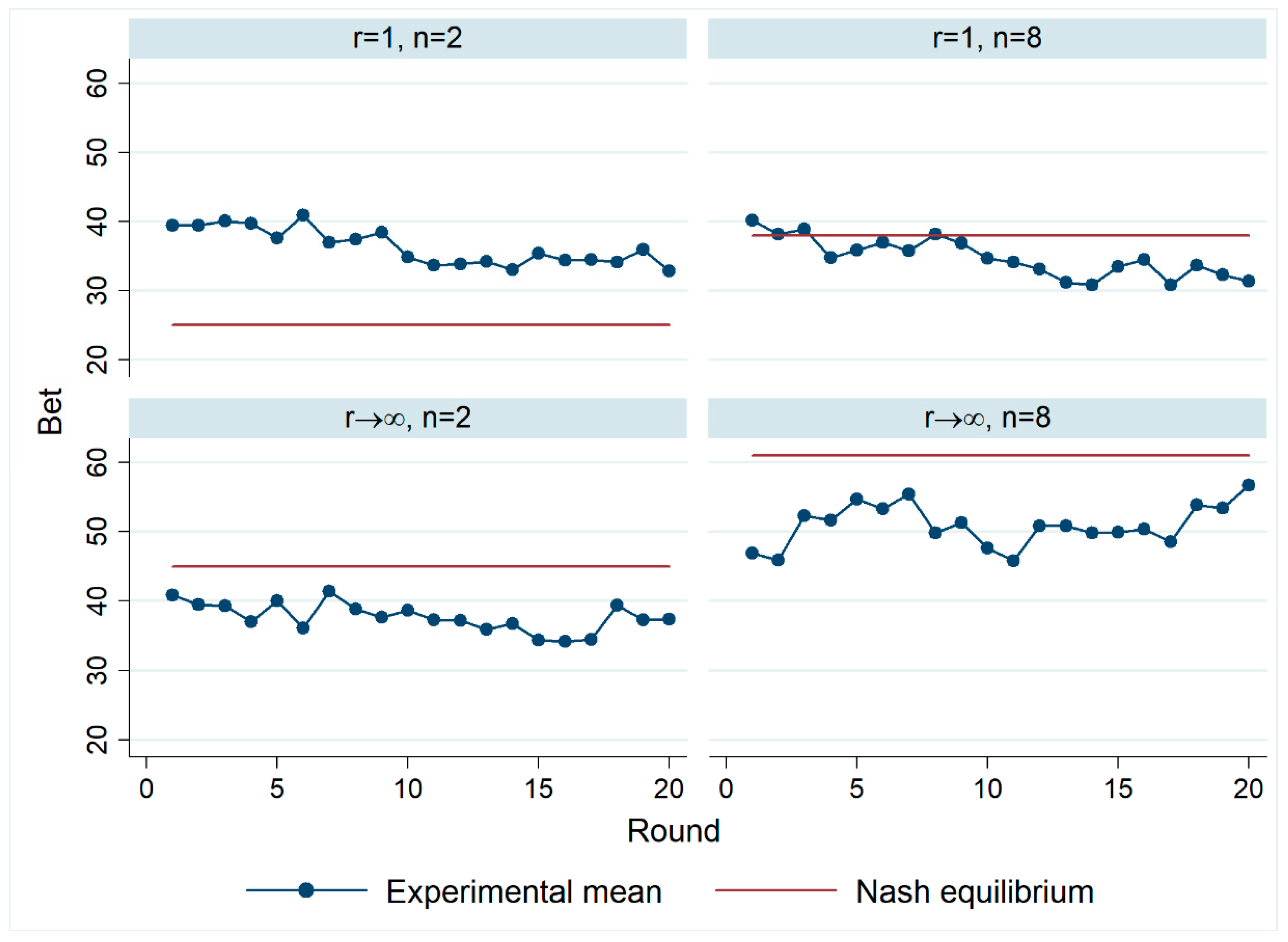
4.2. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Equilibrium Analysis for the Case n = 2
Appendix A.2. Representation of MSNE
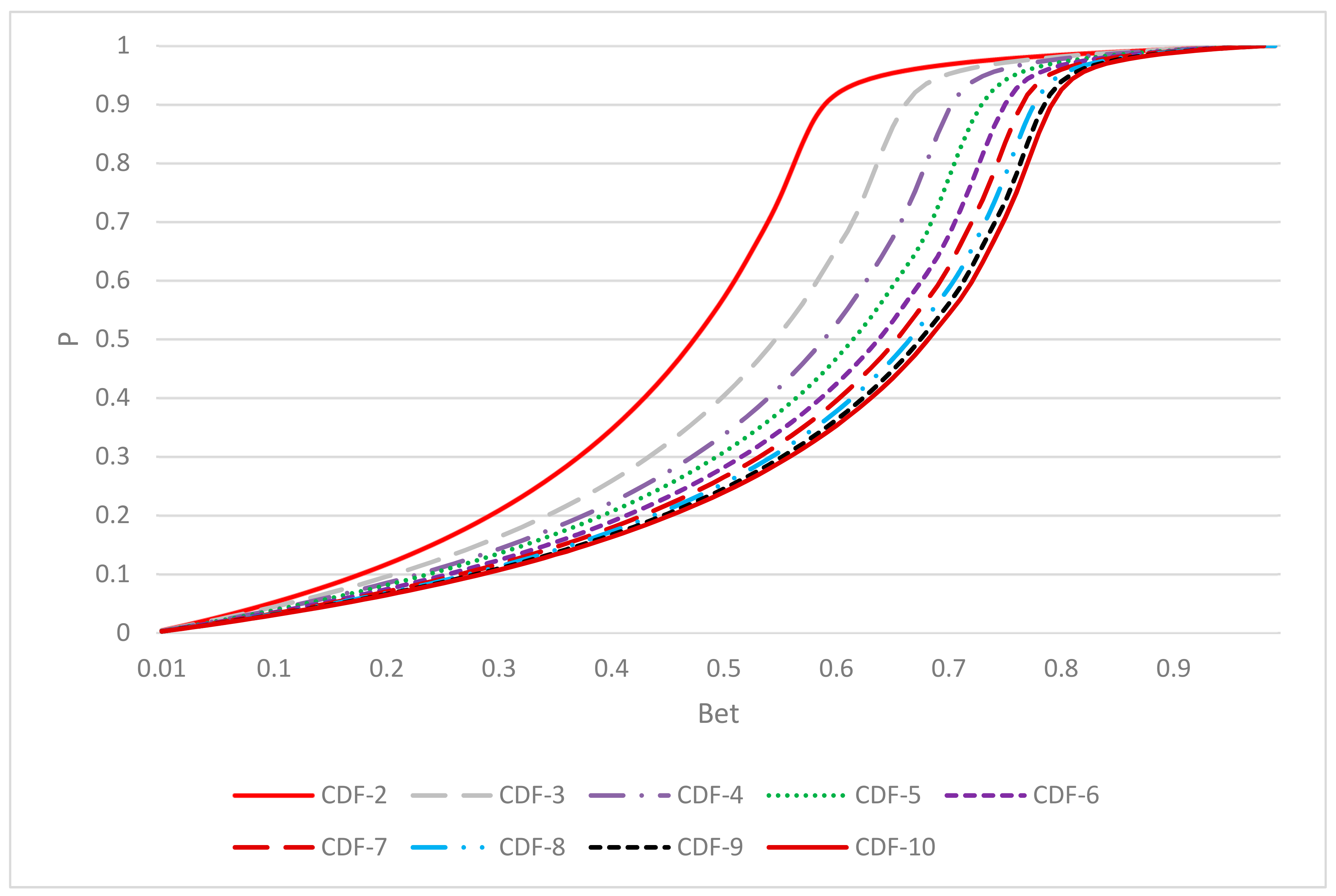

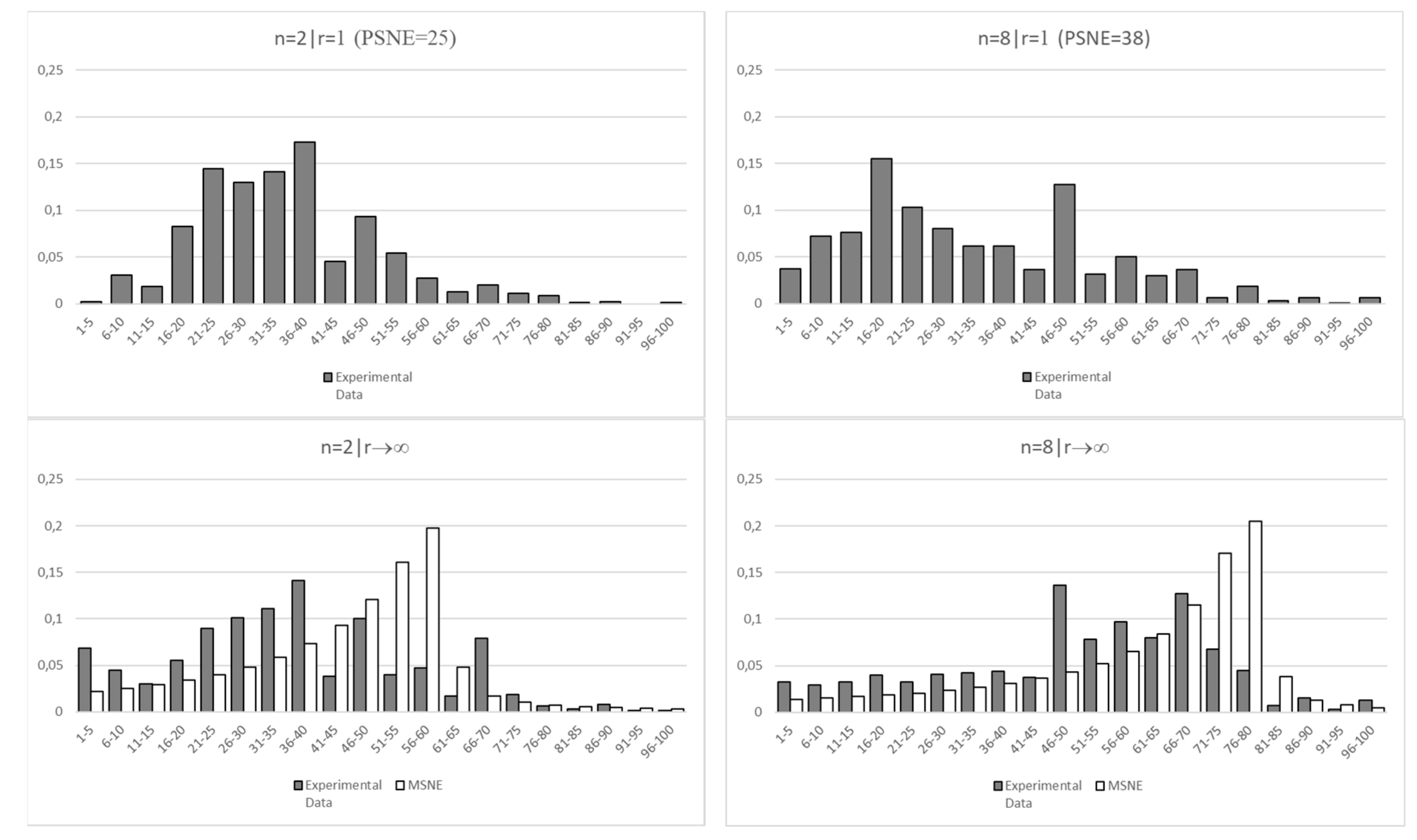
Appendix A.3. Empirical Distribution
Appendix B. Sample Instructions (Treatment n = 8, r = 1)
Appendix B.1. Instructions
Appendix B.2. Competing for a Prize
Appendix B.3. Collecting Green Chips
- Green chips may help you to win the prize of 1000 ECU; but they have no other value.
- If you collect the red chip you will have to pay a penalty of 50 ECU (and in addition all your green chips are destroyed).
- The seven other participants in your group is faced with his or her own set of 100 boxes. Your decisions and whether or not you collect a red chip are completely independent.
- If both you and all the other seven participants happen to collect a red chip, all of you win the prize with equal probability (12.5%).
- In each period you will face a new and fresh set of 100 boxes. Outcomes in a period are completely independent of those in other periods.
Appendix B.4. Information
Appendix B.5. Earnings and Questionnaire
Appendix B.6. Final Remarks
Appendix C. Power Analysis
| Treatment | n | Power M-W Test | ||
|---|---|---|---|---|
| 2 | 8 | |||
| r | 1 | 30 (8.07) [22] | 40 (5.08) [6] | 1−β = 0.856 |
| ∞ | 47 (8.90) [19] | 65 (5.63) [6] | 1−β = 0.998 | |
| power M-W test | 1−β = 0.999 | 1−β = 0.999 | ||
References
- Dechenaux, E.; Kovenock, D.; Sheremeta, R.M. A survey of experimental research on contests, all-pay auctions and tournaments. Exp. Econ. 2014, 18, 609–669. [Google Scholar] [CrossRef]
- Konrad, K.A. Strategy and Dynamics in Contests, 1st ed.; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Bronars, S.; (University of Texas at Austin, Austin, TX, USA). Unpublished Working Paper. 1987.
- Hvide, H.K. Tournament rewards and risk taking. J. Labor Econ. 2002, 20, 877–898. [Google Scholar] [CrossRef]
- Gaba, A.; Tsetlin, I.; Winkler, R.L. Modifying variability and correlations in winner-take-all contests. Oper. Res. 2004, 52, 384–395. [Google Scholar] [CrossRef]
- Gilpatric, S.M. Risk taking in contests and the role of carrots and sticks. Econ. Inq. 2009, 47, 266–277. [Google Scholar] [CrossRef]
- Crosetto, P.; Antonio, F. The “bomb” risk elicitation task. J. Risk Uncertain. 2013, 47, 31–65. [Google Scholar] [CrossRef]
- Bothner, M.S.; Kang, J.; Stuart, T.E. Competitive crowding and risk taking in a tournament: Evidence from NASCAR racing. Adm. Sci. Q. 2007, 52, 208–247. [Google Scholar] [CrossRef]
- Blundell, R.; Griffiths, R.; Van Reenen, J. Market share, market value and innovation in a panel of British manufacturing firms. Rev. Econ. Stud. 1999, 66, 529–554. [Google Scholar] [CrossRef]
- Aghion, P.; Bloom, N.; Blundell, R.; Griffith, R.; Howitt, P. Competition and innovation: An inverted-U relationship. Q. J. Econ. 2005, 120, 701–728. [Google Scholar]
- Boyd, J.H.; De Nicolo, G. The theory of bank risk taking and competition revisited. J. Financ. 2005, 60, 1329–1343. [Google Scholar] [CrossRef]
- Martinez-Miera, D.; Repullo, R. Does competition reduce the risk of bank failure? Rev. Financ. Stud. 2010, 23, 3638–3664. [Google Scholar] [CrossRef]
- Davis, D.D.; Reilly, R.J. Do too many cooks always spoil the stew? An experimental analysis of rent-seeking and the role of a strategic buyer. Public Choice 1998, 95, 89–115. [Google Scholar] [CrossRef]
- Potters, J.; de Vries, C.G.; van Winden, F. An experimental examination of rational rent-seeking. Eur. J. Political Econ. 1998, 14, 783–800. [Google Scholar] [CrossRef]
- Cason, T.N.; Masters, W.A.; Sheremeta, R.M. Entry into winner-take-all and proportional-prize contests: An experimental study. J. Public Econ. 2010, 94, 604–611. [Google Scholar] [CrossRef]
- Sheremeta, R.M. Contest design: An experimental investigation. Econ. Inq. 2011, 49, 573–590. [Google Scholar] [CrossRef]
- Morgan, J.; Orzen, H.; Sefton, M. Endogenous entry in contests. Econ. Theor. 2012, 51, 435–463. [Google Scholar] [CrossRef]
- Gneezy, U.; Smorodinsky, R. All-pay auctions—An experimental study. J. Econ. Behav. Organ. 2006, 61, 255–275. [Google Scholar] [CrossRef]
- Harbring, C.; Irlenbusch, B. An experimental study on tournament design. Labour Econ. 2003, 10, 443–464. [Google Scholar] [CrossRef]
- Orrison, A.; Schotter, A.; Weigelt, K. Multiperson tournaments: An experimental examination. Manag. Sci. 2004, 50, 268–279. [Google Scholar] [CrossRef]
- List, J.; Van Soest, D.; Stoop, J.; Zhou, H. On the Role of Group Size in Tournaments: Theory and Evidence from Lab and Field Experiments; No. w20008; National Bureau of Economic Research: Cambridge, MA, USA, 2014. [Google Scholar]
- Eriksen, K.W.; Kvaløy, O. No guts, no glory: An experiment on excessive risk-taking. Rev. Financ. 2016, 21, 1327–1351. [Google Scholar] [CrossRef]
- Gneezy, U.; Potters, J. An experiment on risk taking and evaluation periods. Q. J. Econ. 1997, 112, 631–645. [Google Scholar] [CrossRef]
- Baye, M.R.; Kovenock, D.; De Vries, C.G. The all-pay auction with complete information. Econ. Theor. 1996, 8, 291–305. [Google Scholar] [CrossRef]
- Chatterjee, B. An optimization formulation to compute nash equilibrium in finite games. In Proceedings of the 2009 Proceeding of International Conference on Methods and Models in Computer Science (ICM2CS), Delhi, India, 14–15 December 2009. [Google Scholar] [CrossRef]
- Fischbacher, U. Z-tree: Zurich toolbox for ready-made economic experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar] [CrossRef]
- Huck, S.; Normann, H.-T.; Oechssler, J. Two are few and four are many: Number effects in experimental oligopolies. J. Econ. Behav. Organ. 2004, 53, 435–446. [Google Scholar] [CrossRef]
- Füllbrunn, S.; Neugebauer, T. Varying the number of bidders in the first-price sealed-bid auction: Experimental evidence for the one-shot game. Theory Decis. 2013, 75, 421–447. [Google Scholar] [CrossRef]
- Müller, W.; Schotter, A. Workaholics and dropouts in organizations. J. Eur. Econ. Assoc. 2010, 8, 717–743. [Google Scholar] [CrossRef]
- Camerer, C.F.; Ho, T.H.; Chong, J.K. A cognitive hierarchy model of games. Q. J. Econ. 2004, 119, 861–898. [Google Scholar] [CrossRef]
- Ederer, F. Feedback and motivation in dynamic tournaments. J. Econ. Manag. Strat. 2010, 19, 733–769. [Google Scholar] [CrossRef]
| 1 | |
| 2 | Of course, the level of resources spent may also affect the level of risk involved. We, however, focus on the level of risk as a strategic variable not as a by-product of the level of effort. |
| 3 | The analysis can be easily extended to cover the following more general specification: The parameter does not affect the equilibrium; it drops out of the analysis as it enters the numerator and the denominator of the contest success function in the same way. The parameter has the same effect on the equilibrium as the parameter r; both parameters enter the contest success function in the same way. |
| 4 | The payoff tables are available upon request. |
| 5 | For the case n = 2 | r = 1, the equilibrium can be presented in closed-form as it follows from solving a quadratic equation (see Appendix A.1). With n players, the symmetric Nash equilibrium for the case r = 1 requires solving a polynomial equation of degree n, which is impossible to do in closed-form for n > 3. Also, for n > 3 we could not establish comparative statics analytically by applying the implicit function theorem. |
| 6 | In Appendix A.2 we present the cumulative density functions of the mixed strategy equilibria for n = 2, 3, …, 10. This illustrates that levels of risk taking are predicted to increase with n in the sense of first-order stochastic dominance (and not just in terms of average bets). For the two cases we implement in the experiment, r → ∞|n = 2 and r → ∞|n = 8, we also present the density functions of the mixed strategy equilibria. |
| 7 | Originally 210 subjects participated but due to a programming error we had to discard the data from 4 groups of 8 subjects. |
| 8 | One reason to focus on these two values of the sensitivity parameter is that they are relatively intuitive schemes and easy to explain to subjects, unlike for example the case r = 3 which involves cubed numbers. |
| 9 | Since in one treatment we have a 8-player game it was impractical to implement random matching. Implementing fixed matching is quite common in experiments that study the effect of the number of players in games (e.g., Harbring and Irlenbusch [19]; Huck et al. [27]; Gneezy and Smorodinsky [18]; Füllbrunn and Neugebauer [28]). |
| 10 | This method of risk taking closely follows the Bomb Risk Elicitation Task of Crosetto and Filippin [7] in which their bomb corresponds to our red chip. A feature of our design is that the chips collected have no monetary value but are entered into a contest for a prize. |
| 11 | A reasonable hypothesis is that the variance of the bids is higher if the Nash equilibrium is in mixed strategies (r → ∞) than if the Nash equilibrium is in pure strategies (r = 1). We find substantial support for this hypothesis. In the games with r = 1 the variance of the bids is significantly lower than in the games with r → ∞ (at 5%-level with a one-sided test). This holds both for the variance of the bids across players within a group, and for the variance of the bids across rounds for the same player. |
| 12 | One might think that this effect is due to selection (reverse causality) where subjects who take more risk are more likely to draw the red chip. However, even in a fixed effects regression the positive effect remains. |
| 13 | For the risk neutral case, equilibrium depends on the value of c/v. Let u(.) be a concave utility function incorporating risk aversion. Equilibrium will then depend on the value of u(c)/u(v) which is larger than c/v, since c < v. Hence, due to risk aversion, the cost c gets a “larger weight” relative to the prize v. This leads to lower risk-taking levels. The same holds for loss aversion. |
| 14 | One might worry that, despite the random assignment over treatments, subjects in treatment n = 2|r = 1 have different risk preferences than subjects in the other three treatments. We find no indication for this. Subjects’ self-reported ‘proneness to take risk’ does not differ between the treatments. |
| 15 | At the same time, it can be seen that risk-taking levels increase in the final three rounds in both treatments with r → ∞. This could hint at an end-effect during which collusion breaks down. So, even though from a theoretical perspective collusion should be more difficult to support with r → ∞ than with r = 1, we cannot rule out that some groups manage to attain at least some degree of tacit collusion which then breaks down near the end of the experiment. |
| 16 | The CH model assumes that there is distribution of player types with varying levels of cognition. Level-0 types have the lowest level of cognition and are assumed to pick a strategy at random. Level-1 types believe that other players are level-0 and choose a best response to that belief. Level-2 types believe that others players consist of a mixture level-0 and level-1 types and best respond to that belief. Generally, level-k types believe that other players are a mixture of lower types. The CH is then closed by assuming a specific distribution of types, usually a Poison distribution. For our implementation we have used a Poison distribution with parameter τ = 1.5 but the model predictions are quite robust to assuming other values of τ. Details are available from the authors upon request. |
| 17 | Note that in our experiment, subjects did not receive feedback on the choices of the other player(s). Hence, learning dynamics based on such information, such as best response learning or fictitious play, are not applicable. |
| 18 | The estimates are very similar if we use only the early rounds of the experiments. |
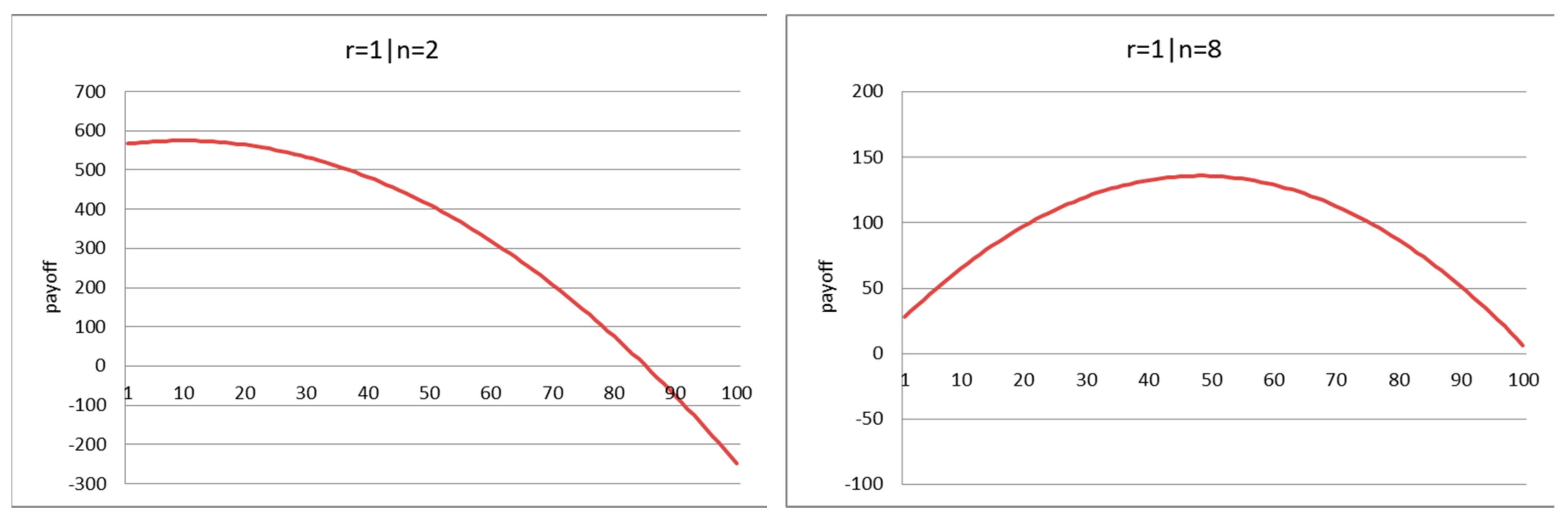
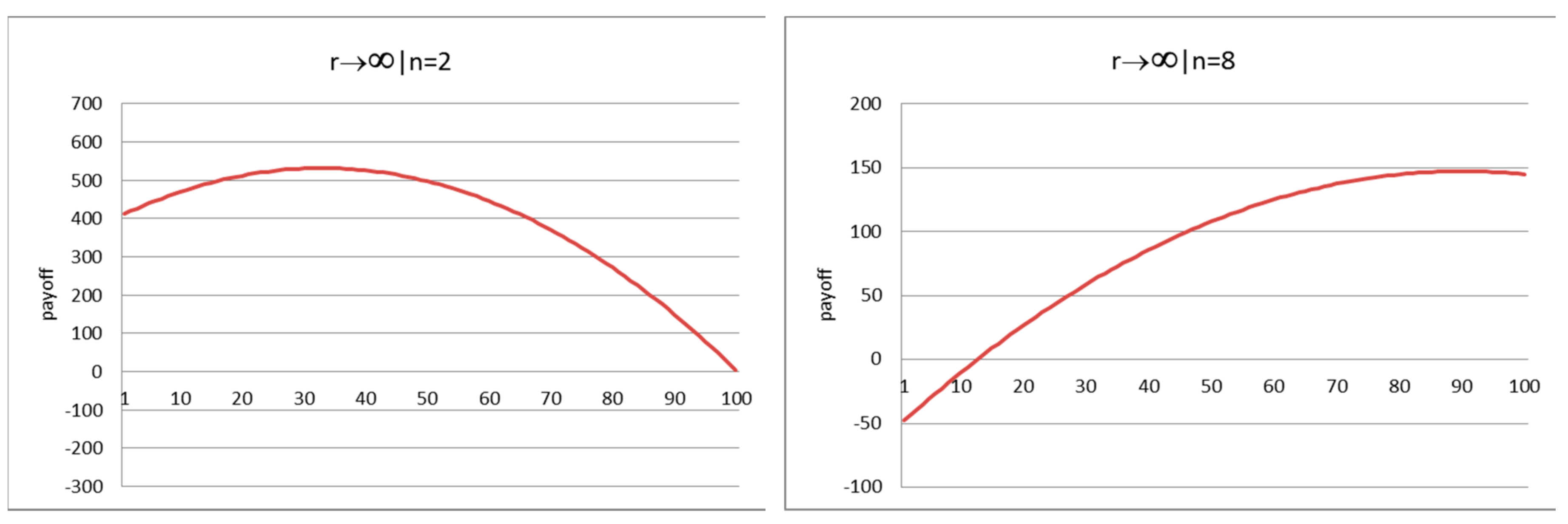
| 19 | Note that these maxima do not necessarily coincide with Nash equilibrium. Still, of course, there is a relationship as both equilibrium and realized payoffs are based on the same payoff structure. |
| n | r = 1 | r → ∞ |
|---|---|---|
| 2 | 0.25 | 0.449 |
| 3 | 0.31 | 0.509 |
| 4 | 0.34 | 0.545 |
| 5 | 0.36 | 0.566 |
| 6 | 0.37 | 0.586 |
| 7 | 0.38 | 0.600 |
| 8 | 0.38 | 0.610 |
| 9 | 0.39 | 0.619 |
| 10 | 0.39 | 0.625 |
| Treatment | n | M-W Test | Row Total | ||
|---|---|---|---|---|---|
| 2 | 8 | ||||
| r | 1 | 36.33 (8.07) [22] | 34.76 (5.08) [6] | p = 0.956 | 36.00 (7.48) [28] |
| ∞ | 37.68 (8.90) [19] | 50.97 (5.63) [6] | p = 0.006 | 40.87 (9.98) [25] | |
| M-W test | p = 0.583 | p = 0.004 | p = 0.069 | ||
| Column Total | 36.96 (8.38) [41] | 42.86 (9.89) [12] | p = 0.044 | 38.29 (9.00) [53] | |
| Indep. Variable | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| r → ∞ | 4.725 | 1.347 | 1.347 | 1.347 |
| (2.303) ** | (2.631) | (2.633) | (2.634) | |
| n = 8 | 5.736 | −1.568 | −1.568 | −1.568 |
| (2.575) ** | (2.561) | (2.562) | (2.564) | |
| r → ∞ × n = 8 | 14.855 | 14.85 | 10.27 | |
| (3.886) *** | (3.888) *** | (4.301) ** | ||
| round | −0.252 | −0.301 | ||
| (0.110) ** | (0.122) ** | |||
| round × r → ∞ × n = 8 | 0.436 | |||
| (0.175) ** | ||||
| cons | 34.77 | 36.33 | 38.98 | 39.49 |
| (1.632) *** | (1.700) *** | (2.164) *** | (2.243) *** | |
| R2 | 0.080 | 0.146 | 0.161 | 0.165 |
| number of observations | 1060 | 1060 | 1060 | 1060 |
| Indep. Variable | (1) | (2) | (3) |
|---|---|---|---|
| r → ∞ | 1.347 | 2.727 | 2.631 |
| (2.830) | (2.701) | (2.701) | |
| n = 8 | −1.568 | −1.173 | −1.091 |
| (2.641) | (2.605) | (2.608) | |
| r → ∞ × n = 8 | 14.86 | 13.135 | 13.276 |
| (4.046) *** | (3.923) *** | (3.92) *** | |
| round | −0.202 | −0.202 | −0.197 |
| (0.093) ** | (0.093) ** | (0.095) * | |
| female | −1.092 | −0.972 | |
| (1.954) | (0.196) | ||
| age | −0.317 | −0.335 | |
| (0.286) | (0.281) | ||
| find game complex | 0. 638 | 0.592 | |
| (0.361) * | (0.363) * | ||
| prone to take risk | 1.511 | 1.491 | |
| (0.45) *** | (0.453) *** | ||
| L.redchip | 2.298 | ||
| (0.767) ** | |||
| L.win | 0.575 | ||
| (0.75) | |||
| cons | 38.45 | 36.85 | 36.113 |
| (1.832) *** | (7.65) *** | (7.608) *** | |
| R2 (overall) | 0.108 | 0.144 | 0.165 |
| number of observations | 3560 | 3560 | 3382 |
| number of subjects | 178 | 178 | 178 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spadoni, L.; Potters, J. The Effect of Competition on Risk Taking in Contests. Games 2018, 9, 72. https://doi.org/10.3390/g9030072
Spadoni L, Potters J. The Effect of Competition on Risk Taking in Contests. Games. 2018; 9(3):72. https://doi.org/10.3390/g9030072
Chicago/Turabian StyleSpadoni, Lorenzo, and Jan Potters. 2018. "The Effect of Competition on Risk Taking in Contests" Games 9, no. 3: 72. https://doi.org/10.3390/g9030072
APA StyleSpadoni, L., & Potters, J. (2018). The Effect of Competition on Risk Taking in Contests. Games, 9(3), 72. https://doi.org/10.3390/g9030072





