Instrumental Reciprocity as an Error

Abstract

We study the strategies used by experimental subjects in repeated sequential prisoners’ dilemma games to identify the underlying motivations behind instrumental reciprocity, that is, reciprocation of cooperation only if there is future interaction. Importantly, we designed the games so that instrumental reciprocity is a mistake for payoff-maximizing individuals irrespective of their beliefs. We find that, despite the fact that instrumental reciprocity is suboptimal, it is one of the most frequently used cooperative strategies. Moreover, although the use of instrumental reciprocity is sensitive to the costs of deviating from the payoff-maximizing strategy, these costs alone cannot explain the high frequency with which subjects choose to reciprocate instrumentally.

1. Introduction

Experiments have shown that individuals often use reciprocal strategies in repeated games and seem well aware of the fact that reciprocity can be used instrumentally. Namely, when playing with the same partners, reciprocating cooperation in early repetitions of a finitely repeated game before switching to defection often leads to higher earnings than simply defecting from the beginning. For example, it is often observed that subjects cooperate more frequently if they know that they will play at least once more with each other than if they know that they are playing one last time, the so-called “end-game effect” [1,2,3,4]. More recently, in their meta-analysis of finitely repeated prisoners’ dilemma games, Embrey et al. [5] establish that most subjects converge to using strategies that reciprocate cooperation until a threshold repetition, after which they start defecting.1

Why would subjects use reciprocal strategies instrumentally in games with a known end? The most common view about instrumental reciprocity is that it is used by players who want to maximize their own material payoff and who are sophisticated enough to understand that, in finitely repeated games, the presence or believed presence of cooperative player types results in the existence of equilibria with high levels of cooperation, at least in early repetitions of the game (as shown by the seminal paper of Kreps et al. [8]).2 However, it is also possible that instrumental reciprocity instead reflects the use of general reputation-building heuristics individuals have learned to apply over the course of their lives [13]. Deciding whether it is optimal or not to reciprocate someone’s cooperation in situations where there is possible future interaction is not a trivial task, even for calculative individuals. In this view, subjects use instrumental reciprocity strategies even if they do not maximize material payoffs. Previous repeated-game experiments, including the ones cited above, cannot differentiate between these two views because in all of them it is possible to rationalize cooperation through a reputation-building framework à la Kreps et al. [8]. In the current paper, we design an experiment that allows us to observe the use of instrumental reciprocity among experienced subjects in a setting where we are certain that it is an error from the point of view of material-payoff maximization.

The key features of our design are as follows. First, we use a sequential prisoners’ dilemma (SPD) game and allow for possible future interaction by repeating the game once with a known probability. Second, to detect instrumental reciprocity and avoid the confounding effects of beliefs, we elicit the strategies of second movers. Specifically, we allow second movers to condition their choice in each repetition of the SPD game on whether the first mover cooperates or defects. This design allows us to identify players who use instrumental reciprocity because they are willing to reciprocate cooperation by first movers in the first repetition of the SPD game but plan to defect if first movers cooperate in the second repetition of the SPD game (if played). We refer to this strategy as reciprocate then defect. Third, we choose payoffs in the game such that instrumental reciprocity is not a rational strategy for second movers who maximize material payoffs irrespective of their beliefs about the behavior of their matched first mover.

Our results can be summarized as follows. In line with the literature, we find that almost all of the second movers’ cooperative behavior in the SPD games is accounted for by reciprocal strategies. Overall, about $80\%$ of the cooperative strategies of experienced players can be attributed to two reciprocal strategies: reciprocate then defect and the strategy to always reciprocate (which is basically tit-for-tat, i.e., reciprocate cooperation in both the first and the second repetition of the game). Instrumental reciprocity is particularly prevalent, corresponding to $47\%$ of the observed cooperative strategies, if the gains to mutual cooperation are relatively high. If the gains to mutual cooperation are low, so that instrumental reciprocity becomes a more costly error from the point of view of a material payoff maximizer, the strategy reciprocate then defect accounts for just $22\%$ of the cooperative strategies. Finally, we find that the strategy always reciprocate is not sensitive to the gains to cooperation.

2. Experimental Design and Procedures

2.1. Experimental Game

In the experiment, pairs of participants play a SPD. The SPD is played once with certainty (period 1), and it is played a second time by the same two players (period 2) with a known continuation probability equal to 0.5. When playing the game, first movers make their decisions using the direct-response method: at the beginning of period 1 and period 2 (if played), they choose to cooperate (c) or to defect (d). Second movers make their decisions using the contingent-response method: they can condition their choice on the decision of the first mover and on the period being played.3 In particular, they are asked to choose to cooperate or to defect in four cases: (i) in period 1 when the first mover cooperates; (ii) in period 1 when the first mover defects; (iii) in period 2 when the first move cooperates; and (iv) in period 2 when the first mover defects.

The game develops as follows. After first movers make their initial decisions and second movers submit their strategies, players learn the outcome of the game in period 1. Subsequently, a coin toss is used to determine whether period 2 is played. If period 2 is played, first movers submit their second choice, which is then matched with the strategy that had already been entered by the second mover. Thereafter, both players learn the choice made by the partner (not the strategy) and the outcome of the game in period 2.

This method allows to directly observe the second movers’ strategy choice. To be precise, we observe Markov strategies since second movers can condition their choice in period 2 on the first mover’s decision in period 2 but not on decisions in period 1.4

Table 1. Possible strategies of second movers.

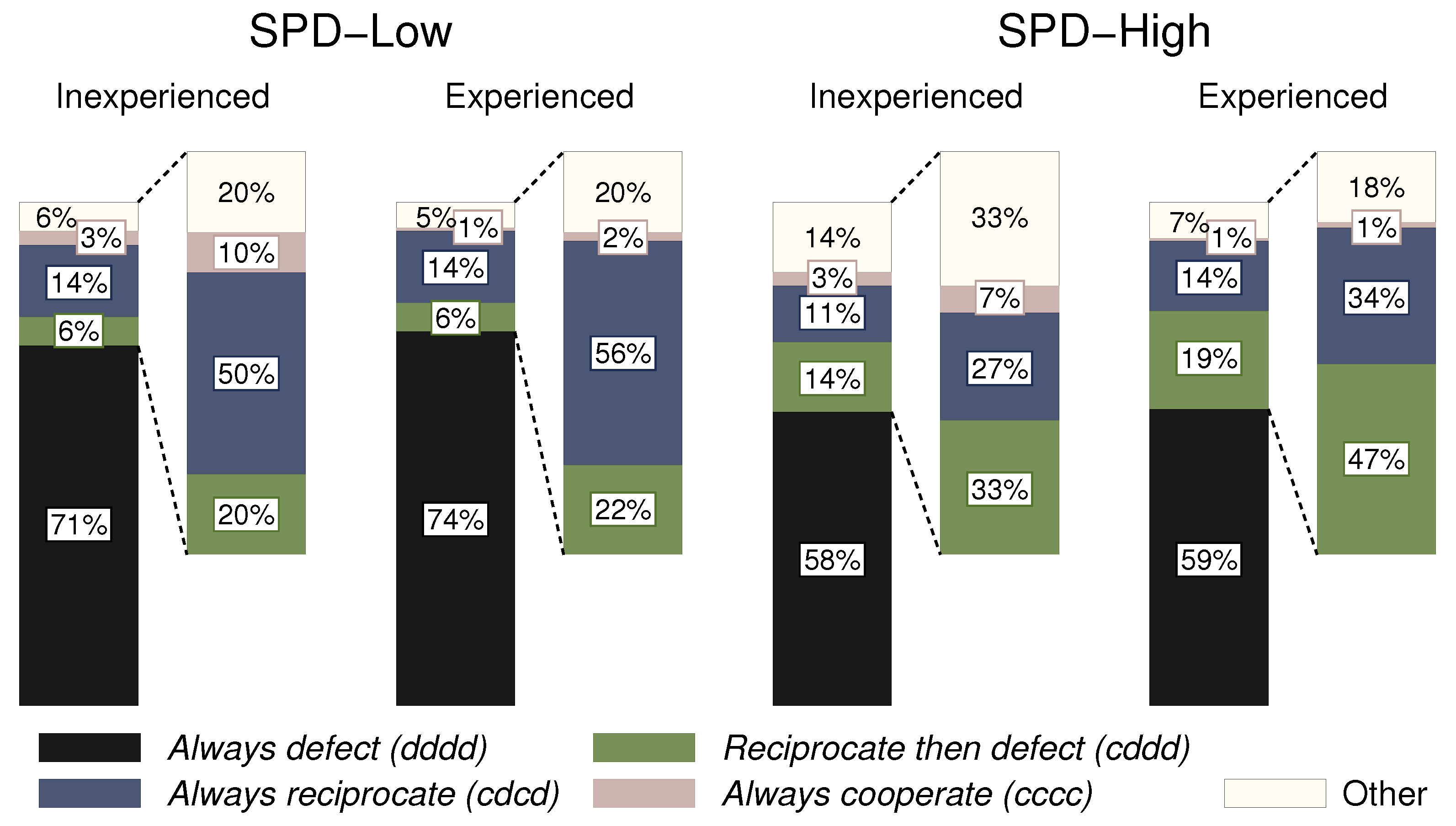
First Mover’s Action In:	Period 1		Period 2
	$\mathit{c}$	$\mathit{d}$	$\mathit{c}$	$\mathit{d}$
Second mover’s strategies:
always defect	d	d	d	d
reciprocate then defect	c	d	d	d
	d	c	d	d
	d	d	c	d
	d	d	d	c
	c	c	d	d
always reciprocate	c	d	c	d
	c	d	d	c
	d	c	c	d
	d	c	d	c
	d	d	c	c
	c	c	c	d
	c	c	d	c
	c	d	c	c
	d	c	c	c
always cooperate	c	c	c	c

Note: The table shows the possible strategies a second mover can use in the experiment. Strategies depend on the period (period 1 or period 2) and on the first mover’s choice (c or d).

shows the sixteen possible strategies second movers may adopt, highlighting four strategies that are of interest. Two of these strategies refer to the above-mentioned reciprocal strategies: reciprocate then defect (instrumental reciprocity) and always reciprocate.

2.2. Treatments

We implement two treatments, SPD-High and SPD-Low, which differ solely in the gains from mutual cooperation. Both treatments have the same mutual defection payoff (equal to 25 points), the same temptation payoff (equal to 50 points), the same sucker payoff (equal to 9 points), but a different mutual cooperation payoff (equal to 37 points in SPD-High and to 30 points in SPD-Low).

Given that we are interested in whether individuals reciprocate when it is not optimal to do so from a monetary perspective, the payoffs in the two treatments were selected so that second movers can never maximize their material payoff in the two-period SPD by choosing either reciprocal strategy. Specifically, in both treatments, the expected material payoff of the strategy to always defect dominates reciprocate then defect, which in turn dominates always reciprocate.5 To see this, first note that in period 2 a second mover is never worse off from a monetary perspective if she defects, which implies that reciprocate then defect weakly dominates always reciprocate (both strategies imply the same actions in period 1). Second, to see that always defect dominates reciprocate then defect, define $p_1$ as the probability the first mover cooperates in period 1. For a first mover who cooperates in period 1, define $p_2^{cc}$ as the probability that he cooperates in period 2 given that the second mover cooperates in period 1 and $p_2^{cd}$ as the probability that he cooperates in period 2 given that the second mover defects in period 1. Similarly, for a first mover who defects in period 1, define $p_2^{dc}$ as the probability that he cooperates in period 2 given that the second mover cooperates in period 1 and $p_2^{dd}$ as the probability that he cooperates in period 2 given that the second mover defects in period 1. The expected payoff of reciprocate then defect for a second mover equals

$$(1-p_1)\left[25+\frac{1}{2}\left(50p_2^{dd}+25\left(1-p_2^{dd}\right)\right)\right]+p_1\left[X+\frac{1}{2}\left(50p_2^{cc}+25\left(1-p_2^{cc}\right)\right)\right],$$

(1)

where $X=30$ in SPD-Low and $X=37$ in SPD-High. The expected payoff of always defect equals

$$(1-p_1)\left[25+\frac{1}{2}\left(50p_2^{dd}+25\left(1-p_2^{dd}\right)\right)\right]+p_1\left[50+\frac{1}{2}\left(50p_2^{cd}+25\left(1-p_2^{cd}\right)\right)\right].$$

(2)

It is easy to see that (1) is smaller than (2) as long as $X<50-25\frac{1}{2}(p_2^{cc}-p_2^{cd})$, which is true for any $p_1,p_2^{dd},p_2^{cc},p_2^{cd}\in [0,1]$ if $X<37.5$.

The payoffs of SPD-Low and SPD-High were chosen to systematically vary the magnitude by which the expected payoff of reciprocate then defect and that of always defect differ. In the “best” case for reciprocate then defect—that is, when in period 1 the first mover cooperates and in period 2 he reciprocates period-1 cooperation by the second mover, so that $p_1=1$, $p_2^{cc}=1$ and $p_2^{cd}=0$—the expected payoff of (1) in SPD-Low equals 55 points and that of (2) 62.5 points. By contrast, in SPD-High, the expected payoff of (1) equals 62 points and that of (2) 62.5 points.

2.3. Procedures

The experiment took one hour and was conducted in the laboratory of Northwestern University using z-Tree [18]. Participants were contacted through an online recruitment system. In total, 70 students participated in PD-Low and 72 in PD-High. Each student participated only once in a session of 10 to 12 people. After their arrival, participants drew a card to be randomly assigned to a seat in the laboratory and consequently to a treatment and role. Once everyone was seated, participants were given the instructions of the experiment. The instructions were written with neutral language. Participants were informed that the experiment consists of multiple parts and that the instructions for the subsequent parts would be provided after the first part had finished. After reading the instructions, they answered control questions to corroborate their understanding of the game. Thereafter, participants learned whether their role would be that of the first or the second mover. They kept the same role throughout the experiment. At the end of the session, participants were paid in private. Mean earnings were $16.10 and ranged from $11.70 to $24.40.

In the first part of the experiment, participants play the one-or-two-period SPD once. We refer to these data as coming from inexperienced participants. In the second part, participants play the game 15 times with randomly matched opponents. After each repetition they are informed of the choice(s) of their partner and their own payoff in that repetition. The reason we included the second part is that participants might need some experience to fully understand the use of reciprocal strategies [1,5,11]. We refer to data based on the last five repetitions of the SPD in the second part as coming from experienced participants. See Section C of the Supplementary for more detailed experimental procedures and a sample of the instructions.

3. Results

3.1. Cooperation and Reciprocation Rates

We distinguish between behavior when participants are “inexperienced” (in the first part of the experiment) and behavior once they have had time to learn (the last five repetitions of the second part), which we label as “experienced”. The observed cooperation rate of first movers is 14% in SPD-Low and 26% in SPD-High when participants are inexperienced and drops to respectively 5% and 9% once they have gained some experience. The realized cooperation rate of second movers is 10% in SPD-Low and 17% in SPD-High when inexperienced and drops to respectively 4% and 7% when experienced.

For our purposes, however, it is of more interest to look at how second movers condition their behavior on the period and action of the first mover. These conditional cooperation rates are provided in

Table 2. Cooperation rates for inexperienced and experienced second movers.

Period	SPD-Low				SPD-High
	Inexperienced		Experienced		Inexperienced		Experienced
	1	2	1	2	1	2	1	2
If first mover cooperates	23%	23%	21%	19%	31%	19%	35%	19%
If first mover defects	6%	9%	2%	1%	11%	11%	3%	3%

Note: The table shows cooperation rates of inexperienced and experienced second movers in SPD-Low and SPD-High. The label “inexperienced” refers to behavior when participants play the experimental game for the first time. The label “experienced” refers to behavior in the last five repetitions of the experiment.

. From the table, it is clear that second movers reciprocate the first mover’s choice. A probit regression clustering standard errors on independent observations (sessions) confirms that second movers in both treatments cooperate significantly more when the first mover cooperates than when the first mover defects in period 1 ($p<0.004$).6 In period 2, second movers significantly reciprocate in all cases ($p<0.040$) except for inexperienced second movers in SPD-High ($p=0.359$). Overall, these results suggest an important role for reciprocal strategies. We now turn to the paper’s main results.

3.2. Strategies of Second Movers

The observed distribution of strategies of second movers by treatment is shown in Figure 1. The figure also shows the distribution of strategies conditional on them containing some cooperation. Although the most common strategy is always defect, which is the payoff-maximizing choice, a large share of the strategies involves some cooperation or reciprocation even after second movers have had plenty of opportunities to learn: 41% if strategies in SPD-High and 26% in SPD-Low. Next to always defect, reciprocate then defect and always reciprocate are the two most common strategies (the complete distribution of observed strategies is available in Section B of the Supplementary). To illustrate, for experienced players, these two strategies account for 33% of all strategies in SPD-High and 20% in SPD-Low.

If we concentrate on strategies that include cooperative actions by second movers, we can see that reciprocate then defect and always reciprocate account for over 60% of the strategy choices for inexperienced second movers, and this percentage goes up to 78% once second movers have gained experience.7 A similar picture emerges if we concentrate on the second movers’ realized cooperation. In SPD-High, reciprocate then defect is the most common strategy behind the realized cooperation while in SPD-Low it is always reciprocate. In the same way, but not illustrated in the figure, these two strategies account for most of the second movers’ reciprocity (i.e., the willingness in a given period to cooperate if the first mover cooperates and to defect if the first mover defects). Specifically, for both experienced and inexperienced second movers, they account for over 81% of the strategies that include reciprocity. In SPD-High, reciprocate then defect is the most common strategy behind reciprocation while in SPD-Low it is always reciprocate.

Looking at the change in the frequency at which strategies are used over time, we find that reciprocate then defect and always reciprocate are not used less frequently over time. Instead, the fraction of times second movers use these strategies increased slightly by the end of the experiment. In contrast, other strategies involving cooperation become less prevalent over time.

Finally, to test whether the distribution of strategies differs significantly depending on the treatment, we run a multinomial probit regression clustering standard errors on sessions (see Section B of the Supplementary for details). We find a significantly lower frequency of always defect and a significantly higher frequency of reciprocate then defect in SPD-High compared to SPD-Low for experienced participants ($p=0.044$ and $p=0.025$ respectively, $p>0.169$ for the other cases).

3.3. Is Instrumental Reciprocity a Simple Mistake?

Our results thus far are consistent with payoff-maximizing individuals mistakenly choosing strategies consistent with instrumental reciprocity as long as doing so is not too costly. In particular, the difference between SPD-High compared to SPD-Low in the frequency in which reciprocate then defect is used suggests that the costs of making mistakes plays a role in strategy choice. The fact that behavior is sensitive to errors but that individuals are less likely to make mistakes when doing so is more costly has been observed in many different games [21,22]. However, the high fraction of second movers choosing reciprocate then defect relative to other strategies suggests that the cost of deviating from the payoff-maximizing strategy is not sufficient to explain the observed distribution of strategies.

To evaluate whether the cost of deviation from profit maximization alone is enough to explain the high frequency of reciprocate then defect, we calculated the expected monetary payoff of each of strategy second movers could choose when we pit it against the distribution of choices made by first movers (see Section B of the Supplementary for details). We find evidence that reciprocate then defect is chosen too often compared to the cost one incurs by choosing it. In particular, the second movers’ strategy to defect in period 1 and reciprocate in period 2 (ddcd) has a higher expected payoff than reciprocate then defect but it is chosen considerably less often: it is chosen 3% of the time in both SPD-High and SPD-Low.8 This finding suggests that the popularity of reciprocate then defect is not simply the result of mere confusion or random mistakes due to low costs of deviating from the payoff-maximizing strategy.

4. Conclusions

We report the results of an experiment where individuals play a sequential prisoners’ dilemma with possible future interaction where always defect is the only rational strategy for second movers who maximize material payoffs, even if they believe that first movers are reciprocators. We find that a large fraction of the strategies adopted by second movers in this game involve some cooperation or reciprocation: 41% of the strategies with high gains to mutual cooperation and 26% of strategies with low gains to mutual cooperation. Of the cooperative strategies, reciprocate then defect (i.e., instrumental reciprocity) and always reciprocate are clearly the most common ones.

In addition to finding that these types of reciprocal strategies are used, we also find that the use of instrumental reciprocity is sensitive to the gains from mutual cooperation. When the payoff of mutual cooperation is relatively high, reciprocate then defect accounts for 19% of all strategies of experienced second movers. In comparison, when the payoff of mutual cooperation is relatively low, reciprocate then defect accounts for just 6% of all strategies. By contrast, always reciprocate is not responsive to changes in the gains to cooperation in our setting: it accounts for 14% of all strategies in both cases.

The findings related to the strategy always reciprocate may not come as a surprise since the use of this strategy has been extensively discussed in the literature (it is often referred to as “strong reciprocity” [23]). Individuals who strongly reciprocate can be modeled as being motivated by social preferences [24], as following a social norm [25,26], or as acting in accordance with a relatively hard-wired heuristic to conditionally cooperate [27,28].

In contrast, for instrumental reciprocity we think that our findings are more surprising. Reciprocate then defect is typically thought of as a strategy adopted by sophisticated material-payoff maximizers who realize that cooperating in early periods to build a reputation and then defecting in later periods is in their best interest [8]. Since in our experiment reciprocate then defect is strictly dominated by always defect for any belief the second movers can hold, and subjects played the game multiple times, which gives them the opportunity to learn, our findings suggest that reputation-building strategies are at least partly chosen for reasons other than rational material-payoff maximization.

What are the reasons that a significant number of experienced second movers use instrumental reciprocity in our experiment? As mentioned previously, our findings suggest that choosing reciprocate then defect is not simply due to random mistakes by rational material-payoff maximizers, even if one takes into account the costs of deviating from the payoff-maximizing strategy (always defect). We believe that this leaves us with two broad explanations.The simplest explanation for the occurrence of instrumental reciprocity in our setting is that it is a pre-established heuristic to reputation-build that might be well-adapted for everyday life but happens to be ill-suited for this particular experiment, in line with the arguments found in Todd and Gigerenzer [29] and Delton et al. [13]. A basic reputation-building heuristic explains why reciprocate then defect is chosen per se, but it is less straightforward to see why it would predict a difference between games with high and low gains to mutual cooperation. To predict this difference, one would need a model that explains when the heuristic is more or less likely to be used. Models of dual processes have been developed to explain the use of social heuristics for reciprocal strategies such as always reciprocate [28]. Hence, a fruitful line for future theoretical research would be to develop a similar model for reputation-building heuristics. In this respect, we think that an interesting extension to our work is to study how changes in the parameters of the game affect the popularity of reciprocate then defect when the cost of deviating from payoff maximization is kept constant. In particular, it would be interesting to vary the continuation probability in order to vary the salience of future interaction while changing the payoff of mutual cooperation such that the difference between reciprocate then defect and always defect is the same across treatments.9 If the continuation probability has an effect on the frequency of instrumental reciprocity in this setting, it would provide further evidence that the use of this strategy is driven by more than payoff maximization.

Another potential explanation for the use of reciprocate then defect is that it is chosen by utility-maximizing individuals with “weak” social preferences. For example, it can be shown that there exist beliefs for which reciprocate then defect is the utility-maximizing strategy of second movers who are averse to advantageous inequality but who are not adverse enough to prefer always reciprocate (see the inequity aversion model of Fehr and Schmidt [30]).10 The advantage of this explanation is that, within one utility-maximizing framework, one can potentially explain the use of both reciprocate then defect and always reciprocate as well as changes in the popularity of these two strategies depending on the parameters of the game. The drawback of this explanation is that it is difficult to derive the precise equilibrium beliefs and strategies of players if one assumes individuals with selfish, “weak”, and “strong” social preferences coexist. Hence, it is not surprising that, to the best of our knowledge, there is no theoretical work that shows that the interaction between these three types can result in an equilibrium where all the three commonly observed strategies (always defect, reciprocate then defect, and always reciprocate) are used.11 Showing the conditions for such an equilibrium is an interesting question for future research.