Abstract
Debates on an EU-leaving referendum arose in several member states after Brexit. We want to highlight how the exit of an additional country affects the power distribution in the Council of the European Union. We inspect the power indices of the member states both with and without the country which might leave the union. Our results show a pattern connected to a change in the number of states required to meet the 55% threshold. An exit that modifies this number benefits the countries with high population, while an exit that does not cause such a change benefits the small member states. According to our calculations, only the exit of Poland would be supported by the qualified majority of the Council.
1. Introduction
The withdrawal of the United Kingdom (UK) from the European Union (EU), Brexit, and its possible effects have become the subject of political debate in several countries like the Czech Republic, France, or Greece since the membership referendum in 2016 [1]. In 2021, a possible Polexit (Poland’s exit) has emerged [2]. Although numerous political and economic effects of an exit from the European Union might be worth inspecting, in this paper we look at one aspect: how the power distribution changes in the Council of the European Union. The voting system of the Council of the European Union has long been the subject of academic interest. Brams and Affuso [3] have used the example of the Council to show real-life occurrence of the new member paradox: Luxembourg has gained more voting power with the joining of Denmark, Ireland, and the United Kingdom in 1973. In the past the voting weights have changed several times, most recently in 2014.
Grech [4], Göllner [5], Kirsch [6], Kirsch et al. [7], Kóczy [8] and Szczypińska [9] have shown independently that Brexit mainly benefits large countries. Bertini et al. [10] have examined the issue in the case of the European Parliament. We first try to explore whether the same result would hold if another country leaves. Secondly, we want to answer the question: what would be the effect of Brexit if Croatia had not joined the EU?
The Council of the European Union, often referred to as the Council of Ministers, is an institution that represents the governments of the member states. It approves EU law and synchronizes the policy of the EU. Along with the European Parliament, the Council of the European Union is the main decision-making body of the EU. Every member state is represented by an individual. The difference in size among the member states appears in a weighted qualified majority voting. Under the Treaty of Lisbon, voting is successful if
- At least 55% of the member states (member quota);
- Represent at least 65% of the habitants (population quota).
Support the decision. Furthermore, any blocking minority should include at least four member states (blocking minority rule). Such creation of the weights enables us to calculate how the power distribution changes if a country leaves the European Union.
Several studies have addressed how voting power affects the overall likelihood of decision-making [11,12]. Contrary to expectations, some studies have found no connection or even a negative relationship between the voting power of individual member states and bargaining success [13,14]. However, Warntjen [15] has shown empirically that there is a robust positive relationship between the number of votes backing a member state request to change European legislation and its success probability. Therefore, it is an important question to measure how much power the countries have in the Council of the European Union.
Concerning our methodology, we use two well-known power indices: (1) the Shapley–Shubik index [16]; and (2) the Banzhaf index [17,18,19]. These measures reflect the probabilities of the players to be instrumental in making decisions. As far as votes on the spending of the budget are concerned, the index value of a player reflects the probability of spending one (or a million) euro in the interest of that player. For several cases of departure, we show the change made by an exit until 2030, which can be called a ‘farsighted’ sense.
We find a pattern connected to a change in the number of states required to meet the 55% threshold. An exit that changes the absolute value of the member quota (for example, from 15 to 14) benefits the large, an exit that does not cause such a change benefits the small countries. These results may suggest that a renegotiation of weights may become relevant.
Our results point in the direction that if the UK had left the European Union before the entry of Croatia, the effect would have been reversed: it would have favored the power of the small countries. According to the calculations, the exit of only one country from the EU27 would be supported by the qualified majority of the Council, Poland.
The paper is structured in the following way. The power indices to be used are defined and presented in Section 2. The results and their interpretation are detailed in Section 3. Section 4 summarises the main findings. Numerical results are presented in Appendix A, Appendix B, Appendix C and Appendix D. Details about the blocking minority rule can be found in Appendix E.
2. Methodology
It is popular to study voting situations as simple cooperative games, where the players are the voters. The value of any coalition (a subset of the player set) is 1 if it can decide a question, or 0 if not. According to Felsenthal and Machover [20,21], there are two interpretations of voting power. One conception, the influence power (I-power) focuses on voting power conceived of as a voter’s potential impact on the result of divisions of the decision-making institution: whether the policies proposed are adopted or rejected. The second conception, prize power (P-power) focuses on a voter’s expected share of a fixed prize given to the winning coalition, while both seek to quantify the potential influence that a member of a decision-making body has over the possible outcomes, they differ fundamentally in what they regard as the outcome. The I-power notion takes the outcome to be the immediate one, passage or defeat of the proposed bill. The P-power view is that the passage or defeat of a bill is merely the ostensible and proximate outcome.
There are historical reasons for this differentiation. The first scientific study of a priori voting was Penrose [19], however, it remained unnoticed for almost two decades. His original definition was ‘half the likelihood of a situation in which an individual vote can be decisive—that is to say, a situation in which the remaining votes are equally divided upon the issue at stake’ ([19], p. 53). Later Penrose [22] changed the value to its double. Without knowing of Penrose’s writings, Banzhaf [17] reinvented the idea.
Another approach proposed by Shapley and Shubik [16] derived from the theory of cooperative games with transferable utility. In such a game, every player receives some payoff of transferable utility. The amount that a given player receives depends on the strategies chosen by all the players. So the Shapley–Shubik index is interpretable as a prior probabilistic estimation of the payoff that the voter can expect on average.
Penrose and Banzhaf’s approach is the I-power, while Shapley–Shubik’s is a P-power notion [21].
They are used extensively for determining power in the Council of the European Union [12,23,24,25]. Since we investigate a phenomenon that belongs to the P-Power, it is better to focus more on analyzing the power distribution of the Council of the European Union with the Shapley–Shubik index [20].
Let N denote the set of players and let be an arbitrary subset of N. We use the corresponding lower-case letters to denote the cardinality of sets, so that and .
Definition 1
(Simple (voting) game). A game is a simple game if it satisfies the relation
Coalitions S such that are called winning coalitions, while coalitions S as are the losing ones.
Definition 2
(Weighted voting game). Let v be a game on the set of players N which is defined by an input as follows:
This simple game represented by () is known as a weighted voting game.
The Shapley–Shubik index is an application of the Shapley value [26] for voting games. Its principle can be described as follows: voters arrive in a random order, and when a coalition becomes winning, the full credit is given to the pivotal player arriving last. A player’s power is specified by the proportion of orders in which it plays this role.
Definition 3
(Shapley–Shubik index). For any simple game v, the Shapley–Shubik index of player i is as follows:
The Banzhaf index, which is the normalized Banzhaf value [17,18,19], uses a different approach. A player is called critical if it can turn a winning coalition into a losing one. The index shows what is the probability that a player influences a decision.
Definition 4.
Player i’s Banzhaf value is:
where is player i’s Banzhaf score, the number of coalitions where i is critical.
Usually, its normalized value is reported as the measure of voting power.
Definition 5.
The Banzhaf index is the normalized Banzhaf score:
The indices somehow show the voter’s expected relative share of the total payoff. When a country leaves, its payment to the EU budget is assumed to cease, therefore the remaining countries do not share the same prize as before. This is a simplification, as some non-EU member countries, like Norway, also contribute to the EU budget in a certain sense. Taking this into account, we correct the power index by the following fraction:
We compute for every country and each exit the adjusted power index as a percentage of the pre-exit power index.
Adjusted power indices have not been normalized for the comparison. Thus, the change in the power index reflects two effects, a shift in power on the one hand and a reduction in the budget on the other.
To illustrate how the indices are affected by changes in the player set, we analyze the situation of the European Economic Community in 1958. This example is well known in the voting literature. Its first academic discussion is probably Brams and Affuso [3], but it has appeared in several other studies [11,27,28,29].
Example 1.
In the predecessor of the EU, the European Economic Community (EEC), the six founding states already used a weighted voting system. The weight of the large countries (France, Germany, Italy) was 4, the weight of the medium-sized states (Belgium, The Netherlands) was 2, and the weight of the smallest state (Luxembourg) was 1. The decision threshold was 12.
According to Table 1, Luxembourg’s power was 0. France, Germany, and Italy each contributed 28% to the EEC budget, Belgium and the Netherlands paid 7.9%, while Luxembourg paid only 0.2%. If Luxembourg had exited and the decision-threshold (12) not changed, the remaining countries’ Shapley–Shubik and Banzhaf indices would have remained the same, but the adjusted indices would have decreased (see Table 2).

Table 1.
Decision-making in the Council of Ministers in 1958, Shapley–Shubik (S–S) and Banzhaf (Bz) indices.

Table 2.
The effect of Luxembourg’s departure from the Council of Ministers in 1958, Shapley–Shubik (S–S) and Banzhaf (Bz).
If a large country, for example, France, departs, and the threshold decreases to 9, then the change is more spectacular. The correction ratio, according to Formula (1), is 0.72. Table 3 shows the power measured by the adjusted Shapley–Shubik and Banzhaf indices. The arrows show the direction of power change. The only winner of this exit is Luxembourg.

Table 3.
The effect of France’s departure from the Council of Ministers in 1958, Shapley–Shubik (S–S) and Banzhaf (Bz).
3. Results
In this section, our findings are presented. Currently, pursuant to the Treaty of Lisbon, the qualified majority voting is successful in the Council of the European Union if
- At least 55% of the member states (member quota );
- Represent at least 65% of the inhabitants (population quota).
Support the decision. Furthermore, a blocking minority must include at least four Council members, failing which the qualified majority shall be deemed attained [30]. This condition is called the blocking minority rule, for further details about this, please see Appendix E.
We use population projections for 2015 and 2030 from Eurostat [31] and budget contribution data from the European Parliament [32]. The values are given in Table 4. The software IOP-Indices of Power [33] is used to calculate the Shapley–Shubik and Banzhaf indices. The software cannot handle large numbers, thus population data are entered in 100,000 s that may have a marginal effect on the indices. For the sake of simplicity, we disregarded the blocking minority rule in the calculations of adjusted power indices, which also has some minor effect (see Appendix E).

Table 4.
Member states of the EU—population (in 100,000 s) and financial contribution.
Kóczy [8] has shown that if the United Kingdom leaves the European Union, which has 28 member states, the smallest member states’ power indices decrease. We have found the same result after repeating the calculation for every other member state (see Appendix A). However, a further question remains: what happens if another member state leaves the EU? Here, we discuss the effects of the Czech Republic (Czexit) and Germany leaving the EU after Brexit. Secondly, building on our previous finding, we inspect what the effect of Brexit would be on the power distribution of the EU had the United Kingdom left it before Croatia entered. Is Brexit in this sense a belated threat? Our results show that it is.
In the following, we will call a country large or small depending on its population size. We observe a pattern, which connects the change in the member state quota to a change in the power distribution: when the departure modifies this threshold, the power indices of the large countries increase. When the departure does not evoke such a change, the power indices of the small countries increase.
3.1. The Impact of Additional Departures to Brexit
In the computations which investigate the results of an additional departure to Brexit, we base our calculations on the 27-member Union without the UK. As mentioned in the previous section, it is also considered that the exit of a country decreases the budget. The example of the Czech Republic is presented first because the EU-skeptical sentiment has recently become stronger in this country. The budget correction ratio is 0.989 according to Formula (1). Figure 1 shows the budget-adjusted change in power indices due to Czexit as a function of the population.
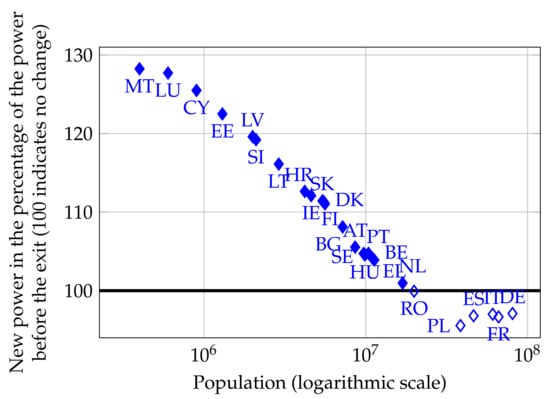
Figure 1.
Effect of Czexit with populations for 2015, adjusted Shapley–Shubik index.
We find that in the case of Czexit, the power indices of the small countries increase, and the power indices of the large countries such as France, Germany, Italy, Poland, and Spain slightly decrease. The main winners from Czexit are Cyprus, Estonia, Luxembourg, and Malta.
The same can be said if one investigates Czexit in a farsighted sense, meaning to repeat the analysis with population predictions for 2030. The only country whose power index change differs is Romania: from a slight decrease (see Figure 1), its power modestly increases (see Figure 2).
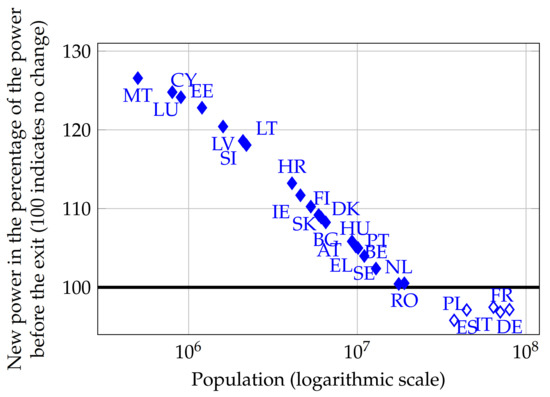
Figure 2.
Effect of Czexit with population projections for 2030, adjusted Shapley–Shubik index.
We get similar results for other departures from a 27-member EU, the power indices of the small countries increase significantly. The detailed results for all member states can be seen in Appendix B. What has created more variation in these cases is the contribution of the particular country to the EU budget. To illustrate this point, let us look at the exit of Germany.
In the case of Germany’s exit (Figure 3a), the adjusted Shapley–Shubik indices of the smallest countries and Poland increase, while the all the other countries lose power. This is because countries with large populations are also the ones that contribute the most, so the budget loss exceeds the power gains caused by the departure of Germany. The correction ratio (1) is 0.711.

Figure 3.
Effect of the German exit with populations for 2015.
The results concerning Poland are especially interesting. If one of the four large countries (Germany, France, Italy, or Spain) leaves, Poland is much better off than Romania or Spain which are the closest countries in the size of the population. In all four cases, its Shapley–Shubik index increases despite the power of the other remaining large countries decreases.
The simulations have been repeated with the other popular power measure, the Banzhaf index. We get the same results, the power of small countries increases. The most considerable difference is in the case of Germany. As one can see in Figure 3b, with the use of the Banzhaf index all countries, including Poland, lose power. As there is no significant difference and the Banzhaf index rather represents the I-Power approach [21], the Shapley–Shubik index is applied in the following.
Calculations for another country leaving the 26-member EU, for instance, if the Czech Republic leaves after Germany show a similar pattern to Brexit (Figure 4). This can be elucidated by the fact that as the number of member states decreases from 26 to 25, the Council of the European Union’s threshold for the number of supporting member states (determined by the member quota) decreases from 15 to 14. In this case, small countries would lose while the power of the large countries would increase.
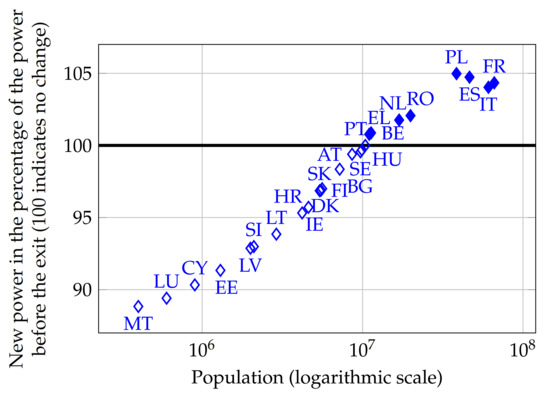
Figure 4.
Change in power due to Czexit in the 26-member EU (after Brexit and Germany’s exit) with populations for 2015, adjusted Shapley–Shubik index.
3.2. The Effect of Brexit before the Accession of Croatia
Since our findings on an additional departure show an impact that is the inverse of Brexit’s [8], Brexit might have had a different impact before the accession of Croatia compared to the exit from the 28-member EU.
This has significance because if Brexit had decreased the power of large countries such as France and Germany, the impact of the potential Brexit would have been calculated differently by these states that usually dominate the policy of the EU: Brexit would have been a greater risk for them. In other words, if Brexit would have had the reverse impact before Croatia joined, it could be seen as a belated threat.
We find that Brexit before the accession of Croatia would have favored smaller countries (Figure 5). In this case, the power of larger countries slightly increased, but not nearly as much as what Kóczy [8] found after the enlargement of EU. The results are similar not only for Brexit but for the case of an exit of any other member state from the EU without Croatia (see Appendix C).
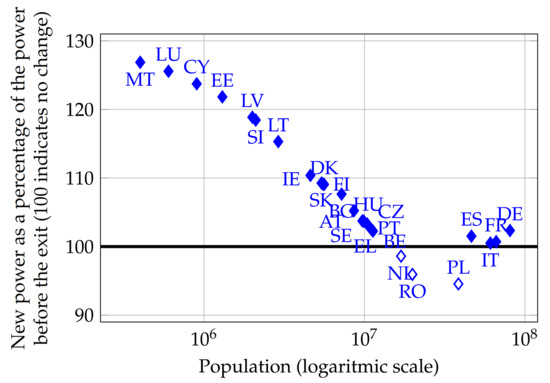
Figure 5.
Effect of Brexit before Croatia joined the EU with populations for 2015, adjusted Shapley–Shubik index.
4. Discussion
Note that an additional departure to Brexit has an inverted impact compared to Brexit’s impact from the 28-member EU, but it is similar to the potential effect of Brexit if it had happened before Croatia’s membership. Results for a departure from the hypothetical 26-member European Union have a strong resemblance to the consequences of Brexit. The inverted impact of an additional departure to Brexit is due to the fact that 15 countries are necessary to make the vote successful in the case of both 26 and 27 members. However, the population threshold decreases after an additional exit.
The voting rule states two main requirements: the support of a given number of countries and a certain percentage of the population. A country will turn a losing coalition into a winning one if (a) the coalition just misses a member state to pass the threshold, and/or (b) if the coalition has the required participation, but the supporting countries are too small to reach the population quota.
With Czexit after Brexit, the population threshold decreases while the member state threshold remains the same, so coalitions with smaller countries become winning, which shifts power from the large to the small member states. This pattern is quite prevalent, we find similar results using population projections for 2030 (Figure 2).
It seems to be a pattern that an exit triggering a decrease in the member quota benefits more the large, while an exit not triggering such a change benefits the small member states (see Appendix A and Appendix B). Since the adjustment is only a vertical downward shift, the direction of the results, meaning which countries are the largest beneficiaries, remains the same even for unadjusted indices (Appendix D).
Any exit induces three types of effects: (1) The increase/decrease in the relative share of the (rounded) numerical quota may increase/decrease the equality among countries of different sizes; (2) in the presence of the double quota, there is a complementarity/substitution effect such that an exit benefits similar countries, finally (3) there is a complex packaging issue with an ambiguous effect, and any of these three can dominate in a given numerical problem.
In the case of 27 member states, voting is successful if at least 15 countries, having together at least a population of 288 million vote in favor. We have examined the number of countries whose power increases if a particular country leaves, which can be considered as a yes vote for the exit of the departing country. Figure 6 presents the number of countries and their total population with an increasing power. Most of the countries would get a positive vote for leaving from 20 or 21 countries, but without the required population. However, in the case of Poland, both thresholds are met, because the power of small and large countries increases, and merely some medium countries (Belgium, Czech Republic, Greece, the Netherlands, Portugal, Romania) lose power. If we ignore the correction for the budget change, the result is unanimous: all countries would increase their influence in the Council in the case of Polexit.
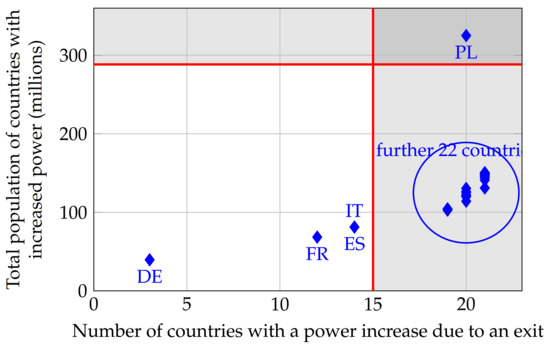
Figure 6.
Effect of a departure from the EU after Brexit with populations for 2015, adjusted Shapley–Shubik index.
Inspired by Brexit, the goal of our investigation has been to examine what would happen in the Council of the European Union after a country’s exit from the EU. For this purpose, the potential changes in the influence of each country have been measured with adjusted power indices.
We find that, not just Brexit, but any other exit from the 28-member EU would have favoured countries with high population. However, an additional exit would increase the power of small countries. Furthermore, we observe a pattern that is linked to the change in the member-state threshold. An exit, which changes the number of member states required for a decision, benefits the large, while an exit that does not cause such a change benefits the small countries. Thus, a hypothetical Brexit before the accession of Croatia would have favored the power of smaller countries in the Council. An exception to this general pattern is the exit of Poland, which would result in an increase of power for most countries.
Author Contributions
Conceptualization, D.G.P., M.F.R. and L.Á.K.; methodology, L.Á.K. and D.G.P.; data curation, writing—original draft preparation, visualization, D.G.P. and M.F.R.; writing—review and editing, supervision, L.Á.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Research, Development and Innovation Office grant number K-128573.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
See references.
Acknowledgments
We are grateful to L ászló Csató and Balázs Sziklai for useful advice.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AT | Austria |
| BE | Belgium |
| BG | Bulgaria |
| CY | Cyprus |
| CZ | Czech Republic |
| DE | Germany |
| DK | Denmark |
| EE | Estonia |
| EL | Greece |
| ES | Spain |
| FI | Finland |
| FR | France |
| HR | Croatia |
| HU | Hungary |
| IE | Ireland |
| IT | Italy |
| LT | Lithuania |
| LU | Luxembourg |
| LV | Latvia |
| MT | Malta |
| NL | Netherlands |
| PL | Poland |
| PT | Portugal |
| RO | Romania |
| SE | Sweden |
| SI | Slovenia |
| SK | Slovakia |
| UK | United Kingdom |
| EU | European Union |
Appendix A. The Impact of Any Member State Leaving the 28-Member EU
The following table presents the impact of any member state leaving the 28-member EU. The country labels in the columns refer to the country that is leaving the EU, the rows show the remaining member states. The values represent the change (new adjusted S–S power index)/(old adjusted S–S power index) in basis points (1/100th of 1%). Bold indicates increasing, while italic signs decreasing power.

Table A1.
The impact of any member state leaving the 28-member European Union with populations for 2015.
Table A1.
The impact of any member state leaving the 28-member European Union with populations for 2015.
| AT | BE | BG | CY | CZ | DE | DK | EE | EL | ES | FI | FR | HR | HU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AT | ↓287 | ↓124 | ↓261 | ↓121 | ↓1250 | ↓317 | ↓254 | ↓151 | ↓481 | ↓287 | ↓966 | ↓213 | ↓113 | |
| BE | ↓68 | ↓19 | ↓119 | ↓5 | ↓1137 | ↓184 | ↓112 | ↓34 | ↓419 | ↓153 | ↓868 | ↓67 | ↑13 | |
| BG | ↓285 | ↓375 | ↓359 | ↓227 | ↓1380 | ↓427 | ↓354 | ↓248 | ↓490 | ↓398 | ↓1075 | ↓319 | ↓206 | |
| CY | ↓1170 | ↓1223 | ↓1140 | ↓1090 | ↓2472 | ↓1299 | ↓1279 | ↓1100 | ↓929 | ↓1278 | ↓1852 | ↓1227 | ↓1073 | |
| CZ | ↓105 | ↓192 | ↓35 | ↓155 | ↓1159 | ↓211 | ↓148 | ↓54 | ↓418 | ↓180 | ↓878 | ↓109 | ↓14 | |
| DE | ↑348 | ↑215 | ↑426 | ↑369 | ↑398 | ↑257 | ↑369 | ↑360 | ↑544 | ↑293 | ↑297 | ↑386 | ↑418 | |
| DK | ↓434 | ↓529 | ↓392 | ↓500 | ↓374 | ↓1545 | ↓476 | ↓398 | ↓522 | ↓541 | ↓1178 | ↓451 | ↓344 | |
| EE | ↓1067 | ↓1138 | ↓1042 | ↓1192 | ↓1002 | ↓2349 | ↓1206 | ↓1013 | ↓889 | ↓1184 | ↓1782 | ↓1124 | ↓963 | |
| EL | ↓78 | ↓185 | ↓28 | ↓126 | ↓14 | ↓1146 | ↓192 | ↓120 | ↓403 | ↓160 | ↓877 | ↓79 | ↑12 | |
| ES | ↑297 | ↑137 | ↑388 | ↑350 | ↑323 | ↑16 | ↑231 | ↑350 | ↑284 | ↑266 | ↑125 | ↑369 | ↑354 | |
| FI | ↓454 | ↓542 | ↓408 | ↓506 | ↓385 | ↓1555 | ↓575 | ↓499 | ↓409 | ↓527 | ↓1182 | ↓457 | ↓358 | |
| FR | ↑346 | ↑207 | ↑429 | ↑382 | ↑393 | ↑160 | ↑266 | ↑380 | ↑355 | ↑526 | ↑302 | ↑400 | ↑416 | |
| HR | ↓586 | ↓682 | ↓524 | ↓649 | ↓529 | ↓1713 | ↓695 | ↓640 | ↓553 | ↓624 | ↓667 | ↓1294 | ↓502 | |
| HU | ↓124 | ↓234 | ↓62 | ↓186 | ↓68 | ↓1191 | ↓253 | ↓171 | ↓96 | ↓425 | ↓222 | ↓887 | ↓139 | |
| IE | ↓552 | ↓637 | ↓484 | ↓604 | ↓485 | ↓1655 | ↓662 | ↓600 | ↓513 | ↓590 | ↓634 | ↓1269 | ↓540 | ↓469 |
| IT | ↑327 | ↑184 | ↑406 | ↑367 | ↑368 | ↑54 | ↑241 | ↑367 | ↑330 | ↑535 | ↑277 | ↑71 | ↑375 | ↑393 |
| LT | ↓739 | ↓810 | ↓678 | ↓848 | ↓672 | ↓1914 | ↓855 | ↓841 | ↓685 | ↓769 | ↓830 | ↓1445 | ↓768 | ↓649 |
| LU | ↓1248 | ↓1300 | ↓1206 | ↓1401 | ↓1176 | ↓2568 | ↓1389 | ↓1369 | ↓1168 | ↓962 | ↓1364 | ↓1931 | ↓1311 | ↓1136 |
| LV | ↓901 | ↓975 | ↓865 | ↓1028 | ↓826 | ↓2130 | ↓1045 | ↓1014 | ↓850 | ↓841 | ↓1018 | ↓1629 | ↓960 | ↓809 |
| MT | ↓1308 | ↓1368 | ↓1278 | ↓1451 | ↓1234 | ↓2632 | ↓1444 | ↓1437 | ↓1247 | ↓996 | ↓1423 | ↓1986 | ↓1359 | ↓1208 |
| NL | ↑96 | ↑6 | ↑141 | ↑63 | ↑172 | ↓1008 | ↓31 | ↑66 | ↑142 | ↓455 | ↑1 | ↓853 | ↑83 | ↑187 |
| PL | ↑213 | ↑62 | ↑292 | ↑235 | ↑244 | ↓645 | ↑134 | ↑237 | ↑209 | ↓873 | ↑167 | ↓582 | ↑263 | ↑277 |
| PT | ↓112 | ↓202 | ↓42 | ↓160 | ↓28 | ↓1163 | ↓216 | ↓153 | ↓60 | ↓420 | ↓184 | ↓879 | ↓118 | ↓26 |
| RO | ↑186 | ↑82 | ↑253 | ↑134 | ↑251 | ↓1043 | ↑69 | ↑136 | ↑219 | ↓582 | ↑101 | ↓889 | ↑187 | ↑264 |
| SE | ↓133 | ↓239 | ↓79 | ↓195 | ↓76 | ↓1196 | ↓260 | ↓188 | ↓103 | ↓418 | ↓229 | ↓885 | ↓144 | ↓50 |
| SI | ↓868 | ↓934 | ↓843 | ↓1001 | ↓801 | ↓2102 | ↓1013 | ↓985 | ↓827 | ↓829 | ↓990 | ↓1611 | ↓932 | ↓777 |
| SK | ↓465 | ↓553 | ↓416 | ↓513 | ↓392 | ↓1565 | ↓582 | ↓506 | ↓421 | ↓526 | ↓553 | ↓1187 | ↓465 | ↓366 |
| UK | ↑346 | ↑201 | ↑425 | ↑376 | ↑387 | ↑136 | ↑262 | ↑376 | ↑347 | ↑541 | ↑298 | ↑142 | ↑398 | ↑415 |
| IE | IT | LT | LU | LV | MT | NL | PL | PT | RO | SE | SI | SK | UK | |
| AT | ↓276 | ↓652 | ↓233 | ↓275 | ↓258 | ↓264 | ↓359 | ↑215 | ↓163 | ↑153 | ↓349 | ↓261 | ↓203 | ↓252 |
| BE | ↓140 | ↓502 | ↓88 | ↓129 | ↓107 | ↓119 | ↓227 | ↑243 | ↓31 | ↑272 | ↓221 | ↓112 | ↓65 | ↓219 |
| BG | ↓386 | ↓705 | ↓353 | ↓371 | ↓365 | ↓361 | ↓445 | ↑164 | ↓251 | ↑42 | ↓436 | ↓368 | ↓315 | ↓407 |
| CY | ↓1287 | ↓1400 | ↓1265 | ↓1328 | ↓1285 | ↓1320 | ↓1280 | ↓495 | ↓1099 | ↓890 | ↓1292 | ↓1282 | ↓1208 | ↓1234 |
| CZ | ↓181 | ↓547 | ↓129 | ↓171 | ↓139 | ↓161 | ↓257 | ↑248 | ↓50 | ↑247 | ↓248 | ↓141 | ↓93 | ↓238 |
| DE | ↑309 | ↑586 | ↑378 | ↑360 | ↑373 | ↑370 | ↑90 | ↑826 | ↑367 | ↑582 | ↑178 | ↑366 | ↑387 | ↑1002 |
| DK | ↓523 | ↓822 | ↓473 | ↓513 | ↓485 | ↓503 | ↓577 | ↑11 | ↓400 | ↓90 | ↓576 | ↓487 | ↓459 | ↓535 |
| EE | ↓1187 | ↓1322 | ↓1168 | ↓1206 | ↓1186 | ↓1202 | ↓1195 | ↓437 | ↓1012 | ↓790 | ↓1187 | ↓1184 | ↓1112 | ↓1132 |
| EL | ↓151 | ↓545 | ↓110 | ↓139 | ↓119 | ↓129 | ↓236 | ↑246 | ↓39 | ↑260 | ↓223 | ↓123 | ↓72 | ↓228 |
| ES | ↑287 | ↑502 | ↑367 | ↑340 | ↑366 | ↑352 | ↓79 | ↓48 | ↑295 | ↑318 | ↑116 | ↑359 | ↑359 | ↑861 |
| FI | ↓532 | ↓825 | ↓480 | ↓520 | ↓494 | ↓515 | ↓580 | ↑3 | ↓407 | ↓102 | ↓588 | ↓495 | ↓464 | ↓536 |
| FR | ↑323 | ↑474 | ↑394 | ↑372 | ↑393 | ↑382 | ↑47 | ↑732 | ↑364 | ↑487 | ↑176 | ↑386 | ↑395 | ↑853 |
| HR | ↓661 | ↓938 | ↓618 | ↓662 | ↓643 | ↓669 | ↓742 | ↓86 | ↓548 | ↓263 | ↓731 | ↓643 | ↓588 | ↓638 |
| HU | ↓208 | ↓553 | ↓163 | ↓205 | ↓179 | ↓194 | ↓286 | ↑233 | ↓97 | ↑217 | ↓279 | ↓184 | ↓136 | ↓239 |
| IE | ↓907 | ↓569 | ↓619 | ↓595 | ↓606 | ↓694 | ↓57 | ↓506 | ↓219 | ↓697 | ↓595 | ↓554 | ↓612 | |
| IT | ↑294 | ↑370 | ↑358 | ↑370 | ↑369 | ↑21 | ↑647 | ↑338 | ↑460 | ↑154 | ↑363 | ↑370 | ↑791 | |
| LT | ↓820 | ↓1078 | ↓861 | ↓848 | ↓861 | ↓912 | ↓157 | ↓689 | ↓431 | ↓876 | ↓847 | ↓751 | ↓792 | |
| LU | ↓1375 | ↓1482 | ↓1353 | ↓1374 | ↓1407 | ↓1364 | ↓557 | ↓1197 | ↓961 | ↓1358 | ↓1369 | ↓1296 | ↓1335 | |
| LV | ↓1021 | ↓1198 | ↓1004 | ↓1053 | ↓1046 | ↓1072 | ↓294 | ↓846 | ↓613 | ↓1032 | ↓1020 | ↓943 | ↓1004 | |
| MT | ↓1425 | ↓1517 | ↓1400 | ↓1490 | ↓1446 | ↓1419 | ↓631 | ↓1248 | ↓1015 | ↓1429 | ↓1439 | ↓1357 | ↓1366 | |
| NL | ↑12 | ↓567 | ↑67 | ↑52 | ↑67 | ↑58 | ↑223 | ↑143 | ↑503 | ↓50 | ↑61 | ↑90 | ↓200 | |
| PL | ↑181 | ↓287 | ↑244 | ↑226 | ↑234 | ↑238 | ↓155 | ↑216 | ↑234 | ↑36 | ↑230 | ↑257 | ↑91 | |
| PT | ↓185 | ↓548 | ↓134 | ↓177 | ↓144 | ↓166 | ↓268 | ↑238 | ↑237 | ↓261 | ↓147 | ↓96 | ↓236 | |
| RO | ↑111 | ↓634 | ↑163 | ↑123 | ↑146 | ↑133 | ↑55 | ↑154 | ↑220 | ↑23 | ↑140 | ↑191 | ↓250 | |
| SE | ↓218 | ↓553 | ↓171 | ↓206 | ↓184 | ↓198 | ↓299 | ↑226 | ↓101 | ↑206 | ↓188 | ↓143 | ↓232 | |
| SI | ↓996 | ↓1178 | ↓970 | ↓1029 | ↓997 | ↓1019 | ↓1053 | ↓270 | ↓821 | ↓587 | ↓1002 | ↓913 | ↓982 | |
| SK | ↓539 | ↓849 | ↓492 | ↓529 | ↓498 | ↓521 | ↓595 | ↓0 | ↓412 | ↓109 | ↓596 | ↓499 | ↓549 | |
| UK | ↑317 | ↑434 | ↑392 | ↑366 | ↑391 | ↑378 | ↑32 | ↑722 | ↑358 | ↑484 | ↑176 | ↑384 | ↑391 |
Appendix B. The Impact of Additional Departures to Brexit
The following table presents the impact of any member state leaving the 27-member EU, after the United Kingdom departed. The country labels in the columns refer to the country that is leaving the EU, the rows show the remaining member states. The values represent the change (new adjusted S–S power index)/(old adjusted S–S power index) in basis points (1/100th of 1%). Bold indicates increasing, while italic signs decreasing power.

Table A2.
The impact of additional departures to Brexit with populations for 2015.
Table A2.
The impact of additional departures to Brexit with populations for 2015.
| AT | BE | BG | CY | CZ | DE | DK | EE | EL | ES | FI | FR | HR | HU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AT | ↑337 | ↑599 | ↑553 | ↑553 | ↓1038 | ↑418 | ↑553 | ↑502 | ↓38 | ↑451 | ↓485 | ↑557 | ↑570 | |
| BE | ↑356 | ↑482 | ↑365 | ↑389 | ↓1059 | ↑253 | ↑377 | ↑329 | ↓172 | ↑287 | ↓618 | ↑390 | ↑415 | |
| BG | ↑748 | ↑578 | ↑711 | ↑811 | ↓884 | ↑708 | ↑717 | ↑745 | ↑184 | ↑742 | ↓279 | ↑855 | ↑816 | |
| CY | ↑2427 | ↑2238 | ↑2569 | ↑2548 | ↓39 | ↑2270 | ↑2352 | ↑2434 | ↑2003 | ↑2322 | ↑1159 | ↑2379 | ↑2535 | |
| CZ | ↑370 | ↑244 | ↑488 | ↑408 | ↓1043 | ↑305 | ↑417 | ↑409 | ↓129 | ↑338 | ↓581 | ↑439 | ↑487 | |
| DE | ↓343 | ↓462 | ↓298 | ↓364 | ↓290 | ↓473 | ↓363 | ↓311 | ↓346 | ↓436 | ↓402 | ↓335 | ↓255 | |
| DK | ↑1052 | ↑885 | ↑1067 | ↑926 | ↑1105 | ↓763 | ↑930 | ↑1034 | ↑420 | ↑907 | ↓17 | ↑985 | ↑1121 | |
| EE | ↑2207 | ↑1990 | ↑2349 | ↑2069 | ↑2249 | ↓177 | ↑2062 | ↑2171 | ↑1753 | ↑2094 | ↑924 | ↑2171 | ↑2248 | |
| EL | ↑380 | ↑188 | ↑447 | ↑384 | ↑414 | ↓1056 | ↑260 | ↑387 | ↓167 | ↑297 | ↓604 | ↑403 | ↑438 | |
| ES | ↓358 | ↓503 | ↓271 | ↓319 | ↓319 | ↓495 | ↓442 | ↓322 | ↓354 | ↓405 | ↓617 | ↓299 | ↓287 | |
| FI | ↑1077 | ↑891 | ↑1099 | ↑936 | ↑1133 | ↓746 | ↑888 | ↑958 | ↑1066 | ↑444 | ↑10 | ↑999 | ↑1135 | |
| FR | ↓373 | ↓511 | ↓320 | ↓364 | ↓334 | ↓249 | ↓485 | ↓366 | ↓359 | ↓530 | ↓448 | ↓342 | ↓303 | |
| HR | ↑1173 | ↑1044 | ↑1302 | ↑1175 | ↑1263 | ↓635 | ↑1063 | ↑1180 | ↑1204 | ↑714 | ↑1097 | ↑132 | ↑1265 | |
| HU | ↑403 | ↑292 | ↑531 | ↑451 | ↑455 | ↓1031 | ↑345 | ↑450 | ↑454 | ↓102 | ↑378 | ↓563 | ↑467 | |
| IE | ↑1109 | ↑1081 | ↑1224 | ↑1076 | ↑1209 | ↓673 | ↑1027 | ↑1080 | ↑1259 | ↑627 | ↑1060 | ↑93 | ↑1108 | ↑1206 |
| IT | ↓354 | ↓473 | ↓287 | ↓359 | ↓300 | ↓383 | ↓469 | ↓359 | ↓324 | ↓316 | ↓432 | ↓980 | ↓333 | ↓262 |
| LT | ↑1494 | ↑1353 | ↑1622 | ↑1522 | ↑1611 | ↓485 | ↑1417 | ↑1545 | ↑1526 | ↑1093 | ↑1451 | ↑414 | ↑1561 | ↑1603 |
| LU | ↑2561 | ↑2456 | ↑2736 | ↑2483 | ↑2769 | ↑51 | ↑2435 | ↑2498 | ↑2645 | ↑2203 | ↑2465 | ↑1313 | ↑2549 | ↑2711 |
| LV | ↑1866 | ↑1706 | ↑2051 | ↑1790 | ↑1960 | ↓314 | ↑1804 | ↑1822 | ↑1877 | ↑1475 | ↑1843 | ↑704 | ↑1923 | ↑1972 |
| MT | ↑2693 | ↑2575 | ↑2836 | ↑2553 | ↑2823 | ↑102 | ↑2529 | ↑2580 | ↑2773 | ↑2331 | ↑2561 | ↑1429 | ↑2660 | ↑2795 |
| NL | ↑54 | ↓99 | ↑166 | ↑116 | ↑96 | ↓1147 | ↑10 | ↑117 | ↑54 | ↓396 | ↑45 | ↓787 | ↑148 | ↑123 |
| PL | ↓468 | ↓638 | ↓372 | ↓365 | ↓444 | ↑201 | ↓528 | ↓368 | ↓490 | ↑1535 | ↓490 | ↑196 | ↓376 | ↓404 |
| PT | ↑381 | ↑257 | ↑494 | ↑409 | ↑474 | ↓1040 | ↑305 | ↑422 | ↑417 | ↓119 | ↑341 | ↓575 | ↑447 | ↑497 |
| RO | ↓45 | ↓204 | ↑40 | ↑7 | ↓6 | ↓1180 | ↓123 | ↑9 | ↓50 | ↓421 | ↓89 | ↓852 | ↑19 | ↑17 |
| SE | ↑417 | ↑249 | ↑529 | ↑463 | ↑472 | ↓1037 | ↑342 | ↑463 | ↑408 | ↓102 | ↑380 | ↓552 | ↑461 | ↑488 |
| SI | ↑1825 | ↑1657 | ↑2002 | ↑1773 | ↑1920 | ↓333 | ↑1783 | ↑1783 | ↑1845 | ↑1447 | ↑1816 | ↑682 | ↑1890 | ↑1916 |
| SK | ↑1105 | ↑919 | ↑1109 | ↑954 | ↑1142 | ↓746 | ↑904 | ↑970 | ↑1084 | ↑465 | ↑937 | ↑34 | ↑1012 | ↑1162 |
| IE | IT | LT | LU | LV | MT | NL | PL | PT | RO | SE | SI | SK | ||
| AT | ↑475 | ↓11 | ↑572 | ↑545 | ↑561 | ↑557 | ↑189 | ↑149 | ↑523 | ↑674 | ↑305 | ↑559 | ↑552 | |
| BE | ↑304 | ↓129 | ↑385 | ↑349 | ↑373 | ↑361 | ↑16 | ↓150 | ↑355 | ↑498 | ↑148 | ↑371 | ↑385 | |
| BG | ↑769 | ↑243 | ↑769 | ↑705 | ↑742 | ↑708 | ↑427 | ↑493 | ↑775 | ↑975 | ↑538 | ↑742 | ↑844 | |
| CY | ↑2293 | ↑1666 | ↑2363 | ↑2300 | ↑2345 | ↑2293 | ↑2121 | ↑3289 | ↑2503 | ↑2726 | ↑2221 | ↑2351 | ↑2438 | |
| CZ | ↑350 | ↓95 | ↑428 | ↑392 | ↑416 | ↑401 | ↑54 | ↓40 | ↑434 | ↑547 | ↑218 | ↑414 | ↑438 | |
| DE | ↓419 | ↓259 | ↓357 | ↓375 | ↓361 | ↓363 | ↓593 | ↑42 | ↓318 | ↓112 | ↓504 | ↓369 | ↓341 | |
| DK | ↑899 | ↑407 | ↑964 | ↑906 | ↑945 | ↑916 | ↑644 | ↑918 | ↑1068 | ↑1179 | ↑824 | ↑934 | ↑1012 | |
| EE | ↑2103 | ↑1439 | ↑2125 | ↑2059 | ↑2091 | ↑2076 | ↑1851 | ↑2872 | ↑2206 | ↑2504 | ↑1945 | ↑2095 | ↑2203 | |
| EL | ↑310 | ↓116 | ↑395 | ↑357 | ↑393 | ↑371 | ↑26 | ↓117 | ↑380 | ↑517 | ↑175 | ↑392 | ↑396 | |
| ES | ↓382 | ↓218 | ↓310 | ↓331 | ↓317 | ↓321 | ↓639 | ↑1320 | ↓346 | ↓158 | ↓538 | ↓325 | ↓308 | |
| FI | ↑926 | ↑415 | ↑988 | ↑930 | ↑960 | ↑936 | ↑669 | ↑959 | ↑1098 | ↑1211 | ↑855 | ↑954 | ↑1025 | |
| FR | ↓424 | ↓709 | ↓360 | ↓374 | ↓365 | ↓361 | ↓650 | ↑124 | ↓361 | ↓148 | ↓551 | ↓373 | ↓352 | |
| HR | ↑1097 | ↑583 | ↑1182 | ↑1164 | ↑1175 | ↑1176 | ↑948 | ↑1344 | ↑1229 | ↑1459 | ↑972 | ↑1175 | ↑1204 | |
| HU | ↑383 | ↓73 | ↑458 | ↑443 | ↑453 | ↑454 | ↑89 | ↑8 | ↑424 | ↑565 | ↑214 | ↑451 | ↑477 | |
| IE | ↑531 | ↑1086 | ↑1065 | ↑1103 | ↑1083 | ↑851 | ↑1212 | ↑1169 | ↑1377 | ↑915 | ↑1104 | ↑1163 | ||
| IT | ↓417 | ↓352 | ↓371 | ↓356 | ↓360 | ↓604 | ↑326 | ↓327 | ↓105 | ↓511 | ↓363 | ↓336 | ||
| LT | ↑1483 | ↑886 | ↑1503 | ↑1553 | ↑1512 | ↑1377 | ↑1846 | ↑1567 | ↑1890 | ↑1295 | ↑1557 | ↑1557 | ||
| LU | ↑2447 | ↑1834 | ↑2537 | ↑2529 | ↑2437 | ↑2301 | ↑3598 | ↑2717 | ↑2944 | ↑2368 | ↑2540 | ↑2581 | ||
| LV | ↑1837 | ↑1227 | ↑1937 | ↑1770 | ↑1792 | ↑1609 | ↑2377 | ↑1912 | ↑2312 | ↑1652 | ↑1876 | ↑1949 | ||
| MT | ↑2560 | ↑1913 | ↑2645 | ↑2532 | ↑2621 | ↑2380 | ↑3782 | ↑2771 | ↑3037 | ↑2492 | ↑2626 | ↑2678 | ||
| NL | ↑71 | ↓327 | ↑144 | ↑92 | ↑125 | ↑104 | ↓569 | ↑65 | ↑158 | ↓133 | ↑121 | ↑143 | ||
| PL | ↓463 | ↑705 | ↓373 | ↓373 | ↓365 | ↓364 | ↓867 | ↓468 | ↓507 | ↓648 | ↓374 | ↓392 | ||
| PT | ↑361 | ↓85 | ↑437 | ↑400 | ↑424 | ↑412 | ↑59 | ↓41 | ↑559 | ↑230 | ↑424 | ↑438 | ||
| RO | ↓63 | ↓368 | ↑16 | ↓2 | ↑14 | ↑8 | ↓401 | ↓778 | ↓37 | ↓235 | ↑8 | ↑8 | ||
| SE | ↑392 | ↓64 | ↑467 | ↑451 | ↑464 | ↑463 | ↑101 | ↑35 | ↑438 | ↑574 | ↑463 | ↑479 | ||
| SI | ↑1792 | ↑1189 | ↑1892 | ↑1743 | ↑1858 | ↑1755 | ↑1584 | ↑2329 | ↑1879 | ↑2253 | ↑1626 | ↑1928 | ||
| SK | ↑929 | ↑430 | ↑991 | ↑944 | ↑974 | ↑960 | ↑692 | ↑988 | ↑1103 | ↑1223 | ↑880 | ↑972 |
Appendix C. The Impact of Any Member State Leaving before the Accession of Croatia
The following table presents the impact of any member state leaving the 27-member EU before the accession of Croatia. The country labels in the columns refer to the country that is leaving the EU, the rows show the remaining member states. The values represent the change (new adjusted S–S power index)/(old adjusted S–S power index) in basis points (1/100th of 1%). Bold indicates increasing, while italic signs decreasing power.

Table A3.
The impact of any member state leaving before the accession of Croatia with populations for 2015.
Table A3.
The impact of any member state leaving before the accession of Croatia with populations for 2015.
| AT | BE | BG | CY | CZ | DE | DK | EE | EL | ES | FI | FR | HU | IE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AT | ↑584 | ↑758 | ↑648 | ↑756 | ↓553 | ↑573 | ↑654 | ↑730 | ↑424 | ↑605 | ↓181 | ↑773 | ↑595 | |
| BE | ↑454 | ↑512 | ↑411 | ↑514 | ↓719 | ↑332 | ↑414 | ↑481 | ↑51 | ↑365 | ↓455 | ↑535 | ↑376 | |
| BG | ↑860 | ↑762 | ↑797 | ↑954 | ↓413 | ↑746 | ↑800 | ↑914 | ↑597 | ↑778 | ↓45 | ↑959 | ↑772 | |
| CY | ↑2648 | ↑2542 | ↑2733 | ↑2770 | ↑659 | ↑2509 | ↑2531 | ↑2714 | ↑2750 | ↑2537 | ↑1530 | ↑2775 | ↑2527 | |
| CZ | ↑515 | ↑410 | ↑591 | ↑486 | ↓670 | ↑407 | ↑489 | ↑560 | ↑157 | ↑440 | ↓380 | ↑608 | ↑431 | |
| DE | ↓373 | ↓498 | ↓301 | ↓349 | ↓332 | ↓459 | ↓350 | ↓363 | ↓186 | ↓425 | ↓422 | ↓308 | ↓413 | |
| DK | ↑1079 | ↑973 | ↑1149 | ↑1023 | ↑1159 | ↓295 | ↑1026 | ↑1125 | ↑940 | ↑984 | ↑136 | ↑1179 | ↑966 | |
| EE | ↑2411 | ↑2317 | ↑2492 | ↑2297 | ↑2515 | ↑525 | ↑2292 | ↑2480 | ↑2442 | ↑2327 | ↑1337 | ↑2540 | ↑2313 | |
| EL | ↑470 | ↑360 | ↑534 | ↑437 | ↑536 | ↓702 | ↑364 | ↑438 | ↑79 | ↑398 | ↓432 | ↑564 | ↑400 | |
| ES | ↓372 | ↓521 | ↓295 | ↓314 | ↓343 | ↓661 | ↓449 | ↓312 | ↓384 | ↓416 | ↓538 | ↓313 | ↓399 | |
| FI | ↑1092 | ↑980 | ↑1165 | ↑1038 | ↑1171 | ↓291 | ↑961 | ↑1045 | ↑1138 | ↑962 | ↑154 | ↑1195 | ↑976 | |
| FR | ↓384 | ↓528 | ↓318 | ↓358 | ↓355 | ↓554 | ↓477 | ↓359 | ↓391 | ↓227 | ↓443 | ↓326 | ↓427 | |
| HU | ↑572 | ↑460 | ↑628 | ↑514 | ↑637 | ↓646 | ↑455 | ↑520 | ↑606 | ↑228 | ↑487 | ↓318 | ↑487 | |
| IE | ↑1241 | ↑1118 | ↑1308 | ↑1195 | ↑1316 | ↓198 | ↑1090 | ↑1215 | ↑1279 | ↑1180 | ↑1120 | ↑285 | ↑1350 | |
| IT | ↓368 | ↓506 | ↓299 | ↓346 | ↓335 | ↓634 | ↓461 | ↓346 | ↓371 | ↓177 | ↓428 | ↓619 | ↓310 | ↓418 |
| LT | ↑1687 | ↑1574 | ↑1799 | ↑1665 | ↑1778 | ↑102 | ↑1599 | ↑1680 | ↑1743 | ↑1746 | ↑1632 | ↑722 | ↑1806 | ↑1636 |
| LU | ↑2836 | ↑2758 | ↑2925 | ↑2699 | ↑2968 | ↑771 | ↑2715 | ↑2716 | ↑2905 | ↑2976 | ↑2742 | ↑1656 | ↑2972 | ↑2701 |
| LV | ↑2076 | ↑1969 | ↑2201 | ↑1973 | ↑2183 | ↑327 | ↑1967 | ↑2000 | ↑2143 | ↑2091 | ↑1999 | ↑1055 | ↑2206 | ↑1979 |
| MT | ↑2975 | ↑2867 | ↑3066 | ↑2808 | ↑3090 | ↑831 | ↑2821 | ↑2841 | ↑3042 | ↑3139 | ↑2854 | ↑1776 | ↑3097 | ↑2821 |
| NL | ↑205 | ↑98 | ↑265 | ↑137 | ↑264 | ↓965 | ↑69 | ↑136 | ↑239 | ↓408 | ↑104 | ↓806 | ↑287 | ↑105 |
| PL | ↓226 | ↓364 | ↓131 | ↓180 | ↓186 | ↓1278 | ↓285 | ↓175 | ↓224 | ↓1592 | ↓254 | ↓1177 | ↓159 | ↓243 |
| PT | ↑528 | ↑425 | ↑603 | ↑480 | ↑594 | ↓661 | ↑411 | ↑502 | ↑569 | ↑176 | ↑445 | ↓367 | ↑620 | ↑442 |
| RO | ↑45 | ↓49 | ↑112 | ↑33 | ↑117 | ↓1180 | ↓56 | ↑34 | ↑88 | ↓670 | ↓23 | ↓1042 | ↑131 | ↓14 |
| SE | ↑586 | ↑474 | ↑636 | ↑531 | ↑652 | ↓644 | ↑472 | ↑535 | ↑618 | ↑255 | ↑504 | ↓296 | ↑681 | ↑502 |
| SI | ↑2021 | ↑1914 | ↑2150 | ↑1936 | ↑2136 | ↑298 | ↑1926 | ↑1963 | ↑2085 | ↑2044 | ↑1960 | ↑1016 | ↑2154 | ↑1935 |
| SK | ↑1113 | ↑1000 | ↑1177 | ↑1056 | ↑1187 | ↓283 | ↑975 | ↑1063 | ↑1149 | ↑991 | ↑1006 | ↑163 | ↑1219 | ↑980 |
| UK | ↓398 | ↓533 | ↓318 | ↓355 | ↓364 | ↓579 | ↓473 | ↓358 | ↓396 | ↓196 | ↓439 | ↓594 | ↓336 | ↓428 |
| IT | LT | LU | LV | MT | NL | PL | PT | RO | SE | SI | SK | UK | ||
| AT | ↑204 | ↑684 | ↑639 | ↑671 | ↑642 | ↑513 | ↑1123 | ↑725 | ↑100 | ↑520 | ↑665 | ↑757 | ↑523 | |
| BE | ↓108 | ↑431 | ↑403 | ↑421 | ↑411 | ↑250 | ↑837 | ↑483 | ↑80 | ↑286 | ↑417 | ↑515 | ↑225 | |
| BG | ↑304 | ↑838 | ↑780 | ↑815 | ↑793 | ↑664 | ↑1343 | ↑918 | ↑120 | ↑700 | ↑810 | ↑929 | ↑764 | |
| CY | ↑2081 | ↑2587 | ↑2501 | ↑2575 | ↑2514 | ↑2380 | ↑3176 | ↑2726 | ↑300 | ↑2482 | ↑2568 | ↑2735 | ↑2373 | |
| CZ | ↑0 | ↑510 | ↑455 | ↑499 | ↑468 | ↑319 | ↑929 | ↑553 | ↑90 | ↑358 | ↑502 | ↑581 | ↑314 | |
| DE | ↓131 | ↓343 | ↓359 | ↓352 | ↓350 | ↓618 | ↑111 | ↓357 | ↓16 | ↓536 | ↓353 | ↓293 | ↑234 | |
| DK | ↑552 | ↑1044 | ↑1013 | ↑1047 | ↑1023 | ↑920 | ↑1584 | ↑1126 | ↑150 | ↑920 | ↑1030 | ↑1137 | ↑906 | |
| EE | ↑1854 | ↑2367 | ↑2268 | ↑2346 | ↑2278 | ↑2164 | ↑2932 | ↑2471 | ↑280 | ↑2252 | ↑2327 | ↑2506 | ↑2182 | |
| EL | ↓76 | ↑455 | ↑428 | ↑452 | ↑430 | ↑272 | ↑878 | ↑506 | ↑80 | ↑313 | ↑442 | ↑545 | ↑254 | |
| ES | ↓193 | ↓314 | ↓324 | ↓315 | ↓312 | ↓726 | ↓920 | ↓368 | ↓39 | ↓538 | ↓319 | ↓281 | ↑152 | |
| FI | ↑556 | ↑1052 | ↑1021 | ↑1059 | ↑1041 | ↑931 | ↑1582 | ↑1138 | ↑150 | ↑937 | ↑1046 | ↑1148 | ↑912 | |
| FR | ↓290 | ↓354 | ↓367 | ↓362 | ↓357 | ↓691 | ↓32 | ↓380 | ↓27 | ↓554 | ↓365 | ↓311 | ↑71 | |
| HU | ↑79 | ↑558 | ↑507 | ↑542 | ↑520 | ↑368 | ↑960 | ↑607 | ↑90 | ↑409 | ↑532 | ↑636 | ↑369 | |
| IE | ↑718 | ↑1242 | ↑1182 | ↑1240 | ↑1202 | ↑1074 | ↑1700 | ↑1280 | ↑160 | ↑1082 | ↑1228 | ↑1282 | ↑1038 | |
| IT | ↓344 | ↓355 | ↓349 | ↓344 | ↓670 | ↓105 | ↓359 | ↓26 | ↓536 | ↓351 | ↓298 | ↑50 | ||
| LT | ↑1187 | ↑1640 | ↑1711 | ↑1659 | ↑1510 | ↑2168 | ↑1738 | ↑210 | ↑1532 | ↑1703 | ↑1805 | ↑1530 | ||
| LU | ↑2285 | ↑2789 | ↑2771 | ↑2689 | ↑2567 | ↑3354 | ↑2919 | ↑330 | ↑2665 | ↑2746 | ↑2926 | ↑2556 | ||
| LV | ↑1503 | ↑2076 | ↑1952 | ↑1972 | ↑1830 | ↑2586 | ↑2137 | ↑250 | ↑1917 | ↑2024 | ↑2172 | ↑1886 | ||
| MT | ↑2407 | ↑2885 | ↑2787 | ↑2894 | ↑2708 | ↑3480 | ↑3038 | ↑340 | ↑2795 | ↑2874 | ↑3042 | ↑2686 | ||
| NL | ↓538 | ↑153 | ↑125 | ↑137 | ↑135 | ↑453 | ↑235 | ↑60 | ↑44 | ↑131 | ↑242 | ↓139 | ||
| PL | ↓899 | ↓169 | ↓195 | ↓169 | ↓183 | ↓549 | ↓214 | ↓17 | ↓387 | ↓176 | ↓116 | ↓544 | ||
| PT | ↑15 | ↑519 | ↑466 | ↑510 | ↑480 | ↑330 | ↑928 | ↑90 | ↑370 | ↑502 | ↑593 | ↑328 | ||
| RO | ↓785 | ↑52 | ↑23 | ↑38 | ↑28 | ↓89 | ↑149 | ↑90 | ↓108 | ↑38 | ↑115 | ↓405 | ||
| SE | ↑46 | ↑557 | ↑525 | ↑555 | ↑533 | ↑390 | ↑981 | ↑623 | ↑90 | ↑546 | ↑655 | ↑374 | ||
| SI | ↑1454 | ↑2030 | ↑1912 | ↑2000 | ↑1927 | ↑1795 | ↑2539 | ↑2092 | ↑240 | ↑1877 | ↑2133 | ↑1844 | ||
| SK | ↑575 | ↑1070 | ↑1042 | ↑1077 | ↑1055 | ↑953 | ↑1595 | ↑1152 | ↑150 | ↑949 | ↑1060 | ↑926 | ||
| UK | ↓277 | ↓356 | ↓363 | ↓359 | ↓355 | ↓683 | ↓54 | ↓389 | ↓27 | ↓562 | ↓362 | ↓309 |
Appendix D. The Impact of Additional Departures to Brexit, Unadjusted Indices
The following table presents the impact of any member state leaving the 27-member EU, after the United Kingdom departed. The country labels in the columns refer to the country that is leaving the EU, the rows show the remaining member states. The values represent the change (new S–S power index)/(old S–S power index) in basis points (1/100th of 1%). Every value indicates increasing power.

Table A4.
The impact of additional departures to Brexit with populations for 2015, unadjusted indices.
Table A4.
The impact of additional departures to Brexit with populations for 2015, unadjusted indices.
| AT | BE | BG | CY | CZ | DE | DK | EE | EL | ES | FI | FR | HR | HU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AT | 1703 | 1664 | 1588 | 1705 | 2604 | 1646 | 1591 | 1701 | 1942 | 1639 | 2527 | 1617 | 1682 | |
| BE | 1512 | 1536 | 1382 | 1522 | 2574 | 1461 | 1398 | 1508 | 1780 | 1456 | 2351 | 1434 | 1510 | |
| BG | 1948 | 1976 | 1762 | 1991 | 2821 | 1970 | 1772 | 1971 | 2208 | 1963 | 2797 | 1944 | 1954 | |
| CY | 3815 | 3855 | 3832 | 3918 | 4010 | 3716 | 3568 | 3853 | 4389 | 3722 | 4692 | 3621 | 3853 | |
| CZ | 1528 | 1598 | 1542 | 1429 | 2597 | 1519 | 1442 | 1597 | 1832 | 1512 | 2399 | 1487 | 1589 | |
| DE | 734 | 797 | 677 | 580 | 768 | 649 | 584 | 794 | 1571 | 650 | 2635 | 634 | 768 | |
| DK | 2286 | 2323 | 2180 | 1997 | 2317 | 2990 | 2006 | 2293 | 2491 | 2147 | 3143 | 2088 | 2291 | |
| EE | 3570 | 3573 | 3591 | 3253 | 3586 | 3816 | 3483 | 3560 | 4090 | 3468 | 4383 | 3392 | 3535 | |
| EL | 1539 | 1534 | 1497 | 1402 | 1550 | 2578 | 1470 | 1409 | 1786 | 1468 | 2369 | 1447 | 1536 | |
| ES | 717 | 751 | 707 | 629 | 736 | 3368 | 683 | 629 | 746 | 684 | 2352 | 674 | 733 | |
| FI | 2314 | 2330 | 2215 | 2009 | 2348 | 3014 | 2171 | 2037 | 2329 | 2521 | 3179 | 2104 | 2305 | |
| FR | 701 | 742 | 652 | 580 | 720 | 3714 | 635 | 581 | 740 | 1351 | 637 | 626 | 716 | |
| HR | 2420 | 2504 | 2438 | 2271 | 2492 | 3171 | 2366 | 2281 | 2483 | 2844 | 2358 | 3340 | 2450 | |
| HU | 1565 | 1652 | 1590 | 1476 | 1596 | 2613 | 1564 | 1478 | 1647 | 1865 | 1557 | 2423 | 1518 | |
| IE | 2350 | 2544 | 2353 | 2162 | 2432 | 3117 | 2327 | 2170 | 2544 | 2740 | 2316 | 3288 | 2224 | 2384 |
| IT | 723 | 784 | 688 | 586 | 758 | 3525 | 653 | 589 | 779 | 1608 | 654 | 1875 | 636 | 761 |
| LT | 2777 | 2853 | 2791 | 2652 | 2878 | 3382 | 2763 | 2681 | 2842 | 3299 | 2753 | 3711 | 2722 | 2823 |
| LU | 3964 | 4101 | 4016 | 3708 | 4163 | 4137 | 3901 | 3728 | 4088 | 4629 | 3881 | 4895 | 3809 | 4048 |
| LV | 3192 | 3253 | 3263 | 2947 | 3265 | 3622 | 3196 | 2986 | 3232 | 3756 | 3188 | 4093 | 3120 | 3231 |
| MT | 4111 | 4236 | 4127 | 3784 | 4222 | 4209 | 4006 | 3818 | 4230 | 4783 | 3988 | 5047 | 3931 | 4141 |
| NL | 1177 | 1208 | 1189 | 1108 | 1198 | 2451 | 1190 | 1113 | 1201 | 1512 | 1187 | 2129 | 1167 | 1187 |
| PL | 595 | 597 | 595 | 579 | 598 | 4348 | 587 | 579 | 594 | 3828 | 590 | 3424 | 589 | 604 |
| PT | 1540 | 1612 | 1549 | 1430 | 1617 | 2602 | 1520 | 1447 | 1606 | 1845 | 1516 | 2408 | 1496 | 1600 |
| RO | 1066 | 1089 | 1049 | 988 | 1083 | 2404 | 1040 | 995 | 1084 | 1482 | 1036 | 2043 | 1025 | 1071 |
| SE | 1581 | 1603 | 1588 | 1490 | 1615 | 2606 | 1561 | 1493 | 1595 | 1865 | 1559 | 2438 | 1511 | 1591 |
| SI | 3146 | 3197 | 3209 | 2928 | 3221 | 3596 | 3172 | 2943 | 3197 | 3722 | 3159 | 4064 | 3084 | 3169 |
| SK | 2345 | 2362 | 2226 | 2029 | 2358 | 3014 | 2189 | 2050 | 2349 | 2546 | 2180 | 3211 | 2118 | 2336 |
| IE | IT | LT | LU | LV | MT | NL | PL | PT | RO | SE | SI | SK | ||
| AT | 1630 | 2484 | 1626 | 1589 | 1607 | 1585 | 1819 | 1476 | 1705 | 1844 | 1684 | 1613 | 1634 | |
| BE | 1440 | 2337 | 1421 | 1373 | 1401 | 1370 | 1618 | 1137 | 1518 | 1648 | 1506 | 1406 | 1450 | |
| BG | 1956 | 2803 | 1844 | 1764 | 1806 | 1751 | 2095 | 1866 | 1985 | 2177 | 1948 | 1814 | 1956 | |
| CY | 3649 | 4583 | 3597 | 3517 | 3568 | 3490 | 4061 | 5027 | 3907 | 4120 | 3856 | 3584 | 3714 | |
| CZ | 1491 | 2380 | 1468 | 1420 | 1448 | 1414 | 1662 | 1262 | 1606 | 1703 | 1585 | 1454 | 1509 | |
| DE | 637 | 2175 | 604 | 576 | 593 | 574 | 910 | 1356 | 768 | 971 | 765 | 591 | 650 | |
| DK | 2100 | 3008 | 2058 | 1985 | 2029 | 1979 | 2347 | 2345 | 2311 | 2404 | 2272 | 2025 | 2142 | |
| EE | 3437 | 4299 | 3335 | 3252 | 3289 | 3252 | 3748 | 4555 | 3577 | 3874 | 3543 | 3302 | 3456 | |
| EL | 1447 | 2353 | 1432 | 1382 | 1423 | 1381 | 1630 | 1174 | 1546 | 1669 | 1536 | 1429 | 1463 | |
| ES | 677 | 2226 | 656 | 624 | 641 | 620 | 857 | 2801 | 737 | 919 | 727 | 640 | 686 | |
| FI | 2131 | 3019 | 2084 | 2011 | 2045 | 2001 | 2377 | 2392 | 2344 | 2440 | 2307 | 2048 | 2156 | |
| FR | 630 | 1612 | 601 | 577 | 588 | 577 | 845 | 1448 | 721 | 930 | 712 | 587 | 637 | |
| HR | 2320 | 3229 | 2297 | 2269 | 2282 | 2264 | 2700 | 2828 | 2490 | 2715 | 2440 | 2291 | 2353 | |
| HU | 1528 | 2408 | 1501 | 1476 | 1488 | 1472 | 1704 | 1317 | 1595 | 1723 | 1580 | 1494 | 1552 | |
| IE | 3163 | 2192 | 2160 | 2203 | 2162 | 2587 | 2679 | 2423 | 2624 | 2375 | 2213 | 2309 | ||
| IT | 638 | 610 | 581 | 598 | 578 | 898 | 1677 | 758 | 979 | 758 | 597 | 655 | ||
| LT | 2749 | 3607 | 2641 | 2698 | 2632 | 3197 | 3395 | 2866 | 3193 | 2806 | 2710 | 2743 | ||
| LU | 3819 | 4792 | 3788 | 3770 | 3648 | 4269 | 5376 | 4145 | 4362 | 4023 | 3792 | 3872 | ||
| LV | 3142 | 4033 | 3127 | 2934 | 2940 | 3466 | 3996 | 3249 | 3661 | 3211 | 3061 | 3175 | ||
| MT | 3945 | 4891 | 3907 | 3772 | 3871 | 4361 | 5585 | 4205 | 4466 | 4164 | 3886 | 3979 | ||
| NL | 1182 | 2089 | 1156 | 1090 | 1128 | 1087 | 663 | 1195 | 1271 | 1186 | 1131 | 1184 | ||
| PL | 588 | 3381 | 586 | 578 | 588 | 573 | 593 | 602 | 532 | 602 | 586 | 593 | ||
| PT | 1503 | 2392 | 1479 | 1429 | 1457 | 1426 | 1669 | 1260 | 1716 | 1599 | 1465 | 1509 | ||
| RO | 1032 | 2039 | 1015 | 986 | 1006 | 982 | 1134 | 427 | 1081 | 1070 | 1007 | 1035 | ||
| SE | 1538 | 2418 | 1512 | 1484 | 1500 | 1482 | 1717 | 1347 | 1610 | 1733 | 1508 | 1555 | ||
| SI | 3092 | 3986 | 3078 | 2905 | 3033 | 2899 | 3437 | 3941 | 3213 | 3596 | 3181 | 3152 | ||
| SK | 2134 | 3037 | 2088 | 2027 | 2061 | 2027 | 2403 | 2425 | 2350 | 2453 | 2336 | 2067 |
Appendix E. The Blocking Minority Rule
According to the Article 16(4) of the Treaty on European Union ‘as from 1 November 2014, a qualified majority shall be defined as at least 55% of the members of the Council, comprising at least fifteen of them and representing Member States comprising at least 65% of the population of the Union. A blocking minority must include at least four Council members, failing which the qualified majority shall be deemed attained.’ (https://eur-lex.europa.eu/resource.html?uri=cellar:2bf140bf-a3f8-4ab2-b506-fd71826e6da6.0023.02/DOC_1&format=PDF, accessed on 1 September 2021).
For the sake of simplicity, we left out the blocking minority rule in the calculations of the adjusted power indices. In the following, the effect of this modification will be calculated.
In the past 28-member state case, there were only 10 variants of coalitions that are winning only due to the blocking minority rule. Table A5 shows all coalitions that are not blocking minorities even though they reach the population quota.

Table A5.
Coalitions which reach the population quota but cannot reject a decision in the 28-member EU.
Table A5.
Coalitions which reach the population quota but cannot reject a decision in the 28-member EU.
| 1 | Germany | France | United Kingdom |
| 2 | Germany | France | Italy |
| 3 | Germany | France | Spain |
| 4 | Germany | France | Poland |
| 5 | Germany | United Kingdom | Italy |
| 6 | Germany | United Kingdom | Spain |
| 7 | Germany | United Kingdom | Poland |
| 8 | Germany | Italy | Spain |
| 9 | Germany | Italy | Poland |
| 10 | France | United Kingdom | Italy |
In the case of small countries, in other words, for countries not appearing in Table A5 (their number is 23), we do not take them as a pivotal player in 10 possible variations, by ignoring the blocking minority rule, but they are. Thus, their Shapley–Shubik index should be increased by .
In the case of France, Germany, Italy, Poland, Spain, and the United Kingdom, we need to reduce the index. If France, Italy, and the United Kingdom oppose a decision, they cannot block it until another country joins them, so Germany is not considered as a pivotal player despite it plays this role. At the same time, we have counted Germany in nine variants as a pivotal player (for example, in the blocking coalition of France, Germany, and the United Kingdom), but it does not play such a role. Therefore, the correction for Germany is:
After Brexit, in the 27-member EU, there are 27! possible coalitions, and 19 variants involved in the correction needed due to the blocking minority rule.
By ignoring the blocking minority rule, in the case of countries not appearing in Table A6 (their number is 12), we do not take them as a pivotal player in 19 possible variants despite the fact that they are. Their Shapley–Shubik index should be increased by .
We show the overall effect of these corrections for Malta. The Shapley–Shubik index of Malta, calculated by the IOP software without the blocking minority rule, is 0.008487, which needs to be increased by . After Brexit, the Shapley–Shubik index of Malta is 0.008036. As mentioned, it should be increased by 19/70200. With the payment correction, the adjusted Shapley–Shubik index will be 0.007574. Therefore, the accurate change in power is . The original result was 0.863331, the difference is only 0.016421. Since Malta has the smallest Shapley–Shubik value, the adjustment for the other countries is lower. Consequently, ignoring the blocking minority rule does not have a significant effect on our results.

Table A6.
Coalitions that reach the population quota but cannot reject a decision in the 27-member EU after Brexit.
Table A6.
Coalitions that reach the population quota but cannot reject a decision in the 27-member EU after Brexit.
| 1 | Germany | France | Italy |
| 2 | Germany | France | Spain |
| 3 | Germany | France | Poland |
| 4 | Germany | France | Romania |
| 5 | Germany | France | Netherlands |
| 6 | Germany | France | Belgium |
| 7 | Germany | France | Greece |
| 8 | Germany | France | Czech Republic |
| 9 | Germany | France | Portugal |
| 10 | Germany | France | Hungary |
| 11 | Germany | France | Sweden |
| 12 | Germany | France | Austria |
| 13 | Germany | Italy | Spain |
| 14 | Germany | Italy | Poland |
| 15 | Germany | Italy | Romania |
| 16 | Germany | Italy | Netherlands |
| 17 | Germany | Spain | Poland |
| 18 | France | Italy | Spain |
| 19 | France | Italy | Poland |
References
- Lyons, K.; Darroch, G. Frexit, Nexit or Oexit? Who Will be Next to Leave the EU. The Guardian. 27 June 2016. Available online: https://www.theguardian.com/politics/2016/jun/27/frexit-nexit-or-oexit-who-will-be-next-to-leave-the-eu/ (accessed on 20 January 2018).
- Easton, A. Poland Stokes Fears of Leaving EU in ‘Polexit’. BBC News. 9 October 2021. Available online: https://www.bbc.com/news/world-europe-58840076 (accessed on 15 November 2021).
- Brams, S.J.; Affuso, P.J. Power and size: A new paradox. Theory Decis. 1976, 7, 29–56. [Google Scholar] [CrossRef]
- Grech, P.D. Power in the Council of the EU: Organizing theory, a new index, and Brexit. Soc. Choice Welf. 2021, 56, 223–258. [Google Scholar] [CrossRef]
- Göllner, R. The Visegrád Group—A rising star post-Brexit? Changing distribution of power in the European Council. Open Political Sci. 2017, 1, 1–6. [Google Scholar] [CrossRef]
- Kirsch, W. Brexit and the Distribution of Power in the Council of the EU. CEPS Online Publication. Available online: https://www.ceps.eu/publications/brexit-and-distribution-power-council-eu (accessed on 1 January 2020).
- Kirsch, W.; Słomczyński, W.; Stolicki, D.; Życzkowski, K. Double majority and generalized Brexit: Explaining counterintuitive results. arXiv 2018, arXiv:1812.07048. [Google Scholar]
- Kóczy, L.Á. Brexit and power in the Council of the European Union. Games 2021, 12, 51. [Google Scholar] [CrossRef]
- Szczypińska, A. Who gains more power in the EU after Brexit? Financ. Uver 2018, 68, 18–33. [Google Scholar]
- Bertini, C.; Gambarelli, G.; Stach, I.; Zibetti, G. Seat apportionment by population and contribution in European Parliament after Brexit. In Transactions on Computational Collective Intelligence XXXIV; Springer: Berlin/Heidelberg, Germany, 2019; pp. 109–126. [Google Scholar]
- Felsenthal, D.; Machover, M. The weighted voting rule in the EU’s Council of Ministers 1958–95: Intentions and outcomes. Elect. Stud. 1997, 16, 33–47. [Google Scholar] [CrossRef]
- Felsenthal, D.; Machover, M. The Treaty of Nice and qualified majority voting. Soc. Choice Welf. 2001, 18, 431–464. [Google Scholar] [CrossRef] [Green Version]
- Arregui, J. Determinants of bargaining satisfaction across policy domains in the European Union Council of Ministers. JCMS J. Common Mark. Stud. 2016, 54, 1105–1122. [Google Scholar] [CrossRef]
- Cross, J.P. Everyone’s a winner (almost): Bargaining success in the Council of Ministers of the European Union. Eur. Union Politics 2013, 14, 70–94. [Google Scholar] [CrossRef]
- Warntjen, A. Do votes matter? Voting weights and the success probability of member state requests in the Council of the European Union. J. Eur. Integr. 2017, 39, 673–687. [Google Scholar] [CrossRef] [Green Version]
- Shapley, L.S.; Shubik, M. A method for evaluating the distribution of power in a committee system. Am. Political Sci. Rev. 1954, 48, 787–792. [Google Scholar] [CrossRef]
- Banzhaf, J.F. Weighted voting does not work: A mathematical analysis. Rutgers Law Rev. 1965, 19, 317–343. [Google Scholar]
- Coleman, J.S. Control of collectives and the power of a collectivity to act. In Social Choice; Lieberman, B., Ed.; Gordon and Breach: New York, NY, USA, 1971; pp. 192–225. [Google Scholar]
- Penrose, L. The elementary statistics of majority voting. J. R. Stat. Soc. 1946, 109, 53–57. [Google Scholar] [CrossRef]
- Felsenthal, D.; Machover, M. The Measurement of Voting Power: Theory and Practice, Problems and Paradoxes; Edward Elgar: Cheltenham, UK, 1998. [Google Scholar]
- Felsenthal, D.; Machover, M. A priori voting power: What is it all about? Political Stud. Rev. 2004, 2, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Penrose, L.S. On the Objective Study of Crowd Behavior; HK Lewis: London, UK, 1952. [Google Scholar]
- Herne, K.; Nurmi, H. The distribution of a priori voting power in the EC Council of Ministers and the European Parliament. Scand. Political Stud. 1993, 16, 269–284. [Google Scholar] [CrossRef]
- Kóczy, L.Á. Beyond Lisbon: Demographic trends and voting power in the European Union Council of Ministers. Math. Soc. Sci. 2012, 63, 152–158. [Google Scholar] [CrossRef] [Green Version]
- Widgrén, M. Voting power in the EC decision making and the consequences of two different enlargements. Eur. Econ. Rev. 1994, 38, 1153–1170. [Google Scholar] [CrossRef]
- Shapley, L.S. A value for n-person games. In Contributions to the Theory of Games Volume II; Kuhn, H.W., Tucker, A.W., Eds.; Annals of Mathematical Studies; Princeton University Press: Princeton, NJ, USA, 1953; Volume 28, pp. 307–317. [Google Scholar]
- Brams, S.J.; Affuso, P.J. New paradoxes of voting power on the EC Council of Ministers. Elect. Stud. 1985, 4, 135–139. [Google Scholar] [CrossRef]
- Kóczy, L.Á. Measuring Voting Power: The paradox of new members vs. the null player axiom. In Towards Intelligent Engineering and Information Technology; Rudas, I.J., Fodor, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 67–78. [Google Scholar]
- Le Breton, M.; Montero, M.; Zaporozhets, V. Voting power in the EU Council of Ministers and fair decision making in distributive politics. Math. Soc. Sci. 2012, 63, 159–173. [Google Scholar] [CrossRef] [Green Version]
- Council of the European Union. Qualified Majority Voting. 2017. Available online: http://www.consilium.europa.eu/en/council-eu/voting-system/qualified-majority/ (accessed on 6 January 2017).
- Eurostat. EUROPOP2013—Convergence Scenario, National Level, Population Predictions [tps00002]. 2014. Available online: http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=tps00002&lang=en (accessed on 6 January 2017).
- European Parliament. EU Budget Explained: Expenditure and Contribution by Member State. 2015. Available online: http://www.europarl.europa.eu/news/en/headlines/eu-affairs/20141202IFG82334/eu-budget-explained-expenditure-and-contribution-by-member-state/ (accessed on 20 January 2017).
- Bräuninger, T.; König, T. Indices of Power IOP 2.0. 2005. Available online: http://www.tbraeuninger.de/download/ (accessed on 6 January 2017).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).