Promotion of Green Technology under Different Environmental Policies
Abstract
1. Introduction
2. Results
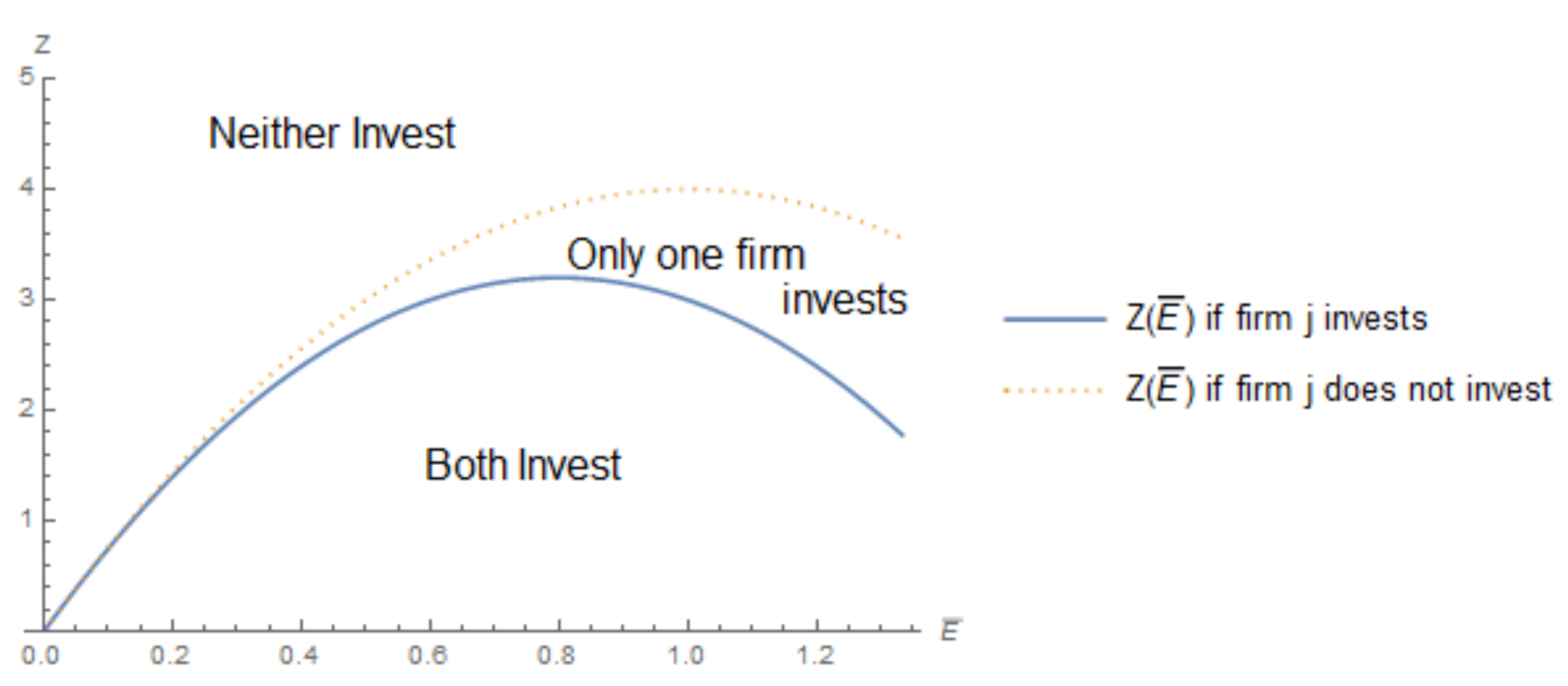
2.1. Emission Fee
- 1.
- Both firms adopt the technology if .
- 2.
- Neither firm adopts the technology if .
- 3.
- Only one firm adopts the technology if .10
2.2. Quota
- 1.
- Both firms adopt the technology if .
- 2.
- Neither firm adopts the technology if .
- 3.
- Only one firm adopts the technology if .14
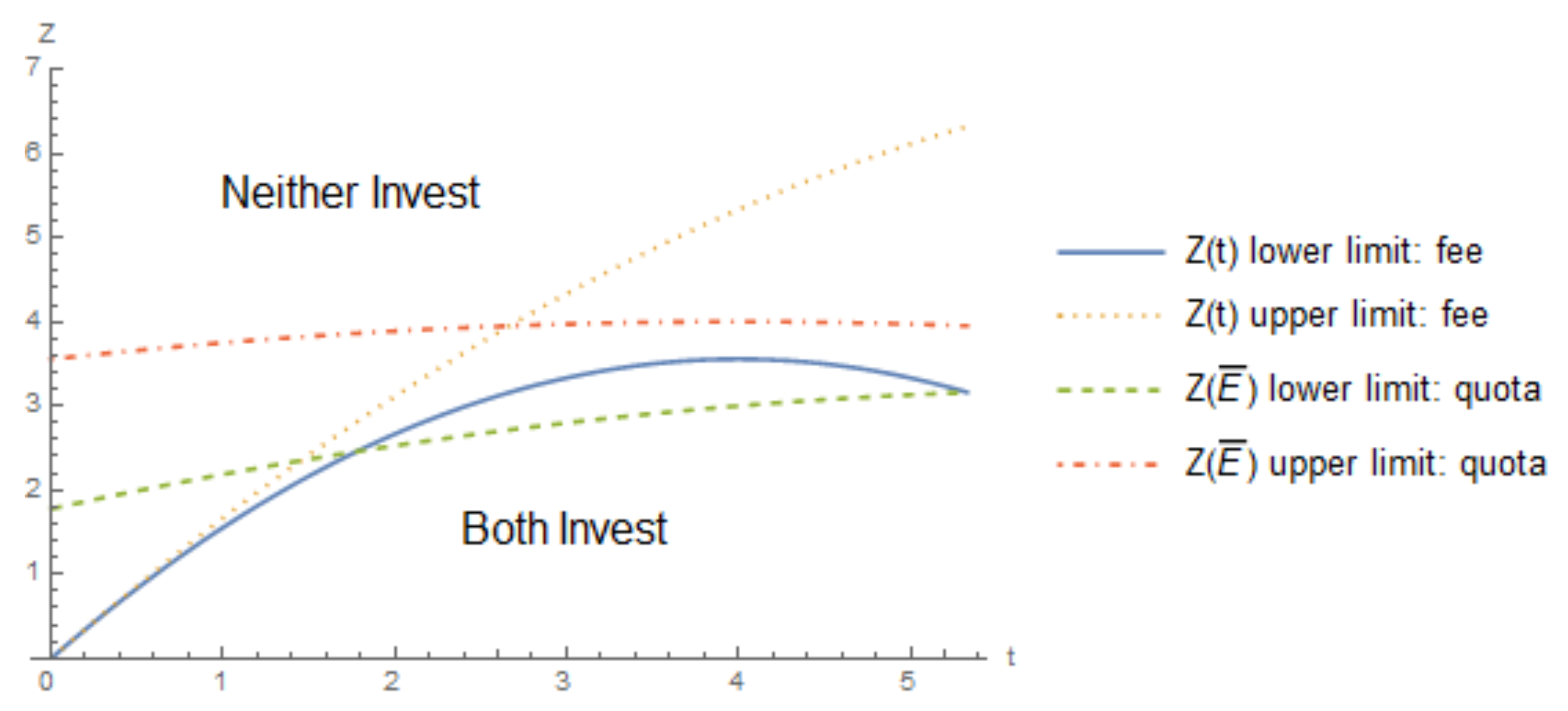
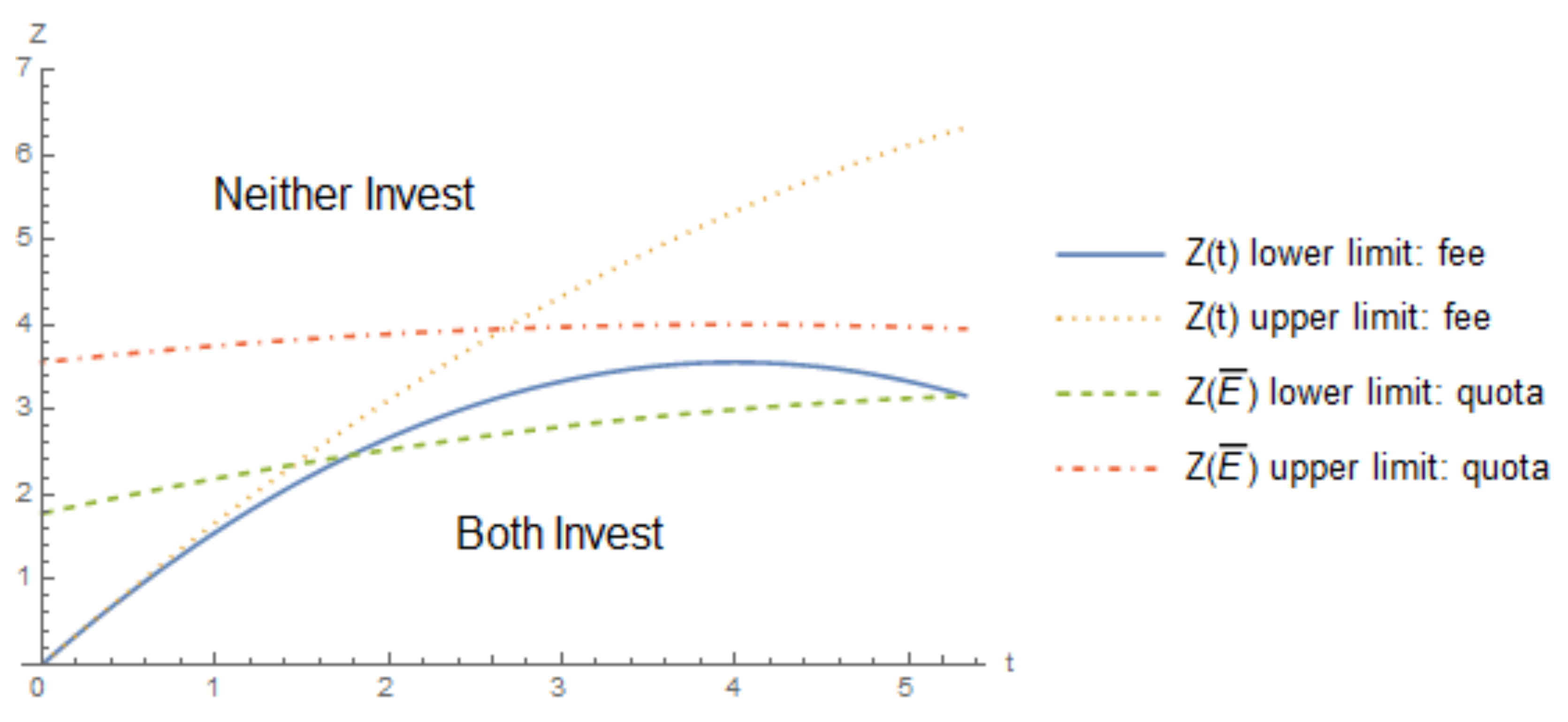
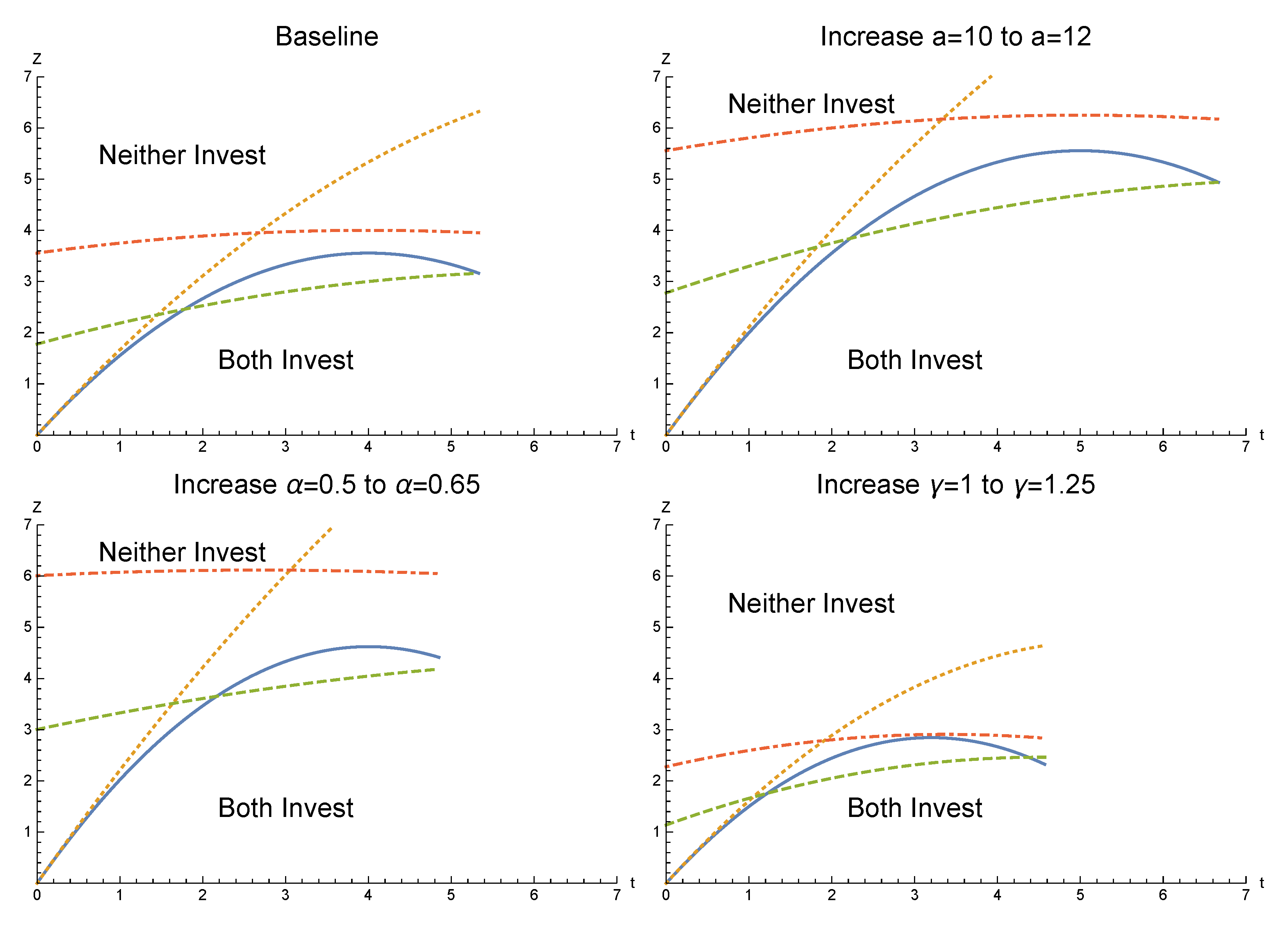
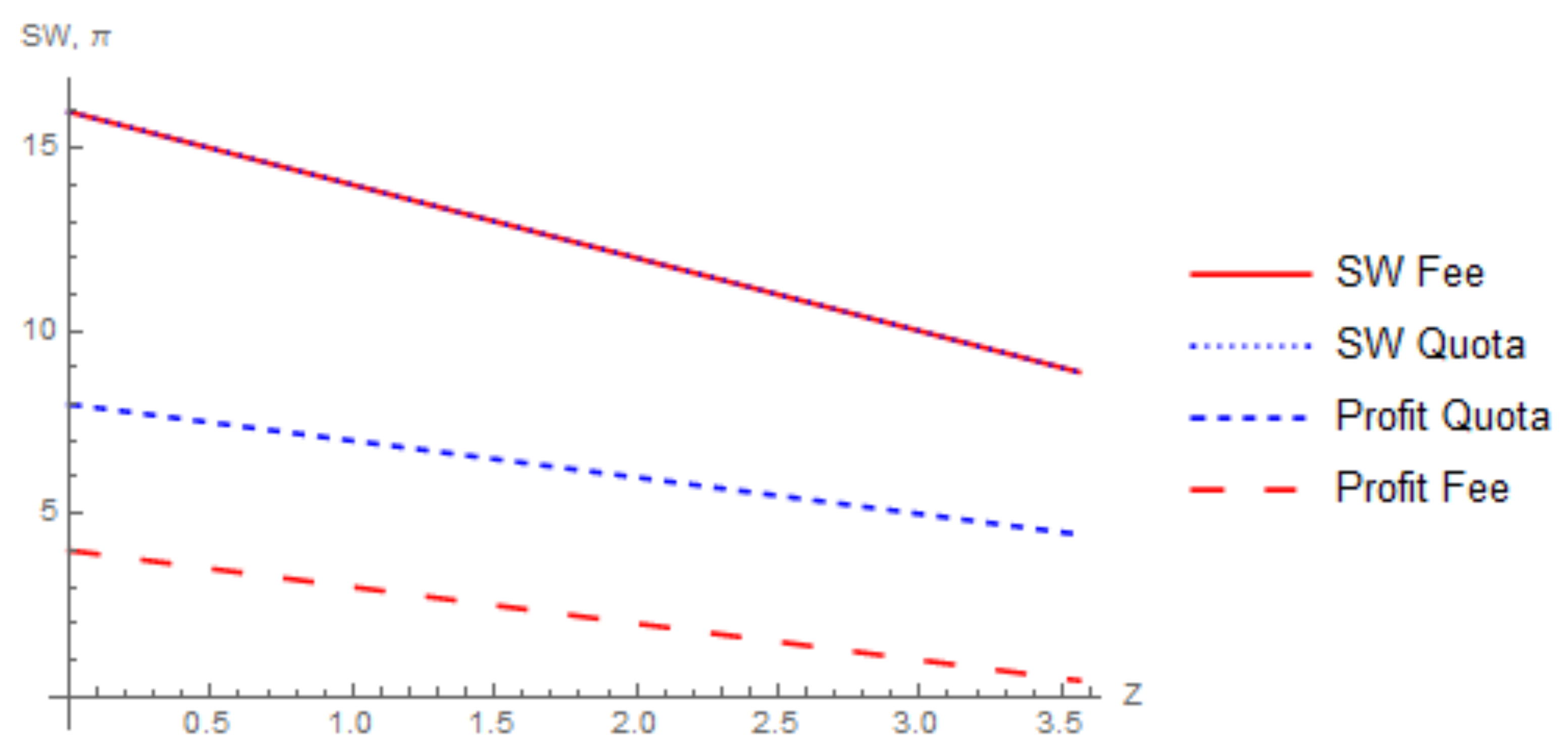
2.3. Comparison of the Fee and Quota
| Market size: | , and | |
| Emissions: | , and | |
| Abatement: | , and |
2.4. Asymmetric Cost of Adoption under an Emission Fee
- 1.
- Both of the firms adopt the technology if .
- 2.
- Neither firm adopts the technology if .
- 3.
- Only one firm adopts the technology if .20
- 4.
- Only the low cost firm i adopts the technology if .
2.5. Investment Increases Marginal Cost of Production under an Emission Fee
- 1.
- Both of the firms adopt the technology if .
- 2.
- Neither firm adopts the technology if .
- 3.
- Only one firm adopts the technology if .23
2.6. Type-Dependent Fee
- 1.
- Both firms adopt the technology if .
- 2.
- Neither firm adopts the technology if .
- 3.
- Only one firm adopts the technology if .25
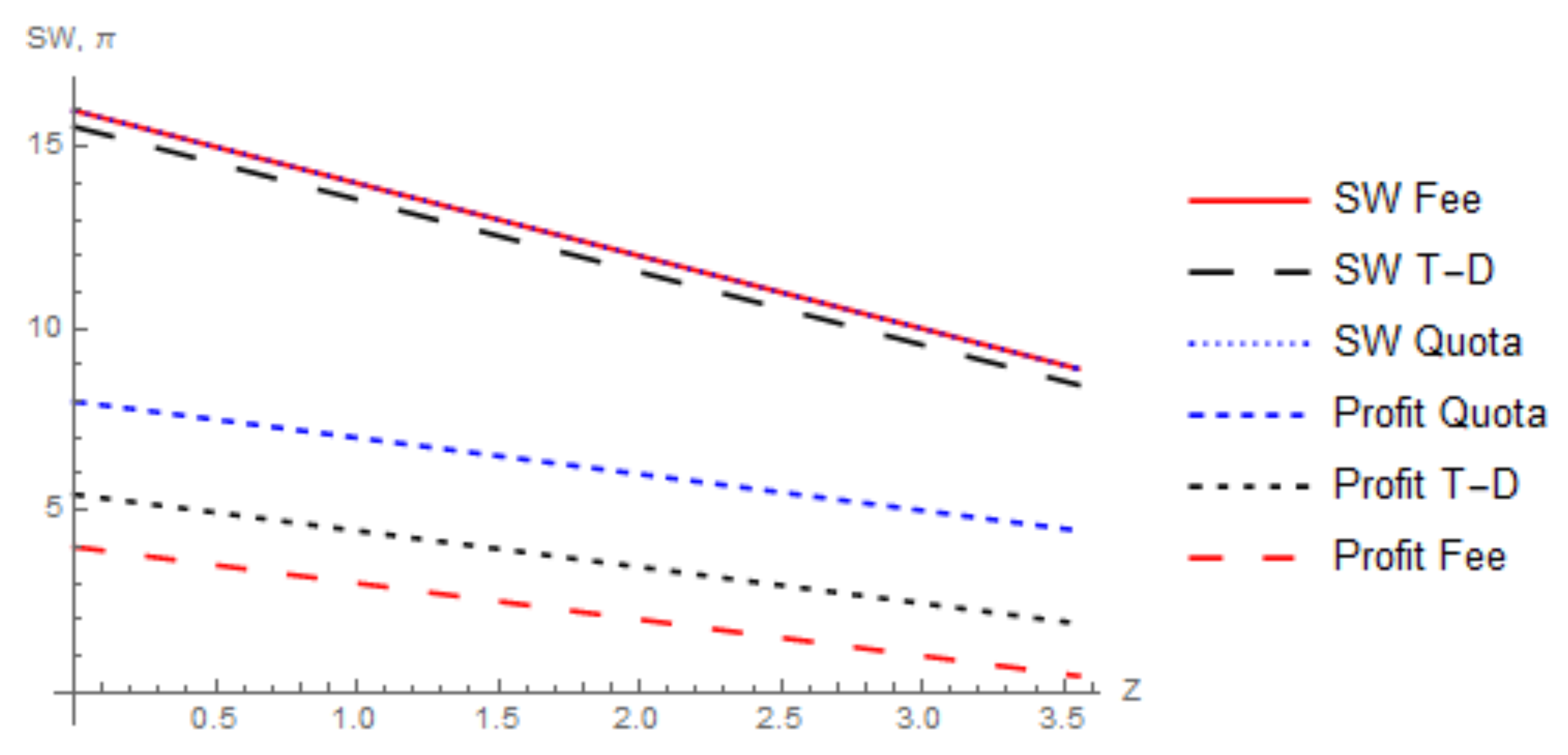
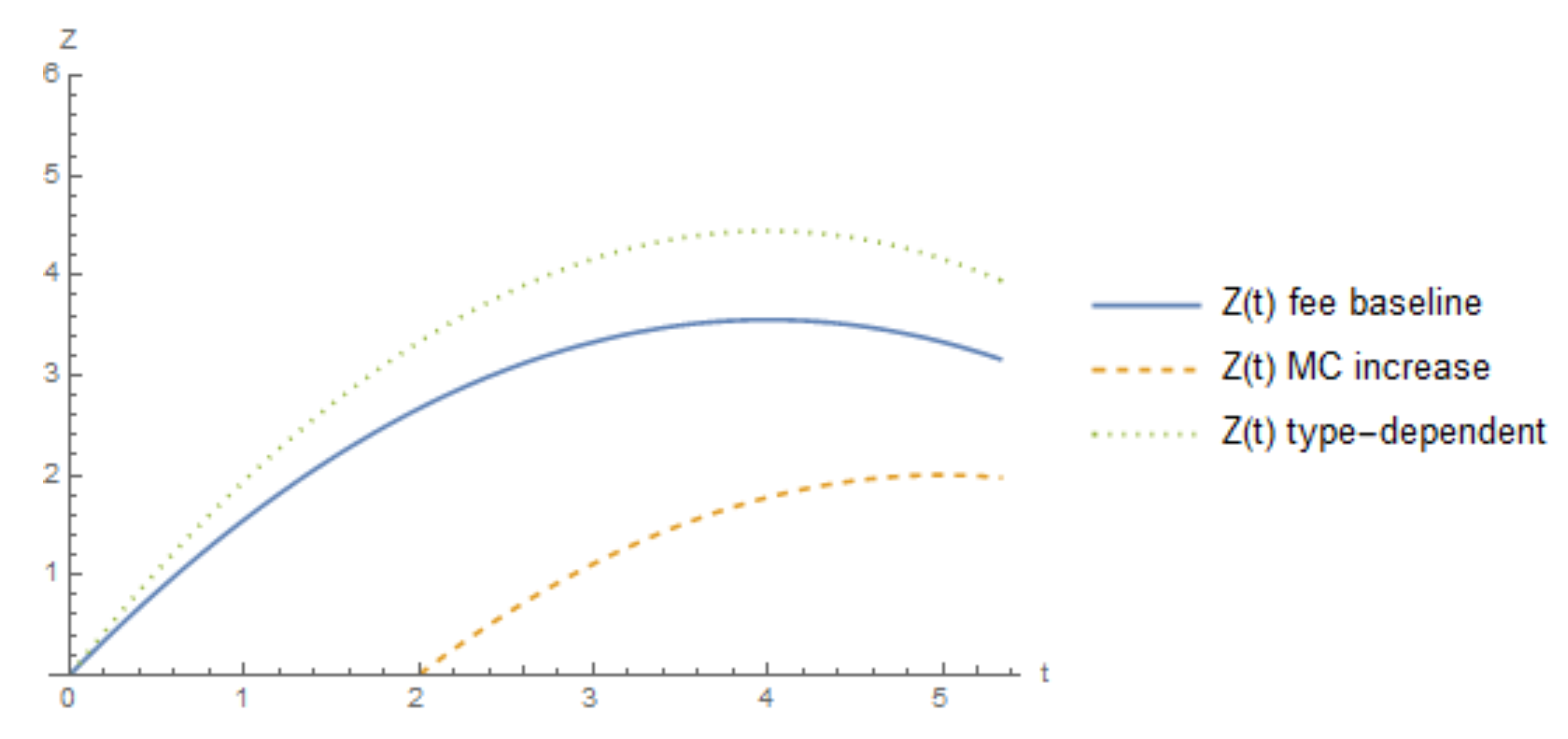
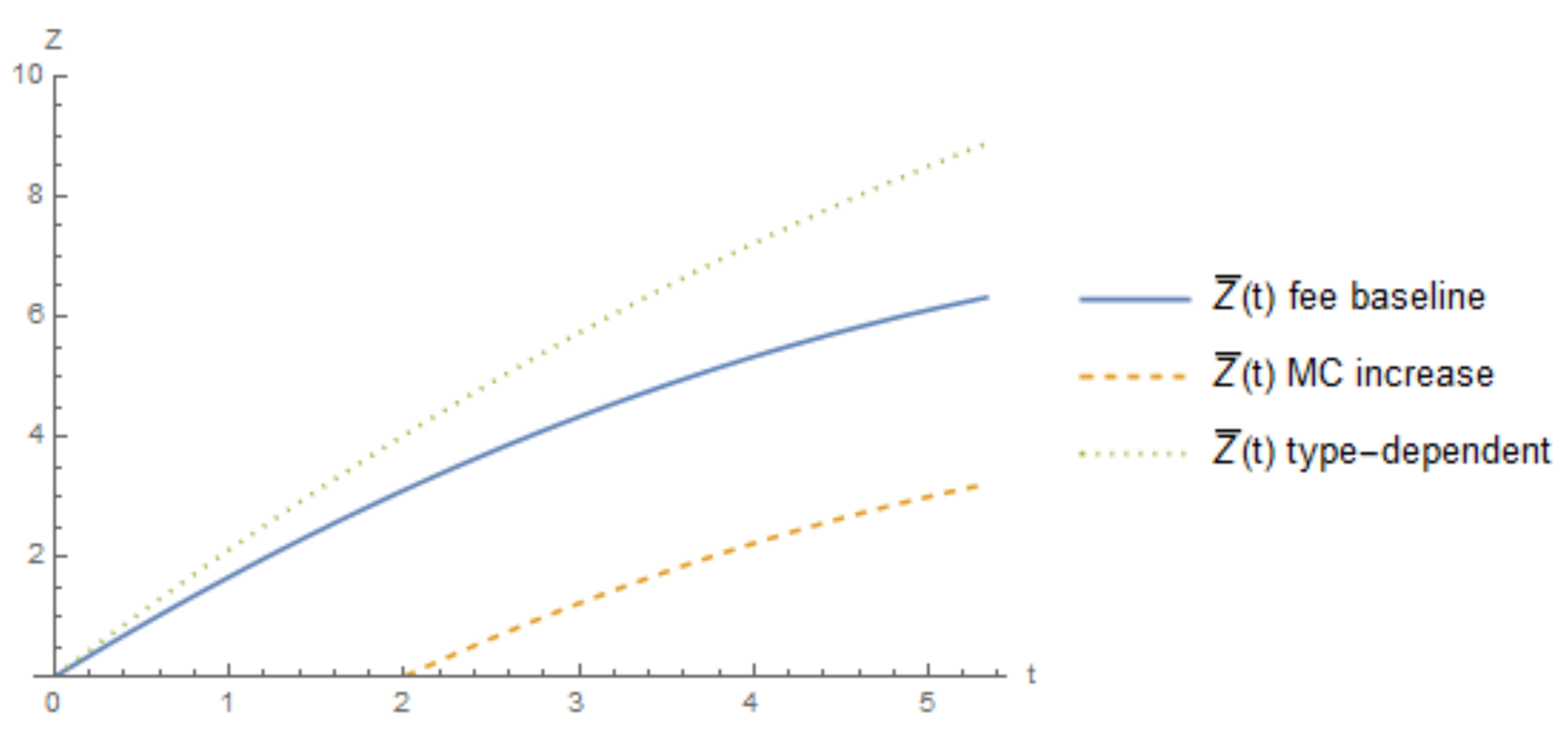
2.7. Comparison of Investment Limits under a Fee
2.8. Tradeable Permit Scheme
2.9. Asymmetric Cost of Adoption under a Quota
- 1.
- Both of the firms adopt the technology if .
- 2.
- Neither firm adopts the technology if .
- 3.
- Only one firm adopts the technology if.27
- 4.
- Only the low cost firm i adopts the technology if .
2.10. Investment Increases Marginal Cost of Production under a Quota
- 1.
- Both firms adopt the technology if , and .
- 2.
- Neither firm adopts the technology if
- 3.
- Only one firm adopts the technology if, and .28
3. Discussion
4. Materials and Methods
4.1. Outline of Proof of Proposition 1
4.2. Quota
4.3. Proof of Lemma 1
Comparative Statics
4.4. Asymmetric Cost of Adoption under a Fee
- If both firms invest, each firm has profit
- If one firm invests, the investing firm has profit , and the firm that does not invest has profit
- If neither firm invests, each firm has profit
4.5. Investment Increases Marginal Cost of Production under a Fee
4.6. Type-Dependent Fee
4.7. Asymmetric Cost of Adoption under a Quota
- If both firms invest, each firm has profit
- If one firm invests, the investing firm has profit , and the firm that does not invest has profit
- If neither firm invests, each firm has profit
4.8. Investment Increases Marginal Cost of Production under a Quota
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| INV | Invest in (or adopt) the green technology |
| NI | Not invest in (or adopt) the green technology |
| R&D | Research and development |
References
- Kemp, R.; Volpi, M. The diffusion of clean technologies: A review with suggestions for future diffusion analysis. J. Clean. Prod. 2008, 16S1, S14–S21. [Google Scholar] [CrossRef]
- Wenders, J.T. Methods of pollution control and the rate of change in pollution abatement technology. Water Resour. Res. 1975, 11, 393–396. [Google Scholar] [CrossRef]
- Magat, W. The Effects of Environmental Regulation on Innovation. Law Contemp. Probl. 1979, 43, 4–25. [Google Scholar]
- Downing, P.B.; White, L.J. Innovation in pollution control. J. Environ. Econ. Manag. 1986, 13, 18–29. [Google Scholar] [CrossRef]
- Milliman, S.R.; Prince, R. Firms incentives to promote technological change in pollution control. J. Environ. Econ. Manag. 1989, 17, 247–265. [Google Scholar] [CrossRef]
- Carraro, C.; Soubeyran, A. Environmental policy and the choice of production technology. In Environmental Policy and Market Structure; Carraro, C., Katsoulacos, Y., Xepapadeas, A., Eds.; Springer: Dordrecht, The Netherlands, 1996; pp. 151–180. [Google Scholar]
- Jung, C.; Krutilla, K.; Boyd, R. Incentives for advanced pollution abatement technology at the industry level: An evaluation of policy alternatives. J. Environ. Econ. Manag. 1996, 30, 95–111. [Google Scholar] [CrossRef]
- Montero, J.-P. Permits, Standards, and Technology Innovation. J. Environ. Econ. Manag. 2002, 44, 23–44. [Google Scholar] [CrossRef]
- Requate, T.; Unold, W. Environmental policy incentives to adopt advanced abatement technology: Will the true ranking please stand up? Eur. Econ. Rev. 2003, 47, 125–146. [Google Scholar] [CrossRef]
- Amacher, G.S.; Malik, A.S. Pollution Taxes When Firms Choose Technologies. South. J. Econ. 2002, 68, 891–906. [Google Scholar] [CrossRef]
- Requate, T. Incentives to innovate under emission taxes and tradeable permits. Eur. J. Political Econ. 1998, 14, 139–165. [Google Scholar] [CrossRef]
- Jensen, R. Innovation adoption and welfare under uncertainty. J. Ind. Econ. 1992, 40, 173–180. [Google Scholar] [CrossRef]
- Zhang, Y.; Mei, S.; Zhong, W. New technology adoption in a Cournot oligopoly with spillovers. J. Econ. 2014, 112, 115–136. [Google Scholar] [CrossRef]
- Pal, R. Technology adoption in a differentiated duopoly: Cournot versus Bertrand. Res. Econ. 2010, 64, 128–136. [Google Scholar] [CrossRef]
- Poyago-Theotoky, J.A. The Organization of R&D and Environmental Policy. J. Econ. Behav. Organ. 2007, 62, 63–75. [Google Scholar]
- Strandholm, J.C.; Espínola-Arredondo, A.; Muñoz-García, F. Regulation, Free-Riding Incentives, and R&D investment with Spillover. Resour. Energy Econ. 2018, 53, 133–146. [Google Scholar]
- Strandholm, J.C.; Espínola-Arredondo, A. Investment in Green Technology and Entry Deterrence. BE J. Econ. Anal. Policy 2020, 20, 1–18. [Google Scholar] [CrossRef]
- Espínola-Arredondo, A.; Muñoz-García, F.; Liu, B. Strategic Emission Fees: Using Green Technology to Deter Entry. J. Ind. Compet. Trade 2019, 19, 313–349. [Google Scholar] [CrossRef]
- Parlfrey, T.R.; Rosenthal, H. Participation and the provision of discrete public goods: A strategic analysis. J. Public Econ. 1984, 24, 171–193. [Google Scholar] [CrossRef]
- Diekmann, A. Volunteer’s Dilemma. J. Confl. Resolut. 1985, 29, 605–610. [Google Scholar] [CrossRef]
- Rose, S.K.; Clark, J.; Poe, G.L.; Rondeau, D.; Schulze, W.D. The private provision of public goods: Tests of a provision point mechanism for funding green power programs. Resouc. Energy Econ. 2002, 24, 131–155. [Google Scholar] [CrossRef]
| 1. | According to the World Health Organization: http://www.who.int/mediacentre/news/releases/2014/air-pollution/en/. |
| 2. | A summary of the situation is explained by Lydia Heida in a Yale Environment 360 article titled, “Can Waterless Dyeing Processes Clean Up the Clothing Industry?”, found at https://e360.yale.edu/features/can_waterless_dyeing_processes_clean_up_clothing_industry_pollution. |
| 3. | Another line of literature focuses on endogenous environmental R&D; see Poyago-Theotoky [15], Strandholm, Espinola-Arredondo, and Munoz-Garcia [16], Strandholm and Espinola-Arredondo [17], and Espinola-Arredondo, Munoz-Garcia, and Liu [18]. I, instead, focus on the adoption of an already developed technology that firms can adopt to lower their emissions. This paper does not consider a knowledge spillover. |
| 4. | Strandholm, Espinola-Arredondo, and Munoz-Garcia [16] focus on the free-riding effects of investing in green technology as optimal policy is set based on expected emissions after the technology is in place, so as one firm invests in a green technology all firms benefit from facing a lower fee. |
| 5. | I use the terms ‘adopt’ and ‘invest’ interchangeably. |
| 6. | This paper assumes an industry where a green technology is already developed and firms only focus on the implementation of it into their production process. Examples of abatement technology include smoke stack scrubbers that remove pollutants from entering the air, underground liners to prevent leakage of pollution into the soil and entering groundwater, and treating waste water before disposal. Thus, considering the case where the firms are price takers in the abatement technology market. |
| 7. | In this game, it is not necessary for the environmental policy to be set optimally, since I am analyzing firms’ reaction to policy. If an optimal policy is set, the analysis would not be affected. |
| 8. | It is trivial to consider production in the first stage as the profit from production in the first stage is the same, regardless of the decision to invest in the green technology as the two decisions are independent. |
| 9. | Profit functions for the different policies and cost asymmetries, as well as all proofs are provided Section 4. |
| 10. | Additionally, a mixed-strategy Nash equilibrium exists where each firm adopts the technology with probability , . |
| 11. | Parameter values for all figures, unless otherwise noted, are: , , , , , , and . |
| 12. | By assumption, the figure’s parameters require that . |
| 13. | The quota is binding if . In the case of adoption, this means that the quota must be set such that . Further explanation is provided in Section 4.5. |
| 14. | A mixed strategy exists where each firm adopts the technology with probability . |
| 15. | This means that Figure 2 is mirrored, so that a high quota corresponds to a low emissions. It is also the case that the allowable range for the fee is smaller than that of the quota, so only the appropriate subsection of the quota appears in Figure 3. The parameter values for all figures in this section are the same as Figure 1. |
| 16. | |
| 17. | Because output, environmental damage, and adoption costs are identical in the first stage in every setting, they have no effect on the comparison of social welfare in each setting and are left out of the social welfare function. The social welfare function is under the assumption that the emission fee is revenue neutral. |
| 18. | At , both firms adopt the technology if and only if , according to Proposition 1. When , the equivalent emissions quota is . |
| 19. | The type-dependent fee is analyzed in Section 2.6. Note that this is bigger than the change in Figure 7 and Figure 8 to better illustrate the difference in profits and social welfare under the type-dependent fee visually. |
| 20. | Additionally a mixed strategy Nash equilibrium exists where each firm adopts the technology with probability . Note that since firm j faces a higher adoption cost, and the low cost firm is more likely to adopt in the mixed strategy. |
| 21. | The cost of adoption is symmetric, i.e., . |
| 22. | Carbon capture and storage (CCS) is an example of a green technology that increases the marginal cost of production. The production process of the good is relatively unchanged; however, there are additional costs to the capture, transport, and store captured carbon dioxide. |
| 23. | A mixed strategy Nash equilibrium exists, where each firm adopts the technology with probability . |
| 24. | A type-dependent fee is the focus of Strandholm et al. [16], who look at it in the context of incremental investment in R&D. The type-dependent fee is set by a regulator that can observe emissions at the plant-level and setting a fee that is based on that plant’s marginal environmental damage. |
| 25. | A mixed strategy Nash equilibrium exists, where each firm adopts the technology with probability . |
| 26. | This figure has the same parameter values as Figure 1 with additional parameters and . In the case of the type-dependent fee, the post-adoption fee is a 25% reduction in the emission fee. |
| 27. | A mixed strategy exists where each firm adopts the technology with probability . |
| 28. | A mixed strategy exists where each firm adopts the technology with probability . |
| Quantity | Profit | |
|---|---|---|
| Neither firm invests | ||
| Both firms invest | ||
| Firm i invests, firm j does not | ||
| Firm j invests, firm i does not |
| Firm j | |||
|---|---|---|---|
| Invest | No Invest | ||
| Firm i | Invest | ||
| No Invest |
| Quantity | Profit | |
|---|---|---|
| Neither firm invests | ||
| Both firms invest | ||
| Firm i invests, firm j does not | ||
| Firm j invests, firm i does not |
| Quantity | Profit | |
|---|---|---|
| Neither firm invests | ||
| Both firms invest | ||
| Firm i invests, firm j does not | ||
| Firm j invests, firm i does not |
| Quantity | Profit | |
|---|---|---|
| Neither firm invests | ||
| Both firms invest | ||
| Firm i invests, firm j does not | ||
| Firm j invests, firm i does not |
| Quantity | Profit | |
|---|---|---|
| Neither firm invests | ||
| Both firms invest | ||
| Firm i invests, firm j does not | ||
| Firm j invests, firm i does not |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strandholm, J.C. Promotion of Green Technology under Different Environmental Policies. Games 2020, 11, 32. https://doi.org/10.3390/g11030032
Strandholm JC. Promotion of Green Technology under Different Environmental Policies. Games. 2020; 11(3):32. https://doi.org/10.3390/g11030032
Chicago/Turabian StyleStrandholm, John C. 2020. "Promotion of Green Technology under Different Environmental Policies" Games 11, no. 3: 32. https://doi.org/10.3390/g11030032
APA StyleStrandholm, J. C. (2020). Promotion of Green Technology under Different Environmental Policies. Games, 11(3), 32. https://doi.org/10.3390/g11030032





