Market Power in Output and Emissions Trading

Abstract

This article focuses on the strategic behavior of firms in the output and the emissions markets in the presence of market power. We consider the existence of a dominant firm in the permit market and different structures in the output market, including Cournot and two versions of the Stackelberg model, depending on whether the permit dominant firm is a leader or a follower in the output market. In all three models, the firm that dominates the permit market is more sensitive to its initial allocation than its competitor in terms of abatement and less sensitive in terms of output. In all three models, output is decreasing and the permit price is increasing in the permit dominant firm’s initial allocation. In the Cournot model, permit dominance is fruitless in terms of output and profit if the initial allocation is symmetric. Output leadership is more relevant than permit dominance since an output leader always tends to, ceteris paribus, produce more and make more profit whether it also dominates the permit market or not. This leadership can only be overcompensated for by distributing a larger share of permits to the output follower, and only if the total number of permits is large enough. In terms of welfare, Stackelberg is always superior to Cournot. If the initial permit allocation is symmetric, welfare is higher when the same firm dominates the output and the permit market at the same time.

1. Introduction

A coordinated and effective global agreement to cut down greenhouse gas emissions is far from being reached after 20 years of formal negotiations since the first big attempt in Kyoto, 1997. Meanwhile, some market-based climate change policies have been put in place at regional levels, the European Trading Scheme (ETS) and the China’s National ETS being the most important experiences.1

The efficiency of emission permit markets deserved academic attention well before their practical implementation.2 The role of market power and the method used to do the initial allocation of permits (mainly grandfathering or auctioning) are among the main issues that have attracted the attention of researchers. Reference [3] established that, under perfect competition, the equilibrium allocation of a permit market is cost-effective, regardless of the initial allocation method. Reference [5] considered market power in the permit market for the first time and showed that the equilibrium allocation fails to be efficient in the presence of a dominant firm (i.e., a firm with some capacity to set the market price), because such a firm has an incentive to manipulate the permit price in order to increase its profits. The resulting allocation is efficient only if the dominant firm is initially allocated with the same number of permits that it would get in a competitive equilibrium.

In its basic version, both results (the result in [3] about the efficiency of a competitive market and the result in [5] about the lack of efficiency of a non-competitive market) refer to the permit market alone and abstract from the existence of an associated output market and its corresponding structure. As has been later acknowledged by several authors, the output market must be taken into account to complete a fully-fledged analysis, since the cost associated with the purchase of permits impacts the overall profits that firms aim to maximize, and therefore, a profit-maximizing firm should act in the permit market in accordance with its output market strategy.

The setting in [5] was extended by [6], which considered the output market and showed that a dominant firm can manipulate the permit price to raise the costs of the price-taking firms. In the same line, Reference [7] found that a dominant firm has an incentive to set the permit price above its marginal abatement cost whenever its initial permit allocation is above a specific threshold that is below its optimal level of emissions. As a consequence, modifying the permit allocation is not enough to achieve overall efficiency. Reference [8] pointed out that a dominant net permit buyer may want to increase the permit price, provided that the increase in compliance costs is more than offset by the sum of the revenue increase in the output market and the rents embedded in the initial allocation. For a survey of the literature on output and permit markets with market power, see [9].

The present study is concerned about situations in which firms interact strategically in two markets simultaneously: output and emission permits. As an example, consider the California NO_x permit market. Around 25% of the NO_x permits were allocated to power companies operating in the Californian electricity market, which is known to have market power problems. According to [10] the electric utilities used the permit market to increase their market power in the electricity market.3

The connections between the permit markets and the output markets are very important, not only at the firm level, but also at the country level. According to [12], some of the large countries involved in an eventual global carbon market are also important players in the energy markets. In this context, Reference [13] analyzes the optimal strategies of Russia, which is a very relevant player in the international emissions market and also an important fuel exporter. The conclusion is that Russia could benefit by coordinating its permit and energy exports through the framework of the Kyoto Protocol.

This paper studies the strategic interaction of polluting firms (or countries)4 taking part in the output and the permit market, paying attention to the market power position of each firm in each market. To this aim, we use a duopoly model under different output market structures while assuming that there is a dominant firm operating in the permit market. We study the effect of market power under three different situations, depending on the role that each firm plays in the product market and, specifically, if the firm that is dominant in the permit market also leads the product market.

We first set up a simple model of a permit market with a dominant firm. The equilibrium of such a market turns out to be crucially determined, first, by the output market equilibrium and, second, by the initial permit allocation. We also restate the classical result of [5], which implies that, as long as some permit trade is taking place in the market, the dominant firm will take advantage of its position whether it acts as a net buyer or as a net seller of permits.

In order to investigate the role of the product market with some detail, we consider three output market structures. The first one is a Cournot duopoly, in which both firms play a symmetric role, whereas the other two are characterized by the existence of a Stackelberg leader and a follower. In the second version (Stackelberg 1), the dominant firm in the emission permit market is also an output market leader. In the third version (Stackelberg 2), we consider that the output leader (firm 1) acts as a price taker in the permit market.

The aim of the first version (Cournot) is to study a case in which a firm dominates the permit market, but the firms are symmetric in the output market. This allows us to ask to what extent the dominant position in the permit market can break the symmetry in the output market or, the other way around, how symmetry in the output market can soften the dominance of a firm in the permit market. This version is similar to the one in [14]. The main difference lies in the timing. In our version, the output market is cleared first, and the permit market comes afterwards, while it is the other way around in [14]. Our timing is consistent with the belief that firms’ main activity is output production and permits are traded only as a secondary or implied activity, not as the main one. This difference has a reflection in some of the findings, as is discussed at the end of Section 4.

The second version (Stackelberg 1) depicts a situation in which a single firm has the ability to lead both markets at the same time, which a priori is the most favorable case for the leading firm itself, but the less favorable for the following firm and, one may expect, also for the sake of market efficiency. Similar versions of this model have been addressed in the literature in the form of a Stackelberg leader-follower setting or a leader-fringe structure.5 Reference [15] studies a permit market considering spatial and intertemporal trading, with a big dominant company and many small nonstrategic but forward-looking firms. The monopoly equilibrium and some intermediate cases are addressed. Reference [16] simulates the California electricity market by building a Cournot-fringe setting in term of output and permits and show that the Cournot firms can raise energy and permit prices, resulting in a loss of social welfare. Our approach in this second version is similar to [7] but with a couple of significant differences. While [7] considers a dominant firm and a fringe of competitive firms in the product market, we focus on a duopoly. Therefore, in the product market, our follower behaves strategically according to its reaction curve, while in [7], the fringe firms are price takers. A second difference is that, by using specific demand and cost functions, we can obtain the closed solution of the model, which makes it easier to compare the results across the different versions.

As far as we know, our third case, (Stackelberg 2) has not been analyzed in the literature yet. The motivation for this version is to look for conditions under which being a leader in each of the two markets represents a competitive advantage. The underlying question is: which is the best place to exercise market power? With this version of the model, we try to get some insight about the relative importance of having a leadership position in the output market or in the permit market. As a motivation for this approach, consider the role of Russia and the USA in the Kyoto Protocol. For example, Reference [17] argues that the USA’s rejection to join this Protocol was due to the fact that its least costly strategy to meet the Kyoto requirements would involve buying a large number of emissions credits from Russia. This situation can be captured in a simple stylized way by stating that Russia was (or the USA thought it was) a leader in the permit market. Simultaneously, one can argue that the USA has a stronger leadership position than Russia in the output market.6 One can be interested in assessing the relative strength of both leaderships. With our third model, we aim to address this question about the best place to exercise market power in a simple and tractable way.

The remainder of this article proceeds as follows: Section 2 presents the main elements of the theoretical model. Section 3 derives the permit market equilibrium. The next three sections explore the impact of the initial allocation on the firms’ output and profit under three different market structures: Cournot (Section 4) and the two versions of the Stackelberg model (Section 5 and Section 6). Section 7 compares all three models in terms of aggregate output and welfare. Section 8 states our conclusions. The Appendix A contains the proofs of all the analytical results.

2. Basic Elements of the Model

Consider a duopoly where the two firms interact in an output market and an emission permit market. Denote individual output as $x_i$ ($i=1, 2$), total output as $X$ and the inverse demand function as $P\left(X\right)=1-X$, where $P$ is the output price. We set the production cost equal to zero, so that the only cost for firms is the abatement cost. Gross emissions are proportional to the firms’ output where one unit of output generates one unit of emissions. 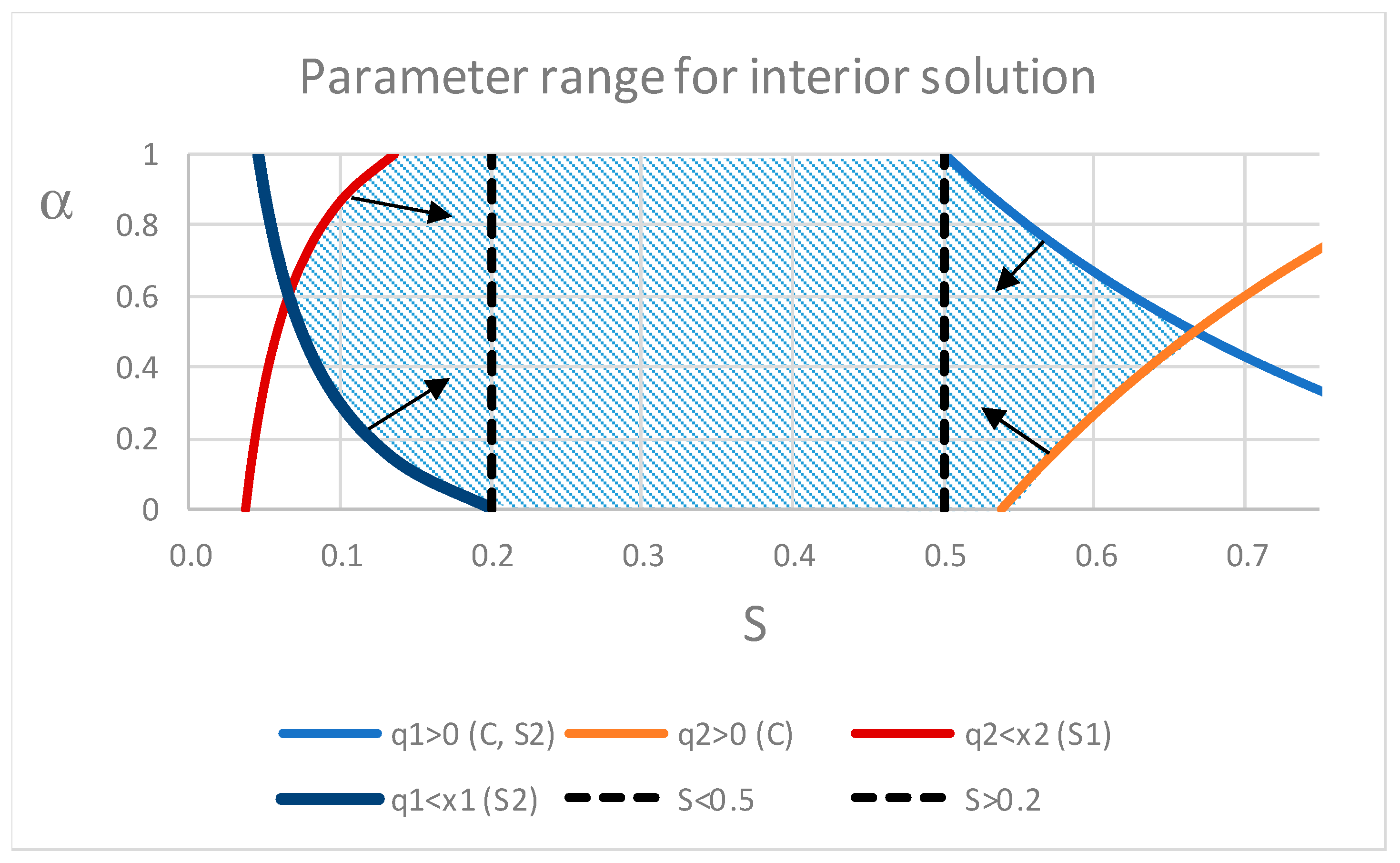Each firm, $i$, enjoys an initial permit allocation, $S_i$ ($i=1, 2$), such that firms 1 and 2 receive a given proportion, $\alpha$ and $1-\alpha$ respectively, of a total given amount, $S$, with $S_1=\alpha S$ and $S_2=\left(1-\alpha \right)S$.7 A necessary condition for the environmental policy to have some effect is that $S$ is not larger than the laissez faire level of emissions (i.e., $2/3$ in the Cournot model and $3/4$ in the Stackelberg model). Moreover, we focused on interior solutions regarding the relevant variables (output, abatement, and net emissions). This makes the presentation simpler without losing any relevant insight. For this reason, we assumed $S\le 0.5$ throughout the article. This constraint ensures that abatement is non-negative for both firms in all the considered models and for any initial allocation.8

Each firm can reduce its emissions by producing less output or by making some abatement effort. Abated quantities are denoted by $q_i$ ($i=1, 2$) and net emissions, $e_i$, are given by gross emissions minus abatement, i.e., $e_i=x_i-q_i$. We assumed the same abatement technology for both firms, with abatement cost given by the quadratic function $C\left(q_i\right)=\frac{q_i^2}{2}$.9 Regarding permit trading, we denoted permits purchased by firm $i$ as $y_i$ if it has a positive value. A negative value of $y_i$ means that firm $i$ is selling rather than buying permits. The market equilibrium condition implies $y_1=-y_2$. The permit price was denoted as $p$. We also assumed that the regulator can perfectly monitor emissions without cost and, thus, firms’ emissions cannot exceed the number of permits they hold.

The timing was as follows.10 The first stage is the output market and the second stage involves abatement and emission trading. In the output game, we considered three alternative classic versions. In the first one (Cournot), both firms decide simultaneously and thus the first stage is one shot. In the second and the third versions (Stackelberg 1 and 2), the first stage has two sub-stages: the output leader moves in the first sub-stage and then the output follower moves in the second. In order to capture the fact that there is a dominant firm in the permit market, the emissions game always has two sub-stages: in the first one, the firm that dominates the permit market (firm 1) sets the price (or, equivalently, its own demand for permits) and firm 2 decides its demand in the second sub-stage taking the permit price as given. The analysis was restricted to interior solutions. All the versions are solved by using backwards induction. Thus, we started by analyzing the emissions game.

3. Permit Market Equilibrium with a Dominant Firm

We first focused on firm 2′ decisions on abatement and permit trading as follows (Equation (1)):

$$\begin{array}{l}\underset{\left\{q_2,y_2\right\}}{Min} \frac{q_2^2}{2}+p{y}_2\\ s.t. x_2-q_2=S_2+y_2\end{array}$$

(1)

where the objective is to minimize total cost, which includes abatement cost plus permit purchase cost (or minus permit revenue if firm 2 is a net seller) and the constraint states that net emissions (gross emissions minus abatement) must be equal to the amount of permits held by firm 2 (initial allocation plus net purchases).

We could solve the constraint in (1) for $y_2$, substitute into the objective function and differentiate with respect to $q_2$, to get the familiar first-order condition, according to which, the permit price equals the marginal abatement cost. The second order condition was satisfied because the objective function is strictly convex in $q_2$. By solving the first order condition for $q_2$ we obtained firm 2′s demand for abatement, and combining such expression with the constraint, we obtained the net permit demand of firm 2 in terms of the permit price (Equations (2) and (3)):

$$q_2\left(p\right)=p,$$

(2)

$$y_2=x_2-p-S_2.$$

(3)

Moving one stage backwards, the dominant firm minimizes its own costs anticipating the reaction of the follower and taking into consideration the permit market-clearing condition, which is given by (Equation (4))

$$y_1=x_1-q_1-S_1=-x_2+q_2\left(p\right)+S_2=-y_2.$$

(4)

The optimal abatement of the dominant firm turns is given by (Equation (5), see the Appendix A, subsection entitled “Leader’s Solution in the Permit Market”, for details)

$$q_1=\frac{\left(2x_1+x_2\right)-\left(1+\alpha \right)S}{3}.$$

(5)

Combining (2)–(5) we obtained firm 2’s optimal abatement and demand for permits as a function of output and the initial allocation of permits (Equation (6)):

$$q_2=\frac{\left(2x_2+x_1\right)-\left(2-\alpha \right)S}{3},$$

(6)

$$y_2=-y_1=q_2-q_1=\frac{\left(2\alpha -1\right)S-\left(x_1-x_2\right)}{3}=\frac{\left(S_1-S_2\right)-\left(x_1-x_2\right)}{3}=\frac{\left(x_2-S_2\right)-\left(x_1-S_1\right)}{3}.$$

(7)

According to Equation (7), the dominant firm turns out to be a net permit buyer (y₁ > 0) in those cases in which it abates more than the follower. In equilibrium, the dominant firm will pay a price for permits that is below its marginal cost of abatement. To see this, we combined Equations (2) and (7) to get (Equation (8)):

$$p=\underset{MA{C}_2}{\underbrace{q_2}}<\underset{MA{C}_1}{\underbrace{q_1}}.$$

(8)

In the same way, when the dominant firm is a net permit seller, it sets a price larger than its marginal abatement cost. In both cases, firm 1 can use its dominant position to reduce its cost and increase its profit. This conclusion simply restates the classical result by [5].

We can determine which of these two scenarios will arise in equilibrium by again inspecting Equation (7). In fact, the permit market equilibrium is driven by two main forces: the product market equilibrium (specifically, the difference in firms’ output), and the initial permit allocation. Equation (7) reveals that the firm with a larger excess of gross emissions over its initial allocation, $\left(x_i-S_i\right)$, is the one that will abate more and behave as a permit buyer in equilibrium. In a particular case where both firms have the same initial allocation, the net permit demand is proportional to the output difference, meaning that the firm that produces more (less) product will be a net permit buyer (seller). If, apart from receiving the same number of permits, both firms produced the same output, in equilibrium both firms would abate the same number of emissions and there would not be any trade of permits. In the next section, we show that this is the case under Cournot competition.

The following sections focus on the output market and how it is influenced by the initial allocation.

4. Cournot Competition in the Output Market

Assume, first, that both firms choose their output simultaneously, maximizing their individual profit a la Cournot. When doing so, they anticipate the consequences of their actions on the permit market. The profit maximization problem of firm 2 (the one that acts as a price taker in the permit market) is (Equation (9)):

$$\begin{array}{c}\underset{\left\{x_2\right\}}{Max}\left[1-\left(x_1+x_2\right)\right]x_2-\frac{q_2^2}{2}-p·\left(x_2-q_2-S_2\right).\\ s.t. Eqs. \left(2\right) and \left(6\right)\end{array}$$

(9)

and, from the first order condition, we derived the reaction function of firm 2, which is given by (Equation (10))

$$x_2=\frac{9+\left(8-7\alpha \right)S-10x_1}{26}.$$

(10)

Similarly, we derived the reaction curve of the dominant firm (Equation (11), where, here, “dominant” refers only to the permit market):

$$x_1=\frac{3+\left(1+\alpha \right)S-4x_2}{8}.$$

(11)

Solving the system given by Equations (10) and (11), we obtained the optimal output of both firms (Equations (12) and (13)):

$$x_1=\frac{7+\left(9\alpha -1\right)S}{28},$$

(12)

$$x_2=\frac{7+\left(9-11\alpha \right)S}{28}.$$

(13)

Since the reaction functions of both firms are different, their output is not necessarily equal in equilibrium, as would happen in a standard Cournot model with symmetric firms. This is due to the different role that the firms play in the permit market. To have a more accurate understanding of the difference between both firms’ output, we combined (12) and (13) to get (Equation (14))

$$x_1-x_2=\frac{5\left(2\alpha -1\right)S}{14}=\frac{5\left(S_1-S_2\right)}{14}.$$

(14)

Plugging Equations (12) and (13) into (5) and (6) and rearranging, we obtained the equilibrium abatement (Equations (15) and (16)):

$$q_1=\frac{1-\left(1+\alpha \right)S}{4},$$

(15)

$$q_2=\frac{7+\left(5\alpha -13\right)S}{28}$$

(16)

and combining both expressions, we derived the difference between the values of both firms’, which in turn, according to (7), also provides the number of permits traded in equilibrium (Equation (17)):

$$y_1=q_1-q_2=\frac{3\left(1-2\alpha \right)S}{14}=\frac{3\left(S_2-S_1\right)}{14}.$$

(17)

It turns out that, if both firms have the same initial allocation (i.e., $S_1=S_2$, or $\alpha =0.5$), the dominant position of firm 1 in the emissions permits market does not result in any advantage in effective terms. In fact, according to Equation (14), in this scenario both firms would produce the same amount of output $\left(x_1=x_2\right)$ and, according to (17), both firms would also abate the same amount. Consequently, no permits would be traded and both firms would also make the same profit (see Proposition 1 below).

Thus, the dominant position of firm 1 plays a relevant role only when the permit allocation is not symmetric. Since the initial allocation can be seen as an environmental policy instrument, it is a useful comparative statics exercise to check the sensitivity of each firm to its own permit allocation. From Equations (12) and (13) we concluded that firm 2′s output is more sensitive than firm 1′s. Formally (Equation (18)),

$$\frac{\partial x_2}{\partial \left(1-\alpha \right)}=-\frac{\partial x_2}{\partial \alpha }=\frac{11\alpha }{28}>\frac{9\alpha }{28}=\frac{\partial x_1}{\partial \alpha }.$$

(18)

On the other hand, the dominant firm’s abatement is more sensitive to its permit allocation than its competitor’s. Formally (Equation (19)),

$$\frac{\partial q_1}{\partial \alpha }=\frac{-S}{4}<-\frac{5S}{28}=\frac{\partial q_2}{\partial \left(1-\alpha \right)}.$$

(19)

Summing up, the firms use different strategies due to the different role they play in the permit market. When endowed with more permits, both firms would react by increasing output and decreasing abatement, but the dominant firm would decrease abatement more and increase output less than the price-taking one does in the same circumstances. The reason lies in the strategic behavior of the dominant firm, as it can buy permits at a price below its marginal abatement cost.

This feature has a straightforward implication on total output, given by (Equation (20))

$$X=\frac{7+\left(4-\alpha \right)S}{14},$$

(20)

which is decreasing in $\alpha$, i.e., the more permits are initially allocated to the dominant firm (given a fixed overall number of permits), the less output is produced in equilibrium.

The equilibrium price of permits is given by (Equation (21))

$$p=\frac{7+\left(5\alpha -13\right)S}{28},$$

(21)

which is increasing in $\alpha$ because, the more permits are allocated to the dominant firm, the more it will exert its market power to increase the price.

The following proposition summarizes the main results regarding firms’ behavior in the Cournot case.

Proposition 1.

Equilibrium in the Cournot case.

(a) 

The dominant firm’s output (abatement) is less (more) sensitive than the permit price-taking firm to its own permit allocation.

(b) 

If the initial permit allocation is higher for firm i (i = 1, 2) than firm j ($j\ne i$), in equilibrium firm i produces more output and, thus more emissions, and abates less than firm j. In this case, firm i (j) becomes a seller (buyer, respectively) of permits.

(c) 

Total output is decreasing, and the permit price is increasing in firm 1′s initial allocation.

(d) 

The firm with a larger initial allocation makes more profit in equilibrium.

Statement (b) to (d) in Proposition 1 highlight the role of the initial allocation. According to (b), this allocation fully determines which firm produces more, which one abates more, and which one is a net buyer or seller or permits. Permits can be seen as an asset, which firms decide how to manage. Assume that, starting from a symmetric situation, a firm is endowed with some additional permits. Such a firm has several options: (i) selling the additional permits to earn some revenue, (ii) producing more output and, thus, emitting more (keeping abatement unchanged), and (iii) keeping output (and thus, gross emissions) unchanged, while decreasing abatement in order to save on abatement cost. Statement (b) implies that, in practice, the firm will choose a combination of these three actions: it will produce more, but not as much as the number of additional permits. Some of those additional permits (but not all of them) will be sold and some will be retained to save some abatement costs.

Statement (d) implies that, if the dominant firm is endowed with fewer permits than the competitive one, its advantage due to the market power position is not enough to compensate for the disadvantage associated to the initial allocation, although such a dominant position will serve to strengthen its advantage (when endowed with more permits) or weaken its disadvantage (when endowed with fewer permits).

It is illustrative to compare this case with the one without market power in the permit market (so the permit market is competitive) and the firms still compete a la Cournot in the first stage. In such a case, total output is given by

$$X=\frac{2+S}{4}.$$

Direct comparison with (20) shows that, whenever $\alpha <0.5 \left(>0.5\right)$, total output is larger (smaller) if there is a dominant firm than if there is not. When $\alpha =0.5$ output is the same in both cases, because the dominant firm cannot exert its market power and the result is the same as if the permit market were competitive. Moreover, as expected, the price of permits with a dominant firm is higher than without a dominant firm if and only if the dominant firm receives more permits than the price-taking one ($\alpha >0.5$).11

The results of the Cournot version of our model are in line with the ones by [14] in the sense that a follower in the permit market may adopt a rival´s cost raising strategy if it is exerting some degree of market power in the output market. But, as discussed above,8 the different timing of the game leads to somewhat different results. Specifically, in [14], the firm that dominates the permit market can buy permits at a price above their marginal abatement cost, while this result can never happen in our case (see Equation (8)).

5. A Firm Leading Both Markets (“Stackelberg 1”)

Assume now that firm 1, apart from having a dominant position in the permit market, is also a Stackelberg leader in the output market. We solved the output model by standard methods: the leader chooses its output considering the reaction function of firm 2, which is given by Equation (10). Solving the leader’s problem and substituting into the follower’s reaction function, we obtained the equilibrium output of both firms (Equations (22) and (23)):

$$x_1=\frac{167+\left(159\alpha +4\right)S}{538},$$

(22)

$$x_2=\frac{61+\left(82-103\alpha \right)S}{269}.$$

(23)

Comparing the expressions for the individual outputs, we concluded that, as happens in the Cournot model, the dominant firm’s output is less sensitive and its abatement is more sensitive to its own allocation than its competitor’s (Equations (24) and (25)):

$$\frac{\partial x_1}{\partial \alpha }=\frac{159S}{538}<\frac{103S}{269}=-\frac{\partial x_2}{\partial \alpha }=\frac{\partial x_2}{\partial \left(1-\alpha \right)}.$$

(24)

$$\frac{\partial q_1}{\partial \alpha }=-\frac{71S}{269}<-\frac{95S}{538}=\frac{\partial q_2}{\partial \left(1-\alpha \right)}.$$

(25)

From (22) and (23), we concluded that the dominant firm tends to produce more output than the follower, as is the case in a standard Stackelberg model. This result is reinforced by the fact that it enjoys a double leadership position in the permit and the output market. It is straightforward to show that $x_1>x_2$ holds when both firms have the same initial allocation ($\alpha =0.5$), but the following proposition shows that it can hold even with very low values of $\alpha$, i.e., with very asymmetric distributions in favor of the follower. If the total number of permits is small enough, this result holds even for the extreme case $\alpha =0$.

Proposition 2.

Output equilibrium in the Stackelberg-1 case.

(a) 

If$S\ge \frac{9}{32}$, there exists a threshold${\overline{\alpha }}^{S1}<0.5$, such that the dominant firm produces more output than the price-taking firm if and only if$\alpha >{\overline{\alpha }}^{S1}$.

(b) 

If$S<\frac{9}{32}$, the dominant firm produces more output than the price-taking firm for any allocation of permits$\alpha \in \left[0,1\right]$.

Proposition 2 states that the only way to counterbalance the strong leadership position of the dominant firm is to allocate more permits to its competitor. Nevertheless, if the total number of permits is too small, it is not possible to generate a large enough counterbalancing effect by reallocating them. Proposition 3 shows a related result for firms’ profits:

Proposition 3.

Profit in the Stackelberg-1 model.

(a) 

If$S\ge \raisebox{1ex}{$19$}\!\left/ \!\raisebox{-1ex}{$321$}\right.$, there exists a threshold${\tilde{\alpha }}^{S1}<0.5$such that the profit of the dominant firm is larger than that of the price-taking firm if and only if$\alpha >{\tilde{\alpha }}^{S1}$.

(b) 

If$S<\raisebox{1ex}{$19$}\!\left/ \!\raisebox{-1ex}{$321$}\right.$, the profit of the dominant firm is larger than that of the price-taking firm for any value of$\alpha \in \left[0,1\right]$.

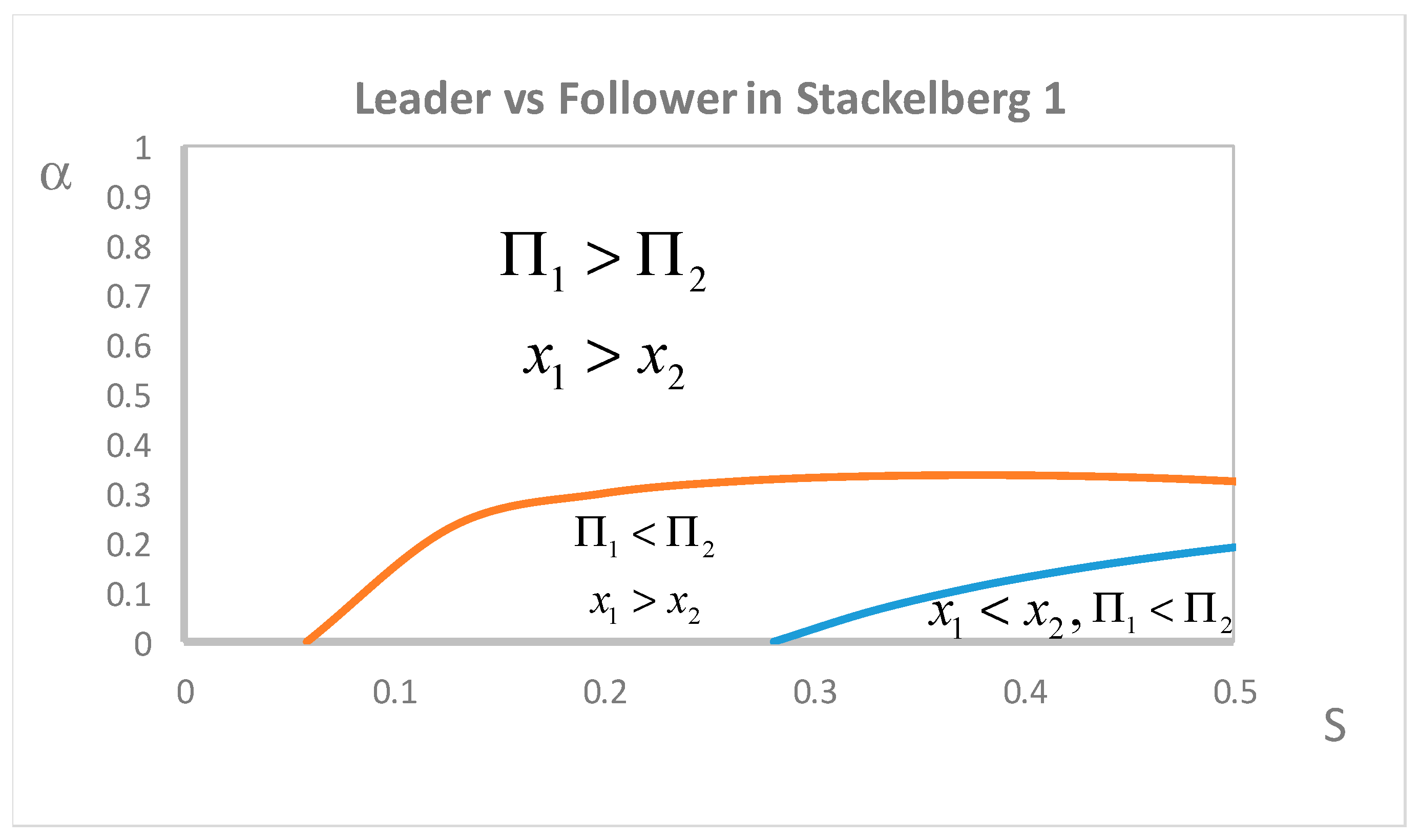
Proposition 3 states that, apart from producing more output, the dominant firm also tends to make a larger profit, as expected. This is always the case for a symmetric distribution of permits ($\alpha =0.5$), but it could also be true for very asymmetric permit allocations, even for $\alpha =0$ if the total number of permits is small enough. Because of Propositions 2 and 3, the relevant $S-\alpha$ space was divided in three regions, as illustrated in Figure 1.

Figure 1 confirms that the dominant firm tends to produce more and make more profit than its competitor, except if a large enough number of permits is allocated to the price-taking firm. There is an intermediate range where the dominant firm produces more but makes less profit, which means that it is easier for the price-taking firm to leapfrog the dominant one in terms of profit than in terms of output. In this intermediate range, the price-taking firm can take advantage of its larger permit allocation to reduce abatement costs and make some revenue by selling permits. This allows it to make more profit, but not to overcome the Stackelberg leadership position in terms of output.

Total output and the price of permits are given, respectively, by (Equations (26) and (27))

$$X=\frac{289+\left(168-47\alpha \right)S}{538},$$

(26)

$$p=\frac{137+\left(95\alpha -248\right)S}{538}.$$

(27)

Expressions (26) and (27) reveal that, as happens in the Cournot model, total output increases and the permit price decreases in the dominant firm’s initial permit share, $\alpha$.

It is also of interest to consider the implications of the double leadership position (output and permits) as compared to the more traditional Stackelberg model, only with output leadership (without market power in the permit market). It can be shown that if the permits are allocated evenly ($\alpha =0.5$), then total equilibrium output is lower if there is a firm that dominates both markets as compared to the situation with output leadership and a competitive permit market. The reason is that the possibility to dominate the permit market increases the capacity of the dominant firm to manipulate the market to its own profit. Moreover, as we show in the following proposition, if the total number of permits is small enough, then the result holds for any permit allocation:

Proposition 4.

Output with double leadership vs. single leadership.

Consider that there a Stackelberg leader in the output market and consider two alternative scenarios: one in which the output leader also dominates the permit market and another one in which the permit market is competitive. Then,

(a) 

If$S\ge \raisebox{1ex}{$85$}\!\left/ \!\raisebox{-1ex}{$1438$}\right.$, there exists a threshold${\widehat{\alpha }}^{S1}<0.5$such that total output is smaller with than without market power in the permit market if and only if$\alpha >{\widehat{\alpha }}^{S1}$.

(b) 

If$S<\raisebox{1ex}{$85$}\!\left/ \!\raisebox{-1ex}{$1438$}\right.$, total output is smaller with than without market power in the permit market, for any value of$\alpha \in \left[0,1\right]$.

The results in this case resemble the ones in [7], as in the latter there is also a firm that dominates both markets. Our results are similar regarding the impact of the initial allocation and the lack of efficiency due to strategic behavior of firms. The difference is that, in our case, the dominant firm makes a profit when buying permits and in [7] the dominant firm sets the permit price above its own marginal cost of abatement when its initial allocation is above a certain threshold. This difference is due to the timing of the game because [7] solves both markets simultaneously in a one-stage model, whereas we adopted a sequential approach, which is based on the idea that the output maker somewhat precedes the permit market.

6. A Stackelberg Model with Reversed Leadership

We then analyzed a different situation where one firm dominates the permit market and the other one leads the output market. For the sake consistency, we assumed that firm 2 is the one that leads the product market (and acts as a price taker in the permit market) while firm 1 behaves as a follower in the output market but dominates the permit market.

The permit game had already been solved in Section 3. By using standard methods, we solved the output game and obtained the following equilibrium values (Equations (28)–(30)):

$$x_1=\frac{3+\left(5\alpha -1\right)S}{14},$$

(28)

$$x_2=\frac{9+\left(11-13\alpha \right)S}{28},$$

(29)

$$X=\frac{15+\left(9-3\alpha \right)S}{28}$$

(30)

and the equilibrium permit price was given by (Equation (31))

$$p=\frac{2+\left(\alpha -3\right)S}{7}.$$

(31)

From Equations (28) and (29), we noticed that, again, firms 1′s output is less sensitive to its allocation than firm 2′s, and using (28) and (29) in (5) and (6) we concluded that firm 1′s abatement is more sensitive than firm 2′s (Equations (32) and (33)):

$$\frac{\partial x_1}{\partial \alpha }=\frac{5S}{14}<\frac{13S}{28}=\frac{\partial x_2}{\partial \left(1-\alpha \right)},$$

(32)

$$\frac{\partial q_1}{\partial \alpha }=-\frac{S}{4}<-\frac{S}{7}=\frac{\partial q_2}{\partial \left(1-\alpha \right)}.$$

(33)

Thus, wrapping up from all three models, we concluded that, whatever the leadership position in the output market, the dominant firm in the permit market reacts to a change in its permit allocation by modifying its abatement more and its output less than its competitor. It is also common to the three models that output decreases and the permit price increases in the initial share of the permit dominant firm, $\alpha$.

Direct inspection of (28) and (29) shows that if the permits are allocated evenly ($\alpha =0.5$), the output leader produces more output than the permit dominant firm. This means that the permit dominant position cannot reverse, per se, the usual result that the Stackelberg output leader produces more output than the follower. Moreover, as is shown in the following proposition, if the total number of permits is not very large, then the output leader will always produce more than firm 1 for any permit allocation:

Proposition 5.

Output in Stackelberg-2 model.

Consider that firm 1 has a dominant position in the permit market and firm 2 is a leader in the output. Then,

(a) 

If$S\le \frac{3}{10}$, in equilibrium the output leader produces more output than the permit dominant firm for any permit allocation$\alpha \in \left[0,1\right]$.

(b) 

If$S>\frac{3}{10}$there exists a threshold,${\overline{\alpha }}^{S2}>0.5$, such that the output leader produces more output than the permit dominant firm if and only if$\alpha <{\overline{\alpha }}^{S2}$.

Proposition 6 shows a related result about profits.

Proposition 6.

Firms’ profit in Stackelberg 2 model.

There is a threshold,$\tilde{S}\simeq \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$16$}\right.$such that

(a) 

If$S\ge \tilde{S}$, there is a threshold${\tilde{\alpha }}^{S2}<0.6$such that the profit of the output leader is larger than its competitor’s if and only if$\alpha <{\tilde{\alpha }}^{S2}$.

(b) 

If$S<\tilde{S}$, then the profit of the output leader is larger than its competitor’s for any admissible value of$\alpha$.

Summing up, under a symmetric allocation of permits, the output and profit of the output leader are larger than those of the permit dominant firm. The permit dominance is not enough to overcome the output leadership unless the permit dominant firm is endowed with a larger enough number of permits than the output leader. In that context, the leadership position in the output market seems more relevant than the dominant position in the permit market. As shown in Figure 2, there is a range of permit allocations such that the permit dominant firm can use its advantage in the permit market to make more profits than the output leader, although it still produces less output.

Equations (30) and (31) show that, as in the two previous models, output is decreasing, and the permit price is increasing in the share of permits initially allocated to the permit dominant firm.

7. Comparison across Models and Welfare Analysis

In this section, we care about the overall results of all three models in terms of output and welfare. We first care about output in the following proposition.

Proposition 7.

Output comparison across models.

(a) 

In the Stackelberg 1 and the Stackelberg 2 models, total output in equilibrium is higher than in the Cournot model for any allocation of permits$\alpha \in \left[0,1\right]$.

(b) 

If$S<\raisebox{1ex}{$11$}\!\left/ \!\raisebox{-1ex}{$69$}\right.$, total equilibrium output is higher in the Stackelberg 1 model than in the Stackelberg 2 model for any value of$\alpha \in \left[0,1\right]$.

(c) 

If$S\ge \raisebox{1ex}{$11$}\!\left/ \!\raisebox{-1ex}{$69$}\right.$, there exists a threshold${\overline{\alpha }}^{S12}<0.5$such that the total output in equilibrium is higher in the Stackelberg 1 model than in the Stackelberg 2 model if and only if$\alpha >{\overline{\alpha }}^{S12}$.

Statement (a) in Proposition 7 restates the classical result that output in a Stackelberg model is higher than in a Cournot model and it is interesting to note this is true for any distribution of the permits. Moreover, this is a feature of both versions of the Stackelberg model; thus, this result is not affected by the way in which the market power (in output and permits) is distributed between the firms.

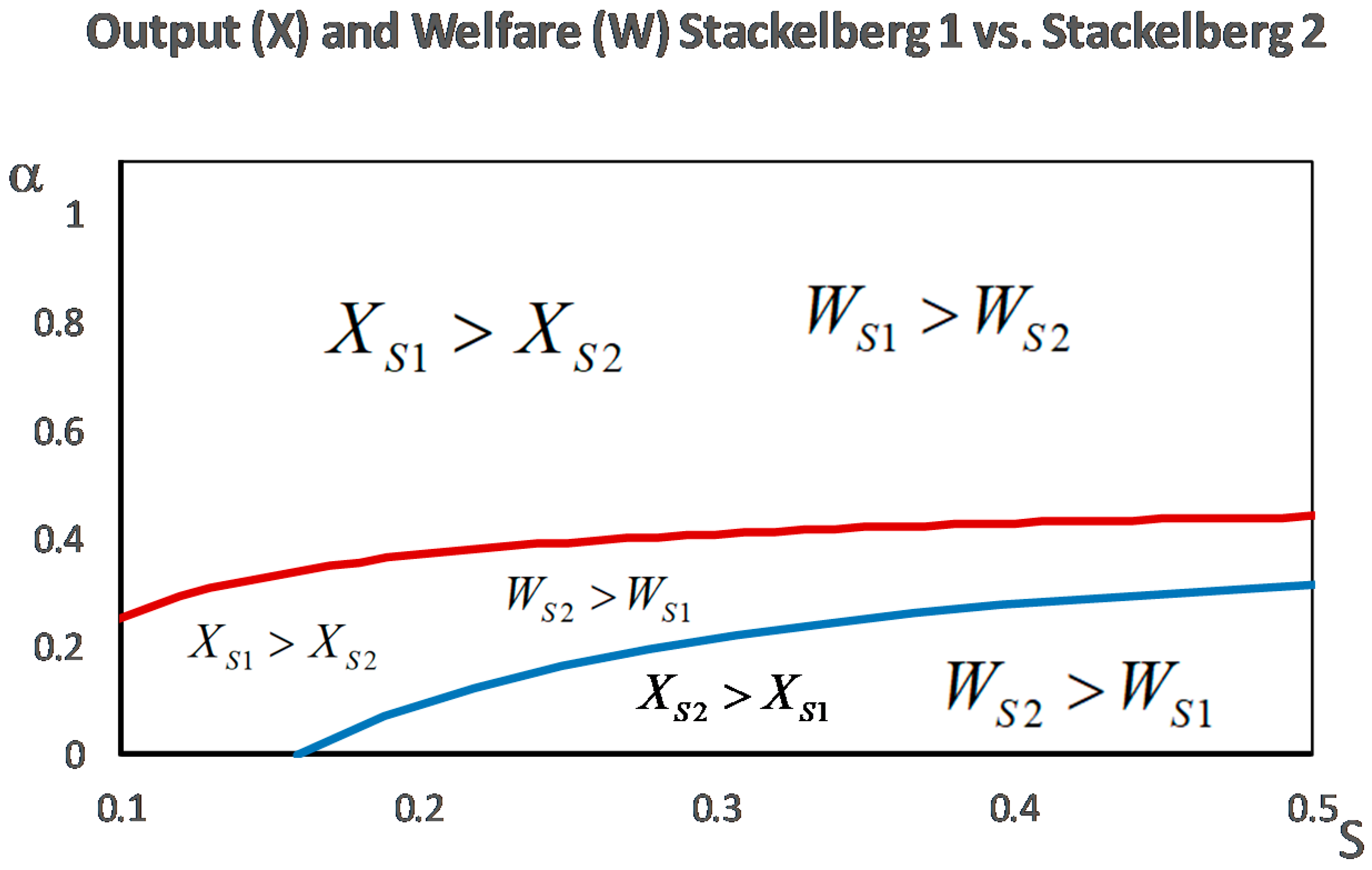
Statements (b) and (c) are illustrated in Figure 3 in combination with the results about welfare (which are proved below). The main conclusion is that output tends to be larger in the Stackelberg 1 model than in the Stackelberg 2 model. To understand the intuition behind this result, it is useful to recall the relationship between the classical Cournot and Stackelberg models. In Stackelberg, the leader uses its advantageous position to produce more output and make more profit, which ultimately increases total output in the market. In our Stackelberg 1 model, this mechanism is reinforced by the double leadership position of a single firm. In Stackelberg 2, the position of the output leader (firm 2) is somewhat undermined by the permit power of firm 1. The output leadership tends to prevail over the permit leadership, except if the number of permits is large enough and a large enough share of them are allocated to the permit leader.

Now, we focus on about the welfare comparison across scenarios. We measured welfare by adding up consumers’ surplus and the profit of both firms. The third component that should be included in social welfare is (minus) the social damage caused by pollution. Nevertheless, since total net emissions are fixed by construction (and equal to $S$) in all three models, the associated damage would also be constant across models and we could focus just on the two first components (consumers’ surplus and firms’ profit).

Proposition 8.

Welfare comparison across models.

(a) 

In the Stackelberg 1 and the Stackelberg 2 models, total social welfare in equilibrium is higher than in the Cournot model for any allocation of permits$\alpha \in \left[0,1\right]$.

(b) 

Considering interior solutions for both models, there is a threshold${\tilde{\alpha }}_W^{S12}<0.5$such that the total welfare in equilibrium is higher in the Stackelberg 1 model than in the Stackelberg 2 model if and only if$\alpha >{\tilde{\alpha }}_W^{S12}$.

According to Proposition 8, total welfare in any of the Stackelberg scenarios turns out to be larger than in the Cournot model for any permit distribution, mainly because the output is larger. The comparison between the two Stackelberg versions is illustrated in Figure 3. When output is higher in one of the models (Stackelberg 1 if $\alpha$ is large enough and Stackelberg 2 if $\alpha$ is small enough), aggregate welfare also tends to be higher in the same model. Nevertheless, there is a range of permit allocations such that welfare is higher in Stackelberg 2, although output is higher in Stackelberg 1. The reason is that, in those cases, the dominant position in the permit market helps to counterbalance the output leadership in such a way that abatement effort (and thus, abatement cost) is distributed more evenly between firms, which results in lower total cost and, thus, a higher overall profit of the firms (which, in this case, more than compensates the lower consumers’ surplus due to lower production).

Our last research question refers to the (socially) optimal allocation of permits, or in other words, the optimal value of $\alpha$ in each of the scenarios. This question is answered in Proposition 9.

Proposition 9.

Optimal allocation of permits.

The initial allocation of permits that maximizes welfare in the Cournot (C), the Stackelberg 1 (S1) and the Stackelberg 2 (S2) models are given, respectively, by (Equation (34))

$$\begin{array}{l}{\alpha }_C^{*}=\{\begin{array}{ccc}0& & if S\le \raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$16$}\right.\simeq 0.44\\ \frac{16S-7}{39S}& & otherwise\end{array}\\ {\alpha }_{S1}^{*}=\{\begin{array}{ccc}0& & if S\le \raisebox{1ex}{$1567$}\!\left/ \!\raisebox{-1ex}{$7066$}\right.\simeq 0.22\\ \frac{7066S-1567}{15699S}& & otherwise\end{array}\\ {\alpha }_{S2}^{*}=\begin{array}{ccc}0& & for any acceptable S\end{array}\end{array}$$

(34)

By direct inspection of the values shown in Proposition 9, we obtained the following conclusions. First, in any market scenario, the permit share of the dominant firm that maximizes welfare is always smaller than 0.5. This means that, for the sake of social welfare, a firm that dominates the permit market should not be allocated a large proportion of the permits. The rationale behind this result is to prevent such a firm from using its dominant position to inefficiently increase the permit price.

Second, if the total number of permits is small enough, it is socially optimal to allocate all of them to the one that acts competitively in the permit market. Third, the distribution of permits that maximizes welfare is ranked as follows across scenarios: ${\alpha }_{S2}^{*}\le {\alpha }_C^{*}\le {\alpha }_{S1}^{*}$.

To understand these results, note that, by construction, total welfare can be split in three summands: first, consumers’ surplus, second, firms revenue, i.e., $P·X$, and third, (minus) total abatement costs of both firms. For convenience, we labeled the sum of the two first components as “output surplus”. As shown above, in all three models, output is decreasing in $\alpha$ and so is output surplus. If we cared only about this part of welfare, the optimal value of $\alpha$ would be zero. On the other hand, since (individual) abatement costs are quadratic, minimizing the sum of them requires a certain balance in the distribution of abatement across firms. This is illustrated in Figure 4 for the Stackelberg 1 model (with $S=0.5$).

The right panel shows that output surplus (the light blue line) is always decreasing in $\alpha$ and thus it is maximized at $\alpha =0$. Nevertheless, total abatement cost (the orange line) is U-shaped as it is illustrated in the left panel. If $\alpha =0$ abatement would be very asymmetric and, thus, total abatement cost would be too high. As a result, total welfare is inverted U-shaped and achieves a maximum at an interior value of $\alpha$. In Cournot and Stackelberg 1 models the latter effect shows up if $S$ is large enough and, otherwise, the optimal allocation involves $\alpha =0$. In Stackelberg 2 model, the second effect never shows up for admissible values of $S$ and, thus, it is always optimal to allocate all the permits to the firm that acts competitively in the permit market (which, in this case, is also the output leader).

8. Concluding Remarks, Policy Implications, and Future Research

This article has analyzed the impact of a given emission permit allocation on the equilibrium outcomes in terms of output, profit, and social welfare in the presence of market power under different makers structures in a duopoly.

Some of our results qualitatively hold across our three scenarios. Specifically, we conclude that, in all three scenarios, when endowed with some additional permits, the permit dominant firm tends to increase output less and reduce abatement more than the price-taking firm in the same situation, whatever their respective roles in the output market. It is also true across scenarios that total output is decreasing and the permit price is increasing in the share of permits allocated to the firm that dominates the permit market.

If both firms have a symmetric role in the output market (i.e., the Cournot model) and enjoy the same initial permit allocation, they produce the same amount of output, make the same profit, and no permits are traded in equilibrium. Thus, the dominant position in the permit market does not lead to any practical advantage. Under asymmetric allocations, the firm initially endowed with more permits produces more output and makes more profit.

When there is a single leader in both markets, it tends to produce more and make more profit than its rival, although each one of these implications (or both) can be reversed if the total number of permits is large enough and a large enough share of them is allocated to the following firm.

When each market is dominated (or led) by a different firm, we conclude that the output leadership tends to be more relevant as the output leader produces more and makes more profits than the permit dominant firm. This is true under a symmetric permit allocation but, if we consider that the firm that dominates the permit market is endowed with more permits, then the output of both firms tends to equalize first and it comes to a point where the firm that dominates the permit market may produce more and make more profit than the output leader.

Any of the two Stackelberg models results in more output and social welfare than Cournot. The case in which firm 1 leads both markets simultaneously tends to generate more output and more welfare than the case with two different leaders except if enough permits are allocated to the permit dominant firm.

From a policy design point of view, we conclude that, whenever a firm dominates the permit market, it is desirable to prevent it from being allocated too many permits, as this would be detrimental for welfare. Paradoxically, this conclusion is particularly strong when the firm that dominates the permit market is a follower in the output market and somewhat softer when a single firm dominates both markets simultaneously.

This paper attempts to provide a first exploratory approach for studying the different implications of output market structures in combination with imperfect permit markets. In order to keep the analysis manageable, we have included some simplifying assumptions that could be relaxed in future work. One first obvious extension would be to check more general functional forms, although this would come at the cost of a larger calculation burden and probably less clear-cut results. Additional extensions would involve considering other market structures such as price rather than output competition and considering heterogenous products.

Finally, in order to focus our attention on the output and the permit secondary market, we have taken the initial allocation as given. This approach is consistent with simple and direct assignment mechanisms such as grandfathering and benchmarking. Since auctioning is becoming more relevant as a way to distribute the permits (for recent developments see [20,21,22]), a relevant (although technically complex) extension would be to endogenize the initial allocation by considering auctioning mechanisms.