Abstract
Epilepsy patients who do not have their seizures controlled with medication or surgery live in constant fear. The psychological burden of uncertainty surrounding the occurrence of random seizures is one of the most stressful and debilitating aspects of the disease. Despite the research progress in this field, there is a need for a non-invasive prediction system that helps disrupt the seizure epileptiform. Electroencephalogram (EEG) signals are non-stationary, nonlinear and vary with each patient and every recording. Full use of the non-invasive electrode channels is impractical for real-time use. We propose two frontal-temporal electrode channels based on ensemble empirical mode decomposition (EEMD) and Relief methods to address these challenges. The EEMD decomposes the segmented data frame in the ictal state into its intrinsic mode functions, and then we apply Relief to select the most relevant oscillatory components. A deep neural network (DNN) model learns these features to perform seizure prediction and early detection of patient-specific EEG recordings. The model yields an average sensitivity and specificity of 86.7% and 89.5%, respectively. The two-channel model shows the ability to capture patterns from brain locations for non-fontal-temporal seizures.
1. Introduction
Epilepsy is a severe neurologic condition with a high incidence and prevalence worldwide, affecting more than 50 million people. The disability, and the adjusted life imposed on patients, ranks the disease as the second-most burdensome neurologic disorder [1,2,3,4]. An epileptic seizure is a sudden rush of abnormal neural activity in the cortex of the brain. The economic cost and unpredictable recurrent nature make the condition difficult to bear for patients and hinders the design of treatments by physicians. Seizure symptoms challenge the patient to face independent life, stigma and social misunderstandings [5,6].
The electroencephalogram (EEG) is widely recognized for assessing brain activities and remains effective for epilepsy research due to its excellent temporal resolution [7,8]. For epilepsy seizure detection, scalp EEGs (sEEGs) and intracranial EEGs (iEEGs) are used to measure the ictal changes that lead to a biomarker for the presence of a seizure. The iEEG reading has a higher specificity, but a limited sampling coverage of the cerebral cortex compared with sEEG readings [9]. More than 40 years have been devoted to predicting epileptic seizures, with the challenge of forecasting seizures before they happen [10]. Most methods look for patterns in the pre-ictal transition and contrast them with the interictal signal for high sensibility [11,12]. For a real-time application, the detection and prediction model must run in an embedded device with limited computation resources and then be able to run state-of-the-art algorithms [13].
Noninvasive methods have emerged as a demanding alternative in medicine to monitor health and treatment [14,15,16,17,18]. The majority of the advancements in noninvasive seizure prediction and detection use the full scalp EEG electrode channels in their research [3,12,15,16,17,19]. It is impractical for epilepsy patients to wear the complete electrode channels EEG cap in a real-time application. The International League Against Epilepsy (ILAE) in 2017 classified seizures based on the seizure onset area, consciousness level during a convulsion and other characteristics of seizures. Temporal lobe seizures and frontal lobe seizures are the most common types of focal impaired awareness seizure, occurring in up to 80% of patients [20].
The main objective of this paper is to implement a two frontal-temporal channel seizure prediction method based on ensemble empirical mode decomposition (EEMD)-Relief and deep neural networks (DNNs). Figure 1 shows the proposed model. The EEMD-Relief combination extracts features from a segmented data frame in the ictal and preictal times and retains the most informative components. The model runs on 23 patient-specific epileptic data. A deep neural network is trained to predict the seizure 23 min before it happens, with early detection of 3.9 s in the ictal period.
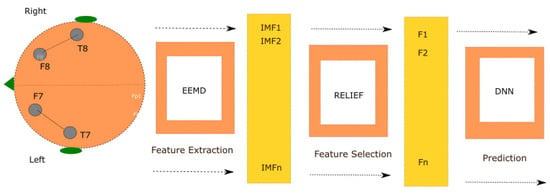
Figure 1.
The proposed patient-specific two temporal-frontal channels with ensemble empirical mode decomposition (EEMD)-Relief.
2. Literature Review
Researchers have developed all kinds of methods that attempt to detect a biological signal pattern using an EEG. From signal processing to classification, state-of-the-art algorithms have been implemented with different levels of success [21]. Several theoretical investigations examine the pre-ictal state to find a signature that helps anticipate and predict an epileptiform seizure [22,23,24,25,26]. The authors in [27] presented a pseudo-prospective seizure prediction. A deep learning classifier was trained to distinguish between pre-ictal and interictal signals. The model was deployed in a neuromorphic chip. However, the study only implemented a real-time testing model on a device for one subject. The mean sensitivity of the system was 69%. They also benchmarked the system against three recent studies. Senger et al. [26] addressed the seizure prediction problem by using an algorithm based on cellular neural networks (CNNs). They used principal components analysis (PCA) to feed a nonlinear CNN for the first method in the preprocessing stage, followed by level-crossing behavioral analysis. For future work, they propose to limit the number of channels for a seizure-warning device.
Daoud et al. [28] proposed four deep learning prediction models with limited preprocessing. The raw data were direct inputs to the multilayer perception (MLP) to classify between pre-ictal and interictal states. The model integrated four layers and backpropagation for optimization. Data from eight subjects were used to evaluate the patient-specific model. In the second model, the authors implemented deep convolutional neural network (DCNN) architecture. This model was designed for front-end feature extraction, reporting a drastic reduction in the number of trainable parameters. The authors implemented a channel selection algorithm to decrease the number of channels, the dimensionality of variables and the demand for memory. Thus, the model is a candidate for real-time application. In addition, the algorithm selects the channels with the highest variance entropy.
The authors in [29] developed a hybrid neural network prediction model by combining ensemble empirical mode decomposition (EEMD) and a stochastic recurrent wavelet neural network, applied to a nonlinear time series energy indexes price. The EEMD extracted feature frequencies from four energy indexes. The proposed wavelet neural network model was implemented by adding stochastic functions to add different timely weight to the historical data, and then recurrent layers were used to improve the learning process. The proposed method exhibits good performance forecasting of the time-series energy price. Zhou et al. [30] proposed a methodological approach to study hippocampal rhythmicity using different spectral decomposition methods. The study compared the spectral features of the wavelet, Fourier transform and EEMD to characterize hippocampal oscillations. The results showed that the wavelet and the EEMD failed to represent the local field potential oscillations accurately in the hippocampal under similar parameters. Additional research with more decomposition methods in a broader brain lobes region is needed for the authors to accomplish their primary objectives.
Kanagaraj et al. [31] extracted features from images of patients with lung cancer using gray level co-occurrence (GLMC). Four image texture features were extracted and calculated from GLMC: energy, contrast, homogeneity and correlation. The contrast feature was reported to be the best suited for differentiating between textures in the lung tissue’s spatial distribution. In the preprocessing, they first conducted image denoising of the original computer tomography images, and secondly, a segmentation process of the lung’s tumor area was implemented. An artificial neural network is used for classifying normal and tumor tissues with an accuracy of 85.5%. The authors in [32] implemented an artificial neural network, multilayer perception (MLP), to explain the economic and financial variables that explain construction industry productivity. The study used nine economic variables. Value-added variables and gross revenues were related to productivity. These features were the inputs to the MPL model for training and testing. The classification score was 94.8%, and the receiving operating curve (ROC) score was 98.1%. The study showed that management variables are closely related to productivity, and using the MLP only addresses the management variables and leaves out other criteria, such as human capital and innovation. A study in [33] presented a comparative method of feature selection and extraction using the original empirical mode decomposition (EMD) and the ensemble empirical mode decomposition (EEMD). The authors extracted intrinsic mode functions (IMFs) from correlation, energy, power spectral density and statistical significance measurements. The extracted features were classified using four algorithms: K-nearest Neighbors (KNN), Support Vector Machine (SVM), Logistic Regressions and Naive Bayes. They demonstrated that the selection of IMFs affects classifications, where EEMD features increase all four classifiers’ performance results.
3. Materials and Methods
3.1. Scalp Time Series Data
The EEG dataset from the Children’s Hospital Boston and the Massachusetts Institute of Technology (CHB-MIT) [34] was used to validate the proposed method. The dataset consists of EEG recordings from pediatric subjects with intractable seizures. Table 1 shows the 23 cases, collected from 22 subjects (5 males, ages 3–22 and 17 females, ages 1.5–19). The sampling rate of the recording was 256 Hz. The international 10–20 electrode positions system was used in the recordings. These were the 23 channels: C3-P3, P3-O1, FP2-F4, F4-C4, C4-P4, P4-O2, FP2-F8, F8-T8, T8-P8, P8-O2, FZ-CZ, CZ-PZ, P7-T7, T7-FT9, FT9-FT10, FT10-T8, and T8-P8. The lobe seizure location for each patient is shown in Table 2. The frontal-temporal channels F7-T7 and F8-T8 shown in Figure 2 are used in this study.

Table 1.
CHB-MIT dataset for 23 subjects.

Table 2.
Seizure location by subjects [16].
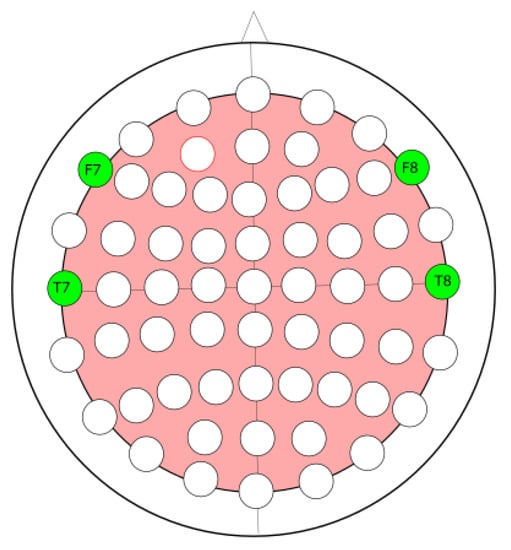
Figure 2.
Channels F7-T7 and F8-T8, used for prediction of the ictal state in all patients.
3.2. Preprocessing
The original signal had a physiological artifact (eyes blinking, muscle movement, involuntary movement) and noise from the power line and EEG equipment. A sixth-order Butterworth band-pass filter (2 Hz to 40 Hz) was applied to the time-series EEG signal to eliminate noise, power harmonics and muscle artifacts.
3.3. Ensemble Empirical Mode Decomposition
The EEMD overcomes the noise mixing effect of the empirical mode decomposition (EMD) by allowing better scale separation. The algorithm adds a different series of white noise into the signal in several iterations [35]. There was no correlation in IMFs among trials, since the added noise was different in each trial. Averaging the IMFs of different trials eliminated the added noise and preserved the signal. The EEMD has been successfully applied to biomedical signals and other noisy nonlinear and nonstationary processes [36,37,38]. The formulation of the EEMD algorithms can be explained with the following two equations [39]:
where M-1 is the total number of IMFs, is the mth IMF and is the residual in the nth trial. The final step of the EEMD involves averaging the total m IMFs related to N trials:
3.4. ReliefF
Relief is a filter-based feature selection method. Contrary to a wrapper, filters use a measurement calculated from the general characteristics of the training data to score features and elicit new feature subsets prior to modeling. Filters are much faster algorithms than wrappers and function independently of the model algorithm [40]. The basic idea of Relief in Algorithm 1 is to weigh attributes between the two nearest instances in a binary classification [5,6].
| Algorithm 1: Original Relief Algorithm |
| set all weights W[A] := 0.0; |
| for i := 1 to m do |
| begin |
| randomly select an instance Ri; |
| find nearest hit H and nearest miss M; |
| for A := 1 to all_atrribuites do |
| W[A] := W[A] − diff(A,Ri,H)/m + diff(A,Ri,M)/m; |
| end; |
| where the function diff calculates the difference of values of attributes between the two nearest instances: |
Multiple versions of Relief, from A to F, have been proposed to overcome the original algorithm problem of dealing with incomplete data sets and multiclass labels. ReliefF is the best known and most adopted Relief filter-based version. Many other improvements have been proposed in succeeding versions [40]. The ReliefF variant deals with noisy and incomplete data sets and can efficiently deal with multiclass problems. The algorithm finds one near-miss class M(C) for each instance in the data set and averages their contribution for updating attribute weights W[A]. ReliefF estimates the ability of attributes to separate each pair of classes, regardless of if they are closest to each other. Here is a ReliefF version algorithm proposed by Kononenko [41]:
3.5. Prediction and Early Detection
We implemented a seizure-specific methodology in which a model was elicited for each patient. The duration of a seizure varies from 10 s to 63 s. For early detection, shown in Figure 3a, the goal is to find a signature of information in the first 3.9 s of the seizure’s ictal stage. The vectors of the EEMD-Relief features extracted in this period were used for training the DNN. The seizure prediction scheme is shown in Figure 3b. The seizure prediction horizon (SPH) is the time between the alarm and the seizure onset, as defined in [11]. We used two SPHs of 23 min and 5 min, respectively. In each prediction horizon, we are using two windows of 3.9 s with an overlapping one of 2.9 s. IMFs were extracted in each window for the corresponding ictal and interictal states. The best IMF futures of ReliefF were given as input to the DNN for training.
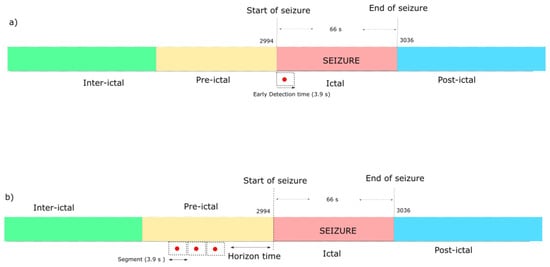
Figure 3.
Scheme for subject S01 for (a) early detection and (b) prediction.
3.6. Statistical Analysis and Validation
Statistical procedures were applied to analyze the sample size of the patient-specific data and the performance score of the prediction model. The sample per subject had a high variability because it depended on the patient’s number of seizures per trial. The minimum number of seizures in this study was three to split the training and testing time segments. The sensitivity of the area for different brain lobes was evaluated using a coefficient of variation and standard deviation as a measure of spread. The DNN model performance was estimated using a one-way analysis of variance (ANOVA) and ten-fold cross-validation. The training features were time-series signals with sequential meanings. The procedure differed from non-sequential data points. Folds for training in our time-series cross-validation were created by chaining the state segments of patient seizures. Therefore, we selected a new train and test set of features for fitting and evaluating the model.
3.7. Deep Neural Network
A DNN of eight hidden layers was designed for classification. The sigmoid and ReLU activation functions for output and input layers were defined in the model. The network ran with a 10% batch size and 100 epochs. Keras, a python deep learning Application Programming Interface (API), was used for running the model.
4. Results
4.1. Early Detection
Within the patient-specific EEG signal, we identified an early indicator in the first 3.9 s of seizure initiation. The empirical mode functions extracted in this seizure state showed a significant contrast to the IMFs of the interictal state in the same time window. A deep neural network prediction algorithm using this feature as input was evaluated on each patient’s EEG recording, in which 143 seizures in 23 patients were analyzed. The proposed method showed an average sensitivity of 86.77% and specificity of 89.52%. Table 3 and Table 4 show the statistics for early detection and prediction.

Table 3.
Early detection statistics in a 3.9 second horizon for each subject.

Table 4.
Patient-specific performance for 5 min and 23 min horizon times.
4.2. Prediction
From the patient EEG signal, we used two prediction horizons of 23 min and 5 min, respectively. Each prediction horizon had a window of 3.9 s with an overlapping one of 2.9 s. IMFs were extracted in each window for the corresponding ictal and interictal states. The best IMF features for ReliefF were given as input to the DNN for training. The DNN model showed a sensitivity of 80.00% and a specificity of 72.85%. Figure 4 and Figure 5 show the intrinsic mode function for the ictal and interictal transitions.
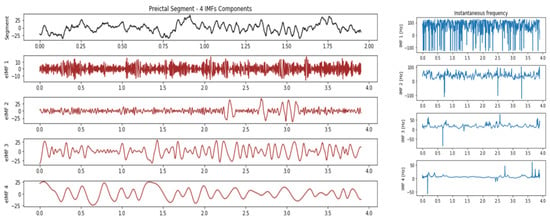
Figure 4.
Intrinsic mode functions of IMF1, IMF2, IMF3 and IMF4 and their instant frequencies in the preictal period of patient S01.
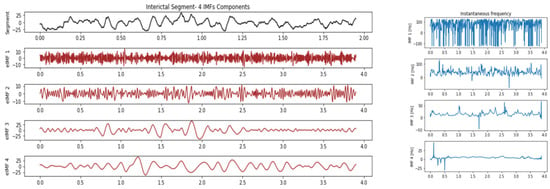
Figure 5.
Intrinsic mode functions of IMF1, IMF2, IMF3 and IMF4 and their instant frequencies in the interictal period of patient S01.
4.3. ReliefF
The contribution of twelve IMFs from the two scalp EEG channels is shown in Figure 6. The score for the left and right hemisphere is presented.
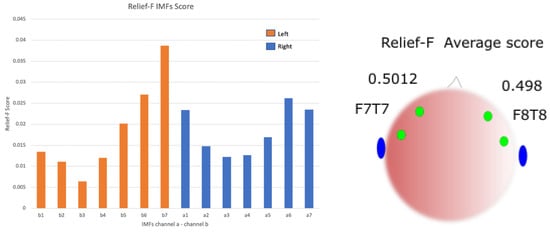
Figure 6.
ReliefF score contributions of twelve IMFs from the two channels of patient S01.
4.4. Early Detection in Different Brain Locations
The sensitivity and specificity of the frontal-temporal model in diffrerent brain locations are shown in Table 5. Frontal and temporal lobes seizure are present in 14 of the 23 subjects.

Table 5.
Performance of the frontal-temporal method in different brain locations.
4.5. Statistical Significance
The high variance of sample size per subject is shown in Figure 7, which depends directly on seizure duration and frequency. Table 6 shows the statitics for subject sensitivity score on brain lobes in the 5 min. and 23 min. horizon time. Table 7 shows the one-way ANOVA analysis of the prediction performance in the 23 min. horizon for all subjects.
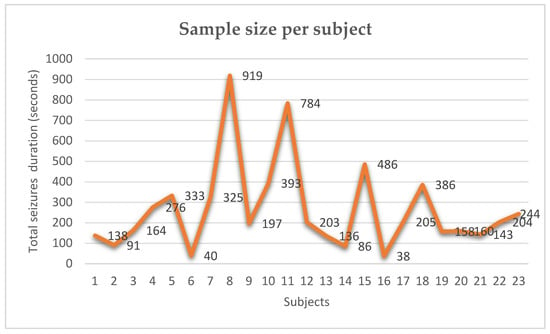
Figure 7.
Sample size per subjects (number of seizures) used in this study. Total seizures = 66, Mean = 265.60, STD = 213.65 and Variance = 47,559.52.

Table 6.
Statistics for brain lobes prediction sensitivity in two horizon times (HTs).

Table 7.
One-way analysis of variance (ANOVA) of prediction score performance in the 23 min horizon.
4.6. Validation and Performance Comparison
Table 8 shows a performance comparison of the most recent work in seizure prediction. Ten-fold cross-validation average for each 23 subject for early detection is shown in Table 9.

Table 8.
Performance comparison of recent works in seizure prediction.

Table 9.
Ten-fold cross-validation average score for each subject model for early detection (D).
5. Discussion and Conclusions
This study focused on the analysis of two frontal-temporal channel prediction systems. We used 23 subjects from the CHB-MIT dataset and scalp EEG recordings to validate this work. A patient-specific DNN classification model for each subject was trained for early detection and prediction. We extracted all the intrinsic mode functions in the segmented preictal and interictal states from the two temporal-frontal channels of each patient. Sixteen intrinsic mode functions were elicited per channel. Then, a ReliefF filter selected the most informative features. This new subset of oscillatory components helped the DNN learn a segment of 1000 data points, representing 3.9 s EEG windows in the ictal and interictal periods. The proposed model achieved excellent results for the two electrodes in each brain hemisphere, F7T7 and F8T8. The performance scores in early detection and prediction are shown in Table 3 and Table 4. Early detection showed an average sensitivity and specificity of 86.77% and 89.52%, respectively, while in the prediction method, the average sensitivity and specificity were 81% and 97% in the 5 min and 23 min horizon times. The area under the curve (AUC) of the receiving operating curve (ROC), ROC-AUC, shows how well the patient-specific DNN model distinguishes between classes, with an overall score of 85.39%.
The ensemble IMFs, and their instantaneous frequencies in the ictal and interictal states, were extracted for early detection. The use of EEMD allowed for discriminating between the segmented ictal and interictal periods. For the prediction analysis, the preictal to interictal signals are shown in Figure 4 and Figure 5, where the preictal state shows higher IMFs of instantaneous frequencies than the corresponding interictal state. These signature patterns in the ictal and preictal enabled the DNN to perform as a successful classifier model. The ReliefF analysis shows an almost similar score feature selection for the F7T7 and F8T8 electrode channels in both early detection and prediction, as shown in Figure 6. This feature pattern is present in each of the 23 subjects, suggesting an equal contribution by each hemisphere in seizure prediction.
The intracranial EEG had a better spatial resolution and signal-to-noise ratio than the scalp EEG. However, not all patients were candidates for surgery. In addition, there are some time complications during craniotomy and risks of potential post-operative deficits [48]. Scalp EEGs promote a more realistic acceptance of real-life scenarios for a patient, but have the limitations of wearing all the electrode arrays in an outpatient setting [9]. A performance comparison of recent research in this field is presented in Table 8. The authors in [46] used a reduced montage of eight electrodes in seizure detection. The algorithm implemented detected seizures from EEG, surface, Electromyogram (EMG) and Electrocardiogram (ECG). Results encouraged the use of reduced electrode sets based on frontal-temporal electrodes. In our study, the two electrode channels of F7-T7 and F8-T8 covered a partial frontal-temporal area on the subject’s scalp. Table 7 shows a one-way analysis of variance (ANOVA) of prediction score performance in the 23 min horizon with a p-value < 0.05. The parietal, temporal-occipital and temporal-parietal seizure locations exhibited an average sensitivity of 94%, 93.3% and 91.9%. The overall performance in Table 5 demonstrates the ability of the proposed model to capture patterns from non-fontal-temporal seizure brain locations. Table 7 shows the validation score for each subject, yielding an average of 80.5%.
Further work can assess the feasibility of running the model on restricted resource devices with frontal and temporal epilepsy subjects. Also, a more extended prediction horizon time can be explored with adjustable windows in the ictal period. The subrogation of the two frontal-temporal channels can also be studied to produce a single, condensed channel (e.g., common spatial pattern). For visual inspection and seizure validation for a physician, we recommend the full use of the 10–20 electrode montage.
We have demonstrated that the proposed method represents a compelling alternative for reducing the number of channels in a patient’s scalp. We proposed an EEMD-ReliefF approach to extract and select the most relevant oscillatory components in two frontal-temporal channels. Investigating and computing the frontal-temporal two-channel signals promises to be a suitable candidate for developing a miniaturized warning and intervention device for therapy in epilepsy patients. Although the detection and prediction results are promising, further studies are needed to validate their utility for broad clinical applications in epilepsy patients.
Author Contributions
Data curation, A.R.; methodology, A.R. and V.M.; supervision, V.M.; validation, A.R.; writing—original draft, A.R.; writing—review and editing, V.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fiest, K.M.; Sauro, K.M.; Wiebe, S.; Patten, S.B.; Kwon, C.S.; Dykeman, J.; Pringsheim, T.; Lorenzetti, D.L.; Jetté, N. Prevalence and incidence of epilepsy. Neurology 2017, 88, 296–303. [Google Scholar] [CrossRef] [PubMed]
- The Economic Burden of Epilepsy in Australia, 2019–2020 | Epilepsy Foundation. Available online: https://epilepsyfoundation.org.au/2020/02/08/the-economic-burden-of-epilepsy-in-australia-2019-2020/ (accessed on 6 August 2020).
- Khan, H.; Marcuse, L.; Fields, M.; Swann, K.; Yener, B. Focal onset seizure prediction using convolutional networks. IEEE Trans. Biomed. Eng. 2018, 65, 2109–2118. [Google Scholar] [CrossRef] [PubMed]
- Zhou, M.; Tian, C.; Cao, R.; Wang, B.; Niu, Y.; Hu, T.; Guo, H.; Xiang, J. Epileptic Seizure Detection Based on EEG Signals and CNN. Front. Neuroinform. 2018, 12, 95. [Google Scholar] [CrossRef] [PubMed]
- Sirven, J.I. Epilepsy: A Spectrum Disorder. Cold Spring Harb. Perspect. Med. 2015, 5, a022848. [Google Scholar] [CrossRef] [PubMed]
- Prathap, P.; Devi, T.A. EEG spectral feature based seizure prediction using an efficient sparse classifier. In Proceedings of the 2017 International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT), Kannur, India, 6–7 July 2017; pp. 721–725. [Google Scholar] [CrossRef]
- Alotaiby, T.N.; Alshebeili, S.A.; Alshawi, T.; Ahmad, I.; Abd El-Samie, F.E. EEG seizure detection and prediction algorithms: A survey. EURASIP J. Adv. Signal Process. 2014, 2014, 1–21. [Google Scholar] [CrossRef]
- Lasefr, Z.; Ayyalasomayajula, S.S.V.N.R.; Elleithy, K. Epilepsy seizure detection using EEG signals. In Proceedings of the 2017 IEEE 8th Annual Ubiquitous Computing, Electronics and Mobile Communication Conference, UEMCON, New York, NY, USA, 19–21 October 2017; Institute of Electrical and Electronics Engineers Inc.: Piscataway Township, NJ, USA, 2017; Volume 2018-January, pp. 162–167. [Google Scholar] [CrossRef]
- Baumgartner, C.; Koren, J.P.; Rothmayer, M. Automatic computer-based detection of epileptic seizures. Front. Neurol. 2018, 9, 639. [Google Scholar] [CrossRef]
- Kuhlmann, L.; Lehnertz, K.; Richardson, M.P.; Schelter, B.; Zaveri, H.P. Seizure prediction—Ready for a new era. Nat. Rev. Neurol. 2018, 14, 618–630. [Google Scholar] [CrossRef]
- Zhang, Z.; Parhi, K.K. Low-Complexity Seizure Prediction From iEEG/sEEG Using Spectral Power and Ratios of Spectral Power. IEEE Trans. Biomed. Circuits Syst. 2016, 10, 693–706. [Google Scholar] [CrossRef]
- Myers, M.H.; Padmanabha, A.; Hossain, G.; De Jongh Curry, A.L.; Blaha, C.D. Seizure prediction and detection via phase and amplitude lock values. Front. Hum. Neurosci. 2016, 10, 1–9. [Google Scholar] [CrossRef]
- Samie, F.; Paul, S.; Bauer, L.; Henkel, J. Highly efficient and accurate seizure prediction on constrained IoT devices. In Proceedings of the 2018 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 19–23 March 2018; pp. 955–960. [Google Scholar] [CrossRef]
- Ponciano, V.; Pires, I.M.; Ribeiro, F.R.; Garcia, N.M.; Villasana, M.V.; Lameski, P.; Zdravevski, E. Machine Learning Techniques with ECG and EEG Data: An Exploratory Study. Computers 2020, 9, 55. [Google Scholar] [CrossRef]
- Alotaiby, T.N.; Alshebeili, S.A.; Alotaibi, F.M.; Alrshoud, S.R. Epileptic seizure prediction using CSP and LDA for scalp EEG signals. Comput. Intell. Neurosci. 2017, 2017. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Guo, Y.; Yang, P.; Chen, W.; Lo, B. Epilepsy Seizure Prediction on EEG Using Common Spatial Pattern and Convolutional Neural Network. IEEE J. Biomed. Heal. Inform. 2020, 24, 465–474. [Google Scholar] [CrossRef]
- Cho, D.; Min, B.; Kim, J.; Lee, B. EEG-Based Prediction of Epileptic Seizures Using Phase Synchronization Elicited from Noise-Assisted Multivariate Empirical Mode Decomposition. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 1309–1318. [Google Scholar] [CrossRef] [PubMed]
- Chu, H.; Chung, C.K.; Jeong, W.; Cho, K.H. Predicting epileptic seizures from scalp EEG based on attractor state analysis. Comput. Methods Programs Biomed. 2017, 143, 75–87. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Sharma, S. Seizure, Complex Partial; StatPearls Publishing: Treasure Island, FL, USA, 2018. [Google Scholar]
- Tzallas, A.T.; Tsipouras, M.G.; Fotiadis, D.I. Automatic Seizure Detection Based on Time-Frequency Analysis and Artificial Neural Networks. Comput. Intell. Neurosci. 2007, 80510, 13. [Google Scholar] [CrossRef]
- Osman, A.H.; Alzahrani, A.A. New Approach for Automated Epileptic Disease Diagnosis Using an Integrated Self-Organization Map and Radial Basis Function Neural Network Algorithm. IEEE Access 2019, 7, 4741–4747. [Google Scholar] [CrossRef]
- Stojanović, O.; Kuhlmann, K.; Pipa, G. Predicting epileptic seizures using nonnegative matrix factorization. PLoS ONE 2019. [Google Scholar] [CrossRef]
- Eberlein, M.; Hildebrand, R.; Tetzlaff, R.; Hoffmann, N.; Kuhlmann, L.; Brinkmann, B.; Müller, J. Convolutional Neural Networks for Epileptic Seizure Prediction. In Proceedings of the 2018 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Madrid, Spain, 3–6 December 2018; pp. 2577–2582. [Google Scholar] [CrossRef]
- Hu, W.; Cao, J.; Lai, X.; Liu, J. Mean amplitude spectrum based epileptic state classification for seizure prediction using convolutional neural networks. J. Ambient Intell. Humaniz. Comput. 2019. [Google Scholar] [CrossRef]
- Senger, V.; Tetzlaff, R. Cellular nonlinear network-based signal prediction in epilepsy: Method comparison. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015; pp. 397–400. [Google Scholar] [CrossRef]
- Kiral-Kornek, I.; Roy, S.; Nurse, E.; Mashford, B.; Karoly, P.; Carroll, T.; Payne, D.; Saha, S.; Baldassano, S.; O’Brien, T.; et al. Epileptic Seizure Prediction Using Big Data and Deep Learning: Toward a Mobile System. EBioMedicine 2018, 27, 103–111. [Google Scholar] [CrossRef]
- Daoud, H.; Bayoumi, M.A. Efficient Epileptic Seizure Prediction Based on Deep Learning. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 804–813. [Google Scholar] [CrossRef]
- Li, J.; Wang, J. Stochastic recurrent wavelet neural network with EEMD method on energy price prediction. Soft Comput. 2020, 1–19. [Google Scholar] [CrossRef]
- Zhou, Y.; Sheremet, A.; Qin, Y.; Kennedy, J.P.; Dicola, N.M.; Burke, S.N.; Maurer, A.P. Methodological considerations on the use of different spectral decomposition algorithms to study hippocampal rhythms. eNeuro 2019, 6. [Google Scholar] [CrossRef]
- Kanagaraj, G.; Kumar, S. Pulmonary Tumor Detection by virtue of GLCM. J. Sci. Ind. Res. 2020, 79, 132–134. [Google Scholar]
- Manuel Gutiérrez-Ruiz, A.; Valcarce-Ruiz, L.; Becerra-Vicario, R.; Ruíz-Palomo, D. Identifying Industrial Productivity Factors with Artificial Neural Networks. J. Sci. Ind. Res. 2020, 79, 534–536. [Google Scholar]
- Karabiber Cura, O.; Kocaaslan Atli, S.; Türe, H.S.; Akan, A. Epileptic seizure classifications using empirical mode decomposition and its derivative. Biomed. Eng. Online 2020, 19. [Google Scholar] [CrossRef] [PubMed]
- CHB-MIT Scalp EEG Database v1.0.0. Available online: https://physionet.org/content/chbmit/1.0.0/ (accessed on 3 August 2020).
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Papadaniil, C.D.; Hadjileontiadis, L.J. Efficient heart sound segmentation and extraction using ensemble empirical mode decomposition and kurtosis features. IEEE J. Biomed. Health Inform. 2014, 18, 1138–1152. [Google Scholar] [CrossRef]
- Ben Ali, J.; Fnaiech, N.; Saidi, L.; Chebel-Morello, B.; Fnaiech, F. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals. Appl. Acoust. 2015, 89, 16–27. [Google Scholar] [CrossRef]
- Guo, W.; Tse, P.W. A novel signal compression method based on optimal ensemble empirical mode decomposition for bearing vibration signals. J. Sound Vib. 2013, 332, 423–441. [Google Scholar] [CrossRef]
- Gaci, S. A New Ensemble Empirical Mode Decomposition (EEMD) Denoising Method for Seismic Signals. Energy Procedia 2016, 97, 84–91. [Google Scholar] [CrossRef]
- Urbanowicz, R.J.; Meeker, M.; La Cava, W.; Olson, R.S.; Moore, J.H. Relief-based feature selection: Introduction and review. J. Biomed. Inform. 2018, 85, 189–203. [Google Scholar] [CrossRef] [PubMed]
- Kononenko, I. Estimating attributes: Analysis and extensions of RELIEF. In Proceedings of the European Conference on Machine Learning: ECML-94, Catania, Italy, 6–8 April 1994; Springer: Berlin/Heidelberg, Germany, 1994; pp. 171–182. [Google Scholar]
- Truong, N.D.; Nguyen, A.D.; Kuhlmann, L.; Bonyadi, M.R.; Yang, J.; Ippolito, S.; Kavehei, O. Convolutional neural networks for seizure prediction using intracranial and scalp electroencephalogram. Neural Netw. 2018, 105, 104–111. [Google Scholar] [CrossRef] [PubMed]
- Parvez, M.Z.; Paul, M. Seizure prediction using undulated global and local features. IEEE Trans. Biomed. Eng. 2017, 64, 208–217. [Google Scholar] [CrossRef] [PubMed]
- Aarabi, A.; He, B. Seizure prediction in patients with focal hippocampal epilepsy. Clin. Neurophysiol. 2017, 128, 1299–1307. [Google Scholar] [CrossRef] [PubMed]
- Eftekhar, A.; Juffali, W.; El-Imad, J.; Constandinou, T.G.; Toumazou, C. Ngram-derived pattern recognition for the detection and prediction of epileptic seizures. PLoS ONE 2014, 9, e96235. [Google Scholar] [CrossRef] [PubMed]
- Birjandtalab, J.; Pouyan, M.B.; Cogan, D.; Nourani, M.; Harvey, J. Automated seizure detection using limited-channel EEG and non-linear dimension reduction. Comput. Biol. Med. 2017, 82, 49–58. [Google Scholar] [CrossRef]
- Fürbass, F.; Kampusch, S.; Kaniusas, E.; Koren, J.; Pirker, S.; Hopfengärtner, R.; Stefan, H.; Kluge, T.; Baumgartner, C. Automatic multimodal detection for long-term seizure documentation in epilepsy. Clin. Neurophysiol. 2017, 128, 1466–1472. [Google Scholar] [CrossRef]
- Shah, A.K.; Mittal, S. Invasive electroencephalography monitoring: Indications and presurgical planning. Ann. Indian Acad. Neurol. 2014, 17. [Google Scholar] [CrossRef]
- Herta, J.; Koren, J.; Fürbass, F.; Hartmann, M.; Gruber, A.; Baumgartner, C. Reduced electrode arrays for the automated detection of rhythmic and periodic patterns in the intensive care unit: Frequently tried, frequently failed? Clin. Neurophysiol. 2017, 128, 1524–1531. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).