Towards a RINA-Based Architecture for Performance Management of Large-Scale Distributed Systems †
Abstract
1. Introduction
Structure of the Paper
- In Section 2, we refine the notion of ‘performance’ using a precise measure called quality attenuation (referred to in other literature as ‘quality impairment’ or ‘quality degradation’);
- In Section 3, we apply this to managing the performance of distributed systems;
- In Section 4, we consider overbooking and correlation hazards to the delivery of good performance;
- In Section 5, we discuss how the features of RINA assist in managing performance hazards;
- In Section 6, we propose metrics to assess the effectiveness of a performance management system;
- In Section 7, we briefly outline an architecture for performance management;
- In Section 8, we draw some conclusions and consider directions for further work.
- Background information on RINA and detail on how it interacts with performance management;
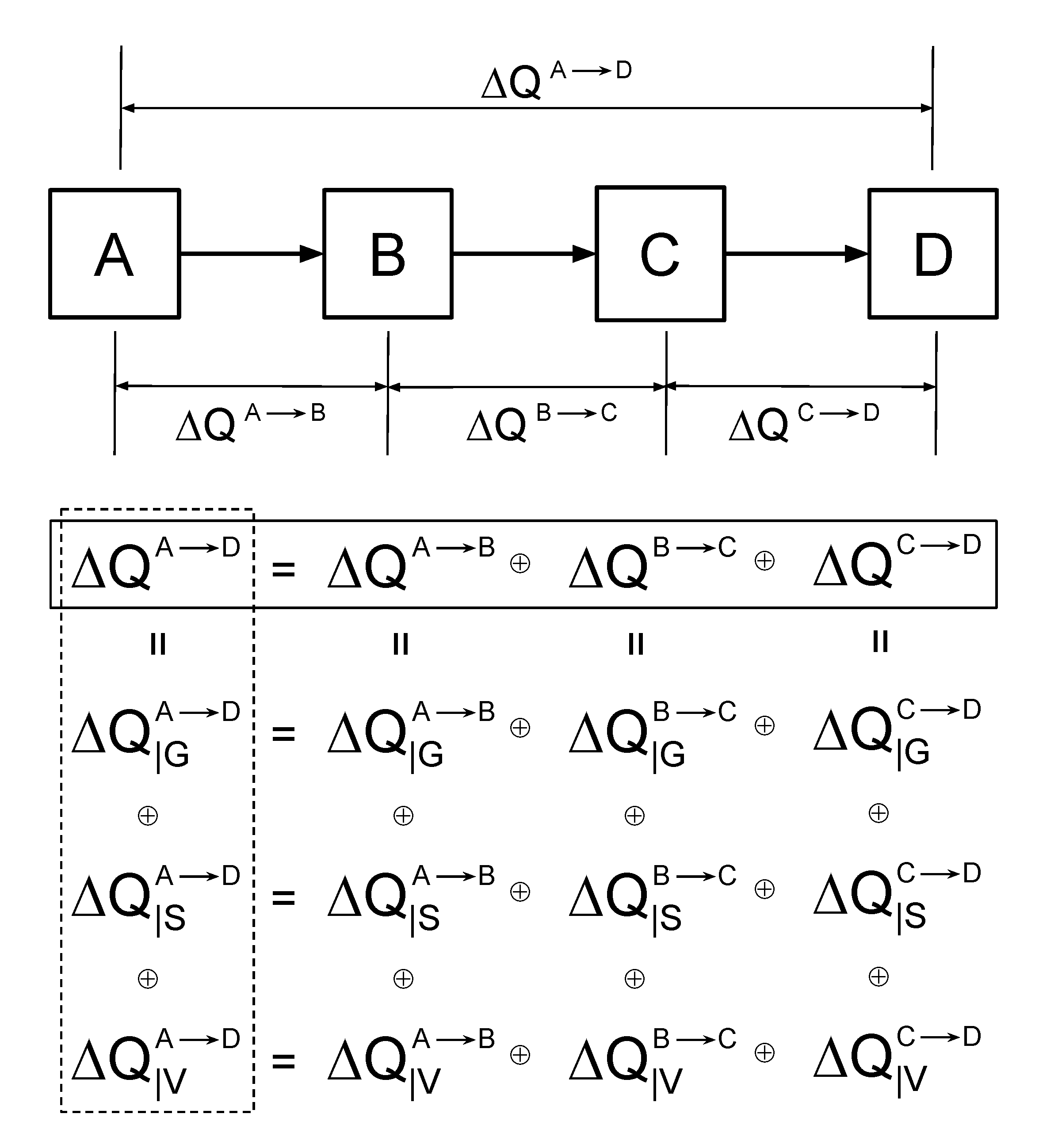
- More detail on the decomposition of ;
- A description of the process of aggregating QTAs;
- A new section on dealing with bursty traffic;
- Expanded conclusions and discussion of directions for future work;
- An appendix showing how can be calculated from application behaviour.
2. Defining Performance
2.1. Service Performance
- VoIP: audio glitches per call minute;
- Web page download: time from request to rendering of the initial part of the web page;
- Web page rendering: time from requesting the page to rendering of the last element;
- Online gaming: enjoyment-impacting game response delays per playing hour;
- Bank transfers: time from requesting transfer to funds appearing in the other account.
2.2. Quality Attenuation:
2.2.1. Mathematical Representation of
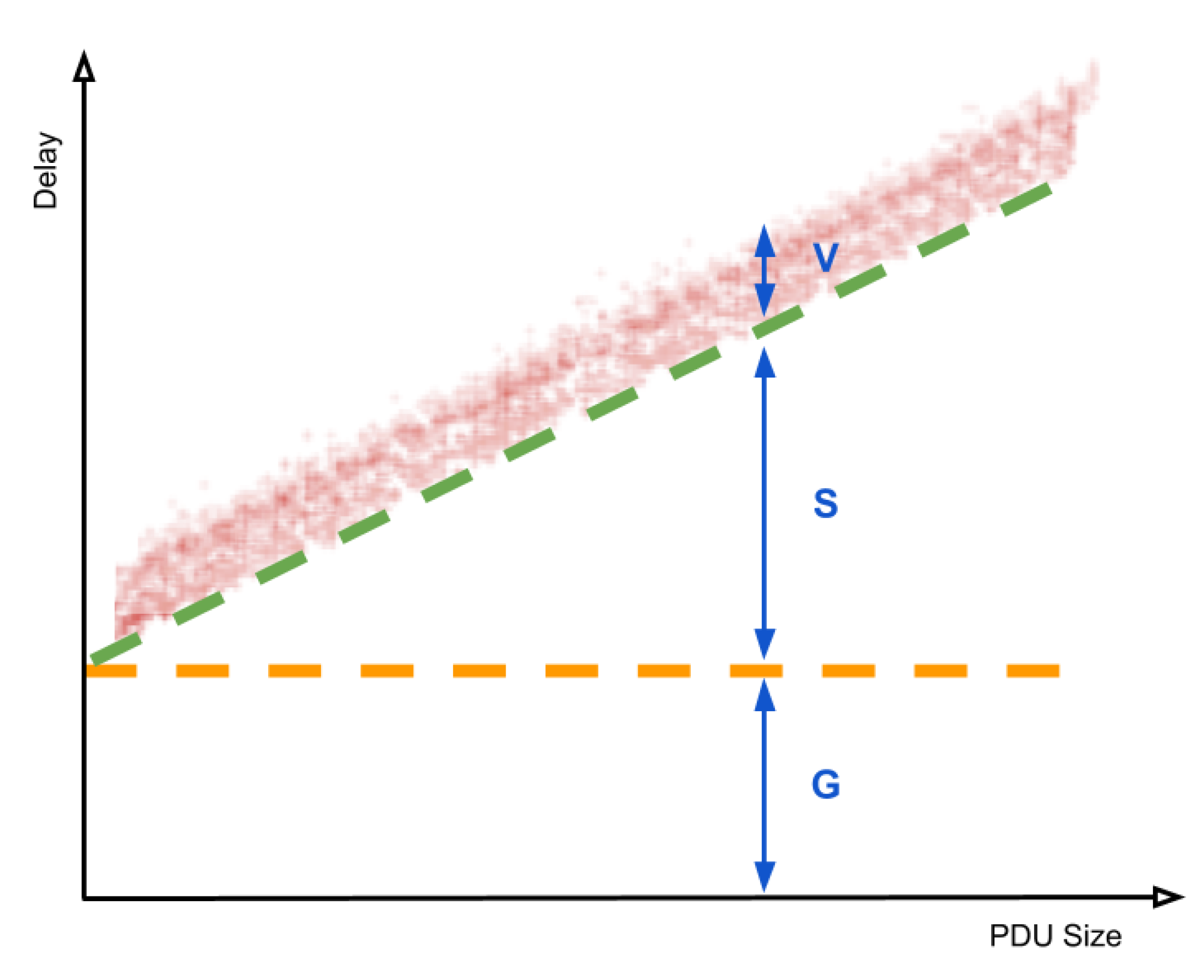
2.2.2. Components of Quality Attenuation
- Physical constraints: for example, an outcome involving transmission of information from one place to another cannot complete in less time than it takes light to travel the distance between them;
- Technological constraints: for example, a computation requiring a certain number of steps depends on a processor executing the corresponding instructions at a certain rate; and communicating some quantity of data takes time depending on the bit-rate of the interfaces used;
- Resource sharing constraints: when an outcome depends on the availability of shared resources, the time to complete it depends on the other use of those resources (and the scheduling policy allocating them).
- The infimum of outcome completion times with the effects of outcome size and resource sharing removed; in the case of packet transmission, it can be thought as the minimum time taken for a hypothetical zero-length packet to travel the path;
- A function from the outcome size to the additional time to complete it, with the infimum time and the effects of resource sharing removed;
- The additional time to complete the outcome due to sharing of resources, with the infimum time and the effects of outcome size removed.
- A failure rate that is intrinsic, independent of both outcome size and load, is the intangible mass of ;
- A failure rate that depends on the outcome size is the intangible mass of ;
- A failure rate that depends on the load is the intangible mass of .
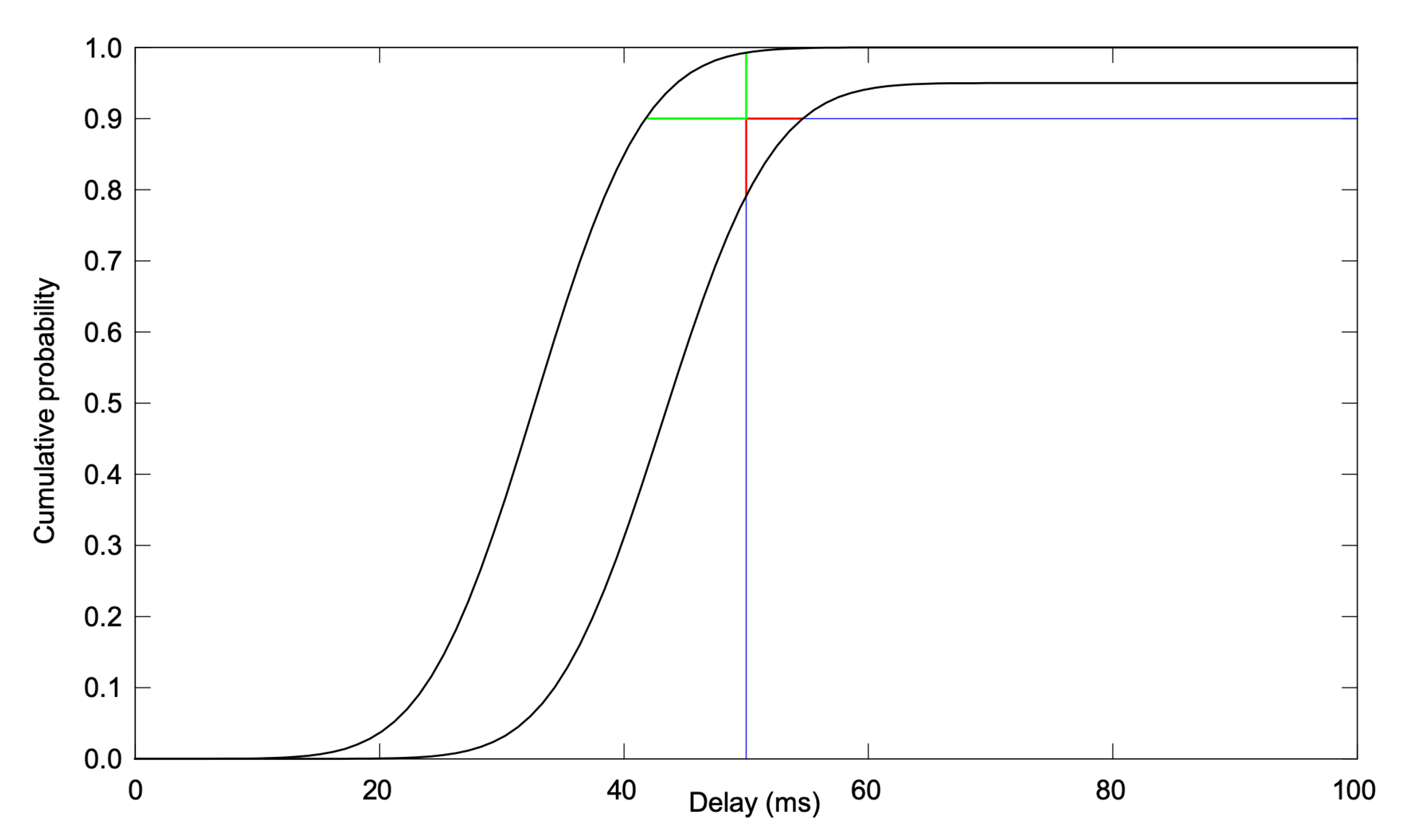
2.2.3. Compositionality of Quality Attenuation
3. Managing Performance
- Observing a single failure gives little information about the relevant probabilities;
- Waiting for a statistically significant number of failures makes the system response too slow to avoid undesirable service degradation.
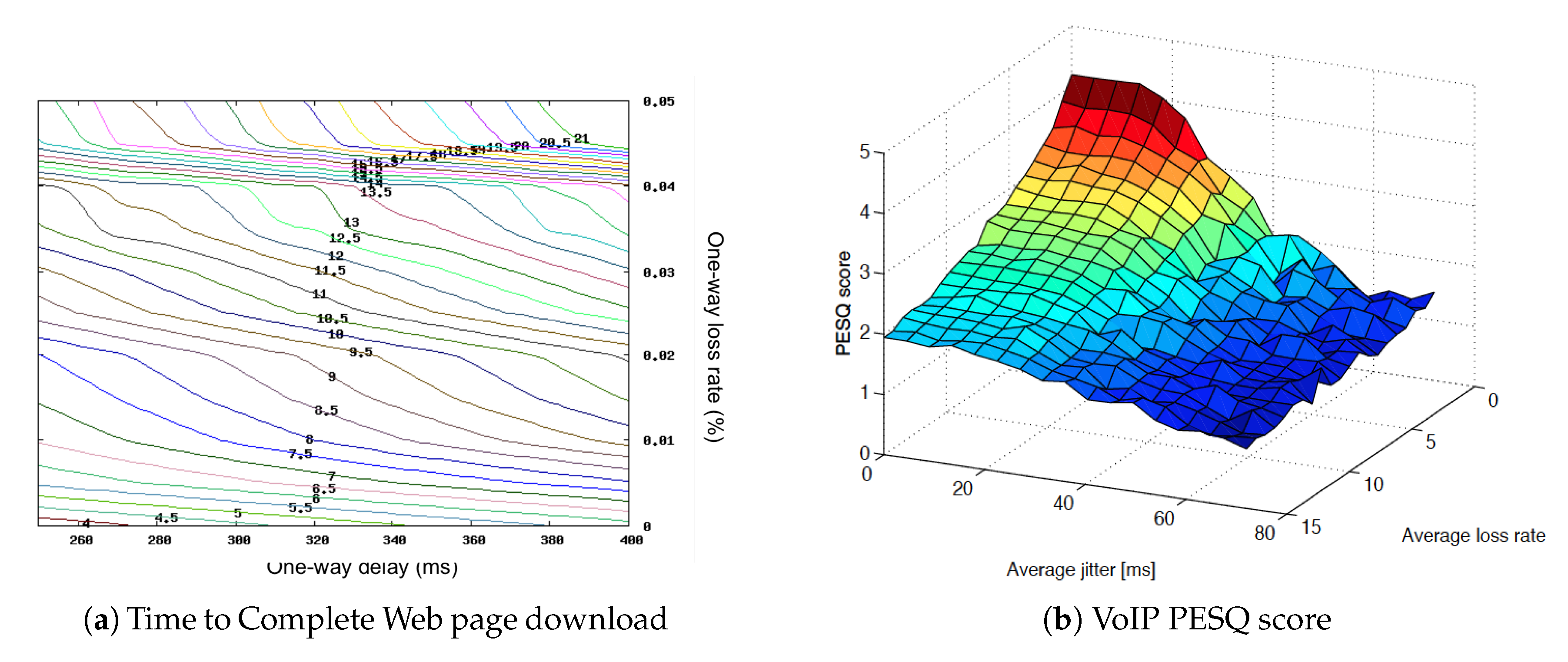
3.1. Measuring Quality Attenuation
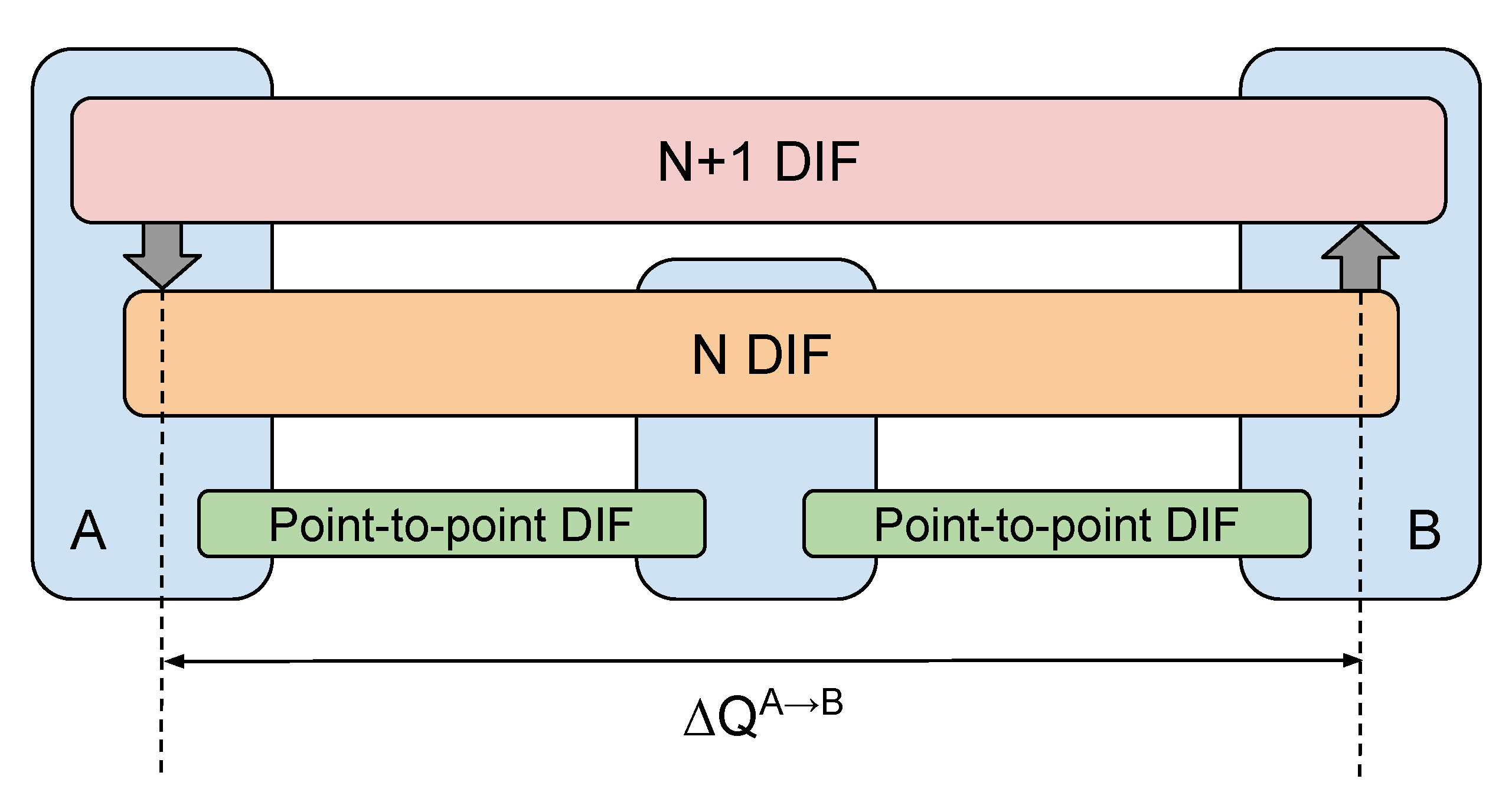
- Timestamping PDUs (measuring quality attenuation within the N-layer);
- Introduce additional SDUs containing a timestamp (measuring quality attenuation across the N-layer using a special-purpose N+1-layer DIF).
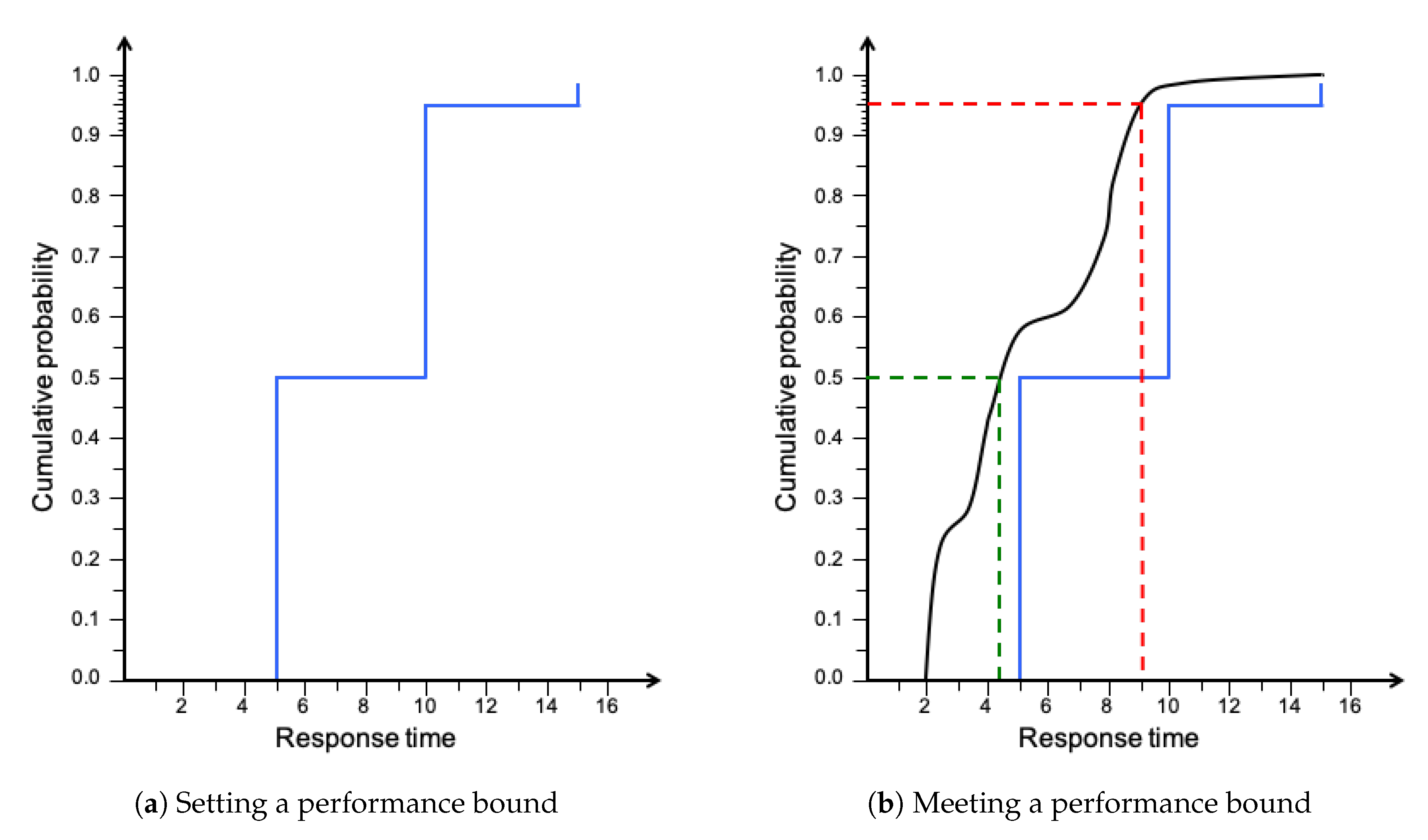
3.2. Setting a Performance Bound
3.3. Managing Demand: Quantitative Timeliness Agreements
3.4. Aggregation of QTAs
3.4.1. Allocation to Peak
3.4.2. Service Time Effects of Aggregate Bearer
3.4.3. Statistical Multiplexing Gain in a Setting
4. Managing Performance Hazards
4.1. Managing Overbooking Risks
- Loads tend to be intermittent, and thus this approach potentially wastes considerable resources;
- Available resources may vary, for example when communicating across a wireless bearer, or when subject to a denial-of-service attack.
4.1.1. Capacity, Urgency and Overbooking
- other traffic getting service worse than its natural urgency;
- this stream (or others) experiencing loss; or
- under-utilisation of the capacity.
4.1.2. Cost of Servicing Bursty Traffic
4.1.3. Urgency, Utilisation and Schedulability
- 0th order: Causality
- The required is not attainable over the end-to-end path.
- 1st order: Capacity
- The loss bounds of cannot be delivered as the capacity along the end-to-end path is insufficient.
- 2nd order: Schedulabilty
- The combined urgency requirements under normal operation cannot be met.
- 3rd order: Internal Behavioural Correlations
- There are correlations (under the control of the system operator) that cause aggregated traffic patterns such that their collective can no longer be met.
- 4th order: External Behavioural Correlations
- As above, but where the external environment imposes the correlations.
4.1.4. Flow Admission
4.1.5. Traffic Shaping
4.2. Timescales of Management
4.3. Supply Variation
- Adapt the local scheduling policy so as to concentrate the performance hazard into less important traffic (not necessarily the traffic with the largest attenuation tolerance.), for example favouring traffic required for maintaining network stability;
- In the case of loss variability, one option is to renegotiate the loss concealment strategy of connections achieving lower loss at the cost of increased load and/or delay (e.g., using Fountain codes [21]).
- Seek additional resources in the form of new/alternative lower-level DIFs, similar to the classic solution to mobility [4]; the difference here is that a lower-layer DIF may be offering connectivity and even capacity, but be unable to satisfy the quality attenuation bounds, forcing an alternate route to be sought.
4.4. Demand Variability
4.5. Correlated Load
- Internal correlations due to the behaviour of the system (for example, sending a large SDU creates a burst of lower-layer PDUs);
- External correlations due to the behaviour of the users of the service (for example, an early evening ‘busy hour’).
5. RINA and Performance Management
5.1. Connection Life-Cycle and QTAs
5.1.1. Allocation and Call Admission Control
5.1.2. Allocation and Slack/Hazard
5.1.3. Active Data Transport and Scheduling
6. Performance Management Metrics
6.1. Slack/Hazard
6.2. Capacity Utilisation
6.3. Coefficient of Variation
7. An Outline Architecture
- On short timescales,
- this is a matter of distributing the quality attenuation due to resource sharing according to the requirements of a set of QTAs. This is the domain of queuing and scheduling mechanisms, which must deliver predictable outcomes regardless of the instantaneous load [19].
- On medium timescales,
- it involves:
- Selecting appropriate routes for traffic and configuring queuing and scheduling mechanisms according to the current set of requirements [15];
- Managing demand so that such configuration is feasible. For elastic flows, this additionally means managing congestion with protocol control loops, and for inelastic flows controlling admission and, if necessary, gracefully shedding load while maintaining the critical functions of the system;
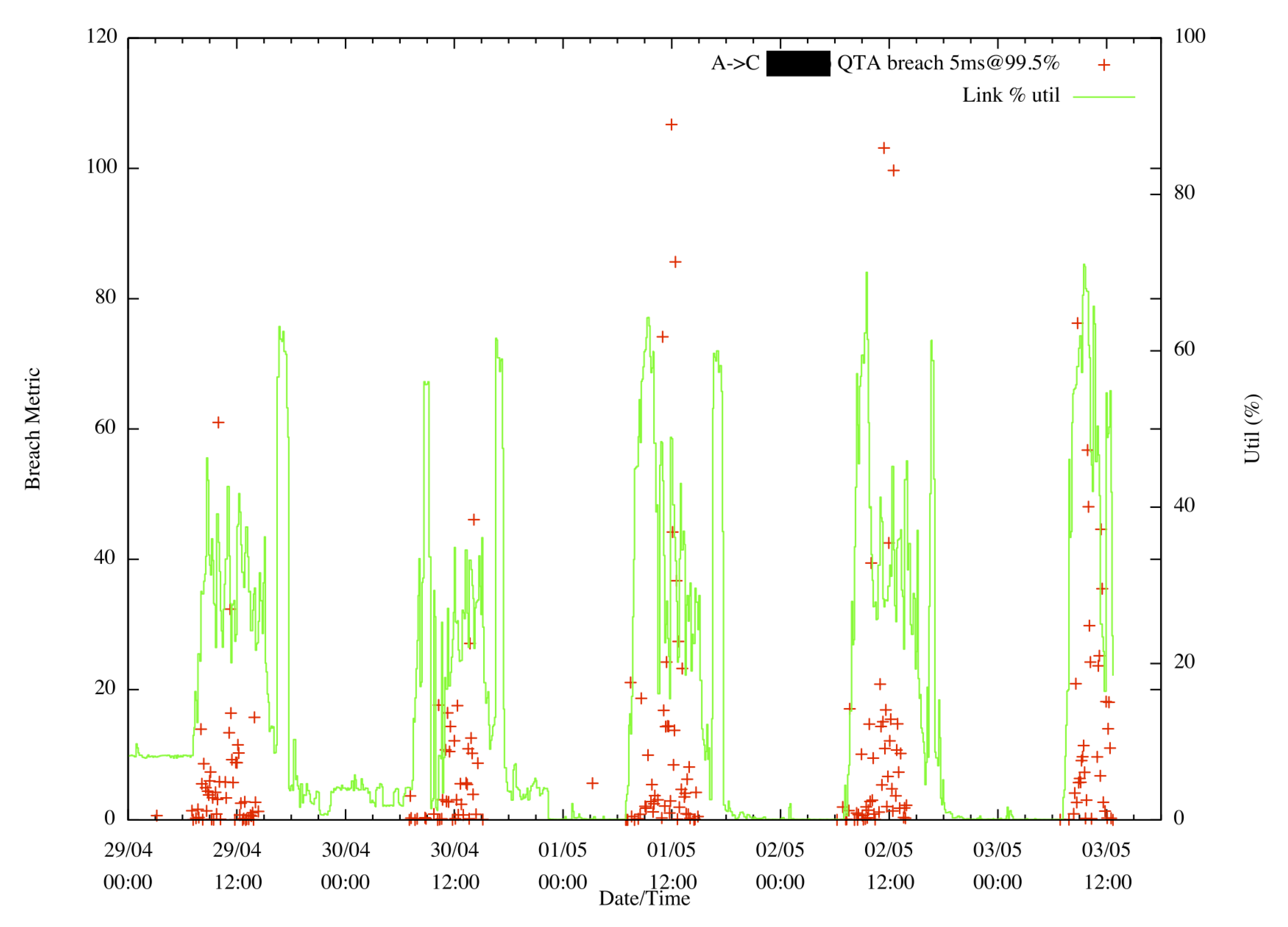
- Measuring performance hazards, particularly those resulting from overbooking and load correlation, and adjusting routing and scheduling configurations to minimise them. Where performance hazards result in QTA breaches, this should be recorded and related to service-level agreements that specify how frequent such breaches are allowed to be.
RINA supplies both the required control mechanisms and signalling (e.g., via QoS-cubes) so that higher network layers and, ultimately, applications, can adapt. - Over longer timescales,
- there are options for RINA management functions to trade quality attenuation budget between elements whose schedulability constraints vary, assuming some stationarity of applied load and a scheduling mechanism within the elements that allows trading of between flows at a multiplexing point. This would allow an overbooking hazard to be spread more evenly, and avoid rejection of new flow requests just because a single element along the path is constrained [27].
- On the longest timescales,
- it requires provisioning new capacity; requests for this could be generated automatically, although fulfilling them might involve manual processes.
8. Conclusions
8.1. Requirements for Delivering Performance
8.2. Managing Performance at Scale
8.3. Benefits of Performance Management
8.4. Directions for Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Quality Attenuation | |
| DDoS | Distributed Denial of Service |
| DIF | Distributed Interprocess communication Facility |
| PDU | Protocol Data Unit |
| IRV | Improper Random Variable |
| QTA | Quality Transport Agreement |
| RIB | Resource Information Base |
| RINA | Recursive InterNetworking Architecture |
| SDN | Software Defined Networking |
| SDU | Service Data Unit |
| SLA | Service Level Agreement |
| UX | User eXperience |
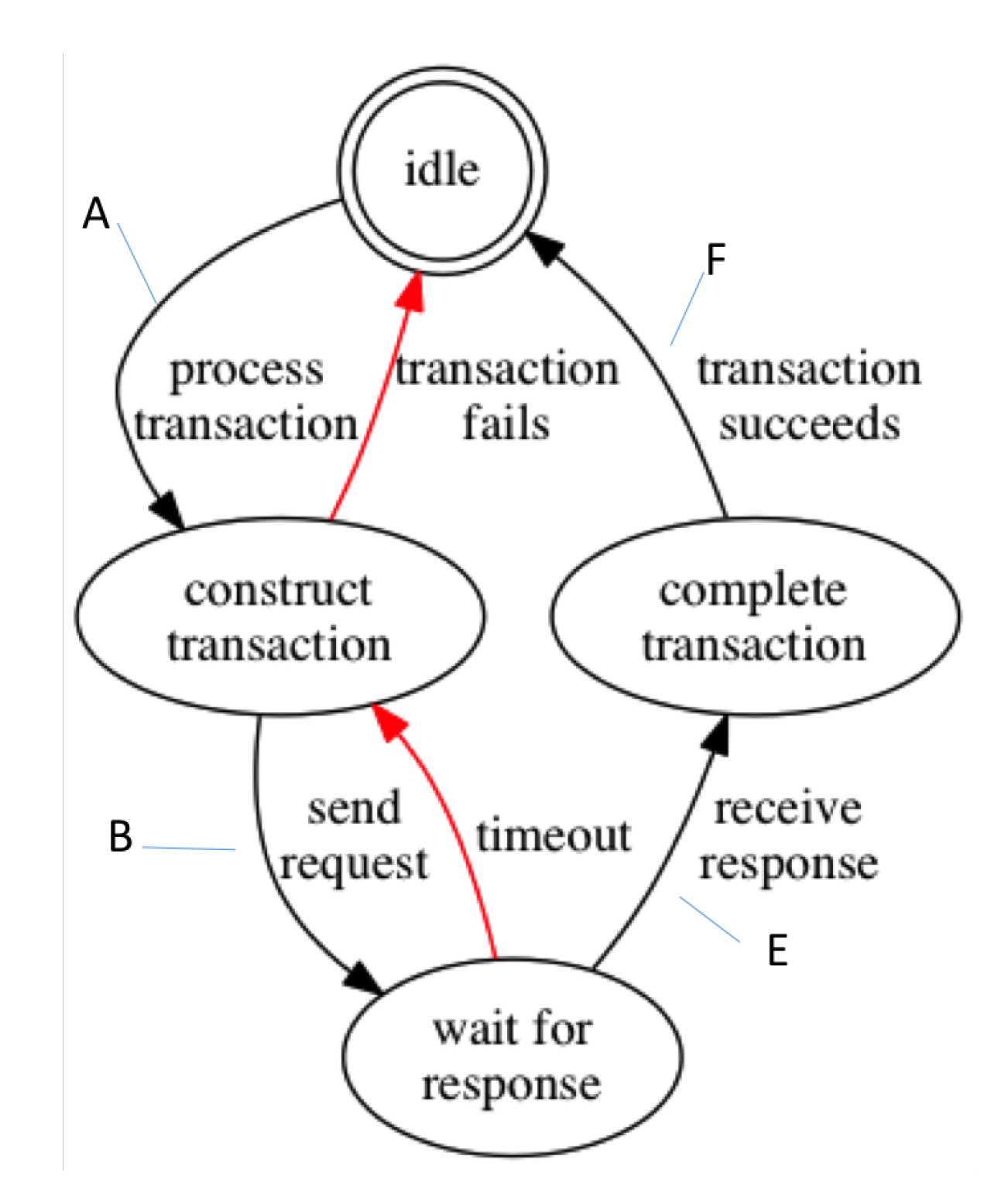
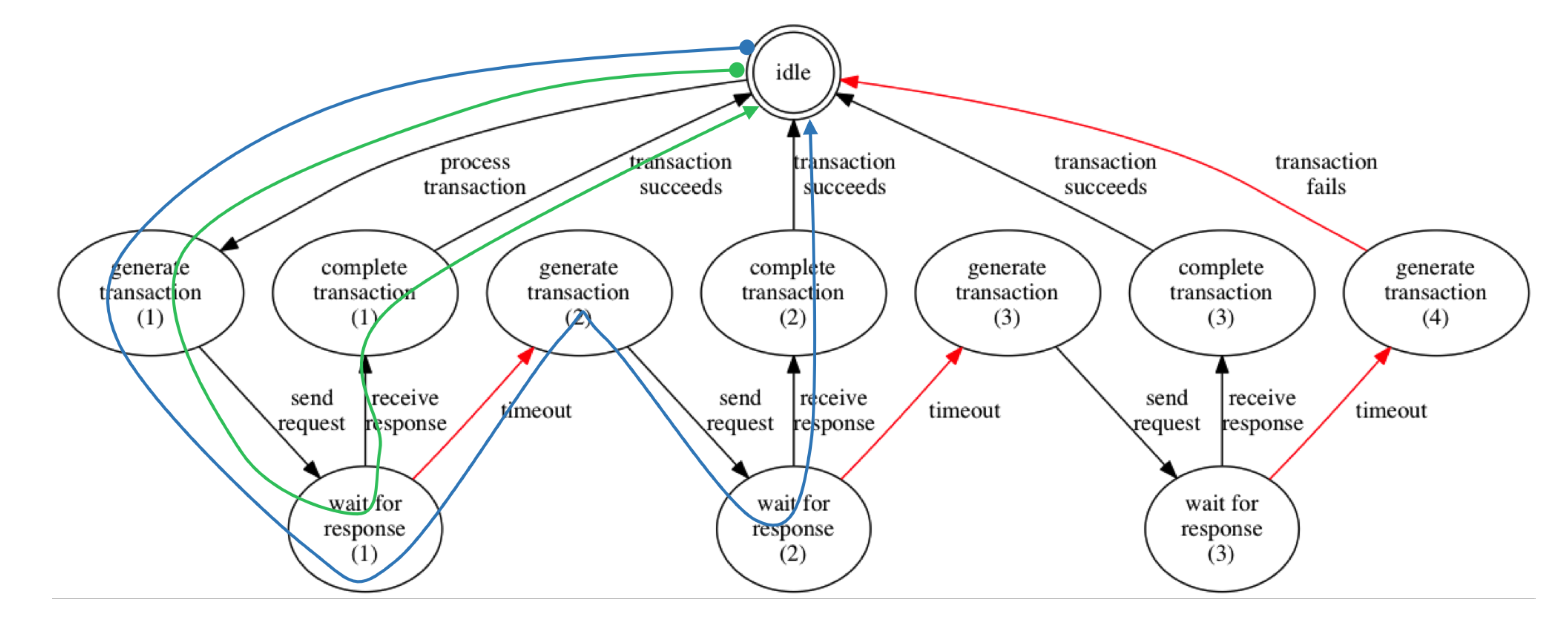
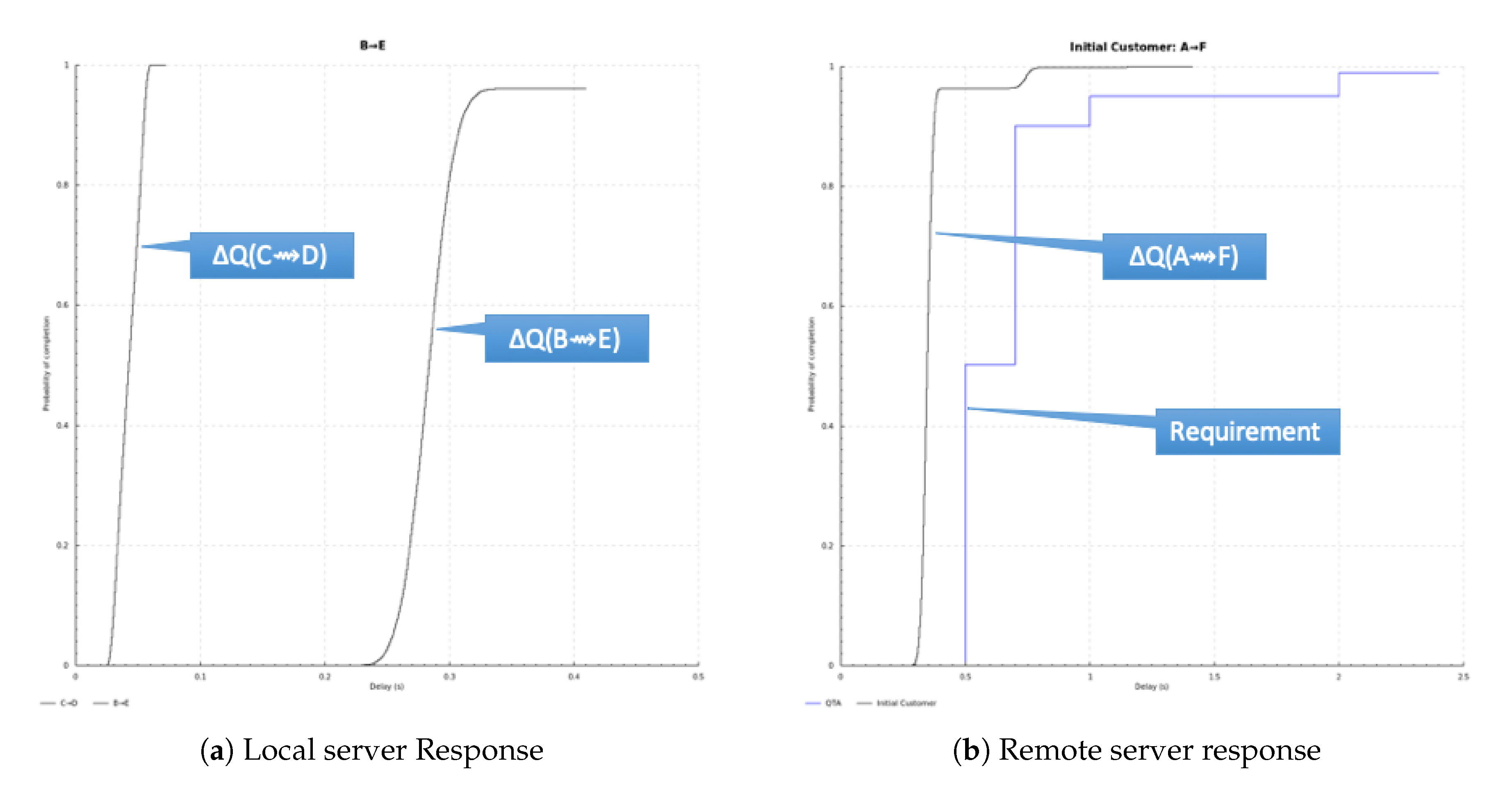
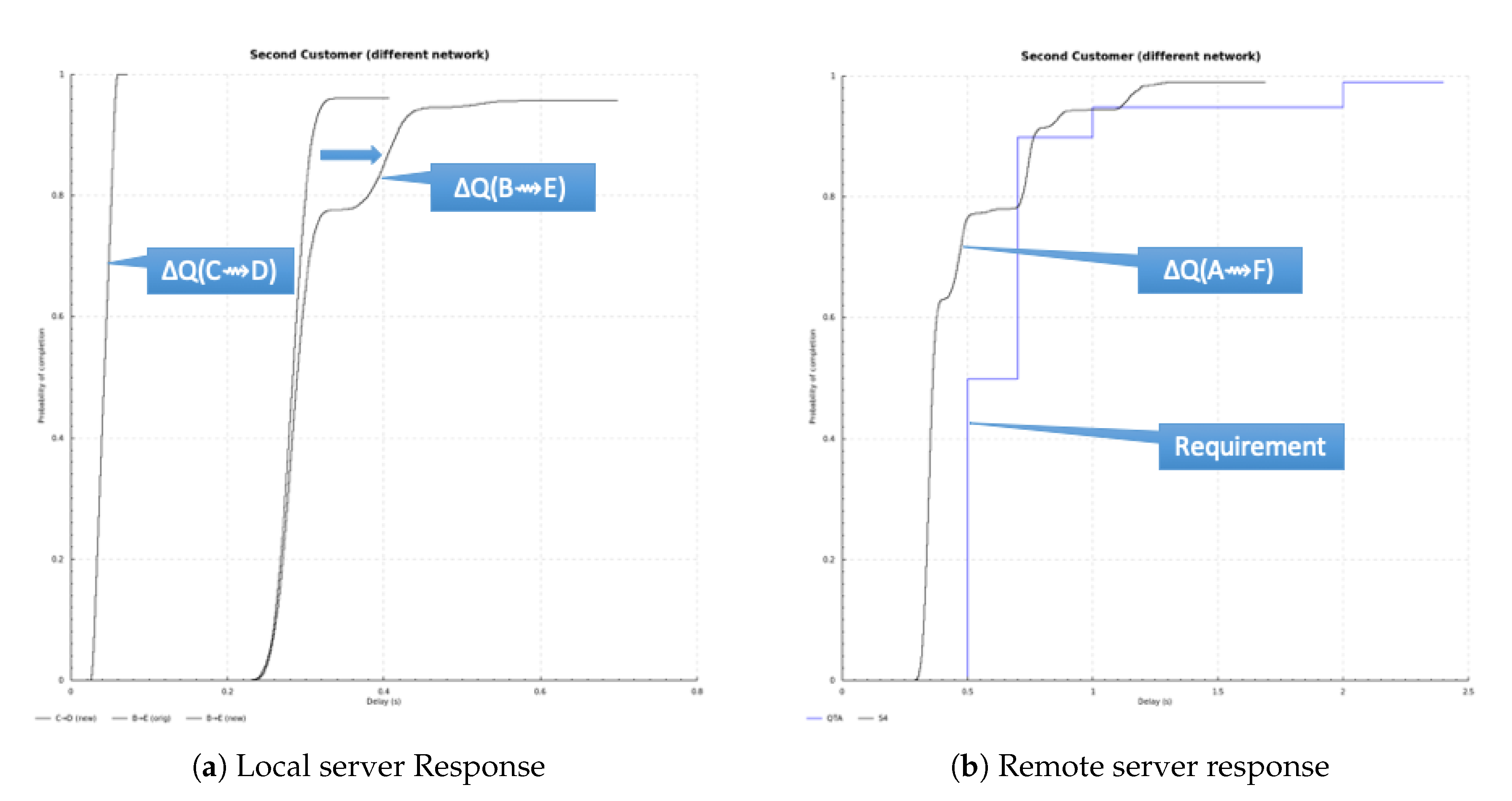
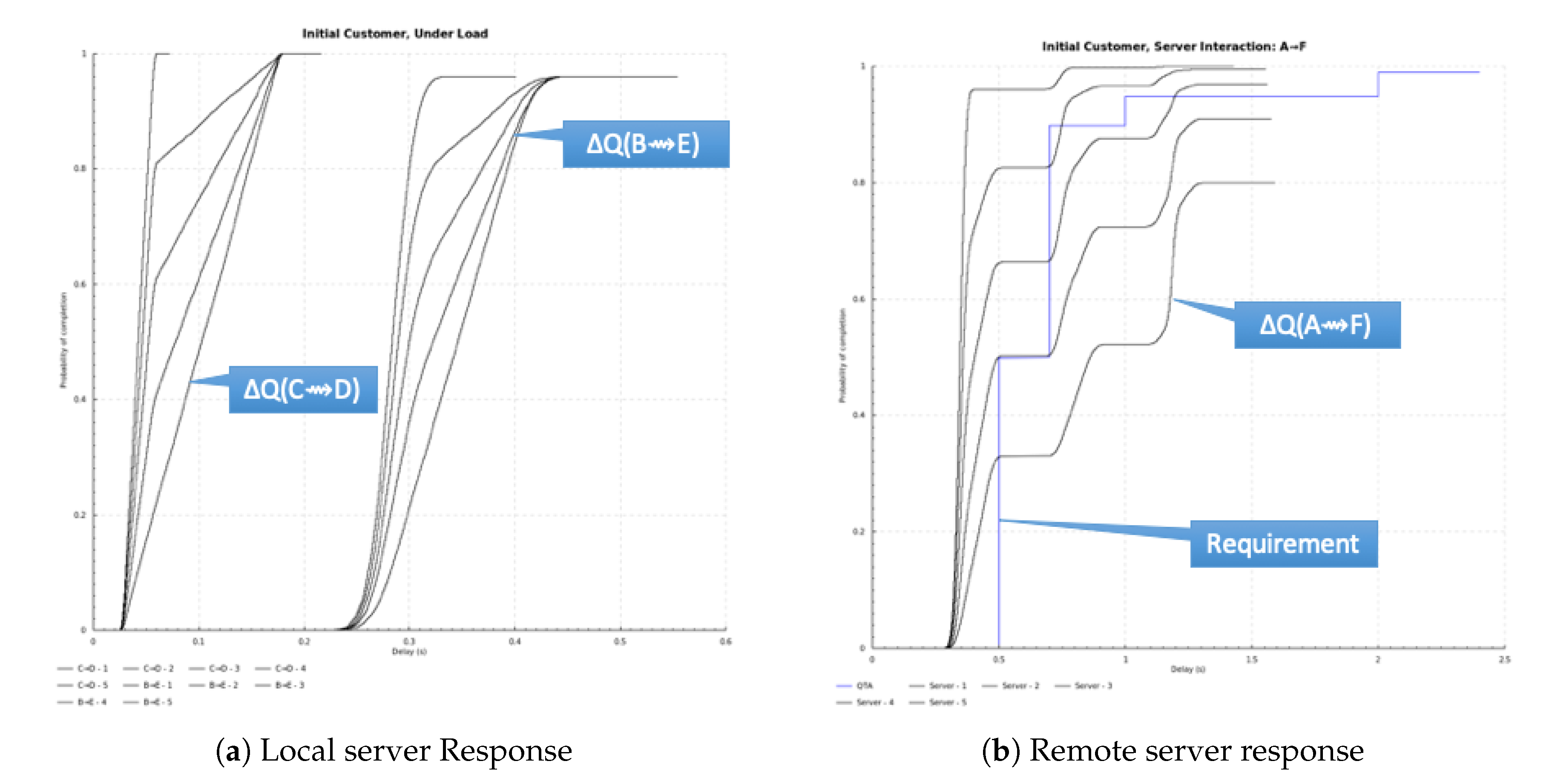
Appendix A. Worked Example of Composition of Quality Attenuation

- 50% within 500 ms;
- 90% within 700 ms;
- 95% within 1 s;
- 99% within 2 s;
- 1% chance of failure to respond within 2.5 s, considered a failed RPC.
References
- Collinson, P. RBS and Barclays asked to explain addition to litany of IT failures. The Guardian, 21 September 2018. [Google Scholar]
- Drescher, D. Blockchain Basics: A Non-Technical Introduction in 25 Steps; Apress: Frankfurt am Main, Germany, 2017. [Google Scholar]
- Rausch, K.; Riggio, R. Progressive Network Transformation with RINA. IEEE Softwarization. January 2017. Available online: https://sdn.ieee.org/newsletter/january-2017/progressive-network-transformation-with-rina (accessed on 25 June 2020).
- Day, J. Patterns in Network Architecture: A Return to Fundamentals; Prentice-Hall: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Tarzan, M.; Bergesio, L.; Gras, E. Error and Flow Control Protocol (EFCP) Design and Implementation: A Data Transfer Protocol for the Recursive InterNetwork Architecture. In Proceedings of the 2019 22nd Conference on Innovation in Clouds, Internet and Networks and Workshops (ICIN), Paris, France, 19–21 February 2019; pp. 66–71. [Google Scholar] [CrossRef]
- Welzl, M.; Teymoori, P.; Gjessing, S.; Islam, S. Follow the Model: How Recursive Networking Can Solve the Internet’s Congestion Control Problems. In Proceedings of the 2020 International Conference on Computing, Networking and Communications (ICNC), Big Island, HI, USA, 17–20 February 2020; pp. 518–524. [Google Scholar] [CrossRef]
- Thompson, P.; Davies, N. Towards a performance management architecture for large-scale distributed systems using RINA. In Proceedings of the 2020 23rd Conference on Innovation in Clouds, Internet and Networks and Workshops (ICIN), Paris, France, 24–27 February 2020; pp. 29–34. [Google Scholar]
- Burns, A.; Davis, R.I. A Survey of Research into Mixed Criticality Systems. ACM Comput. Surv. 2017, 50. [Google Scholar] [CrossRef]
- Goodwin, G. Control System Design; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- PNSol. Assessment of Traffic Management Detection Methods and Tools; Technical Report MC-316; Ofcom: London, UK, 2015. [Google Scholar]
- Reeve, D.C. A New Blueprint for Network QoS. Ph.D. Thesis, Computing Laboratory, University of Kent, Canterbury, Kent, UK, 2003. [Google Scholar]
- Trivedi, K.S. Probability and Statistics with Reliability, Queuing, and Computer Science Applications, 2nd ed.; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Simovici, D.A.; Djeraba, C. Mathematical Tools for Data Mining: Set Theory, Partial Orders, Combinatorics; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Leahu, L. Analysis and Predictive Modeling of the Performance of the ATLAS TDAQ Network. Ph.D. Thesis, Technical University of Bucharest, Bucharest, Romania, 2013. [Google Scholar]
- Leon Gaixas, S.; Perello, J.; Careglio, D.; Grasa, E.; Tarzan, M.; Davies, N.; Thompson, P. Assuring QoS Guarantees for Heterogeneous Services in RINA Networks with ΔQ. In IEEE International Conference on Cloud Computing Technology and Science (CloudCom); IEEE: Piscataway, NJ, USA, 2016; pp. 584–589. [Google Scholar]
- Davies, N.; Thompson, P. Performance Contracts in SDN Systems. IEEE Softwarization eNewsletter. May 2017. Available online: https://sdn.ieee.org/newsletter/may-2017/performance-contracts-in-sdn-systems (accessed on 25 June 2020).
- Chang, C. Performance Guarantees in Communication Networks; Telecommunication Networks and Computer Systems; Springer: London, UK, 2000; Chapter 7. [Google Scholar]
- Saltzer, J.; Reed, D.; Clark, D. End-to-end arguments in system design. ACM Trans. Comput. Syst. 1984, 2. [Google Scholar] [CrossRef]
- Davies, N.; Holyer, J.; Thompson, P. An Operational Model to Control Loss and Delay of Traffic at a Network Switch. In The Management and Design of ATM Networks; Queen Mary and Westfield College: London, UK, 1999; Volume 5, pp. 20/1–20/14. [Google Scholar]
- Lee, M.; Rai, P.; Yip, F.; Eagle, V.; McCormick, S.; Francis, B.; Reeve, D.; Davies, N.; Hammond, F. Emergent Properties of Queuing Mechanisms in an IP Ad-Hoc Network; Technical Report; Predictable Network Solutions Ltd.: Stonehouse, UK, 2005. [Google Scholar]
- Byers, J.; Luby, M.; Mitzenmacher, M.; Rege, A. A Digital Fountain Approach to Reliable Distribution of Bulk Data. In Proceedings of the ACM SIGCOMM ’98 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communication; Association for Computing Machinery: New York, NY, USA, 1998. [Google Scholar]
- Kelly, F. Charging and accounting for bursty connections. In Internet Economics; McKnight, L.W., Bailey, J.P., Eds.; MIT Press: Cambridge, MA, USA, 1997; pp. 253–278. [Google Scholar]
- Perros, H.G.; Elsayed, K.M. Call admission control schemes: A review. IEEE Commun. Mag. 1996, 34, 82–91. [Google Scholar] [CrossRef]
- Watson, R.W. The Delta-t transport protocol: Features and experience. In Proceedings of the 14th Conference on Local Computer Networks, Mineapolis, MN, USA, 10–12 October 1989; pp. 399–407. [Google Scholar]
- Clegg, R.G.; Di Cairano-Gilfedder, C.; Zhou, S. A critical look at power law modelling of the Internet. Comput. Commun. 2010, 33, 259–268. [Google Scholar] [CrossRef]
- Davies, N.; Holyer, J.; Stephens, A.; Thompson, P. Generating Service Level Agreements from User Requirements. In The Management and Design of ATM Networks; Queen Mary and Westfield College: London, UK, 1999; Volume 5, pp. 4/1–4/9. [Google Scholar]
- Davies, N.; Holyer, J.; Thompson, P. End-to-end management of mixed applications across networks. In IEEE Workshop on Internet Applications; IEEE: Piscataway, NJ, USA, 1999; pp. 12–19. [Google Scholar]
- RINArmenia. e-Hayt Research Foundation. Available online: https://rinarmenia.com/ (accessed on 25 June 2020).
- Doffman, Z. Russia In addition, China ‘Hijack’ Your Internet Traffic: Here’s What You Do. Forbes.com, 18 April 2020. [Google Scholar]
| Risk to StdDev | |||||||
|---|---|---|---|---|---|---|---|
| (pkts/sec) | (pkts/sec) | 1.00 × 10−5 | 4.265 | ||||
| on Rate | Duty Cycle | Equiv Rate | Variance | # Std Dev | 1.00 × 10−4 | 3.72 | |
| 50 | 38.53% | 19.265 | 19.265 | 3.1 | 1.00 × 10−3 | 3.1 | |
| 1.00 × 10−2 | 2.33 | ||||||
| No of Sources | Peak Rate | Average Rate | Variance of Estimator | Interesting Centile | Allocated Rate to Achieve | Ratio: Rate/Average | Allocation |
| 1 | 50 | 19.27 | 19.27 | 13.61 | 32.87 | 1.70628 | 32.87 |
| 2 | 100 | 38.53 | 9.63 | 9.62 | 57.77 | 1.49942 | 57.77 |
| 3 | 150 | 57.80 | 6.42 | 7.86 | 81.36 | 1.40777 | 81.36 |
| 4 | 200 | 77.06 | 4.82 | 6.80 | 104.27 | 1.35314 | 104.27 |
| 5 | 250 | 96.33 | 3.85 | 6.09 | 126.75 | 1.31586 | 126.75 |
| 10 | 500 | 192.65 | 1.93 | 4.30 | 235.68 | 1.22335 | 235.68 |
| 15 | 750 | 288.98 | 1.28 | 3.51 | 341.67 | 1.18236 | 341.67 |
| 20 | 1000 | 385.30 | 0.96 | 3.04 | 446.15 | 1.15793 | 446.15 |
| 25 | 1250 | 481.63 | 0.77 | 2.72 | 549.66 | 1.14126 | 549.66 |
| 50 | 2500 | 963.25 | 0.39 | 1.92 | 1059.46 | 1.09988 | 1059.46 |
| 60 | 3000 | 1155.90 | 0.32 | 1.76 | 1261.30 | 1.09118 | 1261.30 |
| 70 | 3500 | 1348.55 | 0.28 | 1.63 | 1462.39 | 1.08442 | 1462.39 |
| 80 | 4000 | 1541.20 | 0.24 | 1.52 | 1662.90 | 1.07896 | 1662.90 |
| 90 | 4500 | 1733.85 | 0.21 | 1.43 | 1862.93 | 1.07445 | 1862.93 |
| 100 | 5000 | 1926.50 | 0.19 | 1.36 | 2062.56 | 1.07063 | 2062.56 |
| 125 | 6250 | 2408.13 | 0.15 | 1.22 | 2560.25 | 1.06317 | 2560.25 |
| 150 | 7500 | 2889.75 | 0.13 | 1.11 | 3056.39 | 1.05767 | 3056.39 |
| 175 | 8750 | 3371.38 | 0.11 | 1.03 | 3551.37 | 1.05339 | 3551.37 |
| 200 | 10,000 | 3853.00 | 0.10 | 0.96 | 4045.42 | 1.04994 | 4045.42 |
| 250 | 12,500 | 4816.25 | 0.08 | 0.86 | 5031.39 | 1.04467 | 5031.39 |
| 300 | 15,000 | 5779.50 | 0.06 | 0.79 | 6015.17 | 1.04078 | 6015.17 |
| Order | Subject of Concern |
|---|---|
| 0: Causality | Does best case low-level permit the system to deliver any successful top-level outcomes within the demanded? |
| 1: Capacity | Will the delivered be within the requirement at economic/expected levels of load? |
| 2: Schedulability | Can the QTAs be maintained during (reasonable) periods of operational stress? |
| 3: Behaviour | Does the system contain (or is it sensitive to) internal correlation effects/events: how does that influence QTA breach hazards? |
| 4: Stress | Is the system sensitive to load correlation effects created outside the system(s) under consideration? |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thompson, P.; Davies, N. Towards a RINA-Based Architecture for Performance Management of Large-Scale Distributed Systems. Computers 2020, 9, 53. https://doi.org/10.3390/computers9020053
Thompson P, Davies N. Towards a RINA-Based Architecture for Performance Management of Large-Scale Distributed Systems. Computers. 2020; 9(2):53. https://doi.org/10.3390/computers9020053
Chicago/Turabian StyleThompson, Peter, and Neil Davies. 2020. "Towards a RINA-Based Architecture for Performance Management of Large-Scale Distributed Systems" Computers 9, no. 2: 53. https://doi.org/10.3390/computers9020053
APA StyleThompson, P., & Davies, N. (2020). Towards a RINA-Based Architecture for Performance Management of Large-Scale Distributed Systems. Computers, 9(2), 53. https://doi.org/10.3390/computers9020053






