1. Introduction
Procedural content generation is progressively becoming an established tool in the development of video games. This is especially true in the case of virtual environments and landscapes, which is particularly labour-intensive when designed by hand. Due to the advent of procedural generation, content can be automatically generated, tackling this issue by reducing development time and production costs. Furthermore, procedural generation also enables the possibility of pseudo-infinite worlds and on-the-fly content creation, amongst other things. These are just a few reasons that has driven research in this area, with approaches seeking to generate a diverse range of environmental assets. One area which particularly receives little to no attention is the prodedural creation of forest and woodland bodies. In the case of natural landscapes, vegetation is a common and important element within the virtual environment. This is especially evident in modern video games, where forestry is frequently used as part of the in-game world. Virtual forests may not only be used as scenery elements, but to enhance game mechanics for, say, providing cover to players in first-person shooter games.
The alternative to a procedural methodology is through a manual or semi-automatic design process. In the case of in-game forest scenes, this would involve the manual distribution of individual trees within the virtual world by an environment artist. However, a few problems arise when following this approach. Namely, this process is not only time-consuming, but the quality of the resulting scene is reliant on the subjective considerations of the designer. One method of circumventing these issues is by randomly sampling positions where trees are subsequently placed at. However, this approach is not representative of the way natural, real-life forests propagate. Instead, natural forests are governed by the developmental cycles of an ecosystem, spanning hundreds of years [
1]. Approaches to model the distribution of these trees, should, therefore, ideally, reflect this process. As a result, there has been a handful of papers which delve into ecosystem models and methods of generating plant communities, which are explored later in our discussion.
This paper extends our previous effort [
2] to undertake this challenge, by introducing a handful of generation techniques and placement strategies, followed by a survey, evaluating each method in terms of perceived realism and playability. Furthermore, the attributes of the generated forestry (such as the density of the trees) are also studied to measure their impact on a player’s perception of a generated forest. This has a clear application in the games development sector, as forestry is a common asset found in games, and designers need to consider which procedural approach best suits the experience they try to create for a player. With this in mind, the hypotheses for this paper are:
Hypothesis 1 (H1)
. A method which is an approximation of a real-life process (a bio-inspired approach) is perceived to generate more enjoyable and realistic content, over a stochastic method which uses randomness to distribute trees.
Hypothesis 2 (H2)
. The canopy coverage of each forest is a significant variable in the perceived playability and realism of it.
The structure of this paper is as follows:
Section 2 provides an overview of procedural content generation algorithms, and a review of their use in generating virtual foliage and flora communities.
Section 3 presents three different approaches in procedural forest generation and spatial distribution of trees within a virtual environment.
Section 4 and
Section 5 discuss our pilot and main evaluations, respectively, whereas
Section 6 presents an extended set of results.
Section 7 presents a frequency analysis of the user’s subjective selection counts and
Section 8 provides the conclusions, also discussing future work.
2. Background
In procedural content generation, content is generated stochastically via algorithms [
3,
4]. This category of approaches has found success in a number of domains, including both research and commercial applications [
5,
6]. Interest in procedural content generation for games was born from early computer systems of the time and their inherent technical limitations [
7]. Today, such approaches can be applied to synthesize a broad spectrum of virtual content, ranging from terrain height-maps [
8,
9,
10,
11], buildings and their furnishings [
12,
13], to the placement of assets for an entire level for a video game [
14], such as settlements [
15] or, as in our case, plant ecosystems [
16].
Procedural generation techniques have been applied specifically to the generation of simulated vegetation. The majority of existing research into procedurally generated vegetation focuses on generating individual items of vegetation, rather than an ecosystem built from individual plants. One of the most prominent methods for generating virtual trees procedurally is through the use of Lindenmayer Systems (L-Systems) [
17]. L-Systems can be used to create fractal-like patterns, using re-writable grammars [
18]. These types of systems are often used to generate the skeletal branches and stems of virtual trees [
19,
20,
21,
22]. In the work of Livny et al. [
23], the authors even proposed an algorithm which reconstructed the skeletal system of a tree from a point-cloud through the use of L-Systems. The generation of other parts of a tree’s structure, such as the bark, can also be generated procedurally. This was demonstrated by Dale et al. [
24], in which the authors proposed a procedural technique for generating bark patterns, through a biomechanical physics model which emulated fractures in a tree’s surface over time.
Procedural methods have also been applied to generate other forms of vegetation, such as mushrooms [
25] or lichens [
26]. An example of the earliest research in procedurally generating of systems of multiple plants is by Reeves and Blau [
27], who explored the problem of how to generate virtual forests. A technique was developed which uses particle systems to approximate individual trees. The designer first defines a few parameters, such as the minimum distance between trees and the height-map of the terrain to place trees on. The algorithm then randomly distributes procedurally generated trees within the environment suited to the supplied parameters. Another related class of algorithms are point distribution methods. There have been a number of papers which show their use in the procedural placement of objects, including trees and forestry [
28,
29]. A recent example of this is by Ecormier et al. [
30], in which a variance-aware disk-based distribution algorithm is presented. In particular, the authors highlight its usage in synthesising virtual forest scenes.
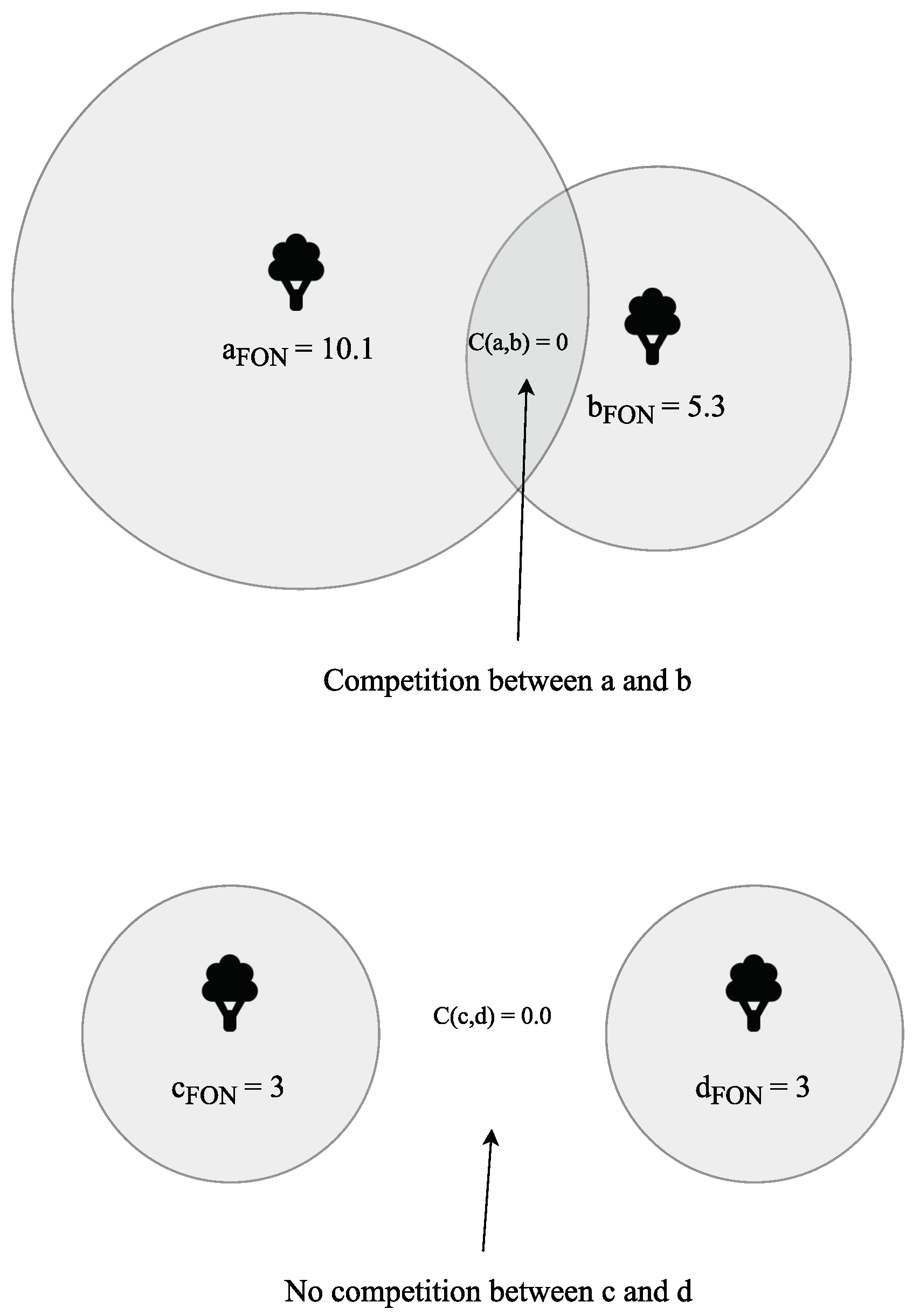
Other approaches, which consider plant competition models, have been developed. Plant competition models consider the simulation of each plant in an ecosystem, and interactions with its neighbours. Such an approach is presented by Bauer et al. [
16] where the authors describe the
field-of-neighbourhood (FON) model. The FON is a circular radius around each tree which determines the zone in which this tree competes with others in the community. If the FON of a tree overlaps with another tree’s FON, then these trees are in competition with each other for resources. Otherwise, if there is no overlap between a tree’s FON and another, then this tree is not in competition with any others. An illustration of this can be seen in
Figure 1. There are two competition models to consider if the FON of two or more plants overlaps: symmetric competition and asymmetric competition. Alsweis and Deussen [
31] define these as:
Symmetric competition: When considering the competition between two plants, resources are split evenly between the two. This infers that the two plants are of the same size, and pose an equal threat to one another:
where
yields the competition/FON-overlap between the two plants.
Asymmetric competition: In the case of two plants, resources are split unevenly between the two, based on which FON is larger. This means that the tree with the smaller FON will be dominated by its competitor, resulting in no access to resources and its eventual death:
Alsweis and Deussen [
31] use bio-inspired rules coupled with the FON model to generate plant communities through asymmetric competition. The development of plants depends on a designer-supplied map that represents the amount of nutrition found throughout the terrain. Members of the simulated plant community reproduce by spreading their seed locally once they reach a certain size. The seed production of each tree also grows alongside its size—as it increases in size, it produces more seeds as a result. A ‘mortality risk’ is also introduced into the system, in which plants which fall below the average plant size are culled due to competition. Computer applications such as GREENLAB [
32] have also been developed to generate and study various bio-inspired growth models. Cournede et al. [
33] used this application to study forest growth and propose a software system to compose virtual forest scenes. Lane and Prusinkiewicz [
34] use a similar approach to develop plant communities. In their method, a plant community is represented as a multiset L-System, in which individual strings of the L-System represent a tree. This multiset of strings is then added to or removed from to simulate growth within the forest. The authors also describe similar concepts, such as a radius around each tree in which it interacts with others (similar to the FON model) and domination of resources through asymmetric competition. To do this, the authors introduce the following three steps for each tree in the multiset:
Cordonnier et al. [
9] draw attention to some scalability issues of FON-based competition models. In particular, the computational expense of FON models is moderate in smaller-scale simulations but infeasible at larger scales. The authors introduce an approach to procedurally generate ecosystems with combined terrain generation. Instead of using a FON-based model, a non-competitive cell-based approach is used to simulate growth. In this approach, the landscape is subdivided into cells, and ecosystem events are generated at random in a given cell. Plant growth, death, and germination are simulated based on plant viability. Plant viability is calculated by taking into account local temperature, soil moisture, and sun exposure, amongst other factors.
3. Forest Generation Approaches
In this section, we introduce three algorithms for the spatial distribution of trees within an environment. The first, the Naive algorithm, is provided as a baseline to evaluate the other methods against. This algorithm uniformly distributes trees randomly within the environment and is commonly used in games development. The second method is Propagation, based on a asymmetric plant competition technique, which implements the FON model discussed previously. This algorithm is a bio-inspired approach intended to approximate how natural forests grow over time. The third algorithm, the Clustering method, is provided as an intermediary between the Naive and Propagation algorithms by using an iterative random distribution technique. We have selected these three algorithms to examine the differences between plant competition models and methods, which randomly sample from a distribution.
3.1. Method 1: Naive
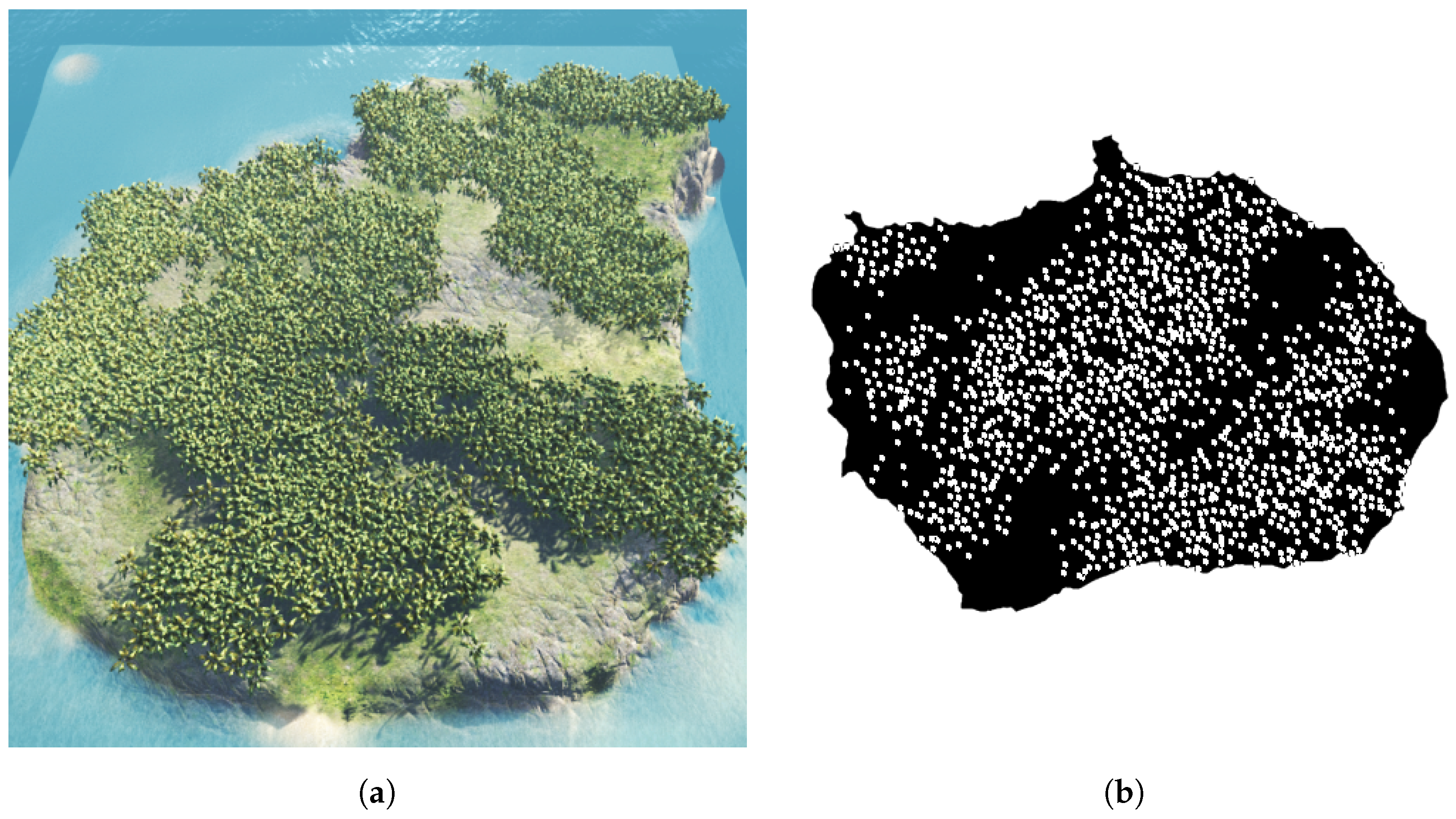
The Naive method randomly distributes trees within a given area. The algorithm distributes trees by sampling a random point in a uniform distribution, and places a tree at the sampled point. The algorithm used throughout this paper was adapted slightly to create forests at various densities. Instead of specifying a number of trees to spawn initially, a target density was specified and the algorithm ran until this target density was matched. Of all the methods described throughout this paper, the Naive method requires the least computational resources due to its simplicity.
The algorithms used in our studies are modified slightly to create forests at various densities. Instead of specifying a number of trees to spawn initially, a target density for the virtual forest is specified instead, and the algorithm is followed until this target density is matched. For example, the density
d for the virtual forest in
Figure 2a is
), which is measured as the percentage of canopy cover across the island.
3.2. Method 2: Propagation
The
Propagation method takes its inspiration from the rules that govern how forests develop in nature. This method should not be considered a faithful reflection of a natural process, but rather a bio-inspired approximation. To do this, this method is based on the asymmetric plant competition approach described by Lane and Prusinkiewicz [
34]. We also similarly make use of a FON-based approach to represent competition between trees. Furthermore, the three steps introduced by Lane and Prusinkiewicz within our algorithm are applied:
Succession: In each simulation iteration, every tree ages (and grows) until it reaches a mature age. Once a tree reaches a certain age, it dies and is culled from the population.
Plant propagation: Once trees have reached a mature age, they can reproduce by sowing seeds locally to their position.
Self-thinning: If a tree is growing close to another tree, then the oldest (and largest) tree will outgrow the other, thereby killing it and culling it from the environment. This is an approximation of asymmetric plant competition.
In addition to these rules, the wind direction and wind magnitude are also simulated whilst generating the virtual forest. It is important to note that this is not an accurate simulation of nature, and various factors (such as evolutionary forces) are ignored. We accept this, and have simply taken inspiration from biology to try and generate something which is visually appropriate.
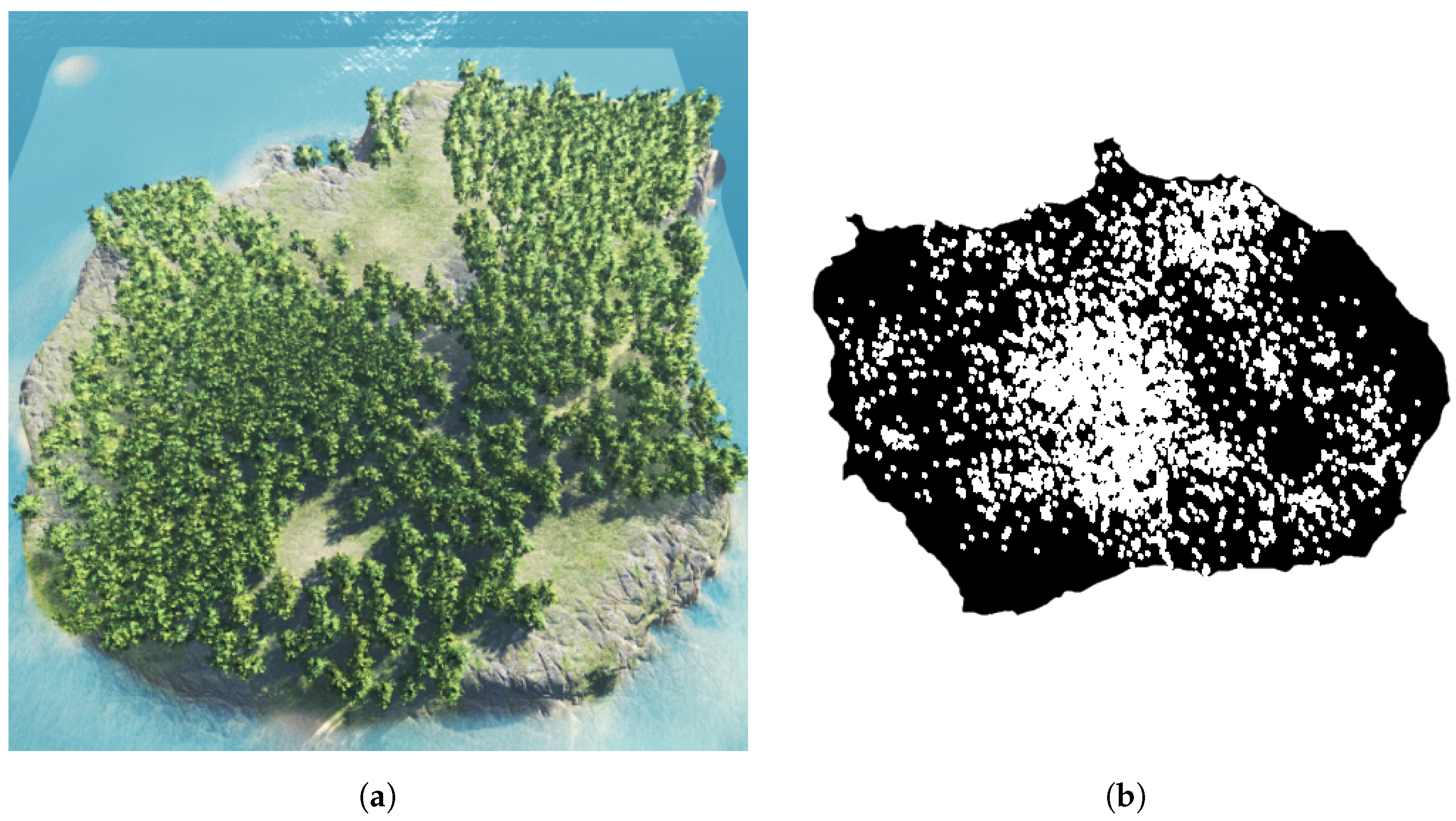
This method has the advantage of spacing trees in a fairly regular manner, which can be seen in
Figure 3a,b. Due to the nature of the approach, trees should remain equidistant, as competition results in the smaller tree’s death. However, this approach is generally more computationally expensive than point distribution methods, as it requires successive iterations and significantly more computation. This may be an issue for devices with limited computational power, such as mobile devices.
3.3. Method 3: Clustering
The Clustering method is an iterative random point distribution algorithm, with the goal of creating clustered areas of trees. To do this, the Clustering method initially selects a handful of random positions within the map in the first iteration, which we refer to as ‘spawn points’. These are chosen in a similar fashion to the Naive approach, sampling from a uniform distribution. In the second and final iteration, points are randomly chosen within a predefined radius of each spawn point to produce clusters of trees. Tree meshes are then placed in each of these final points to produce a forest.
Likewise to the
Naive method, the
Clustering approach has the advantage of requiring very minimal resources, as the environment is not continuously updated and rules are not considered for each iteration of the forest’s lifetime. This algorithm produces clustered distributions of trees, rather than an even and uniform distribution.
Figure 4a,b show two examples of virtual forests generated with this algorithm, from an aerial perspective.
4. First Study: 2D Evaluation
An initial study was undertaken to evaluate whether the more complex approaches are preferred by players. The study consisted of an online survey where participants ranked images of aerial 2D representations of forests. The objective of this evaluation was to collect preference data regarding the visual forest representations. For each question in the survey, participants were presented with three images of forests generated by each algorithm. Each image was randomly ordered on the screen, to reduce any selection bias between questions. The participant was then required to select one of these images which best matched the question criteria. The questions presented to each user throughout the survey evaluated two types of criteria. The first question was focused on the perceived realism of the environments. For these questions, the participant was asked to select two images (of the same three images) which they perceive to be the most and least realistic. The second criteria focused on the perceived suitability of the forest as an in-game environment. For these criteria, the participants were asked to imagine which environment they would (not) choose if they were to play a game based within this environment. Both of these metrics are subjective to the observer. The first relies on them comparing the image to their perception/experience of what a forest should look like. The second by comparison explores their game-play preferences, assessing whether the environments perceived to be more (or less) believable are considered more (or less) interesting to play games within.
Each participant was presented with five questions for each criteria, yielding a total of 20 individual questions. For each of the five questions, three new images were selected and presented to the participant.
2D Study Results
The online survey was completed by 86 participants. Of these participants, 53.48% self-identified as female, with the remaining 46.52% as male. Furthermore, we also captured the general location of each participant, as the demographic featured participants from around the world.
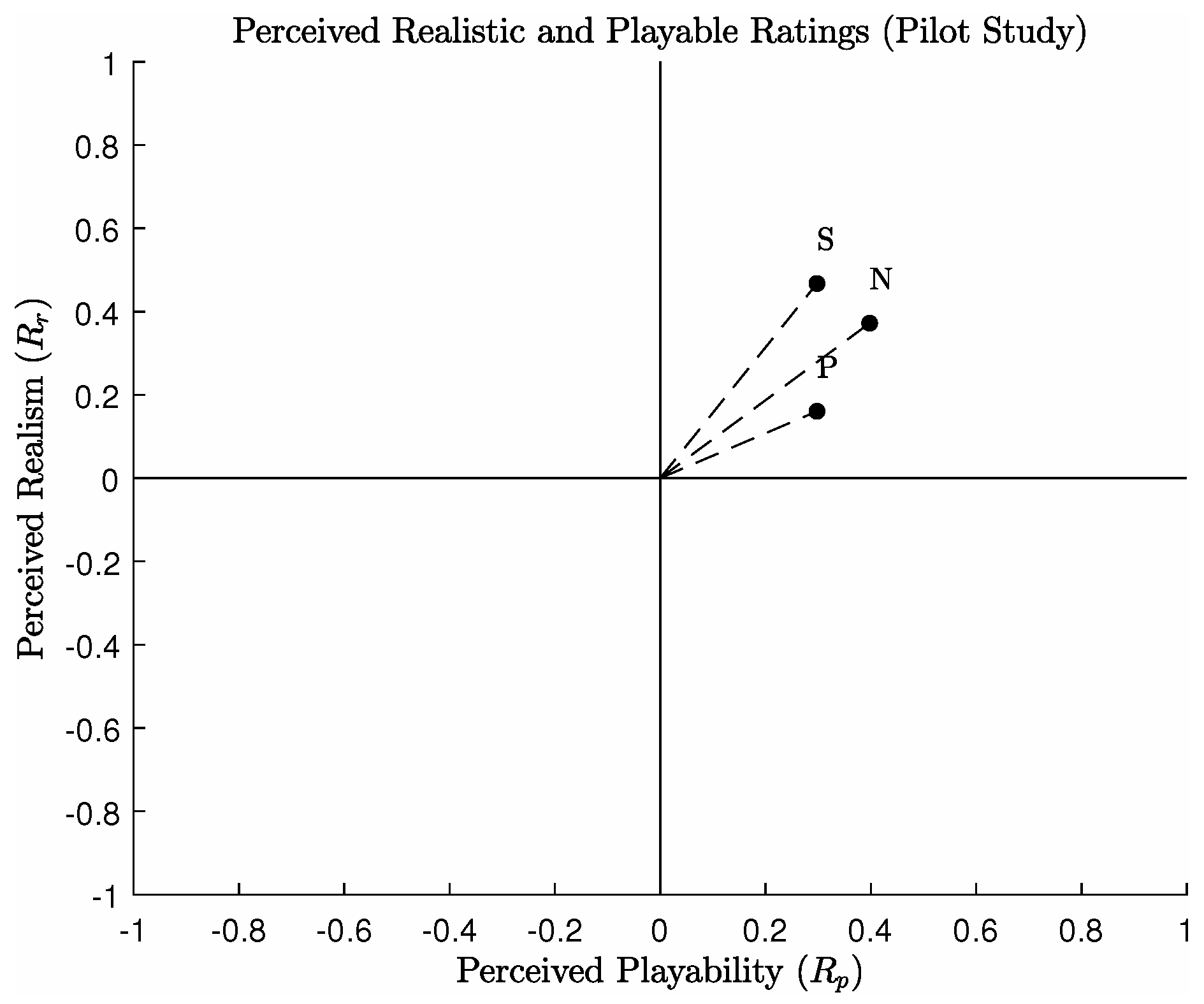
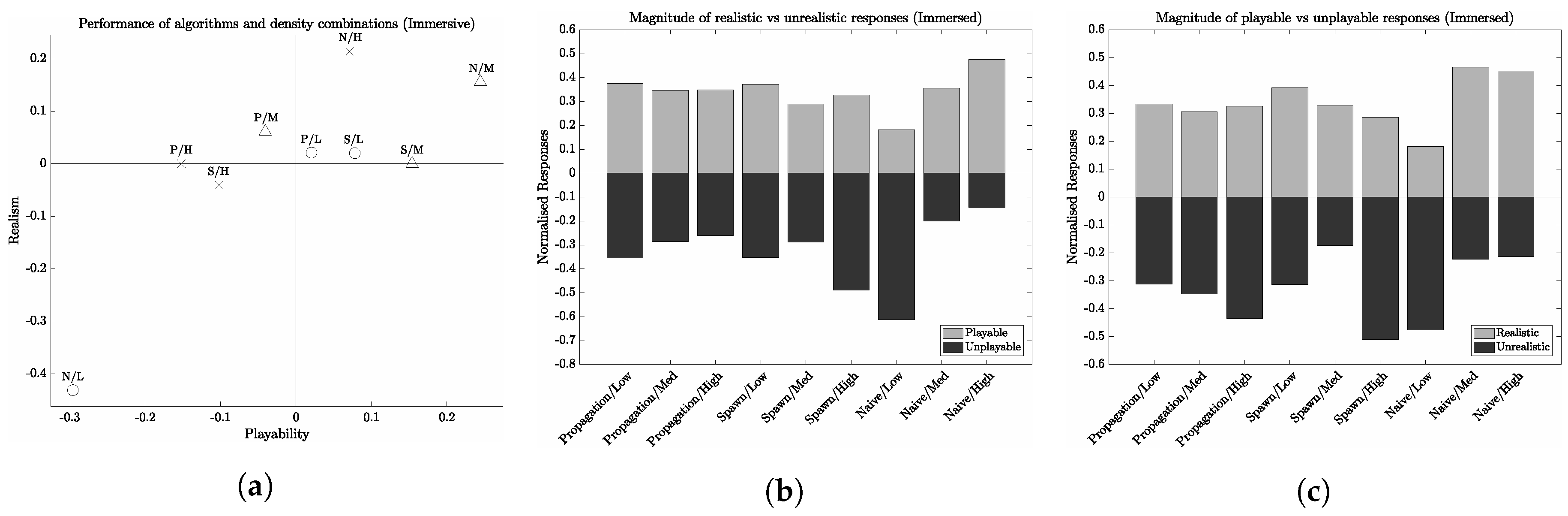
The first and most compelling result found is the performance of the Naive distribution algorithm, which was comparatively rated higher than its competitors in terms of its perceived playability (see
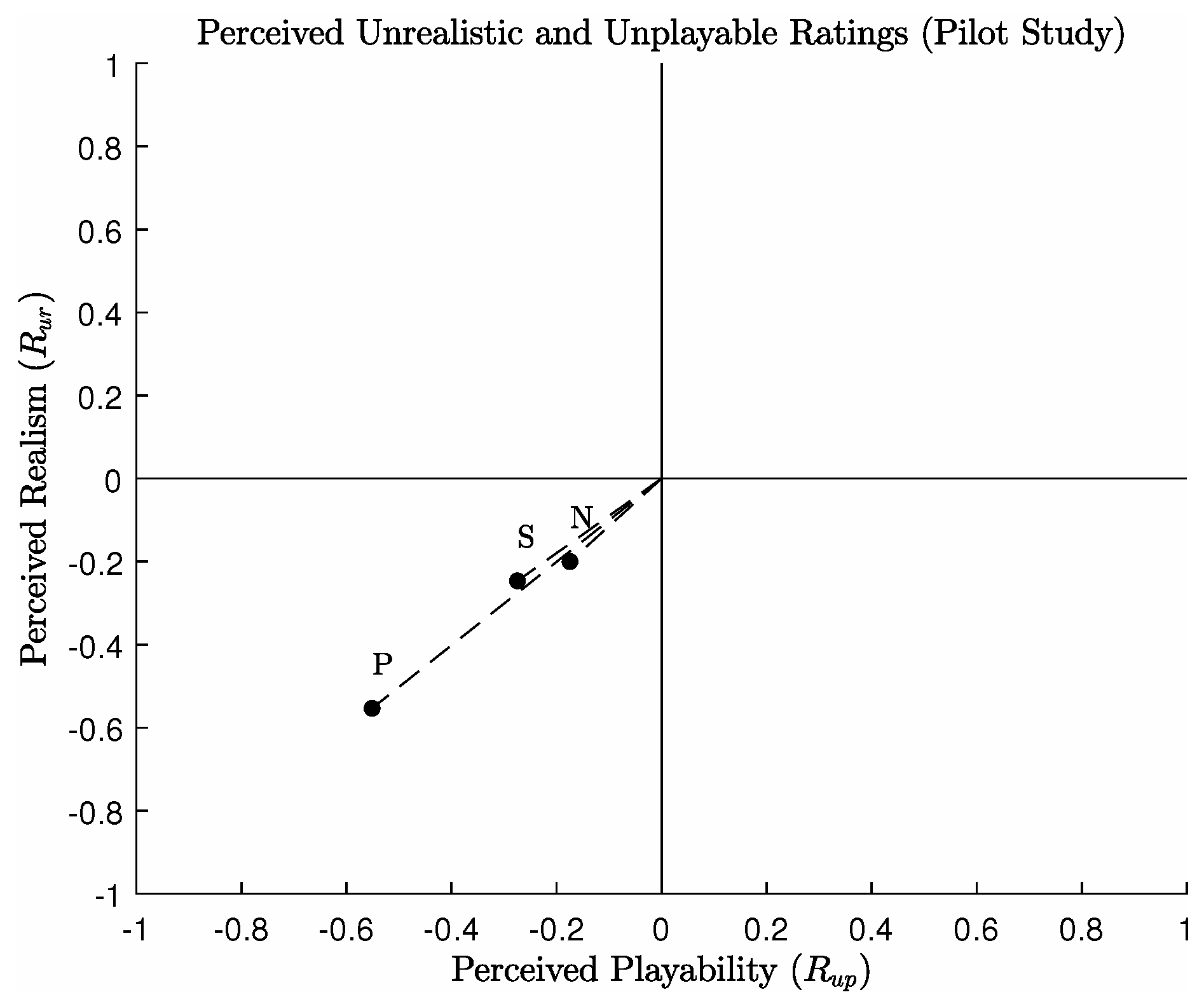
Figure 5). The Clustering method by comparison was rated as the method which produced the most forests perceived as most realistic.
Figure 5 demonstrates that the Propagation distribution method was rated the lowest in terms of realism, but produced forests which were similar to the Clustering method in terms of playability. This same trend can also be seen for the questions which asked for the most unrealistic and unplayable environments (see
Figure 6). For this category of questions, the Naive algorithm was similarly voted as the algorithm which produced the perceivably most realistic and playable environments. The Propagation algorithm however was rated as the most unrealistic and unplayable forest by a considerable margin.
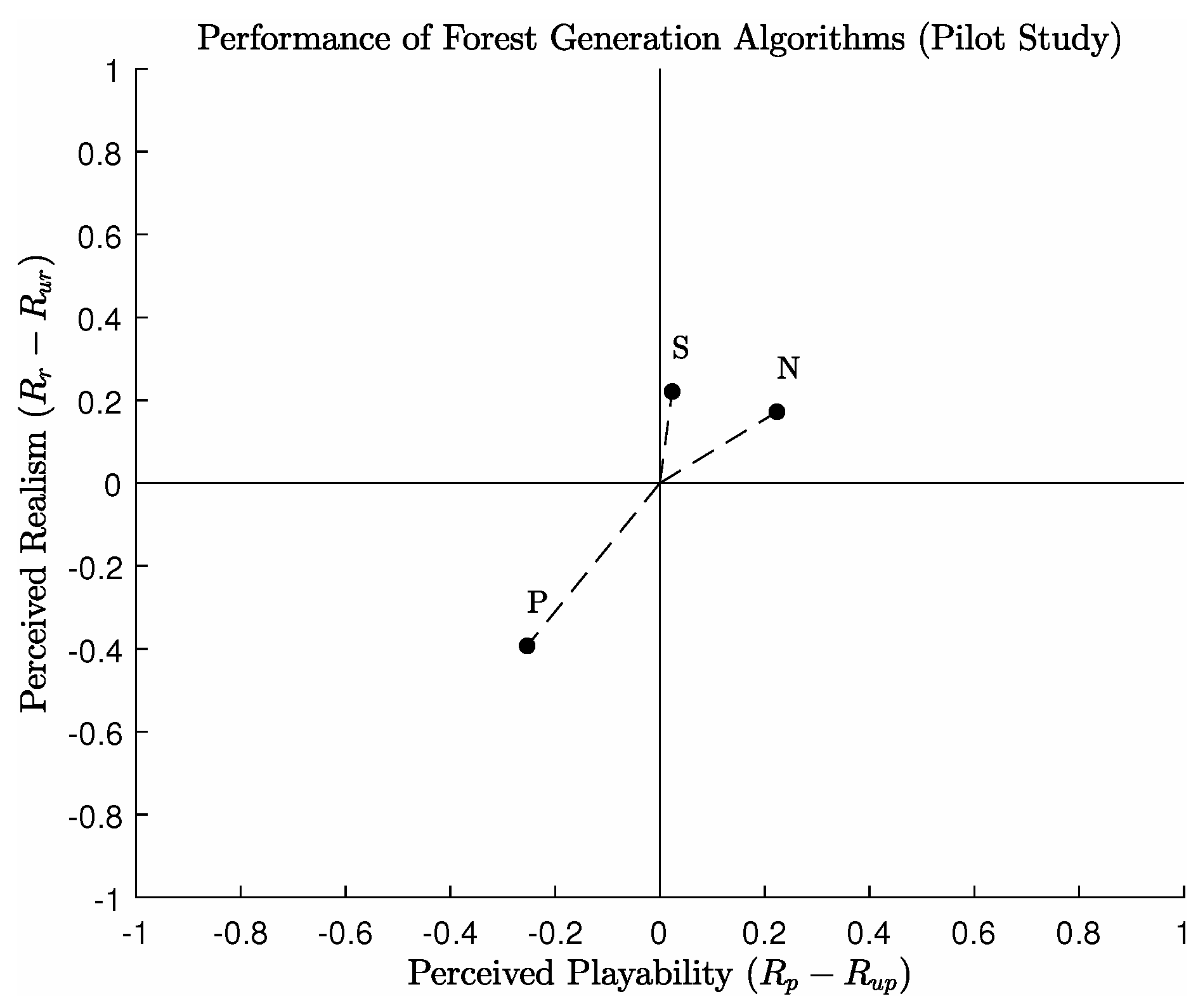
Lastly, the number of ratings for each algorithm were used to provide a metric of performance, to show the overall quality of each algorithm. The metric used is calculated as and . is the number of realistic ratings it received, is the number of unrealistic ratings, is the number of playable ratings received and is the number of unplayable ratings.
Figure 7 shows these two metrics plotted against each other, showing the overall performance of each algorithm. Interestingly, the performance of the Propagation algorithm was the poorest, producing the most unrealistic and unplayable environments. In contrast to this, the Clustering algorithm produced the most realistic environments, and the Naive algorithm yielded the most playable environments. It was hypothesised that the application of the Propagation algorithm would produce more realistic and playable environments, over the other two methods. However, the results show that the non-deterministic algorithms are rated higher in both categories. A further study is required to examine if this is the case under different conditions, and whether or not certain variables (such as forest density) yield similar results.
5. Second Study: 3D and Density Evaluation
A second study was conducted, in order to explore some of the questions raised by the first and to provide a more in-depth analysis of the reasoning behind selections. In this study, the density of each virtual forest, along with the algorithm that produces it, were recorded and analysed. The participant also had the option of providing written feedback at every stage of each question.
As with the previous study, for each question asked, the survey presented the participant with three images to choose from. The participant would then choose the image which best suited the question that was asked. The questions were tailored in such a way to investigate whether the density or algorithm used in virtual forest propagation resulted in more playable or realistic selections. When selecting images to present to the participant, two independent variables were considered.
5.1. Algorithm Chosen
For these questions, the process started by first randomly selecting a forest density from the list of available options (Low, Medium or High). This density was then used to select three images for the participant, each of which was generated with a corresponding algorithm. For example, if the randomly chosen density was ‘Low’, three low density forest images would be selected—one generated with the Naive algorithm, one with the Clustering algorithm, and another with the Propagation algorithm.
5.2. Forest Density
If the independent variable was forest density, then a similar process was followed, but showing varying forest densities generated with a single algorithm. To elaborate, an algorithm from the list of available options is randomly chosen (Naive, Clustering or Propagation). If, for example, the randomly chosen algorithm was ‘Naive’, then three forest images generated by the Naive algorithm would be displayed to the user—one with a low density, another with a medium density, and another with a high density.
Once the three images were selected using these processes, the participant was then asked four questions about the selected images. These questions involved rating the forest images which best suited the question that was asked. These four questions were:
‘Based on these images, which is the most realistic forest?’
‘Based on these images, which is the least realistic forest?’
‘If you were to play a game in one of these forests, which environment would you select to play within based on these top-down images?’
‘If you were to play a game in one of these forests, which environment would you not select to play within based on these top-down images?’
5.3. Image Perspectives
Another limitation of the first study was that the images presented to each participant were from a single, top-down 2D perspective. This was addressed in the second study by introducing images which were rendered in 3D from two perspectives. Additionally, these images allowed further analyse if player perspective had an effect on a participant ratings. The first was a top-down perspective similar to the images from the pilot study, but rendered photo-realistically in 3D. The second used a first-person perspective situated within the forest. An example of the perspectives used in images can be seen in
Figure 8.
These perspectives were also used in the question selection process. The same processes outlined earlier involving the isolation of forest density and the generation algorithm were used but for every perspective. This means that eight questions were asked for each perspective, resulting in a total of 24 questions for the participant to complete. The study ran for three weeks in total, with 71 respondents. Of these 71 respondents, 77.46% were Male, 19.71% were Female, and 2.81% did not specify their gender. The following sections analyse responses given for each perspective.
7. Frequency Analysis of Selection Counts
As mentioned previously, participants could rate images in two criteria: believability and playability. At each stage, participants are asked to choose which image satisfies them in the most and least of these criteria. This gives four possible ratings of images: the most/least believable and the most/least playable. There are also two variables which influence the generated forest, namely the type of algorithm and the forest’s density. Given these two variables, and the possible ratings each image can receive, an interesting question arises regarding the distribution of votes for images presented to participants. Observing frequency distributions will allow for interesting conclusions to be drawn from the data, for example, potential relationships between forest density and the number of times it was selected as the most believable. To achieve this, several contingency tables were created, showing the frequency of selection between different variables. These are each presented and discussed in the following sections.
7.1. Forest Density and Believability
The first area which was considered was the cross-tabulation of forest density types (low, medium, and high) with other variables, which could highlight some interesting relationships. The first of these is the perceived realism of images. In particular, the frequency each density was voted by participants as the most or least believable choice. Cross-tabulations are labelled by image perspective, to explore how this variable impacted the scores given by participants. It is also worth noting that these selections were mutually exclusive, disallowing the same image to be selected for both questions.
Table 1 presents the number of times each image density was selected as most or least believable, for each image perspective. Across all three image perspectives, it can be seen that lower density forests are frequently rated as the least believable selection. This is also true across all densities, with low densities ranking the lowest in terms of believability from a first-person perspective (
(2) = 13.38,
), a 2D aerial perspective (
(2) = 42.28,
), and a 3D aerial perspective (
(2) = 19.12,
). These results seem to suggest that low density distributions are generally unsuitable for generating forests which are similar to real-life, regardless of the user’s viewpoint. Interestingly, the opposite effect can be seen in the case of medium densities, with medium densities being consistently selected as the most believable forest. The distribution of tallies suggests this is the case is also regardless of image perspective, whether it be first-person (
(2) = 10.25,
), 2D aerial (
(2) = 30.78,
) or 3D aerial (
(2) = 10.25352,
).
Of the three image perspectives, the 2D aerial perspective shows the most polarised distribution of positive/negative rating. What is particularly interesting is the differences in perceived realism across the three forest densities. For this perspective, low density forests received a particularly high number of votes as the least believable density. Conversely, both medium and high densities were chosen more frequently as the most believable. However, medium densities were substantially more polarised. It should also be noted that the same pattern of polarisation with regard to medium and high densities can be seen across all three image perspectives. This could signify that participants could more easily determine the believability of medium and low densities, in contrast to high densities.
Another interesting area is the comparison of ratings between the two aerial perspectives. Comparing both aerial perspectives reveals some interesting results. The most noteworthy difference between the two perspectives is the contrast between negative/positive ratings. In this case, 2D aerial perspectives are more polarised with respect to positive/negative selection, suggesting that image dimensionality could impact perceived believability. Curiously, this is not true of high density forests, with little to no difference in selection frequency between 2D and 3D perspectives. However, it is worth noting that a more rigorous investigation is required to conclude if this is the case.
In a similar spirit, how first-person and aerial perspectives differ in selection frequency is another area of consideration. Naturally, it could be assumed that first-person and aerial perspectives receive considerably distinct believability ratings, due to differences in how clearly the distribution of trees can be viewed as a whole. For instance, participants may find it harder to survey distributions wholly from a first-person perspective, due to the lack of a vantage point. A comparison of first-person and aerial perspectives can be seen in
Table 1, highlighting a pattern of votes between the two. For example, low densities are considered significantly less believable across both first-person and aerial perspectives. Similarly, medium and high densities are considered more believable when comparing the two types of perspective. However, there is a substantially less polarisation between positive/negative votes in the case of the first-person perspective. This potentially indicates that judgement of believability may be more difficult from a first-person perspective, due to the inability to survey the distribution as a whole. Further work would be required to ascertain if this is the case, however.
7.2. Forest Density and Playability
In the preceding discussion, forest densities were cross-tabulated with believability to investigate the relationship between the two. However, believability is only one of two criteria in which participants were asked to rate images, the other being playability. Whilst believability is an interesting criteria to examine, how suitable a forest is as an environment in a video game is another important factor. For instance, exploring how the density of a generated forest affects its playability could inform level design in commercial games development. With this goal in mind, a cross-tabulation similar to the previous section was created to investigate relationships between forest density and playability. This is reflected in
Table 2, which displays the frequency each density was selected as the most/least playable choice.
Perhaps the most noteworthy result is that medium density forests were consistently rated as significantly playable environments, across each of the first-person (
(2) = 10.92,
), 2D aerial (
(2) = 40.92,
p < 0.0005) and 3D aerial (
(2) = 15.75,
) perspectives. A similar finding was unearthed in the previous section, revealing that medium forest densities were typically selected as the most believable environments. Compounded with this result, it can be concluded that medium densities were selected most frequently in terms of both believability and playability, regardless of image perspective. One similarity between
Table 1 and
Table 2 is that, in both, the 2D aerial perspective shows the most polarised results. This suggests that participants could most easily determine both believability and playability from this perspective. Whilst this is an unexpected and interesting result, we leave the task of exploring this area to future work.
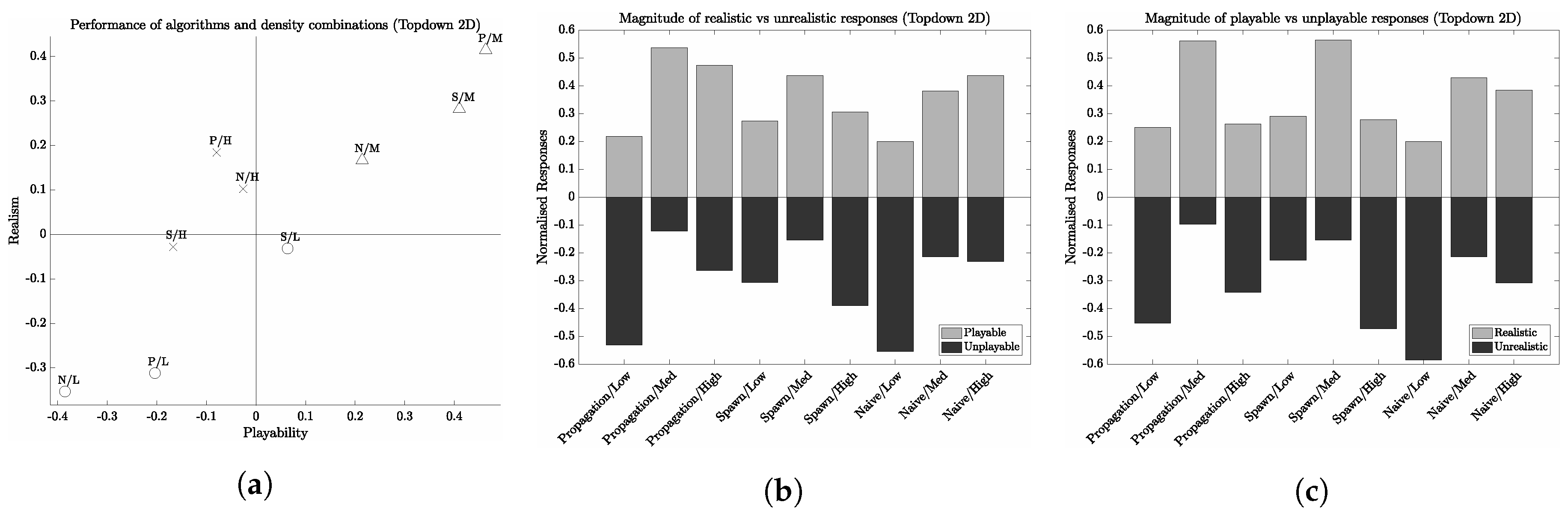
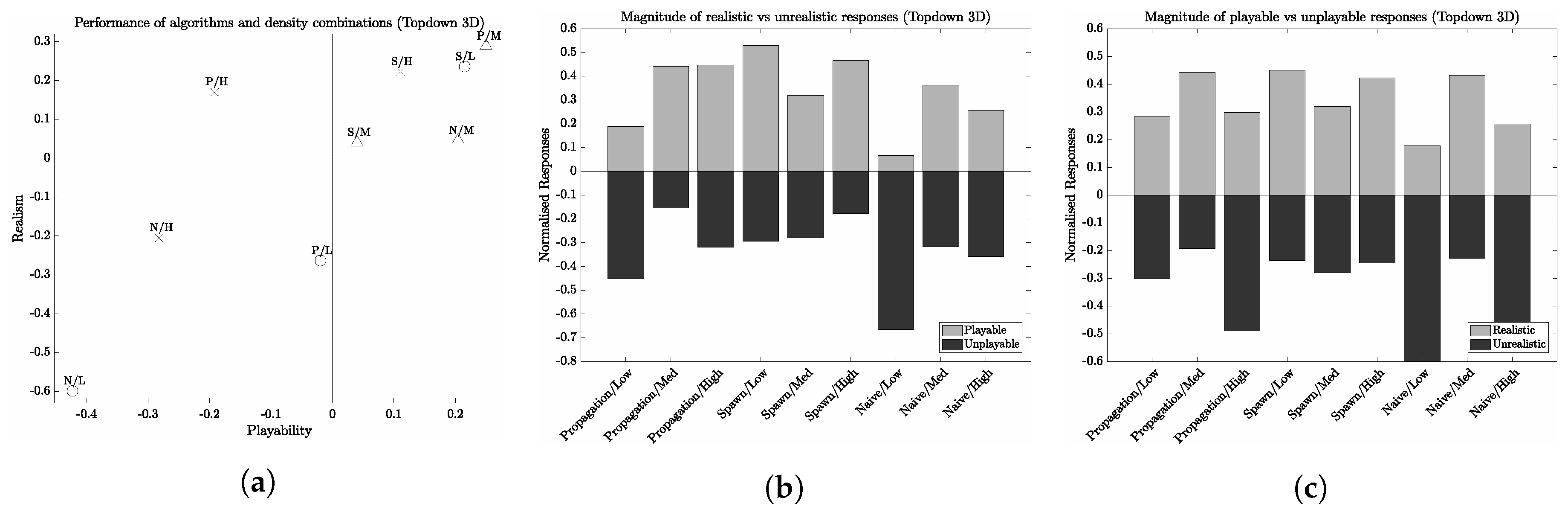
Another interesting discussion is the differences in playability votes between 2D and 3D aerial perspectives. Generally, the distribution of votes share several similarities between the two perspectives. For instance, in each case, both low and high densities are rated more times as the least playable environment than the most playable. An interesting observation is the fact that high densities received more unplayable ratings than playable, with this being the case across all three image perspectives. The fact that high densities are rated so differently in believability and playability could possibly indicate a negative relationship between the two. That is, high density point distributions create believable but unplayable environments. It may be the case for example that high density forests exhibit low tree interspacing which is considered believable, but does not result in a navigable game level. This may be a fascinating avenue of research for future work. It is worth noting, however, that statistical analysis indicates the results for high densities may be subject to noise; across first-person ( (2) = 4.17, ), 2D aerial ( (2) = 2.06, ) and 3D aerial ( (2) = 4.42, ) perspectives.
The comparison of the first person perspective against the two aerial perspectives reveals similar findings to the believability cross-tabulation. More specifically, the distribution of the most/least playable selections across all three densities follows a common pattern. In each case, low and high densities were chosen more frequently as the least playable environment. Similarly, medium densities were selected as the most playable environment. However, there is a considerable difference in polarity of negative/positive votes between first-person and aerial perspectives. In particular, the difference in negative/positive selection frequency are less extreme in the case of the first-person perspective. This is a very similar finding to the previous section, which concerned believability. Furthermore, this implies that participants found it harder to judge both believability and playability from first-person perspectives. As mentioned earlier, the lack of a vantage point could be the issue. However, further investigation would be required to identify if this is the case.
7.3. Generation Algorithm and Believability
Thus far, the impact of forest density on participant preferences has been discussed. Whilst the effects of forest density is an interesting area to explore, another factor in our study was the type of procedural algorithm used to generate virtual forests. Identifying how each of the three algorithms affects perceived believability/playability could give insights into which is the most preferred by players. More importantly, this could be crucial to commercial games development, whose aim is to create immersive and playable virtual environments for players. To achieve this, a similar methodology is used to the previous sections. As mentioned earlier, there were three procedural algorithms used to generate forest images. There were the naive, clustering, and propagation algorithms. A cross-tabulation of generation algorithm and believability ratings can be seen below in
Table 3.
The first noticeable result is that the naive algorithm generally received more votes in favour of it being the most believable image, rather than the least believable. This is also the case across all three image perspectives, which could signify that participants found the naive method to be a method of creating realistic forest distributions. However, this may not be the case, as statistical analysis shows insignificant results across first-person ( (2) = 2.225, ), 2D aerial ( (2) = 1.21, ) and 3D aerial ( (2) = 0.535, p = 0.76) perspectives. Similarly, the clustering algorithm was rated as more believable for the 2D and 3D aerial perspectives, suggesting potential differences between a first-person and aerial perspective. Although the effect observed for the 2D aerial perspective is likely due to noise ( (2) = 2.56, ), there is a significant probability that the 3D aerial perspective is not ( (2) = 12.28, ). This is evidence that the clustering algorithm is a feasible alternative to procedurally generating believable tree distributions, from an aerial perspective. This may have potential impacts on games development, especially given that the clustering algorithm provides a more efficient and suitable alternative to plant growth models.
The opposite can be found for the propagation algorithm, with generated images rated significantly as the least believable, for the 3D aerial perspective ( (2) = 14.73, ). The same effect is observed for the 2D aerial perspective, but lacks statistical significance ( (2) = 2.14, ). Interestingly, the same cannot be said for the first-person perspective, in which the propagation algorithm received more favourable ratings than unfavourable. However, there is a considerable chance that this may be due to noise too ( (2) = 0.535, ). These findings suggest that, generally, the propagation algorithm generates forest distributions which participants deem unbelievable from a 3D perspective. Furthermore, there are some noteworthy results when compared to the previous section, which explored the relationship of forest density and believability. Firstly, the density cross-tabulation featured boldly contrasting results with considerable polarisation between positive/negative selection counts. Furthermore, statistical tests highlighted a number of significant results and relationships. By comparison, cross-tabulating the type of procedural algorithm and selections made by participants reveals very few significant results. One explanation could be that participants find forest density a more distinguishable characteristic in assessing the believability of forest images.
7.4. Generation Algorithm and Playability
Whilst in the previous section the effects on believability were explored, another interesting and related area is how measures of playability are affected by the three algorithms used. Determining this may support games developers to create fun and challenging games, by displaying the most preferred algorithm for creating playable environments. A cross-tabulation of generation algorithm and received playability ratings can be seen in
Table 4.
For the first-person perspective, there are a few contrasting results between the three algorithms. Firstly, forests generated by the Naive algorithm were selected most often as the least playable, of the three algorithms in this perspective. Conversely, forests generated by the Propagation algorithm received the highest number of most playable votes. By the same token, the number of most/least playable selections for the Clustering algorithm are practically identical. These results potentially suggest that plant growth models are the most suitable for creating playable environments from a first-person perspective. On the other hand, uniform point distribution appears to yield the least playable environments in this perspective. Interestingly, almost the opposite effect can be seen from the 2D aerial perspective. Most noticeably, the Propagation algorithm was rated significantly as the algorithm which produces the least playable environments ( (2) = 7.802, ). To contrast, the Clustering algorithm was preferred in creating the most playable environments of the three algorithms, with this perspective in mind. The clear difference in selections between these the first-person and aerial perspectives shows that image perspective is a considerable part of how forests are judged in perceived playability. The 3D aerial perspective also shared a few commonalities to the 2D aerial perspective. For example, the Naive algorithm was rated almost identically to the 2D aerial perspective. Furthermore, the Clustering algorithm was considered the most frequently as creating the most playable environments ( (2) = 11.52, ), and the Propagation algorithm as the least ( (2) = 12.61, ).
There is also a considerable difference between selection counts in the first-person and aerial perspectives. Whilst the two aerial perspectives share different selection counts, they are very similar in nature. Perhaps the most glaring result is the selection frequency of the Propagation algorithm, which is generally rated well from the first-person perspective, but negatively in the two aerial perspectives. Further research would be required to ascertain why this is the case.
7.5. Summary
An in-depth look at forest selection counts has unearthed some results worthy of discussion. The focus of our analysis was to understand how participants perceive generated forests, for different sets of generation parameters. We explored two parameters—forest density and procedural algorithm—which both influence a large part of a forest’s appearance. More specifically, we explored the impacts these two parameters have on the perceived believability and playability of generated forests. Believability and playability were chosen as they represent a desirable goal of procedural environment generation in games development, towards creating realistic immersive worlds, which are fun and engaging to play within.
Analysis of selection counts revealed that forests with a medium density were consistently chosen as the most playable and believable environments. This was also true across all image perspectives. It appears that, if the aim of a game developer is to generate believable and playable forests, using a medium density produces the most optimal results. Another noteworthy result is the difference in selection between the first-person and aerial perspectives, with regard to forest density. In particular, there is considerably higher polarity between positive/negative votes from an aerial perspective. This indicates that participants could more easily determine the playability and believability of forests from an aerial perspective, as opposed to a first-person perspective.
Perhaps the most interesting result of the analysis of how the type of procedural algorithm affected selection counts is that algorithms which were received positively in the first-person perspective were received negatively in the two aerial perspectives, and vice versa. This is an unexpected result, as it signifies a considerable distinction and negative relationship between 1st-person and 3rd-person perspectives. This may be an interesting direction for further work in this area. In addition, both believability and playability selection counts displayed many similar patterns, with very little difference between the two cross-tabulations. This suggests that participants considered believability and playability very similarly, and perhaps implies a relationship between the two.
When comparing the cross-tabulations of forest density and procedural algorithm, there is also a clear distinction in terms of polarity. Specifically, the rankings of different forest densities contain far more polarised positive/negative votes than the type of generation algorithm. This shows that participants could more easily distinguish the playability and believability of forests with distinct densities, rather than distinct types of algorithms. These results may be of importance to the domain of procedural forest generation, since it highlights that forest density has a more crucial role in creating forestry than previously expected. There is also a substantial contrast between 1st-person and aerial perspectives throughout our analysis, indicating that the perspective of the generated forest is an important consideration. This could inform future work and the games development sector of how to generate more realistic and engaging virtual forests. Furthermore, comparing how believability and playability are ranked shows considerable differences in polarity throughout.
8. Conclusions and Future Work
This paper presents a user study into virtual forests, using three different approaches of spatially distributing trees to approximate a plant community. These three approaches consisted of a random uniform distribution algorithm, a asymmetric plant competition model, and an iterative random distribution algorithm for creating clusters of trees. Through this study, the results demonstrate that the asymmetric plant competition model (the ‘Propagation’ algorithm) produces forests which were rated the highest in terms of playability and believability, for both 2D and 3D aerial perspectives. This supports H1, suggesting that a bio-inspired plant competition model can produce forests which were rated the highest in these two criteria, but only for aerial image perspectives. This was not found in the case from a first-person perspective. Interestingly, however, a method which geometrically approximates asymmetric plant competition using pseudo-randomness to distribute trees (the ‘Clustering’ algorithm) received similar ratings for the same perspectives, and has utility as a less expensive alternative to plant competition models. We also found that the algorithms which score highly in the aerial perspective category were not scored as highly when viewed from the perspective of a player situated within the environment. Instead, we found that the control algorithm (pseudo-randomly distributing trees, the Naive approach) scored highly for both criteria when using this perspective. This may be advantageous to game designers who require an efficient alternative to expensive plant competition models. We also found a relationship between the forest density used in images and their rated playability by participants. In particular, forests generated with a high density scored low in playability but highly in realism—whereas forests generated with a low density scored low in realism and high in playability.
From this, we can say that, if the objective of the environment designer is realism and playability, they must consider the perspectives in which the forest is to be viewed when deciding on a procedural algorithm to generate it. If, for example, the virtual forest is to be used within a game where the player is situated within the forest, the Naive approach could be used to create satisfying content while simultaneously conserving computational resources. On the other hand, if the virtual forest to be created is to be used as scenery from an aerial perspective, then employing the asymmetric plant competition approach may generate more satisfying content.
Furthermore, the impacts of forest density and distribution algorithm on participant opinion were explored. More specifically, we were interested in how these two parameters affected believability/playability selection frequencies. Several significant results were unearthed from analysing image selection counts, which may be of interest to game designers. For instance, forest density was found to be a more distinguishable characteristic than the type of procedural algorithm. In addition, forests generated with a medium density were consistently chosen as the most believable and playable distributions. These findings may inform both games developers and researchers of how to improve the quality of generated content. These findings support H2: that the canopy coverage (density) of generated forest images is a significant variable in how it is perceived in terms of believability and playability.
In our experiments, our test group largely consisted of participants who were non-forest experts. One interesting area we would like to investigate in future work is the consideration of forest experts in our experiments. We could then contrast differences in preference between expert and non-expert viewpoints, which could offer some interesting insights. In addition, exploring the impacts of other visual characteristics of forestry is another aspect we are keen to develop in future work. For example, considering elements such as plant types, forest floor coverage, and other types of environments are all interesting questions we wish to address through further investigation.