A Privacy Preserving Cloud-Based K-NN Search Scheme with Lightweight User Loads
Abstract
1. Introduction
- We propose a PPkNN search scheme based on the new encryption method described above, which can perform comparison and addition operations in the encrypted domain, and use an R-tree structure to achieve sub-linear search complexity.
- Benefiting from the new encryption method, the construction of an R-tree can also be done by the cloud server on the encrypted domain, which can reduce the computational overhead of data owners and enhance the query user’s security by preventing data owners from knowing the data access pattern.
- We address and overcome the limitations of related works and make a comparison of our work with them.
- Experimental results over synthetic datasets show that our method is practical and efficient. Moreover, the workloads on user ends are very lightweight.
2. Related Works
2.1. A Brief Survey of the Access Control Mechanisms
2.2. A General Survey of Privacy-Preserving K-NN Problem
2.3. A Survey of the Most Related Works
- The search complexity of our scheme is faster than linear.
- The data owner does not have to share the decryption key to the cloud server or other query users.
- Our approach does not need extra local storage at users’ end and consumes extremely small computational resources.
- The cloud server returns neither the approximate results nor the indexes of resultant data points, but the accurate K-NN values.
- Not only suitable for two dimensional spatial tuples, our approach can be extended to high dimensional dataset, directly.
- Comparing with some methods in which two non-colluding servers are required, one honest-but-curious server is good enough to our scheme.
3. Preliminaries
3.1. Paillier Cryptosystem
- (1)
- Randomly select two large primes and , such that and are relatively prime, i.e., .
- (2)
- Compute and .
- (3)
- Compute and .
- (4)
- Public key is and secret key is .
- (1)
- Select a random number
- (2)
- (1)
- The decryption of the product of two ciphertexts and can be realized by the addition of the two corresponding plaintexts and directly, that is .
- (2)
- The decryption of a ciphertext raised to the power of a plaintext can be realized by computing the product of the corresponding plaintexts and directly, that is = .
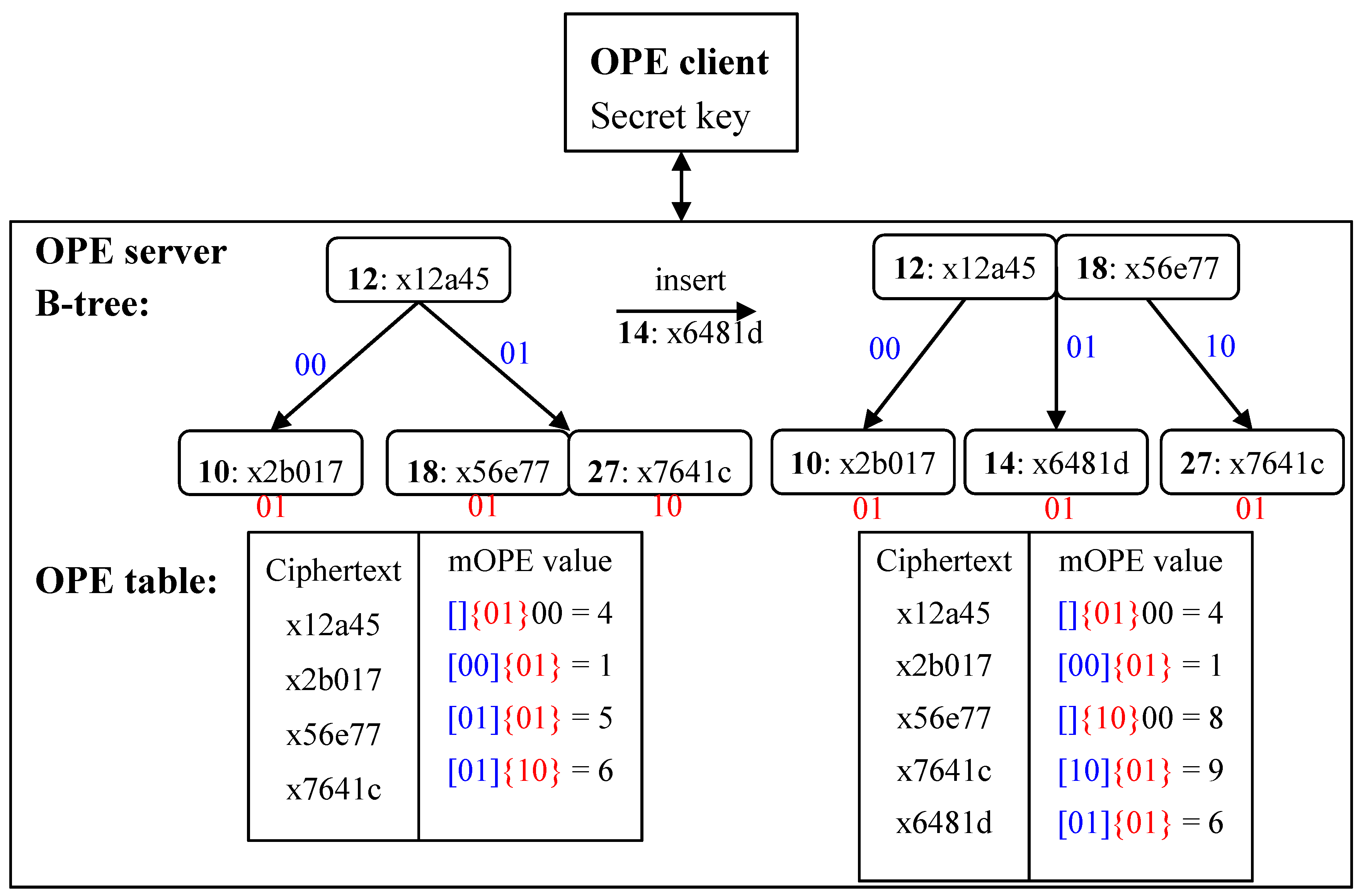
3.2. Order-Preserving Encryption
- (1)
- Client: Encrypt by and send the ciphertext to the server.
- (2)
- Server: If OPE table already contains , do nothing.
- (3)
- Client Server: Otherwise the client helps the server insert to OPE tree by starting a traversal from the root of OPE tree:
- (a)
- The server sends back the ciphertext to the client when it encounters a node.
- (b)
- The client decrypts to . If , the client tells the server to go left, otherwise go right.
- (c)
- Repeat steps a and b until the traversal goes to an empty leaf node and then puts in there.
- (d)
- Rebalance OPE tree if needed and update the OPE table.
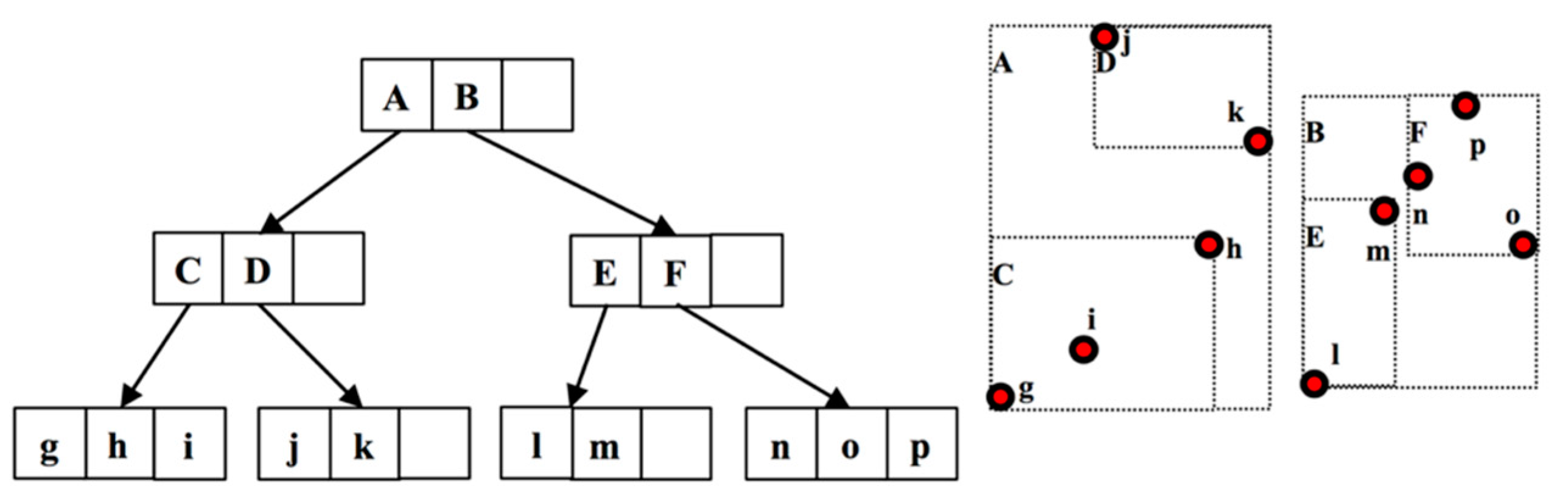
3.3. R-Tree
3.3.1. Bulk-Loading
- (1)
- Set ; if , simply create the root-MBR and end the algorithm.
- (2)
- Calculate the number of leaf-MBR pages, that is , where denotes the ceiling function.
- (3)
- Sort the data points according to the -th coordinate and divide them into slices. Each slice has data points.
- (4)
- Recursively process each slice, by repeating steps 2 and 3, where is the current data number in this slice, and until each slice contains only data points.
- (5)
- Create an MBR for each slice with pointers pointing to all data points in that slice.
- (6)
- Treat MBRs created in step 5 as data points and create higher level MBRs based on step 1.
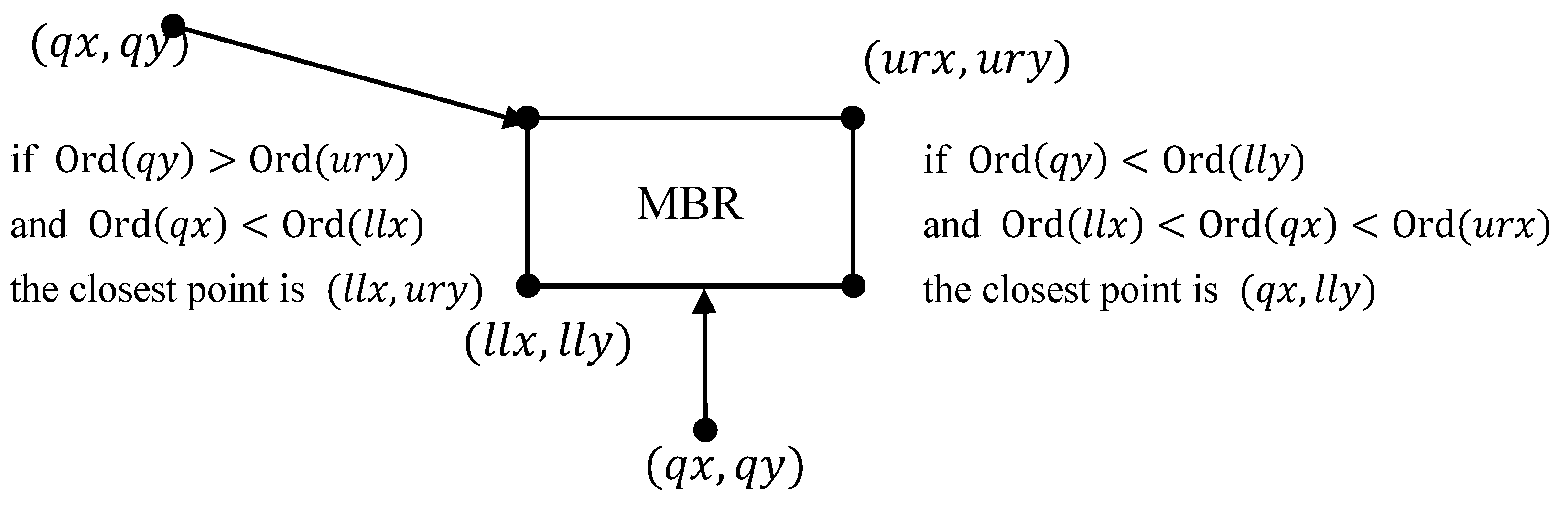
3.3.2. -NN Search over R-Tree
- (1)
- Initialize a priority queue and the result set .
- (2)
- Enqueue the root of into .
- (3)
- While is not empty
- (a)
- Dequeue element from .
- (b)
- If is a data point, put it in . If , return .
- (c)
- Otherwise
- Compute the distance from to each of the children of .
- Enqueue all children of into using their distance to as priority.
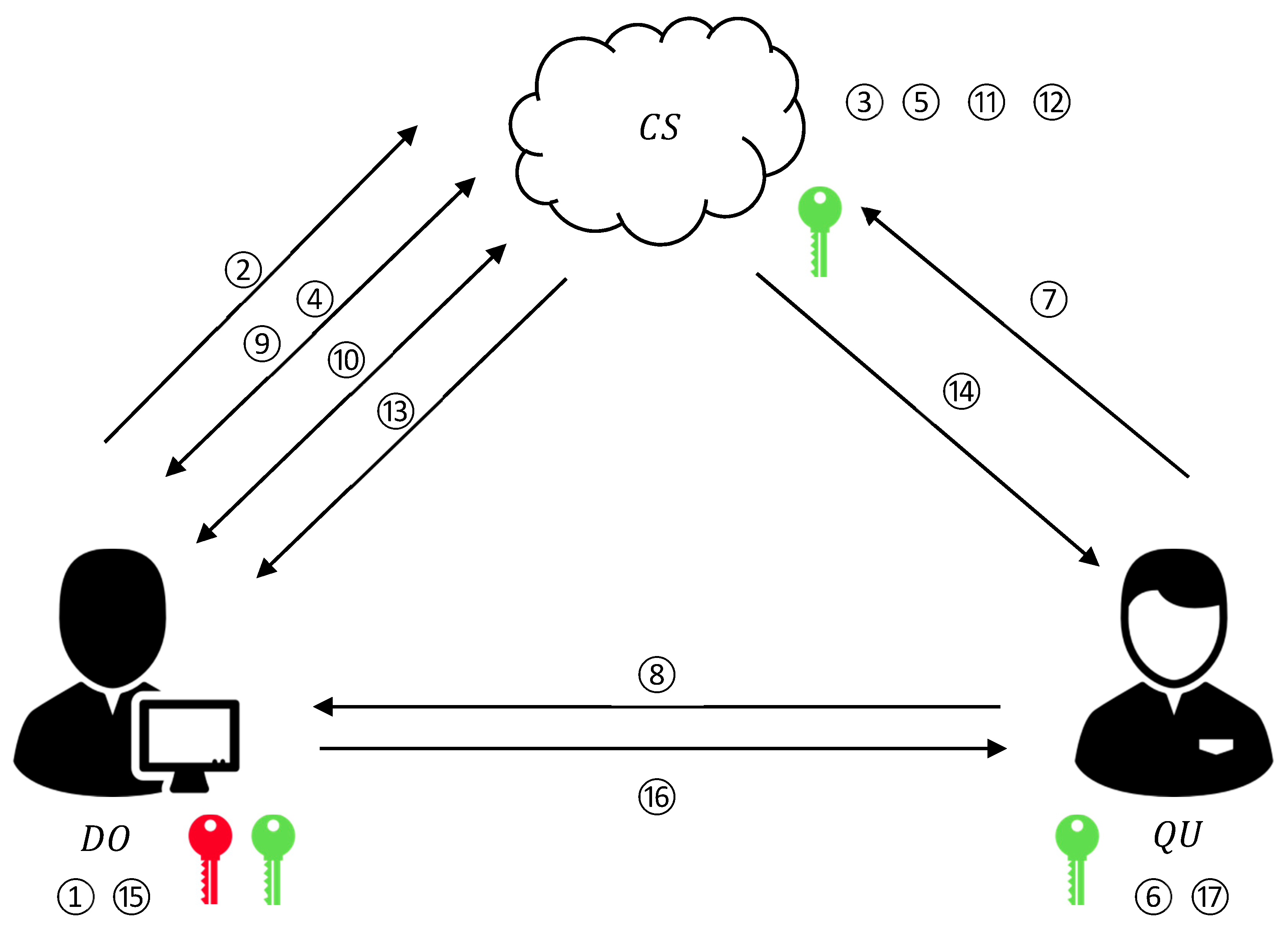
4. The Proposed Scheme
4.1. Overview
4.2. Encryption Method
4.3. Security Building Blocks
4.3.1. R-Tree Construction on the Encrypted Domain
| Algorithm 1. |
Input: -dimensional encrypted data points Output: Encrypted R-tree root pointer
Treat MBRs created in step 6 as data points and create higher level MBRs based on step 2. |
4.3.2. Secure Compare and Secure mOPE
| Algorithm 2. |
Input: two ciphertexts and Output:
|
| Algorithm 3. |
Input: ciphertext Output: the newest state of OPE table
|
4.3.3. Secure Square Euclidean Distance
| Algorithm 4. |
Input: ciphertexts and Output:
|
| Algorithm 5. |
Input: encrypted data points and Output: encrypted square Euclidean distance .
|
4.4. A Newly Proposed Privacy Preserving K-NN Search Scheme (PPKSS)
| Algorithm 6. SBFS |
Input: encrypted query , R-tree and . Output: encrypted resultant set
|
| Algorithm 7. |
Input: generate data points , where , ; make a query , and Results: receive -NN result Setup
Search
|
5. Security Analysis
5.1. Indistinguishability under Order Chosen Plaintext Attack
5.2. Privacy Preserving of Data
- (1)
- is prevented from knowing the actual plaintexts of the original data.
- (2)
- receives only -NN search results in every query request, and has no idea about the rest of the dataset.
5.3. Privacy Preserving of Query
- (1)
- is prevented from knowing the actual value of query.
- (2)
- While running the search scheme, must have no idea about the query, including the plaintext of it, the order relation with any other point in the dataset and the corresponding -NN search result.
6. Performance Evaluation
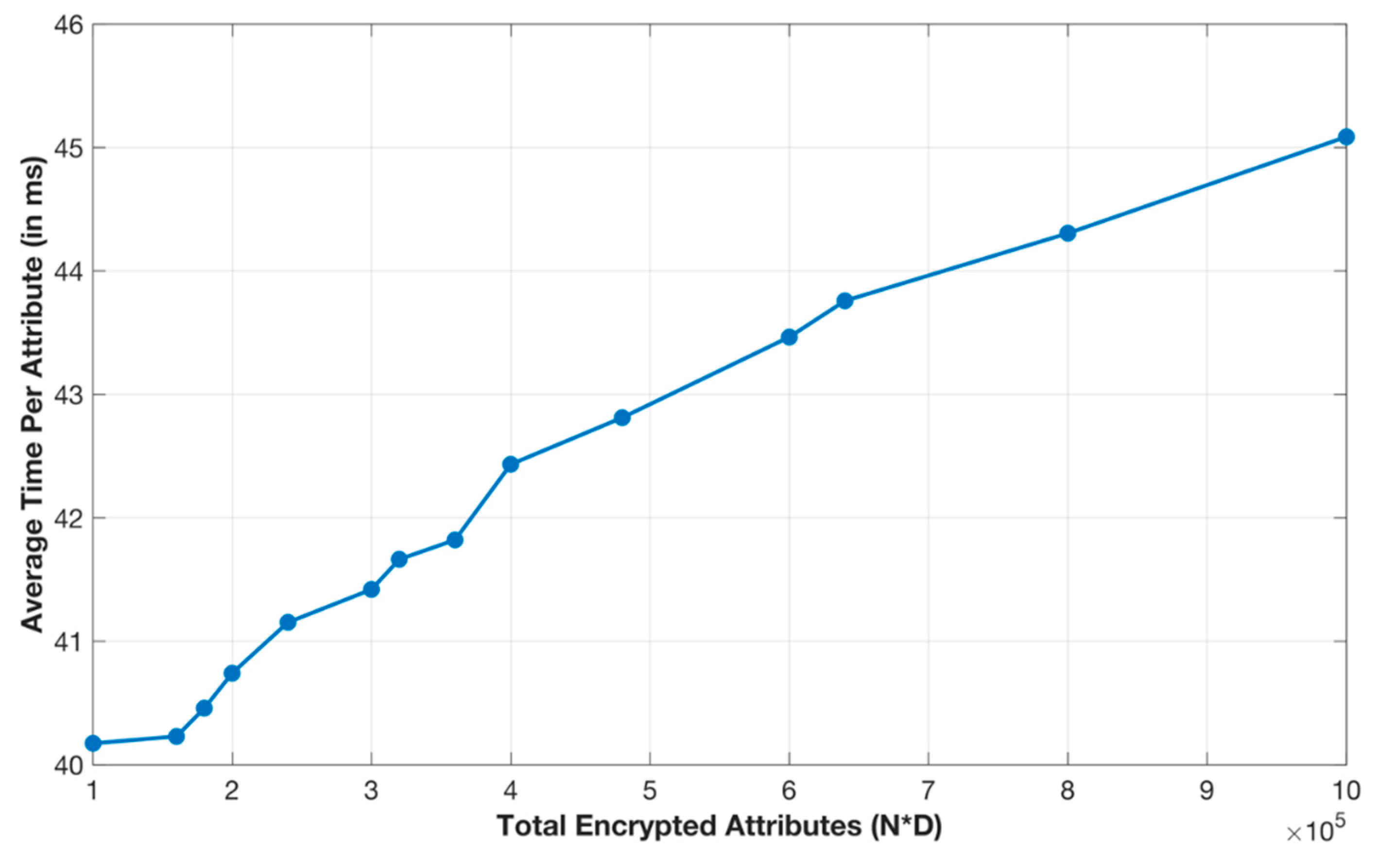
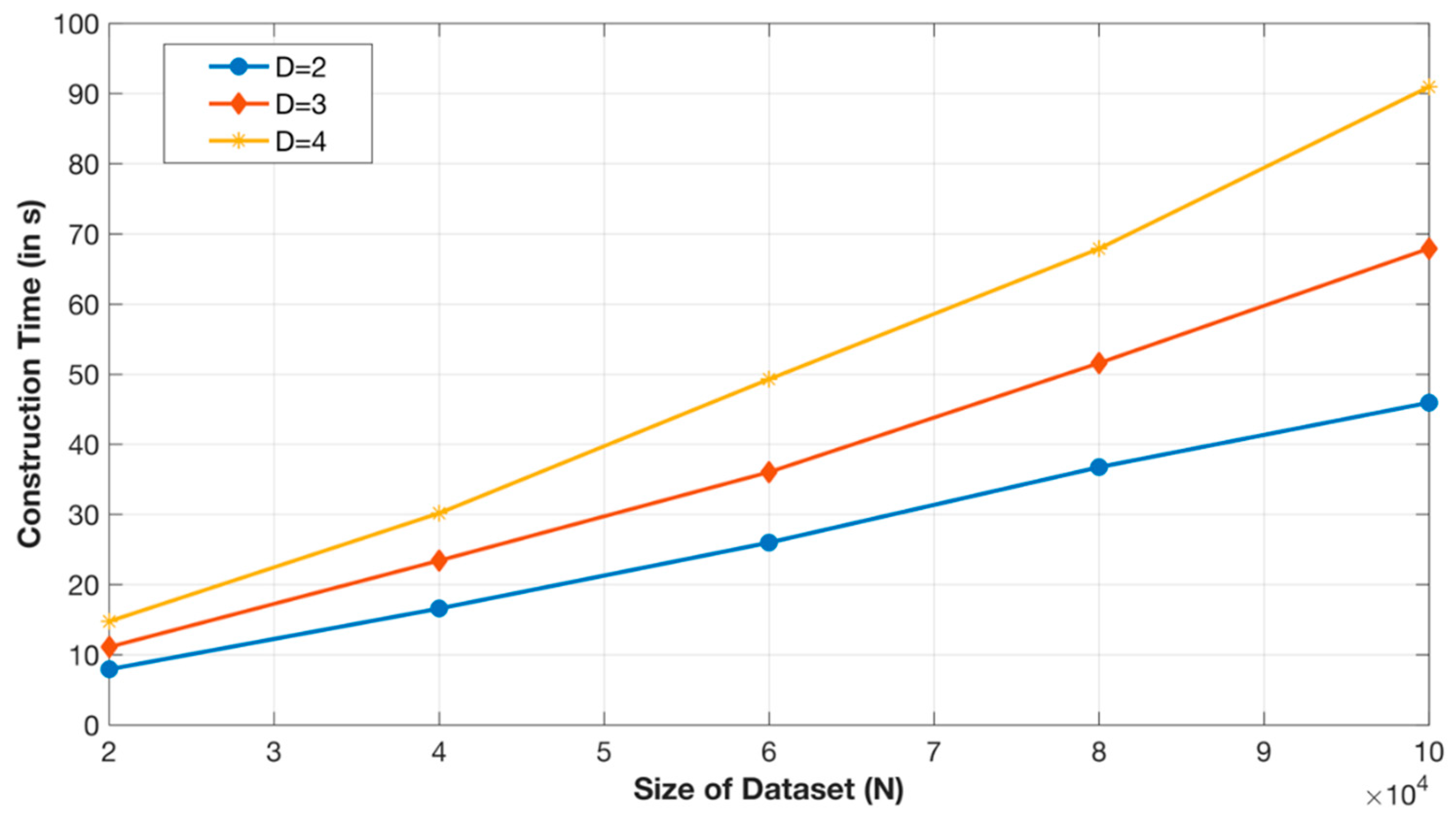
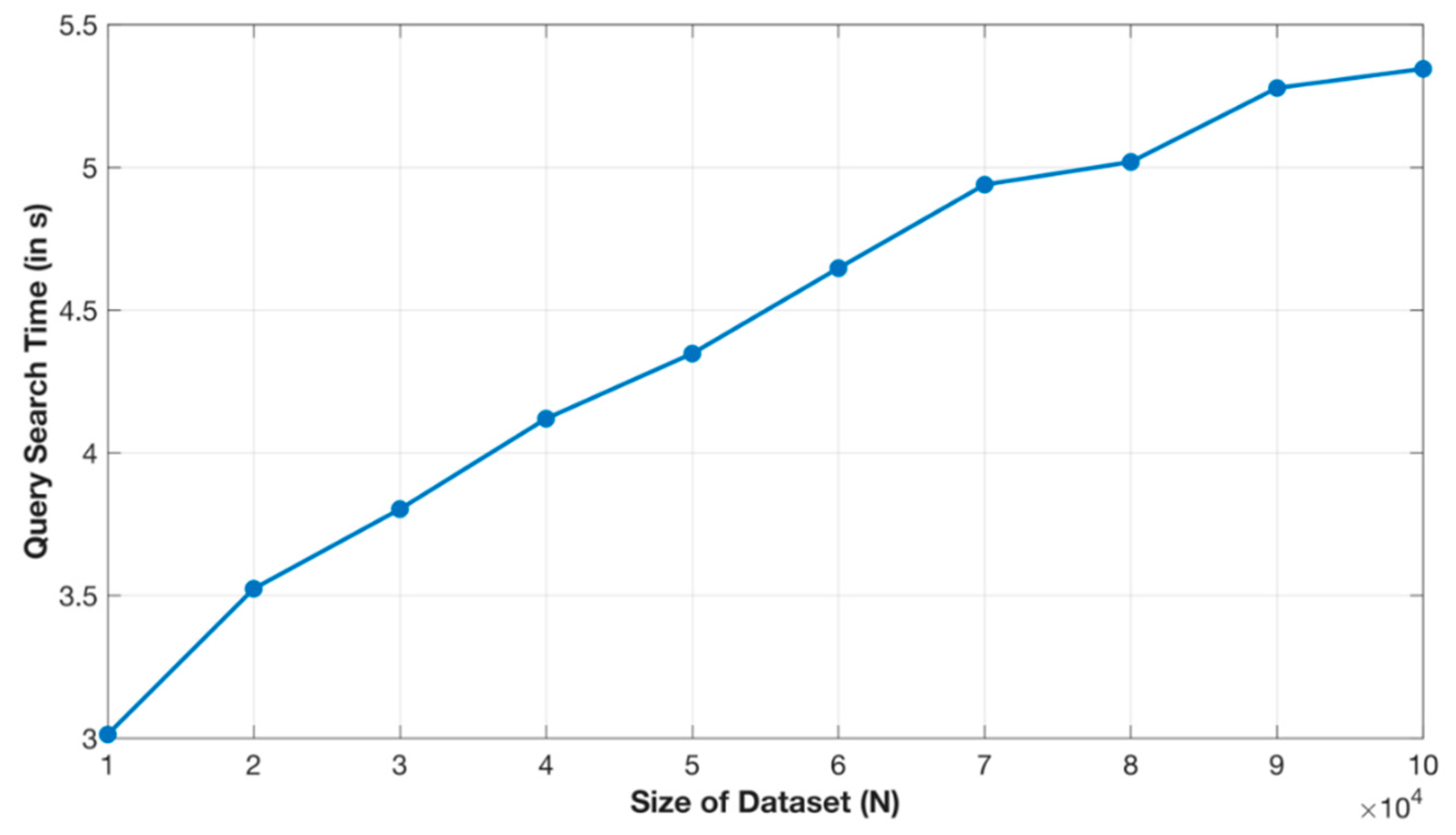
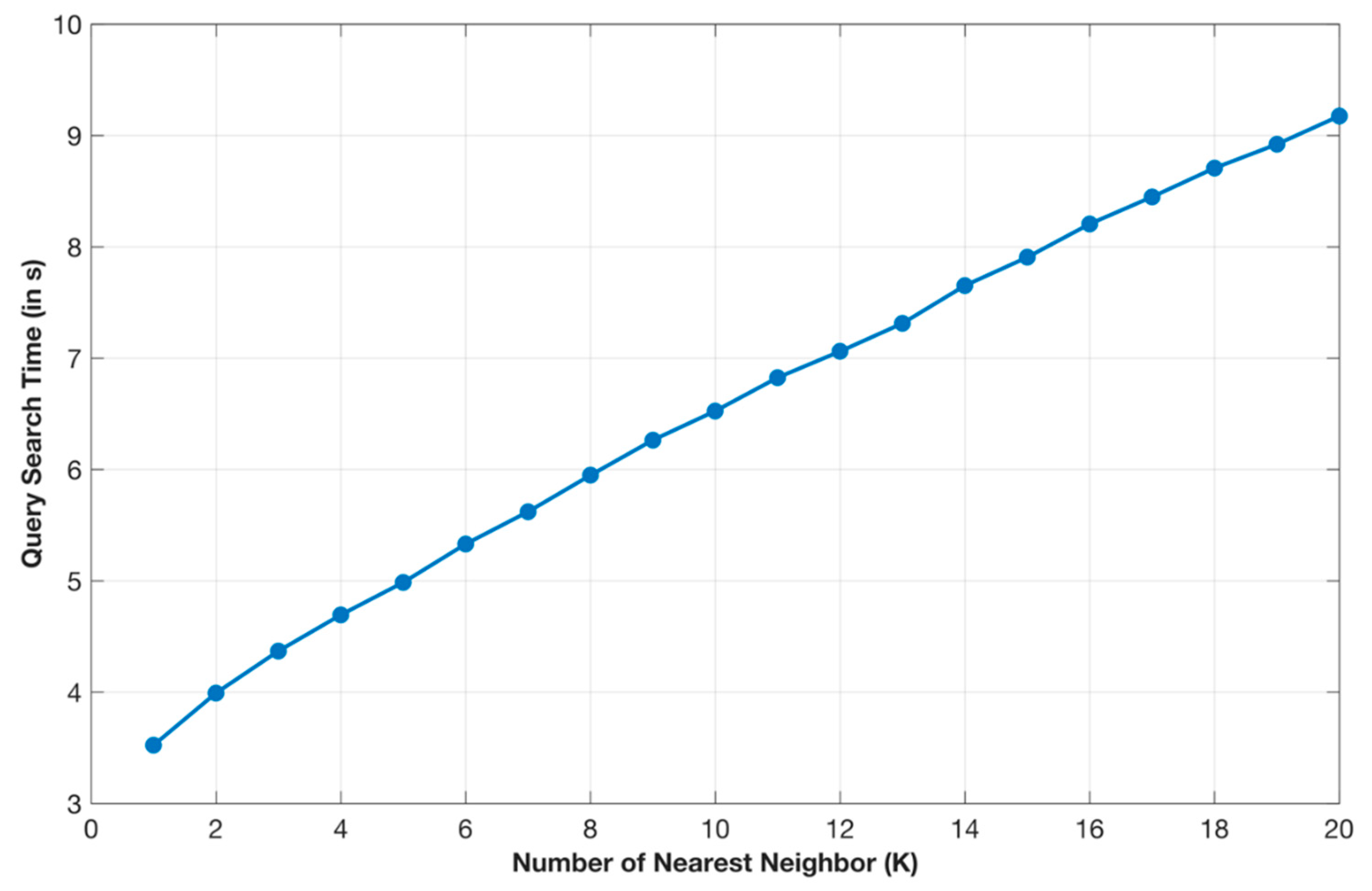
6.1. Complexity Analysis
6.2. Experimental Results
7. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
References
- Guttman, A. R-trees: A Dynamic Index Structure for Spatial Searching. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Boston, MA, USA, 18–21 June 1984; pp. 47–57. [Google Scholar]
- Popa, R.A.; Li, F.H.; Zeldovich, N. An Ideal-Security Protocol for Order-Preserving Encoding. In Proceedings of the IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 19–22 May 2013; pp. 463–477. [Google Scholar]
- Paillier, P. Public-key Cryptosystems Based on Composite Degree Residuosity Classes. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Prague, Czech Republic, 2–6 May 1999; pp. 223–238. [Google Scholar]
- Behera, P.K.; Khilar, P.M. A Novel Trust Based Access Control Model for Cloud Environment. In Proceedings of the International Conference on Signal, Networks, Computing, and Systems, Delhi, India, 25–27 February 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 285–295. [Google Scholar]
- “Mandatory Access Control.” Wikipedia: The Free Encyclopedia. Wikimedia Foundation, Inc. Available online: http://en.wikipedia.org/wiki/Mandatory_access_control (accessed on 21 December 2019).
- Samarati, P.; De Vimercati, S.C. Access control: Policies, models, and mechanisms. In International School on Foundations of Security Analysis and Design; Springer: Berlin/Heidelberg, Germany, 2001; pp. 137–196. [Google Scholar]
- Sandhu, R.S.; Coyne, E.J.; Feinstein, H.L.; Youman, C.E. Role-based access control models. Computer 1996, 29, 38–47. [Google Scholar] [CrossRef]
- Guoyuan, L.; Wang, D.; Bie, Y.; Lei, M. MTBAC: A mutual trust-based access control model in Cloud computing. China Commun. 2014, 11, 154–162. [Google Scholar] [CrossRef]
- Kayers, A.S.M.; Rahayu, W.; Dillon, T.; Chang, E.; Han, J. Context-aware access control with imprecise context characterization for cloud-based data resources. Future Gener. Comp. Syst. 2019, 93, 237–255. [Google Scholar]
- Kwon, Y.; Seo, J.H.; Park, T.B. Dynamic Role-based User Service Authority Control and Management on Cloud Computing. Univers. J. Electr. Electron. Eng. 2019, 6, 79–93. [Google Scholar] [CrossRef]
- Voloch, N.; Levy, P.; Elmakies, M.; Gudes, E. An Access Control Model for Data Security in Online Social Networks Based on Role and User Credibility. The Third International Symposium on Cyber Security Cryptography and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2019; pp. 156–168. [Google Scholar]
- Kayes, A.S.M.; Rahayu, W.; Tharam, T. Critical situation management utilizing IoT-based data resources through dynamic contextual role modeling and activation. Computing 2019, 101, 743–772. [Google Scholar] [CrossRef]
- Rong, H.; Wang, H.-M.; Liu, J.; Xian, M. Privacy-preserving k-nearest neighbor computation in multiple cloud environments. IEEE Access 2016, 4, 9589–9603. [Google Scholar] [CrossRef]
- Park, J.; Lee, D.H. Privacy preserving k-nearest neighbor for medical diagnosis in e-health cloud. J. Healthc. Eng. 2018, 2018, 4073103. [Google Scholar] [CrossRef] [PubMed]
- Burkhart, M.; Dimitropoulos, X. Privacy-preserving distributed network troubleshooting—bridging the gap between theory and practice. ACM Trans. Inf. Syst. Secur. (TISSEC) 2011, 14, 31. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, J.; Xiong, Y.; Huang, X.; Deng, T. PPK-means: Achieving privacy-preserving clustering over encrypted multi-dimensional cloud data. Electronics 2018, 7, 310. [Google Scholar] [CrossRef]
- Wong, W.K.; Cheung, D.W.-L.; Kao, B.; Mamoulis, N. Secure KNN Computation On Encrypted Databases. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Providence, RI, USA, 29 June–2 July 2009; pp. 139–152. [Google Scholar]
- Hu, H.; Xu, J.; Ren, C.; Choi, B. Processing Private Queries over Untrusted Data Cloud Through Privacy Homomorphism. In Proceedings of the IEEE 27th International Conference on Data Engineering, Hannover, Germany, 11–16 April 2011; pp. 601–612. [Google Scholar]
- Yao, B.; Li, F.; Xiao, X. Secure Nearest Neighbor Revisited. In Proceedings of the IEEE 29th International Conference on Data Engineering (ICDE), Brisbane, Australia, 8–12 April 2013; pp. 733–744. [Google Scholar]
- Elmehdwi, Y.; Samanthula, B.K.; Jiang, W. Secure K-nearest Neighbor Query over Encrypted Data in Outsourced Environments. In Proceedings of the IEEE 30th International Conference on Data Engineering, Chicago, IL, USA, 31 March–4 April 2014; pp. 664–675. [Google Scholar]
- Wang, B.; Hou, Y.; Li, M. Practical and Secure Nearest Neighbor Search on Encrypted Large-scale Data. In Proceedings of the IEEE INFOCOM 2016—The 35th Annual IEEE International Conference on Computer Communications, San Francisco, CA, USA, 10–14 April 2016; pp. 1–9. [Google Scholar]
- Xu, R.; Morozov, K.; Yang, Y.; Zhou, J.; Takagi, T. Privacy-preserving K-nearest Neighbour Query on Outsourced Database. In Proceedings of the Australasian Conference on Information Security and Privacy, Melbourne, Australia, 4–6 July 2016; Springer: Berlin/Heidelberg, Germany; pp. 181–197. [Google Scholar]
- Zhou, L.; Zhu, Y.; Castiglione, A. Efficient k-NN query over encrypted Data in cloud with limited key-disclosure and offline data owner. Comput. Secur. 2017, 69, 84–96. [Google Scholar] [CrossRef]
- Zhu, Y.; Huang, Z.; Takagi, T. Secure and controllable k-NN query over encrypted cloud data with key confidentiality. J. Parallel Distrib. Comput. 2016, 89, 1–12. [Google Scholar] [CrossRef]
- Katz, J.; Lindell, Y. Introduction to Modern Cryptography; Chapman and Hall/CRC: Boca Raton, FL, USA, 2014. [Google Scholar]
- Agrawal, R.; Kiernan, J.; Srikant, R.; Xu, Y. Order Preserving Encryption for Numeric Data. In Proceedings of the ACM SIGMOD International Conference on Management of data, Paris, France, 13–18 June 2004; pp. 563–574. [Google Scholar]
- Boldyreva, A.; Chenette, N.; Lee, Y.; O’neill, A. Order-Preserving Symmetric Encryption. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cologne, Germany, 26–30 April 2009; pp. 224–241. [Google Scholar]
- Goldreich, O. Foundations of Cryptography: Volume 1, Basic Tools; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Leutenegger, S.T.; Lopez, M.A.; Edgington, J. STR: A Simple and Efficient Algorithm for R-tree Packing. In Proceedings of the 13th International Conference on Data Engineering, Birmingham, UK, 7–11 April 1997; pp. 497–506. [Google Scholar]
- Hjaltason, G.R.; Samet, H. Distance browsing in spatial databases. ACM Trans. Database Syst. (TODS) 1999, 24, 265–318. [Google Scholar] [CrossRef]
- Henrich, A. A Distance Scan Algorithm for Spatial Access Structures. In Proceedings of the ACM-GIS, Gaithersburg, MD, USA, 1–2 December 1994; pp. 136–143. [Google Scholar]
- Wu, Y.; Wang, K.; Zhang, Z.; Lin, W.; Chen, H.; Li, C. Privacy Preserving Group Nearest Neighbor Search. In Proceedings of the EDBT, Vienna, Austria, 26–29 March 2018; pp. 277–288. [Google Scholar]
- Kayes, A.; Han, J.; Colman, A.; Islam, M.S. Relboss: A Relationship-Aware Access Control Framework for Software Services. In Proceedings of the OTM Confederated International Conferences” On the Move to Meaningful Internet Systems”, Rhodes, Greece, 21–25 October 2014; pp. 258–276. [Google Scholar]
- Khilar, P.M.; Chaudhari, V.; Swain, R.R. Trust-Based Access Control in Cloud Computing Using Machine Learning. In Cloud Computing for Geospatial Big Data Analytics; Springer: Berlin/Heidelberg, Germany, 2019; pp. 55–79. [Google Scholar]
- Kayes, A.S.M.; Rahayu, W.; Dillon, T.S.; Chang, E. Accessing Data from Multiple Sources Through Context-Aware Access Control. In Proceedings of the 17th IEEE International Conference on Trust, Security and Privacy in Computing and Communications, New York, NY, USA, 1–3 August 2018; pp. 551–559. [Google Scholar]

| [13] | [14] | [15] | [16] | [17] | Our Scheme | |
|---|---|---|---|---|---|---|
| Sub-linear search complexity | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ |
| No need to share private key with other | ✕ | ✕ | ✕ | ✕ | ✕ | ✓ |
| No need to store local data at user end | ✓ | ✕ | ✕ | ✓ | ✓ | ✓ |
| Return only accurate K-NN set | ✓ | ✓ | ✕ | ✓ | ✕ | ✓ |
| Applicable to high dimensional data | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ |
| Single Sever | ✓ | ✓ | ✓ | ✕ | ✓ | ✓ |
| Paillier Operation | Plaintext Operation | |||
|---|---|---|---|---|
| for Data | ||||
| for Data | ||||
| for Query | ||||
| for Query | ||||
| Return Results | ||||
| Total Query Time | Per. | Per. | Per. | Communication Cost | ||||
|---|---|---|---|---|---|---|---|---|
| 9.17 | 2.05 | 22.3% | 7.04 | 76.7% | 0.000003 | <0.01% | 469.003 | |
| 19.03 | 3.93 | 20.7% | 14.91 | 78.4% | 0.000003 | <0.01% | 978.568 | |
| 40.24 | 7.85 | 19.5% | 32.01 | 79.5% | 0.000003 | <0.01% | 2091.073 | |
| 77.8 | 14.52 | 18.7% | 62.55 | 80.4% | 0.000004 | <0.01% | 4030.649 | |
| 135.06 | 24.41 | 18.1% | 109.43 | 81.0% | 0.000006 | <0.01% | 7059.019 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsu, Y.-C.; Hsueh, C.-H.; Wu, J.-L. A Privacy Preserving Cloud-Based K-NN Search Scheme with Lightweight User Loads. Computers 2020, 9, 1. https://doi.org/10.3390/computers9010001
Hsu Y-C, Hsueh C-H, Wu J-L. A Privacy Preserving Cloud-Based K-NN Search Scheme with Lightweight User Loads. Computers. 2020; 9(1):1. https://doi.org/10.3390/computers9010001
Chicago/Turabian StyleHsu, Yeong-Cherng, Chih-Hsin Hsueh, and Ja-Ling Wu. 2020. "A Privacy Preserving Cloud-Based K-NN Search Scheme with Lightweight User Loads" Computers 9, no. 1: 1. https://doi.org/10.3390/computers9010001
APA StyleHsu, Y.-C., Hsueh, C.-H., & Wu, J.-L. (2020). A Privacy Preserving Cloud-Based K-NN Search Scheme with Lightweight User Loads. Computers, 9(1), 1. https://doi.org/10.3390/computers9010001





