A New Competitive Binary Grey Wolf Optimizer to Solve the Feature Selection Problem in EMG Signals Classification
Abstract
1. Introduction
2. Materials and Methods
2.1. EMG Data
2.2. Feature Extraction Using STFT
2.2.1. Renyi Entropy
2.2.2. Spectral Entropy
2.2.3. Shannon Entropy
2.2.4. Singular Value Decomposition-Based Entropy
2.2.5. Concentration Measure
2.2.6. Mean Frequency
2.2.7. Median Frequency
2.2.8. Two-Dimensional Mean, Variance, and Coefficient of Variation
2.3. Grey Wolf Optimizer
2.3.1. Binary Grey Wolf Optimization Model 1 (BGWO1)
2.3.2. Binary Grey Wolf Optimization Model 2 (BGWO2)
2.4. Competitive Binary Grey Wolf Optimizer
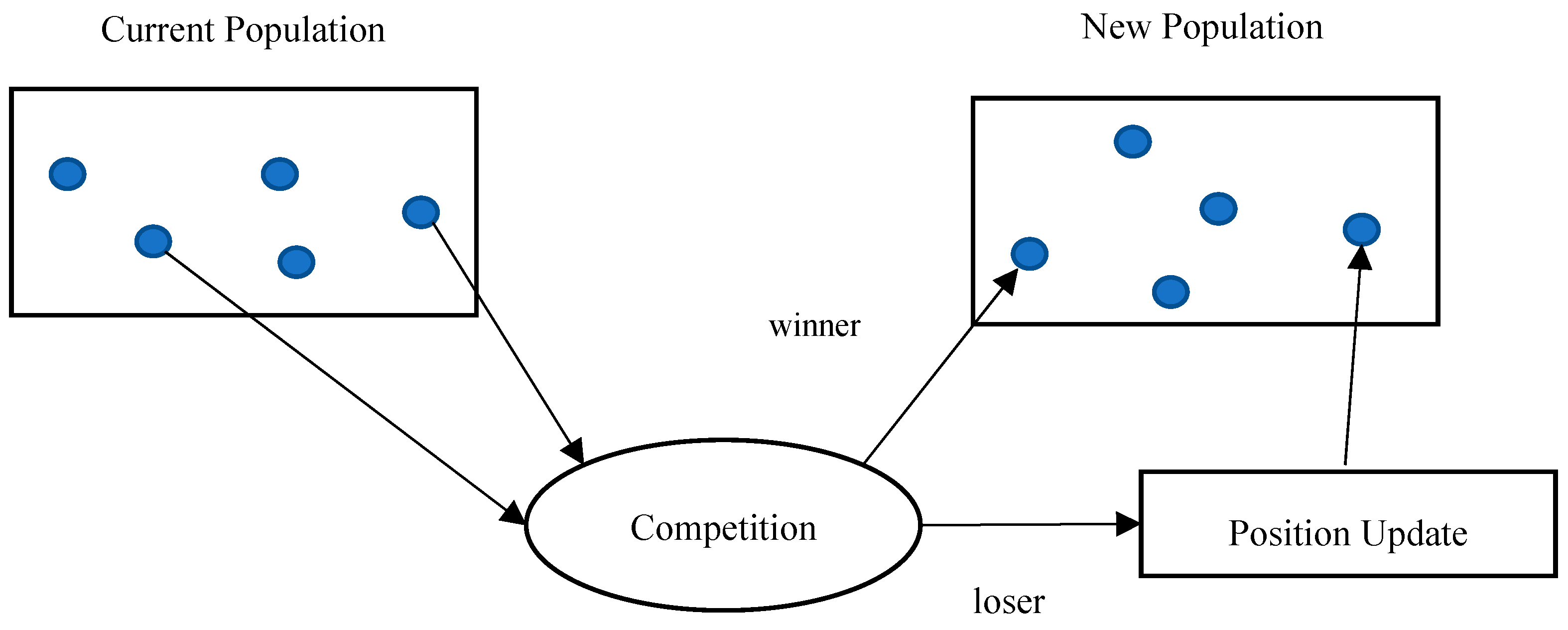
2.4.1. New Position Update
2.4.2. Leader Enhancement
- In CBGWO, only the positions of N/2 (half of the population) wolves are updated. This means that the processing speed of CBGWO is extremely fast.
- CBGWO applies leader enhancement, which has the capability to avoid the leaders (alpha, beta, and delta) from being trapped in the local optimum.
- CBGWO includes the role of winner and loser in the position update. This indicates that the process of hunting and searching prey of wolves, is not only guided by the leaders, but also the winner wolf in each couple.
- CBGWO employs the dynamic change rate, R, in the random walk strategy, which aims to balance the exploration and exploitation in the leader enhancement process.
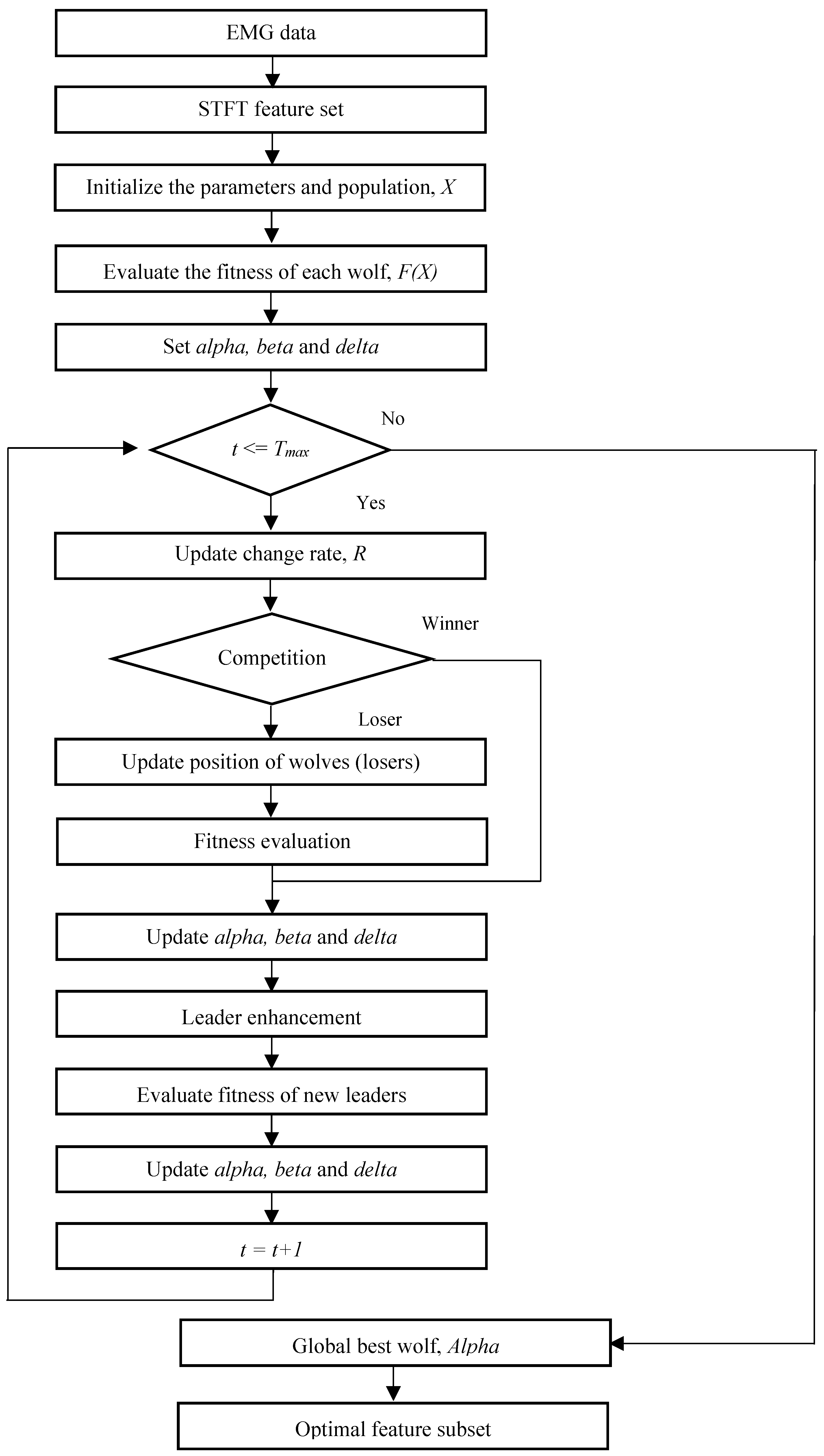
2.5. Proposed CBGWO for Feature Selection
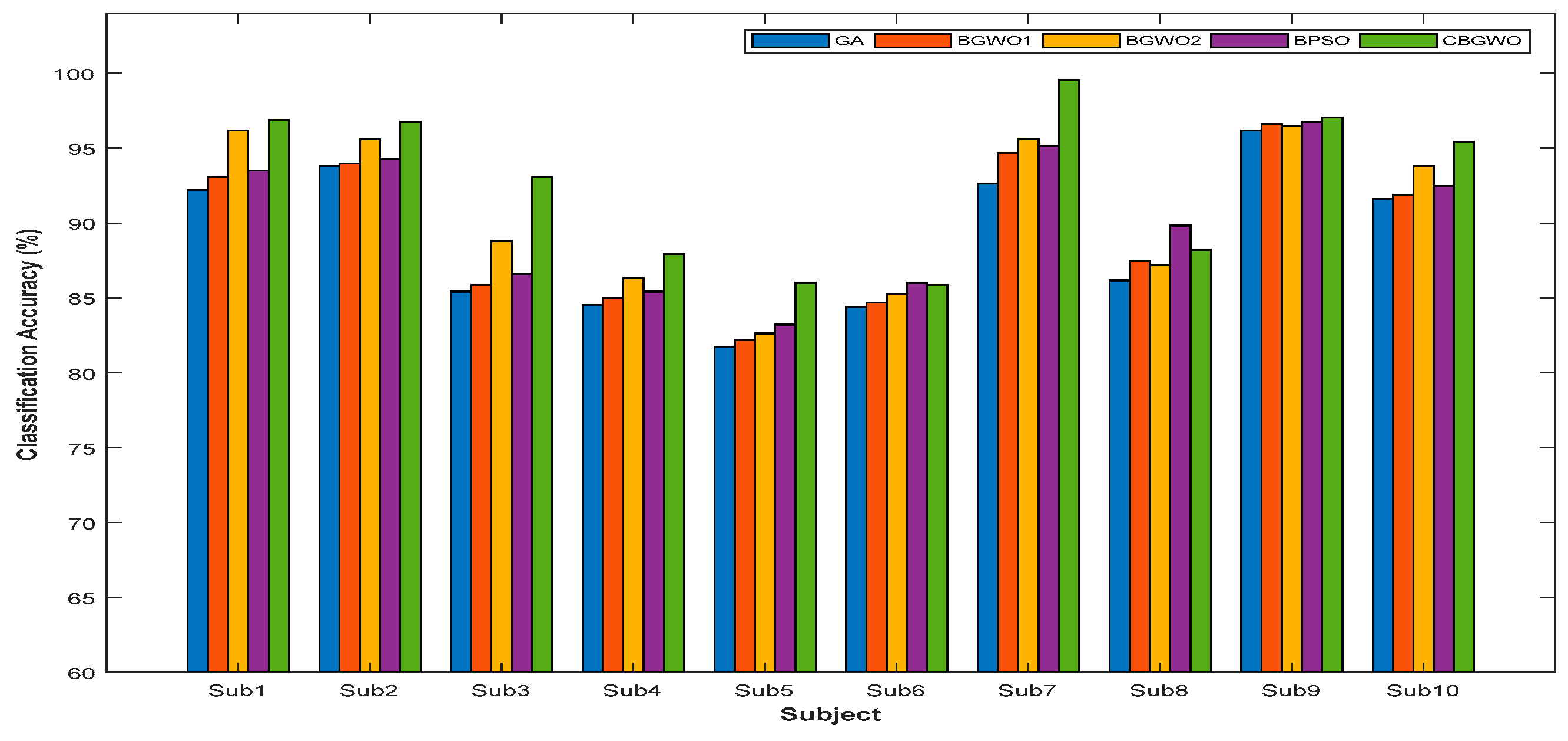
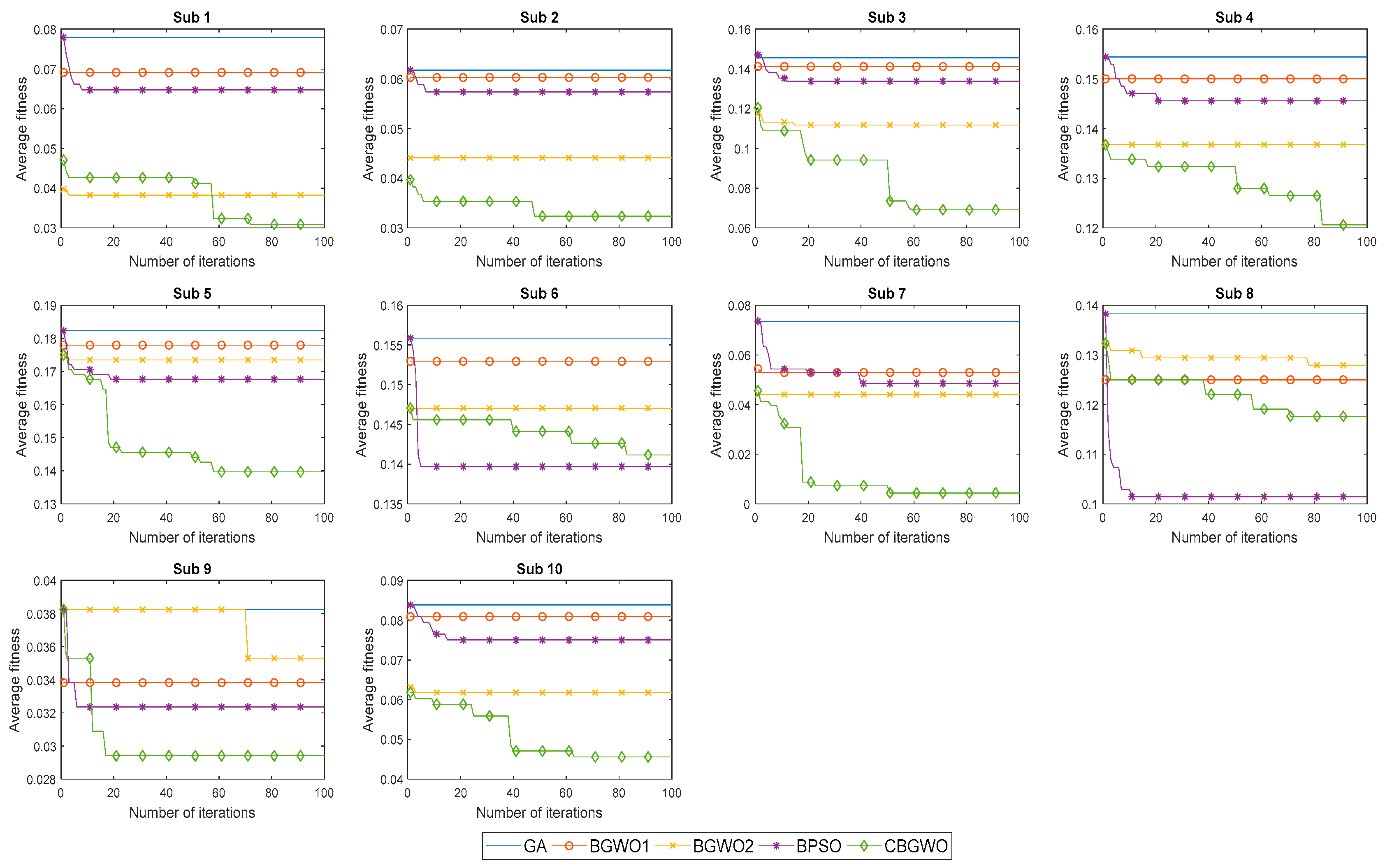
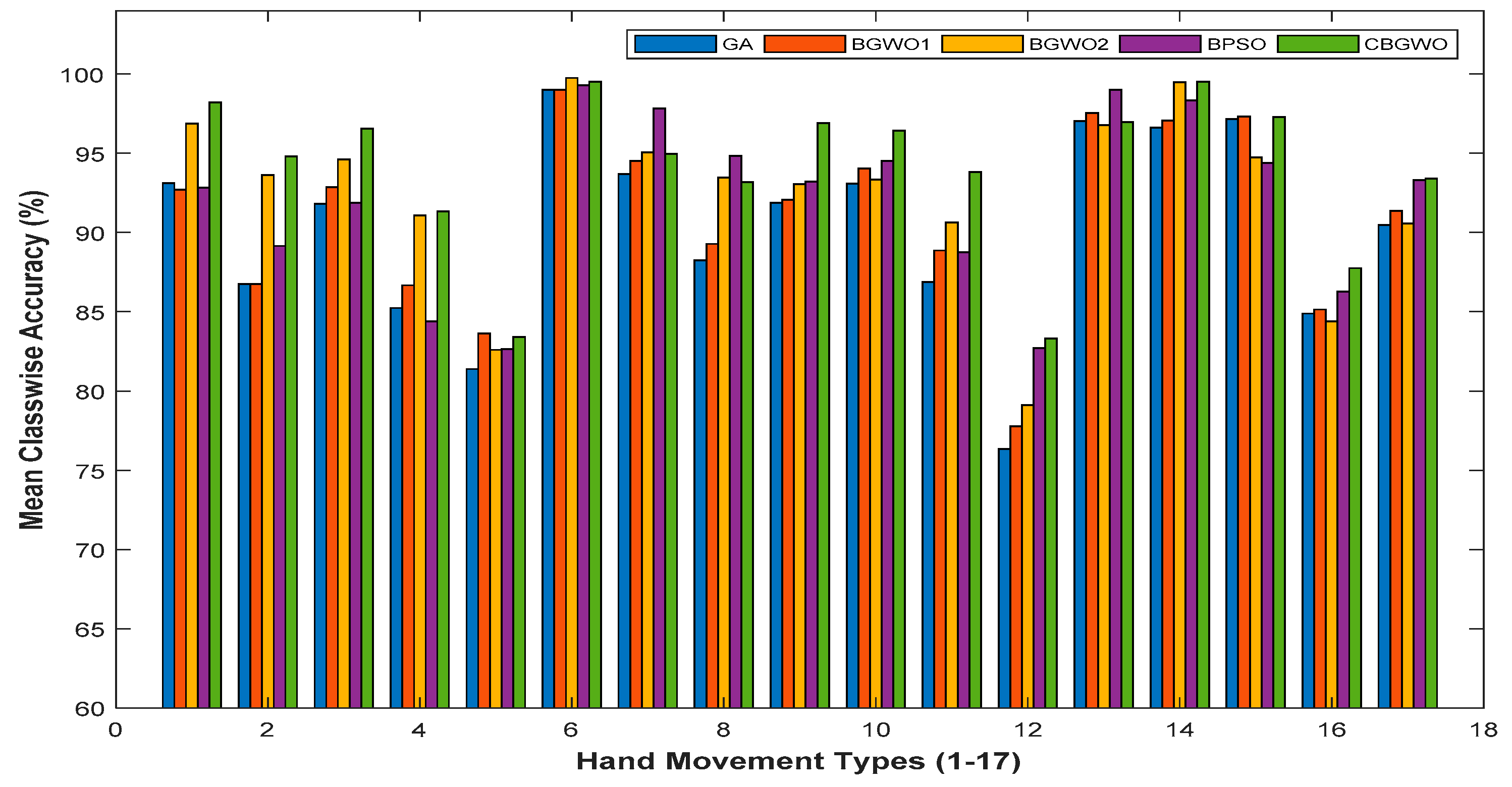
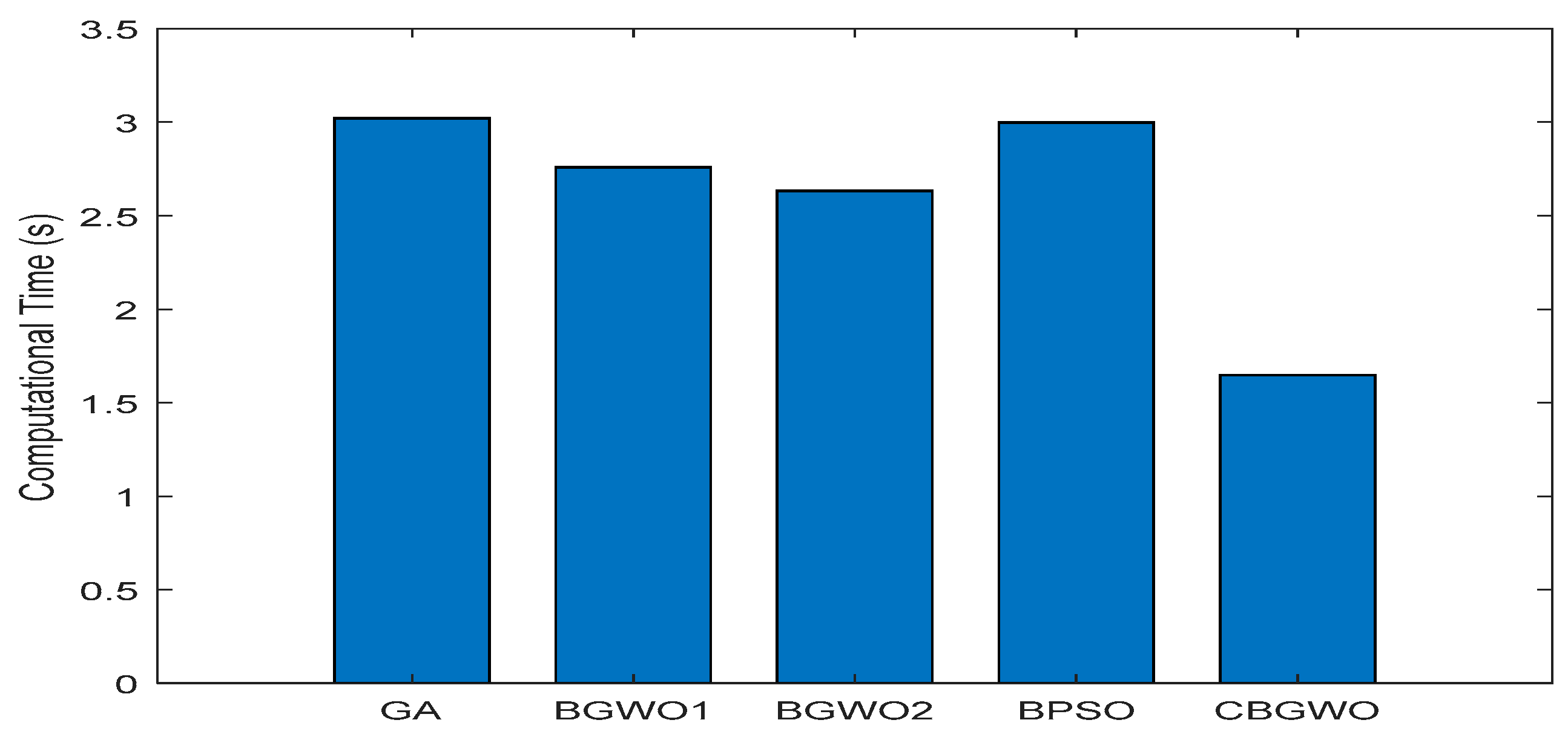
3. Results
Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, J.; Li, X.; Li, G.; Zhou, P. EMG feature assessment for myoelectric pattern recognition and channel selection: A study with incomplete spinal cord injury. Med. Eng. Phys. 2014, 36, 975–980. [Google Scholar] [CrossRef] [PubMed]
- Geethanjali, P. Comparative study of PCA in classification of multichannel EMG signals. Aust. Phys. Eng. Sci. Med. 2015, 38, 331–343. [Google Scholar] [CrossRef] [PubMed]
- Purushothaman, G.; Ray, K.K. EMG based man–machine interaction—A pattern recognition research platform. Robot. Auton. Syst. 2014, 62, 864–870. [Google Scholar] [CrossRef]
- Joshi, D.; Nakamura, B.H.; Hahn, M.E. High energy spectrogram with integrated prior knowledge for EMG-based locomotion classification. Med. Eng. Phys. 2015, 37, 518–524. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Naik, G.R.; Huang, S.; Abraham, A.; Nguyen, H.T. Nonlinear multiscale Maximal Lyapunov Exponent for accurate myoelectric signal classification. Appl. Soft Comput. 2015, 36, 633–640. [Google Scholar] [CrossRef]
- Purushothaman, G.; Vikas, R. Identification of a feature selection based pattern recognition scheme for finger movement recognition from multichannel EMG signals. Aust. Phys. Eng. Sci. Med. 2018, 41, 549–559. [Google Scholar] [CrossRef] [PubMed]
- Xi, X.; Tang, M.; Luo, Z. Feature-Level Fusion of Surface Electromyography for Activity Monitoring. Sensors 2018, 18, 614. [Google Scholar] [CrossRef] [PubMed]
- Tsai, A.C.; Luh, J.J.; Lin, T.T. A novel STFT-ranking feature of multi-channel EMG for motion pattern recognition. Expert Syst. Appl. 2015, 42, 3327–3341. [Google Scholar] [CrossRef]
- Karthick, P.A.; Ghosh, D.M.; Ramakrishnan, S. Surface electromyography based muscle fatigue detection using high-resolution time-frequency methods and machine learning algorithms. Comput. Methods Prog. Biomed. 2018, 154, 45–56. [Google Scholar] [CrossRef] [PubMed]
- Khushaba, R.N.; Takruri, M.; Miro, J.V.; Kodagoda, S. Towards limb position invariant myoelectric pattern recognition using time-dependent spectral features. Neural Netw. 2014, 55, 42–58. [Google Scholar] [CrossRef] [PubMed]
- Chuang, L.Y.; Tsai, S.W.; Yang, C.H. Improved binary particle swarm optimization using catfish effect for feature selection. Expert Syst. Appl. 2011, 38, 12699–12707. [Google Scholar] [CrossRef]
- Xue, B.; Zhang, M.; Browne, W.N. Particle swarm optimisation for feature selection in classification: Novel initialisation and updating mechanisms. Appl. Soft Comput. 2014, 18, 261–276. [Google Scholar] [CrossRef]
- Zorarpacı, E.; Özel, S.A. A hybrid approach of differential evolution and artificial bee colony for feature selection. Expert Syst. Appl. 2016, 62, 91–103. [Google Scholar] [CrossRef]
- Shunmugapriya, P.; Kanmani, S. A hybrid algorithm using ant and bee colony optimization for feature selection and classification (AC-ABC Hybrid). Swarm Evol. Comput. 2017, 36, 27–36. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Chuang, L.Y.; Chang, H.W.; Tu, C.J.; Yang, C.H. Improved binary PSO for feature selection using gene expression data. Comput. Biol. Chem. 2008, 32, 29–38. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Zhang, Q.; Sun, N.; Dong, Y. Feature Selection with Discrete Binary Differential Evolution. In Proceedings of the Artificial Intelligence and Computational Intelligence, Shanghai, China, 7–8 November 2009. [Google Scholar] [CrossRef]
- De Stefano, C.; Fontanella, F.; Marrocco, C.; Di Freca, A.S. A GA-based feature selection approach with an application to handwritten character recognition. Pattern Recognit. Lett. 2014, 35, 130–141. [Google Scholar] [CrossRef]
- Aghdam, M.H.; Ghasem-Aghaee, N.; Basiri, M.E. Text feature selection using ant colony optimization. Expert Syst. Appl. 2009, 36, 6843–6853. [Google Scholar] [CrossRef]
- Huang, H.; Xie, H.B.; Guo, J.Y.; Chen, H.J. Ant colony optimization-based feature selection method for surface electromyography signals classification. Comput. Biol. Med. 2012, 42, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Venugopal, G.; Navaneethakrishna, M.; Ramakrishnan, S. Extraction and analysis of multiple time window features associated with muscle fatigue conditions using sEMG signals. Expert Syst. Appl. 2014, 41, 2652–2659. [Google Scholar] [CrossRef]
- Pizzolato, S.; Tagliapietra, L.; Cognolato, M.; Reggiani, M.; Müller, H.; Atzori, M. Comparison of six electromyography acquisition setups on hand movement classification tasks. PLoS ONE 2017, 12, e0186132. [Google Scholar] [CrossRef] [PubMed]
- Mazher, M.; Aziz, A.A.; Malik, A.S.; Amin, H.U. An EEG-Based Cognitive Load Assessment in Multimedia Learning Using Feature Extraction and Partial Directed Coherence. IEEE Access. 2017, 5, 14819–14829. [Google Scholar] [CrossRef]
- Karthick, P.A.; Ramakrishnan, S. Surface electromyography based muscle fatigue progression analysis using modified B distribution time–frequency features. Biomed. Signal Process. Control. 2016, 26, 42–51. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Elaziz, M.A.; Lu, S. Chaotic opposition-based grey-wolf optimization algorithm based on differential evolution and disruption operator for global optimization. Expert Syst. Appl. 2018, 108, 1–27. [Google Scholar] [CrossRef]
- Al-Betar, M.A.; Awadallah, M.A.; Faris, H.; Aljarah, I.; Hammouri, A.I. Natural selection methods for Grey Wolf Optimizer. Expert Syst. Appl. 2018, 113, 481–498. [Google Scholar] [CrossRef]
- Chuang, L.Y.; Yang, C.H.; Li, J.C. Chaotic maps based on binary particle swarm optimization for feature selection. Appl. Soft Comput. 2011, 11, 239–248. [Google Scholar] [CrossRef]
- Ghareb, A.S.; Bakar, A.A.; Hamdan, A.R. Hybrid feature selection based on enhanced genetic algorithm for text categorization. Expert Syst. Appl. 2016, 49, 31–47. [Google Scholar] [CrossRef]
- Pashaei, E.; Aydin, N. Binary black hole algorithm for feature selection and classification on biological data. Appl. Soft Comput. 2017, 56, 94–106. [Google Scholar] [CrossRef]
- Li, Q.; Chen, H.; Huang, H.; Zhao, X.; Cai, Z.; Tong, C.; Liu, W.; Tian, X. An Enhanced Grey Wolf Optimization Based Feature Selection Wrapped Kernel Extreme Learning Machine for Medical Diagnosis. Comput. Math. Methods Med. 2017, 2017, 9512741. [Google Scholar] [CrossRef] [PubMed]



| Subject | Number of Selected Features (Original = 120) | Precision | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GA | BGWO1 | BGWO2 | BPSO | CBGWO | GA | BGWO1 | BGWO2 | BPSO | CBGWO | ||
| 1 | 59.15 | 61.15 | 57.70 | 42.15 | 40.75 | 0.9427 | 0.9500 | 0.9755 | 0.9500 | 0.9794 | |
| 2 | 62.85 | 61.80 | 56.05 | 43.05 | 37.85 | 0.9569 | 0.9583 | 0.9716 | 0.9613 | 0.9784 | |
| 3 | 61.75 | 61.85 | 58.05 | 48.20 | 46.35 | 0.8993 | 0.9022 | 0.9120 | 0.9103 | 0.9412 | |
| 4 | 62.25 | 61.60 | 58.20 | 44.90 | 42.25 | 0.8863 | 0.8878 | 0.9037 | 0.8936 | 0.9184 | |
| 5 | 59.45 | 60.00 | 58.15 | 46.85 | 46.55 | 0.8708 | 0.8751 | 0.8775 | 0.8710 | 0.9073 | |
| 6 | 62.75 | 62.85 | 59.85 | 48.20 | 44.30 | 0.8962 | 0.9001 | 0.9134 | 0.8961 | 0.9165 | |
| 7 | 60.10 | 60.80 | 56.85 | 46.75 | 42.85 | 0.9466 | 0.9637 | 0.9677 | 0.9628 | 0.9971 | |
| 8 | 61.80 | 61.80 | 60.40 | 44.40 | 43.20 | 0.8885 | 0.9000 | 0.9027 | 0.9340 | 0.9040 | |
| 9 | 61.45 | 60.65 | 59.40 | 44.60 | 41.70 | 0.9740 | 0.9775 | 0.9765 | 0.9784 | 0.9804 | |
| 10 | 62.30 | 62.40 | 56.60 | 46.40 | 38.75 | 0.9414 | 0.9456 | 0.9574 | 0.9461 | 0.9701 | |
| Mean | 61.39 | 61.49 | 58.13 | 45.55 | 42.46 | 0.9203 | 0.9260 | 0.9358 | 0.9304 | 0.9493 | |
| Subject | F-Measure | Matthew Correlation Coefficient (MCC) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GA | BGWO1 | BGWO2 | BPSO | CBGWO | GA | BGWO1 | BGWO2 | BPSO | CBGWO | ||
| 1 | 0.9175 | 0.9273 | 0.9589 | 0.9324 | 0.9671 | 0.9253 | 0.9325 | 0.9641 | 0.9340 | 0.9691 | |
| 2 | 0.9345 | 0.9363 | 0.9533 | 0.9389 | 0.9655 | 0.9379 | 0.9396 | 0.9563 | 0.9426 | 0.9676 | |
| 3 | 0.8322 | 0.8398 | 0.8779 | 0.8452 | 0.9273 | 0.8812 | 0.8803 | 0.8922 | 0.8941 | 0.9278 | |
| 4 | 0.8395 | 0.8432 | 0.8581 | 0.8542 | 0.8746 | 0.8512 | 0.8525 | 0.8658 | 0.8561 | 0.8828 | |
| 5 | 0.8029 | 0.8075 | 0.8131 | 0.8178 | 0.8540 | 0.8500 | 0.8548 | 0.8527 | 0.8551 | 0.8663 | |
| 6 | 0.8416 | 0.8444 | 0.8479 | 0.8611 | 0.8554 | 0.8566 | 0.8599 | 0.8761 | 0.8618 | 0.8735 | |
| 7 | 0.9210 | 0.9425 | 0.9529 | 0.9479 | 0.9953 | 0.9273 | 0.9486 | 0.9551 | 0.9500 | 0.9956 | |
| 8 | 0.8527 | 0.8658 | 0.8604 | 0.8876 | 0.8746 | 0.8676 | 0.8811 | 0.8851 | 0.9082 | 0.8886 | |
| 9 | 0.9574 | 0.9629 | 0.9604 | 0.9635 | 0.9686 | 0.9652 | 0.9680 | 0.9683 | 0.9712 | 0.9706 | |
| 10 | 0.9130 | 0.9151 | 0.9344 | 0.9218 | 0.9516 | 0.9165 | 0.9196 | 0.9380 | 0.9247 | 0.9546 | |
| Mean | 0.8812 | 0.8885 | 0.9017 | 0.8970 | 0.9234 | 0.8979 | 0.9037 | 0.9154 | 0.9098 | 0.9297 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Too, J.; Abdullah, A.R.; Mohd Saad, N.; Mohd Ali, N.; Tee, W. A New Competitive Binary Grey Wolf Optimizer to Solve the Feature Selection Problem in EMG Signals Classification. Computers 2018, 7, 58. https://doi.org/10.3390/computers7040058
Too J, Abdullah AR, Mohd Saad N, Mohd Ali N, Tee W. A New Competitive Binary Grey Wolf Optimizer to Solve the Feature Selection Problem in EMG Signals Classification. Computers. 2018; 7(4):58. https://doi.org/10.3390/computers7040058
Chicago/Turabian StyleToo, Jingwei, Abdul Rahim Abdullah, Norhashimah Mohd Saad, Nursabillilah Mohd Ali, and Weihown Tee. 2018. "A New Competitive Binary Grey Wolf Optimizer to Solve the Feature Selection Problem in EMG Signals Classification" Computers 7, no. 4: 58. https://doi.org/10.3390/computers7040058
APA StyleToo, J., Abdullah, A. R., Mohd Saad, N., Mohd Ali, N., & Tee, W. (2018). A New Competitive Binary Grey Wolf Optimizer to Solve the Feature Selection Problem in EMG Signals Classification. Computers, 7(4), 58. https://doi.org/10.3390/computers7040058





