A Novel Framework for Portfolio Selection Model Using Modified ANFIS and Fuzzy Sets
Abstract
1. Introduction
1.1. Related Work
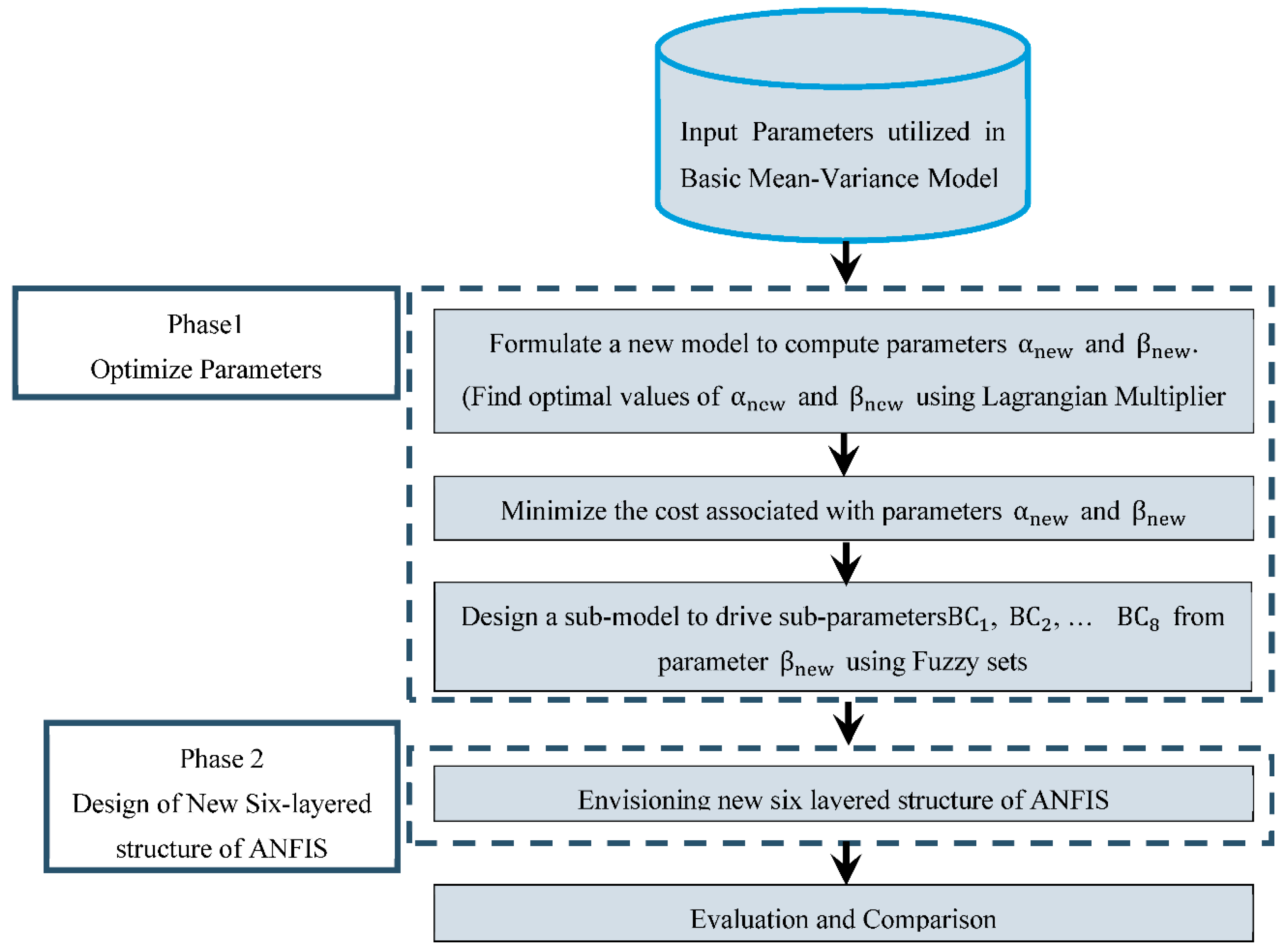
1.2. Concept of the Proposed Framework
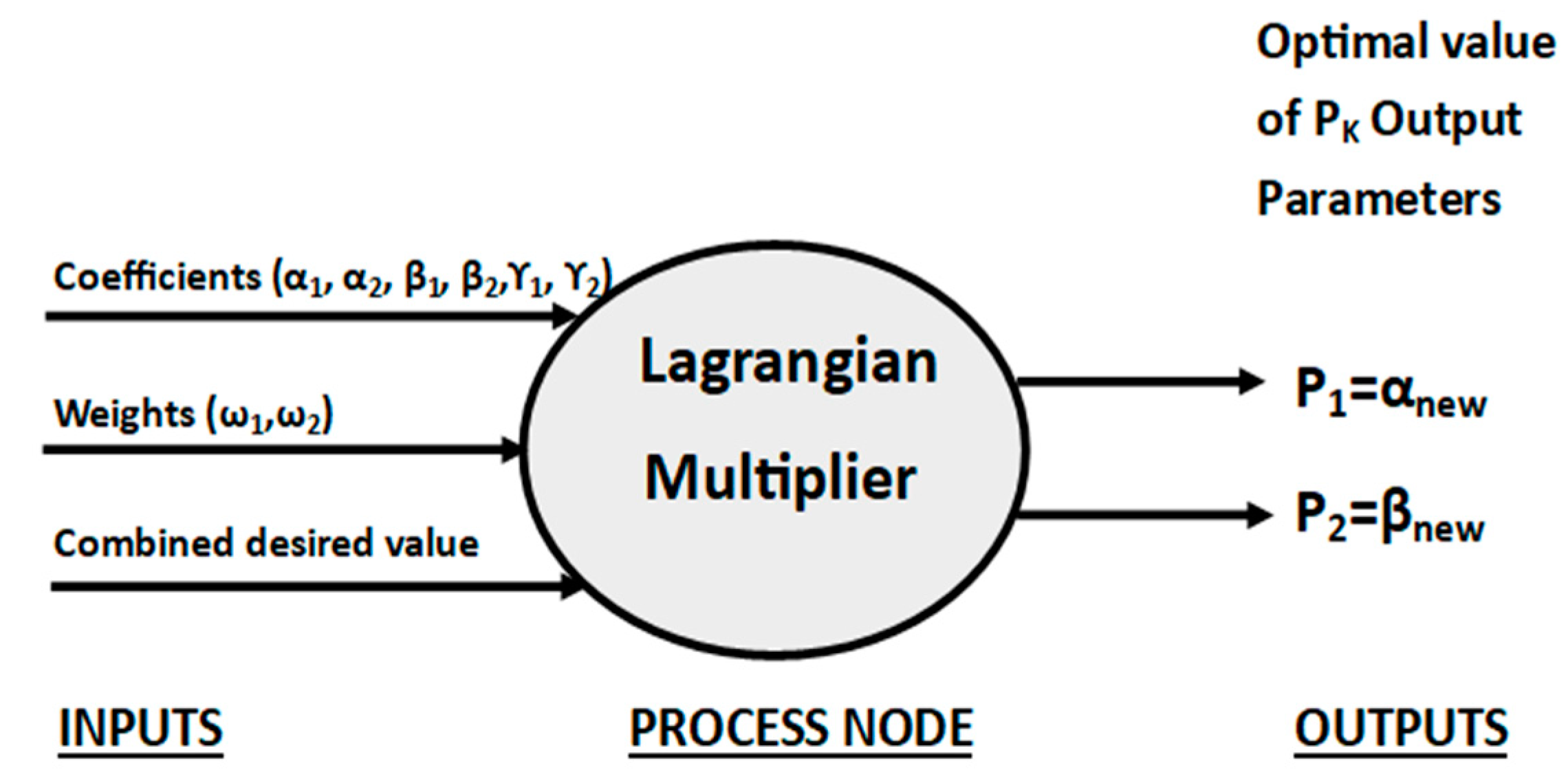
1.2.1. Phase 1. Optimization of Newly Derived Parameters
1.2.2. Phase 2. Design of New Six-Layered Structure of ANFIS
1.2.3. Economic and Statistical Significance of Using the ANFIS Structure
- Statistical Significance: ANFIS structure is utilized for providing a prediction capability in portfolio selection. Since forecast of expected returns may be a desirable feature in view of the investor’s selections. This prediction scheme should be capable of accurately modeling the desired parameters based on existing data points. This can be achieved by means of an ANFIS structure that has a fuzzy inference system. Furthermore, situations where ANFIS with different data points are desirable for selective time duration, an adaptive structure needs to be employed. This adaptive nature is required for a different set of parameters.
- Economic Significance: Designing of efficient models for portfolio selection can be suitably crafted using the computational index represented by the output of the last node in the ANFIS structure. While obtaining the expected returns in case of multi-assets data, this index can be employed as a decision parameter. The expected returns would correspondingly alter in the view of the selected value of this index. Even though a nominal value of this index is employed while designing, this scheme could substantially alter the values of expected returns. These designs may also be employed for finding an optimal solution in the areas beyond financial applications. The investor would like to select an option that yields lower values of risk.
1.2.4. Advantageous of Using the Proposed Methodology
2. Overview of the Basic Mean-Variance Model
| Combined_desired_value | Desired value of (Input). |
| Parameters used while correlating with CVaR. | |
| Parameters used while correlating with CVaR. | |
| , | Nodes of Layer 2 (Modified ANFIS). |
| Nodes of Layer 3 (Modified ANFIS). | |
| Nodes of Layer 5 (Modified ANFIS). | |
| , | Parameters used while correlating with CVaR. |
| Weight associated with and . | |
| The values of parameter of or . | |
| Cost associated with or . | |
| This term is representing loss incurred in the investment process. | |
| , | Weight associated with and respectively. |
| This is a control parameter that represents maximal weighted cost associated with . | |
| Maximum value of risk. | |
| Minimum value of risk. | |
| , | Scaling parameters. |
| ,, | Cost coefficient used in calculating cost, . |
| , , | Parameters used while correlating with CVaR. |
| Lagrangian Function. | |
| Sub parameters generated from using fuzzy sets. | |
| Membership values from fuzzy sets associated with sub parameters . | |
| Membership values of fuzzy sets = . | |
| This parameter represents the total cost associated with parameters | |
| Values used in minimization equation = . | |
| , | Cost coefficients used in minimization problem. |
| Input parameter used in ANFIS. | |
| , | Minimum and maximum value of . |
| Nodes of Layer 1 (Modified ANFIS). |
3. Proposed Novel Portfolio Selection Model Based on Costs Associated with and
3.1. Correlate Parameter with Parameter That Is Being Computed from the Basic Mean-Variance Model
3.2. Correlate Parameter with Conditional-Value-at-Risk (CVaR)
- (c)
- Combined_desired_value:
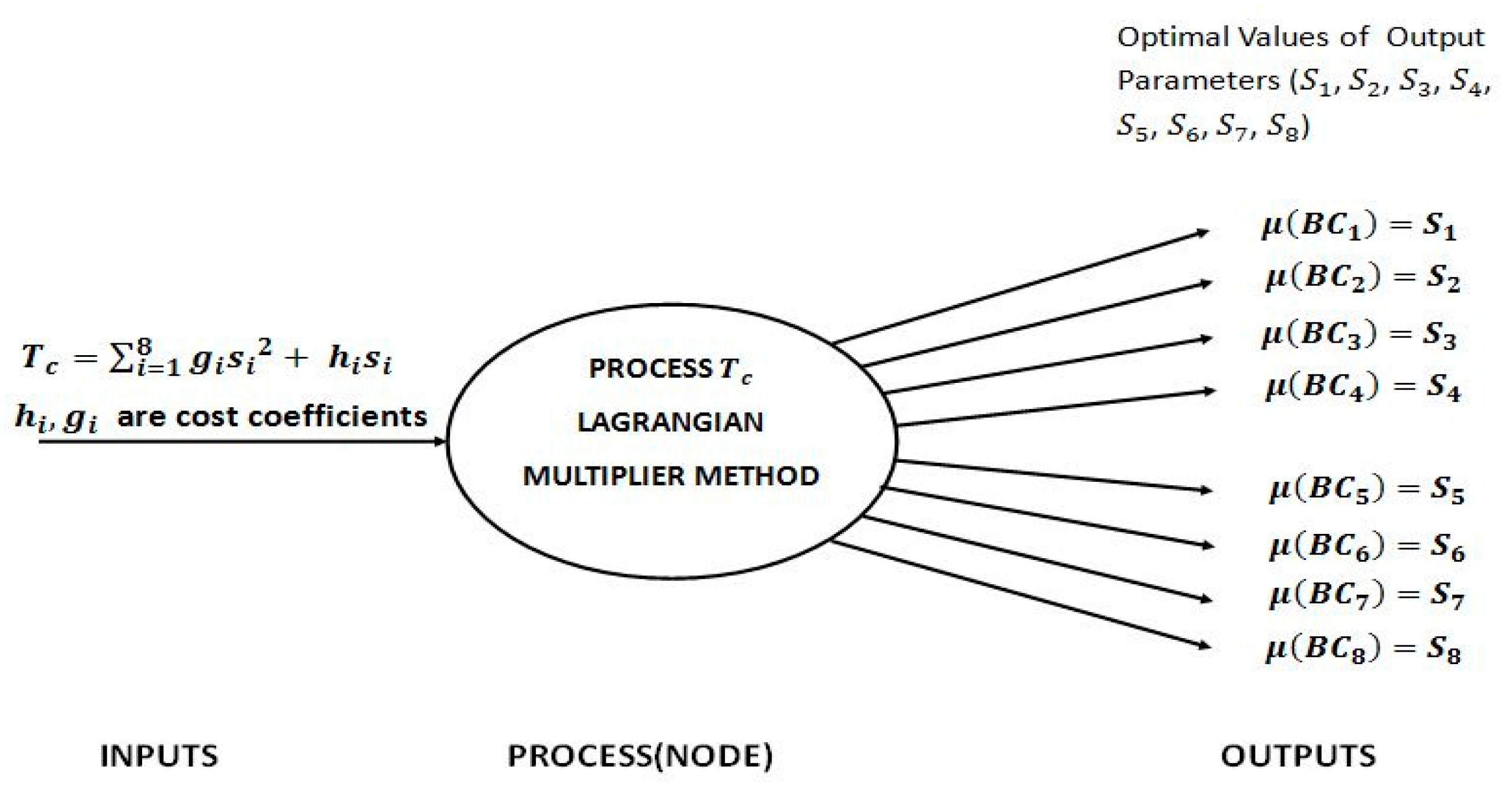
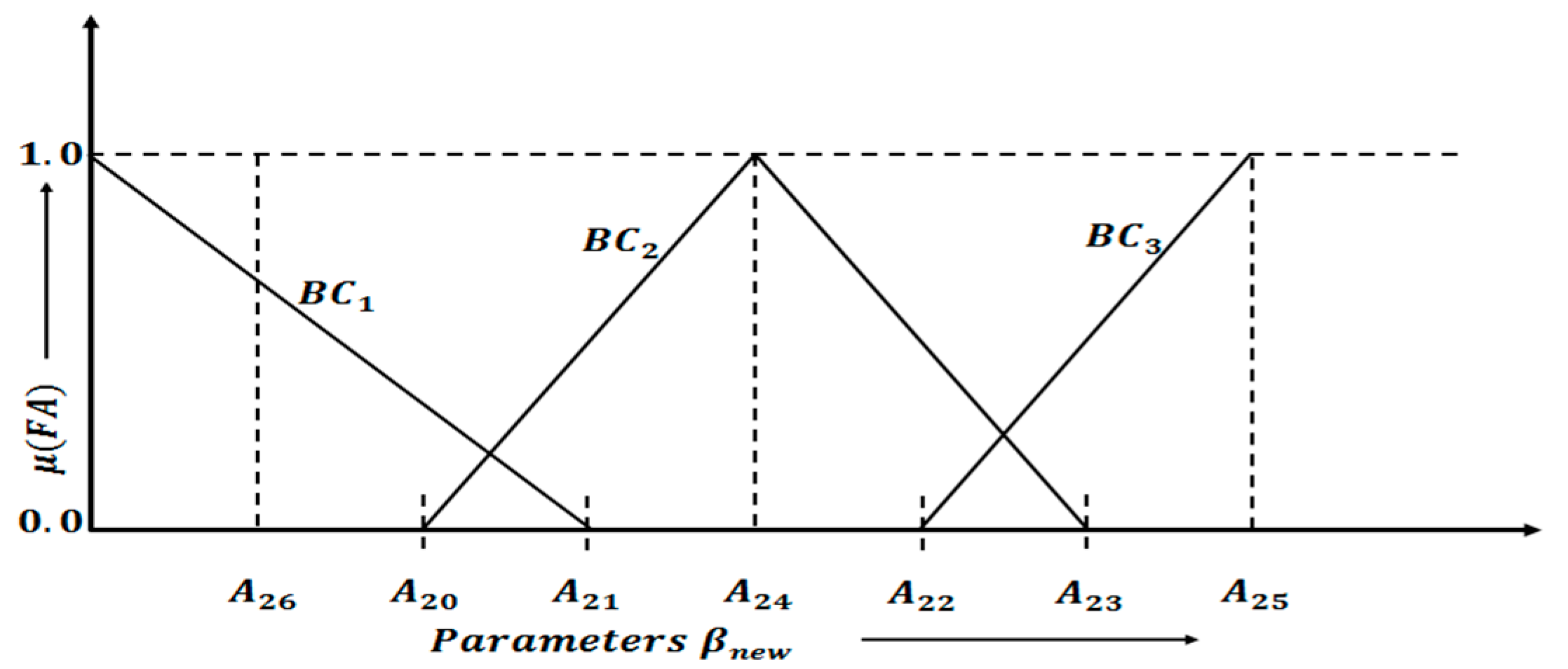
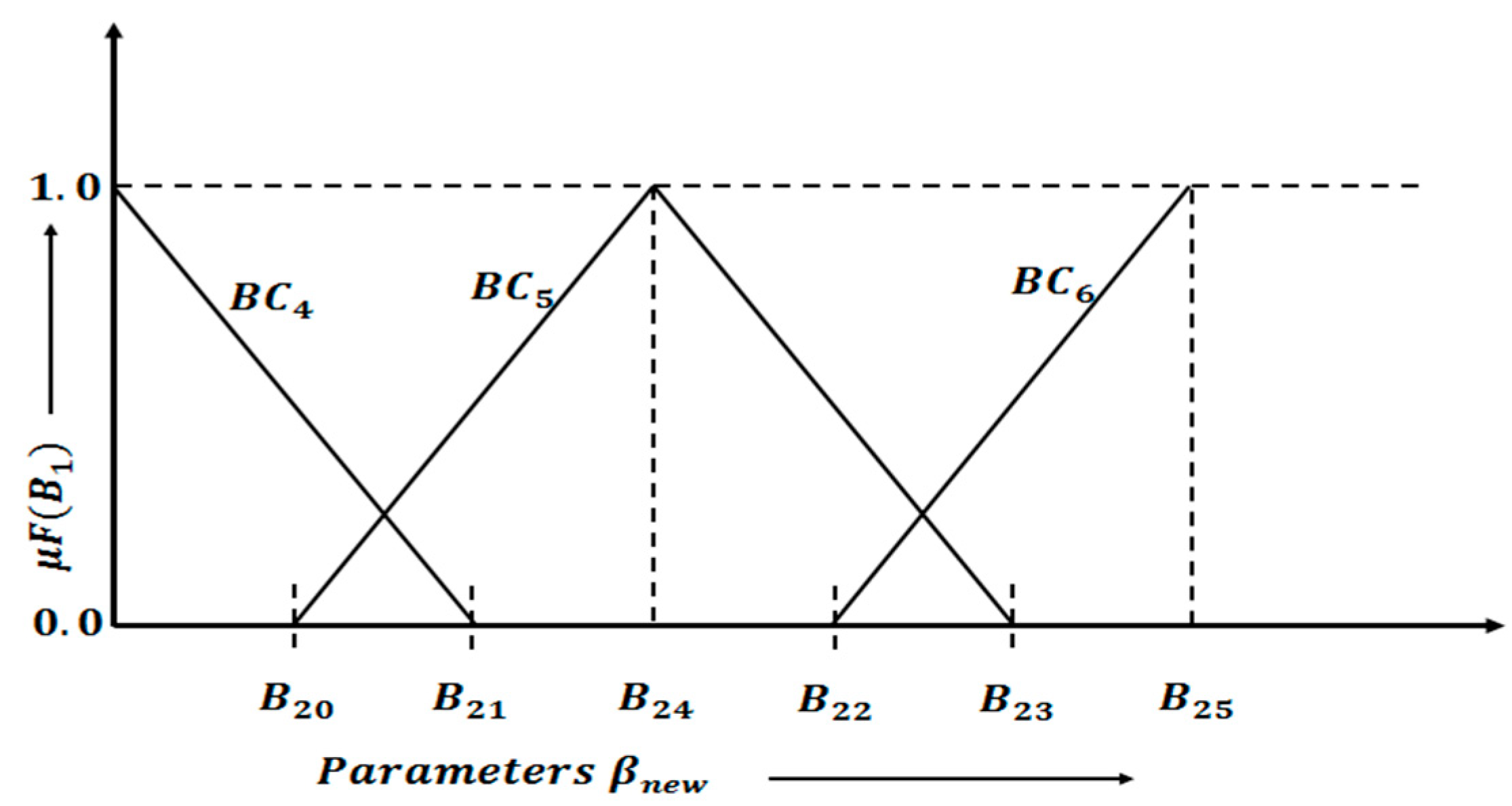
4. Generating Novel Sub-Parameters from Parameters βnew and Finding Optimal Values of Sub-Parameters Using Fuzzy Sets
- Fuzzy Set A is used when the value of parameter β_new lies in Category Awhere A25 is the value = 70.5697 and A0 is the value = 61.5669.Category A: A0 ≤ βnew ≤ A25,
- Fuzzy Set B1 is used when the value of parameter lies in Category Bwhere B20 is the value = 51.3820 and B25 is the value = 58.1558.Category B: B20 ≤ βnew ≤ B25,
- Fuzzy Set B2 is used when the value of parameter lies in Category Cwhere is the value = 47.2518 and is the value = 48.0185.
4.1. Description of Various Equations Used in Fuzzy Sets
4.1.1. Category A: Fuzzy Set-A
4.1.2. Category B: Fuzzy Set-B1
4.1.3. Category C: Fuzzy Set-
- (a)
- The values of cost-coefficients as used in the following equation:
- (b)
- The values of these coefficients are given in Table 4.
- (c)
- The specified value of .
4.2. Mathematical Modeling of Module for Computing Sub Parameters
4.3. Equations for Parameters (i = 1 to 8)
4.4. Description of Different Outputs of the Module for Sub-Parameters
5. Need for Design of a Model Using Fuzzy Logic
- , , ,
- Rule 1:
- Rule 2:
- Rule 3:
- Rule 4:
- Rule 5:
- Rule 6:
- Rule 7:
- Rule 8:
6. New Model Using Modifications in ANFIS: Six-Layered Structure
- Rule 1:
- Rule 2:
Proposed Modifications in Fifth Layer (Layer 5) for Modified ANFIS Using the Cuckoo Intelligence Algorithm
General Framework of the Modification
- Rule 1:
- Rule 2: .
7. Performance Analysis and Experimental Results
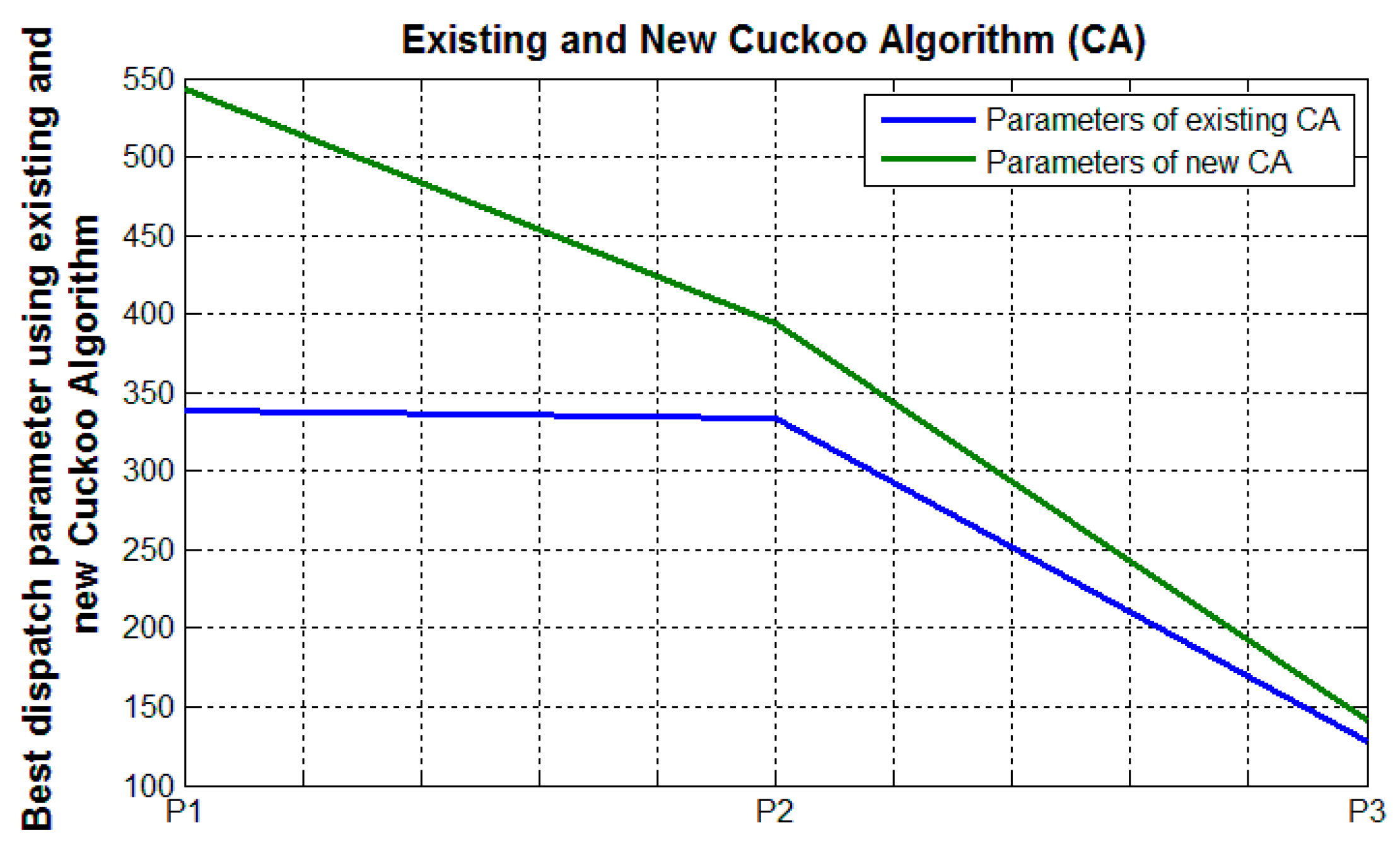
7.1. Discussion on Modifications of the Range Used within a Cuckoo Intelligence Algorithm (Layer 5 of Modified 6 Layered ANFIS)
- = 0.15 = 0.6,
- = 0.1 = 0.4,
- = 0.05 = 0.2.
7.2. Computational Results with Analysis of ANFIS
7.2.1. Comparison of Various Outputs Obtained by Changing Different Layers of ANFIS
7.2.2. Comparison of Values of Output Nodes of the Last Layer in Existing and Modified ANFIS
7.2.3. Economic Significance of the ANFIS Methodology for Additional Constraints
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Markowitz, H.M. Portfolio Selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Huang, X. Fuzzy chance-constrained portfolio selection. Appl. Math. Comput. 2006, 177, 500–507. [Google Scholar] [CrossRef]
- Gupta, P.; Inuiguchi, M.; Mehlawat, M.K.; Mittal, G. Multiobjective credibilistic portfolio selection model with fuzzy chance-constraints. Inf. Sci. 2013, 229, 1–17. [Google Scholar] [CrossRef]
- Huang, X. Portfolio selection with fuzzy returns. J. Intell. Fuzzy Syst. 2007, 18, 383–390. [Google Scholar]
- Huang, X. Mean-semivariance models for fuzzy portfolio selection. J. Comput. Appl. Math. 2008, 217, 1–8. [Google Scholar] [CrossRef]
- Li, X.; Qin, Z.; Kar, S. Mean-variance-skewness model for portfolio selection with fuzzy returns. Eur. J. Oper. Res. 2010, 202, 239–247. [Google Scholar] [CrossRef]
- Huang, X. Risk curve and fuzzy portfolio selection. Comput. Math. Appl. 2008, 55, 1102–1112. [Google Scholar] [CrossRef]
- Gupta, P.; Mittal, G.; Mehlawat, M.K. Multiobjective expected value model for portfolio selection in fuzzy environment. Optim. Lett. 2012, 7, 1765–1791. [Google Scholar] [CrossRef]
- Mehlawat, M.K.; Gupta, P. Fuzzy Chance-Constrained Multiobjective Portfolio Selection Model. IEEE Trans. Fuzzy Syst. 2014, 22, 653–671. [Google Scholar] [CrossRef]
- Wang, B.; Wang, S.; Watada, J. Fuzzy-Portfolio-Selection Models with Value-at-Risk. IEEE Trans. Fuzzy Syst. 2011, 19, 758–769. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Optimization of conditional value-at-risk. J. Risk 2000, 2, 21–41. [Google Scholar] [CrossRef]
- Yao, H.; Li, Z.; Lai, Y. Mean–CVaR portfolio selection: A nonparametric estimation framework. Comput. Oper. Res. 2013, 40, 1014–1022. [Google Scholar] [CrossRef]
- Yan, W.; Miao, R.; Li, S. Multi-period semi-variance portfolio selection: Model and numerical solution. Appl. Math. Comput. 2007, 194, 128–134. [Google Scholar] [CrossRef]
- Yan, W.; Li, S. A class of multi-period semi-variance portfolio selection with a four-factor futures price model. J. Appl. Math. Comput. 2008, 29, 19–34. [Google Scholar] [CrossRef]
- Najafi, A.A.; Mushakhian, S. Multi-stage stochastic mean–semivariance–CVaR portfolio optimization under transaction costs. Appl. Math. Comput. 2015, 256, 445–458. [Google Scholar] [CrossRef]
- Freitas, F.D.; Souza, A.F.D.; Almeida, A.R.D. Prediction-based portfolio optimization model using neural networks. Neurocomputing 2009, 72, 2155–2170. [Google Scholar] [CrossRef]
- Alizadeh, M.; Rada, R.; Jolai, F.; Fotoohi, E. An adaptive neuro-fuzzy system for stock portfolio analysis. Int. J. Intell. Syst. 2010, 26, 99–114. [Google Scholar] [CrossRef]
- Svalina, I.; Galzina, V.; Lujic, R.; Šimunovic, G. An adaptive network-based fuzzy inference system (ANFIS) for the forecasting: The case of close price indices. Expert Syst. Appl. 2013, 40, 6055–6063. [Google Scholar] [CrossRef]
- Chen, Y.-S.; Cheng, C.-H.; Chiu, C.-L.; Huang, S.-T. A study of ANFIS-based multi-factor time series models for forecasting stock index. Appl. Intell. 2016, 45, 277–292. [Google Scholar] [CrossRef]
- Hasuike, T.; Ishii, H. A portfolio selection problem with type-2 fuzzy return based on possibility measure and interval programming. In Proceedings of the IEEE International Conference on Fuzzy Systems, Jeju Island, South Korea, 20–24 August 2009. [Google Scholar]
- Pai, G.A.V. Fuzzy Decision Theory Based Metaheuristic Portfolio Optimization and Active Rebalancing Using Interval Type-2 Fuzzy Sets. IEEE Trans. Fuzzy Syst. 2017, 25, 377–391. [Google Scholar] [CrossRef]
- Pai, G.V.; Michel, T. Metaheuristic multi-objective optimization of constrained futures portfolios for effective risk management. Swarm Evol. Comput. 2014, 19, 1–14. [Google Scholar] [CrossRef]
- Pai, G.A.V.; Michel, T. Fuzzy decision theory based optimization of constrained portfolios using metaheuristics. In Proceedings of the IEEE International Conference on Fuzzy Systems, Hyderabad, India, 7–10 July 2013. [Google Scholar]
- Hassanzadeh, F.; Collan, M.; Modarres, M. A Practical Approach to R&D Portfolio Selection Using the Fuzzy Pay-Off Method. IEEE Trans. Fuzzy Syst. 2012, 20, 615–622. [Google Scholar]
- Nguyen, T.T.; Gordon-Brown, L.; Khosravi, A.; Creighton, D.; Nahavandi, S. Fuzzy Portfolio Allocation Models Through a New Risk Measure and Fuzzy Sharpe Ratio. IEEE Trans. Fuzzy Syst. 2015, 23, 656–676. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Y.; Wang, K.; Chen, Y. Particle Swarm Optimization (PSO) for the constrained portfolio optimization problem. Expert Syst. Appl. 2011, 38, 10161–10169. [Google Scholar] [CrossRef]
- Wang, B.; Watada, J. Multiobjective particle swarm optimization for a novel fuzzy portfolio selection problem. IEEJ Trans. Electr. Electron. Eng. 2012, 8, 146–154. [Google Scholar] [CrossRef]
- Wang, S.; Wang, B.; Watada, J. Adaptive budget-portfolio investment optimization under risk tolerance ambiguity. IEEE Trans. Fuzzy Syst. 2017, 25, 363–376. [Google Scholar] [CrossRef]
- Mishra, S.K.; Panda, G.; Majhi, B. Prediction based mean-variance model for constrained portfolio assets selection using multiobjective evolutionary algorithms. Swarm Evol. Comput. 2016, 28, 117–130. [Google Scholar] [CrossRef]
- Brar, Y.; Dhillon, J.; Kothari, D. Genetic fuzzy logic based weightage pattern search for multiobjective load dispatch problem. Asian J. Inf. Technol. 2003, 4, 365–373. [Google Scholar]
- Brar, Y.; Dhillon, J.S.; Kothari, D. Multiobjective load dispatch by fuzzy logic based searching weightage pattern. Electr. Power Syst. Res. 2002, 63, 149–160. [Google Scholar] [CrossRef]
- Tapia, C.G.; Murtagh, B.A. Interactive fuzzy programming with preference criteria in multiobjective decision-making. Comput. Oper. Res. 1991, 18, 307–316. [Google Scholar] [CrossRef]
- Gupta, P.; Mehlawat, M.K.; Inuiguchi, M.; Chandra, S. Fuzzy Portfolio Optimization Advances in Hybrid Multi-Criteria Methodologies; Springer: Berlin, Germany, 2016. [Google Scholar]
- Padhy, N.P.; Simon, S.P. Soft Computing with MATLAB Programming; Oxford University Press: New Delhi, India, 2015. [Google Scholar]
- Kothari, D.P.; Dhillon, J.S. Power System Optimization; PHI Learning Private Ltd.: New Delhi, India, 2012. [Google Scholar]
- Rubio, J.D.J. Error convergence analysis of the SUFIN and CSUFIN. Appl. Soft Comput. 2018, in press. [Google Scholar]
- Lughofer, E.; Pratama, M.; Skrjanc, I. Incremental Rule Splitting in Generalized Evolving Fuzzy Systems for Autonomous Drift Compensation. IEEE Trans. Fuzzy Syst. 2018, 26, 1854–1865. [Google Scholar] [CrossRef]
- Rubio, J.D.J. USNFIS: Uniform stable neuro fuzzy inference system. Neurocomputing 2017, 262, 57–66. [Google Scholar] [CrossRef]
- Pratama, M.; Lughofer, E.; Er, M.J.; Anavatti, S.; Lim, C.-P. Data driven modelling based on Recurrent Interval-Valued Metacognitive Scaffolding Fuzzy Neural Network. Neurocomputing 2017, 262, 4–27. [Google Scholar] [CrossRef]
- Alder, T.; Kritzman, M. Mean–Variance versus Full-Scale Optimisation: In and Out of Sample. J. Asset Manag. 2007, 7, 302–311. [Google Scholar]
- Cremers, J.N.; Kritzman, M.; Page, S. Optimal Hedge Fund Allocations. J. Portf. Manag. 2005, 31, 70–81. [Google Scholar] [CrossRef]
- Low, R.K.Y.; Faff, R.; Aas, K. Enhancing mean–variance portfolio selection by modeling distributional asymmetries. J. Econ. Bus. 2016, 85, 49–72. [Google Scholar] [CrossRef]
- Kritzman, M.; Page, S.; Turkington, D. In defense of Optimization: The faculty of 1/N. Financ. Anal. J. 2010, 66, 31–39. [Google Scholar] [CrossRef]
- Low, R.K.Y. Vine copulas: Modelling systemic risk and enhancing higher-moment portfolio optimisation. Account. Financ. 2017. [Google Scholar] [CrossRef]
- Hagströmer, B.; Binner, J.M. Stock portfolio selection with full-scale optimization and differential evolution. Appl. Financ. Econ. 2009, 19, 1559–1571. [Google Scholar] [CrossRef]
- Rad, H.; Low, R.K.Y.; Faff, R.W. The Profitability of Pairs Trading Strategies: Distance, Cointegration, and Copula Methods. SSRN Electron. J. 2016, 16, 1541–1558. [Google Scholar] [CrossRef]
- Anderson, R.G.; Binner, J.M.; Elger, T.; Hagströmer, B.; Nilsson, B. Mean-Variance vs. Full-Scale Optimization: Broad Evidence for the UK; Department of Economics, Lund Universtiy: Lund, Sweden, 2008. [Google Scholar]


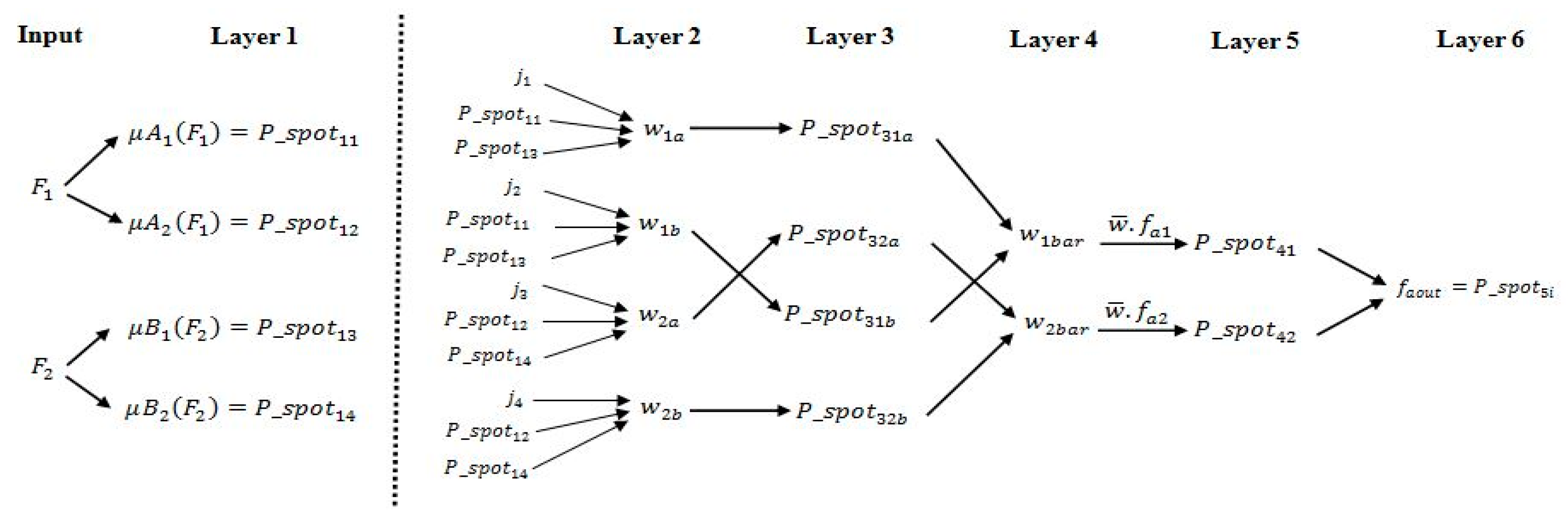


| Existing ANFIS (Number of Layers = 5) | Modified ANFIS (Number of Layers = 6) | ||
|---|---|---|---|
| Inputs = , | |||
| S. No | Layer | Nodes of Existing ANFIS | Nodes of Modified ANFIS |
| 1. | First (Layer 1) | ||
| 2. | Second (Layer 2) | ||
| 3. | Third (Layer 3) | ||
| 4. | Fourth (Layer 4) | ||
| 5. | Fifth (Layer 5) | ||
| 6. | Last layer | None | |
| S. No | Portfolio Return | Portfolio Weights | |||
|---|---|---|---|---|---|
| Risk | Col.5 | Col.8 | Col.10 | ||
| 1 | 0.2572 | 0.1622 | 0.5630 | 0 | 0.4370 |
| 2 | 0.2775 | 0.1641 | 0.5005 | 0 | 0.4995 |
| 3 | 0.2979 | 0.1697 | 0.4379 | 0 | 0.5621 |
| 4 | 0.3183 | 0.1787 | 0.3754 | 0 | 0.6246 |
| 5 | 0.3387 | 0.1905 | 0.3128 | 0 | 0.6872 |
| 6 | 0.3590 | 0.2047 | 0.2502 | 0 | 0.7498 |
| 7 | 0.3794 | 0.2207 | 0.1554 | 0.0580 | 0.7866 |
| 8 | 0.3998 | 0.2376 | 0.0485 | 0.1376 | 0.8139 |
| 9 | 0.4202 | 0.2557 | 0 | 0.1124 | 0.8876 |
| 10 | 0.4405 | 0.2773 | 0 | 0 | 1.000 |
| S. No | ||||
|---|---|---|---|---|
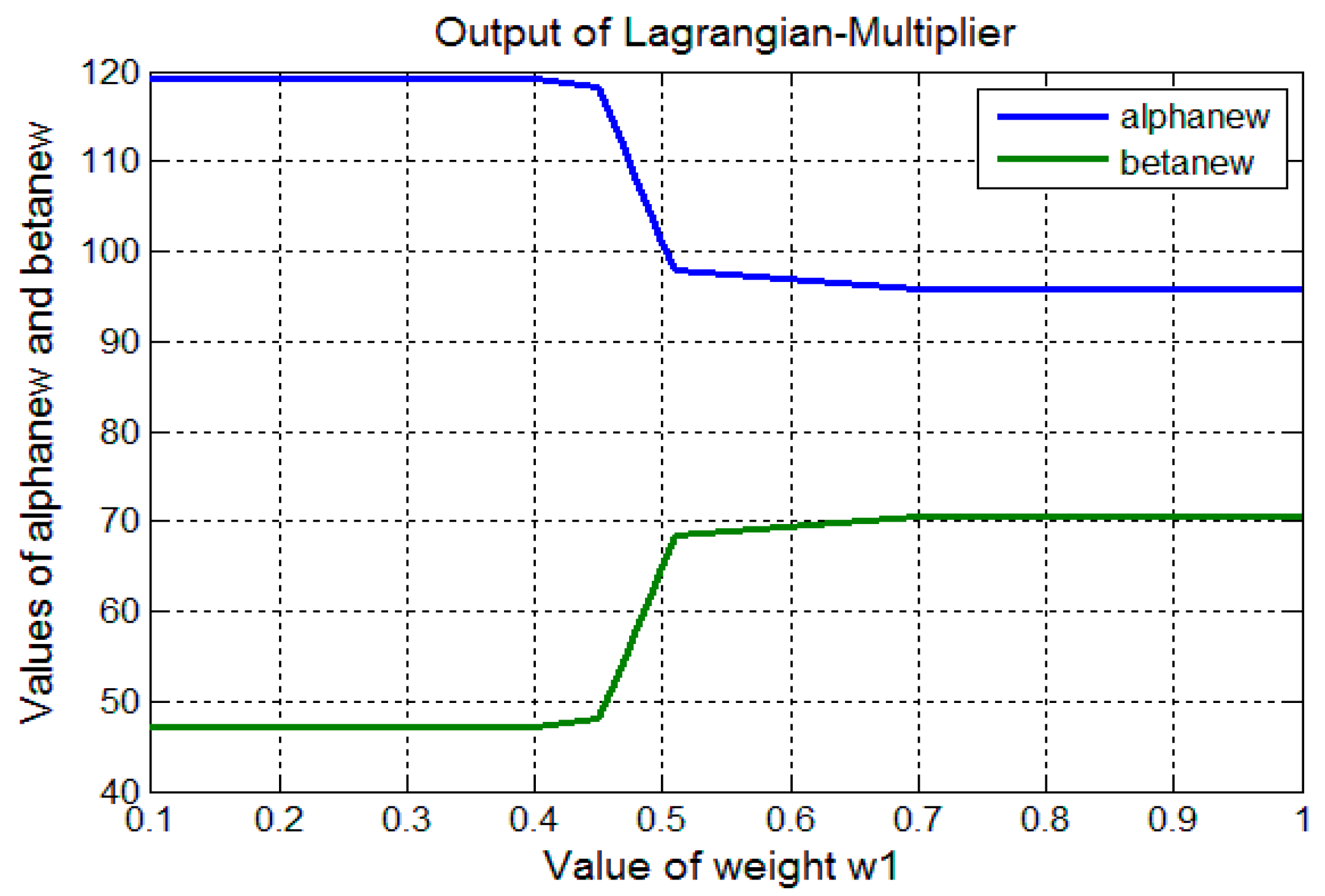
| 1. | 1.0 | 0.0001 | 95.8799 | 70.5697 |
| 2. | 0.9 | 0.1 | 95.8799 | 70.5697 |
| 3. | 0.7 | 0.3 | 95.8800 | 70.5667 |
| 4. | 0.51 | 0.49 | 97.8193 | 68.4395 |
| 5. | 0.5 | 0.5 | 101.0353 | 64.9947 |
| 6. | 0.49 | 0.51 | 104.3293 | 61.5669 |
| 7. | 0.48 | 0.52 | 107.7027 | 58.1558 |
| 8. | 0.47 | 0.53 | 111.1578 | 54.7610 |
| 9. | 0.46 | 0.54 | 114.6992 | 51.3820 |
| 10. | 0.45 | 0.55 | 118.3202 | 48.0185 |
| 11. | 0.4 | 0.6 | 119.1606 | 47.2520 |
| 12. | 0.1 | 0.9 | 119.1606 | 47.2518 |
| S. No | ||
|---|---|---|
| 1 | 0.01 | 0.8 |
| 2 | 0.015 | 0.9 |
| 3 | 0.02 | 0.96 |
| 4 | 0.011 | 0.85 |
| 5 | 0.009 | 0.88 |
| 6 | 0.008 | 0.80 |
| 7 | 0.007 | 0.81 |
| 8 | 0.006 | 0.87 |
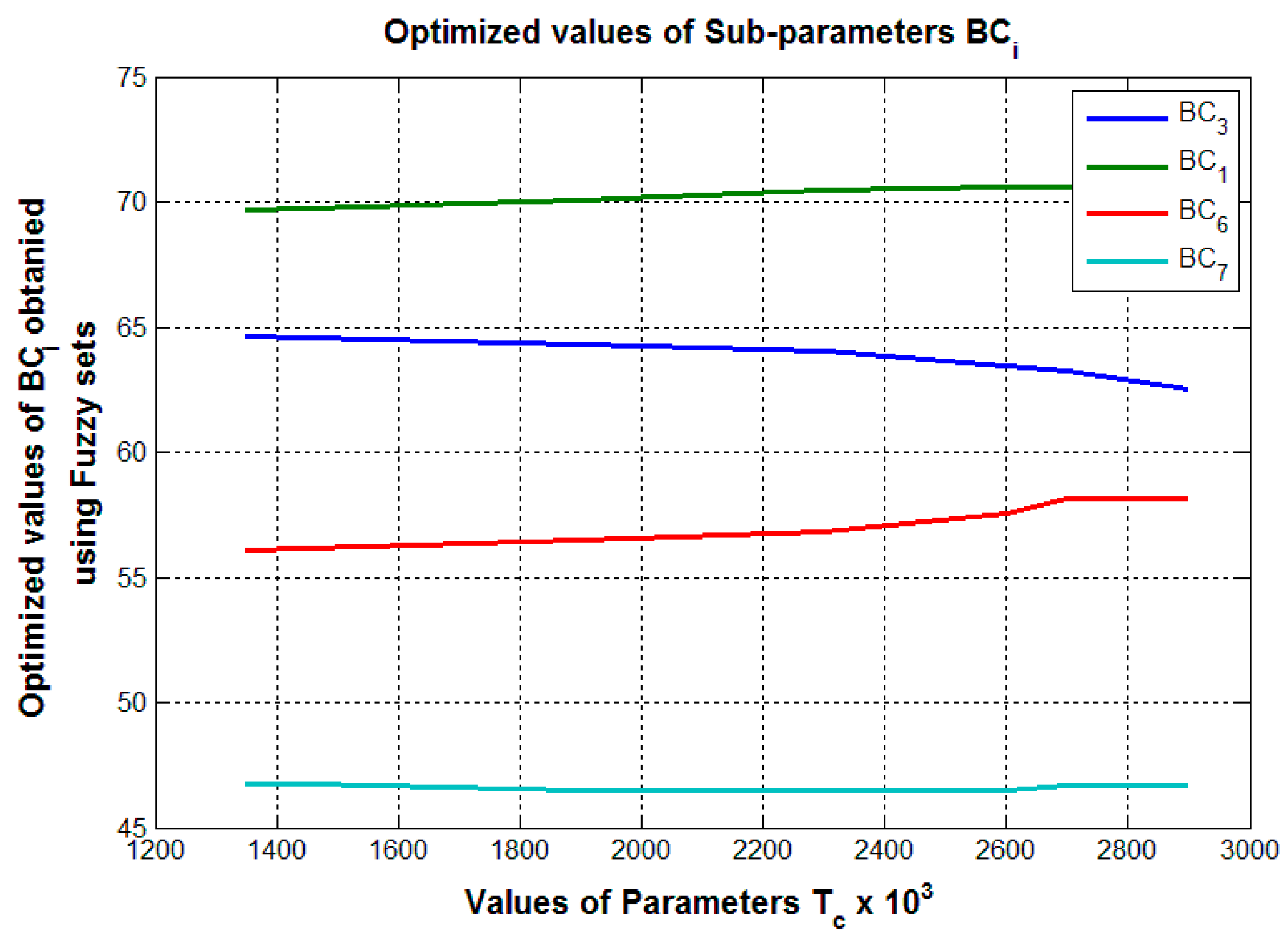
| S. No | Category | Range of Values of βnew | Parameter BCi |
|---|---|---|---|
| 1 | A | 70.56–70.56 | |
| 2 | A | 68.43–70.56 | |
| 3 | A | 61.56–64.99 | |
| 4 | B | 55.00–58.15 | |
| 5 | B | 51.52–54.76 | |
| 6 | B | 49.00–51.38 | |
| 7 | C | 47.25–48.01 | |
| 8 | C | 46.50–47.25 |
| S. No. | Parameter | Si min | Si max |
|---|---|---|---|
| 1 | 0.05 | 0.8 | |
| 2 | 0.21 | 0.21 | |
| 3 | 0.01 | 0.75 | |
| 4 | 0.15 | 0.4 | |
| 5 | 0.31 | 0.31 | |
| 6 | 0.1 | 0.4 | |
| 7 | 0.05 | 0.1 | |
| 8 | 0.05 | 0.15 |
| S. No | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2.9 | 0.579 | 0.210 | 0.750 | 0.400 | 0.310 | 0.400 | 0.100 | 0.150 |
| 2 | 2.7 | 0.414 | 0.210 | 0.750 | 0.400 | 0.310 | 0.365 | 0.100 | 0.150 |
| 3 | 2.6 | 0.355 | 0.210 | 0.750 | 0.400 | 0.310 | 0.324 | 0.100 | 0.150 |
| 4 | 2.3 | 0.221 | 0.210 | 0.676 | 0.400 | 0.310 | 0.232 | 0.100 | 0.150 |
| 5 | 1.9 | 0.155 | 0.210 | 0.393 | 0.400 | 0.310 | 0.188 | 0.92 | 0.150 |
| 6 | 1.45 | 0.99 | 0.210 | 0.153 | 0.336 | 0.310 | 0.149 | 0.70 | 0.120 |
| 7 | 1.35 | 0.88 | 0.210 | 0.104 | 0.314 | 0.310 | 0.142 | 0.66 | 0.113 |
| S. No | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2.9 | 62.51 | 69.5 | 70.57 | 49.0 | 54.56 | 58.15 | 46.5 | 48.01 |
| 2 | 2.7 | 63.22 | 69.5 | 70.57 | 49.0 | 54.56 | 57.87 | 46.5 | 48.01 |
| 3 | 2.6 | 63.47 | 69.5 | 70.57 | 49.0 | 54.56 | 57.55 | 46.5 | 48.01 |
| 4 | 2.3 | 64.05 | 69.5 | 70.46 | 49.0 | 54.56 | 56.82 | 46.5 | 48.01 |
| 5 | 1.9 | 64.33 | 69.5 | 70.06 | 49.0 | 54.56 | 56.48 | 46.5 | 48.01 |
| 6 | 1.45 | 64.57 | 69.5 | 69.71 | 49.38 | 54.56 | 56.17 | 46.72 | 47.82 |
| 7 | 1.35 | 64.61 | 69.5 | 69.64 | 49.51 | 54.56 | 56.12 | 46.75 | 47.82 |
| S. No | Parameters | Lower Limit | Upper Limit | Coefficients | Optimized Values by Executing Cuckoo Intelligence | Scaled Optimized Values | Optimized Value of Fifth Layer (Layer 5) | |
|---|---|---|---|---|---|---|---|---|
| 1. | 150 | 600 | 0.001562 | 338.8589 | 8.1945 | |||
| 7.92 | 0.3388589 | |||||||
| 300 | ||||||||
| 2. | 100 | 400 | 0.00194 | 333.7502 | ||||
| 7.85 | 0.3337502 | |||||||
| 320 | ||||||||
| 3. | 50 | 200 | 0.00482 | 127.3909 | ||||
| 7.97 | 0.1273909 | |||||||
| 329 | ||||||||
| S. No | Parameters | Lower Limit | Upper Limit | Coefficients | Optimized Values by Executing Cuckoo Intelligence | Scaled Optimized Values | Optimized Value of Fifth Layer (Layer 5) | |
|---|---|---|---|---|---|---|---|---|
| 1. | 500 | 800 | 0.001562 | 529.7067 | 0.5297067 | 10.3241 | ||
| 7.92 | ||||||||
| 300 | ||||||||
| 2. | 200 | 600 | 0.00194 | 377.013 | 0.377013 | |||
| 7.85 | ||||||||
| 320 | ||||||||
| 3. | 50 | 300 | 0.00482 | 171.2219 | 0.1712219 | |||
| 7.97 | ||||||||
| 329 | ||||||||
| S. No | Coefficients Used in Modified Fifth Layer | Values |
|---|---|---|
| 1. | 0.45335985 | |
| 2. | 0.27411745 | |
| 3. | 0.49140574 | |
| 4. | 0.34975271 | |
| 5. | 0.01405009 | |
| 6. | 0.02201897 |
| Selected Layer in Existing and Modified ANFIS | Nodes Used in the Selected Layer | Chosen Values of the Selected Nodes |
|---|---|---|
| First layer (layer 1) | 0.3477 | |
| 0.1944 | ||
| 0.6811 | ||
| 0.8250 |
| Selected Layer in Existing ANFIS | Nodes Used in the Selected Layer | Output |
|---|---|---|
| Second layer (Layer 2) | 0.2368 | |
| 0.1604 | ||
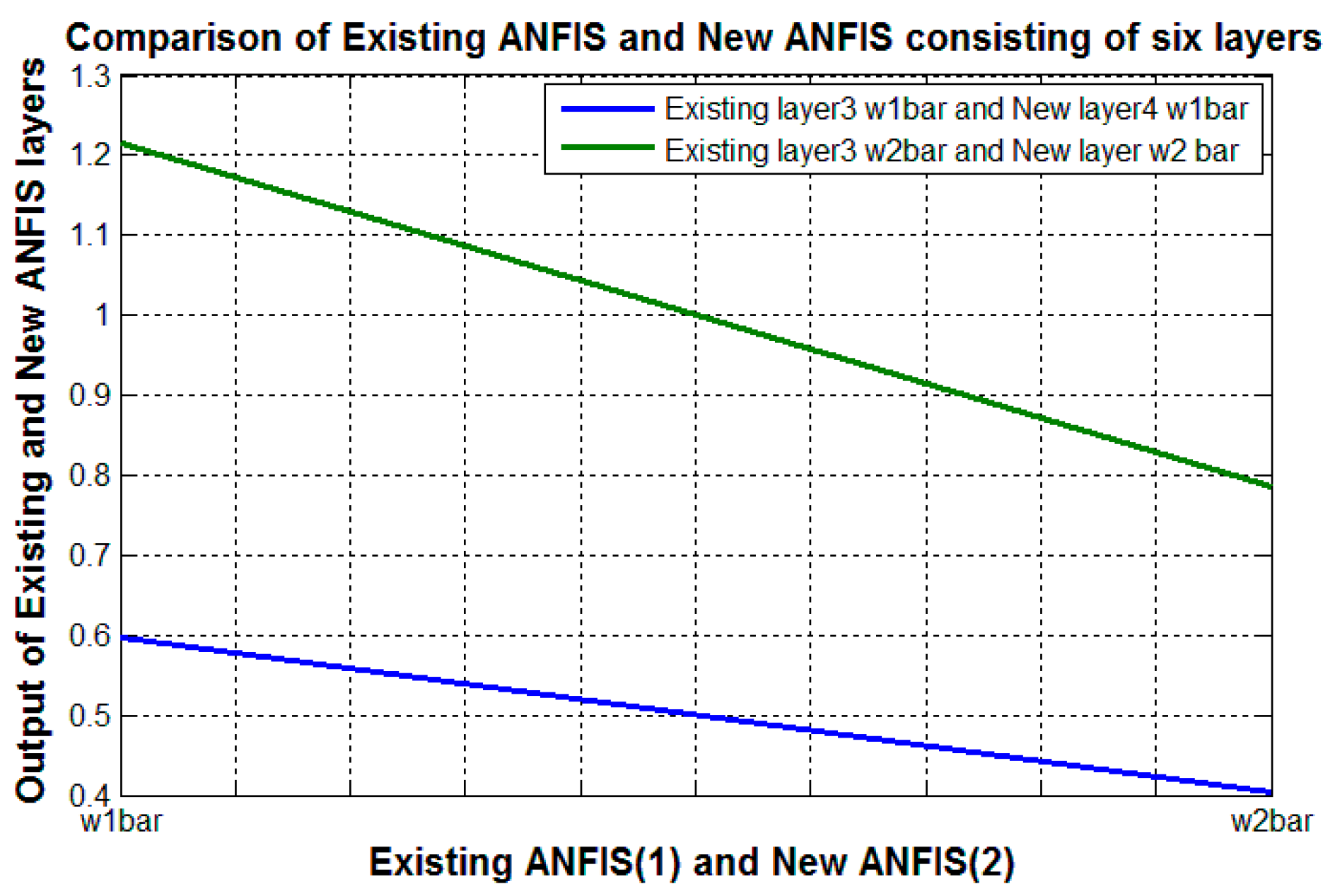
| Third layer (Layer 3) | 0.5963 | |
| 0.4037 | ||
| Fourth layer (layer 4) | 1154.7 | |
| 451.52 | ||
| Last output layer (layer 5) | Output node of Existing ANFIS | 1606.3 |
| Selected Layer in Modified ANFIS | Nodes Used in the Selected Layer | Output |
|---|---|---|
| Second layer (layer 2) | * | 0.4040 |
| * | 0.4050 | |
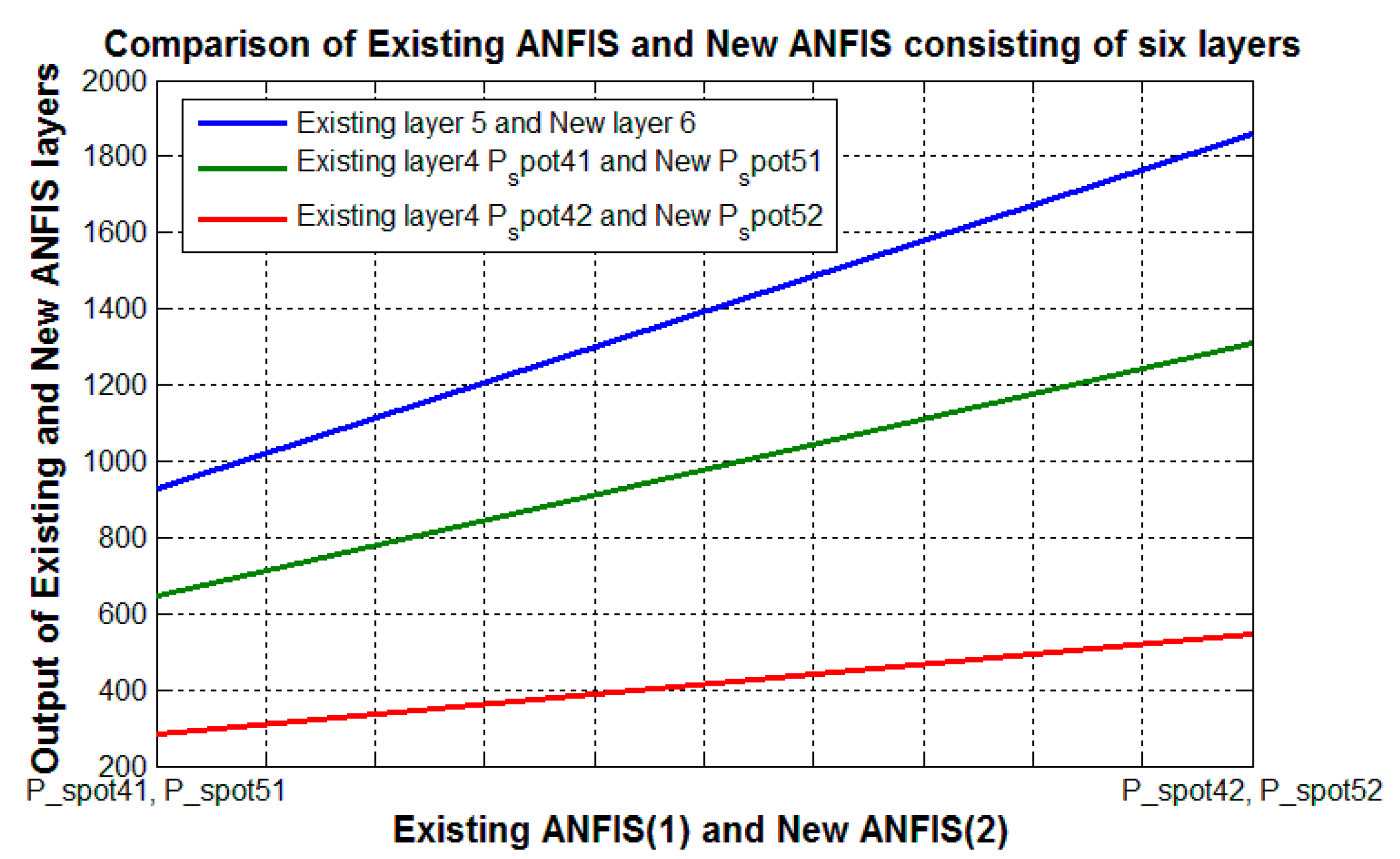
| Fifth layer (layer 5) | 967.1194 | |
| 559.8678 | ||
| Last output layer (layer 6) | Output node of Modified ANFIS | 1527.0 |
| Selected Layer in Modified ANFIS | Nodes Used in the Selected Layer | Output |
|---|---|---|
| Second layer (layer 2) | 0.2368 | |
| 0.1604 | ||
| Fifth layer (layer 5) | 644.3709 | |
| 281.5149 | ||
| Last output layer (layer 6) | Output node of Modified ANFIS | 925.8858 |
| Selected Layer in Modified ANFIS | Nodes Used in the Selected layer | Output |
|---|---|---|
| Second layer (layer 2) | * | 0.4040 |
| * | 0.4050 | |
| Fifth layer (layer 5) | 539.6790 | |
| 349.0620 | ||
| Last output layer (layer 6) | Output node of Modified ANFIS | 888.7410 |
| S. No. | Particular Case | Selected Layers in Which Changes Are Incorporated | Value of Output Node of the Last Layer | ANFIS Structure Used |
|---|---|---|---|---|
| 1. | Case 1 | No layer changed (Existing ANFIS) | 1606.3 | Existing ANFIS |
| 2. | Case 2 | Second layer (layer 2) | 1527.0 | Modified ANFIS |
| 3. | Case 3 | Fifth layer (layer 5) | 925.8858 | Modified ANFIS |
| 4. | Case 4 | Second and Fifth layer | 888.7410 | Modified ANFIS |
| Portfolio Returns (r0) | Allocation | Portfolio Risk | |||||
|---|---|---|---|---|---|---|---|
| B1 | B2 | B3 | B4 | B5 | |||
| PP1 | 0.2560 | - | - | - | - | 0.5628 | 0.1622 |
| PP2 | 0.2786 | - | - | - | - | 0.5002 | 0.1641 |
| PP3 | 0.3012 | - | - | - | - | 0.4377 | 0.1698 |
| PP4 | 0.3238 | - | - | - | - | 0.3752 | 0.1788 |
| PP5 | 0.3464 | - | - | - | - | 0.3126 | 0.1907 |
| PP6 | 0.3690 | - | - | - | - | 0.2501 | 0.2050 |
| PP7 | 0.3916 | - | - | - | - | 0.1876 | 0.2212 |
| PP8 | 0.4142 | - | - | - | - | 0.1251 | 0.2390 |
| PP9 | 0.4368 | - | - | - | - | 0.0438 | 0.2579 |
| PP10 | 0.4594 | - | - | - | - | 0.0 | 0.2779 |
| B6 | B7 | B8 | B9 | B10 | |||
| - | - | - | - | 0.4372 | |||
| - | - | - | - | 0.4998 | |||
| - | - | - | - | 0.5623 | |||
| - | - | - | - | 0.6248 | |||
| - | - | - | - | 0.6874 | |||
| - | - | - | - | 0.7499 | |||
| - | - | - | - | 0.8124 | |||
| - | - | - | - | 0.8749 | |||
| - | - | - | - | 0.9259 | |||
| - | - | - | - | 1.0 |
| Portfolio Returns (r0) | Allocation | Portfolio Risk | |||||
|---|---|---|---|---|---|---|---|
| B1 | B2 | B3 | B4 | B5 | |||
| PP1 | 0.2606 | - | - | - | - | 0.5639 | 0.1622 |
| PP2 | 0.2833 | - | - | - | - | 0.5012 | 0.1642 |
| PP3 | 0.3059 | - | - | - | - | 0.4386 | 0.1698 |
| PP4 | 0.3286 | - | - | - | - | 0.3759 | 0.1789 |
| PP5 | 0.3512 | - | - | - | - | 0.3133 | 0.1908 |
| PP6 | 0.3739 | - | - | - | - | 0.2506 | 0.2052 |
| PP7 | 0.3965 | - | - | - | - | 0.1880 | 0.2215 |
| PP8 | 0.4192 | - | - | - | - | 0.1253 | 0.2393 |
| PP9 | 0.4418 | - | - | - | - | 0.0411 | 0.2583 |
| PP10 | 0.4645 | - | - | - | - | 0.0 | 0.2783 |
| B6 | B7 | B8 | B9 | B10 | |||
| - | - | - | - | 0.4361 | |||
| - | - | - | - | 0.4988 | |||
| - | - | - | - | 0.5614 | |||
| - | - | - | - | 0.6241 | |||
| - | - | - | - | 0.6887 | |||
| - | - | - | - | 0.7494 | |||
| - | - | - | - | 0.8120 | |||
| - | - | - | - | 0.8747 | |||
| - | - | - | - | 0.9240 | |||
| - | - | - | - | 1.0 |
| Portfolio Returns (r0) | Allocation | Portfolio Risk | |||||
|---|---|---|---|---|---|---|---|
| B1 | B2 | B3 | B4 | B5 | |||
| PP1 | 0.2555 | - | - | - | - | 0.5626 | 0.1622 |
| PP2 | 0.2781 | - | - | - | - | 0.5001 | 0.1641 |
| PP3 | 0.3007 | - | - | - | - | 0.4376 | 0.1698 |
| PP4 | 0.3233 | - | - | - | - | 0.3751 | 0.1788 |
| PP5 | 0.3459 | - | - | - | - | 0.3126 | 0.1907 |
| PP6 | 0.3685 | - | - | - | - | 0.2501 | 0.2050 |
| PP7 | 0.3911 | - | - | - | - | 0.1875 | 0.2212 |
| PP8 | 0.4137 | - | - | - | - | 0.1250 | 0.2390 |
| PP9 | 0.4363 | - | - | - | - | 0.0441 | 0.2579 |
| PP10 | 0.4589 | - | - | - | - | 0.0 | 0.2779 |
| B6 | B7 | B8 | B9 | B10 | |||
| - | - | - | - | 0.4374 | |||
| - | - | - | - | 0.4999 | |||
| - | - | - | - | 0.5624 | |||
| - | - | - | - | 0.6249 | |||
| - | - | - | - | 0.6874 | |||
| - | - | - | - | 0.7499 | |||
| - | - | - | - | 0.8125 | |||
| - | - | - | - | 0.8750 | |||
| - | - | - | - | 0.9261 | |||
| - | - | - | - | 1.0 |
| Portfolio | Expected Return with Existing ANFIS | Expected Return with Modified ANFIS |
|---|---|---|
| PP1 | 0.2555 | 0.2606 |
| PP2 | 0.2781 | 0.2833 |
| PP3 | 0.3007 | 0.3059 |
| PP4 | 0.3233 | 0.3286 |
| PP5 | 0.3459 | 0.3512 |
| PP6 | 0.3685 | 0.3739 |
| PP7 | 0.3911 | 0.3965 |
| PP8 | 0.4137 | 0.4192 |
| PP9 | 0.4363 | 0.4418 |
| PP10 | 0.4589 | 0.4645 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, C.; Doja, M.N. A Novel Framework for Portfolio Selection Model Using Modified ANFIS and Fuzzy Sets. Computers 2018, 7, 57. https://doi.org/10.3390/computers7040057
Kumar C, Doja MN. A Novel Framework for Portfolio Selection Model Using Modified ANFIS and Fuzzy Sets. Computers. 2018; 7(4):57. https://doi.org/10.3390/computers7040057
Chicago/Turabian StyleKumar, Chanchal, and Mohammad Najmud Doja. 2018. "A Novel Framework for Portfolio Selection Model Using Modified ANFIS and Fuzzy Sets" Computers 7, no. 4: 57. https://doi.org/10.3390/computers7040057
APA StyleKumar, C., & Doja, M. N. (2018). A Novel Framework for Portfolio Selection Model Using Modified ANFIS and Fuzzy Sets. Computers, 7(4), 57. https://doi.org/10.3390/computers7040057




