Abstract
Features extracted from the electromyography (EMG) signal normally consist of irrelevant and redundant features. Conventionally, feature selection is an effective way to evaluate the most informative features, which contributes to performance enhancement and feature reduction. Therefore, this article proposes a new competitive binary grey wolf optimizer (CBGWO) to solve the feature selection problem in EMG signals classification. Initially, short-time Fourier transform (STFT) transforms the EMG signal into time-frequency representation. Ten time-frequency features are extracted from the STFT coefficient. Then, the proposed method is used to evaluate the optimal feature subset from the original feature set. To evaluate the effectiveness of proposed method, CBGWO is compared with binary grey wolf optimization (BGWO1 and BGWO2), binary particle swarm optimization (BPSO), and genetic algorithm (GA). The experimental results show the superiority of CBGWO not only in classification performance, but also feature reduction. In addition, CBGWO has a very low computational cost, which is more suitable for real world application.
1. Introduction
Electromyography (EMG) signals recorded from the residual muscles have the potential to be used as a control source for assistive rehabilitation device and myoelectric prosthetic [1]. EMG is a bioelectrical signal that offers rich muscle information, which can be used to identify and recognize hand motions [2]. The development of EMG-based rehabilitation devices is becoming of major interest to many biomedical researchers. However, the development of EMG-controlled prosthetics is still a challenging issue in developing countries [3]. In past studies, most researchers have applied advanced signal processing, feature extraction, machine learning, and feature selection algorithms to enhance the performance of the EMG pattern recognition system [4,5,6,7]. Generally, signal processing performs the signal transformation to obtain useful signal information. Feature extraction aims to extract the valuable information from the signal. The feature selection algorithm attempts to evaluate the optimal features from the original feature set. Finally, machine learning acts as the classifier, to classify the features for recognizing the hand movements.
In recent days, many EMG features have been proposed and applied in EMG pattern recognition [8,9,10]. The increment in the number of EMG features not only increases the complexity of the classifier, but also has a negative impact on the classification process [11]. Following this line of thought, feature selection is an essential step to remove redundant and irrelevant information which, in turn, will reduce the number of features and unnecessary complexity [12]. However, feature selection is known as a combinatorial NP-hard problem. The possible combination of the features will be 2D, where D is the dimension of features [13]. For example, if we have 100 features, then, the possible combination of features is 2100, which is impractical for conducting an exhaustive search.
Feature selection can be categorized into filter and wrapper approaches. Filter approach makes use of the dependency, mutual information, distance, and information theory in feature selection [14]. Unlike filter, wrapper approach employs a classifier as the learning algorithm to optimize the classification performance by selecting the relevant features. Commonly, filter approach is often faster than wrapper approach, due to shorter computational time. Nevertheless, wrapper approach can usually provide better performance [13]. Wrapper-based feature selection applies a metaheuristic optimization method, such as binary grey wolf optimization (BGWO), binary particle swarm optimization (BPSO), genetic algorithm (GA), ant colony optimization (ACO), and binary differential evolution (BDE), to select the optimal feature subset [15,16,17,18,19].
In a past study, Huang et al. proposed a new feature selection-based ACO that utilized the minimum redundancy maximum relevance criterion (ACO-mRMR) as the heuristic information for EMG signals classification. The results showed ACO-mRMR outperformed ACO and principal component analysis (PCA) in dimensionality reduction [20]. Venugopal et al. applied GA and information gain (IG) to evaluate the relevant features, and it was observed that GA was good in feature reduction [21]. Emary et al. proposed two binary versions of grey wolf optimization (BGWO1 and BGWO2) to tackle the feature selection problems. The authors indicated proposed methods showed competitive results as compared to other conventional methods [15]. Moreover, Purushothaman et al. made use of particle swarm optimization (PSO) and ACO to identify the best EMG features that optimized the classification performance for finger movement recognition [6]. Recently, Karthick et al. employed BPSO and GA to evaluate promising features for muscle fatigue detection [9]. Previous works imply feature selection is critically important to achieve the optimal classification performance in EMG signals classification.
Binary grey wolf optimization (BGWO) is a recent feature selection algorithm, which usually offers better performance than other conventional methods [15]. However, the new positions of wolves are mostly based on the experience of leaders (alpha, beta, and delta), thus leading to premature convergent. In addition, a proper balance between the exploration (global search) and exploitation (local search) is still the challenging issue in BGWO. In this paper, we propose a new competitive binary grey wolf optimizer (CBGWO) that aims to improve the performance of BGWO in feature selection. Two schemes, namely, competitive and leader enhancement strategies, are introduced in CBGWO. First, a competitive strategy allows the wolves to compete in couples. The winners of competition are directly moved into the new population. On the contrary, the losers will update their positions by learning from the winners and leaders. Second, a leader enhancement strategy is proposed to enhance the leaders, which can prevent the algorithm from being trapped in the local optimal. The performance of CBGWO is tested using the EMG data acquired from NinaPro database. To evaluate the effectiveness of proposed method, CBGWO is compared with BGWO1, BGWO2, BPSO, and GA. The experimental results indicate CBGWO has a very efficient computational complexity, while keeping a comparative performance in feature selection.
The rest of paper is organized as follows. Section 2 introduces the methodology of proposed EMG pattern recognition system. The new feature selection method, CBGWO, is also briefly explained. Section 3 reports the experimental setting and empirical results. Section 4 discusses the results presented in Section 3. At last, the conclusion is outlined in Section 5.
2. Materials and Methods
2.1. EMG Data
In the present study, the fourth version of EMG database (DB4) from Non-Invasive Adaptive Prosthetics (NinaPro) project (https://www.idiap.ch/project/ninapro) is applied [22]. DB4 comprises of the surface EMG signals acquired from 10 healthy subjects. In this work, the EMG signals of 17 hand movement types (Exercise B) are used. There were 12 EMG electrodes that had been implemented in the process of recording. The EMG signals were sampled at 2 kHz. In the experiment, each subject was instructed to perform the hand movement for 5 s each, followed by the resting state of 3 s. Each movement was repeated six times. Note that all the resting states were removed before further processing was conducted.
2.2. Feature Extraction Using STFT
Short-time Fourier transform (STFT) is the most fundamental of time-frequency distributions. As compared to other advance signal processing tools, such as Stockwell transform, B-distribution, and Choi–William distribution, STFT is known to be the simplest and fastest. Mathematically, STFT can be formulated as [8]:
where x(n) is the input EMG signal and w(n − τ) is the Hanning window function. In this study, STFT, with window size of 512 ms (1024 samples), is utilized. Generally, STFT transforms the signal into a two-dimensional matrix. As a result, the signal is represented in both time and frequency planes, which consist of high dimensions. To reduce the dimensionality, ten time-frequency features, namely Renyi entropy, spectral entropy, Shannon entropy, singular value decomposition-based entropy, concentration measure, mean frequency, median frequency, two-dimensional mean, variance, and coefficient of variation, are extracted from STFT coefficients.
2.2.1. Renyi Entropy
Renyi entropy (RE) is a time-frequency feature that estimates the complicacy of the signal itself. A higher RE indicates the signal consists of a high degree of non-stationary component [9]. RE can be defined as
where S is the magnitude of STFT, a is the Renyi entropy order, and L and M are the total length of time and frequency bins, respectively. Previous work affirmed alpha, a, should be an odd integer and must be greater than 2. In this work, the alpha, a, is set at 3 [9].
2.2.2. Spectral Entropy
Spectral entropy (SE) is used to determine the randomness of energy distribution of the signal. A higher SE indicates signal energy is less concentrated to specific region on the time-frequency plane [9,23]. SE can be expressed as
where P is the power spectrum, and L and M are the total length of time and frequency bins, respectively.
2.2.3. Shannon Entropy
Shannon entropy (Sh) is the fundamental of the entropy’s family, and it can be written as
where S is the magnitude of STFT, and L and M are the total length of time and frequency bins, respectively.
2.2.4. Singular Value Decomposition-Based Entropy
Singular value decomposition-based entropy (ESVD) is an entropy estimated from singular value decomposition (SVD). Initially, SVD is applied to decompose the time-frequency amplitude into signal subspace and orthogonal alternate subspace. The entropy based on singular values offers the time-frequency information related to the complexity and magnitude of STFT [9]. Mathematically, ESVD can be formulated as
where is the normalized singular value, and it can be calculated as
where Sk is the singular value of matrix S[n,m] that obtained from the singular value decomposition.
2.2.5. Concentration Measure
Concentration measure (CM) is a time-frequency feature that describes the concentration of signal energy distribution on time-frequency plane [9]. CM can be defined as
where S is the magnitude of STFT, and L and M are the total number of time and frequency bins, respectively.
2.2.6. Mean Frequency
Mean frequency (MNF) is the sum of product of frequencies with its corresponding power spectral that is divided by the total power estimated from the power spectrum [24]. MNF, at each instant of time sample, is represented as
where P is the power spectrum, fm is the frequency value at frequency bin m, and M is the total number of the frequency bin. In this work, the averaged MNF across multiple instants of time sample is calculated.
2.2.7. Median Frequency
Median frequency (MDF) is the frequency that partitions the power spectrum into two equal halves [24]. MDF at each instant of time sample is given by
where P is the power spectrum, and M is the total number of the frequency bin. In this study, the averaged MDF across multiple instants of time sample is calculated.
2.2.8. Two-Dimensional Mean, Variance, and Coefficient of Variation
Generally speaking, statistical features that refer to one-dimensional statistical properties, such as mean, variance (VAR), and coefficient of variation (CoV), can be extended into two dimensions, as follows [9,24]:
where σ is the standard deviation, and μ is the mean value.
2.3. Grey Wolf Optimizer
Grey wolf optimizer (GWO) is a recent metaheuristic optimization method developed by Mirjalili and his colleagues in 2014 [25]. Normally, grey wolves live in a pack with a group size of 5 to 12. GWO mimics the hunting and searching prey characteristic of grey wolves in nature. In GWO, the population are divided into alpha, beta, delta, and omega. Alpha wolf is the main leader which is responsible for decision-making. Beta wolf is the second leader that assists the alpha in making the decision or other activities. Delta wolf is defined as the third leader in the group, which dominates the omega wolves.
Mathematically, the top three fittest solutions in GWO are called alpha (α), beta (β), and delta (δ), respectively. The rest are assumed to be omega (ω). In GWO, the hunting process is guided by α, β, and δ, while ω follows these three leaders. The encircling behavior for the pack to hunt a prey can be expressed as
where Xp is the position of prey, A is the coefficient vector, and D is defined as
where C is the coefficient vector, X is the position of grey wolf, and t is the number of iterations. The coefficient vectors, A and C, are determined by
where r1 and r2 are two independent random numbers uniformly distributed between [0, 1], and a is the encircling coefficient that is used to balance the tradeoff between exploration and exploitation. In GWO, parameter a is linearly decreasing, from 2 to 0, according to Equation (17).
where t is the number of iterations, and T is the maximum number of iterations. In GWO, the leader alpha, beta, and delta wolves are known to have better knowledge about the potential position of prey. Thus, the leaders are guiding the omega wolves to move toward the optimal position. Mathematically, the new position of wolf is updated as in Equation (18).
where X1, X2, and X3 are calculated as follows:
where Xα, Xβ, and Xδ are the position of alpha, beta, and delta at iteration t; A1, A2, and A3 are calculated as in Equation (15); and Dα, Dβ and Dδ are defined as in Equations (22)–(24), respectively.
where C1, C2, and C3 are calculated as in Equation (16).
Generally, GWO is designed to solve the continuous optimization problems. For binary optimization problems, such as feature selection, a binary version of GWO is required. Recently, Emary et al. [15] proposed two novel binary grey wolf optimizations (BGWO1 and BGWO2) to tackle the feature selection problems. The operation of BGWO1 and BGWO2 are described as follows.
2.3.1. Binary Grey Wolf Optimization Model 1 (BGWO1)
For the first approach, BGWO1 utilizes the crossover operator to update the position of wolf as follows:
where Crossover (Y1, Y2, and Y3) is the crossover operation between solutions, and Y1, Y2, and Y3 are the binary vectors affected by the movement of alpha, beta, and delta wolves, respectively. In BGWO1, Y1, Y2, and Y3 are defined using Equations (26), (29) and (32), respectively.
where is the position of alpha, d is the dimension of search space, and represents the binary step that can be expressed as
where r3 is a random vector in [0, 1], and denotes the continuous valued step size that can be calculated as in Equation (28).
where and are determined by applying Equations (15) and (22).
where is the position of beta, d is the dimension of search space, and represents the binary step that can be expressed as
where r4 is a random vector in [0, 1], and denotes the continuous valued step size that can be calculated as in Equation (31).
where and are determined by applying Equations (15) and (23).
where is the position of delta, d is the dimension of search space, and represents the binary step that can be expressed as
where r5 is a random vector in [0, 1], and denotes the continuous valued step size that can be calculated as in Equation (34).
where and are determined by applying Equations (15) and (24). After obtaining Y1, Y2, and Y3, the new position of the wolf is updated using the crossover operation, as follows:
where d is the dimension of search space, and r6 is a random number uniformly distributed between [0, 1].
The pseudocode of BGWO1 is shown in Figure 1. Initially, the population of grey wolves is randomly initialized (either bit 1 or 0). Afterward, the fitness of each wolf is evaluated. The best, second best, and third best solutions are defined as alpha, beta, and delta. For each wolf, Y1, Y2, and Y3 are computed using Equations (26), (29), and (32), respectively. Then, the position of wolf is updated by applying the crossover between Y1, Y2, and Y3. Next, the fitness of each wolf is evaluated. Iteratively, the positions of alpha, beta, and delta are updated. The algorithm is repeated until the terminated criterion is satisfied. At last, the alpha solution is selected as the optimal feature subset.

Figure 1.
The pseudocode of binary grey wolf optimization (BGWO).
2.3.2. Binary Grey Wolf Optimization Model 2 (BGWO2)
For the second approach, BGWO2 updates the position of wolf by converting the position into a binary vector, as shown in Equation (36).
where r7 is a random vector in [0, 1], d is the dimension of search space, and S is the sigmoid function, and it can be expressed as
The pseudocode of BGWO2 is represented in Figure 2. Firstly, the initial population of wolves is randomly initialized (either bit 1 or 0). Secondly, the fitness of grey wolves is evaluated. The three leaders, alpha, beta, and delta, are selected based on the fitness. For each wolf, the X1, X2, and X3 are computed using Equations (19)–(21), respectively. Next, the new position of grey wolf is updated by applying Equation (36). Afterward, the fitness of wolves is evaluated, and the position of alpha, beta, and delta are updated. The algorithm is repeated until the terminated criterion is satisfied. Finally, the alpha solution is selected as the optimal feature subset.

Figure 2.
The pseudocode of BGWO2.
2.4. Competitive Binary Grey Wolf Optimizer
Generally, BGWO has the advantages of being simple, flexible, and adaptable, as compared to other metaheuristic optimizations. However, BGWO also has the limitation of restricting local optimal. BGWO applies the best three solutions (leaders) in the position update, which means all the wolves are trying to move toward the positions of leaders. In this way, the wolves will slowly, or nearly, become the same as the leaders. All the wolves are slowly getting trapped in the local optimal. This will lead to low diversity and premature convergent [26,27]. Therefore, we propose a new competitive binary grey wolf optimizer (CBGWO) to address the limitation of BGWO in feature selection.
The general idea of CBGWO comes to mind from the concept of competition among each couple of wolves in the population. In CBGWO, the wolves are randomly selected, pairwise, from the population, for competition. To explain this concept, the N wolves in the population are randomly divided into N/2 couples, where N is the number of wolves in the population. After that, the competition is made between two wolves in each couple. This indicates that each wolf is only participating once in the competition. From the competition, the wolves with better fitness are called winners. On the contrary, the wolves that lose in the competition are known to be losers. The winners are directly passed to the next generation without performing the position update. On the other side, the losers can update their positions by learning from the winners. In other words, only the position of N/2 wolves in the population will be updated. The general concept and idea of competition in CBGWO is illustrated in Figure 3.
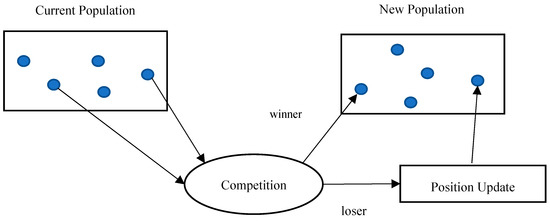
Figure 3.
The competition strategy of competitive binary grey wolf optimizer (CBGWO).
2.4.1. New Position Update
By applying a competition strategy, CBGWO allows the winners (half of the population) to directly pass to the next generation, while the rest N/2 wolves will update their positions according to Equation (38).
where S is the sigmoid function as shown in Equation (37), r8 is a random vector in [0, 1], X1, X2, and X3 are defined as follows:
where Xα, Xβ, and Xδ are the positions of alpha, beta, and delta at iteration t; A1, A2, and A3 are computed as in Equation (15); and , , and are calculated as in Equations (42)–(44), respectively.
where Xw is the winner wolf, Xl is the loser wolf, C1, C2, and C3 are calculated as in Equation (16). As can be seen in Equations (42)–(44), the losers update their positions by learning from the winners. This means that losers are not only instructed by the alpha, beta, and delta wolves, but also guided by the winners to move toward the best prey position. In this way, CBGWO can explore the search region effectively.
2.4.2. Leader Enhancement
The leaders, alpha, beta, and delta, play an important role in CBGWO. Generally, the wolf populations are guided by these leaders to move to a better prey position. To prevent CBGWO from being trapped in the local optimum, these leaders can enhance themselves with a leader enhancement strategy. In this strategy, random walk is used to perform a local search around these leaders (alpha, beta, and delta). The random walk is given by
where R is the change rate, XL is the leader (either alpha, beta or delta), rand (0,1) is a random number generated—either 1 or 0, and r9 is a random number uniformly distributed between [0, 1]. In CBGWO, the R is linearly decreasing from 0.9 to 0, as shown in Equation (46).
where t is the number of iterations, and T is the maximum iteration number. According to Equation (46), a larger R in the beginning of the iteration allows more positions to be changed, thus leading to high exploration. As the time (iteration) passes, a smaller R tends to promote the exploitation around the best solutions. Since there are three leaders in CBGWO, thus, only three new leaders are generated in each iteration using Equation (45). Hence, not much additional computational cost is acquired. In the leader enhancement process, if the fitness value of a new leader is found to be better, then the current leader will be replaced. Otherwise, the current leader is kept for the next generation.
The pseudocode of CBGWO is demonstrated in Figure 4. In the first step, the population of wolves is randomly initialized (either 1 or 0). In the second step, the fitness of the wolves is evaluated. The alpha, beta, and delta wolves are selected according to the fitness value. Next, the population is randomly partitioned into N/2 couples. The competition is made between two wolves in each couple. From the competition, the wolves with better fitness are defined as winners. The winners are directly passed into the new population. On the other hand, the losers update their positions by applying Equation (38). After that, the fitness of new losers is evaluated, and the new losers are added into the new population. The alpha, beta, and delta are then updated. Furthermore, the new leaders are generated by performing the random walk around alpha, beta, and delta. Afterward, the fitness of newly generated leaders is evaluated. The alpha, beta, and delta are again updated according to the newly generated leaders. The algorithm is repeated until the termination criterion is satisfied. In the final step, the alpha solution is chosen to be the optimal feature subset.

Figure 4.
The pseudocode of CBGWO.
The following observations illustrate how the proposed CBGWO theoretically has the ability to tackle the feature selection problem in the classification of EMG signals.
- In CBGWO, only the positions of N/2 (half of the population) wolves are updated. This means that the processing speed of CBGWO is extremely fast.
- CBGWO applies leader enhancement, which has the capability to avoid the leaders (alpha, beta, and delta) from being trapped in the local optimum.
- CBGWO includes the role of winner and loser in the position update. This indicates that the process of hunting and searching prey of wolves, is not only guided by the leaders, but also the winner wolf in each couple.
- CBGWO employs the dynamic change rate, R, in the random walk strategy, which aims to balance the exploration and exploitation in the leader enhancement process.
2.5. Proposed CBGWO for Feature Selection
In this paper, a new CBGWO is proposed to tackle the feature selection problem in EMG signals classification. For feature selection, the solutions are represented in binary form, either bit 1 or 0. Basically, bit 1 denotes the selected feature, while bit 0 represents the unselected feature. For example, given a solution X = {0,1,1,1,0,0,0,0,0,1}, this shows that the second, third, fourth, and tenth features are selected.
Figure 5 illustrates the flowchart of proposed CBGWO for feature selection. Initially, the STFT is employed to transform the EMG signal into time-frequency representation. Next, features are extracted from each STFT coefficient, and form a feature set. Afterward, the STFT feature set is fed into the CBGWO for the feature selection process. The initial population (solutions) is randomized. Iteratively, the initial solutions are evolved in the process of fitness evaluation. Note that the classification error rate obtained by the classifier is used as the fitness function in this work. The classification error rate is defined as the ratio of the number of wrongly classified samples over total number of samples, which can be computed by the classifier. In the fitness evaluation, if the solutions result in same values of fitness, then the solution with the smaller number of features will be selected. At the end of the iteration, the alpha wolf is selected as the global best solution (optimal feature subset).
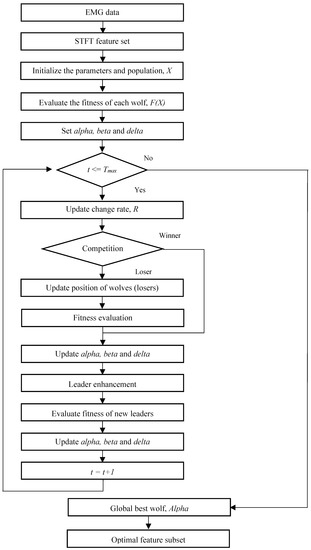
Figure 5.
The flowchart of proposed CBGWO for feature selection.
3. Results
Remarkably, STFT transforms the EMG signal into time-frequency representation. Ten time-frequency features are extracted from STFT coefficient. In total, 120 features (10 features × 12 channels) are extracted from each movement from each subject. For fitness evaluation, k-nearest neighbor (KNN) with k = 1 is used as the learning algorithm, due to its speed and simplicity [16,28]. According to [22], the 2nd and 5th repetitions are used for the testing set, while the remaining four repetitions are applied as training set.
To examine the effectiveness of the proposed method in feature selection, CBGWO is compared with BGWO1, BGWO2, binary particle swarm optimization (BPSO), and genetic algorithm (GA). The parameter setting of feature selection methods are described as follows: the population size, N, and maximum number of iterations, T, are fixed at 30 and 100, respectively. It is worth mentioning that there is no additional parameter setting for BGWO1, BGWO2, and CBGWO. For BPSO, the inertia weight, w, is linearly decreasing from 0.9 to 0.4, acceleration coefficients, C1 and C2, are set at 2, and the maximum and minimum velocity are set at 6 and −6, respectively. For GA, the crossover rate, CR, is set at 0.6, the mutation rate, MR, is set at 0.01, the roulette wheel selection is applied for parent selection, and the single point crossover is implemented.
For performance evaluation, four statistical parameters, including classification accuracy, precision (P), F-measure, and Matthew correlation coefficient (MCC), are determined. Classification accuracy, P, F-measure, and MCC, are calculated as follows [29,30,31]:
where TP, TN, FP, and FN are the true positive, true negative, false positive, and false negative that can be obtained from the confusion matrix. In this study, each feature selection algorithm is executed for 20 runs, with different random seed. The averaged results of 20 runs are used for performance comparison. All the analysis is done in MATLAB 9.3 using a computer with processing Intel Core i5-3340 3.1 GHz with 8 GB random access memory (RAM).
Experimental Results
Figure 6 demonstrates the classification accuracy of proposed methods for individual subjects. As can be seen, eight out of ten subjects obtained the best classification accuracy in CBGWO. For subject 6 and 8, the best results are achieved by BPSO. From the point of view, CBGWO is more capable in selecting the relevant features. Figure 6 shows that BGWO2 is the second-best feature selection method, which provides better results on six subjects compared to GA, BGWO1, and BPSO. Certainly, BGWO performs well in feature selection, which is similar to results in the literature [15].
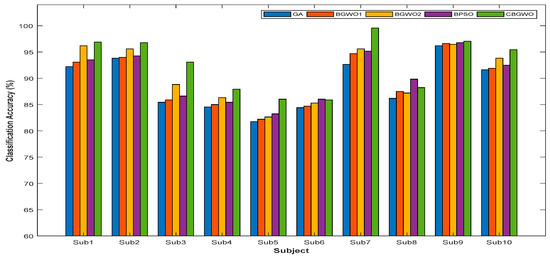
Figure 6.
Classification accuracy of five different feature selection methods for individual subjects.
On average, across all subjects, the best mean classification accuracy is obtained by CBGWO (92.69%), followed by BGWO2 (90.79%). Thanks to leader enhancement, the leaders (alpha, beta, and delta) in CBGWO are allowed to enhance themselves iteratively. Hence, CBGWO has a higher chance to prevent itself from being trapped in the local optimum. By conducting a t-test, it is seen that there is a significant difference in classification performance between CBGWO versus GA (p = 3.8907 × 10−4), CBGWO versus BGWO1 (p = 9.2063 × 10−4), CBGWO versus BGWO2 (p = 0.0023), and CBGWO versus BPSO (p = 0.011). This shows that the performance of CBGWO is significantly better than GA, BGWO1, BGWO2, and BPSO. The statistical results revealed the superiority of CBGWO over other algorithms in feature selection.
Table 1 displays the results of the number of selected features and precision for proposed methods. It is observed that not all the features are required in the classification process. A proper selection of features is more capable of obtaining a higher classification performance with lower complexity. As presented in Table 1, CBGWO contributed the smallest number of features for all ten subjects. This means that CBGWO can achieve promising classification accuracy while keeping a smaller number of features. On one side, GA and BGWO1 have a higher mean number of selected features, 61.29 and 61.49. It can be inferred that GA and BGWO1 did not evaluate the relevant features very well, thus leading to poor classification performance in this work.

Table 1.
Result of feature size and precision of five different feature selection methods.
Table 2 outlines the results of F-measure and MCC of proposed methods. As can be seen in Table 1 and Table 2, CBGWO offered higher precision, F-measure, and MCC values for most of the subjects. Obviously, CBGWO showed a comparative performance compared to GA, BGWO1, BGWO2, and BPSO. The results obtained show the superiority of CBGWO for solving the feature selection problem in EMG signals classification.

Table 2.
Result of F-measure and Matthew correlation coefficient (MCC) of five different feature selection methods.
Figure 7 demonstrates the convergence curve of proposed methods for individual subjects. From this point of view, CBGWO has very good diversity. With the leader enhancement process, CBGWO has the ability to escape from the local optimum. Unlike BGWO1 and BGWO2, CBGWO keeps tracking for the global optimum, thus leading to a very good performance. On the other side, GA and BGWO1 converged faster, but without acceleration. This showed that GA and BGWO1 were easily getting trapped in the local optimum. From Figure 7, it can be inferred that CBGWO is effective and reliable in evaluating the optimal feature subset.
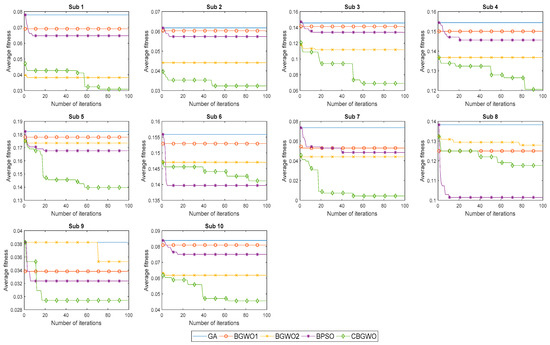
Figure 7.
The convergence curve of five different feature selection methods for individual subject.
Figure 8 shows the mean class-wise accuracy (classification accuracy of 17 hand movement types) across all subjects. Inspecting the result, CBGWO showed competitive performance as compared to GA, BGWO1, BGWO2 and BPSO. By applying CBGWO, 14 out of 17 hand movement types had been successfully recognized (accuracy more than 90%). A similar performance was also found in BGWO2. However, CBGWO overtook BGWO2 in 14 hand movement types. Other algorithms, such as GA and BGWO1, had the difficulty in selecting the relevant features, thus leading to ineffective solutions. The results obtained clearly evinced the effectiveness of CBGWO in EMG feature selection.
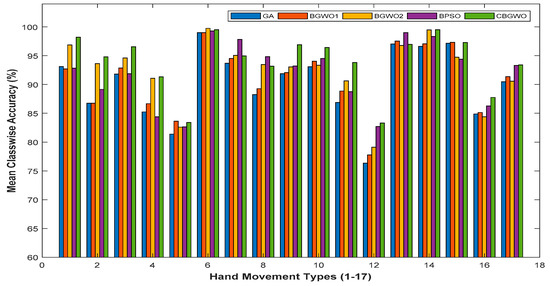
Figure 8.
The mean class-wise accuracy of five different feature selection methods across 10 subjects.
Figure 9 illustrates the average computational time of the proposed methods. Successfully, CBGWO obtained the fastest processing speed in this work. This indicates that CBGWO can achieve the optimal feature subset in a very short period. The reason CBGWO has a very short computational time is because CBGWO utilizes a competition strategy, which performs a position update for only half of the population. Moreover, the leader enhancement was only implemented to three leaders, so there is not much influence on the computational complexity. In short, CBGWO was not only excellent in feature selection, but also computational cost.
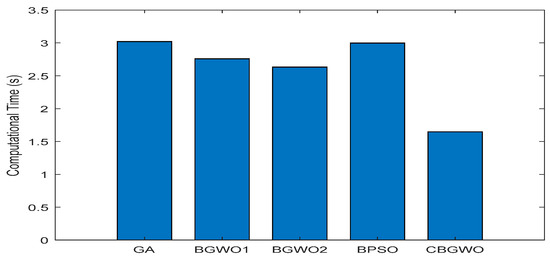
Figure 9.
The average computation time of five different feature selection methods across 10 subjects.
4. Discussion
In this study, a novel CBGWO has been proposed to tackle the feature selection problem in EMG signals classification. CBGWO has been tested and compared with other popular feature selection methods, including BGWO1, BGWO2, BPSO, and GA. The finding of current study shows the superiority of CBGWO in selecting the optimal feature subset. Compared to BGWO1 and BGWO2, CBGWO introduces a competition strategy to keep the high-quality solutions (winners) and promote the cooperation between the competitors. In the hunting and searching prey process, the winner will guide the loser to move toward a better prey position which, in turn, will improve the quality of search. For instance, only half of the population (losers) participate in the position update, while the rest (winners) directly pass into the new population. In other words, CBGWO consumes a very low computational cost, since the updating process is only applied to the losers. Furthermore, CBGWO utilizes the leader enhancement strategy to evolve the quality of the leaders. Iteratively, the leader updates itself if the newly generated leader has a better prey position. In other words, CBGWO keeps tracking for the global optimum, and avoids the algorithm being trapped in a local optimum. By making full use of these mechanisms, CBGWO is known to be successful in feature selection.
Through the analysis, we found that CBGWO is the best feature selection method in this work. CBGWO not only yields the optimal classification performance, but also provides the minimal feature size. It showed that the proposed model is more capable and efficient at solving the feature selection issues in EMG signals classification. Since EMG signal is subject-independent, it is yet to be known the best combination of features for each subject in achieving the optimal classification performance. In practice, users might have difficulty in selecting the best features for each subject. Unlike other traditional feature selection methods, users can apply the CBGWO to select the potential features without prior knowledge. Successively, CBGWO will automatically select the optimal features for specific subjects, and that feature subset will be used in real world application. This, in turn, will reduce the complexity and improve the performance of the recognition system. In sum, the proposed CBGWO is useful in feature selection.
5. Conclusions
A competitive binary grey wolf optimizer (CBGWO) is proposed in this study. CBGWO includes the competitive strategy that allowed the wolves to compete in couples. The winners are directly passed to the new population. On the contrary, the losers update their positions by learning from the winners. In addition, CBGWO implemented a leader enhancement strategy to evolve the quality of leaders in each iteration. As for feature selection, CBGWO is compared with BGWO1, BGWO2, GA, and BPSO. The experimental results revealed CBGWO yielded better performance and overtook other algorithms in feature selection. CBGWO not only offered a very low computational cost, but also ranked as the best in feature selection. In summary, the proposed CBGWO is successful, and more appropriate to be used in clinical and rehabilitation applications. As for future work, a chaotic map can be used to fine-tune the parameters of CBGWO. The number of leaders in CBGWO can be increased to improve the diversity. Moreover, CBGWO will be applied to other optimization areas, such as training neural network, knapsack, and numerical problems.
Author Contributions
Conceptualization, J.T.; Formal analysis, J.T.; Funding acquisition, N.M.A.; Investigation, J.T.; Methodology, J.T. and A.R.A.; Software, J.T.; Supervision, A.R.A.; Validation, J.T., A.R.A. and N.M.S.; Writing—original draft, J.T.; Writing—review & editing, J.T., A.R.A., N.M.S., N.M.A. and W.T.
Funding
This research and the APC were funded by Minister of Higher Education Malaysia (MOHE) under grant number FRGS/1/2017/TK04/FKE-CeRIA/F00334.
Acknowledgments
The authors would like to thank the Skim Zamalah UTeM and Minister of Higher Education Malaysia for funding research under grant FRGS/1/2017/TK04/FKE-CeRIA/F00334.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, J.; Li, X.; Li, G.; Zhou, P. EMG feature assessment for myoelectric pattern recognition and channel selection: A study with incomplete spinal cord injury. Med. Eng. Phys. 2014, 36, 975–980. [Google Scholar] [CrossRef] [PubMed]
- Geethanjali, P. Comparative study of PCA in classification of multichannel EMG signals. Aust. Phys. Eng. Sci. Med. 2015, 38, 331–343. [Google Scholar] [CrossRef] [PubMed]
- Purushothaman, G.; Ray, K.K. EMG based man–machine interaction—A pattern recognition research platform. Robot. Auton. Syst. 2014, 62, 864–870. [Google Scholar] [CrossRef]
- Joshi, D.; Nakamura, B.H.; Hahn, M.E. High energy spectrogram with integrated prior knowledge for EMG-based locomotion classification. Med. Eng. Phys. 2015, 37, 518–524. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Naik, G.R.; Huang, S.; Abraham, A.; Nguyen, H.T. Nonlinear multiscale Maximal Lyapunov Exponent for accurate myoelectric signal classification. Appl. Soft Comput. 2015, 36, 633–640. [Google Scholar] [CrossRef]
- Purushothaman, G.; Vikas, R. Identification of a feature selection based pattern recognition scheme for finger movement recognition from multichannel EMG signals. Aust. Phys. Eng. Sci. Med. 2018, 41, 549–559. [Google Scholar] [CrossRef] [PubMed]
- Xi, X.; Tang, M.; Luo, Z. Feature-Level Fusion of Surface Electromyography for Activity Monitoring. Sensors 2018, 18, 614. [Google Scholar] [CrossRef] [PubMed]
- Tsai, A.C.; Luh, J.J.; Lin, T.T. A novel STFT-ranking feature of multi-channel EMG for motion pattern recognition. Expert Syst. Appl. 2015, 42, 3327–3341. [Google Scholar] [CrossRef]
- Karthick, P.A.; Ghosh, D.M.; Ramakrishnan, S. Surface electromyography based muscle fatigue detection using high-resolution time-frequency methods and machine learning algorithms. Comput. Methods Prog. Biomed. 2018, 154, 45–56. [Google Scholar] [CrossRef] [PubMed]
- Khushaba, R.N.; Takruri, M.; Miro, J.V.; Kodagoda, S. Towards limb position invariant myoelectric pattern recognition using time-dependent spectral features. Neural Netw. 2014, 55, 42–58. [Google Scholar] [CrossRef] [PubMed]
- Chuang, L.Y.; Tsai, S.W.; Yang, C.H. Improved binary particle swarm optimization using catfish effect for feature selection. Expert Syst. Appl. 2011, 38, 12699–12707. [Google Scholar] [CrossRef]
- Xue, B.; Zhang, M.; Browne, W.N. Particle swarm optimisation for feature selection in classification: Novel initialisation and updating mechanisms. Appl. Soft Comput. 2014, 18, 261–276. [Google Scholar] [CrossRef]
- Zorarpacı, E.; Özel, S.A. A hybrid approach of differential evolution and artificial bee colony for feature selection. Expert Syst. Appl. 2016, 62, 91–103. [Google Scholar] [CrossRef]
- Shunmugapriya, P.; Kanmani, S. A hybrid algorithm using ant and bee colony optimization for feature selection and classification (AC-ABC Hybrid). Swarm Evol. Comput. 2017, 36, 27–36. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Chuang, L.Y.; Chang, H.W.; Tu, C.J.; Yang, C.H. Improved binary PSO for feature selection using gene expression data. Comput. Biol. Chem. 2008, 32, 29–38. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Zhang, Q.; Sun, N.; Dong, Y. Feature Selection with Discrete Binary Differential Evolution. In Proceedings of the Artificial Intelligence and Computational Intelligence, Shanghai, China, 7–8 November 2009. [Google Scholar] [CrossRef]
- De Stefano, C.; Fontanella, F.; Marrocco, C.; Di Freca, A.S. A GA-based feature selection approach with an application to handwritten character recognition. Pattern Recognit. Lett. 2014, 35, 130–141. [Google Scholar] [CrossRef]
- Aghdam, M.H.; Ghasem-Aghaee, N.; Basiri, M.E. Text feature selection using ant colony optimization. Expert Syst. Appl. 2009, 36, 6843–6853. [Google Scholar] [CrossRef]
- Huang, H.; Xie, H.B.; Guo, J.Y.; Chen, H.J. Ant colony optimization-based feature selection method for surface electromyography signals classification. Comput. Biol. Med. 2012, 42, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Venugopal, G.; Navaneethakrishna, M.; Ramakrishnan, S. Extraction and analysis of multiple time window features associated with muscle fatigue conditions using sEMG signals. Expert Syst. Appl. 2014, 41, 2652–2659. [Google Scholar] [CrossRef]
- Pizzolato, S.; Tagliapietra, L.; Cognolato, M.; Reggiani, M.; Müller, H.; Atzori, M. Comparison of six electromyography acquisition setups on hand movement classification tasks. PLoS ONE 2017, 12, e0186132. [Google Scholar] [CrossRef] [PubMed]
- Mazher, M.; Aziz, A.A.; Malik, A.S.; Amin, H.U. An EEG-Based Cognitive Load Assessment in Multimedia Learning Using Feature Extraction and Partial Directed Coherence. IEEE Access. 2017, 5, 14819–14829. [Google Scholar] [CrossRef]
- Karthick, P.A.; Ramakrishnan, S. Surface electromyography based muscle fatigue progression analysis using modified B distribution time–frequency features. Biomed. Signal Process. Control. 2016, 26, 42–51. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Elaziz, M.A.; Lu, S. Chaotic opposition-based grey-wolf optimization algorithm based on differential evolution and disruption operator for global optimization. Expert Syst. Appl. 2018, 108, 1–27. [Google Scholar] [CrossRef]
- Al-Betar, M.A.; Awadallah, M.A.; Faris, H.; Aljarah, I.; Hammouri, A.I. Natural selection methods for Grey Wolf Optimizer. Expert Syst. Appl. 2018, 113, 481–498. [Google Scholar] [CrossRef]
- Chuang, L.Y.; Yang, C.H.; Li, J.C. Chaotic maps based on binary particle swarm optimization for feature selection. Appl. Soft Comput. 2011, 11, 239–248. [Google Scholar] [CrossRef]
- Ghareb, A.S.; Bakar, A.A.; Hamdan, A.R. Hybrid feature selection based on enhanced genetic algorithm for text categorization. Expert Syst. Appl. 2016, 49, 31–47. [Google Scholar] [CrossRef]
- Pashaei, E.; Aydin, N. Binary black hole algorithm for feature selection and classification on biological data. Appl. Soft Comput. 2017, 56, 94–106. [Google Scholar] [CrossRef]
- Li, Q.; Chen, H.; Huang, H.; Zhao, X.; Cai, Z.; Tong, C.; Liu, W.; Tian, X. An Enhanced Grey Wolf Optimization Based Feature Selection Wrapped Kernel Extreme Learning Machine for Medical Diagnosis. Comput. Math. Methods Med. 2017, 2017, 9512741. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).