RVR Blockchain Consensus: A Verifiable, Weighted-Random, Byzantine-Tolerant Framework for Smart Grid Energy Trading
Abstract
1. Introduction
- (1)
- A dynamic reputation model to evaluate behavior in real time;
- (2)
- A VRF-driven leader election mechanism that is resistant to Byzantine manipulation;
- (3)
- A universal protocol to support multi-energy transactions.
2. Literature Review
2.1. Traditional BFT Algorithms
2.2. Innovations in Chain-Based Consensus
2.3. Challenges Specific to Smart Grids
2.4. Research Gaps
- Insufficient Byzantine-Resistant Leader Selection: The leader rotation mechanisms inherent in traditional chain consensus are vulnerable to targeted attacks.
- Scenario-Specific Limitations: A predominant focus on isolated energy types or devices restricts the applicability of findings to heterogeneous smart grid environments.
3. Methodology
3.1. Research Design
3.2. Dynamic Reputation Model
3.3. VRF-Driven Leader Election
4. Security Model of Transaction System
4.1. System Model
4.1.1. Entity Layer
4.1.2. Energy Layer
4.1.3. Service Layer
4.1.4. Blockchain Layer
4.2. Transaction Process
4.2.1. Transaction Negotiation
4.2.2. Transaction Execution
- (1)
- Pre-Freezing of Funds
- (2)
- Energy Mortgage
- (3)
- Transaction Settlement
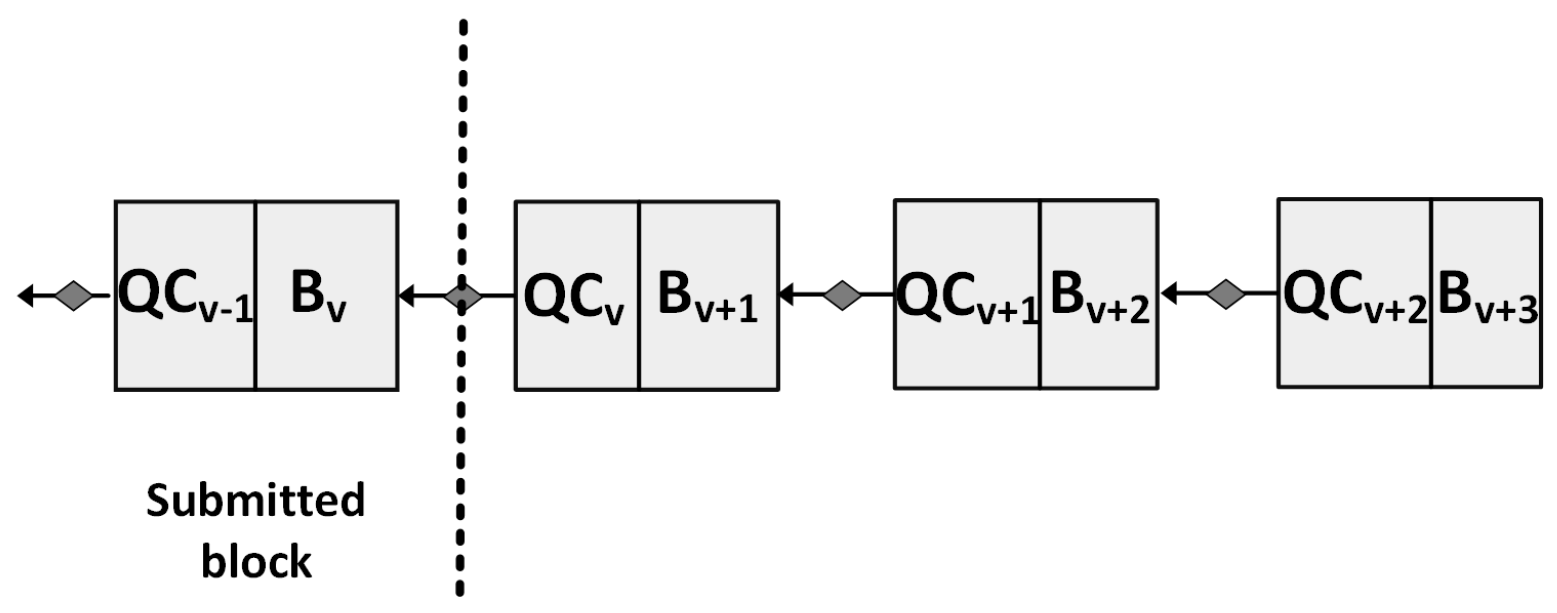
4.3. Chained Leader Consensus Models and Attack Models
4.3.1. Chained Leader Consensus Algorithm
- (1)
- Voting Stage
- (2)
- Block Packaging
- (3)
- Block Addition
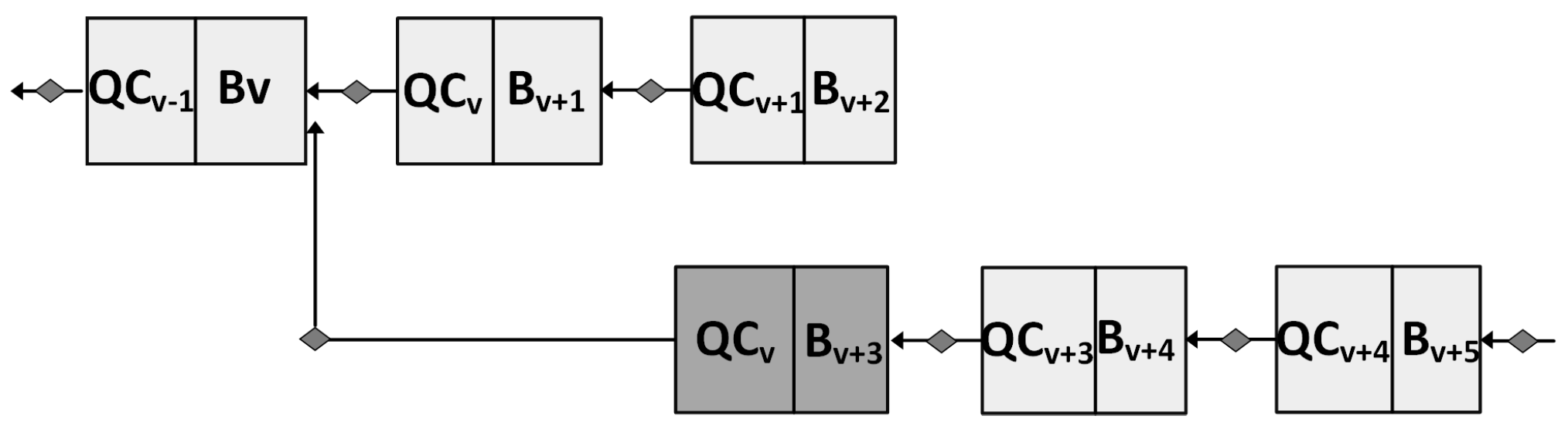
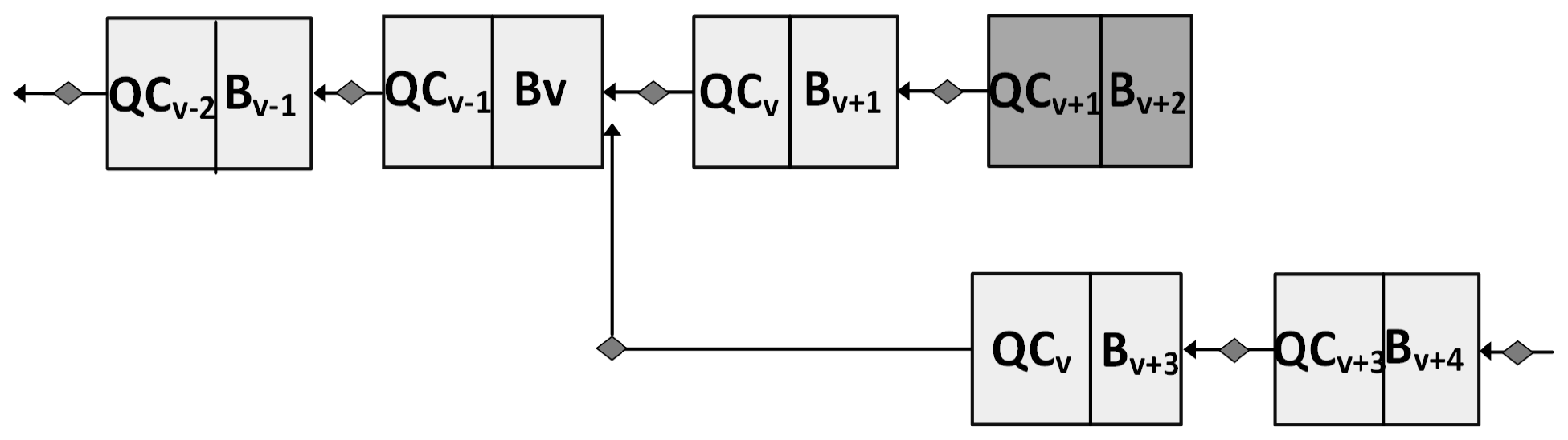
4.3.2. Byzantine Attack Model
Forking Attack
Silence Attack
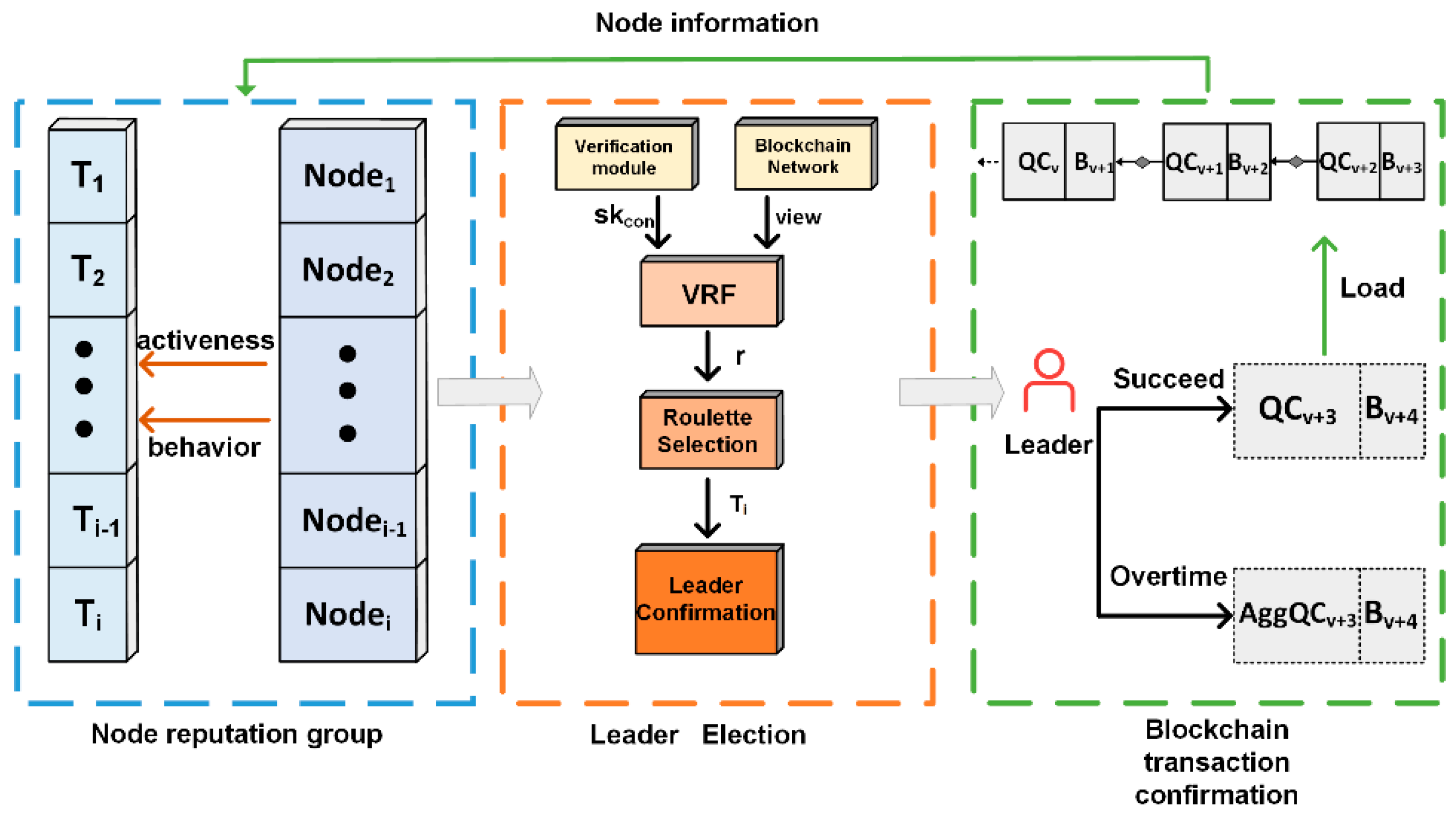
5. Chained Consensus Algorithm Based on Reputation
5.1. The Relationship Among Reputation, VRF, and Roulette
5.2. Node Reputation Mechanisms
5.2.1. Node Activity
5.2.2. Voting Activeness
5.2.3. Behavior Weight
5.3. Leader Election Mechanism
5.3.1. Generating VRF Random Numbers
5.3.2. Leader Confirmation
5.3.3. Verification of Leader Election
5.4. RVR Algorithm Flow
| Algorithm 1: RVR Algorithm Process | |
| 1 | As LeaderNode |
| 2 | Wait msgs from replicas |
| 3 | if n-f η msgs are received |
| 4 | AggQC←CreatAggQC(ηset) |
| 5 | B←CreateMsg(Prepare,view,aggQC,cmd,id) |
| 6 | end |
| 7 | if n-f v msgs are received |
| 8 | QC←CreateQC(V) |
| 9 | B←CreateMsg(Prepare,view,QC,cmd,id) |
| 10 | end |
| 11 | Broadcast B |
| 12 | Update Tarry |
| 13 | nextleader←LeaderElection(view,Tarry) |
| 14 | SendVote(nextleader,V,view+1) |
| 15 | end |
| 16 | As ConsensNode |
| 17 | Wait for B from LeaderNode |
| 18 | if B is accepted successfully |
| 19 | Update Tarry |
| 20 | nextleader←LeaderElection(view,Tarry) |
| 21 | Send Vote(nextleader,V,view+1) |
| 22 | end |
| 23 | if a timeout occurs at any stage |
| 24 | Update Tarry |
| 25 | nextleader←LeaderElection(view,Tarry) |
| 26 | Send η(nextleader,V,view+1) |
| 27 | end |
| 28 | end |
5.5. Theoretical Analysis
5.5.1. Safety Guarantees
5.5.2. Liveness Guarantees
5.6. Comparative Analysis
5.7. Experimental Setup
5.8. Experimental Metrics
6. Results and Discussion
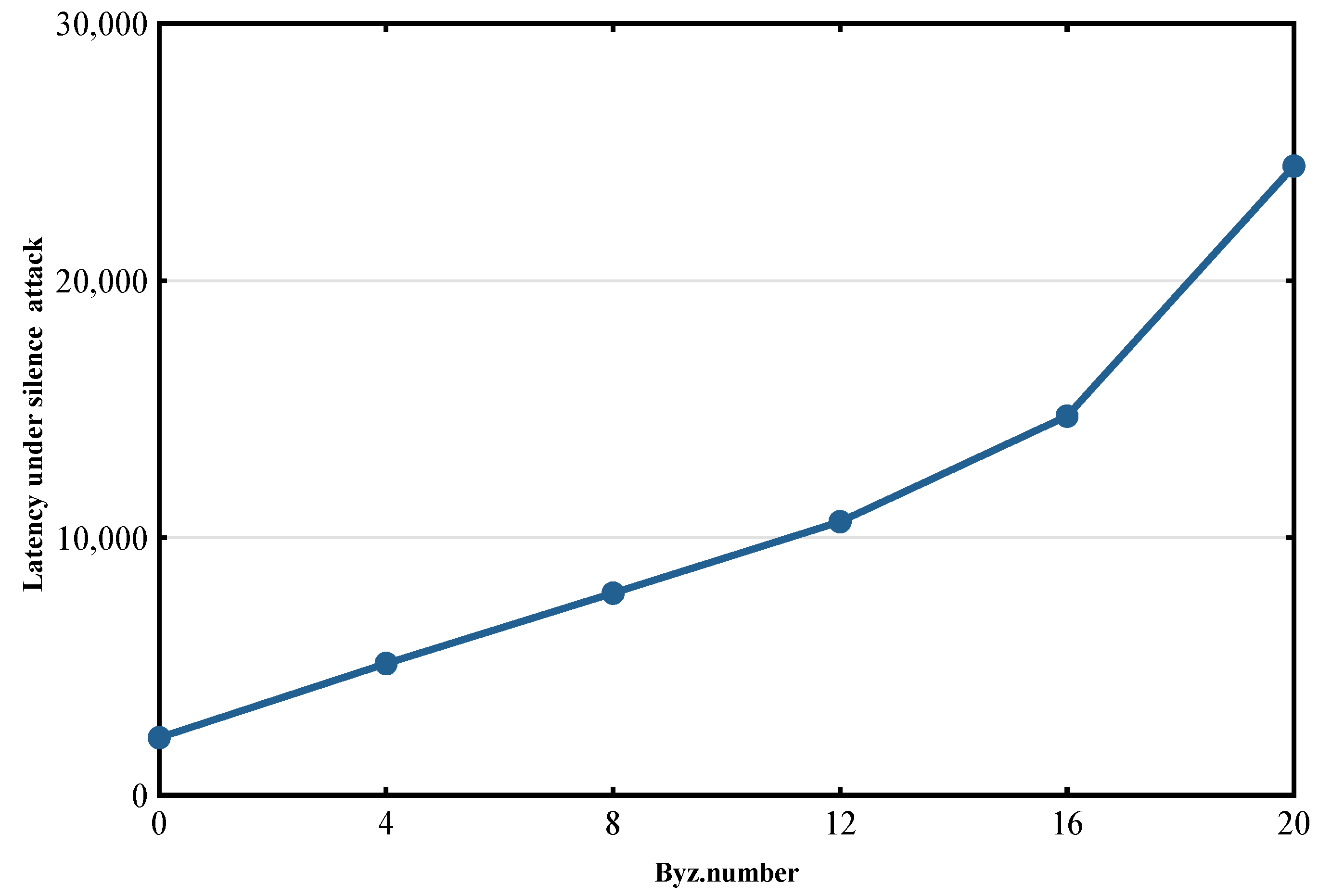
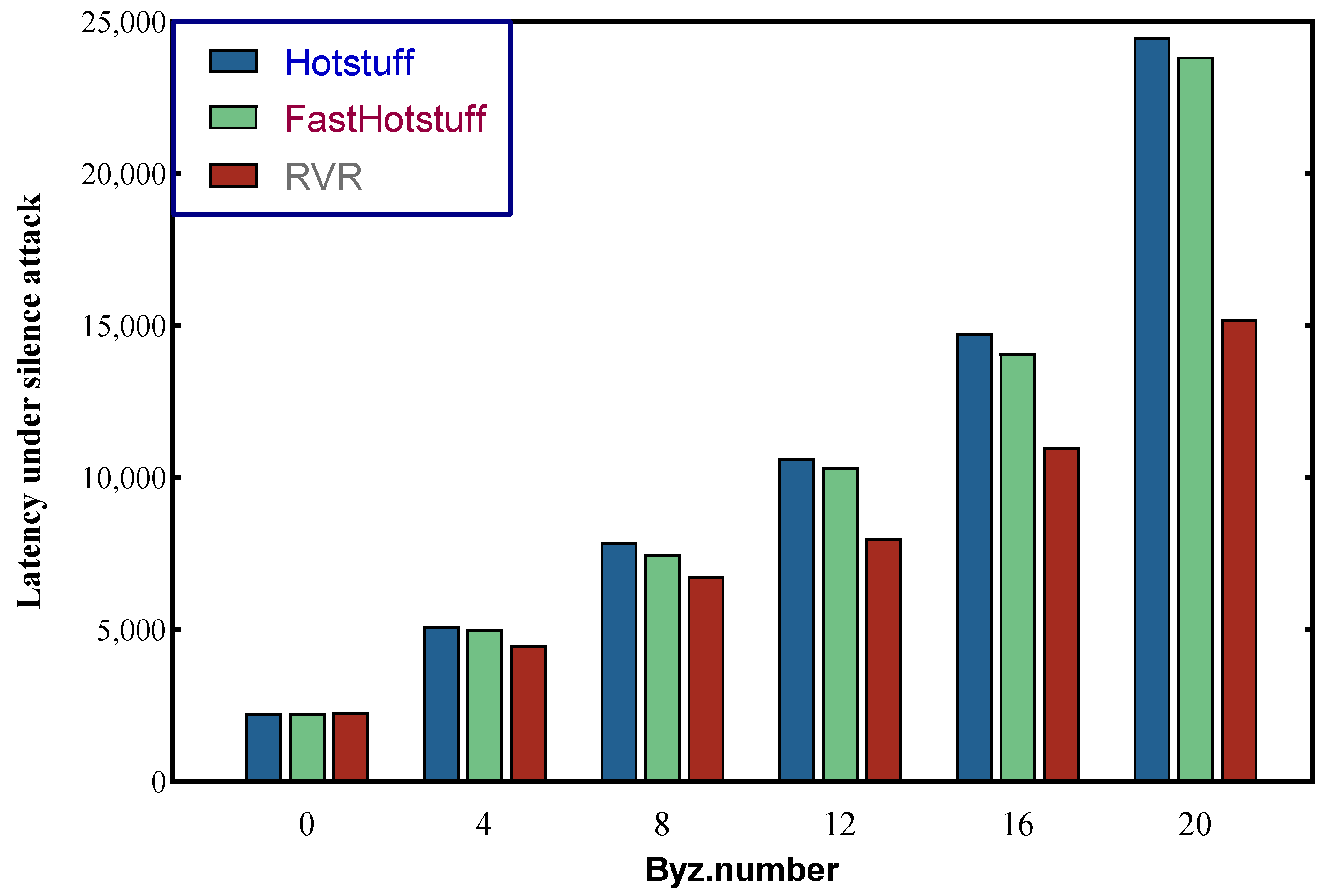
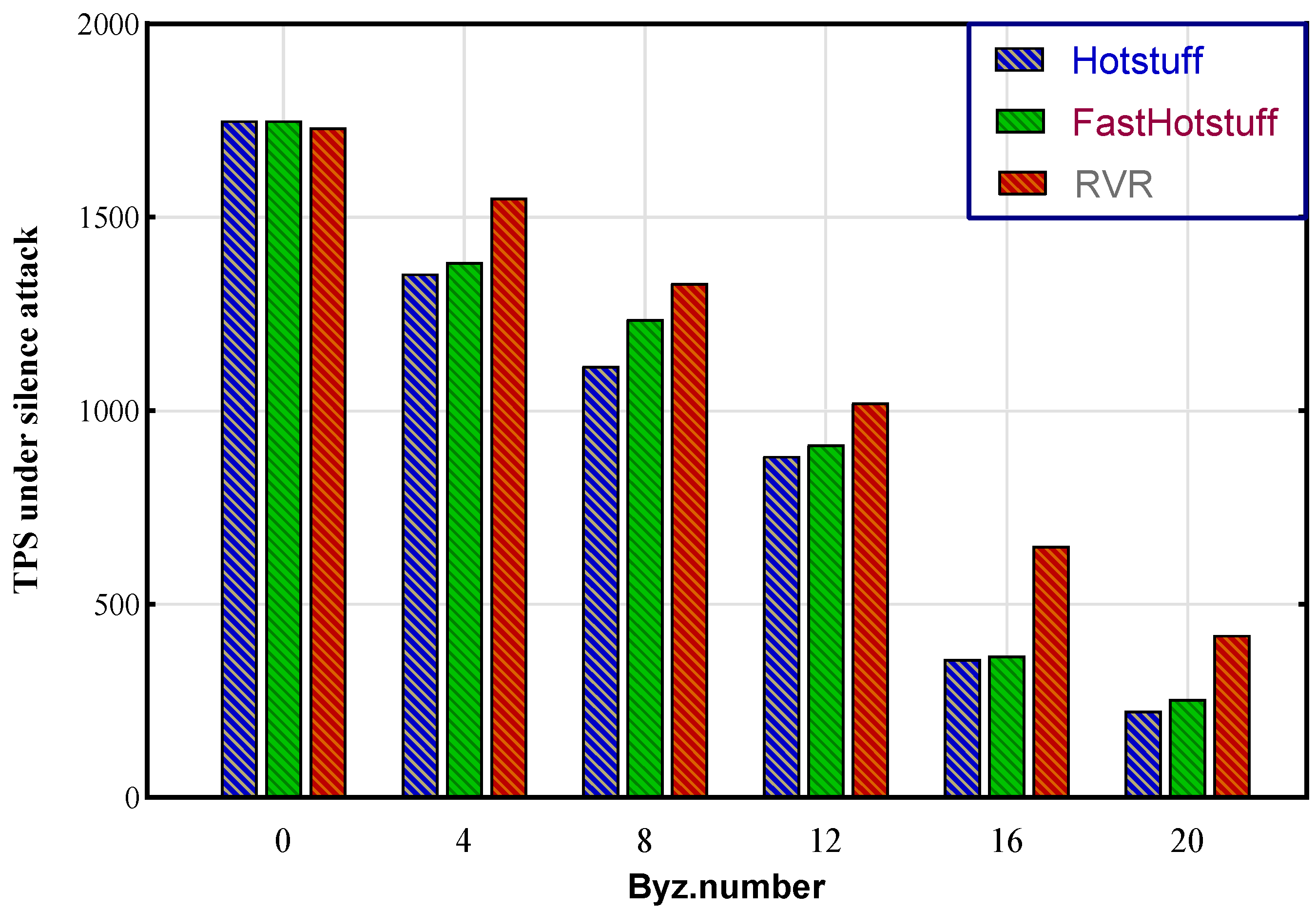
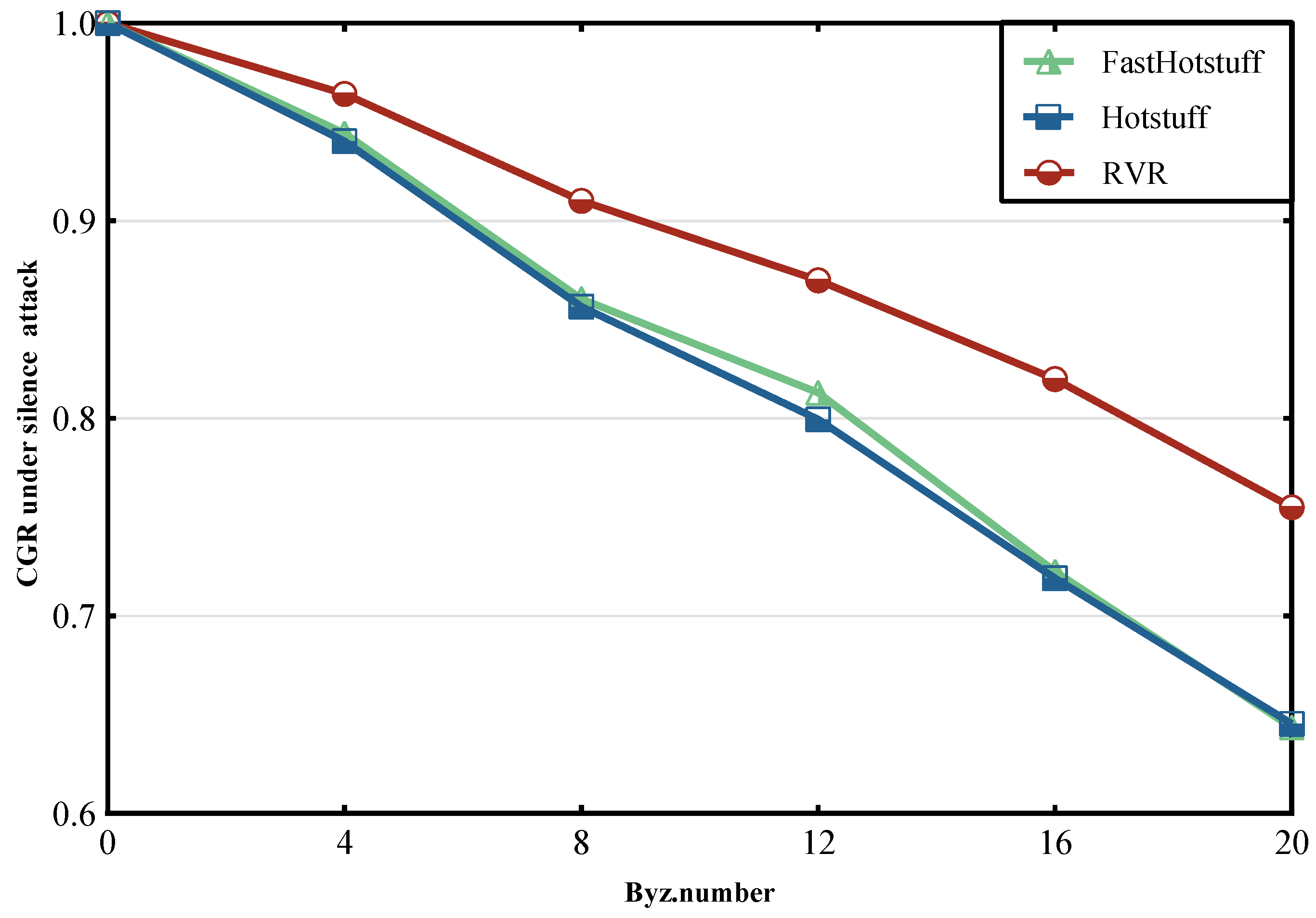
6.1. Under Silence Attack
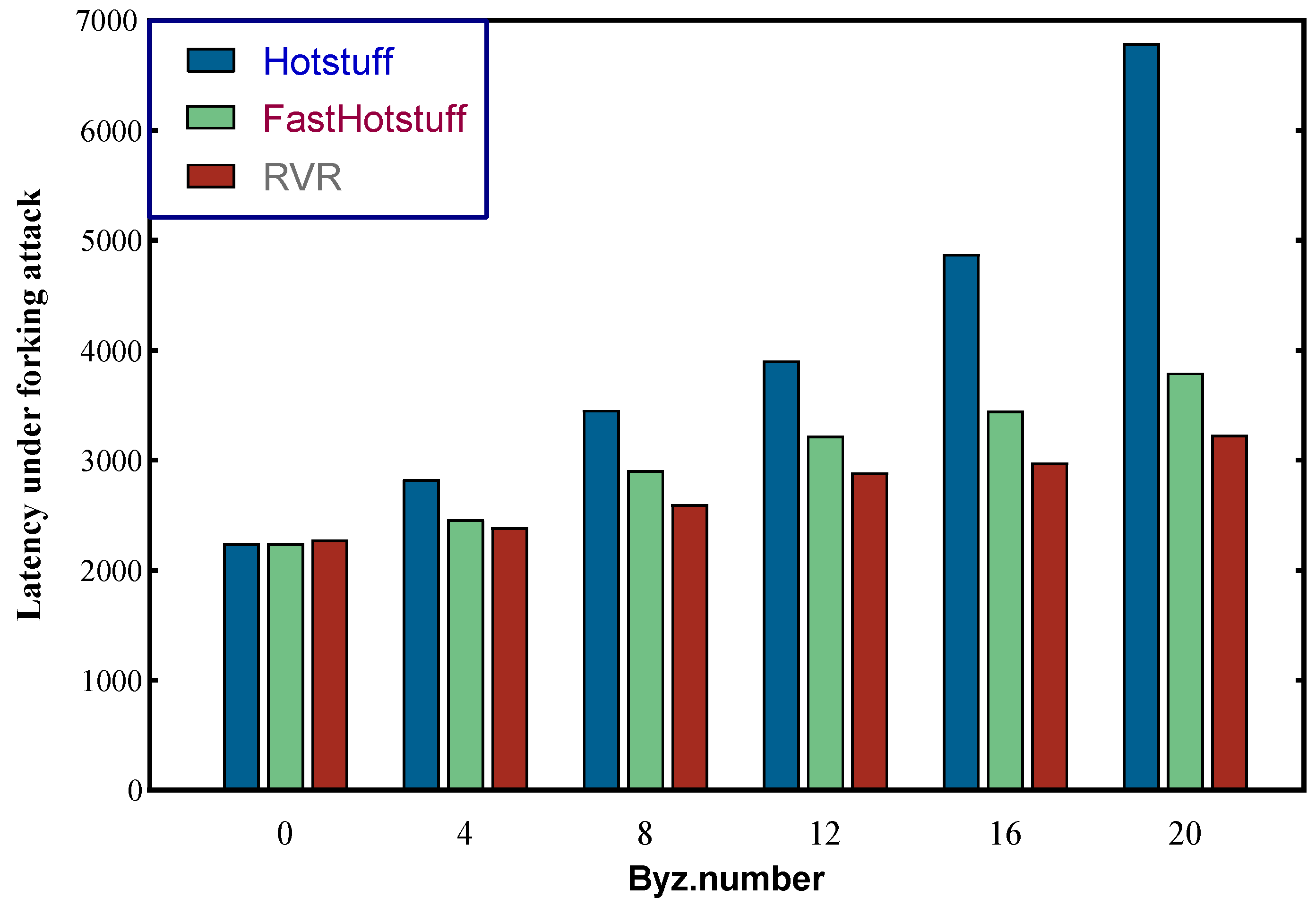
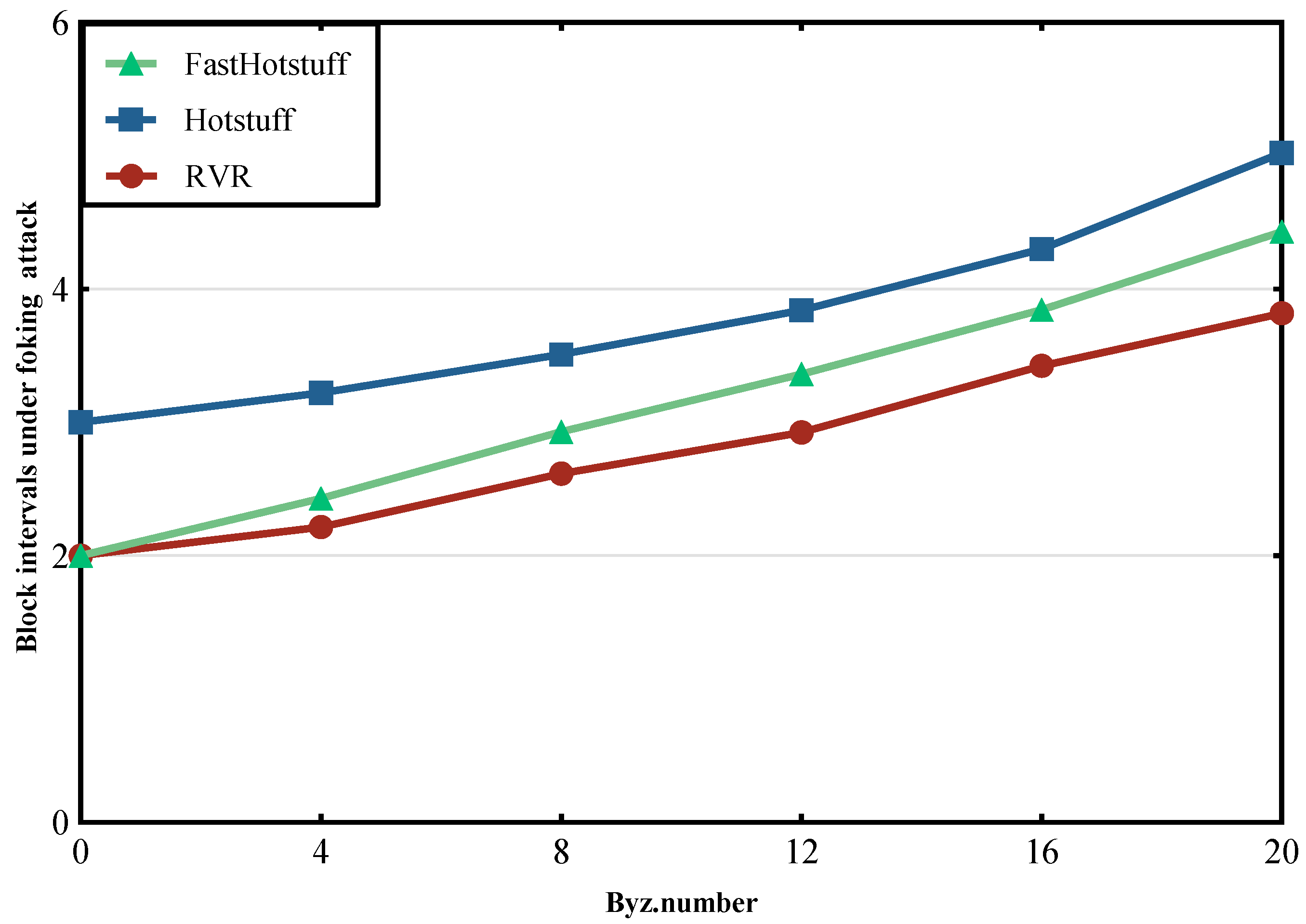
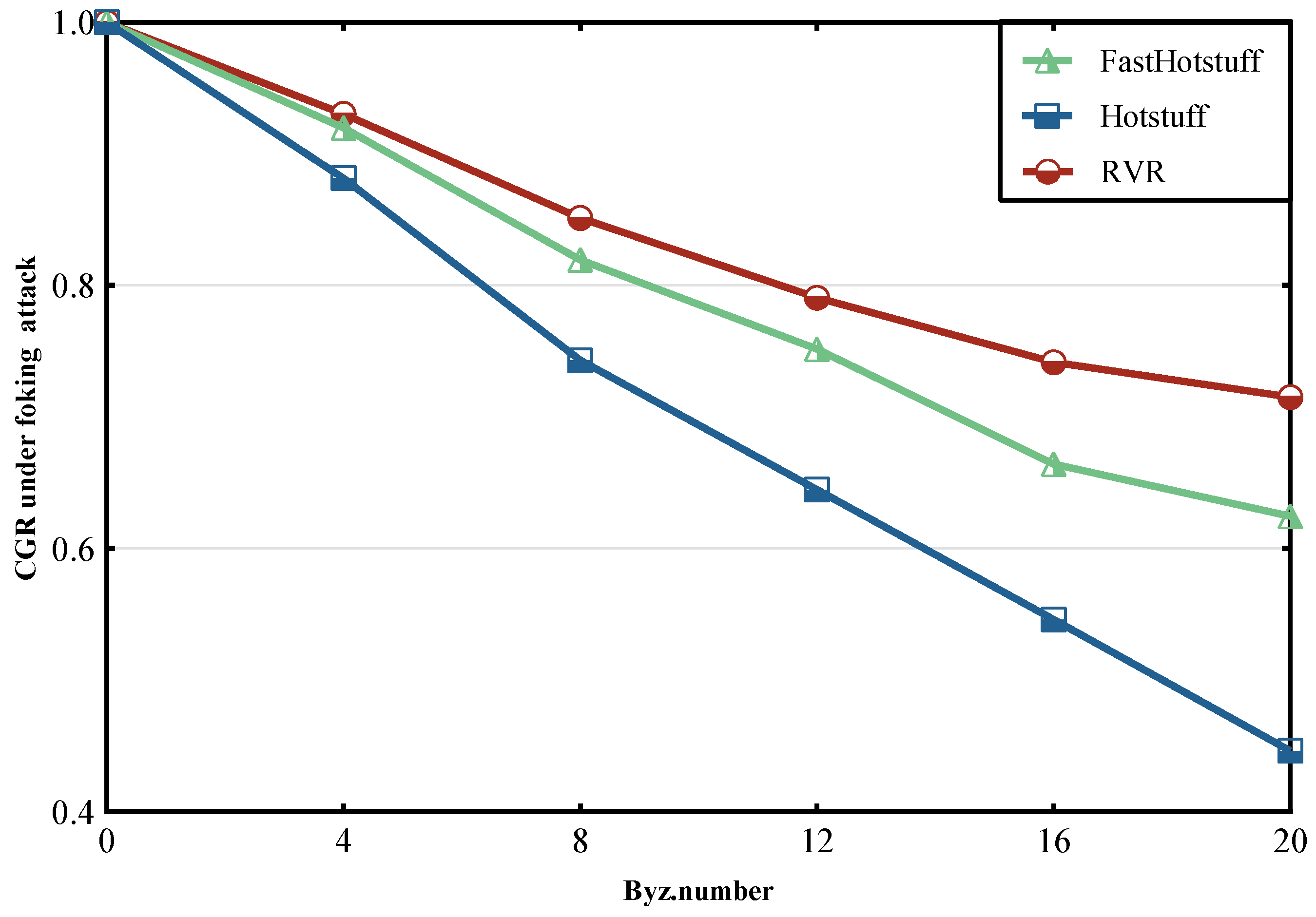
6.2. Under Forking Attack
6.3. Discussion
7. Conclusions
7.1. Technological Advancements and Implications
7.2. Limitations and Directions for Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ha, T.; Lee, D.; Lee, C.; Cho, S. VCG auction mechanism based onblock chain in smart grid. In Proceedings of the 2021 International Conference on Information Networking (ICOIN), Jeju Island, Republic of Korea, 13–16 January 2021; pp. 465–468. [Google Scholar]
- Singla, S.; Dua, A.; Kumar, N.; Tanwar, S. Blockchain-based efficientenergy trading scheme for smart-grid systems. In Proceedings of the 2020 IEEE Globecom Workshops (GC Wkshps), Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Doan, H.T.; Cho, J.; Kim, D. Peer-to-peer energy trading in smart grid through blockchain: A double auction-based game theoretic approach. IEEE Access 2021, 9, 49206–49218. [Google Scholar] [CrossRef]
- Maharjan, S.; Zhang, Y.; Gjessing, S.; Tsang, D.H.K. User-Centric Demand Response Management in the Smart Grid With Multiple Providers. IEEE Trans. Emerg. Top. Comput. 2017, 5, 494–505. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, A.; Zhang, H. Overview of smart grid development in China. Power Syst. Prot. Control 2021, 49, 180–187. [Google Scholar] [CrossRef]
- Xie, J.; Tang, H.; Huang, T.; Yu, F.R.; Xie, R.; Liu, J.; Liu, Y. A survey of blockchain technology applied to smart cities: Research issues and challenges. IEEE Commun. Surv. Tutor. 2019, 21, 2794–2830. [Google Scholar] [CrossRef]
- Wang, T.; Guo, J.; Ai, S.; Cao, J. RBT: A distributed reputation system for blockchain-based peer-to-peer energy trading with fairness consideration. Appl. Energy 2021, 295, 117056. [Google Scholar] [CrossRef]
- Micali, S.; Rabin, M.; Vadhan, S. Verifiable random functions. In Proceedings of the 40th Annual Symposium on Foundations of Computer Science (Cat. No. 99CB37039), New York, NY, USA, 17–19 October 1999; pp. 120–130. [Google Scholar] [CrossRef]
- Castro, M.; Liskov, B. Practical Byzantine fault tolerance and proactive recovery. ACM Trans. Comput. Syst. 2002, 20, 398–461. [Google Scholar] [CrossRef]
- Jakobsson, M.; Juels, A. Proofs of Work and Bread Pudding Protocols (Extended Abstract). In Secure Information Networks; Springer: Berlin/Heidelberg, Germany; Boston, MA, USA, 1999; pp. 258–272. [Google Scholar]
- Kotla, R.; Alvisi, L.; Dahlin, M.; Clement, A.; Wong, E. Zyzzyva: Speculative Byzantine fault tolerance. ACM Trans. Comput. Syst. 2010, 27, 7. [Google Scholar] [CrossRef]
- Miller, A.; Xia, Y.; Croman, K.; Shi, E.; Song, D. The Honey Badger of BFT Protocols. In Proceedings of the ACM SIGSAC Conference on Computer & Communications Security, Vienna, Austria, 24–28 October 2016; ACM: New York, NY, USA, 2016; pp. 31–42. [Google Scholar]
- Zhang, M.; Li, J.; Chen, Z.; Chen, H.; Deng, X. An Efficient and Robust Committee Structure for Sharding Blockchain. IEEE Trans. Cloud Comput. 2023, 11, 2562–2574. [Google Scholar] [CrossRef]
- Pass, R.; Shi, E. Thunderella: Blockchains with Optimistic Instant Confirmation; Springer: Cham, Switzerland, 2018; Volume 10821, pp. 3–33. [Google Scholar]
- Gueta, G.G.; Abraham, I.; Grossman, S.; Malkhi, D.; Pinkas, B.; Reiter, M.; Seredinschi, D.-A.; Tamir, O.; Tomescu, A. SBFT: A Scalable and Decentralized Trust Infrastructure. In Proceedings of the 2019 49th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), Portland, OR, USA, 24–27 June 2019; pp. 568–580. [Google Scholar] [CrossRef]
- Yin, M.; Malkhi, D.; Reiter, M.K.; Gueta, G.G.; Abraham, I. HotStuff: Blconsensus with linearity and responsiveness. In Proceedings of the 2019 ACM Symposium on Principles of Dis-tributed Computing, Toronto, ON, Canada, 29 July–2 August 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 347–356. [Google Scholar]
- Boldyreva, A. Threshold Signatures, Multisignatures and Blind Signatures Based on the Gap-Diffie-Hellman-Group Signature Scheme. In Public Key Cryptography—PKC 2003; Desmedt, Y.G., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2567. [Google Scholar] [CrossRef]
- Jalalzai, M.M.; Niu, J.; Feng, C.; Gai, F. Fast-HotStuff: A Fast and Robust BFT Protocol for Blockchains. IEEE Trans. Dependable Secur. Comput. 2024, 21, 2478–2493. [Google Scholar] [CrossRef]
- Gai, F.; Farahbakhsh, A.; Niu, J.; Feng, C.; Beschastnikh, I.; Duan, H. Dissecting the Performance of Chained-BFT. In Proceedings of the 2021 IEEE 41st International Conference on Distributed Computing Systems (ICDCS), Washington, DC, USA, 7–10 July 2021; pp. 595–606. [Google Scholar] [CrossRef]
- Puthal, D.; Malik, N.; Mohanty, S.; Kougianos, E.; Das, G. Everything you wanted to know about the blockchain: Its promise, components, processes, and problems. IEEE Consum. Electron. Mag. 2018, 7, 6–14. [Google Scholar] [CrossRef]
- Kumar, N.; Aujla, G.; Das, A.; Conti, M. ECCAuth: A secure authentication protocol for demand response management in a smart grid system. IEEE Trans. Ind. Inf. 2019, 15, 6572–6582. [Google Scholar] [CrossRef]
- Kaur, D.; Aujla, G.S.; Kumar, N.; Zomaya, A.Y.; Perera, C.; Ranjan, R. Tensor-based big data management scheme for dimensionality reduction problem in smart grid systems: SDN perspective. IEEE Trans. Knowl. Data Eng. 2018, 30, 1985–1998. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, N.; Lou, W.; Hou, Y.T. A Survey of Distributed Consensus Protocols for Blockchain Networks. IEEE Commun. Surv. Tutor. 2020, 22, 1432–1465. [Google Scholar] [CrossRef]
- Cerf, R. The quasi species regime for the simple genetic algorithm with roulette wheel selection. Adv. Appl. Probab. 2017, 49, 903–926. [Google Scholar] [CrossRef]
- Bianchi, C.; Langner, M.R.; Mishra, V.; Torcellini, P. Accelerating the Adoption of Energy Efficiency and Renewables in Warehouses and Distribution Centers; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2023. [Google Scholar] [CrossRef]
- Kirst, C.; Timme, M.; Battaglia, D. Dynamic information routing in complex networks. Nat. Commun. 2016, 7, 11061. [Google Scholar] [CrossRef] [PubMed]
- Sansone, C.; Vento, M. Signature Verification: Increasing Performance by a Multi-Stage System. Pattern Anal. Appl. 2000, 3, 169–181. [Google Scholar] [CrossRef]
- Hsueh, S.-C.; Kuo, C.-H. Effective Matching for P2P Lending by Mining Strong Association Rules. In Proceedings of the 3rd International Conference on Industrial and Business Engineering (ICIBE ’17), Sapporo, Japan, 17–19 August 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 30–33. [Google Scholar] [CrossRef]
- Li, J.; Wu, J.; Chen, L. Block-secure: Blockchain based scheme for secure P2P cloud storage. Inf. Sci. 2018, 465, 219–231. [Google Scholar] [CrossRef]
- Blue, J.; Condell, J.; Lunney, T. A Review of Identity, Identification & Authentication. Int. J. Inf. Secur. Res. 2018, 8, 794–804. [Google Scholar] [CrossRef]
- Zhang, R.; Bu, S.; Li, G. Multi-market P2P trading of cooling–heating-power-hydrogen integrated energy systems: An equilibrium-heuristic online prediction optimization approach. Appl. Energy 2024, 367, 123352. [Google Scholar] [CrossRef]
- Yu, G.; Wang, X.; Yu, K.; Ni, W.; Zhang, J.A.; Liu, R.P. Survey: Sharding in Blockchains. IEEE Access 2020, 8, 14155–14181. [Google Scholar] [CrossRef]
- Kate, A.; Goldberg, I. Distributed Key Generation for the Internet. In Proceedings of the 2009 29th IEEE International Conference on Distributed Computing Systems, Montreal, QC, Canada, 22–26 June 2009; pp. 119–128. [Google Scholar] [CrossRef]




| Algorithm | Complexity | Energy Consumption | Leader Election Mechanism | Latency | Is Chained Consensus? |
|---|---|---|---|---|---|
| RVR | O(n) | Low | Dynamic reputation weight random verifiable selection | Low | Yes |
| HotStuff [16] | O(n) | Low | Equal probability election | Low | Yes |
| FastHotStuff [18] | O(n) | Low | Equal probability election | Low | Yes |
| PBFT [9] | O(n2) | Low | Fixed sequence rotation | High (large-scale) | No |
| SBFT [15] | O(n) | Low | The one with the highest reputation | Low | Yes |
| Pow [10] | / | Very High | Computational power competition | Very low | Yes |
| Parameter | Description | Value |
|---|---|---|
| N | Total number of nodes | 64 |
| byzNo | Number of Byzantine nodes | 0 to 20 |
| strategy | Byzantine strategy | forking/silence |
| timeout | Maximum waiting time for the next view | 1000 ms |
| hasher | The hash algorithm used | sha3_256 |
| max round | The maximum number of running epochs | 5000 |
| bsize | Number of transactions included in a block | 400 |
| r0 | Basic reward value | 8 |
| p0 | Basic penalty value | 2 |
| α | Punishment growth coefficient | 0.3 |
| β | Reward decay rate | 0.2 |
| k1 | Historical reputation weight | 0.6 |
| k2 | Real-time behavior weight | 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Liu, X.; Chen, J. RVR Blockchain Consensus: A Verifiable, Weighted-Random, Byzantine-Tolerant Framework for Smart Grid Energy Trading. Computers 2025, 14, 232. https://doi.org/10.3390/computers14060232
Wang H, Liu X, Chen J. RVR Blockchain Consensus: A Verifiable, Weighted-Random, Byzantine-Tolerant Framework for Smart Grid Energy Trading. Computers. 2025; 14(6):232. https://doi.org/10.3390/computers14060232
Chicago/Turabian StyleWang, Huijian, Xiao Liu, and Jining Chen. 2025. "RVR Blockchain Consensus: A Verifiable, Weighted-Random, Byzantine-Tolerant Framework for Smart Grid Energy Trading" Computers 14, no. 6: 232. https://doi.org/10.3390/computers14060232
APA StyleWang, H., Liu, X., & Chen, J. (2025). RVR Blockchain Consensus: A Verifiable, Weighted-Random, Byzantine-Tolerant Framework for Smart Grid Energy Trading. Computers, 14(6), 232. https://doi.org/10.3390/computers14060232






