Abstract
In modern data management systems, structured query language (SQL) databases, as a mature and stable technology, have become the standard for processing structured data. These databases ensure data integrity through strongly typed schema definitions and support complex transaction management and efficient query processing capabilities. However, data sparsity—where most fields in large table sets remain unused by most queries—leads to inefficiencies in access optimization. We propose a grouping-based approach (GARMT) that partitions SQL queries into fixed-size groups and applies a modified FP-Growth algorithm (GFP-Growth) to identify frequent table access patterns. Experiments on a real-world dataset show that grouping significantly reduces runtime—by up to 40%—compared to the ungrouped baseline while preserving rule relevance. These results highlight the practical value of query grouping for efficient pattern discovery in sparse database environments.
1. Introduction
User interaction with the database primarily occurs through a series of SQL queries collectively stored as query workloads. These workloads encompass various types of SQL statements, including data retrieval and updates, and they support complex transaction management through efficient query processing. As the volume of SQL queries continues to grow, certain tables experience significantly higher access frequencies, which not only increases the database system’s overall energy consumption [1] but also exacerbates data sparsity (i.e., most table fields remain unused across the majority of queries) [2]. Check Figure 1). This elevated access frequency can further degrade system performance by prolonging response times. Consequently, optimizing queries, judiciously planning table indexes, and adopting efficient data storage and access strategies are essential for reducing energy consumption and enhancing the operational efficiency of database systems. To address these challenges, we propose a grouping-based association rule mining approach that rapidly identifies tables and fields with high access frequency. By clustering query workloads and applying frequent-pattern mining [3], this method uncovers hidden access patterns, enabling database administrators to implement targeted optimizations that improve system performance while reducing energy consumption. For example, consider a web application that generates multiple SQL statements during a user session—such as a SELECT statement for browsing products, an INSERT statement for updating the shopping cart, and a DELETE statement for cleaning up the session. While each query may appear to be unrelated to the other, grouping them together reveals consistent access to the User, Product, and Cart tables. This contextual grouping reveals more meaningful patterns of common access than processing queries in isolation [4]. In addition, strong associations between columns (such as foreign keys or co-occurrences in WHERE clauses) may imply deeper table-level relationships. For example, frequent joint filtering of “orders.user_id” and “users.user_id” may indicate a deeper table-level relationship between “orders” and “users”, implying that they are logically related. Brin et al. [5] have shown that column-level associations can uncover hidden relational dependencies in transactional workloads [6].
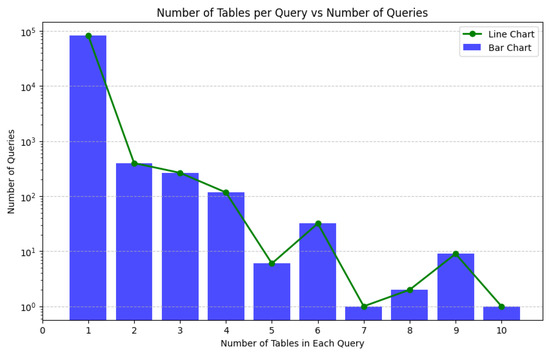
Figure 1.
In SQL databases, there may be a large number of different tables and fields, but any single query may involve only a small fraction of them. This results in highly sparse data, i.e., most items do not appear in most transactions.
This approach makes three original contributions. First, because SQL statements are generally executed line by line, each statement provides only limited information—particularly regarding table usage and data access patterns. Consequently, capturing comprehensive database interaction patterns from a single SQL statement can be exceptionally difficult. To address this limitation, we propose a statement-grouping strategy that aggregates related multi-line SQL statements into a set. The core idea is to treat multiple SQL operations within a time window or logically interrelated SQL operations as a whole, thereby increasing the density and relevance of data items and mitigating the challenges posed by sparse data. Second, by identifying and exploiting relationships and patterns among tables that may be overlooked in traditional SQL log analysis, this research offers novel strategies and tools for database performance optimization and resource management. Third, we theoretically and empirically demonstrate the computational advantages of grouping, including a detailed complexity analysis and runtime evaluations. These insights into the interconnections between tables in real-world applications provide crucial support for designing more efficient database systems and improving data processing strategies.
The reminder of this paper is organized as follows. Section 2 briefly reviews the related literature. In Section 3, we present an approach to optimize table access using association rule mining, which not only accelerates query processing and reduces system load but also improves performance for complex queries. Section 4 introduces a grouping-based data mining algorithm to predict future attributes in SQL databases. In Section 5, we verify the algorithm’s effectiveness and feasibility by testing its performance under various grouping scenarios. Based on these results, Section 6 examines the positive impact of grouping on the generation of association rules. Finally, Section 7 summarizes the key contributions of the article and outlines potential avenues for future research.
2. Related Work
The main goal of frequent-pattern mining is to discover frequently occurring patterns that reveal the intrinsic structure and relationships of data. These patterns can enhance our understanding of data features and support more effective classification, clustering, and prediction.
2.1. Frequent-Pattern Mining
Frequent-pattern mining focuses on identifying and selecting valuable patterns through evaluation metrics such as support, confidence, and lift. Support measures the frequency of an itemset appearing in the entire dataset, defined as , which aids in understanding the prevalence of the pattern in the dataset [7]. Confidence measures the probability of another itemset occurring given that a previous itemset has occurred, expressed as , assessing the dependency relationships between itemsets [8]. Lift evaluates the relevance of itemsets, calculated by , and compares the probability of itemset X occurring given itemset Y to the probability of X occurring independently [5]. These metrics not only help researchers identify significant patterns in the data but are also crucial for interpreting the data relationships behind the patterns. For example, in market basket analysis, analyzing the support and confidence between items can enable the recommendation of products that are frequently purchased together, while lift helps retailers distinguish whether product combinations are coincidental or due to specific consumer habits. Such analyses can greatly optimize inventory management and marketing strategies, thereby enhancing sales efficiency and customer satisfaction.
2.2. FP-Growth
The FP-Growth (Frequent-Pattern Growth) algorithm is a highly efficient method for discovering frequent itemsets in large datasets without generating a multitude of candidate itemsets [9]. The algorithm relies primarily on two database scans and a compressed data structure called the FP-tree (Frequent-Pattern Tree) to achieve performance gains. During the first scan, the algorithm identifies and counts the frequency of individual items, retaining only those that meet a specified minimum support threshold. These frequent items are then sorted in descending order of frequency to form the item header table. In the second scan, each transaction is read, filtered to include only frequent items, reordered according to the item header table, and inserted into the FP-tree. If the corresponding path in the tree already exists, its count is incremented; if not, a new path is created. Subsequent mining of the FP-tree is performed by recursively constructing conditional pattern bases and conditional FP-trees for each item in the item header table. Each conditional FP-tree represents a frequent pattern under a specific itemset prefix, and this process continues until no further frequent itemsets can be identified. By avoiding the generation of large numbers of candidate itemsets and minimizing the number of database scans, FP-Growth significantly reduces computational complexity and execution time, thereby offering a faster and more efficient approach for uncovering important association rules in large datasets.
3. Association Rule Mining for Table Access Optimization
Association rule mining is a powerful data mining technique that optimizes table access in database systems by uncovering patterns in historical query behavior [10]. By analyzing past queries, it identifies relationships among tables that are frequently accessed together, thus forming association rules. These insights can be leveraged to enhance performance by prefetching related tables into memory, optimizing indices, or caching frequently accessed table sets [11]. As a result, query execution times are reduced, and overall resource utilization is improved.
3.1. Grouping-Based Optimization Process
Optimizing table access patterns in SQL databases is crucial for enhancing system performance [12]. This paper introduces a novel optimization method that leverages frequent-pattern mining and predictive modeling to improve table access. The optimization process is structured into several key steps, as outlined below:
- Step 1: Grouping SQL Queries
Assume a sequence of n SQL queries, denoted as . We group these queries into sets of k consecutive queries, with each set denoted as , where
Each contains k consecutive SQL queries.
- Step 2: Table Set Extraction
For each , extract the set of tables accessed by the queries within the group, denoted as :
Here, represents the set of tables accessed by the SQL query .
- Step 3: Frequent-Pattern Mining
Apply frequent-pattern mining algorithms such as FP-Growth to the table sets . The frequent itemsets for each algorithm are denoted as :
These patterns reveal tables that are frequently accessed together, aiding in the optimization of access patterns.
- Step 4: Predicting Future Table Access
Using the frequent-pattern set from the FP-Growth algorithm, construct a prediction model to anticipate future table accesses. Let represent the currently accessed table. The model computes the conditional probability of the next table to be accessed, , given :
where is the number of times table was accessed immediately after table . The next table to be accessed, , is then predicted as follows:
- Step 5: Mapping Table to Corresponding Dataset
Once is identified, it is mapped back to its dataset and the corresponding datasets:
Here, denotes the dataset of the predicted table. This mapping is crucial for optimizing future query operations.
3.2. Problem Statement and Efficiency Analysis
Our primary objective is to allocate computational resources efficiently by minimizing the overall computational complexity [13], which depends on both the size and distribution of query groups. Let n represent the total number of queries and g the designated number of groups. Each group j has a size , with the constraint
The total computational complexity is defined as the sum of the exponential costs across all groups:
The primary objective is to minimize the sum of exponential costs, subject to two potential grouping strategies. In the balanced grouping approach, each group size should approximate , ensuring a more equitable distribution of queries among the groups. In contrast, unbalanced grouping simply requires that each group must include at least one query, thus allowing for greater flexibility in how queries are distributed.
In pursuit of enhanced performance in SQL database systems, a detailed examination of SQL statement processing reveals substantial opportunities for optimization. The following section introduces an innovative technique that involves grouping SQL statements within datasets before applying frequent-pattern mining algorithms. This method not only streamlines query processing but also significantly improves the efficiency of identifying recurring patterns, thus facilitating query optimization. By reorganizing data management, this approach enables more effective analysis and faster response times.
Definition 1.
In balanced grouping, the total number of groups g divides the total number of queries n equally or nearly equally:
Definition 2.
In unbalanced grouping, groups can have different numbers of queries. Let denote the size of group , where .
Theorem 1.
Grouping the SQL statement dataset improves the efficiency of frequent-pattern mining.
where .
Proof.
We use mathematical induction on the number of groups g.
Base Case ():
When , all queries are in a single group. The computational complexity is calculated as follows:
which is the same as the ungrouped case. Thus, the efficiency is the same.
Inductive Hypothesis:
Assume that for , grouping the queries into m balanced groups leads to greater efficiency:
where .
Inductive Step ():
For , the complexities are as follows:
Since frequent-pattern mining algorithms have exponential or super-exponential complexity, i.e., , we have:
Thus, grouping reduces the computational complexity significantly. □
Proof.
We analyze the total computational complexity when the queries are grouped versus when they are not.
Without Grouping: The computational complexity is
With Unbalanced Grouping:
The total computational complexity is the sum of the complexities for each group:
Comparison:
Since the sum of exponentials is less than the exponential of the sum for positive integers,
Thus,
Edge Cases:
Consider the worst-case scenario where one group contains almost all queries, and the others contain minimal queries.
Let and for . Then,
Even in unbalanced grouping, the total computational complexity when grouping is applied is less than the complexity without grouping. This holds true regardless of how the queries are distributed among the groups. □
3.3. Leveraging Column Associations to Infer Table Associations
In large-scale SQL databases, column-to-column associations frequently stem from shared business logic or common dependencies. Building on this observation, we propose the conjecture that “column associations can infer table associations”. Specifically, when multiple columns exhibit high-frequency co-occurrence or strong correlations during querying or data processing, the tables housing these columns may share underlying connections. Verifying this conjecture not only uncovers potential dependencies at the table level but also presents novel strategies for database optimization and query pattern mining. The details are as follows.
To illustrate this concept more clearly, consider a simple schema with two tables: Customers (customer_id, name, email) and Orders (order_id, customer_id, order_date, total_amount). In a typical workload, queries frequently join Customers.customer_id with Orders.customer_id and also filter by Orders.order_date. This demonstrates a divergent pattern: a single column from Customers (customer_id) is frequently associated with multiple columns in Orders. Conversely, imagine that both Customers.email and Customers.name are often used together to filter by or join with Orders.customer_id. This reflects a convergent pattern, where multiple columns in one table point to a common destination column in another table. These examples provide an intuitive understanding of how frequent-column co-occurrence can help infer hidden table-level relationships.
Consider two tables, and , with the respective column sets and . Associations among columns across these two tables can be leveraged to infer relationships between the tables themselves. Such inferences manifest in two principal ways. First, in the case of divergence, when a single column in is associated with multiple columns in , the association propagates from to . In contrast, in the case of convergence, when multiple columns in are associated with the same column in , the association from to is consolidated. The overall strength of these table-level associations is further determined by the frequency and support of the underlying column associations.
- Case 1: Divergence
In the divergence scenario, a single column from is associated with multiple columns from . For example: is associated with both and , denoted as ,
This implies that table is frequently queried in conjunction with table . The support for these associations is as follows:
Given that a single column from is linked to multiple columns from , we infer that table is strongly associated with table . The overall probability of accessing given that has been accessed is proportional to the sum of these individual column associations:
This scenario reflects a divergent association where information from a single column in diverges to multiple columns in , creating a strong overall table association.
- Case 2: Convergence
In the convergence scenario, multiple columns from are associated with a single column from . For example: and are both associated with , denoted as ,
This implies that multiple columns from frequently lead to the same column in , consolidating the association between and . The support for these associations is as follows:
Given that multiple columns from are converging onto a single column in , the association between and is consolidated. The overall probability of accessing given that has been accessed is the product of these individual column associations:
This scenario reflects a convergent association where multiple columns in lead to the same column in , forming a strong, consolidated table association.
Both the divergence and convergence cases demonstrate how column-level associations can infer table-level associations. In the divergence case, a single column from leads to multiple columns in , indicating a broader association between the two tables. In the convergence case, multiple columns from point to a single column in , consolidating the relationship between the tables.
The overall strength of a table association depends on the frequency of its column associations, which can be quantified through the support and conditional probability of specific column pairs. This column-to-table association framework can be applied to optimize query planning and enhance database caching strategies.
4. Algorithm Design
To explore valuable insights from large-scale SQL query logs, we propose an approach based on frequent-pattern mining, which, at its core, utilizes an improved FP-Growth algorithm. The method reveals hidden structural access patterns in database usage by identifying table name combinations that occur frequently in different SQL queries. Unlike traditional FP-Growth, we introduce a “query grouping” strategy, where SQL queries are divided into subsets according to specific criteria, and frequent-pattern mining is performed on each subset separately. As shown in Algorithm 1, this grouping-enhanced algorithm, called “Group FP-Growth” (GFP-Growth), improves processing efficiency, scalability, and pattern recognition accuracy in large-scale data scenarios.
In this study, we adopt a fixed-size sequential grouping strategy. That is, given a query log , we divide it into non-overlapping groups where each group contains k consecutive queries based on their original appearance order. Formally, for . No semantic or user-based information is considered in the grouping process. The entire GFP-Growth process is divided into three key phases, each corresponding to a different task in the data processing pipeline. The first phase is the preprocessing phase, in which we clean and parse the raw query logs and extract key information related to the table name usage; the second phase is the query grouping phase, in which we cluster queries based on their semantic or structural features to form multiple logically similar subsets; and the third phase is the pattern mining phase, in which the FP-Growth algorithm is generated for each query subset. Through this phased and structured process, GFP-Growth effectively improves the efficiency of the algorithm and provides a data-driven decision basis for database optimization and system maintenance.
| Algorithm 1 GFP-Growth |
| Require: SQL queries as a pandas Series |
| Ensure: Frequent patterns from table name sets |
|
Phase I: SQL Query Analysis: The first function, Analyze_SQL, accepts a pandas Series of SQL queries as input. It initializes counters for three critical components: table names, SQL operation types (e.g., SELECT, UPDATE, DELETE, INSERT), and WHERE clauses. Each query is processed using regular expressions to detect these elements. SQL operations are identified through their respective keywords, WHERE clauses by their syntactical structure, and table names from tokens following the FROM keyword. The counts of all components are updated for each query, yielding a comprehensive statistical overview of query usage patterns.
Phase II: Group Analysis: In the data preprocessing phase, we divide the entire SQL query log into subsets (i.e., query groups) according to predefined rules. Such groupings can be divided based on time windows, query structure similarities, user behavior patterns, or other contextual information. Subsequently, the system processes each query group independently by parsing each SQL query statement, extracting the table names involved, and performing frequency statistics within the group. Eventually, each group accumulates the table names used in all queries in the group and their frequency of occurrence, forming group-level table access characteristics. This group-based aggregation process is critical for analyzing local behavioral patterns of database usage. By analyzing smaller, focused groups of queries, we can more easily identify sets of tables that are frequently accessed together. These patterns typically appear in shared business logic, repeated session behavior, or specific time windows. As a result, we can uncover localized access hotspots and usage structures that would be downplayed in a full log analysis. This not only helps to improve the efficiency of frequent-pattern mining, but also provides a more refined reference basis for subsequent index optimization, cache strategy design, and system resource allocation.
Phase III: Frequent-Pattern Mining: After preparing the data and extracting table names, we apply the FP-Growth algorithm. The FP-Growth algorithm was selected because it can efficiently handle large datasets without the need to generate the large candidate sets required by other algorithms, such as Apriori [14]. By identifying frequent patterns in table name usage, FP-Growth reveals common querying behaviors and highlights opportunities for database optimization. FP-Growth is used to uncover frequent patterns in the set of table names that appear in each query group. These patterns represent combinations of structures that are repeatedly accessed by the database in a particular context, thus reflecting the consistent behavior of the user or the system during operation. For example, the frequent co-occurrence of certain table combinations may suggest the existence of implicit business logic associations or joint query requirements between them. By systematically identifying these high-frequency patterns, FP-Growth not only reveals the structural characteristics of the underlying query behavior, but also provides important clues for database optimization, such as index federation optimization, table join strategy tuning, or data partitioning recommendations.
This complexity analysis investigates the computational requirements of both the preprocessing phase and the GFP-Growth algorithm in the context of SQL query analysis. The preprocessing phase involves parsing each m SQL query and extracting tables, operations, and WHERE clauses using regular expressions. This process has linear time complexity, denoted by , where n denotes the average length of the query. While grouping the query imposes only minimal overhead, it requires that each grouping be processed independently, thus maintaining the linear complexity of the overall preprocessing task. However, despite the relatively efficient construction of the FP-tree, its subsequent pattern mining process still faces computational bottlenecks in the worst case. Specifically, the complexity of frequent-pattern mining may reach , where f denotes the number of frequent terms. Several parameters critically influence the algorithm’s runtime. Specifically, smaller group sizes and higher minimum support thresholds (min_sup) reduce computational complexity by limiting the number of transactions and frequent itemsets. In contrast, larger group sizes and lower support thresholds increase processing demands. Thus, the overall efficiency of the approach hinges on striking an appropriate balance between preprocessing overhead and the potential exponential cost of the GFP-Growth algorithm. This underscores the necessity of selecting suitable grouping strategies and support thresholds to ensure scalable and efficient performance.
5. Experiment
The purpose of this experiment is to investigate the impact of dataset size and grouping strategy on the runtime and association rule accuracy of the GFP-Growth algorithm in SQL query analysis. We systematically evaluate the performance, including runtime and rule confidence, under different grouping sizes (5, 10, 20, 30, 50, 100) and support thresholds (0.002, 0.02, 0.2). In the experiments, the ungrouped FP-Growth method (which treats all queries as a transaction set) serves as the baseline, while each grouping configuration represents a different variant of our method, which is used to validate its effectiveness under a wide range of conditions.
5.1. Experimental Setup
5.1.1. Dataset Description
The dataset used in this experiment was provided by Lai et al. [15] and contains SQL queries extracted from a CSV file. These queries originate from the Sloan Digital Sky Survey (SDSS), which stores images, spectra, and catalog data for over three million objects [16]. For each SQL record, the original query statement and session category labels were obtained. The SQL queries were then parsed to identify table names and associated operations, which were subsequently used for frequent-itemset mining.
5.1.2. Preprocessing
Preprocessing played a crucial role in the entire GFP-Growth model construction process. To systematically assess the impact of the grouping strategy on the runtime performance of the GFP-Growth algorithm, we divided the original SQL query logs into multiple query subsets, i.e., ‘query groups’. This process was not only part of the data preparation, but also a key aspect of the experimental design, aiming to explore the specific impact on the algorithm’s efficiency by controlling the number and size of query groups. We adopted two grouping methods: the first was to take the entire query log as a whole, keeping the original structure of the database unchanged without any form of query partitioning; the second was the fixed group size method, which divided the query log into a number of groups by setting the group size artificially, and each group contained 5, 10, 20, 30, 50, or 100 SQL queries. Each grouping approach represented different data granularity and processing complexity, providing us with a multi-dimensional performance evaluation framework. In each query group, all SQL queries were first syntactically analyzed and structurally parsed to extract the table names involved. These table names were then converted into a standardized transaction format so that they could be used as input data for the FP-Growth algorithm. In this way, we mapped the SQL query semantics into structured data that could be used for frequent-itemset mining, thus providing the basis for subsequent GFP-Growth pattern mining. There were two main motivations for introducing these grouping strategies: on the one hand, we want to explore whether smaller group sizes help reduce the runtime of the algorithm, since each group contains fewer transactions, and the FP-tree construction and recursive search process is lighter; on the other hand, we also need to evaluate the potential advantages of larger group sizes, such as more complete frequent-pattern-capturing capabilities, but also the possibility of a higher computational overhead. The ultimate goal is to find an optimal balance between minimizing runtime resource consumption and maximizing the retention of useful information in the data, thus improving the overall execution efficiency and applicability of the GFP-Growth algorithm.
5.2. Experimental Results
In order to perform an in-depth evaluation of the performance of the GFP-Growth algorithm under different parameter settings, we systematically analyzed its runtime performance under a variety of minimum support thresholds (minsup) and query group size conditions. The main goal of the experiments was to clarify how these key parameters interact with each other to affect the efficiency of the algorithm, as shown in Figure 2.
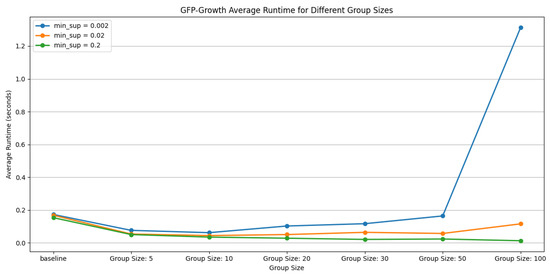
Figure 2.
GFP-Growth performance under different group sizes.
For minimum support, we selected three typical threshold levels: 0.2, 0.02, and 0.002. These values represent high-, medium-, and low-frequency pattern mining scenarios, respectively, and can effectively capture the impact of frequent itemsets on runtime efficiency at different granularities. Figure 3 shows that higher minimum support (e.g., 0.2) significantly reduces the runtime of the algorithm for all query group size settings. Note: “N/A” values indicate that no association rules satisfied both the minimum support (0.2) and confidence (0.8) thresholds for group sizes of 10 and 5. These small groups lacked sufficient frequent-table co-access patterns under strict thresholds. This is due to the fact that only a small number of frequent itemsets satisfy the support requirement under high-threshold conditions, which reduces the construction depth of the FP-tree as well as the scope of the recursive search, and significantly reduces the computational complexity.
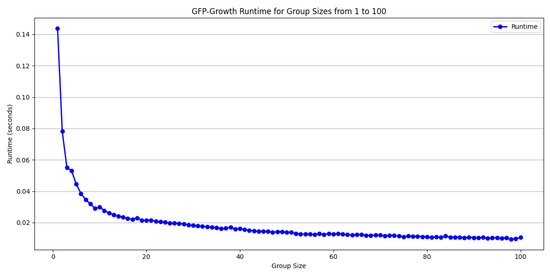
Figure 3.
Support value = 0.2.
Figure 4 shows that lower support thresholds (e.g., 0.002) significantly lengthen the runtime, especially for larger query group sizes (e.g., 50 or 100 queries per group). This is because with lower support, the number of frequent itemsets that the algorithm needs to mine and store increases dramatically, resulting in higher memory consumption and computational burden, especially in the context of large transaction sets.
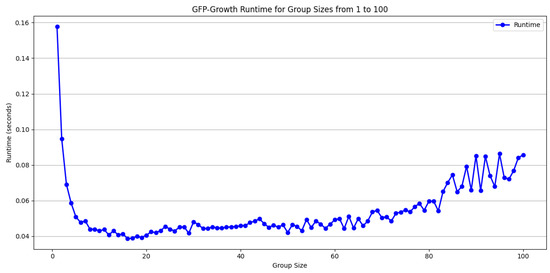
Figure 4.
Support value = 0.02.
In addition, we divided the entire dataset into 5, 10, 20, 30, 50, and 100 query subsets and tested the impact of each grouping size on the operational efficiency separately. The experimental results show that compared to the baseline scenario (i.e., without any grouping processes), the use of small grouping sizes (especially 5 or 10 queries per group) can significantly reduce the runtime, especially when the support threshold is set higher. The main reason for the increased efficiency is the smaller number of transactions in each group, which allows the FP-Growth algorithm to handle smaller FP-trees, greatly reducing the computational overhead.
However, as the size of the query group grows (e.g., to as many as 50 or 100 queries per query group), the runtime starts to increase.This trend is especially noticeable at lower support thresholds. The reason is that, although the grouping strategy was originally intended to reduce computational complexity, the resource consumption during FP-tree construction and recursive mining rises as the size of the set of transactions within each group grows, thus offsetting the original performance advantage.
The runtime efficiency is significantly improved when transitioning from the baseline strategy to a small-sized grouping strategy; however, the runtime bounces back when the group size is too large and the support threshold is too low. This finding highlights the core issue that needs to be considered in the design of grouping policies, that is, how to reduce the runtime while avoiding the growth of computational overhead due to too large a transaction set size. Therefore, choosing the appropriate grouping size and minimum support threshold is key to optimizing the execution efficiency of the GFP-Growth algorithm.
6. Discussion
From the above runtime analysis, it is obvious that the grouping strategy of SQL queries and the setting of the minimum support threshold have a significant impact on the overall performance of the FP-Growth algorithm. Specifically, smaller grouping usually leads to a smaller number of transactions contained in each group, which reduces the computational burden of FP-tree construction and frequent-pattern mining. As a result, smaller group sizes tend to achieve faster runtimes and significantly improve processing efficiency at the same level of support. However, this performance improvement often comes at the expense of the quality of mining results. As fewer transactions are included in each subgroup, the set of frequent items that can be identified is correspondingly reduced, resulting in the final generated association rules being more localized and lacking in global representativeness. By comparing the average confidence metrics, it can be found that although small groupings help to speed up the computation, the rules they generate may have a decreasing trend at the confidence level, which makes it difficult to provide sufficient explanations.
To illustrate the practical utility of the discovered patterns, consider the following representative rule identified under a support threshold of 0.02 and a group size of 20: We have an association rule: {A, B} ⇒ {C} [support = 0.035, confidence = 0.81]. This rule suggests that when a query accesses tables A and B, it is also highly likely to access table C. Such patterns enable database administrators to optimize performance by preloading these frequently co-accessed tables into memory as a group. By proactively bringing A, B, and C into memory during query processing, the system can significantly reduce I/O latency, improve cache hit rates, and enhance overall responsiveness in data-intensive environments.
Selecting an appropriate group size is crucial for maintaining the computational efficiency and stability of the GFP-Growth algorithm. Larger groups significantly expand the search space, leading to increased runtime and volatility in the results, whereas smaller groups generally reduce computational overhead but may limit the algorithm’s ability to capture all relevant patterns. In addition to group size, the choice of support and confidence thresholds also significantly affects both the quality and the quantity of rules generated. In Table 1 and Table 2, it is indicated that a higher support threshold produces a smaller but more representative set of frequent itemsets, facilitating faster calculations and more reliable patterns. Conversely, Figure 5 displays that lower support thresholds can uncover additional frequent itemsets, but risk introducing noise or irrelevant patterns. Combining a high support threshold with a high confidence level yields fewer rules that occur frequently and reliably, reducing the computational burden. However, high support with low confidence may indicate weak correlations between items. Meanwhile, low support with high confidence often requires more extensive computation because the algorithm must process larger itemsets. Finally, low support combined with low confidence produces a voluminous set of rules, many of which may lack practical value. Carefully balancing group size, support, and confidence thresholds is therefore essential to optimize runtime while maintaining the interpretability and practical utility of the discovered patterns.

Table 1.
The association rules generated by GFP-Growth with support value = 0.02.

Table 2.
The association rules generated by GFP-Growth with support value = 0.2.
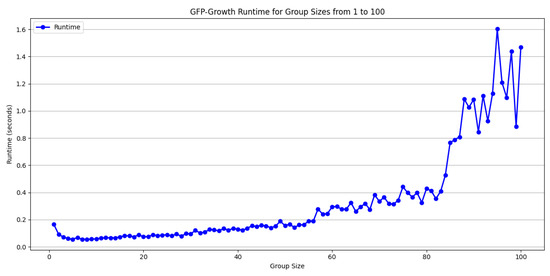
Figure 5.
Support value = 0.002.
7. Conclusions
As the volume of SQL queries continues to grow, database systems increasingly face performance and energy consumption challenges arising from high table access frequency and data sparsity. In this paper, we present a grouping-based association rule mining approach that rapidly identifies the tables and fields with high access frequency, enabling targeted optimizations to reduce energy consumption and enhance system efficiency. Central to our method is a grouping-based analysis strategy that aggregates multiple related SQL statements into a cohesive set, thus mitigating the analytical difficulties posed by data sparsity. By uncovering inter-table relationships and access patterns frequently overlooked in conventional SQL log analyses, this research provides innovative methods and tools for optimizing SQL database performance and managing resources more effectively. While we did not directly measure hardware-level energy consumption, we believe that runtime reduction is a reasonable proxy for computational energy efficiency. In modern database systems, CPU utilization and energy consumption are highly correlated with execution time, especially for analytical workloads. By reducing the number of frequent itemsets generated per grouping and localizing the mining process, our grouping strategy significantly reduces execution time, which, in turn, means lower energy consumption.
In the future, striking a balance between operational efficiency and rule quality will become an important consideration when designing a grouping strategy. Our future work can explore the adaptive grouping mechanism or the combination of clustering [17] to dynamically divide the grouping based on query semantics or structural similarity [18] to balance efficiency and the mining effect. One promising direction is to implement adaptive grouping based on clustering techniques. For example, SQL queries can be dynamically grouped using similarity metrics for query structure (e.g., query templates), user IDs, visited table sets, or query execution time windows. In this way, the grouping strategy can evolve in real time based on workload characteristics. Meanwhile, we will also perform extension of the techniques of association rule mining to non-SQL databases [19], particularly key-value stores that are widely accepted by applications with high requirements for scalability and availability. While most research efforts to date have focused on relational databases and structured query languages, key-value databases present a unique set of challenges and opportunities because they do not require schemas [20]. Studying these not only broadens the scope of frequent-pattern mining, but also tests the adaptability and bounds of established algorithms in less structured data environments. Addressing these challenges can provide insights into the generalization of data mining techniques across different database architectures, which can further enhance their usefulness in a range of computational applications.
Author Contributions
Conceptualization, P.H. and X.Q.; methodology, P.H. and X.Q.; software, P.H.; validation, P.H.; formal analysis, P.H.; investigation, P.H., L.S., X.G., Y.Z. and X.Q.; resources, P.H., Y.Z. and X.Q.; data curation, P.H. and X.Q.; writing—original draft, P.H.; writing—review & editing, L.S., X.G., Y.Z. and X.Q.; visualization, P.H., L.S., X.G., Y.Z. and X.Q.; supervision, X.Q.; project administration, P.H., Y.Z. and X.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zeng, X.; Hui, Y.; Shen, J.; Pavlo, A.; McKinney, W.; Zhang, H. An empirical evaluation of columnar storage formats. Proc. VLDB Endow. 2023, 17, 148–161. [Google Scholar] [CrossRef]
- Yin, H.; Wang, Q.; Zheng, K.; Li, Z.; Zhou, X. Overcoming data sparsity in group recommendation. IEEE Trans. Knowl. Data Eng. 2020, 34, 3447–3460. [Google Scholar] [CrossRef]
- Huang, L.; Chen, H.; Wang, X.; Chen, G. A fast algorithm for mining association rules. J. Comput. Sci. Technol. 2000, 15, 619–624. [Google Scholar] [CrossRef]
- Remil, Y.; Bendimerad, A.; Mathonat, R.; Chaleat, P.; Kaytoue, M. “What makes my queries slow?”: Subgroup Discovery for SQL Workload Analysis. In Proceedings of the 2021 36th IEEE/ACM International Conference on Automated Software Engineering (ASE), Melbourne, Australia, 15–19 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 642–652. [Google Scholar]
- Brin, S.; Motwani, R.; Silverstein, C. Beyond market baskets: Generalizing association rules to correlations. In Proceedings of the 1997 ACM SIGMOD International Conference on Management of Data, Tucson, AZ, USA, 11–15 May 1997; pp. 265–276. [Google Scholar]
- Goethals, B.; Van den Bussche, J. Relational association rules: Getting warmer. In Proceedings of the Pattern Detection and Discovery: ESF Exploratory Workshop, London, UK, 16–19 September 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 125–139. [Google Scholar]
- Han, J.; Kamber, M.; Pei, J. 6-mining frequent patterns, associations, and correlations: Basic concepts and methods. In Data Mining, 3rd ed.; The Morgan Kaufmann Series in Data Management Systems; Morgan Kaufmann: Burlington, MA, USA, 2012; pp. 243–278. [Google Scholar]
- Hipp, J.; Güntzer, U.; Nakhaeizadeh, G. Algorithms for association rule mining—A general survey and comparison. ACM SIGKDD Explor. Newsl. 2000, 2, 58–64. [Google Scholar] [CrossRef]
- Borgelt, C. An Implementation of the FP-growth Algorithm. In Proceedings of the 1st International Workshop on Open Source Data Mining: Frequent Pattern Mining Implementations, Chicago, IL, USA, 21 August 2005; pp. 1–5. [Google Scholar]
- Zaiane, O.R.; Xin, M.; Han, J. Discovering web access patterns and trends by applying OLAP and data mining technology on web logs. In Proceedings of the IEEE International Forum on Research and Technology Advances in Digital Libraries-ADL’98-, Santa Barbara, CA, USA, 22–24 April 1998; IEEE: Piscataway, NJ, USA, 1998; pp. 19–29. [Google Scholar]
- Zhou, Y.; Taneja, S.; Zhang, C.; Qin, X. GreenDB: Energy-efficient prefetching and caching in database clusters. IEEE Trans. Parallel Distrib. Syst. 2018, 30, 1091–1104. [Google Scholar] [CrossRef]
- Che, S.; Sheaffer, J.W.; Skadron, K. Dymaxion: Optimizing memory access patterns for heterogeneous systems. In Proceedings of the 2011 International Conference for High Performance Computing, Networking, Storage and Analysis, Seattle, WA, USA, 12–18 November 2011; pp. 1–11. [Google Scholar]
- Yang, L.; Chen, R.S.; Siu, Y.M.; Soo, K.K. PAPR reduction of an OFDM signal by use of PTS with low computational complexity. IEEE Trans. Broadcast. 2006, 52, 83–86. [Google Scholar] [CrossRef]
- Bodon, F. A Fast APRIORI Implementation; Hungarian Academy of Sciences: Budapest, Hungary, 2003; Volume 3, p. 63. [Google Scholar]
- Lai, E.Y.; Zolaktaf, Z.; Milani, M.; AlOmeir, O.; Cao, J.; Pottinger, R. Workload-Aware Query Recommendation Using Deep Learning. In Proceedings of the EDBT, Ioannina, Greece, 23–31 March 2023; pp. 53–65. [Google Scholar]
- Raddick, M.J.; Thakar, A.R.; Szalay, A.S.; Santos, R.D. Ten years of skyserver i: Tracking web and sql e-science usage. Comput. Sci. Eng. 2014, 16, 22–31. [Google Scholar] [CrossRef]
- Yin, H.; Aryani, A.; Petrie, S.; Nambissan, A.; Astudillo, A.; Cao, S. A rapid review of clustering algorithms. arXiv 2024, arXiv:2401.07389. [Google Scholar]
- Ganesan, S.; Gong, T.; Lee, J. Sqlearn: Automated SQL statement assessment using structure-based analysis. In Proceedings of the 55th ACM Technical Symposium on Computer Science Education V. 2, Toronto, ON, Canada, 20–23 March 2024; pp. 1644–1645. [Google Scholar]
- Han, J.; Haihong, E.; Le, G.; Du, J. Survey on NoSQL database. In Proceedings of the 2011 6th International Conference on Pervasive Computing and Applications, Port Elizabeth, South Africa, 26–28 October 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 363–366. [Google Scholar]
- Zhu, Z.; Saha, A.; Athanassoulis, M.; Sarkar, S. KVBENCH: A key-value benchmarking suite. In Proceedings of the Tenth International Workshop on Testing Database Systems, Santiago, Chile, 9 June 2024; pp. 9–15. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).