LLMPC: Large Language Model Predictive Control
Abstract
1. Introduction
- We formulate a novel framework, LLMPC, that integrates Large Language Models with wodel predictive control principles to enable iterative solving of complex planning problems.
- We highlight that planning methods improve LLM performance by breaking large complex problems down into simpler sub-tasks that can be solved by the LLM due to instruction fine-tuning.
- We show that sampling multiple plans from LLMs and selecting the best according to a cost function significantly improves planning performance as problem complexity increases.
- We empirically validate LLMPC on three diverse planning benchmarks, showing improved performance over few-shot prompting and better computational efficiency than Monte Carlo Tree Search approaches.
2. Model Predictive Control
3. LLM as MPC Plan Sampler
4. Experiments
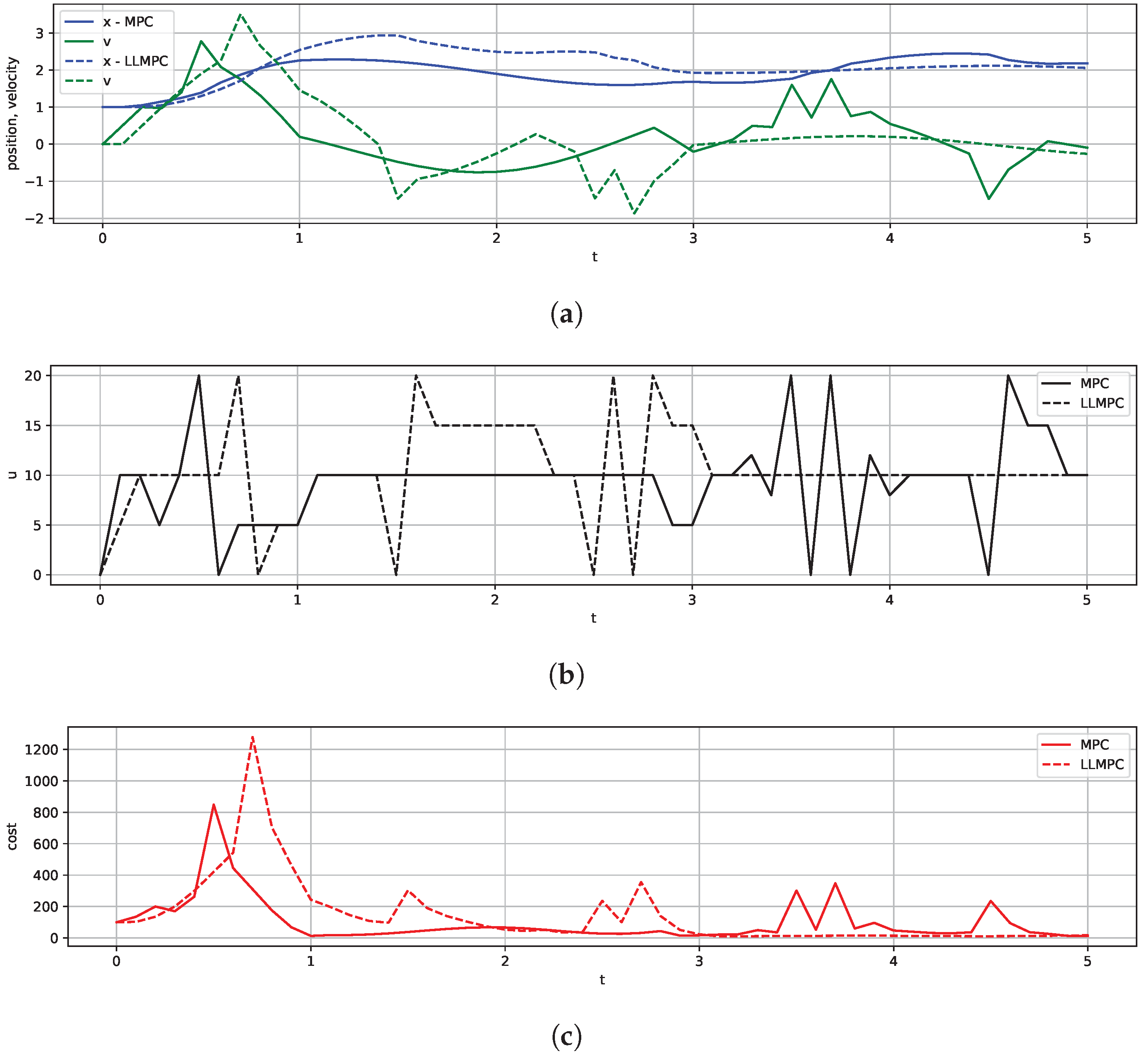
4.1. Control of Spring-and-Mass System
4.2. Trip Planning
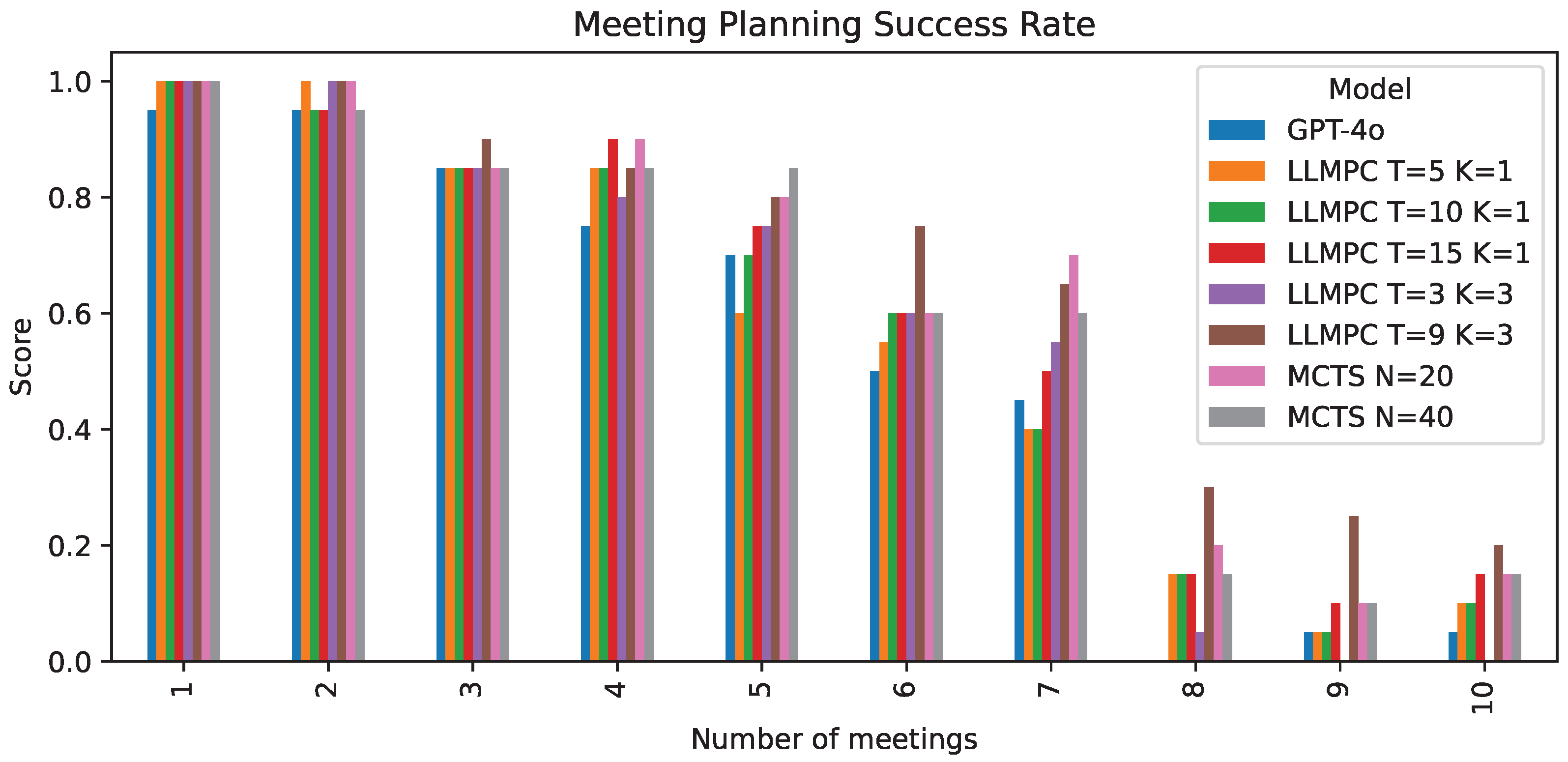
4.3. Meeting Planning
- Varying the number of iterations T to refine plans;
- Sampling multiple plans per iteration (K > 1);
- Combinations of iteration and sampling to balance exploration and refinement.
5. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Mass–Spring System

Appendix B. Trip Planning



Appendix C. Meeting Planning




References
- Wei, J.; Wang, X.; Schuurmans, D.; Bosma, M.; Ichter, B.; Xia, F.; Chi, E.; Le, Q.; Zhou, D. Chain-of-Thought Prompting Elicits Reasoning in Large Language Models. arXiv 2022, arXiv:2201.11903. [Google Scholar]
- Wang, X.; Wei, J.; Schuurmans, D.; Le, Q.; Chi, E.; Narang, S.; Chowdhery, A.; Zhou, D. Self-Consistency Improves Chain of Thought Reasoning in Language Models. arXiv 2022, arXiv:2203.11171. [Google Scholar]
- Wang, A.; Song, L.; Tian, Y.; Peng, B.; Yu, D.; Mi, H.; Su, J.; Yu, D. LiteSearch: Efficacious Tree Search for LLM. arXiv 2024, arXiv:2407.00320. [Google Scholar]
- Jiang, J.; Chen, Z.; Min, Y.; Chen, J.; Cheng, X.; Wang, J.; Tang, Y.; Sun, H.; Deng, J.; Zhao, W.X.; et al. Enhancing LLM Reasoning with Reward-guided Tree Search. arXiv 2024, arXiv:2411.11694. [Google Scholar]
- DeepSeek-AI; Guo, D.; Yang, D.; Zhang, H.; Song, J.; Zhang, R.; Xu, R.; Zhu, Q.; Ma, S.; Wang, P.; et al. DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning. arXiv 2025, arXiv:2501.12948. [Google Scholar]
- Ahn, M.; Brohan, A.; Brown, N.; Chebotar, Y.; Cortes, O.; David, B.; Finn, C.; Fu, C.; Gopalakrishnan, K.; Hausman, K.; et al. Do As I Can, Not As I Say: Grounding Language in Robotic Affordances. arXiv 2022, arXiv:2204.01691. [Google Scholar]
- Wang, G.; Xie, Y.; Jiang, Y.; Mandlekar, A.; Xiao, C.; Zhu, Y.; Fan, L.; Anandkumar, A. Voyager: An Open-Ended Embodied Agent with Large Language Models. arXiv 2023, arXiv:2305.16291. [Google Scholar]
- Song, C.H.; Wu, J.; Washington, C.; Sadler, B.M.; Chao, W.L.; Su, Y. LLM-Planner: Few-Shot Grounded Planning for Embodied Agents with Large Language Models. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–3 October 2023; pp. 2998–3009. [Google Scholar]
- Zhu, Y.; Qiao, S.; Ou, Y.; Deng, S.; Zhang, N.; Lyu, S.; Shen, Y.; Liang, L.; Gu, J.; Chen, H. KnowAgent: Knowledge-Augmented Planning for LLM-Based Agents. arXiv 2024, arXiv:2403.03101. [Google Scholar]
- Yin, S.; Pang, X.; Ding, Y.; Chen, M.; Bi, Y.; Xiong, Y.; Huang, W.; Xiang, Z.; Shao, J.; Chen, S. SafeAgentBench: A Benchmark for Safe Task Planning of Embodied LLM Agents. arXiv 2024, arXiv:cs.CR/2412.13178. [Google Scholar]
- Singh, I.; Traum, D.; Thomason, J. TwoStep: Multi-agent Task Planning using Classical Planners and Large Language Models. arXiv 2024, arXiv:cs.AI/2403.17246. [Google Scholar]
- Zhou, Z.; Song, J.; Yao, K.; Shu, Z.; Ma, L. ISR-LLM: Iterative Self-Refined Large Language Model for Long-Horizon Sequential Task Planning. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024. [Google Scholar] [CrossRef]
- Zhang, C.; Deik, D.G.X.; Li, D.; Zhang, H.; Liu, Y. Planning with Multi-Constraints via Collaborative Language Agents. arXiv 2024, arXiv:cs.AI/2405.16510. [Google Scholar]
- Hao, S.; Gu, Y.; Ma, H.; Hong, J.J.; Wang, Z.; Wang, D.Z.; Hu, Z. Reasoning with Language Model is Planning with World Model. arXiv 2023, arXiv:cs.CL/2305.14992. [Google Scholar]
- Putta, P.; Mills, E.; Garg, N.; Motwani, S.; Finn, C.; Garg, D.; Rafailov, R. Agent Q: Advanced Reasoning and Learning for Autonomous AI Agents. arXiv 2024, arXiv:2408.07199. [Google Scholar]
- Light, J.; Wu, Y.; Sun, Y.; Yu, W.; Liu, Y.; Zhao, X.; Hu, Z.; Chen, H.; Cheng, W. Scattered Forest Search: Smarter Code Space Exploration with LLMs. arXiv 2024, arXiv:cs.SE/2411.05010. [Google Scholar]
- Wang, E.; Cassano, F.; Wu, C.; Bai, Y.; Song, W.; Nath, V.; Han, Z.; Hendryx, S.; Yue, S.; Zhang, H. Planning In Natural Language Improves LLM Search For Code Generation. arXiv 2024, arXiv:cs.LG/2409.03733. [Google Scholar]
- Gu, Y.; Zheng, B.; Gou, B.; Zhang, K.; Chang, C.; Srivastava, S.; Xie, Y.; Qi, P.; Sun, H.; Su, Y. Is Your LLM Secretly a World Model of the Internet? Model-Based Planning for Web Agents. arXiv 2024, arXiv:cs.AI/2411.06559. [Google Scholar]
- Chae, H.; Kim, N.; Iunn Ong, K.T.; Gwak, M.; Song, G.; Kim, J.; Kim, S.; Lee, D.; Yeo, J. Web Agents with World Models: Learning and Leveraging Environment Dynamics in Web Navigation. arXiv 2024, arXiv:cs.CL/2410.13232. [Google Scholar]
- Chen, Y.; Pesaranghader, A.; Sadhu, T.; Yi, D.H. Can We Rely on LLM Agents to Draft Long-Horizon Plans? Let’s Take TravelPlanner as an Example. arXiv 2024, arXiv:2408.06318. [Google Scholar]
- Xiong, S.; Payani, A.; Yang, Y.; Fekri, F. Deliberate Reasoning for LLMs as Structure-aware Planning with Accurate World Model. arXiv 2024, arXiv:cs.CL/2410.03136. [Google Scholar]
- Paul, S.K. Continually Learning Planning Agent for Large Environments guided by LLMs. In Proceedings of the 2024 IEEE Conference on Artificial Intelligence (CAI), Singapore, 25–27 June 2024; pp. 377–382. [Google Scholar] [CrossRef]
- Peng, B.; Li, C.; He, P.; Galley, M.; Gao, J. Instruction Tuning with GPT-4. arXiv 2023, arXiv:cs.CL/2304.03277. [Google Scholar]
- Ghosh, S.; Evuru, C.K.R.; Kumar, S.; S, R.; Aneja, D.; Jin, Z.; Duraiswami, R.; Manocha, D. A Closer Look at the Limitations of Instruction Tuning. arXiv 2024, arXiv:cs.CL/2402.05119. [Google Scholar]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O.M. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Schwenzer, M.; Ay, M.; Bergs, T.; Abel, D. Review on model predictive control: An engineering perspective. Int. J. Adv. Manuf. Technol. 2021, 117, 1327–1349. [Google Scholar] [CrossRef]
- Shi, H.; Zuo, L.; Wang, S.; Yuan, Y.; Su, C.; Li, P. Robust predictive fault-tolerant switching control for discrete linear systems with actuator random failures. Comput. Chem. Eng. 2024, 181, 108554. [Google Scholar] [CrossRef]
- Holtzman, A.; Buys, J.; Du, L.; Forbes, M.; Choi, Y. The Curious Case of Neural Text Degeneration. arXiv 2020, arXiv:cs.CL/1904.09751. [Google Scholar]
- Qin, Y.; Liang, S.; Ye, Y.; Zhu, K.; Yan, L.; Lu, Y.; Lin, Y.; Cong, X.; Tang, X.; Qian, B.; et al. ToolLLM: Facilitating Large Language Models to Master 16000+ Real-world APIs. arXiv 2023, arXiv:2307.16789. [Google Scholar]
- Guo, P.F.; Chen, Y.H.; Tsai, Y.D.; Lin, S.D. Towards Optimizing with Large Language Models. arXiv 2024, arXiv:cs.LG/2310.05204. [Google Scholar]
- Jiang, C.; Shu, X.; Qian, H.; Lu, X.; Zhou, J.; Zhou, A.; Yu, Y. LLMOPT: Learning to Define and Solve General Optimization Problems from Scratch. arXiv 2025, arXiv:cs.AI/2410.13213. [Google Scholar]
- Li, H.; Li, Y.; Tian, A.; Tang, T.; Xu, Z.; Chen, X.; Hu, N.; Dong, W.; Li, Q.; Chen, L. A Survey on Large Language Model Acceleration based on KV Cache Management. arXiv 2025, arXiv:cs.AI/2412.19442. [Google Scholar]
- Hafez, A.; Akhormeh, A.N.; Hegazy, A.; Alanwar, A. Safe LLM-Controlled Robots with Formal Guarantees via Reachability Analysis. arXiv 2025, arXiv:cs.RO/2503.03911. [Google Scholar]
- Wu, Y.; Xiong, Z.; Hu, Y.; Iyengar, S.S.; Jiang, N.; Bera, A.; Tan, L.; Jagannathan, S. SELP: Generating Safe and Efficient Task Plans for Robot Agents with Large Language Models. arXiv 2025, arXiv:cs.RO/2409.19471. [Google Scholar]
- Hua, W.; Yang, X.; Jin, M.; Li, Z.; Cheng, W.; Tang, R.; Zhang, Y. TrustAgent: Towards Safe and Trustworthy LLM-based Agents. arXiv 2024, arXiv:cs.CL/2402.01586. [Google Scholar]
- Zheng, H.S.; Mishra, S.; Zhang, H.; Chen, X.; Chen, M.; Nova, A.; Hou, L.; Cheng, H.T.; Le, Q.V.; Zhou, D. Natural Plan: Benchmarking LLMs on Natural Language Planning. arXiv 2025, arXiv:2406.04520. [Google Scholar]


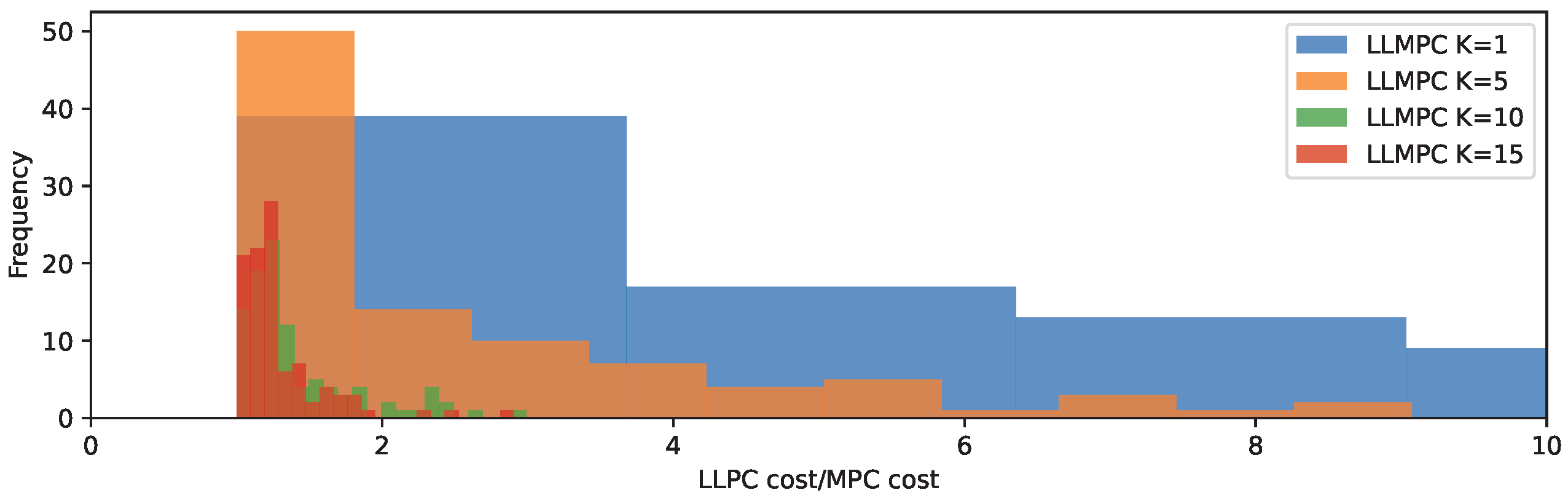

| Ratio LLMPC cost/MPC cost | 8.21 | 2.89 | 1.42 | 1.30 |
| GPT-4o | LLMPC | LLMPC | LLMPC | MCTS | MCTS | |
|---|---|---|---|---|---|---|
| Success Rate | 0.145 | 0.363 | 0.413 | 0.446 | 0.425 | 0.45 |
| GPT-4o | LLMPC | LLMPC | LLMPC | LLMPC | LLMPC | MCTS | MCTS | |
|---|---|---|---|---|---|---|---|---|
| Success Rate | 0.525 | 0.555 | 0.565 | 0.595 | 0.56 | 0.67 | 0.603 | 0.605 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maher, G. LLMPC: Large Language Model Predictive Control. Computers 2025, 14, 104. https://doi.org/10.3390/computers14030104
Maher G. LLMPC: Large Language Model Predictive Control. Computers. 2025; 14(3):104. https://doi.org/10.3390/computers14030104
Chicago/Turabian StyleMaher, Gabriel. 2025. "LLMPC: Large Language Model Predictive Control" Computers 14, no. 3: 104. https://doi.org/10.3390/computers14030104
APA StyleMaher, G. (2025). LLMPC: Large Language Model Predictive Control. Computers, 14(3), 104. https://doi.org/10.3390/computers14030104








