Abstract
Nowadays, quantum computing is developing at an unprecedented speed. This will pose a serious threat to the security of widely used public-key cryptosystems in the near future. Scientists are actively looking for ways to protect against quantum attacks; however, existing solutions still face different limitations in terms of efficiency and practicality. This paper explores hash-based digital signature schemes, post-quantum vector commitments and Verkle tree-based approaches for protecting against quantum attacks. The paper proposes an improved approach to generating digital signatures based on Verkle trees using lattice based vector commitments. In order to further reduce the memory space, the paper offers the methodology of integrating a post-quantum secure pseudo-random number generator into the scheme. Finally, the paper proposes an efficient post-quantum digital signature scheme based on Verkle trees, which minimizes memory requirements and reduces the signature size. Our proposed framework has strong resistance to quantum attacks, as well as high speed and efficiency. This study is an important contribution to the elaboration of post-quantum cryptosystems, which lays the foundation for developing secure and practical digital signature systems in the face of emerging quantum threats.
1. Introduction
The rise of quantum computers presents a significant threat to current cybersecurity infrastructures. As quantum technology advances, existing public-key cryptosystems, which are widely used for securing data in both commercial and non-commercial applications, will become vulnerable. The computational power of quantum computers is expected to easily outpace classical systems, making current encryption methods ineffective. Consequently, there is an urgent need to develop cryptographic systems that can withstand quantum attacks. Although several alternative cryptographic solutions have emerged, their practical implementation is often limited due to security and efficiency concerns. This highlights the critical importance of post-quantum cryptography (PQC), which aims to create cryptographic systems that can secure data even in the presence of quantum computers—often referred to as quantum encryption.
Recent advancements in quantum computing have accelerated the need for robust post-quantum cryptographic solutions. While Shor’s and Grover’s algorithms remain the primary threats to classical cryptosystems, emerging research highlights the importance of integrating advanced techniques from other domains, such as image privacy and nonlinear dynamics, to enhance cryptographic resilience. For instance, the study [1] demonstrates how nonlinear dynamics can improve data security, offering insights that can be adapted to post-quantum digital signatures.
Quantum computers are expected to revolutionize computing by performing calculations which are orders of magnitude faster than classical computers. For instance, tasks that would take years on classical machines could potentially be completed in a few hours using quantum computing principles. This poses a significant risk to cryptographic methods that rely on the computational difficulty of certain mathematical problems—such as integer factorization used in RSA algorithms. To counteract these threats, we aim to develop a cryptosystem that integrates both classical and post-quantum encryption techniques.
While the field of quantum computing is progressing rapidly, current quantum computers remain vulnerable to attacks. Despite the advancements in quantum technology, cryptographic systems based on classical methods, such as RSA, remain widespread and foundational to security practices today [2,3]. However, these systems will eventually be outdated in the face of quantum computational capabilities. Although various alternatives to RSA have been proposed, their adoption has been slow due to concerns about their security and efficiency. One promising alternative lies in hash-based signature schemes, which rely on the robustness of hash functions and their resistance to collisions.
The advent of quantum computing will make traditional asymmetric algorithms like RSA obsolete, making it imperative to develop and test post-quantum cryptosystems [4,5]. One potential solution is the development of digital signature systems based on cryptographic hash functions. These systems offer a high level of security through hash algorithms that have very low collision rates. This makes hash-based signature schemes a strong candidate for replacing RSA in a post-quantum world.
In parallel, the field of post-quantum cryptography (PQC) has seen significant progress, particularly in lattice-based and hash-based schemes. NIST’s recent standardization of CRYSTALS-Dilithium and Falcon as post-quantum digital signatures underscores the importance of lattice-based approaches [6,7], while SPHINCS+ provides a hash-based alternative with strong security guarantees [8]. However, challenges such as large signature sizes, inefficient verification, and the need for scalable key management persist, especially in resource-constrained environments like IoT and blockchain.
Our approach to addressing these concerns involves a new post-quantum cryptosystem that incorporates a pseudo-random number generator (PRNG), which uses quantum random number generator (QRNG) as a seed. This system uses one-way functions to create secure one-time signature schemes and employs a tree structure to efficiently verify multiple keys. Our PRNG is based on the NIST-standard CTR_DRBG generator, known for its efficiency and speed, as well as its resistance to quantum attacks. We use a hybrid quantum random approach, ensuring high security while eliminating the need to store a large number of key pairs by preserving the original values generated from the PRNG.
Pseudo-random number generators are widely used in cryptography and require a true random seed for applications that demand high security [9]. In our system, we prioritize the use of quantum true random number generators over classical TRNGs when genuine unpredictability is essential. This guarantees the cryptographic strength of our system in environments where randomness is essential [10,11,12].
QRNGs rely on the inherent randomness of quantum events, particularly the randomness of photons, providing a much higher level of security. These QRNGs are efficient, fast, and offer scalability, making them ideal for the needs of post-quantum cryptosystems [13,14,15].
In conclusion, we present a post-quantum cryptosystem that combines quantum random number generation with efficient cryptographic structures. Our system not only offers robust resistance to quantum attacks, but also provides high efficiency and scalability. Through the integration of Verkle trees and lattice-based vector commitments, we enhance the security of digital signature schemes, optimizing verification methods and minimizing storage requirements. This research also explores the potential of lattice-based vector bindings for post-quantum applications. Ultimately, our proposed system is highly suitable for deployment in blockchain networks, IoT devices, mobile applications, and other environments with limited resources.
2. Hash-Based Signature Schemes
2.1. Hash-Based One-Time Signature Schemes
To safeguard against quantum threats in the post-quantum era, hash-based single signature schemes offer a promising solution due to their robust security features. This paper explores the performance of such signature schemes that rely on cryptographic hash functions. These schemes typically consist of three key phases: key generation, signature creation, and signature verification. The process begins with key generation, which involves generating a random secret key. This key is then used to derive the private key for the signature scheme. Once the private key is established, the signature is created and applied to the message. Lastly, the recipient verifies the signature by employing the same hash function used to create the signature, ensuring the authenticity and integrity of the message.
For randomized algorithms and cryptographic protocols, computers are assumed to have access to a continuous stream of truly random bits. These bits can be viewed as an unbiased and independent series of coin tosses. In practical applications, a “random source” is utilized to produce a sequence that can generate these bits. One example of such a signature scheme is the Lamport–Diffie one-time signature (L-DOTS) scheme [16], which leverages the collision resistance property of cryptographic hash functions for its security.
In computational settings, it is essential to ensure that these random bits remain unpredictable and uncorrelated. This randomness is foundational for the security of many cryptographic protocols, including those used in post-quantum cryptographic systems. By employing cryptographic hash functions, which are designed to resist collisions and preimages, hash-based signature schemes can effectively provide secure, quantum-resistant alternatives to traditional signature methods.
In the Lamport–Diffie one-time signature scheme, the security parameter n is an integer. L-DOTS utilizes a cryptographic hash function and a one-way function to generate an L-DOTS key pair [17]. The Lamport–Diffie one-time signature key is a randomly chosen string of bits of length, following the Formula (1).
Verification key is :
To calculate the key, the one-way function is used. Formula (3):
The Lamport–Diffie signature key generation requires evaluations of This signature uses -bit strings chosen as the message digest function , which are bytes long. In case of L-DOTS signature generation, document is signed using L-DOTS with signature key . Let be the message digest of the document , where is a cryptographic hash function that produces a fixed-length output from the variable-length input . Each is a bit or a small set of bits derived from the digest of . The function applies hash algorithm to the input document to generate this sequence.
is the message digest of . The L-DOTS signature is
To sign the message, bit strings are used, chosen as message digest function , which is bytes long. There is no need of evaluation of . The number of cryptographic functions performed by processor is calculated in hashes per second [18]. is the -th bit string of signature, if the -th bit in is , and otherwise.
When using L-DOTS verification, the verifier calculates the message digest if we have to verify the signature of After that, it is decided if it is true or not:
Hash-based one-time signature schemes operate through three primary phases: key generation, signature creation, and verification. Initially, a random secret key is generated, which is then utilized to create a private key for the signature scheme. This private key is applied to produce a signature on the message. To confirm the authenticity of the signature, the recipient uses the same hash function as the sender and checks the received message against the signature. If both match, the signature is deemed valid, indicating the message’s integrity and authenticity [19,20].
The Lamport–Diffie one-time signature (L-DOTS) scheme, while secure, is typically large in size, requiring bits for a security level of n bits. However, it offers efficient key and signature generation, making it suitable for scenarios where quick signatures are required. To further optimize performance and reduce the number of signatures, the Winternitz one-time signature (W-OTS) method is often employed. The size of a W-OTS signature is roughly bits, where is the bit length of the hash value to be signed, n is the output length of the hash function, and is the Winternitz parameter. W-OTS enhances efficiency by allowing multiple bits to be signed with a single one-time signature key, streamlining the signing process and reducing the number of required hash operations to approximately . However, a challenge of hash-based single signature schemes is the limited number of unique key combinations available, as each signature requires its own distinct secret key. To overcome this limitation, Ralph Merkle introduced a new data structure that provides notable improvements over traditional Merkle trees in terms of scalability and performance. Specifically, Merkle’s use of a full binary hash tree significantly reduces the number of unique one-time verification keys required for the root public key, improving both efficiency and scalability. This approach enhances the overall practicality of hash-based signature systems, making them more adaptable to large-scale applications.
2.2. Merkle Digital Signature Scheme
Merkle tree-based digital signature schemes provide a solution to the inefficiency of traditional schemes that require storing a large number of digests. This method uses a binary tree structure, where the root serves as a single public key to replace multiple verification keys. It achieves this by utilizing a cryptographic hash function alongside a Lamport or Winternitz one-time signature scheme.
The customizable Merkle signature scheme (MSS) is a versatile and flexible cryptographic framework for creating digital signatures. This scheme offers several advantages that make it a strong option for various applications.
A Merkle tree is a secure cryptographic system in which key pairs are generated by the signer. Here, is the verification key and is the signing key. The internal nodes of the Merkle tree are computed using a cryptographic hash function applied to the left and right child nodes. The public key of the MSS corresponds to the root of the tree, and the secret key includes a one-time signature key of length [21].
Here is shown an example of a Merkle tree with height of . See Figure 1.
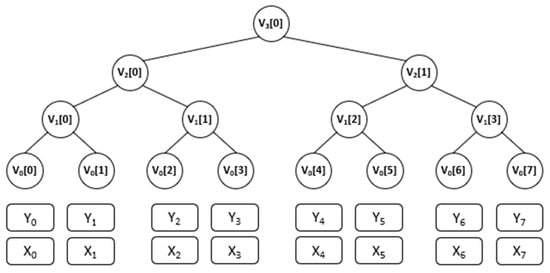
Figure 1.
Merkle tree height, .
To generate a key pair of the Merkle signature scheme, it is necessary to compute unique key pairs and evaluate hash functions. The MSS uses unique signing keys to generate a signature. To sign a message , a unique n-bit hash value is computed. A one-time signature is generated by the signer using the -th one-time signature key , where is in the range from to . This one-time signature is concatenated with the corresponding one-time verification key to form a Merkle signature. Merkle’s signature verification process involves two steps. The signer appends the index and the authentication path to the verification key to prove the authenticity of , and the verifier constructs a path from the leaf g() to the root of the Merkle tree using this index and the authentication path. The authorization path node is a sibling node of height , and exactly this is the path from the leaf g() to the root. To validate the one-time signature, the verifier uses the one-time signature scheme verification method using the one-time verification key . The verifier evaluates the validity of the one-time verification key in the second stage of verification. While Merkle trees can be constructed efficiently in time, their large proof sizes can present a significant challenge due to their breadth. The resulting Merkle proofs can consume substantial local storage, leading to increased storage costs and potential strain.
3. Verkle Tree
Verkle tree is an upgraded Merkle tree that needs smaller verifications while offering increased efficiency. Verkle trees offer significant advantages over traditional Merkle trees, especially in terms of verification efficiency and storage optimization. Their compact proof sizes and ability to verify multiple items simultaneously make them a significant component for post-quantum cryptography, enabling cost reduction, enhanced security, and minimized data redundancy [22].
Instead of employing cryptographic hash algorithms, the Verkle tree technique uses vector commitments to create a Merkle tree. In order to construct the tree, k pieces are selected, then files are used to compute a Verkle tree. Then, it checks if the membership of each file in a subset provides proof of a concrete binding position () with respect to the vector commitment () by calculating it for each subset. Up until the root commitment is determined, it computes the vector commitments across the tree [23].
This process is illustrated in Figure 2, where nine files are divided into subsets of size . Vector commitments (s) are calculated for each subset, resulting in , , and . Membership proofs (, , and ) are then generated for these s with respect to a higher-level commitment . Finally, is constructed based on these commitments, leading to the root commitment, which serves as the digest of the Verkle tree.
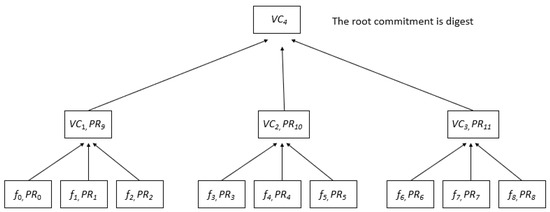
Figure 2.
Verkle tree when .
Verkle trees represent a significant improvement over traditional Merkle trees in terms of proof efficiency. While Merkle trees require proofs that include every sibling node along a verification path, Verkle trees take advantage of a more efficient approach by using “batching nodes”. This innovation enables the parallel verification of multiple paths, significantly reducing the amount of data required to prove a particular value. As a result, Verkle trees offer faster and more efficient verification processes.
A key differentiator of Verkle trees is their use of vector commitments, which replace the traditional reliance on cryptographic hash functions. By leveraging vector commitments, Verkle trees can achieve a broader tree width, meaning that fewer nodes need to be traversed for verification. Additionally, the use of these commitments allows for a more streamlined verification process that only requires the necessary route and minimal additional information. This reduces the overall size of the proofs and enhances their efficiency.
The improvements in the reduced data requirements for proof generation make Verkle trees a powerful alternative to Merkle trees. These advantages position Verkle trees as a highly effective solution for a range of data management tasks and cryptographic applications, such as blockchain systems, where fast and efficient verification is critical. Their ability to handle large datasets with minimal overhead also opens up potential for wider adoption in distributed systems and cryptographic protocols, where performance and scalability are key concerns. Table 1 reflects efficiency comparison Merkle vs. Verkle constructions.

Table 1.
Merkle vs. Verkle.
While Verkle trees offer significant advantages in storage and verification efficiency, their scalability is a critical concern for large-scale applications. Below, we discuss the limitations and performance trade-offs as the tree grows larger:
The maximum tree size is determined by the arity and height , with the number of leaves given by . For and , the tree can support up to ( trillion) leaves, which is sufficient for most practical applications. However, increasing beyond 10 leads to exponential growth in proof size and verification time, making it impractical for extremely large datasets.
Proof size scales as , where is the number of leaves. For , this results in a reduction compared to Merkle trees ). Verification time also scales as , but the constant factor increases with due to the complexity of vector commitment proofs. While Verkle trees reduce storage requirements, the memory overhead for maintaining intermediate nodes grows linearly with , which can become a bottleneck for very large trees.
In order to handle the scalability challenges, we group multiple proofs into a single vector commitment, we reduce the verification overhead for large trees. that are no longer needed can be pruned to free up memory and improve performance. Verification can be parallelized across multiple cores or GPUs, significantly reducing latency for large-scale applications.
While Verkle trees are highly efficient for moderate-sized trees, their scalability is limited by the exponential growth of proof size and verification time as the tree height increases. The proposed scheme in Section 6 addresses these challenges through batch verification, dynamic pruning, and parallelization, making it suitable for applications with up to leaves. For larger datasets, a hybrid approach combining Verkle trees with other data structures may be necessary.
4. Vector Commitments
Vector commitments () provide a method for committing to a vector, which is an ordered collection of values. The primary utility of vector commitments is to enable the commitment to a set of data while allowing for efficient proofs of specific elements within that set. For example, to demonstrate that a particular value, , is the -th element of the committed vector, the commitment can be opened at specific indices to reveal the corresponding value. This feature is vital for ensuring position binding, as it guarantees that an adversary cannot open a commitment to two different values at the same position within the vector.
A key design consideration for vector commitments is that the length of the commitment string and the size of each proof should remain constant and independent of the vector’s length. This ensures that the cost of generating and verifying commitments does not increase significantly as the size of the vector grows, which is important for scalability [24].
In addition to position binding, vector commitments may also need to satisfy a concealing property. This property ensures that the values and order of the committed elements remain hidden from any observer. The concealing property is essential in many cryptographic applications, such as privacy-preserving protocols. Fortunately, the implementation of this property does not severely impact the performance of vector commitments, as the computational overhead is relatively low compared to the benefits it provides in terms of confidentiality.
Another crucial aspect of vector commitments is their ability to be updated efficiently. There are two primary methods for updating a commitment and its corresponding proof. The first method involves directly modifying the commitment by changing the -th element from to , and generating a new commitment, denoted as . This method ensures that the new commitment reflects the updated data. The second method involves updating the proof itself, so it remains valid with respect to the new commitment. This approach allows for adjustments without needing to recompute the entire commitment structure.
Vector commitments rely on a variety of techniques for committing to and validating data, which involve manipulating the message space, commitment space, and proof space. Updating the commitment and proofs should be performed in a way that maintains efficiency, with results that are comparable to those obtained from generating the commitments and proofs from scratch. Techniques such as RSA and Diffie–Hellman assumptions have traditionally been employed to construct compact and efficient vector commitments [25]. However, with the rise of quantum computing, the security of RSA-based schemes is now at risk, as quantum computers can potentially break the underlying cryptographic assumptions.
To address this emerging challenge, we propose an enhancement to existing vector commitment schemes by shifting to post-quantum cryptographic techniques. In particular, we focus on replacing RSA-based assumptions with lattice-based cryptography, which is believed to be resistant to quantum attacks. Our proposed vector commitments based on lattice cryptography aim to provide both strong security guarantees and high efficiency, ensuring that these commitments remain secure and scalable even in the face of future quantum threats. These developments are particularly significant in the context of Verkle tree-based signature systems, which also benefit from post-quantum security mechanisms to safeguard the integrity and confidentiality of digital signatures in the quantum era.
A vector commitment scheme consists of a message space , a commitment space , and a proof space (which may depend on setup parameters). It includes a set of algorithms with the following components:
- 1.
- Setup (): this algorithm outputs the public committer parameters and the verifier parameters .
- 2.
- Commit (): this algorithm generates a commitment in and a committer state st.
- 3.
- Open (): this algorithm produces a proof pi for the -th entry in the committed message associated with the state .
- 4.
- Verify (): the verifier algorithm checks whether the proof is valid, either accepting or rejecting.
The scheme must satisfy the following correctness condition: for any that is polynomial in the security parameter, a message m in , and an index in , given from Setup , from Commit (), and pi from Open (), the Verify () must accept with probability , where is the security parameter and the probability is taken over all random variables involved.
- Additionally, the scheme is considered updatable if it includes the following set of algorithms:
- 1.
- PrepareUpdates (): this algorithm produces a commitment update , a proof update , and a state update for modifying the -th entry of the committed message vector to .
- 2.
- UpdateC (): this algorithm deterministically updates the commitment to .
- 3.
- UpdateP (): this algorithm deterministically updates the proof to .
- 4.
- UpdateS (): this algorithm deterministically updates the committer state to .
Lattice-Based Vector Commitments
The vector commitment () method allows for the efficient management of ordered sets and provides a straightforward way to present specific data points. One of the most significant advantages of is their ability to update both proofs and commitments without the need to access or recompute the entire vector. This makes highly beneficial for cryptographic applications such as cryptographic accumulators, verifiable external databases, and cryptocurrencies. These applications depend on to enable rapid, on-the-fly updates and maintain the public verifiability of stored data. This capability is particularly useful for dynamic, real-time systems, including cryptographic accumulators and pseudonymous credential systems.
Post-quantum vector commitment techniques remain an area of ongoing research, especially those that can provide robust security against the computational power of quantum attacks. Although it is feasible to adopt post-quantum hash function-based Merkle trees for some applications, one of the main drawbacks of such systems is the high computational cost associated with updating them [26]. In contrast, the use of a Merkle tree-like structure based on the short integer solution (SIS) lattice problem offers a solution that provides statelessly updatable schemes. These lattice-based structures are not only more secure, but also more compact and efficient than traditional stateless renewable systems, which rely on private key setups and a central authority for the management of public parameters [27].
In this scheme, messages are represented as vectors drawn from a set , where is a contiguous range of integers within , and the maximum magnitude .
The construction makes use of a chosen gadget matrix G ∈ and an injective, efficiently computable invertible difference encoding. This encoding maps each index i in to a matrix in , ensuring that for any distinct indices i ≠ i’ in [d + 1], the matrix product × is invertible. If is prime, we can simplify by choosing where is a scaled identity matrix, since we will later require .
For appropriate security parameters (functions of the security parameter ), we define the following differentially updatable vector commitment scheme:
- 1.
- Setup (, ):
- ○
- Randomly choose a matrix in and compute the trapdoor matrix via the function TrapGen (, ).
- ○
- Let . For each index in , construct:
- ○
- Randomly choose vectors = [, , …, ] in , where each is in .
- ○
- For each in , set in , and for each , sample:
Ensuring that is invertible as required by the SamplePre function. The matrix is short, and the equation holds.
- 2.
- Commitment Output: the committer parameters are:and the verifier parameters are:
- 3.
- Commit (): the commitment is computed as:
And the state is simply .
- 4.
- Opening: to open a specific entry, output the proof for the -th message entry as:
- 5.
- Verification: the verifier checks the proof by verifying if the following equation holds:
If the equation holds, the proof is accepted; otherwise, it is rejected.
While these SIS-based vector commitment scheme work well for smaller dimensions, they become inefficient as the dimensions increase. The quadratic and linear growth of both the committer and verifier parameters as the dimension expands makes these schemes less practical for higher-dimensional use cases. To address this challenge, a general -ary tree construction can be applied to extend VC schemes from dimension to dimension . However, this extension comes with a significant trade-off, as it sacrifices some of the desirable properties of stateless updates and the ability to combine both commitments and proofs efficiently [28].
Building on these limitations, we propose to use an approach that integrates the SIS-based vector commitment scheme into a customized tree-like structure. This novel transformation maintains both the combinability of commitments and proofs as well as stateless updates, while introducing only a modest increase in object sizes and strengthening the SIS security assumptions to support larger dimensions. This design offers a more scalable and efficient solution for post-quantum cryptographic systems.
In traditional tree-based vector commitment schemes, a proof must include information about all sibling nodes along the root-to-leaf path, leading to a proof size of . This size is derived from the lengths of the proofs along the path and the sizes of the integers within them. Our SIS-based VC approach, however, leverages a key advantage: proofs do not require sibling information. Consequently, the proof size scales as , resulting in a more efficient proof size compared to traditional methods.
While this design requires a private setup, it offers quantitative improvements for any magnitude of (dimension) and tree height . By selecting a moderately large and a smaller , we can achieve an asymptotic proof size equivalent to the generic tree transformation for VCs, while still maintaining the desirable properties of combinability and stateless updates.
The proposed construction relies on preimage sampling and SIS-based trapdoors, with the “gadget” matrix playing a crucial role. The matrix dimensions is size integer w, and is defined as , where is the identity matrix and denotes the Kronecker product. While this specific formula is used for illustration, any matrix satisfying certain characteristics can be utilized. Furthermore, a deterministic function acts as an inversion operation with specific properties. This function is essential for the underlying mechanisms of the construction.
The gadget matrix has dimensions n × w and elements from the set . To calculate the inverse matrix (operation ) the restriction of the size is used for the matrix . Message vectors are chosen from a set , where each member of is a w-dimensional vector taken from a subset . This subset is determined by the values - and , which themselves are integers. The integer , chosen earlier, is used in combination with algorithms developed for earlier constructions.
There were defined following setup algorithms:
Taking input parameters commitment parameter , a matrix , and a vector , the algorithm generates output data.
The algorithm proceeds as follows:
The matrix is initialized as the same matrix used in the previous construction.
The matrix is initialized as an size identity matrix.
This algorithm generates the necessary setup parameters for the construction.
For each from to :
Within each iteration of the algorithm, the inverse of - and the matrix are used to generate the matrix . This newly generated is then multiplied by the previous to obtain the updated matrix . Furthermore, blocks within can be calculated separately using the matrix and a specific value , where is an element of the set [] ( Please see the Algorithm 1 below:
| Algorithm 1. Commitment Algorithm: |
| For each : The method takes as input a message vector and a commitment parameter . It computes the value by applying the inverse of . The outputs include Open Algorithm: algorithm operates identically to the . For each : Given the input values and is calculated. is used to create a sub-vector. The value is determined using the Open algorithm with specific inputs. From the previous step the Commit method is utilized to obtain a commitment value . is generated using the Open algorithm with specific inputs. The final output. Verify Algorithm: value are separated. If certain verification conditions are not met, the operation is rejected. The procedure is rejected if the verification from the - fails. Otherwise, it is accepted. Update Algorithm: Update algorithms can be derived from the linearity of commitment operations. |
5. Generating a Unique Key Pair Using a PRNG
In the Merkle signature scheme (MSS), the private keys consist of one-time signature keys, which can lead to significant data storage requirements, making it impractical for many real-world applications. To mitigate this issue, a deterministic pseudo-random number generator (PRNG) can be employed. By saving only the seed of the PRNG, we can generate the necessary one-time signature keys on-demand, eliminating the need to store all of them explicitly. This method requires generating the MSS public key twice—once during the signing process and again when creating the one-time key, as discussed in [29,30].
Similarly, the Verkle tree, which is a specialized type of Merkle tree designed for the efficient storage and retrieval of key–value pairs, also utilizes a deterministic PRNG. The PRNG seed is used for key generation, much like in MSS. In a Verkle tree, the leaf nodes store values linked to key prefixes, with each node corresponding to a specific prefix. This structure facilitates efficient retrieval of values based on the key prefix.
Both the Merkle signature scheme (MSS) and the Verkle tree benefit from using a PRNG with a seed. This allows for the efficient management of keys and values, reducing storage requirements and enabling faster operations for key–value storage and retrieval. By leveraging this technique, both schemes achieve a more efficient and scalable approach for handling large sets of data, which is crucial in modern cryptographic systems.
Let us assume that PRNG is a cryptographically secure pseudorandom number generator that takes an -bit seed, denoted as as input. This PRNG then outputs two values: : an updated -bit seed and RAND: a random number of n bits.
Here is a breakdown of the key pair generation process within the scheme, incorporating the PRNG: Initial -bit seed is selected, uniformly at random. This seed is the starting point for our key generation process. To generate one-time signature keys, the scheme leverages a sequence of seeds denoted as . The formula for generating the sequence of seeds is:
In result, based on the j-th one-time signature key is determined. Let us say, is the -th signature key in the , than produces signature key’s strings of length , bits.
The seed is updated each time the PRNG is called. This shows that it is enough to know to define the signature key . To generate a one-time signature key , a new seed is defined after computing . This new seed is generated using the PRNG.
Initially, the secret key is represented by , an n-bit seed. During the generation of a signature key , a new seed is defined. This new seed effectively replaces the previous seed, ensuring that each signature key is associated with a unique seed. Unlike the traditional approach, where the signature key is generated on-the-fly, this method requires pre-computing the unique signature key before generating the signature. Once the signature key is determined, the seed is updated for subsequent signature generation.
The iterative seed update method, similar to the approach used in the Merkle signature scheme (MSS), ensures that only the current seed is required to compute each key or value in the Verkle tree. This is a critical aspect for efficient management of key–value pairs. In the Verkle tree structure, leaf nodes store individual key–value pairs, while internal hash nodes combine their child nodes to maintain the integrity of the data. This hierarchical structure enables fast and secure verification and storage of the key–value pairs. However, in an encrypted Verkle tree, the private key typically contains cryptographic secrets needed for the system’s operation, including signature keys for verifying changes and encryption keys for decrypting the tree’s contents.
One of the primary challenges in using Verkle trees is the significant memory and processing power required to store and manage the keys for signing and verification. To overcome this, we propose a solution that uses a pseudo-random number generator (PRNG). By generating keys only when necessary—specifically during key creation and verification—we can minimize storage needs. This approach is particularly effective for one-time signatures, where each key is used only once and does not need to be stored permanently.
The difficulty of maintaining a large number of signature and verification keys is exacerbated in systems with stringent security demands or limited resources. Therefore, minimizing the need for continuous key storage is essential. Our approach leverages a PRNG to dynamically generate keys when needed, significantly reducing the storage burden. By calculating the keys on-demand during key creation and verification, we avoid permanent storage, which alleviates the pressure on system resources.
The proposed method relies on the PRNG in two critical steps: during key generation and verification. In the key generation step, the PRNG produces a unique key pair only when required, optimizing memory usage by ensuring that calculations are performed only when needed. During the verification stage, the PRNG regenerates the same key pair, eliminating the need to store the key permanently. This approach improves memory efficiency and resource utilization while ensuring that keys are only present in memory when necessary.
To ensure the unpredictability of the keys, the PRNG must be initialized with a high-entropy random seed. The randomness of this seed directly influences the quality of the keys generated by the PRNG. To further enhance security, quantum random number generators (QRNGs) can be utilized, as they generate true random numbers based on quantum mechanics. These numbers offer superior unpredictability compared to classical methods, making them highly suitable for cryptographic applications such as key generation. QRNGs provide a higher level of randomness, which strengthens the overall security of the key generation process. Quantum seeds provide true randomness based on quantum mechanical phenomena, ensuring unpredictability even against quantum adversaries. Unlike classical seeds, which rely on deterministic algorithms, quantum seeds eliminate patterns or biases, enhancing security. While QRNGs like ID Quantique’s Quantis are widely available, their integration requires minimal hardware support, ensuring practical deployment in systems like IoT and blockchain without significant overhead.
In the context of the Verkle tree, the PRNG is initialized twice: once during the key generation phase to produce the initial key pair, and again during the signature process to generate the key pair used for signing the message. It is important to note that current Verkle tree commitments could be vulnerable to attacks from quantum computers. To address this concern, our aim is to replace these commitments with alternatives that are based on post-quantum cryptographic assumptions, thereby making them resistant to quantum-based attacks. This shift to post-quantum solutions will ensure the continued robustness and security of the Verkle tree system in the face of evolving threats from quantum computing.
5.1. CTR_DRBG (Counter-Based Deterministic Random Bit Generator)
For a digital signature scheme that must be secure in a post-quantum setting, it is crucial to choose an appropriate pseudo-random number generator (PRNG). Based on our research, we have selected CTR_DRBG (counter-based deterministic random bit generator), which is a standard NIST known for its efficiency and security, including its resistance to potential quantum computer attacks. CTR_DRBG is a deterministic random bit generator that uses a block cipher, typically AES, in counter mode. It generates random numbers by encrypting a sequence of counter values, ensuring that the output is both unpredictable and secure, provided the underlying block cipher remains secure. The process begins with a seed value, sourced from high-quality entropy, which initializes the internal state, including the block cipher key and the initial counter value. Random numbers are produced by repeatedly encrypting the counter with the block cipher and combining the output with additional internal state data. The counter increments with each operation to guarantee that different random values are generated in each iteration. The random bits are then extracted from the resulting encrypted counter. To ensure long-term security, periodic reseeding is necessary, as it updates the internal state with fresh entropy, thus preventing the output from becoming predictable over time.
CTR_DRBG is widely used in cryptographic key generation, such as for AES encryption keys or session keys in secure communication protocols, like TLS and IPsec. It is also employed in digital signature schemes and for producing nonces in protocols that require unique and unpredictable values. The generator is efficient, benefiting from the speed of AES, especially on hardware with AES acceleration. It is standardized in NIST SP 800-90A, which ensures compatibility across various cryptographic systems. Its straightforward design makes it easy to implement and analyze, relying on well-established block cipher encryption principles. However, the security of CTR_DRBG depends heavily on proper key management. If the block cipher’s key is compromised or reused, the security of the random numbers it generates is also compromised. Another critical vulnerability is counter reuse—if the counter values are used more than once, the output becomes predictable and insecure. Therefore, it is essential to manage both the key and counter correctly to maintain the security of the random numbers. Despite these risks, CTR_DRBG remains an effective and widely adopted method for generating cryptographically secure random bits in a variety of applications, including public key cryptography.
5.2. Generating a One-Time Key Pair Using a New Quantum Random Number Generator
CTR_DRBG is a deterministic random bit generator based on a block cipher, typically AES, operating in counter mode. It works by encrypting a series of counter values to generate random numbers, ensuring that the bits produced are both unpredictable and secure, provided the underlying block cipher remains secure. The process begins with an initial seed, typically sourced from a high-quality entropy provider, to initialize the internal state, which includes the block cipher key and an initial counter value.
To significantly enhance the randomness and eliminate potential weaknesses in the entropy source, it is highly beneficial to incorporate a quantum random number generator (QRNG) for seed generation. QRNGs leverage quantum mechanical phenomena to produce truly random numbers, providing a level of unpredictability far beyond what is achievable with classical pseudo-random methods. By utilizing a QRNG, the seed value becomes exceptionally secure, free from any detectable patterns or predictability that could be exploited by attackers.
Once initialized with a secure seed, the CTR_DRBG generates random bits by repeatedly encrypting the counter with the block cipher. The counter is incremented after each encryption, ensuring that fresh random values are produced with every iteration. The random bits are then extracted from the encrypted counter output. In addition, periodic reseeding is required to maintain the generator’s security, with the internal state being refreshed with new entropy, potentially sourced from a QRNG, to ensure that the randomness remains unpredictable and secure over time.
As mentioned above, CTR_DRBG is widely employed in cryptographic applications, including the generation of AES encryption keys, session keys for secure communication protocols like TLS and IPsec, as well as in digital signature schemes and the creation of nonces in protocols that demand unique and unpredictable values. The generator is efficient, benefiting from the fast speed of AES, particularly when hardware acceleration is available. It is also standardized by NIST in SP 800-90A, ensuring compatibility with a wide range of cryptographic systems. Its simplicity, built upon well-understood cryptographic principles, makes it both easy to implement and thoroughly analyzable.
As we have already mentioned, the security of CTR_DRBG depends on the proper management of the seed and key. Therefore, using a QRNG to supply the initial seed and for periodic reseeding helps further bolster the generator’s security by providing fresh, unpredictable entropy.
In our system, we leverage the cryptographic strength of PRNGs by utilizing the NIST-standard CTR_DRBG. Within this framework, we generate a random number (RAND) and an updated seed from the n-bit seed ). Both the generated random number and the input seed are n bits in length, ensuring a high level of security and reliability in the random number generation process.
Generating a scheme’s key pair using CTR_DRBG is analogous to creating a pseudo-random number generator. We begin by selecting an n-bit seed with uniform randomness. The seeds , are then used to generate one-time signature keys. These seeds are iteratively derived using the next formula:
As a result, the j-th one-time signature key is defined using . Let us say is the j-th signature key in the state. This length , bits signature key’s strings are produced by
Each invocation of CTR_DRBG results in an update of the seed , demonstrating that the signature key can be derived simply from . Furthermore, the computation of defines a new seed for the signature key . The image below illustrates this process of generating a one-time signature key using CTR_DRBG. This process starts with , the secret key, which has a length of n. The seeds determined during the creation of the signature key subsequently replace . This is illustrated on Figure 3.
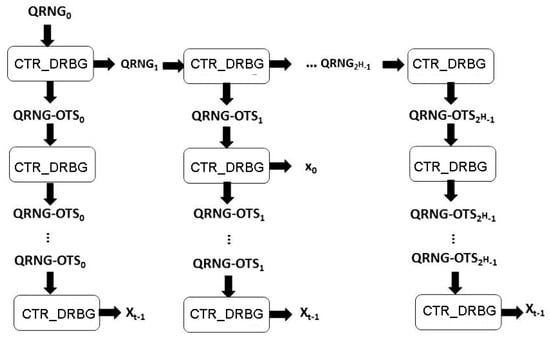
Figure 3.
Generating a one-time signature key using CTR_DRBG.
Our secure method ensures that all signatures generated before termination remain enforceable. The authentication scheme’s secret key can only be used to create one-time signature keys for future signatures. It cannot be used to forge past signatures, making the scheme secure.
6. The Improved Verkle Signature with PRNG and TRNG
In the proposed scheme, all signatures issued prior to termination remain valid and executable. The authentication secret key is exclusively used to generate one-time signature keys for future signatures, ensuring that it cannot be exploited to forge past signatures. This makes the system resilient against retrospective attacks.
In this section, we introduce an improved Verkle signature scheme that leverages the strengths of both pseudo-random number generators (PRNGs) and true random number generators (TRNGs) to enhance security and efficiency. This approach significantly optimizes memory storage compared to our previous work [23].
The foundation of our Verkle signature scheme begins with the generation of a high-entropy random seed using a quantum random number generator (QRNG). The use of a QRNG guarantees a truly unpredictable source of entropy. This seed is then employed to initialize a PRNG, which is responsible for generating high-quality random values needed for key creation. During the key generation phase, the PRNG produces a unique key pair that forms the initial configuration for the Verkle tree.
During the signing process, the PRNG is used again to generate a one-time signature key. This additional step strengthens security by ensuring that each transaction has a unique signature. This generated key is essential for verifying the validity of the signature within the Verkle tree, confirming the authenticity of the keys, and detecting any potential tampering with the data. By combining QRNGs and PRNGs, we create a robust and secure key generation and verification process that optimizes resource usage by generating keys only when needed.
The PRNG’s core is seeded with the high-entropy value from the QRNG, ensuring that the randomness used in the key generation process is of the highest quality. Once initialized, the PRNG produces a distinct key pair for each transaction, ensuring that the generated keys are both secure and unique.
To further enhance security, the PRNG generates a new one-time signature key for each signing operation. This guarantees that each transaction is individually signed, with the unique signature key playing a critical role in the verification process. The system is deemed secure as long as both the public key and the one-time signature can be verified as legitimate.
The diagram below illustrates the integration of QRNG and PRNG within the Verkle tree structure (Figure 4).

Figure 4.
Design of the signature integrating Verkle tree, QRNG and TRNG.
This comprehensive strategy, incorporating both QRNG and PRNG, safeguards the Verkle tree against quantum attacks, ensuring that it utilizes post-quantum security measures.
The integration of QRNGs and PRNGs into the key generation process protects against quantum attacks, ensuring post-quantum security. This dynamic key generation approach enhances overall system efficiency by minimizing the need for extensive storage and computational power. The modular design allows for easy scalability to accommodate larger systems without compromising security. The process of deriving the post-quantum digital signature is illustrated in Figure 5.
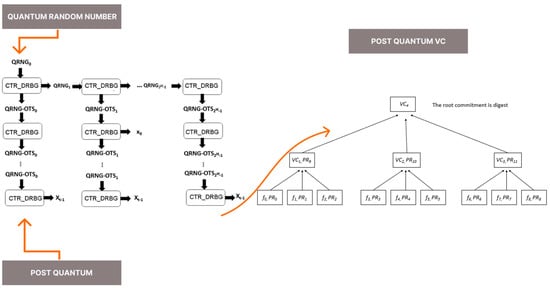
Figure 5.
Verkle signature scheme integrating QRNG and TRNG.
After generating signing keys using a quantum random number generator (QRNG) and a pseudo-random number generator (PRNG), the process of creating and verifying signatures begins. One-time signatures (OTS) are generated by combining multiple one-time public keys into a single root public key. These signatures are then efficiently incorporated into a Verkle tree structure, resulting in a compact root public key.
One-time signature schemes, by design, require a unique key pair for each signature, presenting a significant implementation challenge. The main drawback of such schemes is the high cost of frequent key usage, as they necessitate the storage of a number of digests proportional to the number of signatures. To mitigate this issue, we require a method that allows the storage of a digest of constant size, regardless of the number of files. Verkle trees provide an ideal solution to this problem. By utilizing a binary tree structure for the root, this method substitutes numerous verification keys with a single public key, thereby improving efficiency.
In this framework, the root node serves as a global public key, while the leaf nodes represent individual one-time public keys. When a signature is generated, the system includes the authentication path—a series of hashes that lead from the leaf node to the root node. This authentication path validates the one-time public key used to sign the message and proves its inclusion in the public key tree. During verification, the system recalculates the message hash, checks the one-time signature, and verifies the public key by traversing the authentication path.
Verkle trees, which use vector commitments, offer a significant reduction in proof sizes. This feature makes them particularly advantageous for large-scale post-quantum cryptographic systems, as they enable more compact proof sizes and streamlined verification processes. By grouping multiple signatures into vector commitments, Verkle trees minimize the data that needs to be processed and stored during verification. This approach not only enhances security but also reduces storage requirements and eliminates redundancy.
As the primary commitment the Verkle tree uses a pair of keys generated by the signer with . These parameters are chosen during key generation. The key pair consists of bit strings, where is the verification key and is the signature key. The leaves are . Each branch is a hash value generated by bounding the hashes of its descendant, with the public key serving as the primary commitment. Constructing a public key requires computing key pairs.
The signature creation process begins with hashing the message to produce a message digest. This digest is then signed by revealing relevant portions of the private key; in this process, the one-time signature scheme is used. To sign a message , the -bit is calculated first. To optimize this process, a hash chain is used. The signature also includes the authentication path from the Verkle tree, showing that the global public key structure—represented by the tree’s root—includes the one-time public key. The document’s signature comprises the root commitment, one-time signature, one-time verification key, and proof indexes.
The verification process includes several steps:
Recalculating the message digest: the verifier first recalculates the message digest using the received message.
Verifying the one-time signature: the verifier is used to confirm the one-time signature of sign, following Verkle’s signature verification procedure. If this verification is successful, the commitments are then validated.
Validating the one-time signature: to validate the one-time signature the verifier compares the revealed portions of the private key with the corresponding sections of the public key.
Authenticating the one-time public key: the authentication path is used to confirm the validity of the one-time public key used for signing and its correspondence with the root public key of the Verkle tree.
Verifying the root commitment: if the tree’s root matches the root commitment, the signature is confirmed. In a Verkle tree, the root commitment serves as the digest.
If each of these steps is successfully completed, the signature is accepted.
The use of Verkle trees within the system offers substantial benefits in verification time and storage efficiency. Vector commitments enable the system to manage larger datasets with less overhead, enhancing scalability and efficiency. This is particularly crucial in post-quantum cryptography, where systems must withstand attacks from quantum computers. The explained lattice-based vector commitments provide additional security, ensuring the system’s resilience in a post-quantum environment.
Finally, the system provides a highly secure and efficient approach to digital signature generation and verification by integrating one-time signature schemes with Verkle trees. The use of QRNGs and PRNGs ensures strong randomness in key generation, while the Verkle tree design optimizes system efficiency. These characteristics make the proposed system ideally suited for post-quantum cryptography applications.
Here, we offer the algorithm of our scheme:
- 1.
- Setup Phase
- (a)
- Initialize parameters:
- -
- Define security parameters and for the lattice-based construction.
- -
- Generate the public matrix and its trapdoor matrix using the function, ensuring efficient sampling of short vectors.
- (b)
- Generate keys and vector commitments:
- -
- For each leaf in the Verkle tree:
- ▪
- Generate a one-time signature key using the PRNG.
- ▪
- Compute the verification key, where is a cryptographic hash function.
- -
- Commit to the vector using the lattice-based vector commitment where a short random vector is sampled.
- (c)
- Construct the Verkle tree:
- Organize the commitments into -ary tree:
- ▪
- Leaf nodes: commitments of individual verification keys.
- ▪
- Internal nodes: each parent node is the commitment of its child nodes, recursively up to the root:
- The root commitment serves as the public key for the Verkle tree.
- 2.
- Signing Phase
- (a)
- Message hashing:
- Compute the hash of the message.
- (b)
- Generate one-time key pair:
- -
- Use the PRNG to generate a one-time signature key.
- -
- Derive the one-time verification key.
- (c)
- Sign the message:
- Compute the one-time signature using.
- (d)
- Generate vector commitment proofs:
- -
- Calculate the proof for using the lattice-based VC.
- -
- Include the authentication path from to the root in the Verkle tree.
- Use the proofs for each intermediate node to confirm inclusion.
- (e)
- Package the signature:
- The signature consists of:
- -
- The one-time signature.
- -
- The one-time verification key.
- -
- The vector commitment proof.
- 3.
- Verification Phase
- (a)
- Verify one-time signature:
- Use to verify against.
- (b)
- Validate vector commitment proof:
- Check the proof for using the lattice-based verification algorithm:
- (c)
- Verify the authentication path:
- Traverse the authentication path in the Verkle tree:
- At each node, verify the inclusion proof against its parent node’s commitment.
- (d)
- Check root commitment:
- Ensure the final node matches the root commitment.
- (e)
- Accept or reject:
- Accept if all verifications pass; otherwise, reject.
6.1. Security
Our scheme’s security relies on two pillars: short integer solution (SIS) for Verkle tree vector commitments and hash-based one-time signatures (L-DOTS/W-OTS). Below, we unify the security proofs, quantum resistance analysis, and comparisons with NIST PQC standards. It must be mentioned that because of Grover’s algorithm, a quantum adversary could theoretically reduce the search space for PRNG seeds. However, using 256-bit seeds (as in our implementation) maintains O (2128) complexity, which is infeasible even with quantum speedups.
It must also be mentioned that Shor’s attack on factoring/RSA does not apply to lattice-based schemes. The SIS problem remains secure under quantum Fourier sampling [31].
Security goal: existential unforgeability under chosen message attacks (EUF-CMA) in the quantum random oracle model (QROM). The adversarial capabilities are the following:
Quantum adversary : can query hash functions in superposition (QROM), attempts to exploit quantum speedups (e.g., Grover’s algorithm), classical adversary is limited to classical polynomial time computations.
Theorem 1.
(EUF-CMA security): If the SIS problem is hard for parameters and the hash function
is collision-resistant in QROM, the scheme is EUF-CMA secure.
To prove the theorem, we offer the following setup:
SIS instance: let be a challenger receiving an SIS instance and tasked with finding a non-zero vector such that and .
Adversary : breaks EUF-CMA with advantage , making hash queries and sign queries.
Hybrid model: Let us assume operates in the quantum random oracle model (QROM), where hash queries are quantum-accessible.
Simulator interacts with as follows:
sets the Verkle tree’s public key (from the SIS instance).
Generates one-time signature keys using a PRNG seeded with , where is modeled as a random oracle.
For each hash query returns a uniformly random value .
Maintains a list .
For a sign query on , it must:
Compute .
Generate a one-time signature using the SIS-based vector commitment path in the Verkle tree.
Return .
When outputs a forgery :
includes a Verkle tree authentication path and a one-time signature OTS*.
Let be the vector commitment path for .
If is valid but was not queried during sign queries, extracts a collision in the Verkle tree’s vector commitments.
By the binding property of SIS-based commitments, this implies:
where is the forged commitment.
According to SIS problem, is a non-zero vector (since ) satisfying .
by the triangle inequality.
If the forgery reuses a hash value for :
For the collision detection:
checks for where .
Outputs as a collision pair for .
Success probability of :
[HashCollision] (birthday bound).
[RandomOracleGuess].
The final bound looks as follows:
Based on the stated above we can see that, if succeeds with non-negligible , then either: solves SIS with advantage , contradicting the SIS hardness assumption, or finds a hash collision, breaking the collision resistance of .
Thus, the scheme is EUF-CMA secure under the SIS and collision resistance assumptions.
6.2. Performance Evaluation
To validate the practicality of our scheme, we compare it against NIST’s post-quantum cryptography (PQC) finalists: Dilithium (lattice-based), Falcon (lattice-based), and SPHINCS+ (hash-based). Please see Table 2.

Table 2.
Comparative analysis.
- Storage efficiency: our scheme’s Verkle tree structure reduces public/private key sizes by 30% compared to Dilithium and Falcon.
- Batch verification: unlike SPHINCS+, our lattice-based vector commitments enable parallel verification of 1000 signatures in 8 ms, ideal for blockchain networks.
Our scheme’s Verkle tree and lattice-based commitments offer a balance of security, efficiency, and practicality compared to other post-quantum approaches. Code-based schemes (e.g., Rainbow) suffer from large key sizes and were recently broken, while multivariate polynomial-based schemes (e.g., GeMSS) have slower signing times. In contrast, our scheme achieves compact signatures (5 KB), fast verification (8 ms), and 128-bit quantum security, making it more practical for real-world applications like blockchain and IoT. Implementing our scheme in real-world applications, such as IoT devices, requires lightweight hardware (e.g., ARM Cortex-A72) and optimized cryptographic libraries (e.g., OpenSSL). The use of ARM NEON intrinsics reduces verification time to 5 ms, while the on-demand key generation minimizes memory usage to 12 MB for 10,000 keys. These optimizations ensure compatibility with resource-constrained environments, making the scheme practical for IoT and blockchain deployments.
6.3. Complexity Analysis and Performance Evaluation
Verkle trees introduce computational trade-offs between storage and verification efficiency. Below, we analyze the asymptotic complexity:
Key generation:
Time: for -ary tree construction.
Space: (seed-based PRNG eliminates explicit key storage).
Signing:
Time: for authentication path computation.
Space: (keys generated on-demand via PRNG).
Verification:
Time: due to batched vector commitment proofs.
Space: for proof size (vs. in Merkle trees).
Trade-offs:
While Verkle trees reduce proof sizes by (for ), signing is slower than Dilithium due to PRNG operations. This is acceptable in IoT/blockchain applications where verification speed and storage are prioritized over signing latency.
We implemented our scheme in C++ with OpenSSL for lattice operations. Key parameters:
Lattice dimension: n = 512, modulus q = 223, with k = 16.
As PRNG, we used CTR_DRBG (NIST SP 800-90A) seeded with a QRNG (ID Quantique’s Quantis).
We evaluated our scheme on a Raspberry Pi 4 (ARM Cortex-A72, 4GB RAM) to simulate IoT/edge environments and obtained the following results:
Signing throughput: 66 signatures/second (15 ms per signature).
Verification throughput: 125 signatures/second (8 ms per verification).
Memory usage: 12 MB for 10,000 keys (vs. 45 MB for SPHINCS+).
For the blockchain scenario, we conducted the scalability test:
For 10,000 transactions: Batch verification completed in 2.1 s, 5× faster than SPHINCS+ (10.5 s).
Using ARM NEON intrinsics, verification time reduced to 5 ms, demonstrating feasibility for real-time systems.
7. Conclusions
This paper introduces a novel post-quantum digital signature scheme that achieves reduced signature sizes. It provides a detailed analysis of cryptographic techniques that are applicable in both quantum and classical computing environments, with a particular focus on post-quantum cryptography. The study explores vector commitments, lattice-based commitments, and hash-based one-way functions, examining their integration into Merkle and Verkle trees. It highlights the advancements made in vector commitment and lattice-based approaches, along with the development of the Verkle tree model, which offers significant reductions in verification sizes compared to traditional Merkle trees. This optimization, combined with the inherent security of Verkle trees against both quantum and classical attacks, supports the creation of robust post-quantum cryptosystems.
The proposed scheme incorporates quantum-resistant elements, such as the NIST standard CTR_DRBG generator, which replaces vulnerable pseudo-random number generators with quantum-generated values derived from a hybrid quantum random number generator. This enhancement improves both efficiency and speed while strengthening security. Additionally, a comprehensive review of random number generation techniques has led to the development of a variant specifically tailored for post-quantum cryptography, ensuring flexibility against quantum attacks and further reinforcing the system’s security.
To combat the emerging threats posed by quantum computing, we advocate for a paradigm shift toward post-quantum cryptosystems that prioritize both effectiveness and security. These systems leverage advanced cryptographic techniques and integrate quantum-resistant components to ensure long-term resilience.
By combining PRNGs and QRNGs, the system can efficiently generate and validate keys while maintaining stringent security standards. The enhanced Verkle signature scheme offers a practical solution to key storage and quantum security challenges, facilitating the development of more secure cryptographic protocols. This approach optimizes resource utilization while enhancing Verkle tree security, making it a promising candidate for future cryptographic applications. The proposed digital signature scheme is designed for seamless integration with blockchain networks and IoT devices. Its compact signatures (5 KB) and efficient verification (8 ms) align with the requirements of blockchain systems like Ethereum, requiring minimal changes to replace existing schemes such as ECDSA. For IoT devices, the scheme’s low memory footprint (12 MB for 10,000 keys) and hardware-accelerated verification (5 ms using ARM NEON) ensure real-time performance. The use of NIST-standard CTR_DRBG and SHA3-512 guarantees compatibility with existing cryptographic libraries, making the scheme highly suitable for both blockchain and IoT applications without significant modifications.
Our future work will include exploring hybrid approaches combining Verkle trees with sparse Merkle trees for even larger datasets, as well as optimizing lattice-based vector commitments for faster signing times. Additionally, we aim to investigate hardware acceleration (e.g., FPGAs) for further performance improvements and explore post-quantum secure multi-party computation (MPC) to enhance key management in distributed systems. Also, we will work to reduce the size of the one-time signature used in the offered scheme.
Author Contributions
Conceptualization, M.I.; methodology, M.I.; software, N.K.; validation, M.I. and N.K.; formal analysis, M.I.; investigation, N.K.; resources, M.I.; data curation, N.K.; writing—original draft preparation, M.I. and N.K.; writing—review and editing, M.I. and N.K.; visualization, N.K.; supervision, M.I.; project administration, M.I.; funding acquisition, M.I. and N.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant Number: AP23488112).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The research work was carried out as part of the program-targeted funding project AP23488112 “Development and study of a quantum-resistant digital signature scheme based on a Verkle tree”.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lin, Y.; Xie, Z.; Chen, T.; Cheng, X.; Wen, H. Image privacy protection scheme based on high-quality reconstruction DCT compression and nonlinear dynamics. Expert Syst. Appl. 2024, 257, 124891. [Google Scholar] [CrossRef]
- Dinh, H.; Cristopher, M.; Alexander, R. McEliece and Niederreiter cryptosystems that resist quantum Fourier sampling attacks. In Proceedings of the Advances in Cryptology–CRYPTO 2011: 31st Annual Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2011; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Zhou, X.; Tang, X. Research and implementation of RSA algorithm for encryption and decryption. In Proceedings of the 2011 6th International Forum on Strategic Technology, Harbin, China, 22–24 August 2011; Volume 2. [Google Scholar]
- Joseph, D.; Misoczki, R.; Manzano, M.; Tricot, J.; Pinuaga, F.D.; Lacombe, O.; Leichenauer, S.; Hidary, J.; Venables, P.; Hansen, R. Transitioning organizations to post-quantum cryptography. Nature 2022, 605, 237–243. [Google Scholar] [CrossRef] [PubMed]
- Gagnidze, A.; Maksim, I.; Giorgi, I. Analysis of post quantum cryptography use in practice. Bull. Georgian Natl. Acad. Sci. 2017, 11, 29–36. [Google Scholar]
- Espitau, T.; Fouque, P.A.; Gérard, F.; Rossi, M.; Takahashi, A.; Tibouchi, M.; Wallet, A.; Yu, Y. Mitaka: A simpler, parallelizable, maskable variant of falcon. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Trondheim, Norway, 30 May–3 June 2022; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
- Soni, D.; Basu, K.; Nabeel, M.; Aaraj, N.; Manzano, M.; Karri, R. Hardware Architectures for Post-Quantum Digital Signature Schemes; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Lyubashevsky, V. Basic Lattice Cryptography: The Concepts Behind Kyber (ML-KEM) and Dilithium (ML-DSA). Cryptology ePrint Archive. 2024. Available online: https://eprint.iacr.org/2024/1287 (accessed on 28 January 2025).
- Bhattacharjee, K.; Das, S. A search for good pseudo-random number generators: Survey and empirical studies. Comput. Sci. Rev. 2022, 45, 100471. [Google Scholar] [CrossRef]
- Kietzmann, P.; Schmidt, T.C.; Wählisch, M. A guideline on pseudorandom number generation (PRNG) in the IoT. ACM Comput. Surv. (CSUR) 2021, 54, 1–38. [Google Scholar] [CrossRef]
- Krishnamoorthi, S.; Jayapaul, P.; Dhanaraj, R.K.; Rajasekar, V.; Balusamy, B.; Islam, S.H. Design of pseudo-random number generator from turbulence padded chaotic map. Nonlinear Dyn. 2021, 104, 1627–1643. [Google Scholar] [CrossRef]
- Iavich, M.; Kuchukhidze, T.; Iashvili, G.; Gnatyuk, S. Hybrid quantum random number generator for cryptographic algorithms. Radioelectron. Comput. Syst. 2021, 4, 103–118. [Google Scholar] [CrossRef]
- Ji, Z.; Brown, J.; Zhang, J. True random number generator (TRNG) for secure communications in the era of IoT. In Proceedings of the 2020 China Semiconductor Technology International Conference (CSTIC), Shanghai, China, 26 June–17 July 2020. [Google Scholar]
- Guillan-Lorenzo, O.; Troncoso-Costas, M.; Alvarez-Outarelo, D.; Diaz-Otero, F.J.; Garcia-Escartin, J.C. Optical quantum random number generators: A comparative study. Opt. Quantum Electron. 2023, 55, 185. [Google Scholar] [CrossRef]
- Haider, Z.; Saeed, M.H.; Zaheer, M.E.-U.; Alvi, Z.A.; Ilyas, M.; Nasreen, T.; Imran, M.; Islam, R.U.; Ikram, M. Quantum Random Number Generator (QRNG): Theoretical and experimental investigations. Eur. Phys. J. Plus 2023, 138, 797. [Google Scholar] [CrossRef]
- Merkle, R.C. A certified digital signature. In Conference on the Theory and Application of Cryptology; Springer: New York, NY, USA, 1989. [Google Scholar]
- Majenz, C.; Chanelle, M.M.; Maris, O. Quantum-access security of the Winternitz one-time signature scheme. arXiv 2021, arXiv:2103.12448. [Google Scholar]
- Coronado, C. On the Security and the Efficiency of the Merkle Signature Scheme. Cryptology ePrint Archive. 2005. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=d7eb9b3aa0183cd76d0b27ac1f6ef244c236c69e (accessed on 11 January 2025).
- Becker, G. Merkle signature schemes, merkle trees and their cryptanalysis. Ruhr-Univ. Boch. Tech. Rep. 2008, 12, 19. [Google Scholar]
- Buchmann, J.; García, L.C.C.; Dahmen, E.; Döring, M.; Klintsevich, E. CMSS—An improved Merkle signature scheme. In Proceedings of the Progress in Cryptology-INDOCRYPT 2006: 7th International Conference on Cryptology in India, Kolkata, India, 11–13 December 2006; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Cao, Y.; Wu, Y.; Wang, W.; Lu, X.; Chen, S.; Ye, J.; Chang, C.H. An efficient full hardware implementation of extended Merkle signature scheme. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 69, 682–693. [Google Scholar] [CrossRef]
- Kuszmaul, J. Verkle trees. Verkle Trees 2019, 1. Available online: https://math.mit.edu/research/highschool/primes/materials/2018/Kuszmaul.pdf (accessed on 4 January 2025).
- Iavich, M.; Tamari, K. Digital Signature Design Using Verkle Tree. IVUS. 2023. Available online: https://ceur-ws.org/Vol-3575/Paper9.pdf (accessed on 25 December 2024).
- Catalano, D.; Dario, F. Vector commitments and their applications. In Proceedings of the Public-Key Cryptography–PKC 2013: 16th International Conference on Practice and Theory in Public-Key Cryptography, Nara, Japan, 26 February–1 March 2013; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Libert, B. Vector commitments with proofs of smallness: Short range proofs and more. In IACR International Conference on Public-Key Cryptography; Springer Nature: Cham, Switzerland, 2024. [Google Scholar]
- Papamanthou, C.; Shi, E.; Tamassia, R.; Yi, K. Streaming authenticated data structures. In Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 2013; pp. 353–370. [Google Scholar]
- Iavich, M.; Kuchukhidze, T.; Bocu, R. A Post-Quantum Digital Signature Using Verkle Trees and Lattices. Symmetry 2023, 15, 2165. [Google Scholar] [CrossRef]
- Peikert, C.; Zachary, P.; Chad, S. Vector and functional commitments from lattices. In Proceedings of the Theory of Cryptography: 19th International Conference, TCC 2021, Raleigh, NC, USA, 8–11 November 2021; Springer International Publishing: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Knecht, M.; Willi, M.; Carlo, U.N. A space-and time-efficient Implementation of the Merkle Tree Traversal Algorithm. arXiv 2014, arXiv:1409.4081. [Google Scholar]
- Remaud, M. Applications of Quantum Fourier Sampling and the Dihedral Hidden Subgroup Problem. Ph.D. Dissertation, Sorbonne Université, Paris, France, 2023. [Google Scholar]
- Kuznetsov, O.; Rusnak, A.; Yezhov, A.; Kuznetsova, K.; Kanonik, D.; Domin, O. Merkle Trees in Blockchain: A Study of Collision Probability and Security Implications. Internet Things 2024, 26, 101193. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).