Leveraging Positive-Unlabeled Learning for Enhanced Black Spot Accident Identification on Greek Road Networks
Abstract
1. Introduction
Contributions
2. Literature Review
2.1. Traditional Methods for Black Spot Identification
2.2. Machine Learning in Black Spot Identification
2.3. Weakly Supervised Learning in Defect Detection
2.4. Bridging the Gap
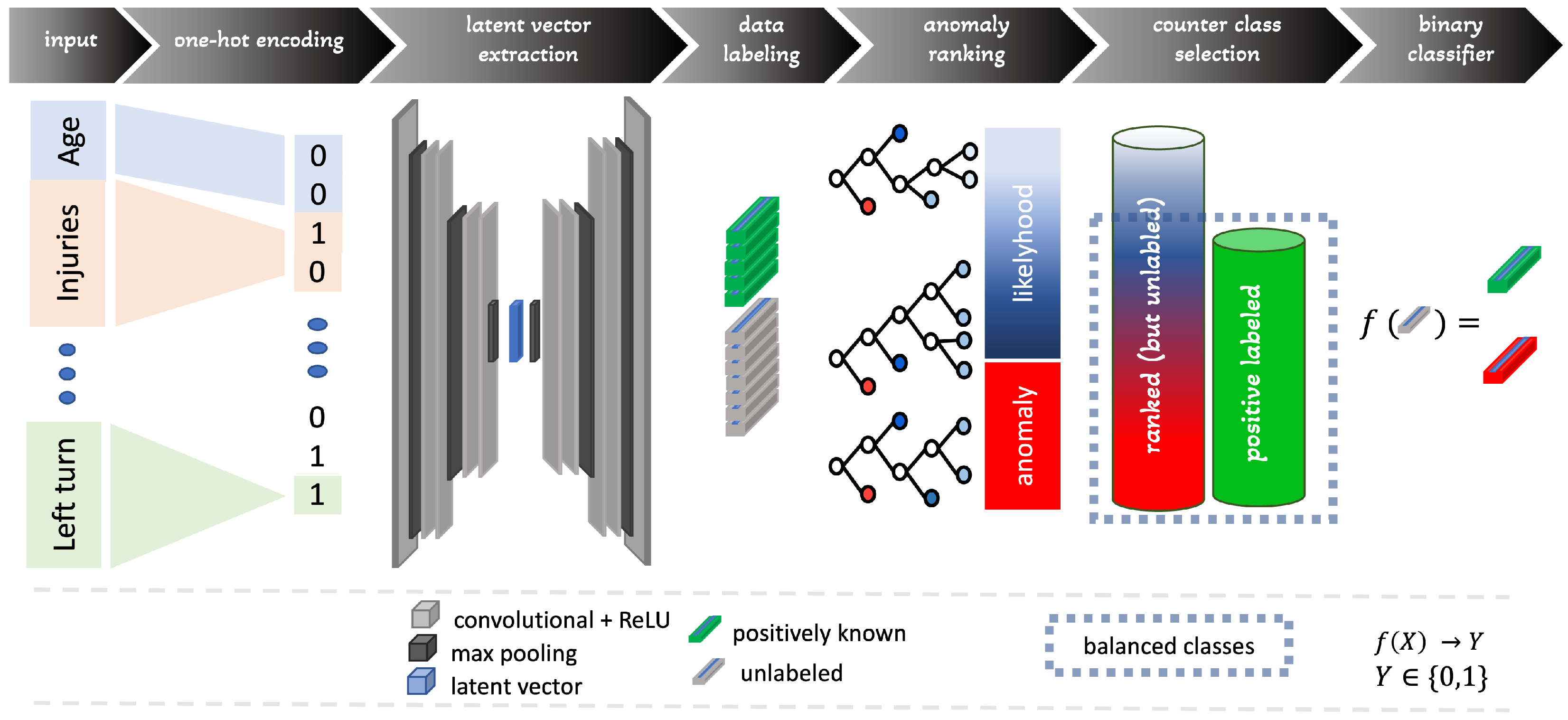
3. Methodology
3.1. Transforming Supervised Learning into Outlier Detection
3.2. Proposed Pipeline
Categorical Encoding
3.3. Self-Supervised Deep Learning Model
3.4. Utilization of Latent Vectors
3.5. Anomaly Ranking with Isolation Forest
3.6. Class Balancing through Counter Example Generation
3.7. Training of the Binary Classifier
4. Experiments
4.1. Dataset and Preprocessing
- Accident location;
- Incident and road environment details (month, week of year, number of deaths, serious injuries, minor injuries, total number of injuries, number of vehicles involved, road surface type, atmospheric conditions, road surface conditions, road marking, lane marking, road width, road narrowness, turn sequence, road gradient, straightness, right turn, left turn, boundary line marking left and right, accident severity, type of first collision);
- Driver information (gender and age);
- Vehicle information (type, age, and mechanical inspection status).
4.2. Experimental Setup
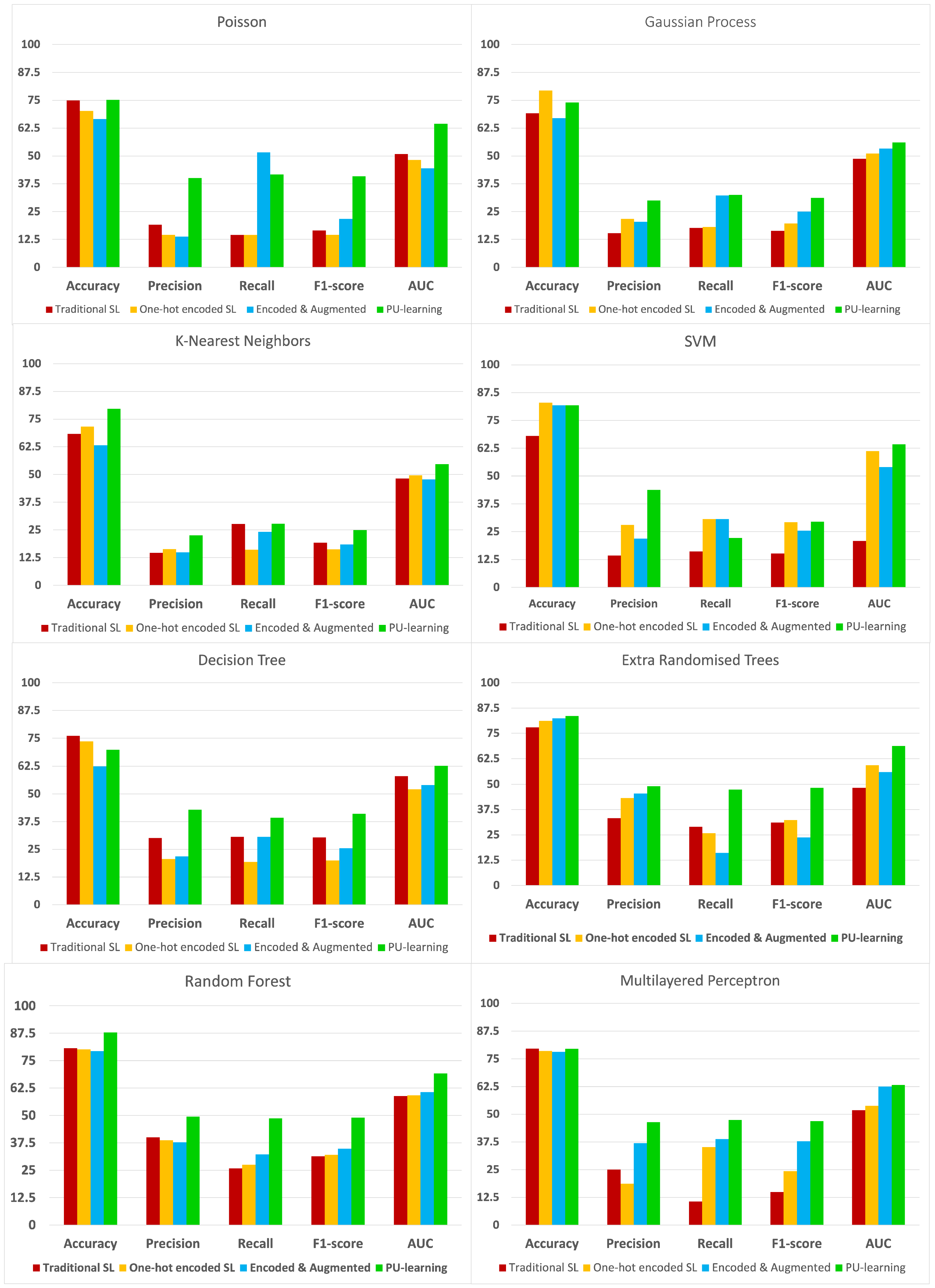
5. Results
5.1. Comparative Analysis
5.2. Discussion
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ML | Machine Learning |
| SL | Supervised Learning |
| PU | Positive-Unlabeled |
| BSNG | Black Spots of North Greece |
| GIS | Geographical Information Systems |
| AUC | Area Under the Curve |
| ROC | Receiver Operational Characteristic |
| SVM | Support Vector Machine |
| RBF | Radial Basis Function |
| DNN | Deep Neural Network |
| ReLU | Rectified Linear Unit |
References
- Debrabant, B.; Halekoh, U.; Bonat, W.H.; Hansen, D.L.; Hjelmborg, J.; Lauritsen, J. Identifying traffic accident black spots with Poisson–Tweedie models. Accid. Anal. Prev. 2018, 111, 147–154. [Google Scholar] [CrossRef]
- Elvik, R. State-of-the-Art Approaches to Road Accident Black Spot Management and Safety Analysis of Road Networks; Transportøkonomisk Institutt: Oslo, Norway, 2007. [Google Scholar]
- Tiwari, M.; Nagar, P.; Arya, G.; Chauhan, S.S. Road Accident Analysis Using ML Classification Algorithms and Plotting Black Spot Areas on Map. In Proceedings of the International Conference on Micro-Electronics and Telecommunication Engineering, Ghaziabad, India, 24–25 September 2021; pp. 685–701. [Google Scholar]
- Karamanlis, I.; Kokkalis, A.; Profillidis, V.; Botzoris, G.; Kiourt, C.; Sevetlidis, V.; Pavlidis, G. Deep Learning-Based Black Spot Identification on Greek Road Networks. Data 2023, 8, 110. [Google Scholar] [CrossRef]
- Božič, J.; Tabernik, D.; Skočaj, D. Mixed supervision for surface-defect detection: From weakly to fully supervised learning. Comput. Ind. 2021, 129, 103459. [Google Scholar] [CrossRef]
- Sevetlidis, V.; Pavlidis, G.; Balaska, V.; Psomoulis, A.; Mouroutsos, S.; Gasteratos, A. Defect detection using weakly supervised learning. In Proceedings of the 2023 IEEE International Conference on Imaging Systems and Techniques (IST) Proceedings, Copenhagen, Denmark, 17–19 October 2023. [Google Scholar]
- Bekker, J.; Davis, J. Learning from positive and unlabeled data: A survey. Mach. Learn. 2020, 109, 719–760. [Google Scholar] [CrossRef]
- Elvik, R. Evaluations of road accident blackspot treatment: A case of the iron law of evaluation studies? Accid. Anal. Prev. 1997, 29, 191–199. [Google Scholar] [CrossRef] [PubMed]
- Alsop, J.; Langley, J. Under-reporting of motor vehicle traffic crash victims in New Zealand. Accid. Anal. Prev. 2001, 33, 353–359. [Google Scholar] [CrossRef] [PubMed]
- Newstead, S.V.; Corben, B.F. Evaluation of the 1992–1996 Transport Accident Commission Funded Accident Black Spot Treatment Program in Victoria; Monash University Press: Clayton, VIC, Australia, 2001; Number 182. [Google Scholar]
- Robinson, D. Changes in head injury with the New Zealand bicycle helmet law. Accid. Anal. Prev. 2001, 33, 687–691. [Google Scholar] [CrossRef] [PubMed]
- Oppe, S. Detection and Analysis of Black Spots with Even Small Accident Figures; Institute for Road Safety Research SWOV: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Dereli, M.A.; Erdogan, S. A new model for determining the traffic accident black spots using GIS-aided spatial statistical methods. Transp. Res. Part A Policy Pract. 2017, 103, 106–117. [Google Scholar] [CrossRef]
- Budzyński, M.; Kustra, W.; Okraszewska, R.; Jamroz, K.; Pyrchla, J. The use of GIS tools for road infrastructure safety management. E3S Web Conf. 2018, 26, 00009. [Google Scholar] [CrossRef]
- Chang, K.T. Introduction to Geographic Information Systems; Mcgraw-Hill Boston: Boston, MA, USA, 2008; Volume 4. [Google Scholar]
- Silva, P.B.; Andrade, M.; Ferreira, S. Machine learning applied to road safety modeling: A systematic literature review. J. Traffic Transp. Eng. (Engl. Ed.) 2020, 7, 775–790. [Google Scholar] [CrossRef]
- Miaou, S.P.; Hu, P.S.; Wright, T.; Rathi, A.K.; Davis, S.C. Relationship between truck accidents and highway geometric design: A Poisson regression approach. Transp. Res. Rec. 1994, 26, 471–482. [Google Scholar]
- Sagamiko, T.; Mbare, N. Modelling road traffic accidents counts in Tanzania: A poisson regression approach. Tanzan. J. Sci. 2021, 47, 308–314. [Google Scholar]
- Abdel-Aty, M.A.; Radwan, A.E. Modeling traffic accident occurrence and involvement. Accid. Anal. Prev. 2000, 32, 633–642. [Google Scholar] [CrossRef] [PubMed]
- Chin, H.C.; Quddus, M.A. Applying the random effect negative binomial model to examine traffic accident occurrence at signalized intersections. Accid. Anal. Prev. 2003, 35, 253–259. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Kockelman, K.M.; Damien, P. A multivariate Poisson-lognormal regression model for prediction of crash counts by severity, using Bayesian methods. Accid. Anal. Prev. 2008, 40, 964–975. [Google Scholar] [CrossRef] [PubMed]
- Lord, D.; Washington, S.P.; Ivan, J.N. Poisson, Poisson-gamma and zero-inflated regression models of motor vehicle crashes: Balancing statistical fit and theory. Accid. Anal. Prev. 2005, 37, 35–46. [Google Scholar] [CrossRef] [PubMed]
- Lord, D.; Persaud, B.N. Accident prediction models with and without trend: Application of the generalized estimating equations procedure. Transp. Res. Rec. 2000, 1717, 102–108. [Google Scholar] [CrossRef]
- Caliendo, C.; Guida, M.; Parisi, A. A crash-prediction model for multilane roads. Accid. Anal. Prev. 2007, 39, 657–670. [Google Scholar] [CrossRef] [PubMed]
- Lord, D.; Mannering, F. The statistical analysis of crash-frequency data: A review and assessment of methodological alternatives. Transp. Res. Part A Policy Pract. 2010, 44, 291–305. [Google Scholar] [CrossRef]
- Savolainen, P.T.; Mannering, F.L.; Lord, D.; Quddus, M.A. The statistical analysis of highway crash-injury severities: A review and assessment of methodological alternatives. Accid. Anal. Prev. 2011, 43, 1666–1676. [Google Scholar] [CrossRef]
- Szénási, S.; Jankó, D. A method to identify black spot candidates in built-up areas. J. Transp. Saf. Secur. 2017, 9, 20–44. [Google Scholar] [CrossRef]
- Aghajani, M.A.; Dezfoulian, R.S.; Arjroody, A.R.; Rezaei, M. Applying GIS to identify the spatial and temporal patterns of road accidents using spatial statistics (case study: Ilam Province, Iran). Transp. Res. Procedia 2017, 25, 2126–2138. [Google Scholar] [CrossRef]
- Erdogan, S.; Ilçi, V.; Soysal, O.M.; Kormaz, A. A model suggestion for the determination of the traffic accident hotspots on the Turkish highway road network: A pilot study. Bol. De CiÊncias Geodésicas 2015, 21, 169–188. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, Y.; Chen, Y. Identification of potential traffic accident hot spots based on accident data and GIS. MATEC Web Conf. 2020, 325, 01005. [Google Scholar] [CrossRef]
- Turki, Z.; Ghédira, A.; Ouni, F.; Kahloul, A. Spatio-temporal analysis of road traffic accidents in Tunisia. In Proceedings of the 2022 14th International Colloquium of Logistics and Supply Chain Management (LOGISTIQUA), El Jadida, Morocco, 25–27 May 2022; pp. 1–7. [Google Scholar]
- Al-Omari, A.; Shatnawi, N.; Khedaywi, T.; Miqdady, T. Prediction of traffic accidents hot spots using fuzzy logic and GIS. Appl. Geomat. 2020, 12, 149–161. [Google Scholar] [CrossRef]
- Gundogdu, I.B. Applying linear analysis methods to GIS-supported procedures for preventing traffic accidents: Case study of Konya. Saf. Sci. 2010, 48, 763–769. [Google Scholar] [CrossRef]
- Shafabakhsh, G.A.; Famili, A.; Bahadori, M.S. GIS-based spatial analysis of urban traffic accidents: Case study in Mashhad, Iran. J. Traffic Transp. Eng. (Engl. Ed.) 2017, 4, 290–299. [Google Scholar] [CrossRef]
- Lasisi, A.; Li, P.; Chen, J. Hybrid Machine Learning and Geographic Information Systems Approach—A Case for Grade Crossing Crash Data Analysis. Adv. Data Sci. Adapt. Anal. 2020, 12, 2050003. [Google Scholar] [CrossRef]
- Azmi, N.N.; Sarif, A.S. The Development of a GIS database for blackspot area in Federal Route 24. Prog. Eng. Appl. Technol. 2023, 4, 949–955. [Google Scholar]
- Thakare, K.; Shete, B.; Bijwe, A. A Review on the Study of Different Black Spot Identification Methods. Int. Res. J. Eng. Technol. 2021, 9, 1758–1763. [Google Scholar]
- Chen, H. Black spot determination of traffic accident locations and its spatial association characteristic analysis based on GIS. J. Geogr. Inf. Syst. 2012, 4, 608–617. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Steyaert, L.T.; Parks, B.O.; Johnston, C.; Maidment, D.; Crane, M.; Glendinning, S. GIS and Environmental Modeling: Progress and Research Issues; John Wiley and Sons Inc.: Canada, 1996. [Google Scholar]
- Iqbal, A.; Rehman, Z.U.; Ali, S.; Ullah, K.; Ghani, U. Road traffic accident analysis and identification of black spot locations on highway. Civ. Eng. J. 2020, 6, 2448–2456. [Google Scholar] [CrossRef]
- Karamanlis, I.; Kokkalis, A.; Profillidis, V.; Botzoris, G.; Galanis, A. Identifying Road Accident Black Spots using Classical and Modern Approaches. WSEAS Trans. Syst. 2023, 22, 556–565. [Google Scholar] [CrossRef]
- Karamanlis, I.; Nikiforiadis, A.; Botzoris, G.; Kokkalis, A.; Basbas, S. Towards Sustainable Transportation: The Role of Black Spot Analysis in Improving Road Safety. Sustainability 2023, 15, 14478. [Google Scholar] [CrossRef]
- Fiorentini, N.; Losa, M. Handling imbalanced data in road crash severity prediction by machine learning algorithms. Infrastructures 2020, 5, 61. [Google Scholar] [CrossRef]
- Theofilatos, A.; Chen, C.; Antoniou, C. Comparing machine learning and deep learning methods for real-time crash prediction. Transp. Res. Rec. 2019, 2673, 169–178. [Google Scholar] [CrossRef]
- Fan, Z.; Liu, C.; Cai, D.; Yue, S. Research on black spot identification of safety in urban traffic accidents based on machine learning method. Saf. Sci. 2019, 118, 607–616. [Google Scholar] [CrossRef]
- Mbarek, A.; Jiber, M.; Yahyaouy, A.; Sabri, A. Black spots identification on rural roads based on extreme learning machine. Int. J. Electr. Comput. Eng. 2023, 13, 3149–3160. [Google Scholar] [CrossRef]
- Vasconcelos, S.P.; de Souza Baptista, C.; de Figueirêdo, H.F. Using a Social Network for Road Accidents Detection, Geolocation and Notification—A Machine Learning Approach. In Proceedings of the Fifteenth International Conference on Advanced Geographic Information Systems, Applications, and Services, Venice, Italy, 24–28 April 2023. [Google Scholar]
- Kwok-Fai Lui, A.; Chan, Y.H.; Lo, K.H.; Cheng, W.T.; Cheung, H.T. Predictive Screening of Accident Black Spots based on Deep Neural Models of Road Networks and Facilities: A Case Study based on a District in Hong Kong. In Proceedings of the 2021 5th International Conference on Computer Science and Artificial Intelligence, Beijing, China, 4–6 December 2021; pp. 422–428. [Google Scholar]
- Paul, A.K.; Boni, P.K.; Islam, M.Z. A Data-Driven Study to Investigate the Causes of Severity of Road Accidents. In Proceedings of the 2022 13th International Conference on Computing Communication and Networking Technologies (ICCCNT), Virtual, 3–5 October 2022; pp. 1–7. [Google Scholar]
- Abdullah, P.; Sipos, T. Exploring the Factors Influencing Traffic Accidents: An Analysis of Black Spots and Decision Tree for Injury Severity. Period. Polytech. Transp. Eng. 2024, 52, 33–39. [Google Scholar] [CrossRef]
- Amorim, B.d.S.P.; Firmino, A.A.; Baptista, C.d.S.; Júnior, G.B.; Paiva, A.C.d.; Júnior, F.E.d.A. A Machine Learning Approach for Classifying Road Accident Hotspots. ISPRS Int. J. Geo-Inf. 2023, 12, 227. [Google Scholar] [CrossRef]
- Sobhana, M.; Rohith, V.K.; Avinash, T.; Malathi, N. A Hybrid Machine Learning Approach for Performing Predictive Analytics on Road Accidents. In Proceedings of the 2022 6th International Conference on Computation System and Information Technology for Sustainable Solutions (CSITSS), Bangalore, India, 21–23 December 2022; pp. 1–6. [Google Scholar]
- Al-Mistarehi, B.; Alomari, A.H.; Imam, R.; Mashaqba, M. Using machine learning models to forecast severity level of traffic crashes by R Studio and ArcGIS. Front. Built Environ. 2022, 8, 860805. [Google Scholar] [CrossRef]
- Megnidio-Tchoukouegno, M.; Adedeji, J.A. Machine learning for road traffic accident improvement and environmental resource management in the transportation sector. Sustainability 2023, 15, 2014. [Google Scholar] [CrossRef]
- Wang, Y.; Zhai, H.; Cao, X.; Geng, X. Cause Analysis and Accident Classification of Road Traffic Accidents Based on Complex Networks. Appl. Sci. 2023, 13, 12963. [Google Scholar] [CrossRef]
- Khattak, A.; Almujibah, H.; Elamary, A.; Matara, C.M. Interpretable Dynamic Ensemble Selection Approach for the Prediction of Road Traffic Injury Severity: A Case Study of Pakistan’s National Highway N-5. Sustainability 2022, 14, 12340. [Google Scholar] [CrossRef]
- Kumeda, B.; Zhang, F.; Zhou, F.; Hussain, S.; Almasri, A.; Assefa, M. Classification of road traffic accident data using machine learning algorithms. In Proceedings of the 2019 IEEE 11th International Conference on Communication Software and Networks (ICCSN), Chongqing, China, 12–15 June 2019; pp. 682–687. [Google Scholar]
- Manzoor, M.; Umer, M.; Sadiq, S.; Ishaq, A.; Ullah, S.; Madni, H.A.; Bisogni, C. RFCNN: Traffic accident severity prediction based on decision level fusion of machine and deep learning model. IEEE Access 2021, 9, 128359–128371. [Google Scholar] [CrossRef]
- Kaur, G.; Kaur, H. Black Spot and Accidental Attributes Identification on State Highways and Ordinary District Roads Using Data Mining Techniques. Int. J. Adv. Res. Comput. Sci. 2017, 8, 2312. [Google Scholar]
- Balakrishnan, S.; Karuppanagounder, K. Accident Blackspot Ranking: An Alternative Approach in the Presence of Limited Data. In Recent Advances in Transportation Systems Engineering and Management: Select Proceedings of CTSEM 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 721–735. [Google Scholar]
- Sevetlidis, V.; Giuffrida, M.V.; Tsaftaris, S.A. Whole image synthesis using a deep encoder-decoder network. In Proceedings of the Simulation and Synthesis in Medical Imaging: First International Workshop, SASHIMI 2016, Held in Conjunction with MICCAI 2016, Athens, Greece, 21 October 2016; pp. 127–137. [Google Scholar]
- Pavlidis, G.; Mouroutsos, S.; Sevetlidis, V. Efficient colour sorting of Chios mastiha. In Proceedings of the 2014 IEEE International Conference on Imaging Systems and Techniques (IST) Proceedings, Santorini, Greece, 14–17 October 2014; pp. 386–391. [Google Scholar]
- Kritsis, K.; Kiourt, C.; Stamouli, S.; Sevetlidis, V.; Solomou, A.; Karetsos, G.; Katsouros, V.; Pavlidis, G. GRASP-125: A Dataset for Greek Vascular Plant Recognition in Natural Environment. Sustainability 2021, 13, 11865. [Google Scholar] [CrossRef]
- Sevetlidis, V.; Pavlidis, G.; Arampatzakis, V.; Kiourt, C.; Mouroutsos, S.G.; Gasteratos, A. Web acquired image datasets need curation: An examplar pipeline evaluated on Greek food images. In Proceedings of the 2021 IEEE International Conference on Imaging Systems and Techniques (IST), Kaohsiung, Taiwan, 24–26 August 2021; pp. 1–6. [Google Scholar]
- Sevetlidis, V.; Pavlidis, G.; Mouroutsos, S.; Gasteratos, A. Tackling dataset bias with an automated collection of real-world samples. IEEE Access 2022, 10, 126832–126844. [Google Scholar] [CrossRef]
- Pavlidis, G.; Solomou, A.; Stamouli, S.; Papavassiliou, V.; Kritsis, K.; Kiourt, C.; Sevetlidis, V.; Karetsos, G.; Trigas, P.; Kougioumoutzis, K.; et al. Sustainable ecotourism through cutting-edge technologies. Sustainability 2022, 14, 800. [Google Scholar] [CrossRef]
- Sevetlidis, V.; Pavlidis, G. Effective Raman spectra identification with tree-based methods. J. Cult. Herit. 2019, 37, 121–128. [Google Scholar] [CrossRef]
- Sevetlidis, V.; Pavlidis, G. Hierarchical Classification For Improved Compound Identification In Raman Spectroscopy. In Proceedings of the 3rd Computer Applications and Quantitative Methods in Archaeology (CAA-GR) Conference, Limassol, Cyprus, 18–20 June 2018; p. 133. [Google Scholar]
- Zhou, Z.H. A brief introduction to weakly supervised learning. Natl. Sci. Rev. 2018, 5, 44–53. [Google Scholar] [CrossRef]
- Foulds, J.; Frank, E. A review of multi-instance learning assumptions. Knowl. Eng. Rev. 2010, 25, 1–25. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, Z.H. A New Analysis of Co-Training. ICML 2010, 2, 3. [Google Scholar]
- Letouzey, F.; Denis, F.; Gilleron, R. Learning from positive and unlabeled examples. In Proceedings of the International Conference on Algorithmic Learning Theory, Sydney, NSW, Australia, 11–13 December 2000; pp. 71–85. [Google Scholar]
- Zhang, D.; Han, J.; Cheng, G.; Yang, M.H. Weakly supervised object localization and detection: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 5866–5885. [Google Scholar] [CrossRef]
- Xu, L.; Lv, S.; Deng, Y.; Li, X. A weakly supervised surface defect detection based on convolutional neural network. IEEE Access 2020, 8, 42285–42296. [Google Scholar] [CrossRef]
- Chatterjee, S.; Saeedfar, P.; Tofangchi, S.; Kolbe, L.M. Intelligent Road Maintenance: A Machine Learning Approach for surface Defect Detection. In Proceedings of the Twenty-Sixth European Conference on Information Systems (ECIS2018), Portsmouth, UK, 23–28 June 2018; p. 194. [Google Scholar]
- Fernandes, A.M.d.R.; Cassaniga, M.J.; Passos, B.T.; Comunello, E.; Stefenon, S.F.; Leithardt, V.R.Q. Detection and classification of cracks and potholes in road images using texture descriptors. J. Intell. Fuzzy Syst. 2023, 44, 10255–10274. [Google Scholar] [CrossRef]
- Boucetta, Z.; Fazziki, A.E.; Adnani, M.E. A Deep-Learning-Based Road Deterioration Notification and Road Condition Monitoring Framework. Int. J. Intell. Eng. Syst. 2021, 14, 503–515. [Google Scholar] [CrossRef]
- Basavaraju, A.; Du, J.; Zhou, F.; Ji, J. A machine learning approach to road surface anomaly assessment using smartphone sensors. IEEE Sens. J. 2019, 20, 2635–2647. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, T.; Li, C.; Zhou, X. A Novel Driver Distraction Behavior Detection Method Based on Self-Supervised Learning with Masked Image Modeling. IEEE Internet Things J. 2023, 11, 6056–6071. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, B.; Yin, J.; Cao, L.; Zhang, C.; Hao, Z. Similarity-based approach for positive and unlabeled learning. In Proceedings of the IJCAI Proceedings-International Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011; Volume 22, p. 1577. [Google Scholar]
- Nam, J.; Kim, S. Clami: Defect prediction on unlabeled datasets (t). In Proceedings of the 2015 30th IEEE/ACM International Conference on Automated Software Engineering (ASE), Lincoln, NE, USA, 9–13 November 2015; pp. 452–463. [Google Scholar]
- Hariri, S.; Kind, M.C.; Brunner, R.J. Extended isolation forest. IEEE Trans. Knowl. Data Eng. 2019, 33, 1479–1489. [Google Scholar] [CrossRef]
- Tsintotas, K.A.; Sevetlidis, V.; Papapetros, I.T.; Balaska, V.; Psomoulis, A.; Gasteratos, A. BK tree indexing for active vision-based loop-closure detection in autonomous navigation. In Proceedings of the 2022 30th Mediterranean Conference on Control and Automation (MED), Athens, Greece, 28 June–1 July 2022; pp. 532–537. [Google Scholar]
- Xu, Y.; Zhang, C.; He, J.; Liu, Z.; Chen, Y.; Zhang, H. Comparisons on methods for identifying accident black spots using vehicle kinetic parameters collected from road experiments. J. Traffic Transp. Eng. (Engl. Ed.) 2023, 10, 659–674. [Google Scholar] [CrossRef]
- Tanprasert, T.; Siripanpornchana, C.; Surasvadi, N.; Thajchayapong, S. Recognizing traffic black spots from street view images using environment-aware image processing and neural network. IEEE Access 2020, 8, 121469–121478. [Google Scholar] [CrossRef]
| Country/Area | Methodology | Sliding Window (m) | Threshold | Severity Included | Time Frame (Years) |
|---|---|---|---|---|---|
| Denmark | Poisson | variable length | 4 | No | 5 |
| Croatia | Segment ranking | 300 | 12 | Implicitly | 3 |
| Flanders | Weighted method | 100 | 3 | Yes | 3 |
| Hungary | Accident indexing | 100 (spot)/1000 (segment) | 4 | No | 3 |
| Switzerland | Accident indexing | 100 (spot)/500 (segment) | Statistical, critical values | Implicitly | 2 |
| Germany | Weighted indexing | Likelihood | 4 | No | 5 |
| Portugal | Weighted method | 200 | 5 | Yes | 5 |
| Norway | Poisson, statistical testing | 100 (spot)/1000 (segment) | 4 | Accident cost | 5 |
| Greece | Absolute count | 1000 | 2 | No | N/A |
| RoadType | IsUrban | IsRural | IsHighway |
|---|---|---|---|
| Urban | 1 | 0 | 0 |
| Rural | 0 | 1 | 0 |
| Highway | 0 | 0 | 1 |
| Dataset | Method | Acc (std) | Prec (std) | Rec (std) | F1 (std) | AUC (std) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | Poisson | 74.93 | (3.20) | 19.14 | (1.67) | 14.51 | (2.08) | 16.51 | (2.54) | 50.94 | (4.12) |
| Gaussian Process | 69.14 | (2.81) | 15.27 | (3.02) | 17.74 | (3.22) | 16.41 | (3.14) | 48.73 | (2.67) | |
| kNN | 68.31 | (2.85) | 14.66 | (2.33) | 27.74 | (3.18) | 16.05 | (2.63) | 48.23 | (2.98) | |
| SVM | 68.04 | (3.12) | 14.28 | (1.98) | 16.10 | (0.89) | 28.00 | (1.06) | 49.80 | (2.77) | |
| Decision Tree | 76.03 | (2.72) | 30.15 | (2.09) | 30.64 | (2.78) | 30.41 | (2.63) | 58.01 | (3.12) | |
| Random Forest | 80.71 | (1.94) | 40.01 | (2.48) | 25.81 | (2.09) | 31.37 | (2.63) | 58.91 | (1.98) | |
| Xtra Trees | 77.96 | (2.47) | 33.33 | (2.73) | 29.03 | (2.28) | 31.03 | (2.67) | 58.53 | (2.42) | |
| MLP | 79.61 | (2.47) | 25.00 | (1.83) | 10.67 | (0.75) | 13.96 | (1.01) | 51.84 | (2.11) | |
| B | Poisson | 70.24 | (0.83) | 14.62 | (1.27) | 14.51 | (0.92) | 14.28 | (1.04) | 48.12 | (1.11) |
| Gaussian Process | 79.33 | (1.01) | 21.73 | (0.84) | 18.10 | (0.06) | 19.54 | (1.02) | 51.04 | (0.92) | |
| kNN | 71.62 | (1.14) | 16.39 | (0.79) | 16.12 | (0.98) | 16.26 | (1.01) | 49.59 | (0.89) | |
| SVM | 82.92 | (0.98) | 50.01 | (1.33) | 30.64 | (0.96) | 28.02 | (0.91) | 61.16 | (1.22) | |
| Decision Tree | 73.55 | (1.02) | 20.68 | (0.91) | 19.35 | (0.83) | 19.99 | (0.95) | 52.03 | (0.99) | |
| Random Forest | 80.16 | (0.94) | 38.63 | (1.12) | 27.41 | (0.79) | 32.07 | (0.87) | 59.22 | (1.09) | |
| Xtra Trees | 81.26 | (1.05) | 43.24 | (0.98) | 25.81 | (0.86) | 32.32 | (1.01) | 59.41 | (1.11) | |
| MLP | 28.65 | (0.78) | 18.32 | (0.89) | 91.93 | (1.34) | 30.56 | (0.93) | 53.77 | (1.01) | |
| C | Poisson | 36.63 | (2.50) | 13.79 | (1.08) | 51.61 | (3.20) | 21.76 | (2.11) | 44.49 | (2.58) |
| Gaussian Process | 66.94 | (2.30) | 20.40 | (1.59) | 32.25 | (2.98) | 25.00 | (2.29) | 53.27 | (3.13) | |
| kNN | 63.25 | (2.02) | 14.85 | (1.56) | 24.19 | (2.26) | 18.42 | (1.90) | 47.81 | (2.60) | |
| SVM | 81.81 | (3.10) | 43.75 | (2.63) | 22.25 | (1.89) | 29.78 | (2.29) | 58.31 | (3.70) | |
| Decision Tree | 69.42 | (2.21) | 21.83 | (1.82) | 30.64 | (2.92) | 25.52 | (2.08) | 54.02 | (2.73) | |
| Random Forest | 79.33 | (2.74) | 37.73 | (2.31) | 32.25 | (2.25) | 34.78 | (2.42) | 60.64 | (3.14) | |
| Xtra Trees | 82.36 | (2.83) | 45.45 | (2.57) | 16.12 | (1.71) | 24.44 | (2.03) | 56.07 | (2.79) | |
| MLP | 78.23 | (2.62) | 36.92 | (2.63) | 38.79 | (2.54) | 37.77 | (2.49) | 62.54 | (3.21) | |
| PU | Poisson | 75.14 | (0.22) | 40.03 | (0.53) | 41.67 | (0.36) | 40.82 | (0.79) | 64.45 | (0.68) |
| Gaussian Process | 74.07 | (0.31) | 30.06 | (0.78) | 32.50 | (0.52) | 31.20 | (0.19) | 56.03 | (0.88) | |
| kNN | 79.66 | (0.66) | 22.60 | (0.35) | 27.79 | (0.17) | 24.93 | (0.51) | 54.72 | (0.69) | |
| SVM | 81.82 | (0.82) | 43.75 | (0.33) | 22.23 | (0.62) | 29.80 | (0.30) | 64.31 | (0.98) | |
| Decision Tree | 69.80 | (0.31) | 42.90 | (0.46) | 39.31 | (0.61) | 41.02 | (0.14) | 62.68 | (0.12) | |
| Random Forest | 87.84 | (0.24) | 49.45 | (0.43) | 48.61 | (0.28) | 49.03 | (0.67) | 69.20 | (0.39) | |
| Xtra Trees | 83.58 | (0.52) | 49.03 | (0.56) | 47.44 | (0.71) | 48.22 | (0.54) | 68.81 | (0.51) | |
| MLP | 79.50 | (0.76) | 46.39 | (0.83) | 47.44 | (0.23) | 46.63 | (0.13) | 63.19 | (0.71) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sevetlidis, V.; Pavlidis, G.; Mouroutsos, S.G.; Gasteratos, A. Leveraging Positive-Unlabeled Learning for Enhanced Black Spot Accident Identification on Greek Road Networks. Computers 2024, 13, 49. https://doi.org/10.3390/computers13020049
Sevetlidis V, Pavlidis G, Mouroutsos SG, Gasteratos A. Leveraging Positive-Unlabeled Learning for Enhanced Black Spot Accident Identification on Greek Road Networks. Computers. 2024; 13(2):49. https://doi.org/10.3390/computers13020049
Chicago/Turabian StyleSevetlidis, Vasileios, George Pavlidis, Spyridon G. Mouroutsos, and Antonios Gasteratos. 2024. "Leveraging Positive-Unlabeled Learning for Enhanced Black Spot Accident Identification on Greek Road Networks" Computers 13, no. 2: 49. https://doi.org/10.3390/computers13020049
APA StyleSevetlidis, V., Pavlidis, G., Mouroutsos, S. G., & Gasteratos, A. (2024). Leveraging Positive-Unlabeled Learning for Enhanced Black Spot Accident Identification on Greek Road Networks. Computers, 13(2), 49. https://doi.org/10.3390/computers13020049









